El presente trabajo contribuye al conocimiento del comportamiento de las descargas térmicas en aguas marinas costeras mediante la implementación y la aplicación de un modelo numérico que resuelve las ecuaciones de Navier-Stokes-Reynolds para aguas someras y la ecuación de la energía para la temperatura. El modelo numérico toma en cuenta el flujo de calor en la capa superficial, donde interactúan la superficie libre del mar y la atmósfera. Como caso de estudio, se analiza la dispersión de la pluma térmica de la Central Nucleoeléctrica Laguna Verde (CNLV), ubicada en el Estado de Veracruz, México. Las simulaciones numéricas se llevan a cabo teniendo en cuenta la información ambiental, que incluye información batimétrica, oceanográfica, meteorológica e hidrológica, y las condiciones de operación de la descarga de la CNLV. Con base en comparaciones con datos medidos en campo y en el criterio de eficiencia de Nash-Suffle para verificar la calidad de la solución numérica, se considera que los resultados obtenidos son bastante satisfactorios.
This work contributes to the study of nuclear plant thermal discharges in coastal areas by using a numerical model which solves the Navier-Stokes-Reynolds equations for shallow waters and the energy equation for computing temperature variations. The numerical model takes into account the heat flux given in the upper layer, where the free surface and the atmosphere interact. In this study, the thermal plume dispersion from the nuclear power plant Laguna Verde, Veracruz, Mexico, is analyzed. Bathymetry, oceanographic, meteorological, hydrologic and plant operating data are used to run numerical simulations. The results are compared against observed data showing good agreement. The Nash-Suffle's criterion is also applied to verify the quality of the numerical solution obtaining suitable results.
Constante de Smagorinsky (adim)
Calor específico del agua (m2/°C s2)
Fuerza de Coriolis por unidad de masa (1/s)
Aceleración de la gravedad (m/s2)
Profundidad total (m)
Constante de von Kármán (adim)
Constante de ajuste en la ecuación de estado (°C)
Coeficiente de dispersión en el plano horizontal (m2C)
Coeficiente de dispersión en el plano vertical (m2/s)
Longitud de mezclado (m)
Presión hidrostática (Pa)
Presión atmosférica (Pa)
Numero de Prandtl turbulento (adim)
Flujo de calor neto (kg/s3)
Salinidad (ups)
Tiempo (s)
Temperatura del agua (°C)
Magnitud de la componente de velocidad en la dirección x (m/s)
Magnitud de la componente de velocidad en la dirección y (m/s)
Magnitud de la componente de velocidad en la dirección z (m/s)
Plano cartesiano de referencia (m)
Distancia vertical desde el fondo hasta un punto cualquiera (m)
Variación de la superficie libre con respecto al nivel medio (m)
Coeficiente de viscosidad turbulenta horizontal (m2/s)
Coeficiente de viscosidad turbulenta vertical (m2/s)
Área de control (m2)
Aporte de temperatura por flujo de calor en la superficie (°C/s)
Incremento del paso de tiempo (s)
Volumen de control (m3)
Ancho de celda en la dirección x (m)
Ancho de celda en la dirección y (m)
Densidad del agua (kg/m3)
Densidad de referencia (kg/m3)
En los últimos años, los cuerpos de agua costeros han sido objeto de contaminación ambiental por obras que ha construido el hombre. Aunque las leyes son cada vez más estrictas, la contaminación de los mares en la zona costera es cada vez más significativa, lo que ocasiona una alteración de los parámetros físicos, químicos y biológicos del agua que afecta directamente al ecosistema [1,2]. Algunas de las principales fuentes de contaminación en la zona costera son las que se derivan de las actividades industriales, agrícolas y domésticas. De manera particular, en lo que se refiere a las actividades de tipo industrial, cabe mencionar las descargas térmicas de plantas de generación de energía que, al verter aguas residuales al mar a temperaturas mayores a las del cuerpo de agua receptor, provocan una contaminación térmica del agua. Desde una perspectiva ambiental, esta variación local de la temperatura del agua puede perturbar considerablemente el ecosistema acuático [3], causando alteraciones en los organismos que ahí se desarrollan. Se ha demostrado que un ligero cambio en la temperatura del agua (1 o 2°C) puede tener un impacto considerable en el ambiente [4,5]. Por otro lado, desde un punto de vista técnico-operacional, en ocasiones se presenta en las plantas de generación de energía el problema de la recirculación de agua caliente por la mala ubicación de la obra de toma o de una o varias descargas, lo que se traduce en una disminución de la capacidad generadora de energía de la planta. De aquí la necesidad de estudiar y monitorizar la dispersión de la pluma térmica en el mar y determinar así su orientación y su área de influencia.
El seguimiento de la pluma térmica de plantas de generación de energía se ha llevado a cabo mediante el uso de diferentes técnicas para medir la temperatura del mar, entre las que destacan las mediciones en sitio con boyas oceanográficas, las mediciones en cruceros oceanográficos, las imágenes de satélites radiométricos y la modelación numérica. El uso de boyas oceanográficas permite obtener información a lo largo de la columna de agua, aunque se limita a mediciones puntuales. Las mediciones realizadas en cruceros oceanográficos, además de que proporcionan información de la columna de agua, permiten medir a lo largo de diferentes transectos, cubriendo una zona determinada. Sin embargo, estas mediciones suelen tomar tiempo y su costo es generalmente elevado. Otra técnica utilizada en el estudio y seguimiento de plumas térmicas es la medición de la temperatura superficial con satélites radiométricos, que proporcionan una visión sinóptica de la temperatura en grandes extensiones de agua [6–8]. Pese a los avances significativos de la tecnología satelital en los últimos años, esta técnica se limita a la capa superficial del mar y a la resolución espacial con que cuentan los satélites actualmente en órbita, 120m en el caso de los Landsat-4 y 5 [9], por citar un ejemplo de los satélites que cuentan con mayor resolución.
La dinámica de fluidos computacional se utiliza cada vez más en estudios de calidad del agua y de otros temas de tipo ambiental. Las ecuaciones que expresan los principios de conservación de cantidad de movimiento, de masa y de energía, sirven para definir las propiedades macroscópicas del movimiento de los fluidos, y ayudan así al estudio de la difusión y el transporte de materia a través de un fluido en movimiento. La solución de dichas ecuaciones a través del desarrollo de modelos numéricos parece ser la técnica más viable en el estudio de contaminantes en general, entre los que se incluyen desde luego las plumas térmicas. La viabilidad en el uso de los modelos numéricos obedece principalmente a 2 razones: la primera es el progreso en la modelación multidisciplinaria en las últimas décadas, en la que se agrupan la mayoría de los factores que interactúan en el medio (hidrodinámicos, meteorológicos y de calidad del agua) en un modelo operacional capaz de reproducir un determinado fenómeno físico; la segunda es el avance en la tecnología computacional, incluyendo el uso de procesos en paralelo, que ha permitido que por primera vez sea factible utilizar modelos físicos y ecológicos de manera acoplada y con la misma resolución [10].
En el presente trabajo se lleva a cabo un estudio de dispersión térmica en el mar mediante la implementación de un modelo numérico. El caso de estudio es la pluma térmica de la Central Nucleoeléctrica Laguna Verde (CNLV), localizada sobre el litoral del Golfo de México (GDM), en el Estado de Veracruz, México (coordenadas 19°43′15″ N 96°24′23″ O). La CNLV es la única planta nuclear en el país y aporta el 3% de la generación total de energía eléctrica. Desde el punto de vista ecológico, los efectos generados por la operación de la CNLV en el ambiente ya han sido estudiados y analizados por varios autores [1,2], así como los efectos producidos por el oleaje incidente debido a las obras de protección [11,12]. Por otro lado, no existe un estudio de la dispersión de la pluma térmica enfocado en determinar un posible problema de recirculación de agua caliente que pudiera afectar a las condiciones de operación de la CNLV. Así pues, el objetivo de este trabajo se plantea en 2 vertientes: validar el código numérico implementado de acuerdo con los datos medidos en sitio, y determinar mediante la modelación numérica si la CNLV se ve afectada por el problema de la recirculación de agua caliente.
En la siguiente sección se muestra el sistema de ecuaciones que resuelve el modelo numérico; en la sección 3 se detalla el esquema de solución numérica; en la sección 4 se hace un planteamiento sobre los aspectos que se consideran importantes para la validación del modelo numérico implementado; en la sección 5 se describen los escenarios de simulación para el caso de estudio de la pluma térmica de la CNLV y se muestran y discuten los resultados. El trabajo termina con las conclusiones finales.
2Ecuaciones gobernantesLas ecuaciones que se resuelven a continuación son las ecuaciones para aguas someras deducidas a partir de las ecuaciones de Navier-Stokes-Reynolds para flujos a superficie libre. Se considera la aproximación de aguas someras, donde las velocidades en el plano horizontal son mayores que la velocidad vertical, y las escalas de las longitudes horizontales son mucho mayores que la escala de longitud vertical, es decir Δx≈Δy≫Δz.
Así, se resuelven las ecuaciones que a continuación se enumeran.
Ecuaciones para las velocidades en el plano horizontal:
Ecuación de continuidad:
Ecuación para la superficie libre:
Las variaciones de densidad (ρ) son función de las variaciones de presión (P), temperatura (T) y salinidad (S), y son estimadas a través de la siguiente ecuación de estado definida por la UNESCO [13]:
donde kp es una constante de ajuste que se determina por módulos [13], y es función de las variaciones de P, T y S.Las ecuaciones para la temperatura y la salinidad son:
En el sistema de ecuaciones que gobiernan las aguas someras se evita la ecuación del movimiento para calcular la velocidad vertical W se aproxima a partir de la ecuación (3) como:
Por otro lado, el término de presión en la ecuación (1) es sustituido, considerando la aproximación hidrostática:
El primer término de la derecha de la ecuación (9) es el término barotrópico, que representa al gradiente de presión horizontal definido por la variación de la superficie libre. El segundo término es el término baroclínico, y describe la diferencia de densidades en la columna vertical de agua. El tercer término considera la contribución de la presión atmosférica. Análogamente, se plantea la misma definición para la variación del gradiente de presión de la ecuación (2).
2.1Los coeficientes de viscosidad turbulentaEl coeficiente de viscosidad turbulenta horizontal νTH que aparece en las ecuaciones (1) y (2) se estima mediante el modelo de Smagorinsky como sigue:
donde Csmag es la constante de Smagorinsky, cuyos valores fluctúan entre 0,02 y 0,5. Un valor típico que es utilizado es de 0,1 [14]. Para el cálculo del coeficiente de viscosidad turbulenta vertical νTV se utiliza el modelo siguiente [15]:donde ℓ es la longitud de mezclado y se define como:donde k es la constante de Von Kármán igual a 0,40 y zb es la distancia vertical desde el fondo hasta el punto donde se calcula νTV.Los coeficientes de difusión de temperatura y salinidad de las ecuaciones (6) y (7) son evaluados como KTH=νTHPrT y KTV=νTVPrT, donde PrT es el número de Prandtl turbulento igual a 0,9 [15,16].
2.2El intercambio de calor océano-atmósferaEn la ecuación (6) aparece el término del flujo de calor neto Q en la superficie libre del agua, que es la suma de la radiación de longitud de onda larga, de la radiación de longitud de onda corta, de la evaporación y del calor sensible. Para cuantificar el flujo de calor neto, el modelo numérico toma en cuenta datos climatológicos y meteorológicos, tales como la magnitud y la dirección del viento, la temperatura ambiente, la nubosidad y la radiación, y la temperatura superficial y del fondo del agua [17]. Para el cálculo de Q se utilizó la forma linearizada de Haney, que permite estimar el flujo de calor neto en la interfase agua-aire como sigue:
3Esquema de solución numéricaEl modelo numérico desarrollado tiene la capacidad de trabajar en 3 dimensiones en multicapas, y en el caso particular en 2 dimensiones se realiza una integración en la vertical. El mallado que se utiliza es de tipo staggered cell o MAC. En la figura 1 se muestran los elementos de la malla, donde el punto negro ubicado al centro de cada celda representa cualquier magnitud escalar como la temperatura y la salinidad, y los círculos en las caras indican la posición de las componentes de los vectores de velocidad U, V y W.
En lo que se refiere a la discretización vertical, se pueden considerar espesores constantes o variables. La distribución de las variables se muestra en la figura 2.
El método de solución numérica se basa en una discretización espacial en diferencias finitas en orden 2, y se considera una formulación temporal euleriana-lagrangiana donde los términos advectivos altamente no lineales de las ecuaciones de movimiento y transporte (1), (2), (6) y (7) se resuelven por el método de las características (parte lagrangiana) en orden 1, el cual evita oscilaciones numéricas introducidas por fuertes gradientes. Por otro lado, los términos de difusión se resuelven mediante un esquema implícito (parte euleriana) en orden 2. Para la solución discreta de la ecuación de la superficie libre (η), ecuación (4), es necesario resolver un sistema lineal pentadiagonal (o heptadiagonal en 3D), donde se utiliza el método de Gradiente Conjugado. Los detalles sobre el algoritmo de solución numérica pueden ser consultados en la bibliografía [15,16,18–20].
4Sobre la implementación y la validación del modelo numéricoEl modelo utilizado es validado en 4 aspectos importantes:
- •
Conceptualmente.
- •
Algorítmicamente.
- •
Informáticamente.
- •
Funcionalmente.
El primero se refiere a que el formulismo matemático que conforman las ecuaciones utilizadas debe incluir los principios físicos fundamentales que garanticen resultados aceptables. El segundo aspecto se refiere al algoritmo de solución utilizado para resolver las ecuaciones; en este caso se utiliza un algoritmo parabólico en el tiempo y elíptico en el espacio, con la implementación de un esquema euleriano-lagrangiano. La parte lagrangiana aproxima los términos advectivos de las ecuaciones de movimiento y transporte, y contempla un algoritmo con delimitador de flujo que ha demostrado eliminar eficazmente las oscilaciones numéricas generadas por estos términos [21]. La parte euleriana del esquema numérico resuelve con eficiencia los términos difusivos. La conjunción de estos esquemas ha sido validada con soluciones de referencia y casos controlados, y los esquemas han mostrado ser bastante precisos y exactos [18,19]. El tercer aspecto hace referencia a la codificación, que es la traducción del algoritmo al lenguaje de programación FORTRAN. Se han utilizado prácticas modernas de programación, como la modularización y la creación de diagramas de flujos de datos. Se han probado por separado los distintos componentes del código en el proceso de su desarrollo, para garantizar la consistencia, la estabilidad y la convergencia de las soluciones, y se han optimizado además los tiempos de solución numérica [20].
Finalmente, el cuarto aspecto se refiere a la validación funcional, la cual consiste en la verificación del modelo con mediciones obtenidas en sitio. La interpretación de un fenómeno físico costero conlleva mediciones con instrumentación que involucran diferentes escalas temporales y espaciales. La medición de la dinámica de estos ecosistemas implica un análisis de estas escalas con métodos particulares, tanto estadísticos como determinísticos. Por ello, la calibración, y por tanto la validación de un modelo en aplicaciones costeras, es bastante compleja ya que, a diferencia de las aplicaciones controladas en laboratorio, los aparatos y mecanismos de medición no son consistentes y traen consigo un cierto grado de aproximación intrínseco. A esto hay que añadirle el factor humano, ya que la interpretación y la apreciación introducen una incertidumbre extra. Para verificar la calidad de la solución numérica con respecto a los datos observados en campo se utiliza la eficiencia de Nash-Sutcliffle [22] determinada por la siguiente expresión:
donde φobs es un dato observado o medido y φsim es un dato obtenido de la simulación numérica, en el mismo punto y en el mismo instante de tiempo. El parámetro φ¯ es la varianza de los datos observados. Evidentemente, si el valor de R es cercano a la unidad, es posible considerar que los datos de la simulación son bastante aproximados a los datos medidos en campo.5Caso de estudio de la descarga térmica de la Central Nucleoeléctrica Laguna VerdeEl sistema de enfriamiento de la CNLV es de tipo abierto, el agua destinada para el enfriamiento de los condensadores no se vuelve a utilizar. Aunque es difícil definir los límites de una descarga, para la CNLV se inicia con el aumento de la temperatura que se produce en el condensador y termina cuando el efluente se mezcla y se enfría en el mar. El gasto necesario para enfriar los condensadores de la CNLV es de 63m3/s, lo mismo que se descarga al mar a través de un canal con un incremento de temperatura. La descarga se localiza a 1.800m de la obra de toma, aproximadamente. A 800m al sur del canal de descarga se ubica la desembocadura del río El Viejón, como se ilustra en la figura 3. En esta misma figura se muestra la ubicación geográfica de 6 boyas de medición que se instalaron en la zona para obtener información oceanográfica y meteorológica, que se reportaron en Silva y Botello [1] y Botello y Rendón [2].
El sitio es topográficamente plano, limitado al oeste por montañas de baja elevación (de 500m aproximadamente) en los primeros 5km de la costa. Batimétricamente, la zona se caracteriza por una pendiente suave que presenta una isóbata máxima en la parte noreste cuyo valor es de -28m respecto al nivel medio del mar. En la figura 4 se muestra el dominio considerado para las simulaciones numéricas y su batimetría, que abarca un área aproximada de 11,7km2, con una longitud de 4.200m en la dirección x y 3.500m en la dirección y.
Para analizar la dispersión de la pluma térmica de la CNLV se simularon 2 escenarios, los cuales corresponden a los periodos de secas (febrero-mayo) y lluvias (junio-septiembre). Dado que se contó con muy poca información histórica medida en campo en la zona de interés, tanto oceanográfica como meteorológica, se tomaron los datos disponibles de zonas aledañas para diferentes periodos anuales, particularmente de la zona del puerto de Veracruz que se ubica al sur de la CNLV. La información se procesó conjuntamente con los datos medidos en la zona de estudio reportados en Silva y Botello [1] y en Botello y Rendón [2] para generar las condiciones iniciales y forzantes de cada escenario. La información sobre gastos de succión y gastos y temperaturas de descarga de la CNLV fue proporcionada por la Comisión Federal de Electricidad del Gobierno Mexicano.
El dominio de estudio se discretizó utilizando una malla rectangular de 88×67 celdas, conformando un total de 5.896 elementos, con espaciamientos constantes de Δx=Δy=50m (véase fig. 5). El incremento del paso de tiempo en las simulaciones fue de Δt=1s.
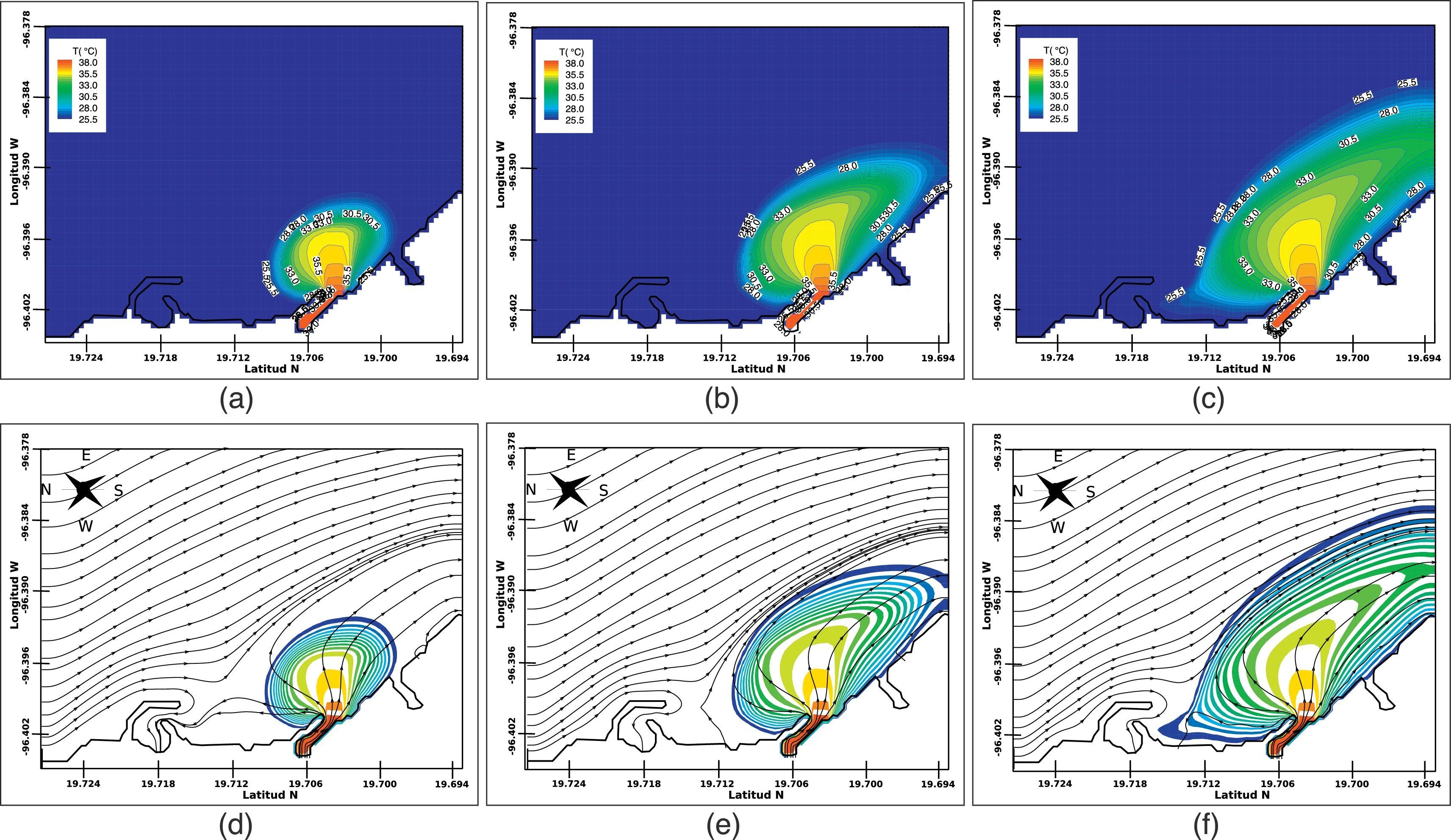
5.1Simulaciones en periodo de secasLos parámetros de inicialización y forzantes que se impusieron en las simulaciones numéricas se indican en la tabla 1. En este caso, no se consideraron los efectos de la marea, la acción del viento sobre la superficie libre, ni el aporte hidrológico del río El Viejón. Los resultados obtenidos con el modelo numérico se validaron cualitativamente con las mediciones en sitio de Silva y Botello [1]. En la figura 6 se muestra la pluma térmica obtenida [1], donde se observa que esta se dispersa hacia el sur, lejos de la obra de toma de la CNLV. De la misma forma, la secuencia de imágenes de la figura 7, que ilustra las isotermas y las líneas de corriente obtenidas con el modelo numérico para 120h de simulación, muestra que la pluma térmica se dispersa con dirección sur, lo que permite concluir que el modelo reproduce el mismo comportamiento que el que se reporta en la referencia con datos medidos en sitio. Además, según estos resultados, la CNLV no se ve afectada por el problema de la recirculación de la pluma térmica hacia la obra de toma.
Pluma térmica medida en marzo de 1996 [1].
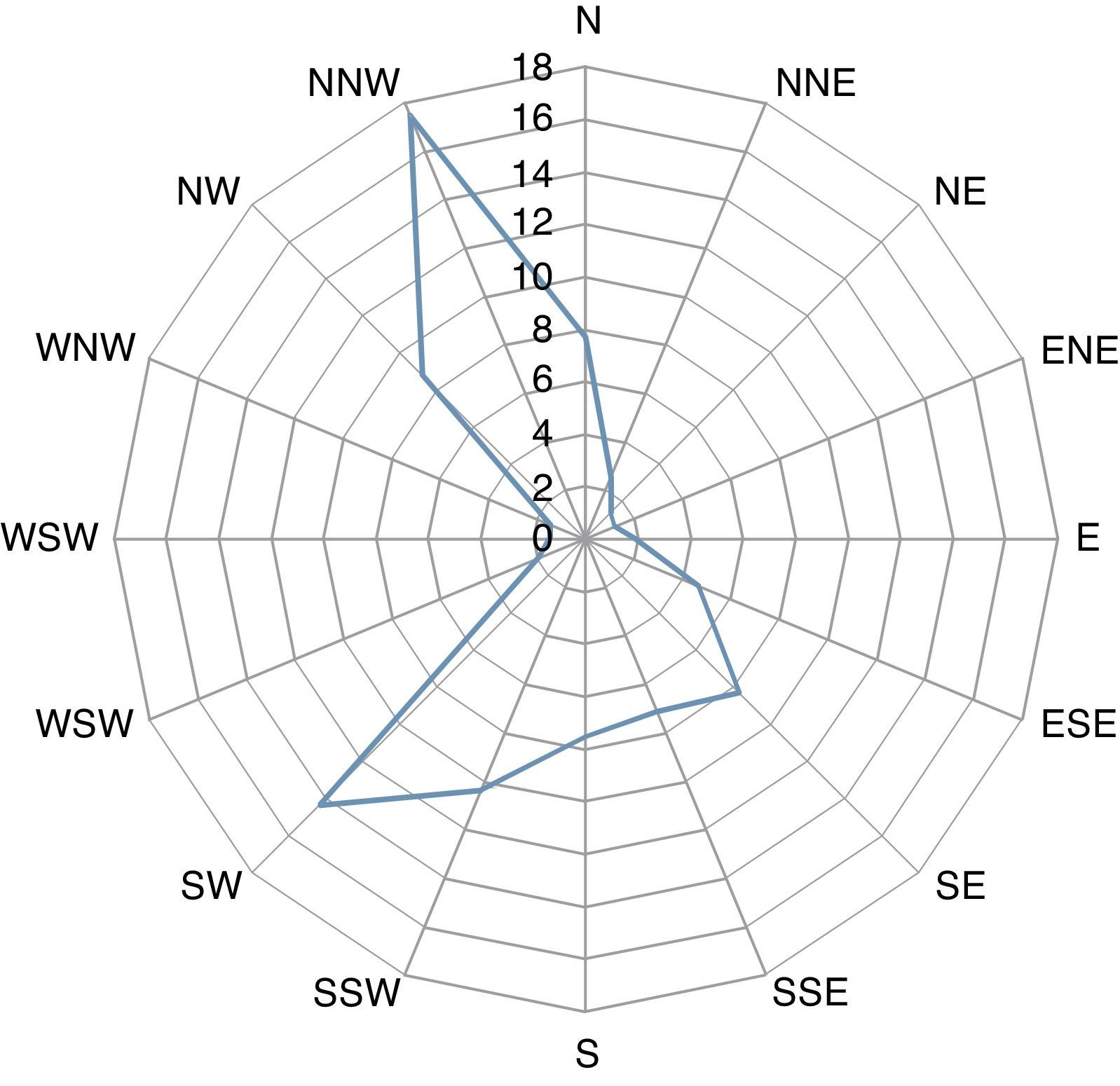
Los valores medios de los parámetros de inicialización y forzantes que se impusieron en las simulaciones numéricas se indican en la tabla 2. En este caso se tuvieron en cuenta los efectos de la marea, gracias a los datos proporcionados por las bases de datos del Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE), Baja California, México (fig. 8). Se consideraron también los efectos del viento sobre la superficie libre, cuyas magnitudes y direcciones se tomaron de datos medidos en la CNLV en el año 2004 (fig. 9). Asimismo, se tuvo en cuenta el flujo de calor en la superficie, caracterizado por el último término del lado derecho de la ecuación (6) y definido en la ecuación (13). Los datos sobre las corrientes litorales se generaron a partir de información aportada por la Dirección General de Puertos y Marina Mercante, México, para el periodo 1982-1984 (fig. 10). Finalmente, se valoró también el aporte hidrológico del río El Viejón, que se estimó de acuerdo con los datos medidos en sitio. El mallado que se utilizó para la simulación numérica cuenta con el mismo número de elementos que en el caso de secas.
Datos utilizados para la simulacion de lluvias
| Parámetro | Valor |
| Corriente litoral | 0,10m/s |
| Dirección de la corriente litoral | Sur-Norte |
| Temperatura media del mar | 28°C |
| Salinidad media del mar | 33ups |
| Gasto de descarga | 63m3/s |
| Temperatura de la descarga | 44°C |
| Gasto del río El Viejón | 6,09m3/s |
| Temperatura del río El Viejón | 25°C |
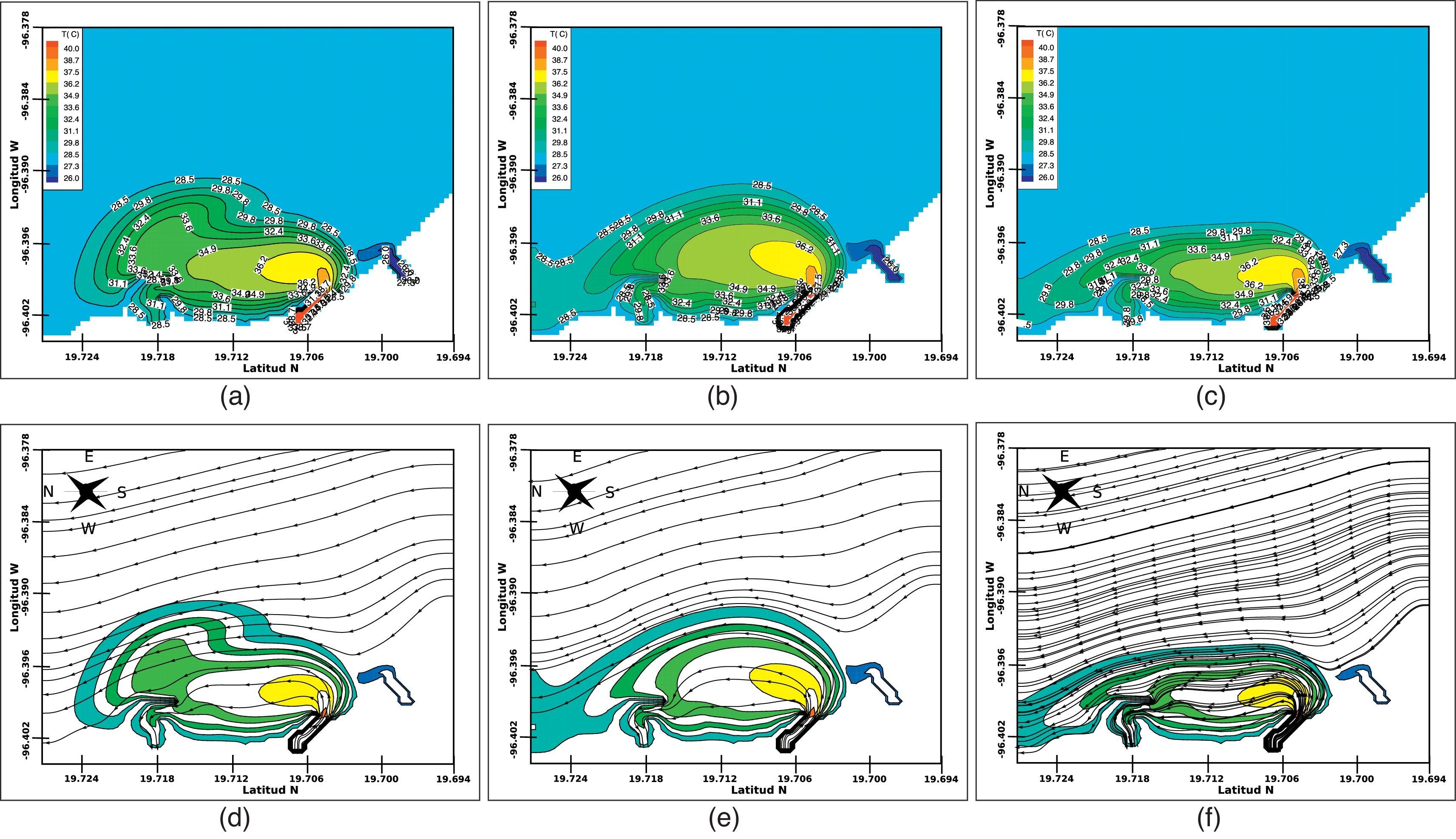
Los resultados obtenidos con el modelo numérico indican que el escenario de lluvias presenta un fenómeno de recirculación de la pluma térmica en la CNLV. En este caso, debido principalmente a la intensidad y a la dirección de las corrientes, la pluma térmica se dispersa con dirección hacia la obra de toma. Los resultados se ilustran en la figura 11, en la que puede observarse la evolución de la pluma térmica por medio de las isotermas (a), (b) y (c). La pluma térmica alcanza a la obra de toma y, consecuentemente, afecta al sistema de enfriamiento de la CNLV al presentarse un incremento de temperatura de 2°C respecto de la temperatura media del mar, justo en la succión. Las líneas de corriente (d), (e) y (f) de la figura 11 ilustran los campos hidrodinámicos correspondientes a los patrones de dispersión antes mencionados, donde se observa que la orientación de la pluma térmica obedece a la dirección predominante de las corrientes.
En la figura 12 se muestra la evolución de la pluma térmica obtenida con el modelo numérico. Para ello, se graficaron los valores de temperatura en diferentes puntos ubicados sobre la trayectoria que se esquematiza con la línea negra gruesa, desde la descarga hasta la obra de toma. En esta misma figura, el cero de las abscisas indica el inicio de la trayectoria en la descarga, y la última coordenada, 2,4km, indica el fin de la trayectoria en la obra de toma. El eje de las ordenadas corresponde a la temperatura. La línea negra fina permite observar que la temperatura de 44°C impuesta en la descarga decae hasta los 30°C en la obra de toma.
Con la información medida en la obra de toma de la CNLV se pudieron verificar los resultados arrojados por el modelo numérico para el periodo de lluvias. En la figura 13 se presenta la comparación entre la temperatura medida en la obra de toma (boya 1 en la fig. 3) y la temperatura estimada por la simulación en el mismo punto. La señal de temperatura mantiene un comportamiento similar en ambos casos, pues la media de los datos medidos en sitio es de 30,02°C, mientras que la media de los valores simulados es de 30,26°C. Con el objetivo de validar y establecer un parámetro cuantitativo de la calidad de la solución numérica se aplicó la ecuación (14) para los datos de la figura 13, y se obtuvo un valor de R cercano a la unidad igual con R=0, 998642, por lo que se considera que la solución numérica tiene una excelente calidad, según el criterio de Nash-Sutcliffle [22].
6ConclusionesEl presente trabajo contribuye al conocimiento del comportamiento de las descargas térmicas en aguas someras mediante el uso de la modelación numérica. El modelo que se implementó para el estudio de la dispersión de la pluma térmica de la Central Nucleoeléctrica Laguna Verde, ubicada en el Estado de Veracruz, México, reprodujo con una excelente calidad de solución 2 escenarios: secas y lluvias. La calidad de los resultados se pudo constatar cualitativamente mediante comparaciones con información de campo y cuantitativamente según el criterio de Nash-Sutcliffle [22]. Así, se demuestra que la modelación numérica es una herramienta útil en el análisis y en el diseño del funcionamiento hidráulico y ambiental de algunas obras y que, si se utiliza con una correcta apreciación de sus limitaciones intrínsecas, permite reproducir diferentes escenarios en menor tiempo y a bajo costo, con excelentes resultados en comparación con otras técnicas o formas de monitoización y análisis.
De acuerdo con los resultados obtenidos, el sistema de enfriamiento de la CNLV se ve afectado por la recirculación térmica para el periodo de lluvias ya que, debido principalmente a las corrientes marinas, la pluma térmica descargada llega a la obra de toma con valores medios cercanos a los 30°C, que son 2°C por encima de los 28°C de temperatura media del mar.
Los autores agradecen a la Comisión Federal de Electricidad, México, y en particular al M. en I. Lázaro Aguilar por las facilidades otorgadas para la realización de este trabajo y al M. en I. Iván Campos Pérez por plantear y participar en el análisis del problema de la recirculación de la pluma térmica de la CNLV.



























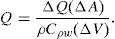






![Pluma térmica medida en marzo de 1996 [1]. Pluma térmica medida en marzo de 1996 [1].](https://static.elsevier.es/multimedia/02131315/0000002900000002/v1_201308020947/S0213131513000163/v1_201308020947/es/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)






