En este trabajo se muestra un modelo computacional tridimensional para la simulación del comportamiento mecánico de la unidad músculo tendón (UMT). El modelo ha sido formulado a través de una función densidad energía de deformación para materiales hiperelásticos que incorpora tanto el comportamiento pasivo de los tejidos conectivos como el activo, considerando para ambos casos direcciones de comportamiento preferencial no necesariamente coincidentes en el espacio. Las tensiones iniciales, presentes habitualmente en tejidos blandos, han sido implementadas mediante la definición de un gradiente de deformación para llevar a cabo la simulación de la UMT. El modelo se ha particularizado para un modelo de experimentación animal. La geometría utilizada se corresponde con la del músculo tibial anterior de rata reconstruido a partir de imagen médica procedente de resonancia magnética obtenida «in-vivo». También se estudia el efecto que sobre el comportamiento pasivo ejerce la fascia ajustando un modelo de comportamiento hiperelástico para la misma a partir de ensayos experimentales.
This paper presents a three dimensional computational model to simulate the mechanical behavior of the muscle-tendon unit (MTU). The model has been formulated through a strain energy density function for hyperelastic materials incorporating both the passive and active behavior of the connective tissues, and taking into account preferential directions for both behaviours, not necessarily coincident. The initial stresses, usually present in soft tissues, have been considered when performing the MTU simulation. The geometry used corresponds to the rat tibialis anterior muscle reconstructed from «in-vivo» magnetic resonance images. This paper also studies the effect of the fascia on the MTU passive behaviour and the setting of a hyperelastic model for this tissue by means of experimental tests.
El tejido músculo-esquelético es un tejido biológico blando responsable, fundamentalmente, del movimiento del cuerpo y de mantener la postura corporal. El cuerpo humano contiene aproximadamente 650 músculos, con formas diferentes en función del tipo de movimiento, representando aproximadamente el 40% del peso corporal [1]. Cada uno de estos músculos puede ser considerado como un conjunto de fibras musculares (elemento contractil) rodeadas, en diferentes niveles, por tejido conectivo (elemento elástico) que, de forma pasiva, es el responsable de absorber los alargamientos del músculo. Es bien sabido además que, las fibras musculares también contribuyen al comportamiento pasivo (elemento elástico en serie) [2,3]. El tejido conectivo está constituido por fibras de colágeno y elastina embebidas en la sustancia fundamental y organizadas en tres niveles, el epimisio, perimisio y endomisio, que juegan un papel importante en la transmisión lateral de las fuerzas generadas por las fibras y, a través de los cuales, se distribuyen los vasos sanguíneos y ramificaciones nerviosas.
Los recientes avances en la adquisición de imágenes, en la caracterización experimental de los tejidos biológicos y en el desarrollo de nuevos algoritmos de comportamiento han permitido el desarrollo de modelos 3D que permiten obtener el campo de tensiones y deformaciones en el interior de los tejidos vivos. En la mayoría de las ocasiones, la construcción de dichos modelos lleva asociada la adopción de hipótesis simplificativas, por ejemplo, las propiedades mecánicas se determinan mediante ensayos «in-vitro» [4,5], o se combinan parámetros de diferentes tejidos [6], o bien se adoptan geometrías idealizadas [7–11], lo que hace difícil validar los resultados obtenidos y por lo tanto poder extrapolar los resultados numéricos a estudios clínicos.
Con el objetivo de minimizar las posibles causas de error atribuidas a las simplificaciones anteriores, en este trabajo se presenta el modelado del músculo tibial anterior (TA) de rata, partiendo de imagen procedente de resonancia magnética (RM). Se ha utilizado un modelo de comportamiento hiperelástico anisótropo capaz de reproducir la respuesta pasiva y activa del músculo partiendo de los resultados experimentales. También se han incorporado las deformaciones iniciales habituales en los tejidos blandos [12,13]. El modelo parte de la caracterización experimental, tanto activa como pasiva de la UMT llevada a cabo por los autores en trabajos previos [14–16].
Los resultados obtenidos en la simulación son validados con los resultados experimentales procedentes de ensayos uniaxiales a tracción «in-vivo» de la UTM, en el caso del comportamiento pasivo [14], y de la estimulación eléctrica en condiciones isométricas, en el caso activo [15].
2Modelo matemáticoEn este apartado se resumen las ecuaciones que definen el modelo de comportamiento hiperelástico anisótropo habitualmente empleado en la simulación de tejidos biológicos blandos, dentro siempre del dominio elástico. Dicho modelo estructural se plantea en el marco de la mecánica del continuo no lineal y teniendo en cuenta la posibilidad de ser incorporado en un código de elementos finitos.
2.1Definición de la deformaciónSe entiende por sólido tridimensional, Ωo, a un subconjunto de ℝ3 cuyos puntos se identifican mediante sus coordenadas en un sistema de referencia. Matemáticamente, podemos interpretar lo anterior a través de una función biunívoca de tres componentes φo aplicada sobre el sólido Ωo tal que, a cada punto P∈Ωo, adscribe tres valores que corresponden a las coordenadas de dicho punto P en el sistema de referencia elegido, es decir:
A φo la denominaremos configuración inicial del sólido Ω0, configuración de referencia o configuración indeformada. A lo largo del movimiento del sólido, la posición de cada uno de los puntos del mismo va variando. La configuración correspondiente define las coordenadas de los puntos del sólido en ese instante Ωt respecto a un sistema de referencia (que en general también puede variar con el tiempo) a través de una expresión similar a (1), es decir:
A φt la denominaremos configuración actual del sólido Ωt o configuración deformada.
Dado un movimiento φt:Ωt→ℝ3C1−regular, se define el gradiente de deformación F, como el campo tensorial sobre la configuración indeformada φo(Ω), F=∂x∂X, siendo J≡detF>0 el jacobiano de la transformación.
Una de las características más relevantes de los tejidos biológicos blandos, en general, y del músculo en particular, es la incompresibilidad. Esta indica que el cuerpo al ser sometido a fuerzas o deformaciones no presenta un cambio de volumen, lo que se representa matemáticamente como que el jacobiano del gradiente de deformación es igual a la unidad, J≅1. Siguiendo a [17], definimos la siguiente descomposición multiplicativa del gradiente de deformación:
el término J13I representa la deformación volumétrica y F¯ la deformación desviadora. Denotamos por F¯, C¯ y b¯ al gradiente de deformación y los tensores de deformación de Cauchy-Green por la derecha e izquierda modificados, respectivamente.La anisotropía del material en un punto X∈Ω0, va asociada a la dirección de la fibras musculares, en el caso del comportamiento activo, y a la dirección de las fibras de colágeno en el caso del comportamiento pasivo. En los músculos fusiformes como es el caso del TA, la dirección de anisotropía coincide para ambos comportamientos, es decir, el comportamiento preferencial pasivo coincide con la dirección de las fibras musculares, pero no es así en músculos planos, como pueden ser los de la pared abdominal [5]. Por tanto, en una situación general, se puede partir de la hipótesis de que la dirección de anisotropía, asociada al comportamiento activo, se define por un vector unitario m0(X), y la asociada al comportamiento pasivo mediante el vector n0(X), con |m0|=1, |n0|=1. Definimos la base Ei=(m0, n0, l0), donde el vector l0=m0⊗n0 está fuera del plano formado por los otros dos vectores.
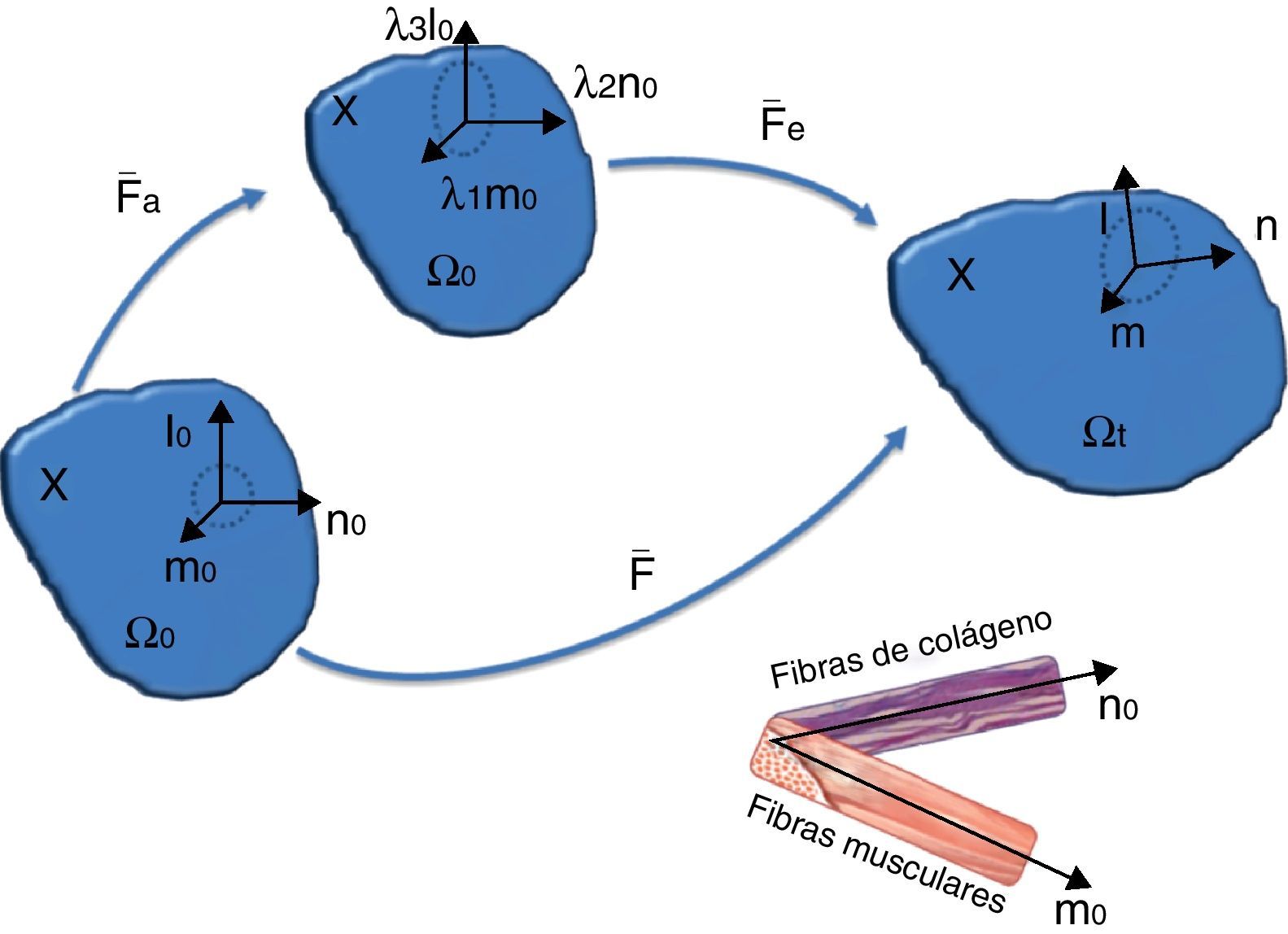
La deformación asociada a la actividad muscular (ver figura 1) se puede modelar mediante un proceso ficticio de dos pasos [18]: el primero de ellos asociado al desplazamiento relativo de las proteínas actina y miosina y, el segundo, a una deformación elástica asociada a los puentes cruzados y a la titina. Esto puede ser expresado mediante una descomposición multiplicativa de F¯[18]:
Esquema de la deformación pasiva y activa [18]. Sobre el punto X de la configuración indeformada Ω0, consideramos dos direcciones preferenciales definidas por m0 y n0. Esta configuración se transforma en la misma dirección por la contracción activa F¯a, donde los nuevos vectores serán λ1m0, λ2n0 y λ3l0. La deformación elástica transforma esta configuración intermedia activa a la configuración deformada Ωt por medio del gradiente de deformación F¯e.
Si las fibras musculares se contraen en la dirección definida por el vector de comportamiento preferencial m0 y se supone que dicha dirección no cambia, el tensor de contracción activo vendrá dado por:
donde los vectores Ei forman una base dual a ei definida como ei·Ej=δij con δij la delta de Kronecker. λ¯1=λ¯a y el valor de λ¯2=λ¯3 se determina al considerar el material incompresible.Sustituyendo los valores de λ¯2 y λ¯3 obtenidos al aplicar (8), la ecuación (7) se reduce a:
el tensor de contracción sólo depende del alargamiento de contracción λ¯a. Aplicando la regla de la cadena, la variación de F¯a con respecto al tiempo (9) viene dada como:donde λ¯˙a es la velocidad de contracción en la dirección de comportamiento preferencial que debe ser conocida y ∂F¯a∂λ¯a puede obtenerse como:Se supone que las fibras de colágeno se mueven de forma conjunta con la matriz extracelular, por lo que, el alargamiento λ¯ es definido como la relación entre las longitudes de las fibras en las configuraciones deformada y de referencia, es decir:
donde C¯=F¯TF¯ es el tensor de deformación de Cauchy-Green por la derecha modificado. Podemos definir C¯e=F¯eTF¯e=F¯a−TC¯F¯a−1 como la medida de deformación de los puentes cruzados y la titina (no es una variable de estado ya que depende de C¯ y λ¯a), m y n son los vectores unitarios que definen la dirección de comportamiento preferencial (asociada a las fibras musculares y de colágeno, respectivamente) en la configuración deformada (fig. 1).2.2Respuesta tensional hiperelásticaPara caracterizar un proceso isotermo en materiales reversibles sin disipación de energía, se suele postular la existencia de una única representación de la función densidad energía de deformación Ψ[19], en este caso, expresada de forma desacoplada como suma de la energía volumétrica y desviadora, para evitar los problemas de incompresibilidad, empleando en la hipótesis cinemática (3) y siguiendo a [20]. A su vez, para el tejido muscular, la energía de deformación desviadora se puede expresar de forma aditiva como la energía pasiva almacenada en el tejido y asociada principalmente al colágeno y elástina, Ψ¯p, más la energía almacenada en la fibra muscular, que denominaremos energía activa, Ψ¯a. La energía almacenada dependerá de F y de las variables de estado λ¯a,β y de los tensores estructurales M, N definidos como M=m0⊗m0 y N=n0⊗n0:
con Ψvol, Ψ¯p y Ψ¯a las partes volumétrica y desviadora asociadas a las componentes pasiva y activa, respectivamente, de la función densidad de energía de deformación. El tensor C¯e no es una variable de estado ya que depende de C¯ y λ¯a, pero es necesario para formular la energía libre. β representa el nivel de activación con el tiempo o, lo que es lo mismo, la variación de la fuerza activa generada con el tiempo.La función densidad energía de deformación Ψ puede expresarse en función de los invariantes definidos por:
I¯1 y I¯2 son el primer y segundo invariante de C¯ y los pseudo-invariantes I¯4,I¯5 caracterizan la anisotropía asociada al comportamiento pasivo. I¯4 tiene un claro significado físico ya que se define como el alargamiento de la fibras de colágeno al cuadrado e I¯5 está asociado a la deformación transversal de las fibras de colágeno. De forma análoga se definirán los pseudo-invariantes asociados a las fibras musculares, donde el tensor de deformación C¯ se ha sustituido por C¯e:Es norma habitual en biomecánica omitir la dependencia de la función Ψ de los invariantes I¯5,J¯5, como consecuencia de la fuerte correlación de I¯5 con I¯4 y de J¯5 con J¯4[21]. Con lo cual se consigue disminuir el número de parámetros del material y, por lo tanto, facilitar el ajuste a los resultados experimentales. Adicionalmente, los invariantes I¯4 y J¯4 poseen una clara interpretación física. En lo que sigue, se planteará la formulación únicamente considerando los invariantes I¯4 y J¯4, con lo que la ecuación (13) vendrá dada como:
La respuesta en tensiones se puede obtener a partir de la Ψ teniendo en cuenta la desigualdad de Clausius-Planck:
siendo Sa la tensión generada por el golpe de fuerza en los puentes cruzados y Sc por la variación del impulso en el tiempo. Teniendo en cuenta las ecuaciones (16) y (17) se obtiene:Si suponemos que el primer término de la ecuación (18) no depende de λ¯˙a y β˙, el segundo tensor de tensiones de Piola-Kirchhoff vendrá dado por:
con:siendo p la presión hidrostática, S˜p y S˜a los tensores de tensiones de Piola-Kirchhoff modificados correspondientes a la parte pasiva y activa respectivamente y DEV el operador desviador en descripción material definido como:El valor del segundo tensor de Piola-Kirchhoff, S, en función de los invariantes I¯1, I¯2,I¯4 y J¯4 vendrá dado por:
El tensor de tensiones de Cauchy σ es 1/J veces el empuje (push-forward) de S (σ=J−1φ*(S)), o en notación indicial, σij=J−1FiIFjJSIJ. Utilizando la relación entre el operador DEV[•], definido en la descripción material, y el operador dev[•], definido en la espacial [22]:
se obtiene la descripción espacial de (22), es decir, el tensor de Cauchy. Para obtener la componente asociada al comportamiento activo, el empuje se ha de realizar con el tensor F¯e en lugar del tensor F¯ utilizado para la componente volumétrica y pasiva. Operando, se obtiene:con 1 el tensor identidad de segundo orden, m⊗m y n⊗n los tensores estructurales asociados a las fibras musculares y de colágeno, respectivamente, en la configuración espacial.2.3Tensor de comportamiento elásticoPara obtener la solución numérica del problema no lineal empleando una técnica iterativa tipo Newton, es necesario obtener la linealización de las ecuaciones constitutivas [23]. Conocido el segundo tensor de tensiones de Piola-Kirchhoff, S, en un punto, su variación con respecto al tensor de Cauchy-Green por la derecha C puede escribirse de la forma:
con ℂel tensor elástico en la configuración material [24]. Partiendo de la ecuación (19) se obtiene la contribución volumétrica y desviadora del tensor, esta última expresada como la suma de la componente pasiva y activa:donde ℂvol, ℂ¯p y ℂ¯a pueden escribirse de la forma siguiente:Por conveniencia, se introduce la función escalar p˜, definida por:con la ecuación constitutiva para p dada por (20).con:yPara calcular la componente desviadora del tensor elástico asociada al comportamiento activo, se parte de la hipótesis de que las actualizaciones de λ¯a se calcularán de forma explícita en cada incremento, por lo tanto S¯a no dependerá de F¯a. Operando se obtiene:
con:como puede observarse el valor de (31) es idéntico a (29) reemplazando C¯ por su componente elástica C¯e y posteriormente realizar la operación tirón (pull-back).El tensor elástico en la configuración espacial, denotado por ℂ, se define como el empuje de ℂ escalado por el factor J−1, esto es:
Operando, se obtiene la expresión volumétrica y desviadora en la configuración deformada:
siendo:con:y ℙ el tensor proyección:Para calcular la parte desviadora de la componente activa en la configuración espacial es necesario realizar el empuje con el tensor F¯e:
con:yℂ¯w¯i, i=p, a, es el empuje de ℂ¯w¯i y su valor también se puede expresar mediante:Operando se puede llegar a la expresión del tensor constitutivo desviador ℂ¯ expresado en función de los invariantes I¯1,I¯2,I¯4 y J¯4.
2.4Imposición de deformaciones inicialesEl músculo, al igual que la mayoría de los tejidos blandos, se encuentra sometido a deformaciones iniciales en la configuración de referencia. Para su incorporación en la formulación hiperelástica se sigue la metodología propuesta por [25]. Se supone que el tensor gradiente de deformación correspondiente al estado deformado Fr se puede expresar mediante una descomposición multiplicativa Fr=FF0, donde, F0 representa el gradiente de deformación correspondiente a las deformaciones iniciales y F es el gradiente de deformación correspondiente a la aplicación de las cargas desde la configuración inicial Ω0 (ver figura 2).
Como F0 no es fácil de evaluar, en este caso se supone que F0 corresponde al alargamiento longifudinal λ0 en la dirección de las fibras musculares m0 en el estado de referencia Ω0[25]. En un sistema local de coordenadas (*) donde la dirección de las fibras musculares m0 está alineada con el eje X1, F0* puede ser expresado por:
y trasformado al sistema global mediante el tensor de rotación F0=RF0*RT[13].2.5Extensión al elemento membranaA la hora de abordar el modelado mediante elementos finitos de distintas unidades musculares, aparece la dificultad de que determinados tejidos presentan un espesor despreciable frente a los tejidos circundantes. Una posible alternativa sería despreciar su contribución mecánica, lo cual es factible siempre que su rigidez sea inferior a la de los otros tejidos. Sin embargo, no es posible despreciar la contribución de las estructuras que aportan rigidez, como es el caso de la fascia. En este caso se ha optado por modelar el tejido fascial mediante elementos membrana, por lo que las tensiones normales en la dirección del espesor se consideran despreciables. Por lo tanto, las seis componentes del tensor de tensiones considerado en la formulación 3D (ecuaciones (22) y (24)) se han de reducir en la formulación de membrana, por lo que la condición de tensiones nulas en el espesor del elemento ha de ser incorporada si se trabaja con la ley constitutiva planteada (ecuaciones (26) y (34)) para materiales hiperelásticos anisótropos. Este ha sido el esquema seguido en este trabajo, para el cual se ha empleado el algoritmo propuesto por [26], que ha sido implementado en el código Abaqus [27] mediante una subrutina UMAT.
Para el modelado del comportamiento de la membrana, se utiliza un sistema de coordenadas local definido por tres vectores. e1 y e2 están incluidos en el plano de la membrana y e3 es perpendicular a dicho plano. Estos vectores giran como lo hace el sólido rígido y las deformaciones se expresan en el sistema local. El gradiente de deformación F en notación matricial, para el elemento membrana, viene dado por:
por lo que las componentes C33 y b33 del tensor de deformaciones de Cauchy Green por la derecha y la izquierda no son nulas, así como las componentes S33 y σ33.Para comenzar con el algoritmo, la ley constitutiva 3D se expresa agrupando los tensores de tensión y deformación en los términos no nulos Sm=(S11, S22, S12, S13, S23)T y los que tendrían que ser nulos Sz=(S33)=0.
Para desarrollar el algoritmo de imposición de tensión plana de forma local, se parte de la ecuación (45) y se considera que Sz=0 y Cz es la componente desconocida del tensor de deformación. Expresando la tensión en serie de Taylor:
donde el superíndice i indica el número de la iteración local. En las iteraciones sucesivas se modifica la componente en z del tensor de deformación de Cauchy Green por la derecha, Cz hasta alcanzar la condición de Sz=0. Despreciando los términos de alto orden en la ecuación (46) se obtiene ℂzz(i)=∂Sz(i)∂Cz(i) y con ello la deformación incremental:con lo que la deformación en la siguiente iteración viene dada por:La matriz de rigidez tangente, utilizada en cada iteración en el algoritmo de Newton-Raphson, podría estar asociada con la variación de Sm con respecto a Cm pero dependerá del estado de deformación completo C. Para obtener la matriz de rigidez tangente consistente, con la condición de tensión impuesta por la formulación del elemento, la matriz de rigidez tangente se ha de condensar. En este caso concreto, la condición es que la tensión sea nula en el espesor de la membrana. Si dCz=0, de la segunda ecuación de (45) se obtiene:
con:donde ℂpsc es la matriz de rigidez tangente correspondiente al elemento membrana.3EjemplosEs esta sección se presentan diferentes resultados obtenidos de la simulación del músculo TA de rata que muestran tanto su respuesta pasiva como activa. Con el objetivo de validar el modelo numérico propuesto en la sección anterior, estas simulaciones se comparan con ensayos experimentales llevados a cabo sobre el mismo músculo.
3.1Modelo geométrico del músculo TALa geometría del músculo TA se reconstruyó a partir de la imagen axial de resonancia magnética (RM) de una rata adulta Wistar de 215±15 g de peso tal y como se describe en [16]. Dicha geometría se discretizó con elementos hexaédricos utilizando el software ABAQUS [27].
Es necesario tener en cuenta que la geometría del músculo se ha obtenido «in-vivo», es decir, en la configuración fisiológica, por lo que está sujeto a tensiones iniciales que es necesario introducir en el modelo numérico. En este caso se introduce un gradiente de deformación inicial, F0, definido por el acortamiento λ0=1.2035 obtenido experimentalmente al diseccionar el tendón en la zona distal (4.54±1.325 mm) [16].
3.2Función densidad energía de deformaciónPara caracterizar el comportamiento pasivo de la UMT, se utilizó la siguiente función densidad energía de deformación:
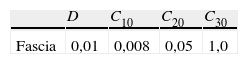
donde I¯1 representa el primer invariante del tensor de deformación de Cauchy-Green modificado, I¯4>I¯40 caracteriza la respuesta mecánica en la dirección de las fibras de colágeno, I¯4ref alargamiento de transición entre la zona lineal y exponencial. c1>0, c3>0, c5>0 y c6<0 son parámetros con unidades de tensión, siendo c3>0 una escala de la parte exponencial, c4>0 es un parámetro adimensional y c7 es un parámetro con unidades de energía de deformación. Nótese que c5>0, c6>0 y c7>0 no son parámetros independientes, sino que vienen determinados por las condiciones de continuidad de la energía, de la tensión y de la primera derivada de la tensión (en términos globales del tensor elástico tangente).Para caracterizar el comportamiento pasivo de la fascia se utilizó la función isótropa de Yeoh:
donde c10>0, c20>0 y c30>0 son parámetros con unidades de tensión. En las ecuaciones (52) y (53) solo se expresa la parte isocórica.Para caracterizar el comportamiento activo, proponemos la función Ψ¯a expresada como una serie de funciones adimensionales que escalan la magnitud de la tensión isométrica máxima σ0[15]. Estas funciones se obtienen de la relación tensión-alargamiento f1(λ¯a) asociada al solapamiento efectivo entre los filamentos de miosina y actina en el elemento contráctil, de la relación tensión-velocidad f2(λ¯˙a), de la deformación asociada a los puentes cruzados f3(J¯4) y del nivel de activación f(fr, t):
La función f1(λ¯a) ha sido formulada por diferentes autores [28,10], en este trabajo utilizamos la función propuesta por [15]:
siendo λopt el alargamiento óptimo del músculo y α corresponde a la curvatura de la función. La relación tensión-velocidad f2(λ¯˙a) tomará el valor unidad en el caso de contracciones isométricas, para el caso en el que varíe la longitud del músculo durante la contracción, se adopta la propuesta por [10]. La deformación asociada a los puentes cruzados:Finalmente la función de activación β(fr, t) puede expresarse como [15]:
siendo T′ el tiempo de contracción aparente para todo el músculo generado en un pulso y P′ es la amplitud aparente de la tensión generada en el mismo pulso, ti es el intervalo de tiempo entre estímulos que corresponde a 1/fr, r determina la tasa entre la tensión en un pulso y un tétano, c es la tasa de incremento de fuerza conforme aumenta la frecuencia y n es el número de estímulos.3.3Simulación ensayo uniaxialPara validar el modelo de comportamiento pasivo se ha reproducido numéricamente un ensayo de tracción uniaxial sobre la UMT de dos formas, considerando la inclusión de la fascia a través de elementos membrana y sin incluirla. Después, se comparan los resultados numéricos obtenidos con los experimentales [14]. En ambos casos, las fibras se consideran en la dirección fusiforme y el espesor de la fascia, medido previamente en ensayos experimentales [29], se toma igual a 0.3 mm. Las constantes de la función densidad energía de deformación para el músculo, tendón y fascia se recogen en las tablas 1 y 2, respectivamente. Es necesario destacar aquí que, si bien los parámetros que caracterizan el comportamiento pasivo de músculo y tendón son bien conocidos de un trabajo previo [14], aquellos que caracterizan la fascia han sido determinados ajustando la respuesta numérica a los ensayos experimentales. Para reproducir el ensayo se fijan los desplazamientos de la zona proximal del músculo TA y se aplica un desplazamiento impuesto de 10 mm en la zona distal (nodos correspondientes al tendón). Como el ensayo se realiza una vez que se ha producido la disección del tendón, se ha de partir en la simulación de la configuración libre de tensiones iniciales (Ωsf), por lo que inicialmente se ha de obtener dicha configuración liberando las tensiones iniciales.
Parámetros que caracterizan el comportamiento pasivo del músculo y tendón. Constantes en MPa [14].
| c1 | c3 | c4 | c5 | c6 | c7 | I¯40 | I¯4ref | |
| Músculo | 0,001 | 0,053915 | 0,782802 | 5,742780 | −9,035709 | −4,875961 | 1,254400 | 3,189796 |
| Tendón | 0,01 | 0,054292 | 6,860021 | 57,738461 | −66,243575 | −57,078409 | 1,0 | 1,44 |
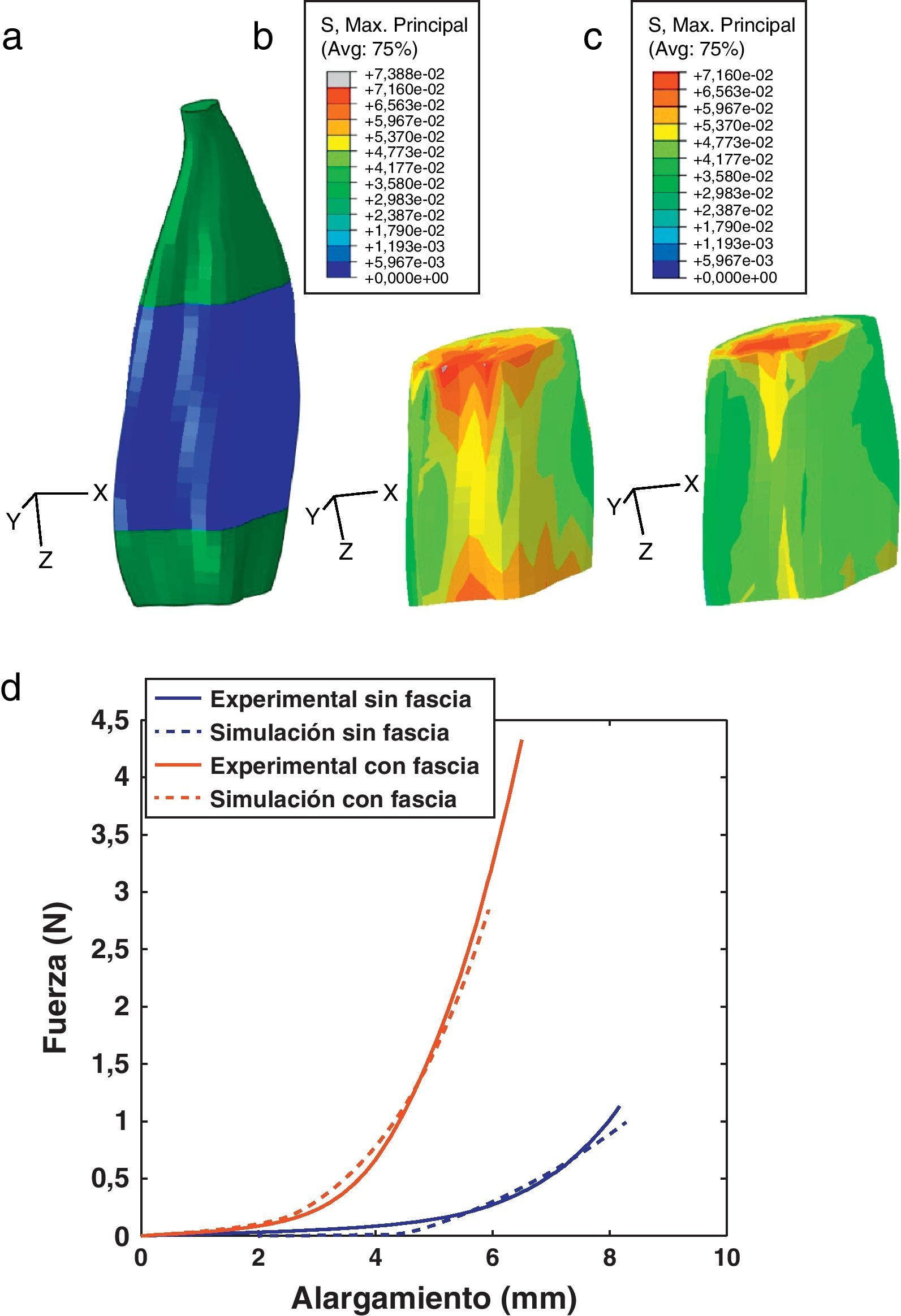
La figura 3a presenta el modelo de elemenos finitos para el músculo TA, donde se ha indicado una región central del vientre muscular sobre la que se visualizan los campos de tensiones máximas principales (TMP). Las TMP que se muestran en la figura 3b se corresponden con la simulación del modelo sin incluir la fascia mientras que la figura 3c incluye este tejido. Para establecer una comparación directa entre ambas imágenes, los elementos correspondientes a la fascia han sido suprimidos en la figura 3.c. Se observa que la distribución de TMP evidencia valores mayores en la figura 3b, donde no está considerada la fascia.
(a) Modelo de elementos finitos del TA. En azul se indica la parte central del músculo, donde se visualizan los campos de TMP. (b) Campo de TMP en el músculo cuando no se incluye la fascia. (c) Campo de TMP en el músculo cuando se considera la fascia. La fascia ha sido retirada para visualizar solamente el músculo y poder comparar con (b). (d) Fuerza vs. alargamiento obtenido de las simulaciones del ensayo uniaxial, con y sin fascia, comparadas con los resultados experimentales [14].
Las relaciones fuerza-desplazamiento obtenidas en las simulaciones numéricas se muestran en la figura 3.d donde, a su vez, se comparan con las curvas experimentales. Aquí se aprecia la diferencia de rigidez entre ambas situaciones, evidenciando una rigidez notablemente mayor para el caso en el que se incluye la fascia.
3.4Simulación de la contracciónSe han llevado a cabo 2 grupos diferentes de simulaciones para estudiar la contracción isométrica (la longitud del músculo es constante) y la contracción concéntrica (la longitud del músculo disminuye) a velocidad constante (isotónica). La tabla 3 recoge los parámetros utilizados para las simulaciones.
Parámetros que caracterizan el comportamiento activo del músculo [15].
| σ0 (MPa) | λopt | α | T′ (s) | P′ (N) | ti (s) | r | c |
| 0,8 | 1 | 0,83616 | 0,04 | 0,11 | 0,01667 | 1,0535 | 1,1245 |
En primer lugar, para estudiar la contracción isométrica, se fijan ambos extremos de la malla manteniendo fijos los grados de libertad de los nodos en dichas regiones. Puesto que en una contracción isométrica, la unidad mínima funcional del músculo (sarcómero) no altera su longitud inicial, no existe desplazamiento relativo entre los filamentos de actina y miosina. Es por ello que, en la descomposición multiplicativa del gradiente de deformación F¯a=1, por lo tanto F¯=F¯e. El valor de la función f(λ¯˙a) en la ecuación (54) al no existir dependencia con la velocidad se toma como f(λ¯˙a)=1.
La figura 4 muestra la fuerza de reacción total registrada en los nodos de la malla del extremo superior para cuatro frecuencias del estímulo. El efecto que la frecuencia del estímulo ejerce sobre la deformación y la TMP del tejido se observa en la figura 5.
Por otro lado, para llevar a cabo la simulación de una contracción concéntrica, se liberan las condiciones de contorno establecidas en el caso anterior para los nodos del extremo superior de la malla. De esta manera, el músculo acortará su longitud inicial libremente.
Bajo estas condiciones, y realizando sucesivos incrementos de tiempo en un análisis estático, es necesario definir la velocidad de la contracción. En las simulaciones llevadas a cabo en este trabajo se ha considerado que la contracción se realiza a velocidad constante (contracción isotónica) tomando un valor λ¯˙a=−5 [1/s] [34] por ello, F¯a se supone conocida y, en la dirección de la fibra muscular tendrá la siguiente forma, con λ¯an+1=λ¯an+λ¯˙a▵t:
En esta situación, el valor de f(λ¯˙a) se ha tomado como f(λ¯˙a)=0.5[10].
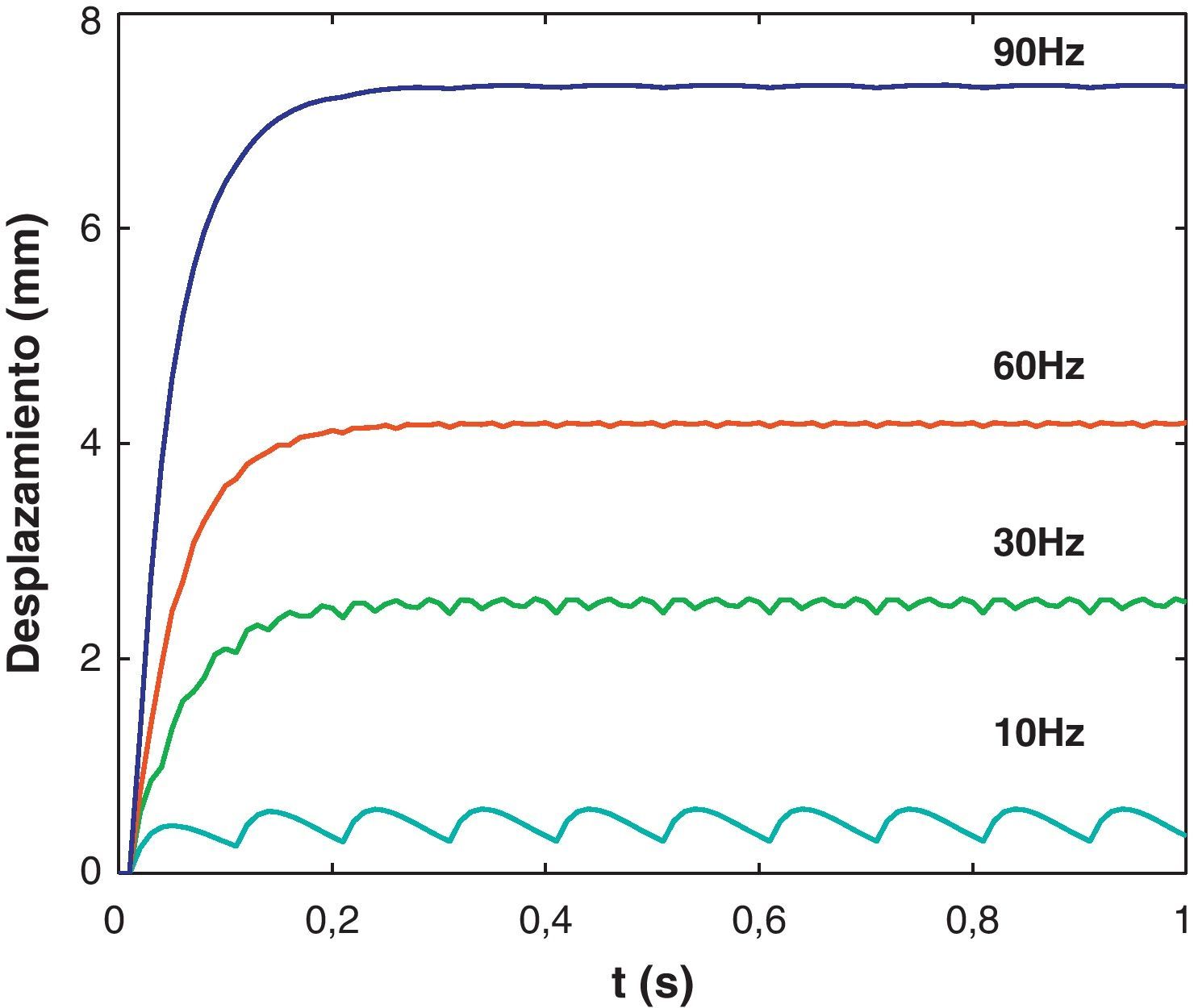
La figura 6 representa el desplazamiento del extremo superior de la UMT para las cuatro diferentes frecuencias consideradas. La figura 7 representa, junto con la configuración inicial del tejido, la deformada y el campo de desplazamientos en la dirección longitudinal para los 4 estímulos. Se observa cómo para la frecuencia mayor se obtiene el mayor acortamiento del músculo.
4ConclusionesEn este trabajo se ha presentado y validado un modelo numérico de comportamiento 3D que permite simular la respuesta mecánica del tejido músculo-esquelético de mamíferos. Esta respuesta está fuertemente influenciada por la geometría y la arquitectura de las fibras musculares [30]. Por ello, en este trabajo se ha modelado el músculo TA partiendo de imagen de RM considerando una distribución de dichas fibras siguiendo la geometría fusiforme del tejido. En la mayoría de los trabajos de la literatura se parte de geometrías de músculos procedentes de cadáveres [31,10] o bien utilizan geometrías idealizadas [9,28,10,32].
El modelo numérico propuesto se ha particularizado para el músculo TA de rata. Para ello, las constantes que definen el comportamiento pasivo y activo se han tomado de trabajos experimentales previos desarrollados por los autores [14,15]. El comportamiento pasivo se ha validado comparando los resultados numéricos con los experimentales cuando a la UMT se le solicita a un estado uniaxial de tracción (fig. 3d). Este procedimiento ha permitido, a través de las curvas fuerza-desplazamiento obtenidas experimentalmente, ajustar un modelo de comportamiento isótropo para la fascia que envuelve el tejido muscular. De esta forma se ha conseguido estimar las constantes que definen su comportamiento indirectamente a través de la simulación computacional. Este hecho permite caracterizar de manera precisa el tejido evitando llevar a cabo ensayos experimentales de extrema dificultad técnica. La figura 3 muestra además el efecto que ejerce la fascia sobre la distribución de tensiones en el vientre muscular. Este tejido, debido a que presenta una rigidez mayor, disminuye la tensión que soporta el músculo para un mismo nivel de extensión pasiva [33].
En el caso de la simulación del comportamiento activo, la fuerza de reacción obtenida para la contracción isométrica (figura 4) coincide con la observada experimentalmente en [15] para las frecuencias de estímulo de 30, 60 y 90 Hz. Una limitación importante del modelo bajo contracción isométrica consiste en haber considerado F¯a=1. Si bien es cierto que para este tipo de contracción no hay desplazamiento de los extremos de la UMT, las fibras musculares se acortan hasta alcanzar una posición de equilibrio en la dirección formada por los dos extremos fijos. En el caso de contracciones concéntricas los resultados presentan la misma tendencia obtenida por otros autores para geometrías diferentes [9,10,34]. La simplificación llevada a cabo de no considerar la masa y efectos inerciales del tejido así como la ausencia de cargas exteriores condiciona que la simulación se acerque a la realidad del comportamiento de la UMT.
Esta investigación ha sido financiada por el Ministerio de Economía y Competitividad de España mediante el proyecto DPI2011-27939-C02-01 y el Instituto de Salud Carlos III (ISCIII) mediante la iniciativa CIBER. Los autores también agradecen al Ministerio de Ciencia e Innovación por la beca (BES-2009-021515) concedida a B. Hernández-Gascón.













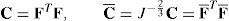

![Esquema de la deformación pasiva y activa [18]. Sobre el punto X de la configuración indeformada Ω0, consideramos dos direcciones preferenciales definidas por m0 y n0. Esta configuración se transforma en la misma dirección por la contracción activa F¯a, donde los nuevos vectores serán λ1m0, λ2n0 y λ3l0. La deformación elástica transforma esta configuración intermedia activa a la configuración deformada Ωt por medio del gradiente de deformación F¯e. Esquema de la deformación pasiva y activa [18]. Sobre el punto X de la configuración indeformada Ω0, consideramos dos direcciones preferenciales definidas por m0 y n0. Esta configuración se transforma en la misma dirección por la contracción activa F¯a, donde los nuevos vectores serán λ1m0, λ2n0 y λ3l0. La deformación elástica transforma esta configuración intermedia activa a la configuración deformada Ωt por medio del gradiente de deformación F¯e.](https://static.elsevier.es/multimedia/02131315/0000002800000003/v1_201305061220/S0213131512000193/v1_201305061220/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)


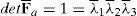



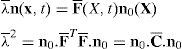



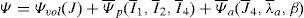
















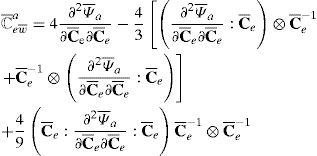
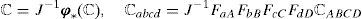





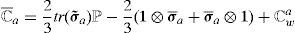





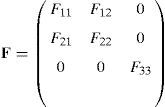




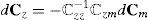
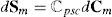




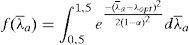
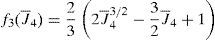
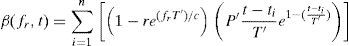
![(a) Modelo de elementos finitos del TA. En azul se indica la parte central del músculo, donde se visualizan los campos de TMP. (b) Campo de TMP en el músculo cuando no se incluye la fascia. (c) Campo de TMP en el músculo cuando se considera la fascia. La fascia ha sido retirada para visualizar solamente el músculo y poder comparar con (b). (d) Fuerza vs. alargamiento obtenido de las simulaciones del ensayo uniaxial, con y sin fascia, comparadas con los resultados experimentales [14]. (a) Modelo de elementos finitos del TA. En azul se indica la parte central del músculo, donde se visualizan los campos de TMP. (b) Campo de TMP en el músculo cuando no se incluye la fascia. (c) Campo de TMP en el músculo cuando se considera la fascia. La fascia ha sido retirada para visualizar solamente el músculo y poder comparar con (b). (d) Fuerza vs. alargamiento obtenido de las simulaciones del ensayo uniaxial, con y sin fascia, comparadas con los resultados experimentales [14].](https://static.elsevier.es/multimedia/02131315/0000002800000003/v1_201305061220/S0213131512000193/v1_201305061220/es/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)




