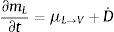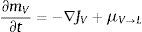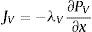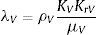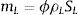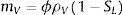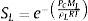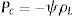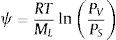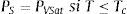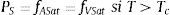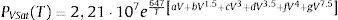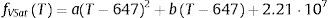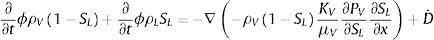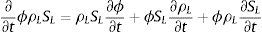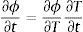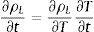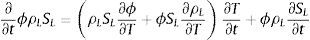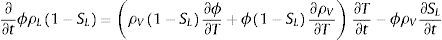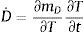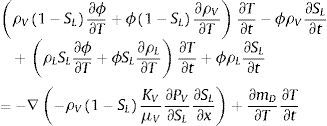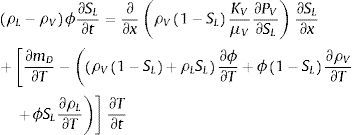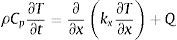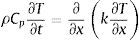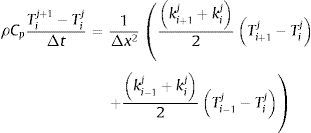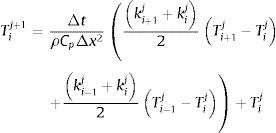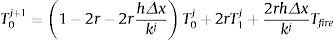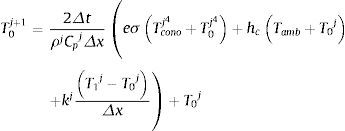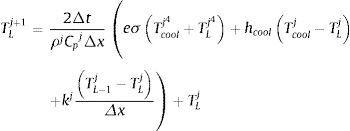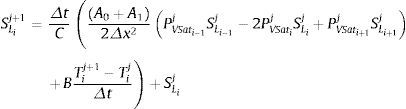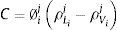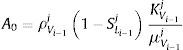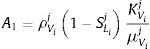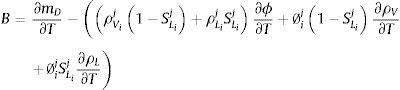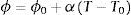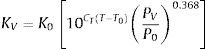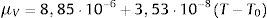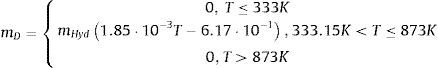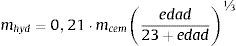En este trabajo se expone un modelo hidrotérmico simplificado para calcular la presión de los poros en hormigones expuestos a temperaturas elevadas, basado en el análisis de la transferencia de masa y energía en medios porosos multifase. El modelo ha sido estructurado de tal forma que permite, realizando una serie de asunciones, minimizar el número de parámetros de entrada sin comprometer los resultados de las predicciones. Se han validado los resultados de la simulación y se ha evidenciado que el modelo de cálculo es capaz de reproducir, con un alto grado de fiabilidad y precisión, la evolución de las temperaturas en el hormigón como resultado de la agresión térmica, tanto en la superficie expuesta como en el interior del elemento. Asimismo, las presiones máximas de los poros estimadas por el modelo ofrecen unos resultados adecuados si se comparan con los valores experimentales.
In the present work, a simplified hydro-thermal model for pore pressure calculation in concrete exposed to high temperatures is presented. The model is based on heat and mass transfer analysis in multi-phase porous media. The model has been structured in such a way that it is possible, due to assumptions, to reduce the numbers of inputs without compromising the results of the predictions. The validation process has been performed, and it has shown that the computational model is capable to reproduce with a high reliability and accuracy the mass losses reported in the experimental tests and the evolution of temperatures on concrete due to thermal exposure, both at the exposed surface and inside the element. Likewise, pore pressure estimated by the model agrees with the experimental results.
El desconchamiento (spalling) del hormigón causado por una agresión térmica es considerado uno de los fenómenos más graves que pueden producirse en caso de incendio [1]. Existen distintos tipos de desconchamiento: de superficie, de los áridos, de esquina, explosivo y postenfriamiento. De todos estos, el desconchamiento explosivo es el que más afecta al hormigón en caso de incendio. Estudios recientes [2–5] demuestran que durante el calentamiento del hormigón se produce un incremento de la presión en los poros y un deterioro del material como consecuencia de los esfuerzos térmicos. A partir de estos estudios, se infiere que la presión en los poros generada en el interior del hormigón no es suficientemente alta para provocar, por sí sola, el desconchamiento. Por ello, lo más probable es que previamente se haya producido un deterioro del hormigón, lo cual conlleva una pérdida de rigidez del material. Cuando la presión interna de los poros sobrepasa la resistencia del hormigón, se produce la expulsión violenta de la capa de hormigón.
Sobre la base de esta hipótesis, se han desarrollado diferentes modelos de predicción, basados en análisis hidrotermomecánicos [2,5–9]. Sin embargo, estos modelos requieren la introducción de propiedades del material variables con la temperatura, las cuales pueden no encontrarse bien definidas incluso a temperatura ambiente [10]. Otros autores [11–15] consideran que las fuerzas de tracción que se generan en el interior del hormigón como consecuencia de la presión de los poros son las responsables de que se produzca el desconchamiento explosivo, una vez superada la resistencia a la tracción del hormigón, la cual disminuye a medida que aumenta la temperatura. Sobre la base de esta hipótesis, se ha propuesto un modelo simplificado para estimar la presión de los poros [11], el cual requiere un número reducido de parámetros de entrada.
En este modelo simplificado se han seleccionado cuidadosamente las variables de estado, con el fin de poder describir el comportamiento del agua (tanto capilar como absorbida) y del vapor dentro de todo el rango de temperaturas y presiones presentes en el hormigón sometido al ataque térmico. Varios autores han estudiado de forma experimental [16–19] el incremento de la presión de los poros en el interior del hormigón como consecuencia del ataque térmico. Sin embargo, los resultados y los dispositivos de ensayo analizados por la literatura [19,20] evidencian la importancia de la preparación experimental y de la configuración del dispositivo utilizado en la medición de la presión de los poros.
Otros autores [21–24] han empleado técnicas de calorimetría de pérdida de masa para evaluar los mecanismos y la velocidad de expulsión de la humedad en el hormigón sometido al ataque térmico bajo determinadas condiciones de ensayo.
2Descripción del modelo hidrotérmicoEl modelo desarrollado se inspira en el modelo hidrotérmico simplificado propuesto por Dwaikat y Kodur [11]. Este modelo, basado en los principios de la mecánica estructural y la termodinámica, utiliza las ecuaciones de conservación de la masa y la energía para predecir la presión de los poros. Presenta la ventaja de que el número de parámetros iniciales para estimar la presión de los poros en el interior del hormigón es mínimo, en comparación con otros modelos hidrotermomecánicos existentes.
En el modelo propuesto se han revisado todas las asunciones iniciales y se han propuesto correcciones de tal forma que el nuevo modelo tiene en cuenta consideraciones no previstas en el modelo original (comportamiento del agua por encima del punto crítico, efectos de la adición de fibras de polipropileno sobre la porosidad y la permeabilidad, efecto de la edad del hormigón en el grado de hidratación). Se considera el hormigón un medio poroso continuo multifase en el cual los poros están rellenos parcialmente por una fase líquida (agua) y por una fase gaseosa constituida solamente por vapor de agua. Para simplificar el modelo, no se ha considerado el efecto del aire en el interior de los poros, debido a que su masa es pequeña en comparación con la del vapor de agua [9,11].
El presente modelo asume que el movimiento de la humedad se produce por evaporación-condensación. Esto significa que todo el movimiento de la humedad en el interior del hormigón se produce en la fase gaseosa, de modo que se obvia la movilidad del agua en estado líquido. Esto se debe a que el coeficiente de permeabilidad de Darcy para el agua líquida es, por término medio, inferior al coeficiente de permeabilidad al gas en 2 o 3 órdenes de magnitud. No obstante, esta asunción puede ser cuestionable para el caso de los hormigones con un alto grado de saturación, en que la permeabilidad relativa al líquido no es despreciable. Sin embargo, según [25], esta asunción es esencialmente correcta en el caso de los sistemas expuestos a gradientes de temperatura, incluso con niveles de saturación de poros relativamente elevados, como es el caso que nos atañe.
El modelo desarrollado es unidimensional, lo cual restringe su aplicabilidad a los elementos planos, como forjados, paredes, muros, losas, etc.
2.1Ecuaciones del submodelo hídricoLas ecuaciones de conservación de la masa pueden expresarse como
donde mL y mV son las masas de agua líquida y de vapor de agua por unidad de volumen; μL→V es la masa de agua líquida que se transforma en vapor por unidad de volumen; μV→L es la masa de vapor que se condensa para transformarse en agua por unidad de volumen; D˙ es la variación de la masa de agua como resultado de la deshidratación del cemento por unidad de volumen y tiempo, y JV es el flujo de masa de vapor de agua que atraviesa el hormigón. Asumimos que toda el agua que se evapora se condensa y, para el caso unidimensional, JV puede relacionarse con el gradiente de presión a través de la ley de Darcy mediante la expresión:donde PV es la presión de vapor y λV es el coeficiente de permeabilidad de Darcy, el cual puede escribirse como:donde KV es la permeabilidad intrínseca al vapor de agua; KrV es la permeabilidad relativa al vapor de agua del hormigón, y μV es el coeficiente de viscosidad dinámica del vapor de agua. Las masas de agua y de vapor de agua presentes en el hormigón han sido consideradas en el modelo como función de la saturación según:donde ϕ es la porosidad del hormigón; ρL es la densidad del agua líquida; SL es la saturación de líquido, y ρV es la densidad del vapor de agua.Tanto la variación de la densidad del agua como la del vapor de agua tienen un comportamiento extremamente no lineal. A partir de la temperatura crítica, Tc=647K, la densidad del agua se iguala a la crítica ρCrit=322kg/m3 y se comporta como un fluido supercrítico [26].
El modelo utiliza la saturación de líquido en función de la presión capilar (Pc) y la temperatura (T) para estimar el contenido de agua líquida
donde ML es la masa molar del agua y R es la constante universal de los gases.La presión capilar puede expresarse, mediante la ecuación de Kelvin, como función del potencial del agua (ψ):
Utilizando el potencial del agua como variable de estado, es posible describir el comportamiento del agua dentro de todo el rango de temperaturas y presiones presentes en los poros del hormigón, tanto para el agua capilar como para el agua adsorbida:
donde PVSat es la presión de saturación del vapor; fASat es la fugacidad de saturación del agua adsorbida, y fVSat es la fugacidad de saturación del vapor, que pueden entenderse como pseudopresiones.Por debajo de la temperatura crítica, la frontera de cambio de fase del agua, de líquido a gas, queda definida por la curva de presión de saturación de vapor. El modelo obtiene esta presión mediante la ecuación propuesta por la IAPWS [27], la cual relaciona la presión de saturación del vapor en función de la temperatura.
con V=1−T647, a=−7,86, b=1,84, c=−11,8, d=22,7, f=−16,0 y g=1,80, T en K y PVSat en Pa.A temperaturas superiores a la temperatura crítica, el agua adsorbida se encuentra en equilibrio termodinámico con el vapor de agua en el interior de los poros del hormigón, por lo cual el valor de la fugacidad del agua adsorbida se corresponde con el valor de la fugacidad del vapor. En los gases ideales, el valor de la fugacidad del vapor se corresponde con el valor de la presión de vapor, de modo que el coeficiente de fugacidad es igual a 1. En el caso del vapor de agua, el coeficiente para el rango de temperaturas y presiones estudiadas sigue siendo próximo a 1 y, por tanto, puede asumirse que el comportamiento del vapor del agua es ideal. En este caso, el valor de la fugacidad del vapor por encima de la temperatura crítica se corresponderá con el valor de la presión en la isocora crítica.
Para calcular esta presión en el modelo, se propone la expresión empírica (13), dependiente de la temperatura, la cual ha sido obtenida mediante un ajuste cuadrático R2=1,00 a partir de las formulaciones de la IAPWS [27]
con a=−29,0 y b=2,91·105, T en K y fVSat en Pa.Sumando las ecuaciones (1) y (2) y sustituyendo las expresiones descritas más arriba se obtiene la siguiente expresión para determinar la masa de agua líquida en el interior del hormigón:
La derivada de la masa de agua líquida en función del tiempo puede expresarse como:
Mediante la regla de la cadena, las derivadas de la porosidad en función del tiempo y la derivada de la densidad de agua líquida son:
Sustituyendo las ecuaciones (16) y (17) en (15) y agrupando términos:
Análogamente, la derivada de la masa de vapor en función del tiempo puede expresarse como:
La variación de la masa de agua como resultado de la deshidratación del cemento por unidad de volumen y tiempo D˙ puede calcularse como:
donde mD es la masa de agua líquida que se produce por la deshidratación. Sustituyendo las ecuaciones (18), (19) y (20) en (14), se obtiene:Y agrupando términos para facilitar el planteamiento del esquema de solución por diferencias finitas, la expresión anterior puede escribirse como:
2.2Ecuaciones del submodelo térmicoPara el caso unidimensional, el análisis de la transferencia de calor en el medio poroso se realiza mediante la ecuación de conservación de la energía (23):
donde ρ es la densidad del hormigón; Cp es el calor específico; kx es la conductividad térmica, y Q es la fuente de calor externa.A efectos del modelo, la aportación del calor latente y el calor de hidratación/deshidratación se tienen en cuenta en la expresión del calor específico, la cual ha sido desarrollada según [28,29], de modo que la expresión anterior puede simplificarse a:
2.3Solución numérica de las ecuaciones del modeloPara la solución numérica de la ecuación (24) se ha empleado el método explícito de diferencias finitas, utilizando una diferencia progresiva de primer orden para la derivada temporal y una diferencia central de segundo orden para la derivada espacial. Aplicando el método, la ecuación (24) puede escribirse como:
donde Δt es la discretización temporal adoptada para la solución y Δx es la discretización espacial. El término Tij+1 representa la temperatura a la profundidad i para el instante de tiempo j+1 y puede determinarse de manera explícita a partir de la expresión:Considerando ΔtρCpΔx2= r, la ecuación es estable si r≤12 para todo el intervalo de tiempo considerado.
Conocido el valor de la temperatura para el instante de tiempo j, es posible obtener el valor correspondiente para el instante de tiempo j+1 a partir de la expresión recurrente anterior. Las fronteras x=0 y x=L, T0j y TLj deberán calcularse a partir de las condiciones de frontera específicas para el caso que se esté analizando.
Para la determinación de las temperaturas en la cara expuesta se han tenido en consideración 3 posibles escenarios: el caso más simple, en que conocemos la temperatura en la superficie; una segunda condición de contorno, en que se simulan las condiciones de diversas curvas de incendio conocidas por la ecuación (27), y una condición de radiación y convección para el caso general de un quemador, según la ecuación (28):
La solución numérica para la condición de contorno térmica de la cara no expuesta se describe mediante la ecuación:
donde Tcool es la temperatura ambiental en el lado frío y hcool es el coeficiente de convección de este lado.De manera análoga al cálculo de la evolución de las temperaturas en el interior del hormigón, se ha utilizado un esquema de solución por diferencias finitas para aproximar la solución de la ecuación de gobierno de la saturación. Para su resolución se emplean los valores de las temperaturas obtenidos de las ecuaciones anteriores. Transformando la ecuación en derivadas parciales mediante el método explícito de diferencias finitas y agrupando térmicos, la ecuación (22) puede expresarse como:
donde:Para resolver la ecuación (30) se requiere plantear las condiciones de frontera de la saturación en ambas superficies del material. A tal efecto, en el modelo se ha considerado una curva de desorción SL=HR[30], de modo que el valor de la saturación en la superficie del material se considera igual al valor de la humedad ambiental relativa.
2.4Ecuaciones para la descripción del estado hidrotérmicoLa porosidad del hormigón varía linealmente con la temperatura mediante la expresión:
donde ϕ0 es la porosidad inicial del hormigón y α es un parámetro que depende de la naturaleza de los áridos [31].La densidad del agua líquida tiene un comportamiento extremamente no lineal a temperaturas próximas a la temperatura crítica. A los efectos del modelo, se han utilizado las ecuaciones propuestas por la IAPWS [26]. La densidad de vapor depende de la temperatura y de la presión. Para temperaturas altas y presiones relativamente bajas, y asumiendo que el vapor de agua se comporta como un gas ideal, la densidad puede estimarse mediante la ley de los gases ideales. La permeabilidad intrínseca al vapor de agua que interviene en el cálculo de su difusión a través del medio poroso se estima, según [31]:
donde K0 es la permeabilidad del gas inicial; P0 es la presión atmosférica, y CT es un coeficiente que tiene en cuenta el incremento de la permeabilidad a elevadas temperaturas. En el modelo se ha considerado CT=0, 0025 [11]. Se asume que la viscosidad cinemática del vapor de agua varía linealmente con el tiempo, según la expresión:La masa de agua líquida que se produce como consecuencia de la deshidratación de la pasta de cemento con la temperatura se ha estimado del modo siguiente:
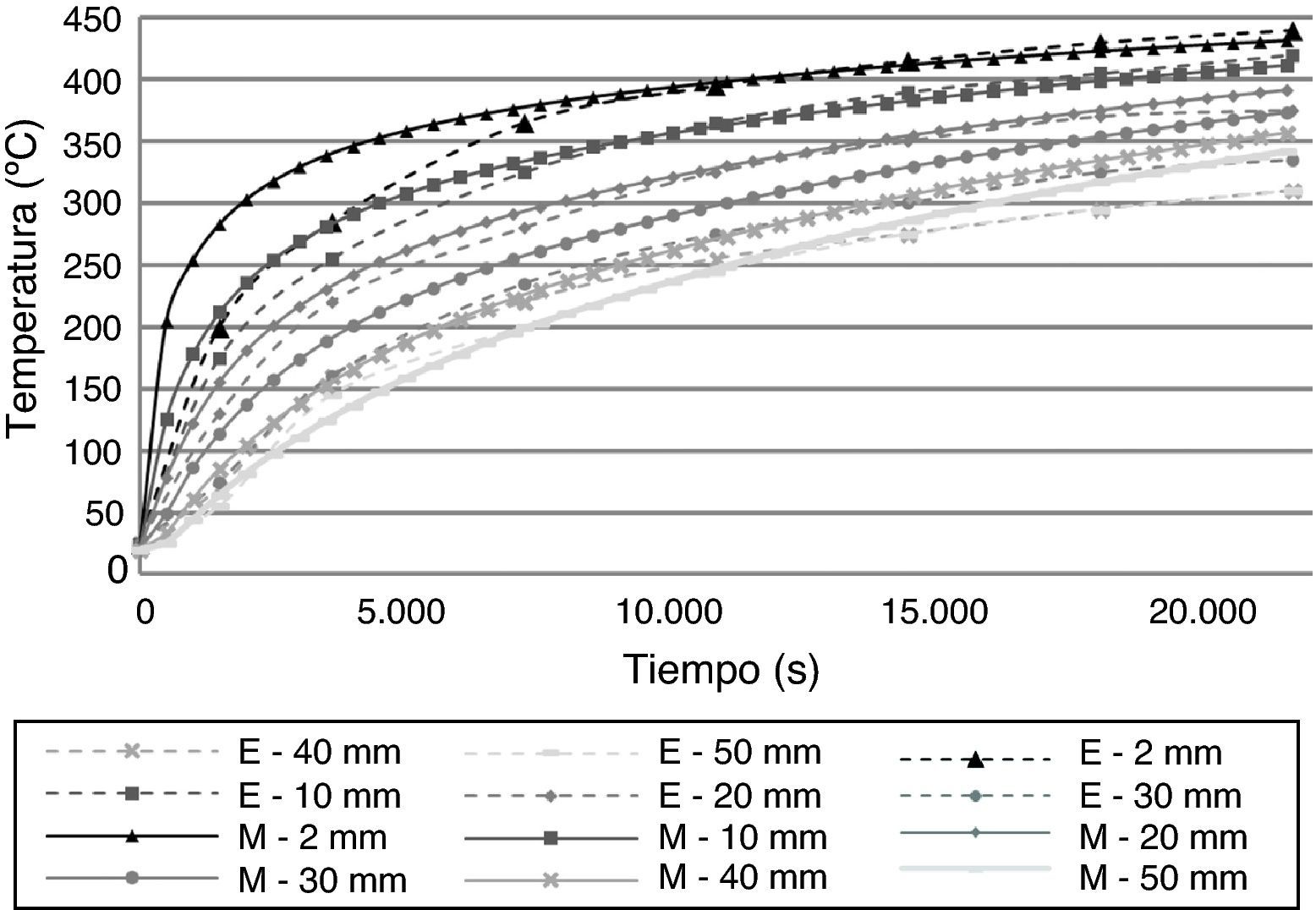
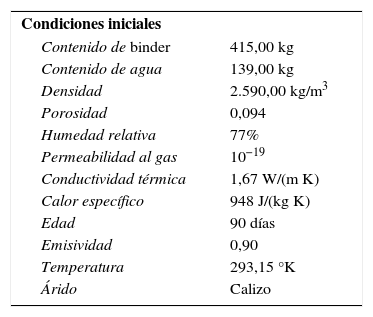
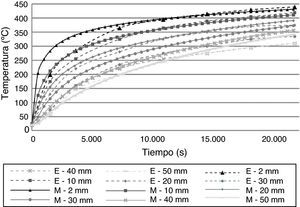
donde mhyd es la masa de agua hidratada, la cual puede estimarse, mediante [32]:siendo mcem el contenido de cemento por metro cúbico de hormigón, y edad, la edad del hormigón en días.3Validación del modeloEn esta sección se valida el modelo ante los resultados de los ensayos presentados por Kalifa [18], realizados con muestras de hormigón de 30×30×12 cm3. En estos ensayos se aplicó una temperatura del calentador de 600°C. El modelo se valida con 2 ensayos de hormigón sin fibras de polipropileno y otros dos con 3kg/m3 de contenido de fibras. Se han introducido en el modelo las condiciones iniciales y de frontera, que se reflejan en la tabla 1. Como condición de frontera térmica para el radiador se ha utilizado la propuesta por [33], que se presenta en la tabla 2. Esta curva consigue un buen ajuste con la temperatura experimental a partir de los 10mm de profundidad, tal como se observa en la figura 1, que indica las temperaturas para distintas profundidades.
Propiedades del hormigón empleado en los ensayos y condiciones de frontera empleadas en la simulación
| Condiciones iniciales | |
| Contenido de binder | 415,00 kg |
| Contenido de agua | 139,00 kg |
| Densidad | 2.590,00 kg/m3 |
| Porosidad | 0,094 |
| Humedad relativa | 77% |
| Permeabilidad al gas | 10−19 |
| Conductividad térmica | 1,67 W/(m K) |
| Calor específico | 948 J/(kg K) |
| Edad | 90 días |
| Emisividad | 0,90 |
| Temperatura | 293,15 °K |
| Árido | Calizo |
| Condiciones de frontera | |
| Cara expuesta | |
| Pg | 101.325 Pa |
| Humedad ambiental | 65% |
| hc | 10,00 W/(m2 K) |
| Emisividad | 0,90 |
| Temperatura | Ver fig. 1 |
| Cara no expuesta | |
| Pg | 101.325 Pa |
| Humedad ambiental | 65% |
| hc | 8,30 W/(m2 K) |
| Emisividad | 0,90 |
| Temperatura | 293,15 K |
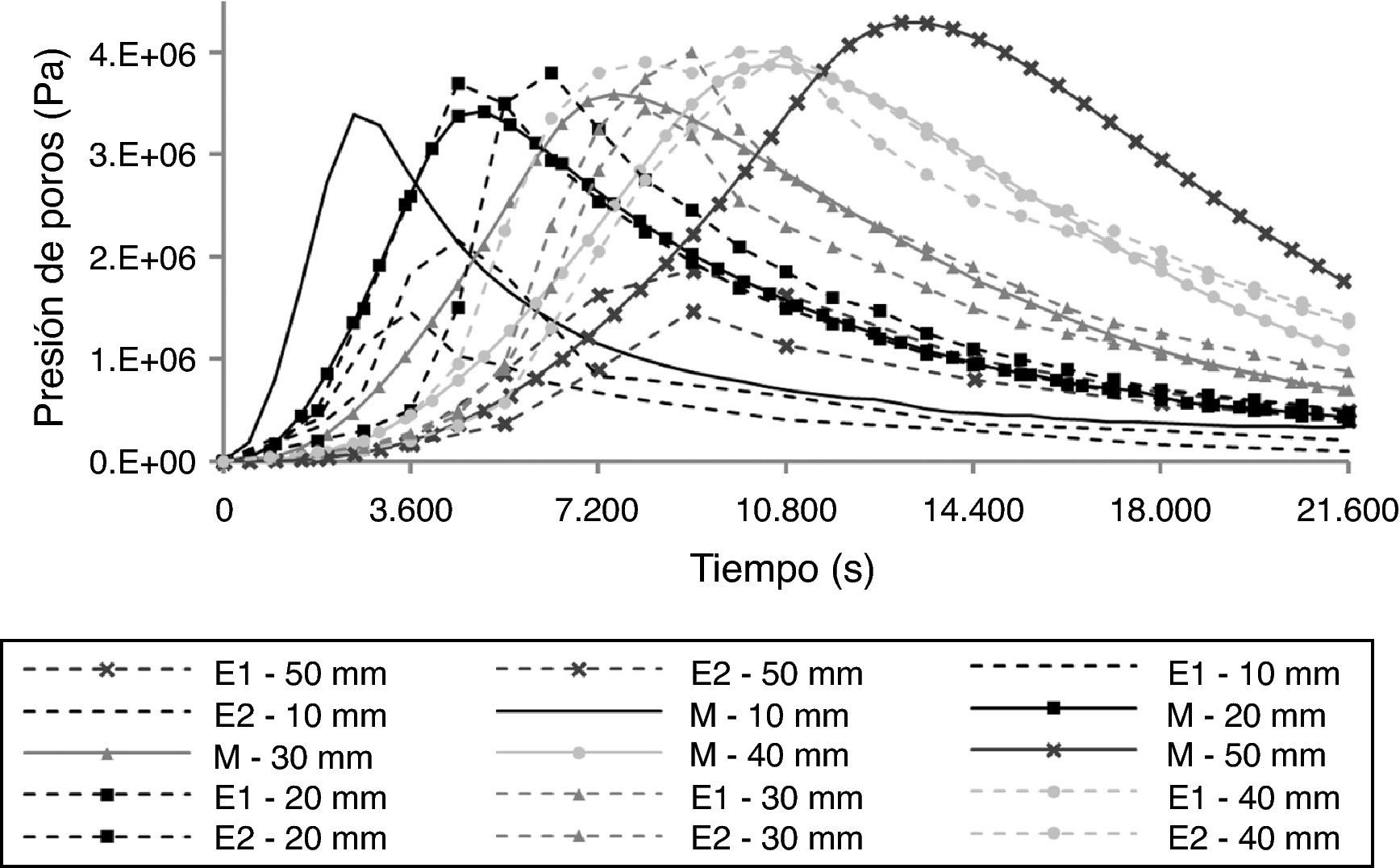
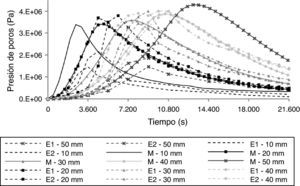
La figura 2 compara los resultados de la presión de los poros que se han obtenido con el modelo (M) en los ensayos sin fibras (E1 y E2) [18] a las profundidades de 10, 20, 30, 40 y 50mm. Como puede apreciarse en la figura, los resultados obtenidos por el modelo concuerdan adecuadamente con los valores experimentales, tanto los valores de las presiones máximas y los intervalos de tiempo a que se producen, como la tendencia general del comportamiento de la presión de los poros en el interior del hormigón en las profundidades de 20 a 40mm. En cambio, el modelo no calcula con la misma precisión en las profundidades de 10 y 50mm. Se obtienen unos resultados similares en el caso del hormigón con 3kg/m3 de fibras de polipropileno. No obstante, se observa que, en general, las presiones de los poros estimadas por el modelo, tanto en los instantes iniciales como al final de la simulación, son superiores a los valores experimentales. Este fenómeno puede atribuirse, en parte, a que el mecanismo de variación de la permeabilidad del hormigón en función de la temperatura y de la presión de poros no se ha estudiado del todo y, en parte, a las simplificaciones realizadas en el modelo, como la consideración de que el agua líquida solo se mueve en el hormigón por efecto de la evaporación y de la condensación en las zonas más frías. Es necesario tener en cuenta también la divergencia de los resultados obtenidos en los ensayos, que se realizaron por duplicado.
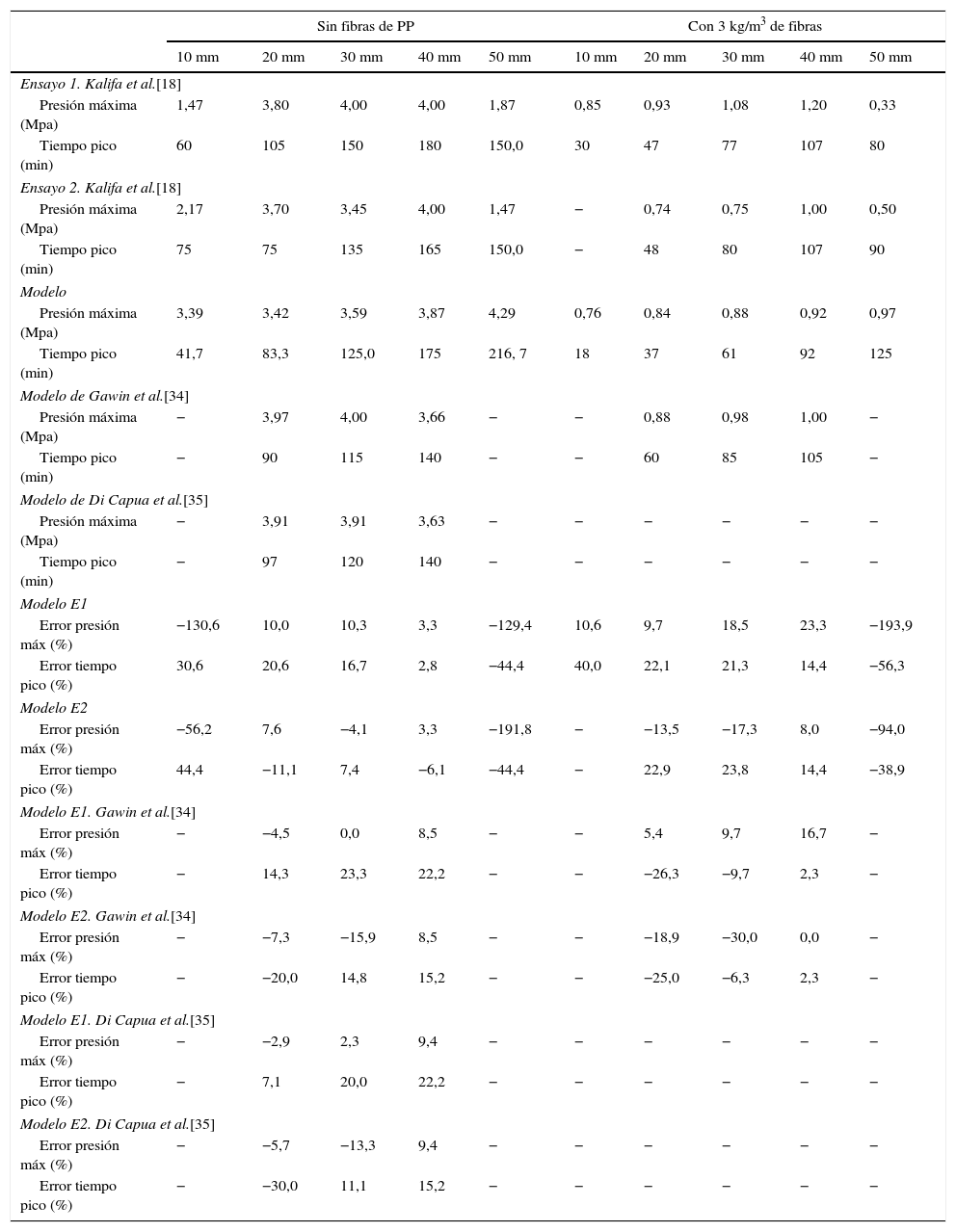
La tabla 3 contiene los resultados de la validación del modelo considerando el hormigón con 3kg/m3 de fibras y sin fibras con respecto a los ensayos experimentales de Kalifa [18], al modelo de Gawin [34] y al modelo de Di Capua [35]. Puede observarse una buena aproximación del modelo a los resultados experimentales y de los demás modelos considerados.
| Sin fibras de PP | Con 3 kg/m3 de fibras | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 mm | 20 mm | 30 mm | 40 mm | 50 mm | 10 mm | 20 mm | 30 mm | 40 mm | 50 mm | |
| Ensayo 1. Kalifa et al.[18] | ||||||||||
| Presión máxima (Mpa) | 1,47 | 3,80 | 4,00 | 4,00 | 1,87 | 0,85 | 0,93 | 1,08 | 1,20 | 0,33 |
| Tiempo pico (min) | 60 | 105 | 150 | 180 | 150,0 | 30 | 47 | 77 | 107 | 80 |
| Ensayo 2. Kalifa et al.[18] | ||||||||||
| Presión máxima (Mpa) | 2,17 | 3,70 | 3,45 | 4,00 | 1,47 | − | 0,74 | 0,75 | 1,00 | 0,50 |
| Tiempo pico (min) | 75 | 75 | 135 | 165 | 150,0 | − | 48 | 80 | 107 | 90 |
| Modelo | ||||||||||
| Presión máxima (Mpa) | 3,39 | 3,42 | 3,59 | 3,87 | 4,29 | 0,76 | 0,84 | 0,88 | 0,92 | 0,97 |
| Tiempo pico (min) | 41,7 | 83,3 | 125,0 | 175 | 216, 7 | 18 | 37 | 61 | 92 | 125 |
| Modelo de Gawin et al.[34] | ||||||||||
| Presión máxima (Mpa) | − | 3,97 | 4,00 | 3,66 | − | − | 0,88 | 0,98 | 1,00 | − |
| Tiempo pico (min) | − | 90 | 115 | 140 | − | − | 60 | 85 | 105 | − |
| Modelo de Di Capua et al.[35] | ||||||||||
| Presión máxima (Mpa) | − | 3,91 | 3,91 | 3,63 | − | − | − | − | − | − |
| Tiempo pico (min) | − | 97 | 120 | 140 | − | − | − | − | − | − |
| Modelo E1 | ||||||||||
| Error presión máx (%) | −130,6 | 10,0 | 10,3 | 3,3 | −129,4 | 10,6 | 9,7 | 18,5 | 23,3 | −193,9 |
| Error tiempo pico (%) | 30,6 | 20,6 | 16,7 | 2,8 | −44,4 | 40,0 | 22,1 | 21,3 | 14,4 | −56,3 |
| Modelo E2 | ||||||||||
| Error presión máx (%) | −56,2 | 7,6 | −4,1 | 3,3 | −191,8 | − | −13,5 | −17,3 | 8,0 | −94,0 |
| Error tiempo pico (%) | 44,4 | −11,1 | 7,4 | −6,1 | −44,4 | − | 22,9 | 23,8 | 14,4 | −38,9 |
| Modelo E1. Gawin et al.[34] | ||||||||||
| Error presión máx (%) | − | −4,5 | 0,0 | 8,5 | − | − | 5,4 | 9,7 | 16,7 | − |
| Error tiempo pico (%) | − | 14,3 | 23,3 | 22,2 | − | − | −26,3 | −9,7 | 2,3 | − |
| Modelo E2. Gawin et al.[34] | ||||||||||
| Error presión máx (%) | − | −7,3 | −15,9 | 8,5 | − | − | −18,9 | −30,0 | 0,0 | − |
| Error tiempo pico (%) | − | −20,0 | 14,8 | 15,2 | − | − | −25,0 | −6,3 | 2,3 | − |
| Modelo E1. Di Capua et al.[35] | ||||||||||
| Error presión máx (%) | − | −2,9 | 2,3 | 9,4 | − | − | − | − | − | − |
| Error tiempo pico (%) | − | 7,1 | 20,0 | 22,2 | − | − | − | − | − | − |
| Modelo E2. Di Capua et al.[35] | ||||||||||
| Error presión máx (%) | − | −5,7 | −13,3 | 9,4 | − | − | − | − | − | − |
| Error tiempo pico (%) | − | −30,0 | 11,1 | 15,2 | − | − | − | − | − | − |
Tras analizar los resultados obtenidos durante el proceso de validación del modelo presentado en este trabajo, se ha podido contrastar que las simplificaciones y las asunciones realizadas no han perjudicado los resultados de las simulaciones, pues los resultados obtenidos concuerdan satisfactoriamente tanto con los resultados experimentales como con los resultados de otros modelos de referencia recogidos en la literatura.
Precisamente estas simplificaciones han permitido obtener unos resultados aceptables para su aplicación práctica minimizando el coste de cálculo, que constituye uno de los principales problemas que limitan el uso de modelos similares. En ese sentido, se han podido reducir los tiempos de cómputo y se han obtenido tiempos de simulación en torno a los 3,5s de media para simulaciones de 180min y elementos de 12cm de espesor.
Por otra parte, la inclusión en el modelo del comportamiento del agua por encima del punto crítico ha ampliado el campo de aplicación del modelo, de manera que se ha podido simular todo el rango de temperaturas que el hormigón puede soportar en un incendio, y en las ecuaciones de balance se ha incorporado la masa de agua que se produce como consecuencia de la deshidratación de los componentes hidratados en el hormigón.
Asimismo, la inclusión de un mecanismo para determinar la influencia de la adición de las fibras de polipropileno en la relajación de las presiones internas permite utilizar el modelo como una herramienta válida para estimar el contenido de fibras más adecuado para prevenir el desconchamiento.
FinanciaciónSubvención BIA2012-37890 otorgada por el proyecto «PYRODESIGN – Modelado de los parámetros térmicos y cinéticos para la caracterización de la reacción al fuego de materiales» financiado con fondos FEDER.
Los autores queremos agradecer a Candesa por el proyecto «Análisis para la Mejora de la Resistencia Mecánica frente al Fuego de Hormigones Autocompactantes y de Alta Resistencia», a IECA por el proyecto «Análisis de parámetros asociados a la ocurrencia de spalling en hormigones de alta resistencia» y al Ministerio de Economía y Competitividad por la subvención BIA2012-37890 otorgada por el proyecto «PYRODESIGN – Modelado de los parámetros térmicos y cinéticos para la caracterización de la reacción al fuego de materiales» financiado con fondos FEDER.