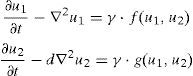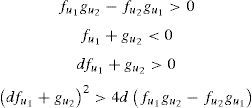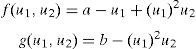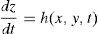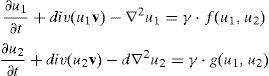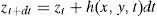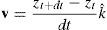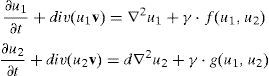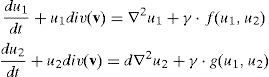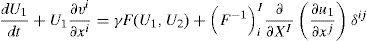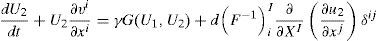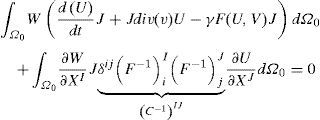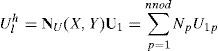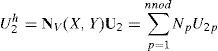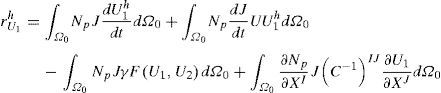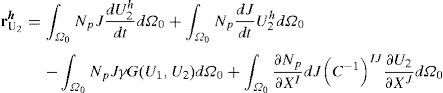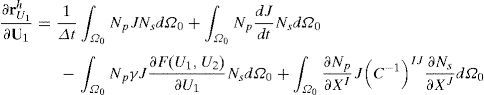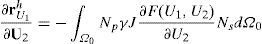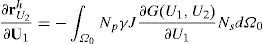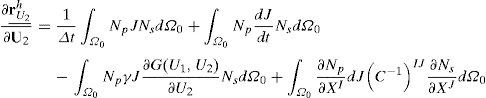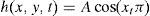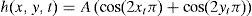En este artículo se desarrollan varios ejemplos numéricos sobre ecuaciones de reacción-difusión con dominio creciente. Para este fin se utiliza el modelo de reacción de Schnakenberg, con parámetros en el espacio de Turing. Por tanto se realizan ensayos numéricos sobre la aparición de los patrones de Turing en superficies que tienen alta tasa de deformación. Para la solución de las ecuaciones de reacción difusión se presenta un método de solución en superficies en 3 dimensiones mediante el método de los elementos finitos bajo el uso de la formulación lagrangiana total. Los resultados muestran que la formación de los patrones de Turing depende de las funciones de deformación de la superficie y la tasa a la cual se presenta el cambio de posición de cada punto del dominio donde se lleva a cabo la solución numérica. Estos resultados pueden esclarecer algunos fenómenos de cambio de patrón en la superficie de la piel de aquellos animales que exhiben manchas características.
In this work we have developed several numerical examples of reaction-diffusion equations with growing domain. For this purpose we have used the Schnakenberg reaction model with parameters in space Turing. Therefore numerical tests are performed on the appearance of Turing patterns on surfaces that have high deformation rate. For the solution of reaction diffusion equations is presented a solution method on surfaces in three dimensions using the finite element method under the use of the total Lagrangian formulation. The results show that the formation of Turing patterns depends on the features of surface deformation and the rate at which change in position of each point of the domain. These results can explain some phenomena of change of pattern on the surface of the skin of animals that exhibit characteristic spots.
Las ecuaciones de reacción-advección-difusión [1–13] (RAD) (1) y otros modelos más complejos, donde intervienen más especies o reactantes, poseen la habilidad para crear patrones espacio-temporales. Un caso particular de estos patrones son las inestabilidades de Turing[14,15], las cuales se caracterizan por la aparición de distribuciones de especies (patrones) estables en el tiempo e inestables en el espacio. Dada su especial respuesta, este tipo de modelos matemáticos han inspirado modelos para el estudio de problemas en muy diversos campos, tales como dinámica de fluidos [16], transferencia de calor [17,18], física de semiconductores [19], ingeniería de materiales [20], química [21], biología [7,8,14,22], dinámica de poblaciones [9,23,24], astrofísica [25], ingeniería biomédica [3,5,26] y matemáticas financieras entre otros.
El análisis de estos sistemas de reacción-difusión (RD), que presentan inestabilidad de Turing, se ha desarrollado tradicionalmente desde 2 marcos de trabajo: mediante análisis matemático [27] y mediante simulación numérica [14,15,28].
Desde el punto de vista analítico, los esfuerzos por entender el comportamiento de los sistemas de RD se han centrado en el estudio de la relación entre las bifurcaciones del espacio de parámetros y la formación de patrones. Desde esta perspectiva, se han estudiado los sistemas de RD mediante comparaciones de sub y super soluciones, teoría de grado, índice de Conley, teoría de puntos críticos y perturbaciones singulares para varios tipos de máximos principales [27]. Estos métodos han sido efectivos para el análisis de soluciones estacionarias y ondas viajeras [29,30]. También se han estudiado escenarios de bifurcaciones complejas en sistemas de RD aplicando métodos de teoría de grupo para problemas con simetrías [31,32]. Los esfuerzos en esta área del análisis matemático y, específicamente, de la dinámica de sistemas han permitido construir un gran conocimiento, el cual se ha comprobado y ampliado con el uso de la simulación numérica.
La simulación numérica de sistemas de RD ha permitido corroborar el conocimiento obtenido analíticamente sobre la formación de patrones, como en: Madzvamuse, [15,28] y Painter et al. [32,33], donde se han desarrollado ejemplos numéricos sobre la formación de patrones en dominios bidimensionales bajo consideraciones de dominio creciente. En [28] se reporta la aparición de diferentes estructuras que pueden variar entre sistemas de bandas, puntos y combinaciones de estos patrones en dominios con decrecimiento exponencial. En [34] se reporta la formación de patrones en presencia de campos convectivos con divergencia nula. Es así como se ha dedicado un gran esfuerzo al estudio de los patrones de Turing bajo la deformación del dominio de la solución y cuando esta sometido a campos de flujo. Es importante notar que el trabajo de Madzvamuse et al. [5,15,22,28,35] se ha centrado en el estudio del efecto que tiene el crecimiento uniforme sobre la dinámica de los patrones de Turing. Adicionalmente, importantes trabajos y aplicaciones se han desarrollado en el área de morfogénesis y movimiento celular [36]. A diferencia de estos trabajos, en este artículo se hace especial énfasis en el crecimiento no uniforme del dominio, con el objeto de estudiar el efecto de los gradientes de desplazamiento en la aparición y formación de los patrones de Turing. Además, en este trabajo se hacen ensayos numéricos con crecimiento perpendicular al plano, por lo que se puede controlar la evolución de cada punto del dominio.
Siguiendo un planteamiento similar al utilizado en [35,36], se utiliza el modelo de reacción de Schnakenberg [14] con parámetros en el espacio de Turing para simular la aparición de los patrones en superficies que tienen alta tasa de deformación. Para la solución de las ecuaciones de reacción difusión se presenta un método de solución en superficies en 3 dimensiones mediante el método de los elementos finitos bajo el uso de la formulación lagrangiana total.
El artículo está organizado como sigue: en primer lugar se muestran las ecuaciones de reacción difusión y las condiciones necesarias para generar patrones de Turing, luego se muestra el procedimiento de solución de las ecuaciones no lineales resultantes. Posteriormente se presentan los ejemplos numéricos para diferentes tipos de patrones. Por último se presenta la discusión y conclusiones.
2Materiales y métodos2.1Sistema de reacción-difusiónUn sistema de reacción difusión (RD) puede controlar la formación de los patrones siempre que sus parámetros reactivos y difusivos se encuentren en el espacio de Turing [14]. Para estudiar los patrones de Turing, se inicia con la definición de un sistema de RD, para 2 especies, dado por (1):
donde u1y u2 son las concentraciones, en su forma adimensional, de las especies químicas presentes las ecuaciones (1), d es el coeficiente de difusión adimensional y ( es una constante de adimensionalización. Por su parte, f y g, son las funciones de reacción que se presentan en cada una de las ecuaciones (1). Estas funciones tienen, en este artículo, un carácter no lineal y tienen una participación importante en la formación de los patrones de Turing.Turing [37] en su libro «The chemical basis of morphogenesis» desarrolló las condiciones necesarias para la formación de patrones espaciales a partir de la ecuación (1). Las condiciones para la formación de patrones determinan el espacio de Turing dado por las siguientes restricciones (2):
donde fl y gl indican las derivadas de las funciones de reacción con respecto a las variables de concentración, por ejemplo fu=∂f∂u[14]. Estas condiciones (2) están evaluadas en el punto de equilibrio que se obtiene haciendo f(u1,u2)0=g(u1,u2)0=0.Las ecuaciones (1) y sus restricciones (2) permitieron el desarrollo de una rama de investigación de los sistemas dinámicos [14]: las inestabilidades de Turing. La teoría acerca de los patrones de Turing ha permitido explicar la formación de patrones biológicamente complejos, como las manchas que se encuentran en la piel de algunos animales [38,39] y en problemas de morfogénesis [40], entre otros. Además, recientemente se ha comprobado, experimentalmente, que el comportamiento de algunos sistemas RD generan patrones de ondas viajeras y patrones espaciales estables [41–43].
Las ecuaciones (1) contienen términos reactivos (f(u1, u2)yg(u1, u2)) que tienen una importante contribución en la formación de los patrones de Turing. En este artículo, las ecuaciones que se han utilizado para el término reactivo son las de Schnakenberg [14,28] dadas por:
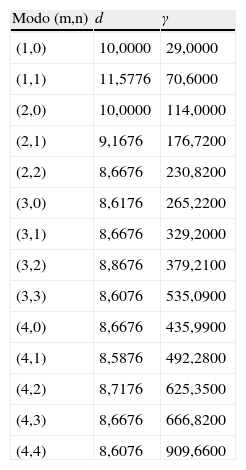
Donde a y b son parámetros adimensionales del modelo. Los puntos de estado estable están dados por u1,u20=a+b,ba+b2. Aplicando las restricciones (2) al modelo (1) en el punto de estado estable u1,u20 se obtiene un conjunto de restricciones que permiten establecer el sitio geométrico de los parámetros en el espacio de Turing [14,28].Haciendo uso del análisis de estabilidad lineal [14,15,28], se pueden calcular los valores de los parámetros adimensionales d y γ, requeridos para la formación de patrones de Turing bajo el modelo de RD. El cálculo de estos parámetros se hace mediante el uso de las ecuaciones (2). En primer lugar se fijan los valores a=0,1 y b=0,9; luego, con las desigualdades descritas en (2) se obtienen intervalos para d y γ. Por último, en estos intervalos se eligen valores particulares, con el objeto de cumplir los requisitos de formación de patrones específicos, como se describe en la tabla 1. Estos patrones pueden ser identificados por los correspondientes números de onda, tal como los que se mencionan en la tabla 1.
Modos de vibración (m, n) para diferentes valores de d y γ del modelo de Schnakenberg con valores constantes a=0, 1 y b=0, 9 [28]
| Modo (m,n) | d | γ |
| (1,0) | 10,0000 | 29,0000 |
| (1,1) | 11,5776 | 70,6000 |
| (2,0) | 10,0000 | 114,0000 |
| (2,1) | 9,1676 | 176,7200 |
| (2,2) | 8,6676 | 230,8200 |
| (3,0) | 8,6176 | 265,2200 |
| (3,1) | 8,6676 | 329,2000 |
| (3,2) | 8,8676 | 379,2100 |
| (3,3) | 8,6076 | 535,0900 |
| (4,0) | 8,6676 | 435,9900 |
| (4,1) | 8,5876 | 492,2800 |
| (4,2) | 8,7176 | 625,3500 |
| (4,3) | 8,6676 | 666,8200 |
| (4,4) | 8,6076 | 909,6600 |
Para deformar la superficie donde se lleva a cabo se solución de las ecuaciones (1) se utilizaron las ideas sugeridas en [44–46]. Con el objeto de estudiar el efecto de la deformación no uniforme del dominio, se desplaza cada punto, con diferente velocidad, en dirección perpendicular al plano xy. Por tanto, la ecuación de desplazamiento normal esta dada por (4):
Donde h(x, y, t) es una función que determina la velocidad de desplazamiento. De esta forma, la velocidad de cada punto de la superficie esta dada por v=h(x,y,t)kˆ, donde kˆ es el vector unitario en dirección z (perpendicular al plano).Al incluirse el término de crecimiento de la superficie [ecuación (4)], se modifican las ecuaciones (1), donde se presenta un nuevo término que tiene en cuenta la convección y la dilatación del dominio dado por:
Donde el término nuevo div(uiv) incluye la convección y dilatación que se debe al crecimiento del dominio.Para solucionar el RD convección descrito en (5) se utiliza el método de los elementos finitos [47] y el método de Newton-Raphson [48] para solucionar el sistema no lineal de ecuaciones en derivadas parciales que se derive de la formulación. La imposición del campo de crecimiento sobre la superficie se hace mediante la solución de la ecuación (4), con lo que se obtiene la nueva configuración (actual) y el campo de velocidades que se incluirá en el problema de RD.
En primer lugar se muestra la solución de las ecuaciones de reacción difusión mediante el método de los elementos finitos.
Para calcular el movimiento de la malla y la velocidad a la cual se deforma el dominio se utiliza la ecuación (4), la cual se integra mediante el método de Euler, dado por [26]:
Donde zt+dt y zt son la configuración de la superficie en el estado t y t+dt. Por tanto la velocidad se obtiene mediante (7):Donde el término de velocidad tiene dirección y magnitud que depende del punto material de la superficie S.2.3Solución del sistema de reacción-convección-difusiónLa formulación del sistema RD incluyendo el transporte convectivo se puede escribir como (8) [14]:
Donde u1y u2 son las variables químicas del RD. Esta ecuación también se puede escribir en términos de la derivada total (9) [14]:Donde se debe tener en cuenta que dudt=∂u∂t+v⋅grad(u)[49,50].Según como se describe en [49] se llega a que, el RD convección en la configuración inicial, o de referencia Ω0 [con coordenadas materiales X(x)], está dada por la siguiente ecuación escrita en términos de las coordenadas materiales y con notación indicial [49]:
Donde U1y U2 son las concentraciones de cada una de las especies en la configuración inicial Ω0, esto es, U(X, t)=u(x(X, t), t). Además, F−1Ii es el inverso del gradiente de deformación dado por FIi=∂xi∂XI[3], xi son las coordenadas actuales (en cada instante de tiempo) y XI son las coordenadas iniciales (de referencia, donde se realizarán los cálculos) [49,50].Multiplicando la ecuación (10) por una función de ponderación W e integrando en el dominio Ω0 se obtiene la forma débil general (11) [47]:
Donde U es cualquiera de las 2 especies en estudio (U1 o U2), W es la función de peso (o ponderación), J es el jacobiano (y es igual al determinante del gradiente de deformación F) y C-1 es el inverso del tensor Cauchy – Green por la derecha [47,48].En el caso de la formulación lagrangiana total, el cálculo se realiza, siempre, en la configuración inicial de referencia Ω0. La integración temporal se lleva a cabo mediante el método de Backward-Euler, el cual es estable para problemas parabólicos [47]. En este caso, todas las variables están calculadas en el nuevo tiempo. Además, gracias a la no linealidad se utiliza el método de Newton Raphson para la solución numérica. Por tanto, la solución del sistema (10a) y (10b) se inicia con la discretización de las variables U1 y U2 (calculadas en el tiempo t) mediante (12) [47]:
donde nnod es el número de nodos, U1 y U2 son los vectores que contiene los valores de U1y U2 en los puntos nodales y el superíndice h indica la discretización de la variable en elementos finitos. Mediante la elección de las funciones de peso igual a las funciones de forma (Galerkin Estándar) se obtienen los vectores residuo del método de Newton-Raphson dado por [47] (13):Con p=1,…, nnod. Donde rU1h y rU2h son los vectores residuos que están calculados en el nuevo tiempo. Se debe notar que, dU1hdt=U1h(t)−U1h(t−Δt)Δt, dU2hdt=U2h(t)−U2h(t−Δt)Δt, U1h=U1h(t) y U2h=U2h(t), donde se han omitido los superíndices izquierdos en las ecuaciones (12) y (13) para facilidad de lectura. Por su parte, cada una de las posiciones (entradas) de la matriz jacobiana está dada por (14):
Donde J es el determinante del gradiente de deformación, C-1 es el inverso del tensor de Cauchy-Green por la derecha y p,s=1,…, nnod e I,J=1,…,dim, donde dim representa la dimensión en la cual se resuelve el problema. Por tanto, utilizando las ecuaciones (13) y (14) se puede implementar el método de Newton-Raphson para solucionar el sistema de reacción-difusión utilizando su descripción material. En este sentido se debe anotar que la integración de (13) y (14) se hace sobre la configuración inicial [49]. Una deducción detallada de las ecuaciones se puede encontrar en [49].2.4Aspectos de la implementación computacionalPara implementar el modelo de reacción-difusión en elementos finitos se utiliza la formulación antes descrita. Es importante anotar que, aunque la superficie se encuentra orientada en el espacio 3D, los cálculos numéricos se hacen en 2D. Para este objetivo, se encuentra la normal a cada elemento (Z’) y se ubican los ejes primos (X’Y’) formando un plano paralelo al plano del elemento (fig. 1). Para enmallar la geometría se utilizan elementos triangulares de primer orden con 3 nodos. Por tanto, el cálculo se simplifica pasando de un sistema 3D a un sistema bidimensional donde se soluciona los modelos de reacción-difusión en cada instante de tiempo. La relación existente entre los ejes X’Y’Z’ y XYZ se puede obtener mediante una matriz de transformación T [49].
Para solucionar el sistema de ecuaciones resultantes del método de los elementos finitos con el método de Newton-Raphson se hizo un programa en FORTRAN y se solucionaron los siguientes ejemplos en un Laptop de 4096 MB en RAM y 800 MHz de velocidad de procesador.
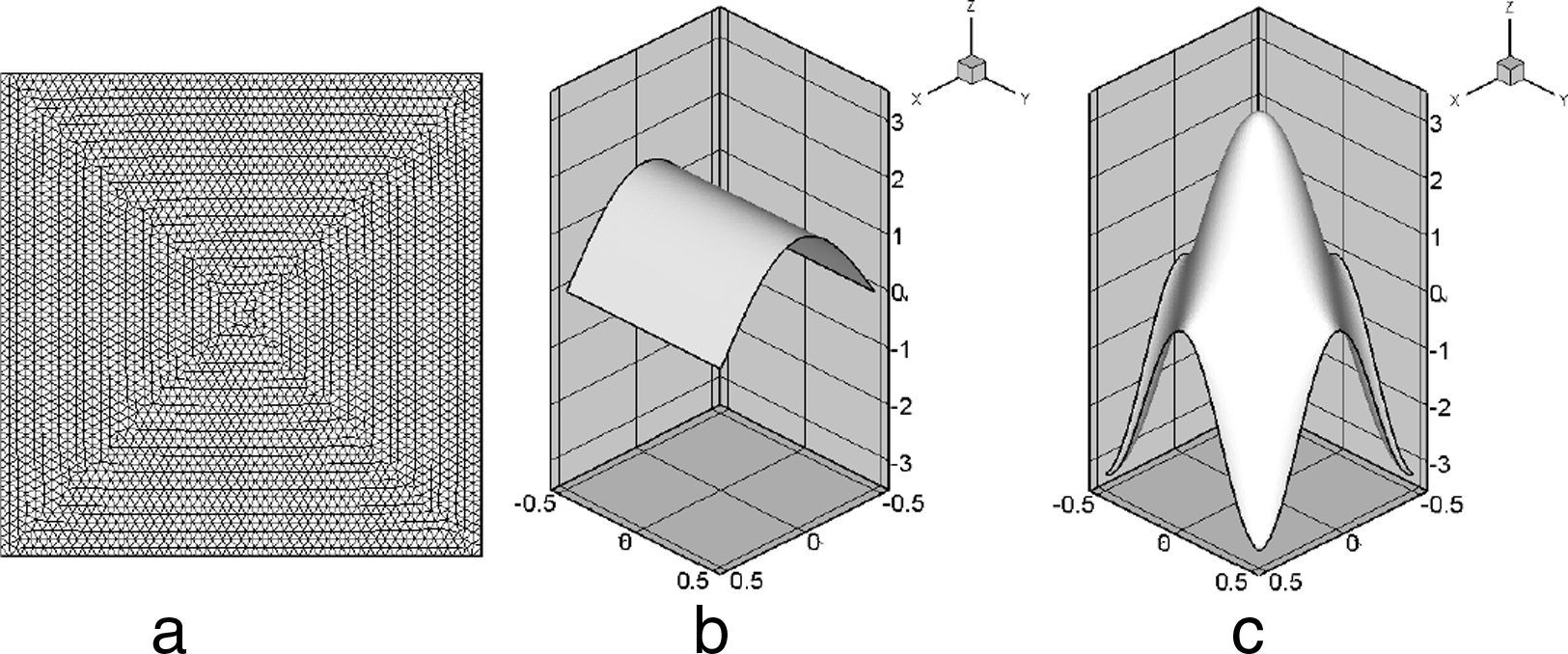
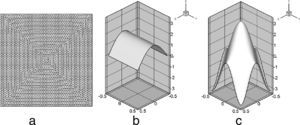
Para llevar a cabo la deformación del dominio se han utilizado las ecuaciones que se describen a continuación (fig. 2):
Deformación senoidal con una oscilación dado por (ver fig. 2b)
con un máximo localizado (ver fig. 2c):Cada una de estas ecuaciones se puede ver representada en la figura 2.
3Ejemplos de aplicación y resultados numéricosTodas las simulaciones se han hecho con un paso de tiempo Δt=0, 05. El tiempo final de la simulación es t=80, 0 adimensional. La malla que se utilizo se muestra en la fig. 2, y contiene 2.944 nodos y 5.686 elementos.
3.1Primer conjunto de parámetrosSe han hecho 2 tipos de simulaciones, según las ecuaciones (15) y (16). En el primer conjunto de parámetros que se ha utilizado esta dado por a=0, 1, b=0, 9, γ=29, 0yd=10, 0, para el sistema de reacción-difusión y A=0,02 para las ecuaciones (15) y (16).
La deformación se lleva a cabo mediante el movimiento de los nodos según un sistema de ecuaciones como los descritos en (15) y (16) (fig. 2). Para la fila A se utiliza la ecuación (15), es decir se utiliza una función senoidal con una oscilación. En la fila B se utiliza la ecuación (16), es decir con un valor máximo en la función de deformación.
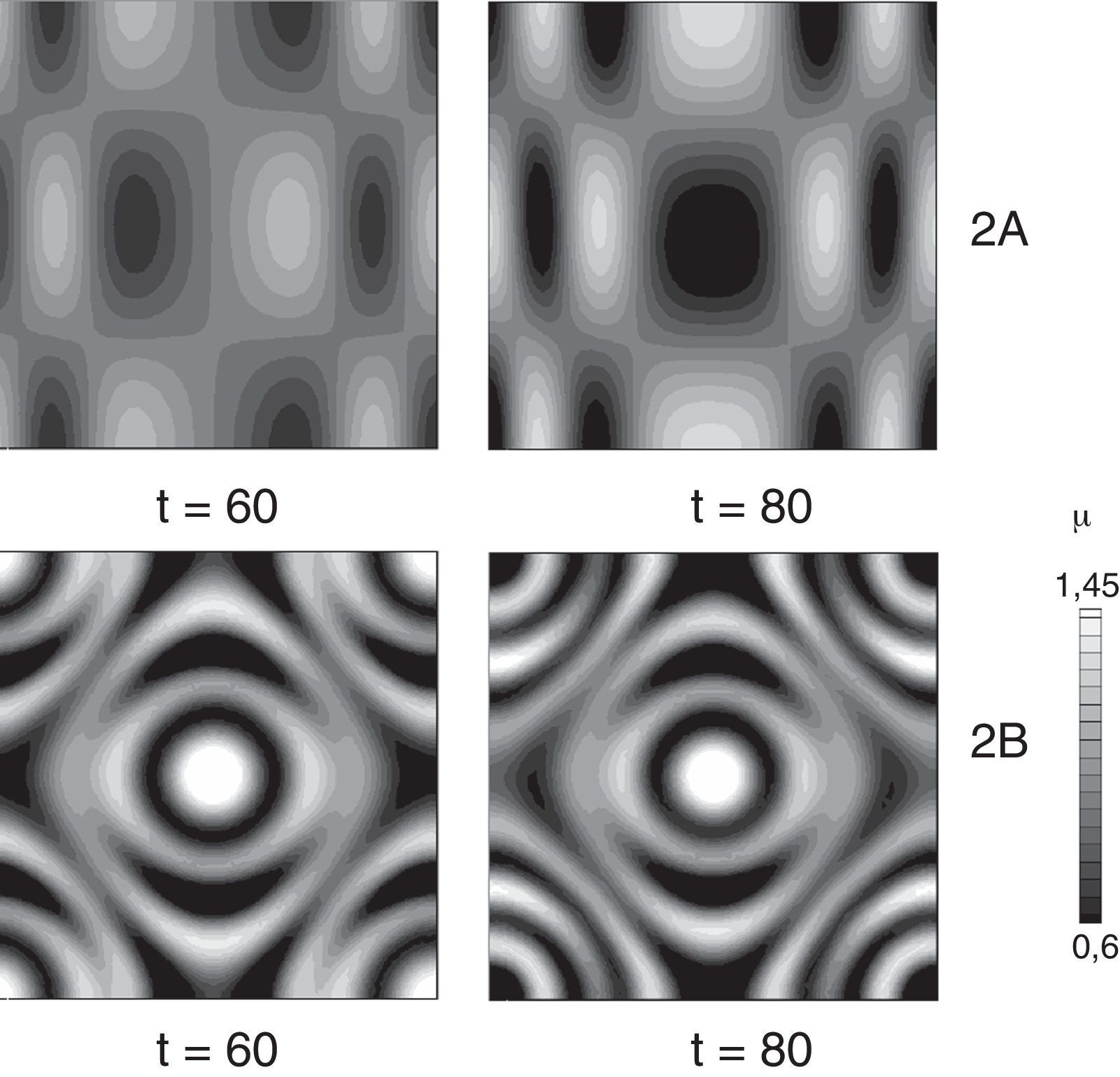
Con la tabla 1, se puede establecer que estos parámetros dan un modo de onda (1,0) [28]. En la figura 3 se observa la formación del patrón de onda (1,0). Se puede notar la formación de un patrón con alta concentración en la parte inferior y baja concentración en la parte superior. Nótese que existe una alta deformación en la parte central del dominio (fig. 2).
En la fila 1B, de la figura 3, se muestran los resultados según la deformación descrita por la ecuación (16). Nótese que, en t=60, la concentración disminuye en el centro del dominio, donde se presenta la mayor deformación (fig. 2). En el siguiente instante de tiempo (t=80) se forma un halo de baja concentración alrededor de aquellas zonas de mayor gradiente de deformación. Se debe advertir que no se llega al estado estable, por tanto se tiene un cambio permanente en los patrones debido a la deformación de la superficie.
3.2Primer conjunto de parámetrosSe han hecho 2 tipos de simulaciones, según las ecuaciones (15) y (16). En el primer conjunto de parámetros que se ha utilizado esta dado por a=0, 1, b=0, 9, γ=230, 82yd=8, 6676, para el sistema de reacción-difusión y A=0,02 para las ecuaciones (15) y (16).
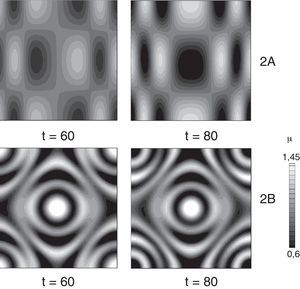
En la fig. 4 se presentan los resultados para un conjunto de parámetros que forman patrones de Turing (2,2), según la tabla 1[28]. En la fila 2a) [con deformación según la ecuación (15)], en t=60, se observa la formación de un patrón con modo de onda (2,2). Conforme pasa el tiempo se establece un patrón con un mínimo en el centro del dominio. En la parte lateral derecha e izquierda se forman manchas con mayor cercanía, más estrechas. En la figura 2B [que se deforma según la ecuación (16)] se forman manchas de alta concentración en el centro y un conjunto de anillos que oscilan entre baja y alta concentración.
4Discusión y conclusionesEn este artículo se utilizó el método de los elementos finitos para solucionar un sistema de ecuaciones de reacción difusión de carácter no lineal. Para estudiar la versatilidad del método se desarrollaron varios ejemplos de reacción-difusión, con un sistema reactivo del tipo Schnakenberg. El sistema no lineal se ha resuelto mediante el método de Newton Raphson. Los parámetros del modelo cumplen las restricciones del espacio de Turing, por tanto, los patrones que se obtienen en la solución exhiben inestabilidades espaciales, denominadas: de Turing.
En este trabajo se logró modelar la deformación de superficies en donde se desarrolla el proceso de reacción y difusión, similar a lo que ocurriría en, por ejemplo, la epidermis de una animal, donde un proceso reactivo permite la formación de manchas características de la piel de algunas especies. Para este fin se utilizó la formulación de mecánica de medio continuo que permite aproximar la solución mediante un esquema lagrangiano total. En este método se utilizó la configuración de referencia [o indeformada (1)] para llevar a cabo los cálculos numéricos en cada instante de tiempo. Esta formulación permite generalizar la metodología propuesta por Madzvamuse et al. [38,39], en donde se desarrolla un modelo de movimiento de malla para problemas bidimensionales planos. En este artículo se logra ampliar dicha formulación para cualquier movimiento espacial de una superficie en deformación.
De los resultados (figs. 3 y 4) se puede concluir que debido a la deformación de la superficie se pueden obtener patrones que no corresponden a aquellos predichos por la teoría de espacios de Turing (ver referencia [28] y tabla 1). La distribución de concentración en cada ejemplo sigue el patrón del movimiento de la malla. En este sentido se pierde el efecto del sistema reacción difusión en el espacio de Turing y se obtienen patrones que tienen máximos (o mínimos) en aquellas zonas de mayor (o menor) desplazamiento de los puntos del dominio. Este resultado puede explicar porque en algunas zonas de la piel de aquellos animales que exhiben manchas en su dermis puede cambiar el patrón superficial, o, inclusive desaparecer.
Estos resultados pueden compararse con los fenómenos que ocurren en la epidermis de los animales que presentan patrones especiales en su piel. Por tanto se puede especular que en aquellas zonas del cuerpo donde se presenta una gran deformación de la piel se puede perder los patrones superficiales y las manchas características. Por el contrario, en zonas de baja deformación pueden cambiar los patrones presentando manchas localizadas diferentes al resto de la distribución de manchas en la piel.