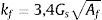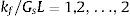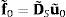Respuesta dinámica de edificaciones producida por campos de ondas incidentes considerando la interacción suelo-estructura

Resumen

En este artículo se presentan 2 metodologías basadas en las formulaciones del Método de los Elementos de Contorno y del Método de los Elementos Finitos para estudiar el efecto de la interacción suelo-estructura en el comportamiento dinámico de edificaciones. Se ha estudiado la respuesta de un edificio de 3 plantas producida por un campo de ondas incidente con los 2 métodos propuestos. Los resultados obtenidos presentan un buen grado de acuerdo entre ellos. A partir de estos resultados se ha validado un modelo aproximado para estudiar este tipo de problemas y se han examinado diferentes tipologías de edificaciones. Las conclusiones alcanzadas muestran que la respuesta global de las estructuras se debe a la deformación de los forjados y depende de su superficie, de las condiciones de apoyo y del acoplamiento con los forjados de la misma planta. Del mismo modo, se ha observado un acoplamiento del comportamiento de pilares y forjados cuando las rigideces de ambos son similares.

Abstract

This paper presents 2 methodologies based on the Boundary Element Method and the Finite Element Method to study soil-structure interaction effect on building behaviour. A 3-story building response induced by an incident wave field is studied using both methods. The results obtained show a good agreement. Then, a simplified model is validated from these methods and several buildings are analysed. Conclusions show that structural responses are due to floor deformation, and depend on their area, support conditions and coupling. A coupling between floors and columns when both elements have similar stiffness is also observed.

1

Introducción

Las vibraciones y el ruido rerradiado en edificaciones como consecuencia del tráfico, de instalaciones industriales y de procesos de construcción son 2 de los aspectos que originan mayor malestar en las personas. Este problema se divide en la emisión de las vibraciones, la propagación de las ondas en el suelo y la inmisión de los campos de ondas incidentes en las edificaciones. El grado de afección depende de la distancia a la fuente de vibraciones, de la intensidad de estas y de las propiedades dinámicas del terreno. Además, las características estructurales de la edificación determinan los niveles de vibración alcanzados. Teniendo en cuenta que dichos niveles pueden ser elevados, es necesario analizar este fenómeno y adoptar medidas correctoras [1].

El estudio de la inmisión de vibraciones en edificaciones requiere modelos numéricos que permitan representar adecuadamente edificios complejos y modelizar los efectos de la interacción suelo-estructura. Los modelos numéricos basados en las formulaciones del Método de los Elementos de Contorno (MEC) [2] y del Método de los Elementos Finitos (MEF) [3,4] permiten estudiar con rigor este tipo de problema. El MEC está especialmente indicado para el análisis de la propagación de ondas en el suelo [5] al considerar su carácter semi-infinito y cumplir implícitamente la condición de radiación de Sommerfeld [6]. Por otra parte, el MEF resulta muy útil para describir el comportamiento dinámico de las estructuras y tener en cuenta efectos no lineales [7–9].

En los últimos años, diferentes autores han estudiado la respuesta dinámica de edificios a consecuencia de ondas incidentes. Los modelos desarrollados se diferencian en su complejidad y en la forma en la que se estudian los mecanismos de emisión, de propagación y de inmisión. Varios autores han investigado las vibraciones en elementos estructurales simples. Auersch [10] y Jean y Villot [11] estudiaron vigas de cimentación y muros; Cryer [12], Talbot [13] y Hassan [14] analizaron forjados, muros y edificios, considerándolos con longitud infinita; Meinhardt [15] y Auersch [16] desarrollaron modelos suelo-forjado y suelo-muro-forjados; las tesis de Breitsamter [17] y Molzberger [18] presentaron modelos más complejos; Appel [19] y Ropars [20] desarrollaron algoritmos simplificados de acoplamiento suelo-estructura para calcular edificaciones complejas con programas MEF comerciales. También han empleado métodos simplificados para reducir el coste computacional de los análisis y para identificar claramente los fenómenos y principios de la interacción suelo-estructura; Pyl [21] y Fiala [22] investigaron el comportamiento de edificaciones con modelos acoplados MEC-MEF.

En este artículo se presentan 2 métodos basados en la formulación tridimensional MEC-MEF en los dominios del tiempo y de la frecuencia que permiten obtener la respuesta de edificios sometidos a ondas incidentes. Además, se evalúa la exactitud de un método simplificado de interacción suelo-estructura presentado por Auersch [16], estudiándose el grado de acuerdo entre los resultados obtenidos con este método simplificado y con los modelos MEC-MEF. Por último, se presentan resultados obtenidos en edificaciones singulares y se estudia la influencia de la tipología estructural.

2

Modelos numéricos de interacción suelo-estructura

Los modelos numéricos propuestos para el análisis elastodinámico de problemas de interacción suelo-estructura se basan en la descomposición de un dominio en 2 subdominios representados mediante el MEC y el MEF. El acoplamiento de las ecuaciones de ambos métodos requiere que se satisfagan las condiciones de equilibrio de fuerzas y de compatibilidad de desplazamientos en la interfase entre los 2 subdominios.

El MEC se utiliza para representar el carácter semi-infinito del suelo, debido a que la condición de radiación se satisface implícitamente. Las estructuras se modelizan mediante el MEF, utilizando elementos viga de Euler-Bernoulli para la discretización de vigas, pilares y pilotes, y elementos placa para la representación de forjados, muros y losas de cimentación. La respuesta de la estructura se estudia en régimen de comportamiento lineal.

2.1

Formulación MEC-MEF en el dominio del tiempo

La ecuación de equilibrio del MEF en el dominio del tiempo se expresa de la siguiente forma [3]:

donde M, C y K son las matrices de masa, amortiguamiento y rigidez del sistema, respectivamente. Los vectores uⁿ, u˙n y u¨n representan los desplazamientos, las velocidades y las aceleraciones nodales, respectivamente, y fⁿ las fuerzas externas aplicadas, en el paso de tiempo n.

La ecuación (1) se expresa de una forma más compacta definiendo una matriz de rigidez dinámica D y agrupando la influencia de los pasos anteriores en el término independiente fⁿ⁻¹[23]:

La integración del sistema de ecuaciones se realiza mediante el algoritmo de Newmark GN22 [3,23].

Por otra parte, la ecuación del MEC que permite describir el comportamiento dinámico del suelo en el domino del tiempo es la siguiente [5]:

donde, uⁿ y pⁿ son los vectores de desplazamientos y de tracciones al final del paso de tiempo n, respectivamente, y Hⁿⁿ y Gⁿⁿ son las matrices del MEC. El sumatorio del término de la derecha representa la influencia de los pasos de tiempo entre m = 1 y m = n − 1.

En este trabajo se utiliza la solución fundamental del espacio completo [6], discretizando la superficie libre del suelo más allá de la zona de interés para evitar efectos espurios relacionados con la difracción de ondas en el contorno [2,24].

Aplicando las condiciones de compatibilidad de desplazamientos y de equilibrio de fuerzas en los nodos de la interfase, se obtiene un sistema global de ecuaciones MEC-MEF:

donde el subíndice c hace referencia a los nodos del dominio asociados a la interfase, y los subíndices b y f al resto de nodos de los subdominios representados con elementos de contorno y finitos, respectivamente. La matriz Gˆ se define como Gˆ=G∑a=1A∫ΓNTNdΓ−1, siendo N las funciones de forma y extendiéndose el sumatorio sobre todos los elementos A que contienen al nodo correspondiente [25].

La resolución de la ecuación (4) requiere utilizar una discretización espacial y temporal adecuada para garantizar la estabilidad del modelo propuesto. La formulación propuesta del MEC en el dominio del tiempo es estable para valores parámetro β = c_sΔt/Δl comprendidos entre 0,3 y 1,2, donde c_s es la velocidad de propagación de las ondas S en el suelo, Δt es el paso de tiempo y Δl es la distancia característica entre nodos de un elemento [8].

La ecuación (4) describe el comportamiento dinámico del sistema suelo-estructura, donde las incógnitas en los nodos de la interfase son los desplazamientos y las fuerzas nodales; en el resto de nodos depende de las condiciones de contorno del problema. Una vez se ha obtenido la evolución temporal de los desplazamientos, el contenido en frecuencia de la respuesta se obtiene aplicando la Transformada Rápida de Fourier (FFT, en sus siglas en inglés).

2.2

Formulación MEC-MEF en el dominio de la frecuencia

La matriz de rigidez dinámica del MEF en el dominio de la frecuencia puede representarse de la siguiente forma [26]:

donde las matrices M, C y K tienen el mismo significado que en la formulación en el dominio del tiempo.

La formulación del MEC en el dominio de la frecuencia permite obtener una matriz de rigidez del suelo [10,27]. Los desplazamientos y las tracciones de la superficie del suelo se pueden expresar a partir de 5 funciones escalares f_k de la siguiente forma:

donde

siendo c_p y c_s las velocidades de propagación de las ondas P y S en el suelo, respectivamente, ω la frecuencia angular y r la distancia entre el punto de aplicación de la carga y el punto de observación. Estas funciones representan los desplazamientos longitudinales y las tracciones normales causadas por una carga longitudinal y, del mismo modo, los desplazamientos transversales y las tracciones coplanarias producidos por una carga transversal. El valor de las constantes a₁, a₂, a₃ y a₄ puede encontrarse en las referencias [10,27]. A partir de estas expresiones se obtienen las matrices H˜ y G˜ del MEC en el dominio de la frecuencia. La matriz de rigidez dinámica del suelo D˜S se calcula como:

Las matrices de rigidez del MEC y del MEF se acoplan estableciendo las condiciones de compatibilidad y equilibrio en los nodos de la interfase, obteniéndose la siguiente expresión:

donde u˜ y f˜ son los desplazamientos y las fuerzas nodales en el dominio de la frecuencia, respectivamente, y los subíndices c y f tienen el mismo significado que en el apartado 2.1.

2.3

Método simplificado

Las formulaciones presentadas en los apartados anteriores permiten resolver con rigor problemas de interacción suelo-estructura. Sin embargo, cuando la modelización del edificio involucra un alto número de grados de libertad, el coste computacional de los modelos MEC-MEF puede ser elevado. Alternativamente, es posible usar un modelo simplificado de interacción. Este método consiste en introducir en el modelo MEF una serie de elementos muelle-amortiguador con propiedades k_f y c_f. Estos elementos representan el efecto de la interacción suelo-estructura y, en su conjunto, aportan una rigidez y un amortiguamiento equivalentes al efecto del terreno.

Pueden encontrarse diferentes aproximaciones para diversos sistemas de cimentación. En las referencias [16,28–30] se recogen correlaciones para cimentaciones basadas en zapatas continuas, grupos de zapatas, pilotes aislados y grupos de pilotes. Los valores de la rigidez y del amortiguamiento equivalente de la cimentación varían en función de la frecuencia de excitación. Sin embargo, la consideración de un valor constante permite simplificar el análisis.

En este trabajo se ha utilizado la siguiente correlación para cimentaciones superficiales [16]:

donde G_s y ρ_s son el módulo de elasticidad transversal y la densidad del suelo, respectivamente, y A_f el área de la cimentación.

Asimismo, en la sección 4, se ha usado la correlación presentada en la referencia [29] para cimentaciones pilotadas:

donde L y R son la longitud y el radio del pilote, respectivamente. La validez de esta correlación está limitada para pilotes rígidos (R/L = 0,005, …, 0,05), para los que la rigidez y el amortiguamiento equivalente son aproximadamente constantes.

De este modo, se puede caracterizar dinámicamente la edificación teniendo en cuenta de una forma simplificada la interacción con el suelo y utilizando únicamente el MEF. La respuesta de la estructura se obtiene directamente en el dominio de la frecuencia.

3

Ejemplo numérico: edificación solicitada por un campo de ondas incidentes

En esta sección se presenta la respuesta de una edificación producida por un campo de ondas incidentes que solicita la base de la estructura. Los resultados se han obtenido empleando las formulaciones descritas en la sección anterior, estudiándose la validez del modelo simplificado.

El campo de ondas incidentes es la respuesta de la superficie libre del suelo producida por una carga dinámica suponiendo que la estructura está ausente. En este trabajo, para evaluar la interacción suelo-estructura, se ha considerado un campo de ondas que se corresponde con una distribución uniforme de desplazamientos verticales en la interfase suelo-estructura. De esta forma, se estudia el comportamiento vertical de los forjados, de especial relevancia cuando se analiza la inmisión de vibraciones producidas por el tráfico ferroviario y por las actuaciones de construcción.

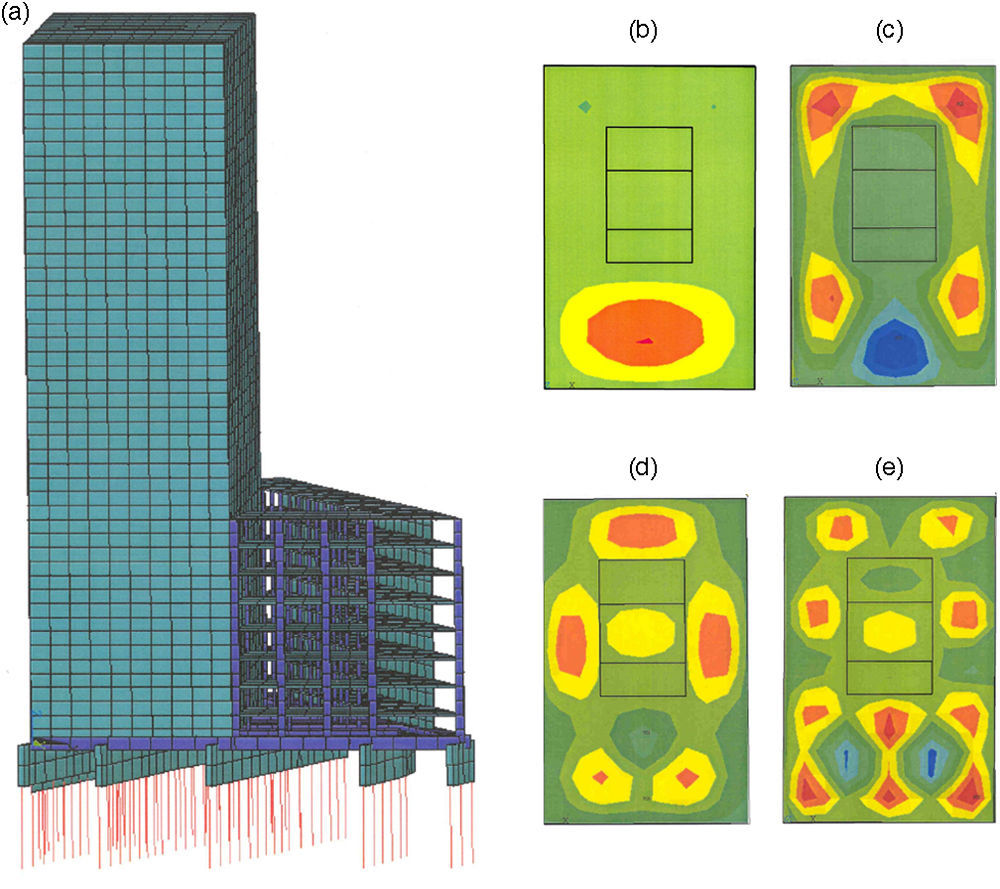
El edificio objeto de estudio está formado por 3 plantas de dimensiones 14,4 m × 10,8 m y altura 3 m (fig. 1). La estructura está constituida por 8 pilares por planta, de sección 0,3 m × 0,3 m y se encuentra reforzada por un núcleo central de 0,15 m de espesor. El sistema de cimentación se corresponde con una losa continua de h_f = 0,3 m de espesor. El material de la estructura es hormigón armado con las siguientes propiedades: módulo de Young, E_c = 30 × 10⁹ N/m², módulo de Poisson, ν_c = 0,2, y densidad, ρ_c = 2.500 kg/m³. El suelo sobre el que se encuentra la edificación se ha representado como un semiespacio homogéneo donde los valores de las velocidades de propagación de las ondas son: c_p = 300 m/s, c_s = 150 m/s y c_R = 140 m/s.

Figura 1.

Planta de una edificación de 3 plantas. Dimensiones y puntos de observación para cada planta: A_i, B_i, C_i, D_i, P_i y W_i (i = 1,2, 3).

La estructura se ha discretizado con elementos finitos utilizando un tamaño de elemento adecuado para obtener la respuesta dinámica del edificio con precisión hasta un valor máximo de la frecuencia f_max = 80 Hz. La longitud de onda mínima de las ondas de flexión en las plantas de la estructura es λ=2πD/ρchf4/fmax=3,6m, donde D=Echf3/12(1−νc2) es la rigidez a flexión de los forjados. El tamaño de los elementos (l = 0,6 m) se ha elegido considerando 6 elementos por longitud de onda. La validez del modelo está restringida al estudio de la respuesta global de la estructura y no permite obtener con exactitud la concentración de tensiones, por ejemplo, alrededor de los puntos de unión entre los pilares y los forjados.

El suelo se ha modelizado utilizando elementos de contorno cuadráticos de 9 nodos, con una distancia característica entre nodos Δl = 0,95 m. La discretización del semiespacio se ha extendido 10,8 m mas allá de la edificación. El paso de tiempo seleccionado para el análisis, Δt = 6 ×10⁻³ s permite resolver el problema con un valor mínimo del parámetro β igual a 0,47.

La edificación está solicitada por una distribución de fuerzas en la interfase suelo-estructura, obtenidas a partir de las siguientes expresiones en el dominio del tiempo y de la frecuencia, respectivamente:

donde u₀ = δ(t) y u˜0=1 representa un campo de desplazamientos uniforme.

En la figura 2 se muestra la amplificación de la respuesta del edificio, u/u₀, obtenida en diferentes instantes de tiempo mediante la metodología presentada en el apartado 2.1. Las mayores amplificaciones se producen por la deformación de las plantas, alcanzándose el nivel máximo en el forjado superior del núcleo central.

Figura 2.

Amplificación de la respuesta de una edificación de 3 plantas debida a un desplazamiento vertical de la base en diferentes instantes de tiempo: (a) t = 0,05 s, (b) t = 0,09 s, (c) t = 0,11 s y (d) t = 0,13 s.

En las figuras 3–5 se muestran las funciones de transferencia del sistema suelo-estructura, obtenidas a partir de las velocidades de vibración de la estructura, v, y del campo de ondas incidente, v₀. La respuesta de la edificación está gobernada por los modos de vibración asociados a la deformación local de los forjados de cada planta (fig. 2), determinados por la configuración de los muros y por los pilares que los soportan. En el núcleo central los forjados se encuentran apoyados en 3 de sus extremos, alcanzándose la máxima amplificación en el rango de frecuencias comprendido entre 20 y 30 Hz (figs. 3–5 (a)). Por el contrario, los forjados laterales que se encuentran soportados por 4 pilares exhiben un comportamiento resonante a 12 Hz (fig. 3–5 (c)). Del mismo modo, el resto de los forjados que están apoyados en una de las paredes del núcleo central y en 2 pilares tienen picos a las frecuencias de 15 Hz (figs. 3–5 (b)) y 12 Hz (figs. 3–5 (d)). Los forjados con frecuencias de resonancia similares presentan un comportamiento acoplado. Por otra parte, la amplitud de la respuesta de los pilares y del núcleo rigidizador es muy inferior al resto de puntos de la estructura (figs. 3–5 (e,f)).

Figura 3.

Funciones de transferencia producidas por un campo uniforme de ondas incidentes en los puntos (a) A_i, (b) B_i, (c) C_i, (d) D_i, (e) W_i y (f) P_i, de las plantas: baja (+), primera (▵), segunda (∘) y tercera (□). Modelo MEC-MEF dominio del tiempo.

Figura 4.

Funciones de transferencia producidas por un campo uniforme de ondas incidentes en los puntos (a) A_i, (b) B_i, (c) C_i, (d) D_i, (e) W_i y (f) P_i, de las plantas: baja (+), primera (▵), segunda (∘) y tercera (□). Modelo MEC-MEF dominio de la frecuencia.

Figura 5.

Funciones de transferencia producidas por un campo uniforme de ondas incidentes en los puntos (a) A_i, (b) B_i, (c) C_i, (d) D_i, (e) W_i y (f) P_i, de las plantas: baja (+), primera (▵), segunda (∘) y tercera (□). Modelo de interacción suelo-estructura simplificado.

En la tabla 1 se resumen los resultados obtenidos con los modelos utilizados en este artículo. Las diferencias en los resultados obtenidos con los modelos en el dominio del tiempo y en el dominio de la frecuencia están originadas por la consideración del amortiguamiento (amortiguamiento viscoso en el dominio del tiempo e histerético en el dominio de la frecuencia). Los resultados obtenidos con el modelo de interacción simplificado presentan un grado de acuerdo aceptable con los resultados obtenidos con los modelos completos.

Tabla 1.

Amplificaciones resonantes en los puntos A, B, C y D de la estructura: influencia de las propiedades dinámicas del suelo y de la cimentación.

Modelo	v/v0 (A)	f (A)	v/v0 (B)	f (B)	v/v0 (C)	f (C)	v/v0 (D)	f (D)	Diferencia
		[Hz]	[–]	[Hz]	[–]	[Hz]	[–]	[Hz]	[%]
Simplificado	6,5	26	4	12	9	13	6,5	15	9-44
Dominio tiempo	6	26	7	12	14,5	12	8	15	33-55
Dominio frecuencia	4,5	26	4,5	12	10	12	5,5	14	-
cs = 200 m/s	6	26	5,5	12	12	12	6	15	-
cs = 300 m/s	7,5	26	6	12	13	13	9	15	-
d = 0,3 m	6	26	4,5	12	10	12	5,5	15	-
d = 0,5 m	6,5	26	4	12	10	12	5,5	15	-
Zapata continua	2	10	5	11	7	11	5	14	-
Zapata	6	6	5,5	6	5	6	4,5	6	-
Sin núcleo	5	10	5,5	10	5,5	10	5	10	-

En la última parte de esta sección, se ha estudiado la influencia del suelo y del sistema de cimentación en el comportamiento de la edificación. Se han analizado 2 tipos de suelos con velocidades de propagación de las ondas S, c_s = 200 m/s, y c_s = 300 m/s. Asimismo, se han estudiado losas de cimentación de espesor d = 0,3 m y d = 0,5 m, zapatas aisladas y zapatas continuas. También se ha obtenido la respuesta del edificio sin considerar el núcleo rigidizador. Todos los resultados se han obtenido utilizando el modelo formulado en el dominio de la frecuencia (sección 2). Los resultados obtenidos se han presentado en la tabla 2.

Tabla 2.

Características de las edificaciones estudiadas: número de plantas (n), área por planta (A_E), relación pilares/muros por planta (α), área de los forjados (A_F), espesor de los forjados (d_F), velocidad de propagación de las ondas S en el terreno (c_s) y rigidez y amortiguamiento equivalente de la cimentación (k_f y c_f, respectivamente).

	Edificio 1	Edificio 2	Edificio 3	Edificio 4	Edificio 5
n	8	8	8	20	24
AE [m^2]	16,5 × 66	160	20 × 25	36 × 61	25 × 35
α	52/0	10/2	4/15	5/4	10/10
dF [m]	0,25	0,22	0,22	0,25	0,25
AF [m^2]	5,5 × 5,5	5,4 × 4,5	6 × 5	4,8 × 7,5	6 × 10
cs [m/s]	200	150	240	200	200
Cimentación	Pilote	Pilote	Losa	Losa	Pilote
Discretización [m]	0,9 − 1,0	9,0 − 1,1	1,5	1,0	1,7 − 2,5
kf [N/m]	1,8 × 10^8	3,0 × 10^10	9,1 × 10^9	4,1 × 10^10	1,1 × 10^11
cf [N/m]	7,2 × 10^8	1,7 × 10^10	4,5 × 10^9	3,0 × 10^9	1,5 × 10^9

Los resultados muestran un incremento de la respuesta de la estructura a medida que aumenta la rigidez del suelo, siendo el valor de las frecuencias de resonancia aproximadamente constante. La influencia del espesor de la losa de cimentación es más reducida, produciéndose solo un cambio significativo de la respuesta en el punto A. Por el contrario, los resultados obtenidos con los diferentes sistemas de cimentación considerados muestran una reducción tanto de las frecuencias de resonancia de los forjados como de la amplificación de la respuesta a medida que la rigidez de la cimentación es menor. Finalmente, el núcleo rigidizador también ocasiona un incremento de las frecuencias de resonancia.

En la siguiente sección se utilizará dicho método para obtener la respuesta de edificaciones con tipologías estructurales más complejas.

4

Comportamiento dinámico de edificaciones singulares

En esta sección, se presenta la caracterización dinámica de edificaciones singulares. Se han calculado las funciones de transferencia de las estructuras solicitadas por un campo uniforme de ondas incidentes en la base, empleando el modelo simplificado presentado anteriormente.

Se han analizado las respuestas de 5 edificaciones con diferentes tipologías, estudiándose la influencia de la superficie de los forjados y de las condiciones de apoyo. En la tabla 2 se presenta un resumen de las características de las edificaciones estudiadas, recogiéndose el número de plantas (n), la superficie de cada planta (A_E), la relación entre el número de pilares y de muros por planta (α) y la superficie (A_F) y el espesor (d_F) de los forjados. Además, se indica la velocidad de propagación de las ondas S en el suelo (c_s), el sistema de cimentación, los valores de la rigidez (k_f) y del amortiguamiento (c_f) equivalente de la cimentación, y el tamaño característico de la discretización utilizada en cada caso.

El primer edificio se corresponde con una estructura regular de 8 plantas sustentada únicamente por pilares. En la figura 6 se muestran los modos de vibración a 5 Hz y 13 Hz de dicha estructura. Debido a la tipología uniforme de la estructura, las funciones de transferencia presentan un comportamiento regular (fig. 7). La amplitud de la respuesta en torno a 6 Hz se incrementa conforme aumenta la altura de las plantas. Por el contrario, para frecuencias superiores se reducen las amplitudes con la altura. Los valores máximos de las funciones de transferencia se producen en el rango de frecuencias entre 10 Hz y 20 Hz, siendo próximos a v/v0=4.

Figura 6.

Modos de vibracion del edificio 1: (a) 5 Hz y (b) 13 Hz.

Figura 7.

Funciones de transferencia producidas por un campo uniforme de ondas incidentes en cada planta del edificio 1: sótano □, baja ∘, primera ▵, segunda +, tercera ×, cuarta ♦, quinta *, sexta ▿ y séptima ★.

La segunda edificación estudiada tiene también 8 plantas, pero en este caso con geometría triangular y sustentada por 11 pilares y un núcleo rigidizador (fig. 8 (a)). En la figura 8 (b) se muestran las funciones de transferencia de las plantas de la estructura. Los resultados obtenidos para cada planta presentan una tendencia similar, alcanzándose una amplificación máxima v/v0=8 en el rango de frecuencias comprendido entre 15 Hz y 20 Hz. Posteriormente, se obtiene un valor inferior a la unidad para frecuencias superiores a 25 Hz.

Figura 8.

(a) Modelización del edificio 2 y (b) funciones de transferencia producidas por un campo uniforme de ondas incidentes en cada planta: primera ∘, segunda ▵, tercera +, cuarta ×, quinta ♦, sexta *, séptima ▿ y octava ★.

El tercer edificio consta de 8 plantas soportadas, principalmente, por muros y una serie de pilares. En la figura 9 se representa uno de sus modos de vibración (20 Hz), observándose una resonancia más moderada que en los casos anteriores y un acoplamiento entre la deformación de los forjados y de los pilares. En la figura 9 (b) se muestra la respuesta de la planta superior, en la que el punto donde se alcanza la amplificación máxima coincide con un pilar de la edificación.

Figura 9.

(a) Modo de vibración a 20 Hz del edificio 3 y (b) detalle de la octava planta.

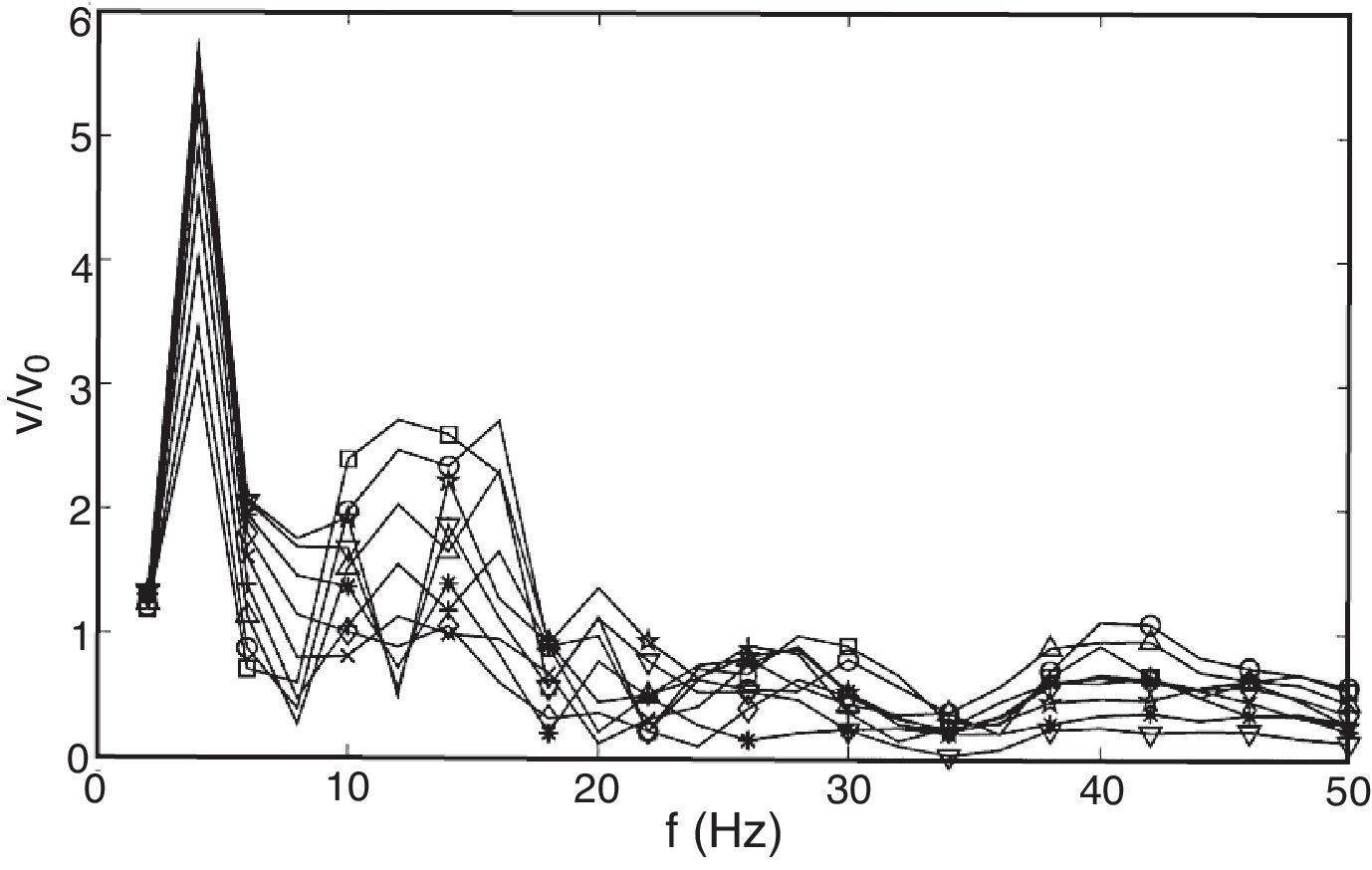
El cuarto edificio estudiado está compuesto por un cuerpo principal de 10 plantas y uno auxiliar de 20 plantas (fig. 10). El edificio está formado por 4 núcleos rigidizadores que albergan las escaleras. En este caso, el número de pilares y muros por plantas es similar. En la figura 10 se muestran la respuesta de la estructura 12 Hz y el comportamiento de la planta superior a 8 Hz. En ambos casos, los desplazamientos máximos se producen en las proximidades de los pilares. En la figura 11 se muestran las funciones de transferencia del cuerpo principal de 10 plantas. La respuesta de los forjados alrededor de las paredes de la edificación (fig. 11 (a)) presenta una componente dominante alrededor de 20 Hz. El valor v/v0 de la amplificación de dicha respuesta varía entre 4 y 6 para todas las plantas. Asimismo, la respuesta de los forjados alrededor de los pilares (fig. 11 (b)) presenta niveles máximos v/v0=6, aproximadamente a 20 Hz. Además, se observa una amplificación a 8 Hz asociada a la frecuencia de resonancia de la masa de los forjados sustentada por los pilares.

Figura 10.

(a) Modo de vibración a 12 Hz del edificio 4 y (b) respuesta a 8 Hz de la décima planta del edificio 4.

Figura 11.

Funciones de transferencia producidas por un campo uniforme de ondas incidentes del cuerpo principal del edificio 4 en forjados sustentados (a) sobre muro y (b) sobre pilares para las plantas: sótano □, baja ∘, primera ▵, segunda +, tercera ×, cuarta ♦, quinta *, sexta ▿, septima ★, octava□ y novena ∘.

La última estructura analizada se corresponde con una torre de 24 plantas, formada por un núcleo central y pilares. En la figura 12 se muestran la modelización del edificio y los modos de vibración de la planta superior. El primer modo de vibración se corresponde con la deformación de un forjado sustentado por 3 pilares, alcanzándose la amplitud máxima junto a los pilares del centro del forjado. El resto de modos se corresponde con la respuesta local de los forjados de acuerdo con la longitud de las ondas de flexión (λ∼1/f). La amplitud máxima de la respuesta, v/v0=6, se produce a la frecuencia de resonancia de 4 Hz (fig. 13). Se observa también una amplificación en el rango de frecuencias comprendido entre 10 Hz y 15 Hz, siendo sus valores inferiores a v/v0=3.

Figura 12.

(a) Modelización del edificio 6 y modos de vibración de la planta 24 a las frecuencias: (b) 4 Hz, (c) 10 Hz, (d) 14 Hz y (e) 20 Hz.

Figura 13.

Funciones de transferencia del edificio 6 en forjados sustentados sobre pilares, producidas por un campo uniforme de ondas incidentes para las plantas: primera □, tercera ∘, sexta ▵, noventa +, decimosegunda ×, decimoquinta ♦, decimoctava *, vigesimoprimera ▿ y vigesimocuarta ★.

Todos los edificios analizados presentan un comportamiento similar. Las funciones de transferencia presentan un nivel v/v0=1 para frecuencias próximas a 0 Hz y, posteriormente, se alcanzan las máximas amplificaciones a las frecuencias de resonancia de la estructura comprendidas entre 10 Hz y 30 Hz con una amplificación de la respuesta entre 3 y 7. Los edificios formados por pilares muestran un comportamiento resonante producido por el acoplamiento pilar-forjado a 4 Hz y 8 Hz. Por otra parte, las funciones de transferencia de las estructuras construidas sobre muros son más regulares y la atenuación a alta frecuencia es mayor.

5

Conclusiones

En este artículo se han presentado 2 métodos basados en las formulaciones MEC-MEF en los dominios del tiempo y de la frecuencia que permiten analizar problemas de interacción suelo-estructura. Además, se ha presentado un método simplificado que permite considerar la influencia del suelo con un coste computacional menor.

Se ha estudiado la respuesta de una edificación de 3 plantas solicitada por un campo uniforme de ondas incidentes en la base y los resultados obtenidos se han comparado con los 3 métodos. Los resultados muestran una correlación aceptable. Asimismo, se han considerado variaciones de esta estructura para evaluar la influencia de las propiedades dinámicas del suelo y del sistema de cimentación en la respuesta resonante de los forjados. Los resultados muestran una influencia baja de la rigidez del suelo cuando la rigidez de la cimentación es elevada, especialmente en el caso en que la estructura está cimentada sobre una losa continua. En otros casos, cuando se considera una cimentación por zapatas (aisladas o continuas) se produce una reducción de las frecuencias de resonancia y un incremento de la amplitud de la respuesta.

Los resultados obtenidos en edificaciones más complejas han permitido alcanzar las siguientes conclusiones:

• 1.

  Las frecuencias de resonancia dependen de las dimensiones de los forjados y de las condiciones de apoyo.

• 2.

  La respuesta de forjados acoplados de una misma planta se produce en un rango de frecuencias comprendido entre 10 Hz y 30 Hz, y no se observan picos dominantes.

• 3.

  En los modos de vibración de forjados sustentados por pilares existe un acoplamiento pilar-forjado. Las frecuencias de resonancia son menores y las amplificaciones que se producen son más elevadas que en los casos en que no existe dicho acoplamiento.

• 4.

  La respuesta dinámica de edificaciones con plantas sustentadas por pilares debe estudiarse empleando modelos que permitan representar con rigor el comportamiento acoplado de los forjados.

Agradecimientos

L. Auersch, A. Romero y P. Galvín han colaborado en la realización de este artículo. Auersch ha desarrollado los modelos formulados en el dominio de la frecuencia y ha obtenido los resultados presentados en la sección 4 con la ayuda de C. Meinhardt (ejemplo 3) y S. Said (ejemplo 4). También ha escrito las secciones correspondientes, así como la primera y última sección. Romero y Galvín han desarrollado el modelo numérico BEM-FEM formulado en el dominio del tiempo [8]. Con este modelo se han obtenido los resultados incluidos en la sección 3, durante una estancia de Romero supervisada por Auersch en el BAM.

El contenido de este artículo se encuentra enmarcado en los trabajos de investigación asociados al proyecto BIA2010-14843. El segundo y tercer autor agradecen el apoyo del Ministerio de Economía y Competitividad y del Centro Informático Científico de Andalucía (CICA). Romero agradece la financiación concedida por la Universidad de Sevilla y por la Consejería de Economía, Innovación, Ciencia y Empleo de la Junta de Andalucía, para la realización de una estancia en el BAM.