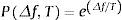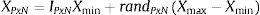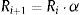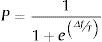Este trabajo propone el empleo de la técnica estocástica de optimización ASAM para sustituir el criterio de optimalidad utilizado dentro del método de optimización topológica propuesto por Andreassen. Para evaluar y validar el desempeño de las técnicas planteadas, se abordaron 3 problemas de elasticidad plana reportados en la literatura especializada. Cada problema fue analizado empleando el Método de Elementos Finitos (MEF) con 3 tipos de mallas diferentes, con el fin de comparar los resultados obtenidos en cuanto a topologías, valor de energía de deformación y tiempos de ejecución promedio. Se logró establecer que el procedimiento que involucra a ASAM arroja menores tiempos computacionales a medida que se analizan los problemas con mallas más refinadas. Finalmente, las distribuciones de material en el dominio de diseño y valores de energía obtenidos fueron similares a los reportados en el trabajo de Andreassen, dando validez a la propuesta aquí presentada.
This work proposes the use of the MSAA stochastic optimization technique to replace the optimality criterion used in the topology optimization method proposed by Andreassen. To evaluate and validate the MSAA performance we studied three plane elasticity problems reported in the literature. Each problem was analyzed with three different finite element mesh types in order to compare the results obtained in terms of topology, strain energy value and average runtimes. It was established that the procedure involving the MSAA, yields lower computational times in problems with more refined meshes. Finally, the material distribution and the energy values obtained were similar to those reported in the work of Andreassen giving validity to the work presented here.
El problema de Optimización Topológica (OT) consiste en buscar una distribución óptima de material en un dominio de diseño que satisfaga las solicitaciones y las condiciones de borde definidas. Generalmente, la OT ha sido formulada en términos de minimizar la energía de deformación de la estructura analizada.
En la mayoría de trabajos sobre OT reportados se encuentra que los métodos de optimización comúnmente empleados son: el criterio de Optimalidad Estándar (Optimality Criteria)[1–3], el Método de la Curva de Nivel (Level Set Method)[4] y la eficiencia de Pareto (Pareto Optimal Tracing)[5], entre otros. Sin embargo, se debe recordar que la OT es un problema con múltiples mínimos locales susceptible de solución a través de métodos estocásticos diseñados para identificar mínimos globales. Por lo tanto, se propone en este estudio emplear el Algoritmo Simulated Annealing Modificado (ASAM) [6] debido a su notable desempeño en comparación con técnicas como Harmony Search, Algoritmos Genéticos y PSO-DE (Particle swarm optimization-differential evolution), entre otras. Para mayores detalles se recomienda consultar [6]. De forma general, todas estas técnicas exploran el espacio de búsqueda de una manera controlada y tienen la ventaja de no depender del cálculo de derivadas para llevar a cabo el proceso de optimización.
En su primera parte este trabajo presenta la descripción del problema de OT y los ejemplos numéricos de benchmark a analizar. Seguidamente se describe brevemente la técnica ASAM, sus fundamentos y los parámetros que la controlan. Finalmente, se muestran los resultados obtenidos con la implementación de este método y se comparan con resultados de la literatura internacional.
2Descripción del problemaCon la finalidad de encontrar la distribución óptima de material para cada una de las estructuras mostradas se procedió a discretizar el dominio de diseño mediante el Método de Elementos Finitos (MEF). En este estudio se emplearon elementos finitos tipo C4 [7], y a cada elemento (e) se le asignó una densidad Xe. El siguiente paso fue utilizar la ecuación (1) definida en el método SIMP modificado [1] (por su sigla en inglés, Solid Isotropic Material with Penalization) para definir el módulo de elasticidad de cada elemento.
donde xeε0,1 es la densidad del material, Emin es un valor de densidad muy pequeño asignado para anular elementos con el fin de que la matriz de rigidez no se convierta en singular, y p es un factor de penalización (generalmente p=3) introducido para garantizar soluciones blanco y negro (black-and-white). La formulación matemática del problema de optimización se basa en una ley potencial, donde el objetivo es minimizar la energía de deformación, y se describe así [1]:Sujeto a:donde c es la energía de deformación a minimizar, U y F son los vectores de desplazamiento y fuerzas globales, respectivamente, K es la matriz de rigidez global, ue es el vector desplazamiento del elemento, Ee está dado por la ecuación 1, k0 es la matriz de rigidez del elemento, x es el vector de variables de diseño (es decir, las densidades de los elementos) y N es el número de elementos usados para discretizar el dominio de diseño, Vx y V0 son el volumen del material y el volumen del dominio de diseño, respectivamente, y f es la fracción de volumen. La fracción de volumen es la cantidad de material que se desea que quede en el elemento. Como se puede ver en la ecuación (1), el problema dado es convexo para p=1 y no convexo para p>1. Por tratarse entonces de un problema no convexo (con múltiples mínimos locales), se justifica el uso de las técnicas estocásticas.Con el objeto de evitar problemas de inestabilidad numérica, el algoritmo de OT emplea una técnica de filtrado de densidad, descrito por Andreassen [1], el cual produce un alisado de las energías de deformación de los elementos, teniendo en cuenta el valor de la energía de los elementos vecinos, y así encontrar soluciones razonables. Para especificar los elementos vecinos (vecindario), se define el área de influencia empleando un radio (equivale a un porcentaje del ancho del elemento 3-4%) para seleccionar el vecindario de cada elemento, que influirá en el valor de la derivada de la energía de deformación (con respecto a xe) de este.
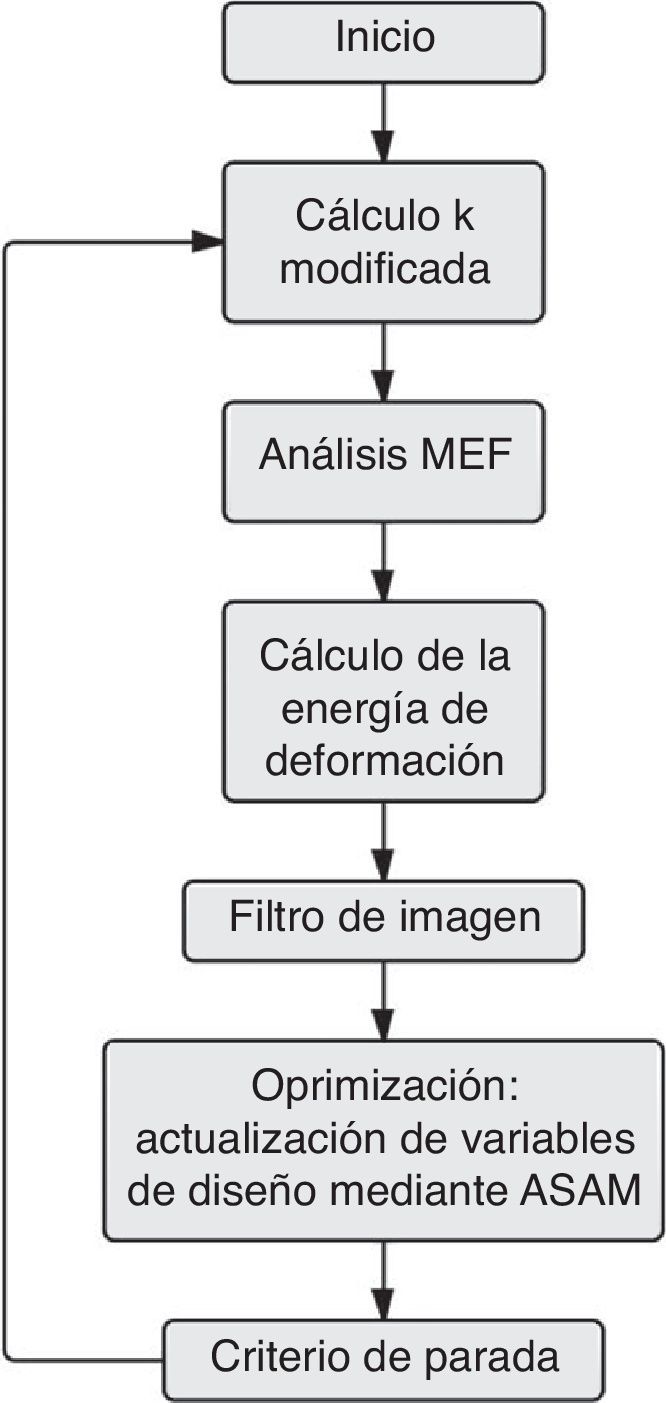
La estructura básica del algoritmo propuesto por Andreassen con la adición propuesta en este trabajo (ver punto 6) se presenta a continuación:
- 1)
Diseño inicial. Se realiza una distribución homogénea del material en la geometría de trabajo.
- 2)
Se calcula la matriz de rigidez global teniendo en cuenta la actual distribución del material.
- 3)
Se calcula mediante elementos finitos el campo de desplazamientos para cierto estado de cargas.
- 4)
Se calcula la energía de deformación con respecto la variable de diseño (densidades).
- 5)
Se aplica un filtro con el objeto de encontrar soluciones menos pixeladas y más continuas, todo esto con el fin de evitar problemas de inestabilidad mencionados anteriormente.
- 6)
Finalmente, mediante una técnica estocástica (ASAM), se calculan las nuevas densidades.
- 7)
Se vuelve al paso 2.
De esta forma, el proceso continúa iterando hasta un punto en que el valor de las densidades no cambia significativamente y el bucle termina. La estructura del algoritmo enunciada anteriormente se representa mediante el diagrama de flujo representado en la figura 1.
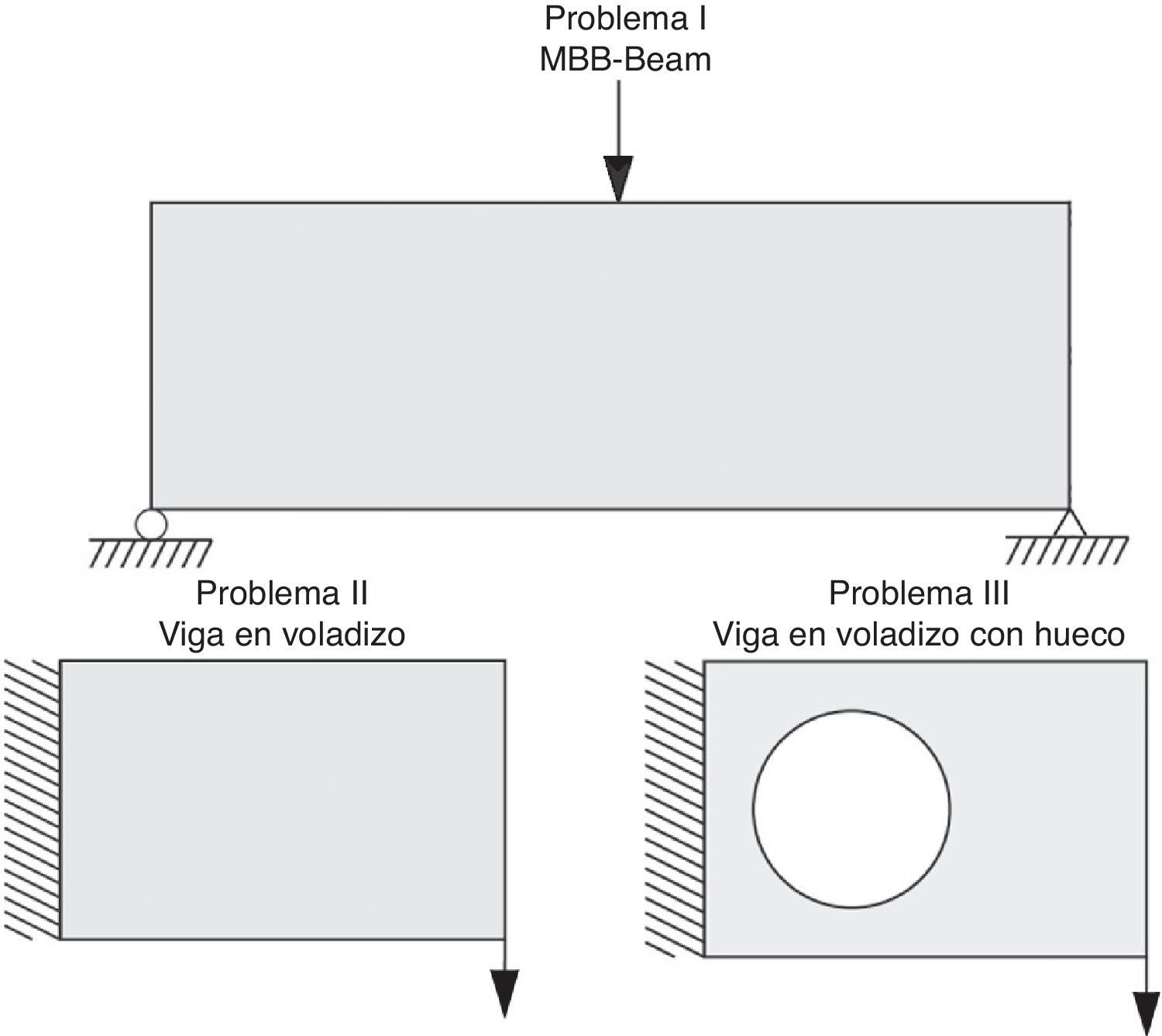
2.1Problemas propuestos de Optimización TopológicaPara evaluar el comportamiento de los algoritmos de optimización en problemas de OT, se realizaron 3 problemas de benchmark reportados en la literatura (fig. 2).
Problemas de optimización [1].
Las técnicas estocásticas están entre los desarrollos más recientes en métodos aproximados para resolver problemas de optimización. Estos métodos usan conceptos basados en inteligencia artificial, biología, matemáticas, ciencia físicas y naturales. Esta sección presenta los fundamentos del Algortimo Simulated Annealing Modificado (ASAM).
3.1Algoritmo Simulated Annealing ModificadoAntes de sintetizar las características del ASAM, vale la pena describir brevemente funcionamiento del Simulated Annealing básico. El Simulated Annealing comienza con un cierto estado S. A través de un proceso único crea un estado vecino S' al estado inicial. Si la energía o la evaluación del estado S' son menores que el estado S, cambia el estado S por S'. Si la evaluación de S' es mayor que la de S puede estar empeorando, por lo que elige S' en vez de S con una cierta probabilidad que depende de las diferencias en las evaluaciones y la temperatura T del sistema. La probabilidad de aceptar un estado peor se calcula por la siguiente ecuación:
donde:P: probabilidad de aceptar el nuevo estado.
Δf: diferencia de las evaluaciones de la función para cada estado.
T: temperatura del sistema.
e: número de Euler.
Inicialmente, con valores grandes de T, frecuentemente se aceptan soluciones con un mayor valor de función objetivo; a medida que el valor de T disminuye, tal tipo de soluciones raramente se aceptan, y cuando T se acerca a cero, solo se aceptan aquellas soluciones que mejoran la anterior. La función para reducción de temperatura más utilizada es: Tk+1=Tk·α, donde Tk+1 es el nuevo valor ajustado de T, Tk corresponde al previo valor de T y α es una constante que está comprendida en el intervalo [0,8, 0,99].
El Simulated Annealing comienza con una solución inicial escogida aleatoriamente en el espacio de búsqueda y la compara con otra que también se selecciona estocásticamente en el espacio de búsqueda, lo que afecta al algoritmo cuando se tienen funciones altamente dimensionales y modales generando mayores tiempos de búsqueda y soluciones subóptimas. Además, la probabilidad de aceptación de una solución peor se encuentra en un intervalo de entre 0 y 1, lo cual causa que a temperaturas iniciales el algoritmo acepte un gran número de soluciones de peor calidad (aumentando el riesgo de quedar atrapado en un óptimo local).
En este contexto, el algoritmo ASAM, desarrollado por Millán, Begambre y Millán [6], tiene 3 características fundamentales que lo hacen diferente respecto al Simulated Annealing básico. Dichas características son las siguientes:
3.1.1Exploración preliminarEn esta etapa el algoritmo realiza una exploración en todo el espacio de búsqueda que viene dado por la siguiente matriz:
donde:P: número de puntos (estados) que se desean en el espacio de búsqueda.
N: número de dimensiones del problema.
IPxN: matriz identidad de tamaño PxN.
Xmin: límite inferior del problema.
Xmax: límite superior del problema.
randPxN: matriz PxN de números aleatorios (aleatoriedad pura) entre 0 y 1.
Para comenzar el proceso de optimización con ASAM se evalúan todos los puntos generados con la ec.(7) mediante la función objetivo del problema y se escoge el que tenga menor valor (en el caso de estar buscando el valor mínimo de la función) como punto inicial de la búsqueda.
3.1.2Paso de búsquedaA partir del punto inicial determinado en la etapa anterior, se genera un paso de búsqueda para determinar el estado vecino. Este paso depende de un radio de acción que se reduce gradualmente a medida que desciende la temperatura del sistema (ver ecuación 8). Es decir, cuando el algoritmo está en determinada temperatura, con radio de acción definido por la ec.(7) para esa temperatura, la transición del punto inicial al nuevo punto (paso de búsqueda) se realiza mediante la adición al punto inicial de números aleatorios que están comprendidos entre cero y el valor del radio. Esto permite que el algoritmo realice una exploración global a temperaturas altas y una exploración local a temperaturas bajas, dando un equilibrio entre la exploración y la explotación del algoritmo.
donde:Ri: radio inicial ciclo.
α: coeficiente de reducción del radio.
En esta propuesta la probabilidad de aceptación de una peor solución (estado) viene dada por:
donde,P: probabilidad de aceptar el nuevo estado.
Δf: diferencia de las evaluaciones de la función para cada estado.
T: temperatura del sistema.
e: número de Euler.
Esta probabilidad se encuentra en un intervalo entre 0 y ½, lo que permite al algoritmo tener un rango menor de aceptación de peores soluciones.
En resumen, las 3 modificaciones propuestas aquí tienen la finalidad de mejorar la exploración inicial, permitir un balance entre exploración inicial y final y controlar la convergencia en la etapa final de la búsqueda.
4Resultados numéricosLos resultados obtenidos fueron comparados con los reportados por Andreassen [1]. La implementación de los algoritmos propuestos fue realizada en MATLAB®, bajo el sistema operativo Windows 7. Cabe mencionar que el equipo utilizado fue un Intel Core™ 2 Duo-1.33GHz, 2.00 GB (RAM).
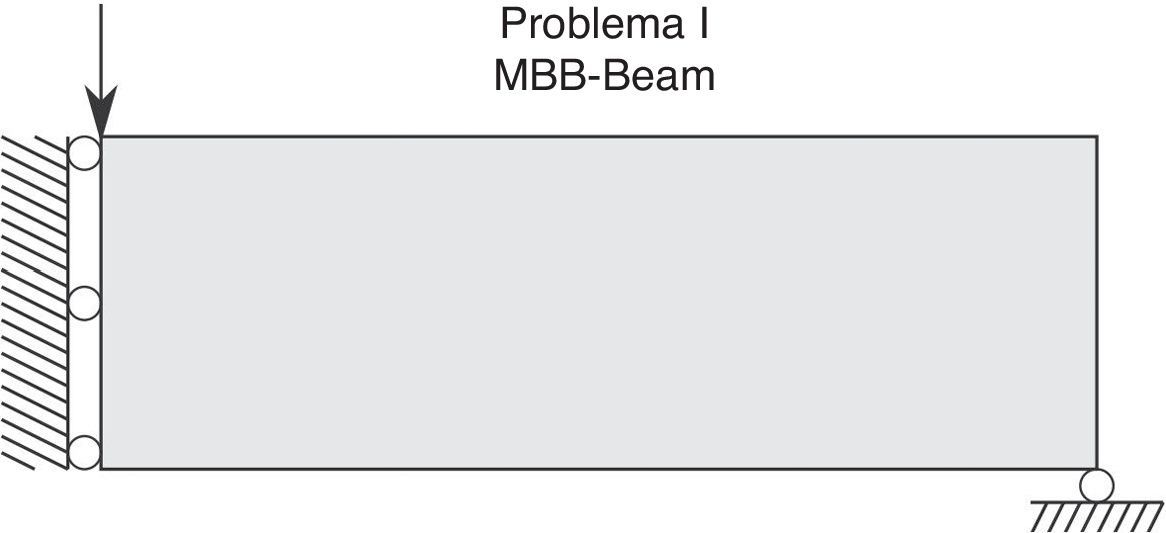
El primer problema simulado es la llamada viga MBB-Beam, denominación originada por la empresa alemana Messerschmitt-Bolkow-Blohm. Las condiciones de contorno predeterminadas corresponden a la mitad de la MBB-Beam (fig. 3). La carga se aplica verticalmente en la esquina superior izquierda; hay condiciones de contorno simétricas a lo largo del borde izquierdo, y la estructura se apoya horizontalmente en la esquina inferior derecha.
La estructura fue discretizada con 3 tipos de mallas, como se indica a seguir: a)60×20 (60 elementos en dirección horizontal y 20 elementos en dirección vertical); b)150×50, y c)300×100. El problemaii es la viga en voladizo (fig. 1), conocida en la literatura internacional como el voladizo de Michell. Este problema se modeló con 3 tipos de mallas: a)80×50; b)160×100, y c)240×150. Por último, el problemaiii, llamado viga en voladizo con hueco (fig. 1), se analizó con las mallas: a)75×50; b)150×100, y c)225×150.
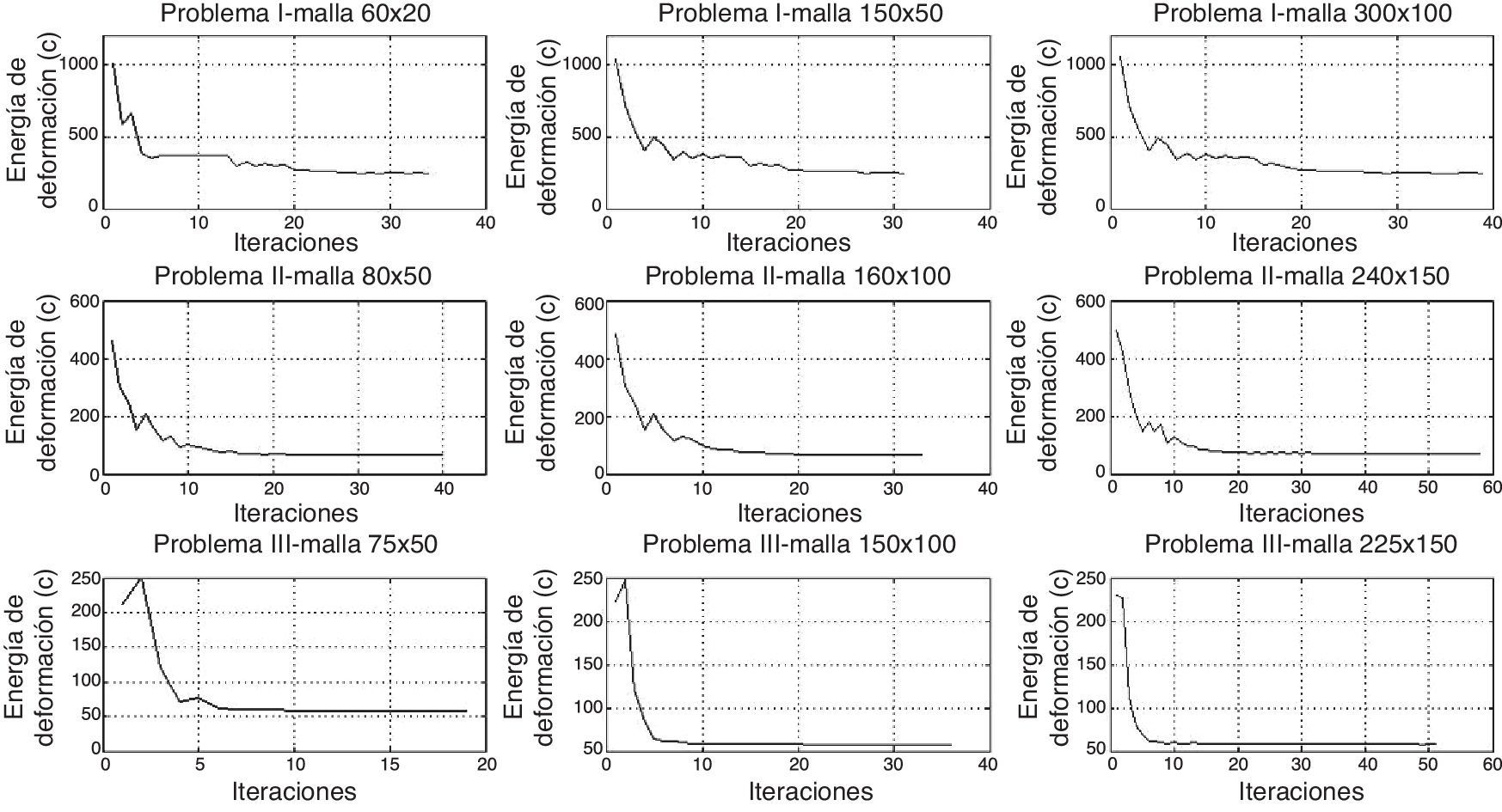
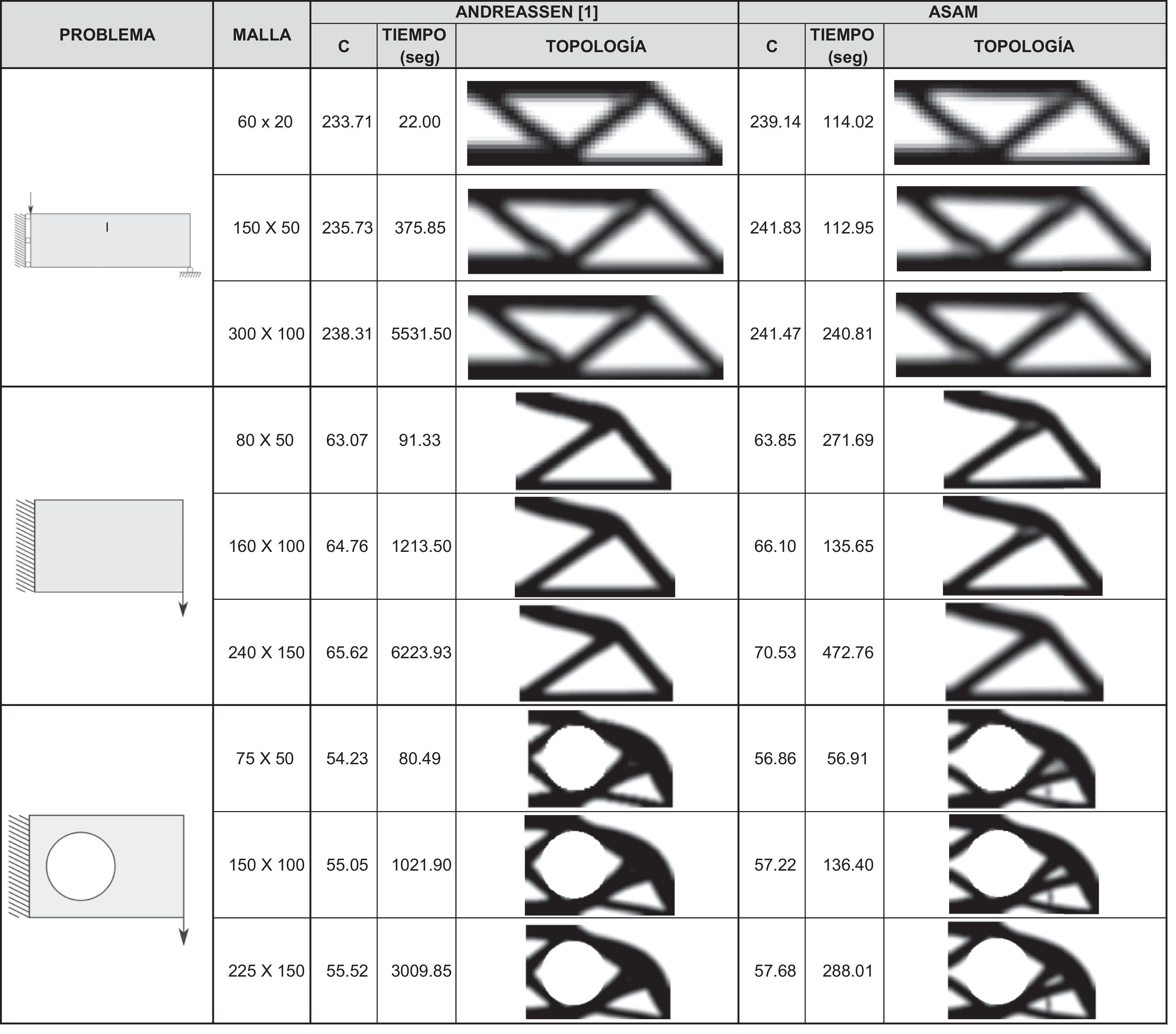
Con el fin de evaluar el desempeño de la metodología aquí empleada, inicialmente se realizaron los experimentos numéricos obteniendo: las topologías, sus valores correspondientes de energía de deformación (c) y los tiempos de ejecución promedio para cada ejemplo. Estos valores se encuentran resumidos en la figura 5. Finalmente, en la figura 4 se presentan las gráficas de convergencia de ASAM para cada problema.
Se puede observar, para el problemai, que ASAM tiene un buen comportamiento en cuanto a distribución del material y energía. En cuanto a tiempos de ejecución, se puede decir que a medida que aumenta el número de elementos finitos (discretización), el ASAM (empleado aquí por primera vez en problemas de OT) emplea menos tiempo en comparación con la referencia [1] y, además, se pueden observar soluciones más suavizadas (es decir, menos dentadas).
Para el problemaii, ASAM, encontró topologías bastantes similares a la referencia, variando un poco en el grosor de los elementos; esto se ve reflejado en los valores de energía de deformación, los cuales difieren mínimamente. Por último, en el problemaiii se puede observar que ASAM obtiene topologías en donde adiciona un pequeño orificio y una barra delgada (fig. 5) que poco alteran los valores de energía de deformación en relación con los de la referencia [1], evidenciando la capacidad de ASAM para encontrar puntos óptimos globales en cualquier tipo de problema.
5ConclusionesSe ha conseguido evaluar el desempeño del Algoritmo Simulated Annealing Modificado (ASAM) en el problema de optimización topológica de estructuras bidimensionales en régimen elástico. Las topologías, los valores de energía y los tiempos de cómputo obtenidos por ASAM fueron comparados con los resultados presentados por Andreassen [1], mostrando que son coherentes y satisfactorios (como se muestra en la fig. 5), dando así validez al trabajo aquí realizado.
En cuanto a la técnica empleada, se puede observar que ASAM tiene una versatilidad para enfrentar diversos tipos de problemas, con diferentes tipos de mallas. Esto se ve reflejado en las distribuciones de material, valores de energía y tiempos logrados. Además, muestra gran ventaja en tiempos de ejecución, cuando los problemas son discretizados con mallas refinadas (aumento de número de elementos).
Finalmente, en cuanto al tipo de malla, se puede afirmar que un refinamiento de esta conlleva a una mejora en la solución (más suavizada y menos dentada), mas no a una topología diferente.
Los autores agradecen a la UIS, al grupo de investigación INME y a la Escuela de Ingeniería Civil-UIS por el soporte ofrecido.
El segundo autor agradece el apoyo de la VIE-UIS (proyecto FM-2013-2: Optimización topológica de elementos estructurales empleando elementos finitos generalizados en formulación variacional mixta y técnicas de optimización estocástica).




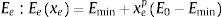
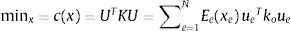
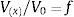
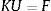
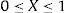

![Problemas de optimización [1]. Problemas de optimización [1].](https://static.elsevier.es/multimedia/02131315/0000003200000002/v1_201604020137/S0213131515000127/v1_201604020137/es/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)