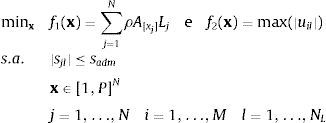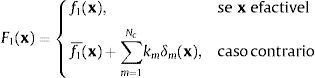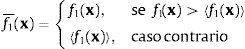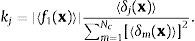Problemas de otimização estrutural visam o aumento do desempenho da estrutura e a diminuição de seus custos garantindo, entretanto, os requisitos de segurança aplicáveis. Devido à natureza conflitante desses aspectos, a formulação de um problema de otimização estrutural como multiobjetivo é natural, embora pouco frequente, e tem a vantagem de apresentar um conjunto diversificado de soluções ao(s) tomador(es) de decisão. A literatura mostra que os algoritmos evolucionários (AE) são eficazes na obtenção de soluções em problemas de otimização multiobjetivo e que aqueles baseados em evolução diferencial (ED) são eficientes na resolução de problemas de otimização estrutural mono-objetivo, especialmente os que utilizam codificação real em suas variáveis de projeto. Por outro lado, nota-se a ausência da aplicação da ED na versão multiobjetivo desses problemas. Esse artigo apresenta uma análise do desempenho de um algoritmo baseado em ED em cinco exemplos de problemas de otimização estrutural multiobjetivo. Os resultados obtidos são comparados aos encontrados na literatura, indicando o potencial do algoritmo proposto.
Structural optimization problems aim at increasing the performance of the structure while decreasing its costs guaranteeing, however, the applicable safety requirements. As these aspects are conflicting, the formulation of the structural optimization problem as multiobjective is natural but uncommon, and has the advantage of presenting a diverse set of solutions to the decision maker(s). The literature shows that Evolutionary Algorithms (EAs) are effective to obtain solutions in multiobjective optimization problems, and that the Differential Evolution (DE) based ones are efficient when solving structural mono-objective structural optimization problems, specially those with a real encoding of the design variables. On the other hand, one can note that DE has not yet been applied to the multiobjective version of these problems. This article presents a performance analysis of a DE-based algorithm in five multiobjective structural optimization problems. The obtained results are compared to those found in the literature, and the comparisons indicate the potential of the proposed algorithm.
A solução de problemas de otimização estrutural (OE) é de grande aplicabilidade na busca por concepções estruturais com baixo custo, alto desempenho, de fácil execução e manutenção e, também, mais recentemente, incorporando aspectos ambientais, desde sua construção até à sua utilização. Na sua quase totalidade, estes problemas apresentam restrições de várias naturezas que devem ser satisfeitas para que se obtenha uma solução candidata viável.
Em geral, os objetivos desejados são conflitantes, como a minimização de custo e a manutenção das condições mínimas de segurança, caracterizando assim um problema multiobjetivo. Devido a essa natureza conflitante, a resolução de um problema multiobjetivo obtém um conjunto diversificado de soluções de onde o(s) tomador(es) de decisão tem a oportunidade de selecionar aquela que melhor se adapta às suas preferências.
Entre as várias técnicas para o tratamento de problemas multiobjetivo estão os algoritmos evolucionários (AE). Os AEs são considerados interessantes na obtenção de soluções desses problemas por serem capazes de lidar com características normalmente encontradas neles, tais como não-linearidade e não-diferenciabilidade [1].
Um exemplo frequente de problema de OE multiobjetivo consiste em encontrar as áreas das seções transversais das barras (variáveis de projeto) de uma treliça buscando minimizar simultaneamente o seu peso e o deslocamento máximo dos seus nós. Neste caso, as restrições podem ser as tensões normais máximas nas barras.
Em Angelo et al. [2] são discutidos 5 problemas desse tipo, comumente encontrados na literatura tratados como mono-objetivo. Naquele artigo os autores utilizaram 2 algoritmos baseados em colônia de formigas: Multi-objective Ant System (MOAS) e Multi-objective Ant Colony System (MOACS). Para o tratamento das restrições adotou-se a técnica de penalização adaptativa (APM), proposta por Barbosa e Lemonge [3], cuja principal vantagem é a ausência de parâmetros a serem definidos pelo usuário. Os resultados apresentados mostraram que os algoritmos MOAS e MOACS foram capazes de gerar uma grande variedade de soluções, algumas delas muito próximas das soluções da versão mono-objetivo encontradas na literatura, sugerindo o bom desempenho dos algoritmos propostos.
Versões mono-objetivo de 4 desses 5 problemas foram testadas por Silva et al. [4] para avaliar o desempenho de um AE baseado em evolução diferencial (ED) em problemas desse tipo. Os autores também utilizaram a técnica APM para o tratamento das restrições e codificação real para suas variáveis de projeto. Os resultados apresentados mostram a potencialidade do uso da ED nesses problemas, pois quando não foram melhores mostraram-se competitivos com os encontrados na literatura.
Um levantamento das pesquisas existentes sobre AE aplicados a problemas de OE multiobjetivo é apresentado por Zavala et al. [1]. Os autores não encontraram publicações utilizando AE baseados em ED para a obtenção de soluções de problemas de OE multiobjetivo. Eles afirmam que o surgimento de trabalhos nessa direção é esperado nos próximos anos visto que a maioria dos estudos analisados utilizavam codificação real para suas variáveis de projeto e a ED tem uma potencialidade com esse tipo de codificação. O algoritmo The Third Step of Generalized Differential Evolution (GDE3), proposto por Kukkonen e Lampinen [5], é citado pelos autores como um algoritmo que pode ser utilizado nesses próximos trabalhos.
Baseado na argumentação apresentada e na sugestão de Zavala et al. [1], o presente trabalho analisou o desempenho do algoritmo GDE3 nos 5 problemas de OE de treliças tratados no trabalho de Angelo et al. [2]. Os resultados foram comparados aos obtidos pelos algoritmos MOAS e MOACS nas mesmas métricas de análise de desempenho utilizadas por esses autores.
Apesar do GDE3 já possuir um tratamento de restrições próprio, a mesma técnica APM usada em Angelo et al. [2] foi adotada aqui para permitir o enfoque dessa análise na eficiência da ED. Ela foi acoplada ao GDE3, substituindo a original. Além disso, foi adotada a mesma codificação real para as variáveis de projeto utilizadas por Silva et al. [4]. As descrições dos problemas e os parâmetros foram idênticos àqueles utilizados por Angelo et al. [2]. Os resultados obtidos mostram que o GDE3 apresentou desempenho superior aos algoritmos MOAS e MOACS e o conjunto de soluções obtido pelo GDE3 contém elementos muito próximos das soluções obtidas por Silva et al. [4], mostrando que o tratamento desses problemas através da versão multiobjetivo não acarreta perda significativa da qualidade das soluções obtidas pela sua versão mono-objetivo.
O restante do texto é organizado da seguinte forma: a Seção 2 faz uma introdução dos conceitos básicos de OE multiobjetivo, enquanto a Seção 3 destaca o algoritmo GDE3. A técnica APM é mostrada na Seção 4 e o algoritmo proposto é descrito em detalhes na Seção 5. Os experimentos numéricos, bem como seus resultados e sua discussão, são mostrados na Seção 6, enquanto a Seção 7 descreve as conclusões do trabalho.
2Otimização estrutural multiobjetivoSeja uma treliça de N barras com M graus de liberdade de translação de seus nós, com material de massa específica ρ e comprimento da j-ésima barra denotada por Lj. Considere sjl a tensão normal da j-ésima barra no caso de carregamento l, sadm a tensão normal máxima que esta barra pode estar submetida e uil o deslocamento do nó i no caso de carregamento l. O problema de OE multiobjetivo pode ser escrito como:
Os problemas de OE multiobjetivo tratados neste artigo têm como variáveis de projeto as áreas das seções transversais das barras das treliças, as quais devem ser selecionadas entre os P elementos do conjunto discreto ordenado de forma crescente AP={A1, …, AP}, definido um espaço de busca discreto. Apesar disso, adota-se aqui uma codificação real para as variáveis de projeto conforme sugerido por Kaveh e Shahrouzi [6] e utilizada por Silva et al. [4]. O vetor x=(x1, …, xN) representa a treliça de N barras onde a área da seção transversal da j-ésima barra é A[xj] ([xj]-ésimo elemento de AP), onde [xj] é o inteiro mais próximo de xj∈[1, P], j=1, …, N.
Os objetivos f1(x) (minimização de custo, aqui representado pelo peso da estrutura) e f2(x) (minimização dos deslocamentos, aqui representado pelo deslocamento máximo de cada nó) são conflitantes. Isso significa que minimizar os deslocamentos pode acarretar um aumento considerável no peso da estrutura e vice-versa. Assim, a relação de dominância exibida a seguir deve ser observada.
Considerando os vetores x, y∈[1, P]N, se f1(x)≤f1(y) e f2(x)<f2(y), ou equivalentemente, se f1(x)<f1(y) e f2(x)≤f2(y), então o vetor x domina o vetor y. Dado 2 vetores x, y∈[1, P]N, uma, e somente uma, das 3 possibilidades ocorre: 1) x domina y; 2) y domina x; 3) x e y são não-dominados entre si.
Resolver o Problema 1 através de um AE significa encontrar um conjunto de vetores factíveis SPO={x1, …, xλ} onde cada par de elementos de SPO são não-dominados entre si e nenhum outro vetor factível que domina algum elemento de SPO foi obtido pelo AE. O conjunto das imagens dos elementos de SPO é chamado de Frente de Pareto.
A relação de dominância definida aqui não leva em consideração as violações das restrições dos vetores x e y. No algoritmo utilizado neste trabalho, essas violações são tratadas através de penalização de suas funções objetivo, conforme é detalhado na Seção 4. Dessa forma, vetores factíveis e infactíveis podem aparecer na população. Entretanto, como factibilidade é condição necessária para a entrada de um vetor no conjunto SPO, não existem soluções infactíveis nesse conjunto.
3Generalized Differential EvolutionA ED, proposta originalmente em [7] para problemas mono-objetivos, é sem dúvida um dos mais eficientes AE que utiliza codificação real [8]. Ele se destaca pela sua simplicidade de implementação, incluindo o pequeno número de parâmetros de controle, e pelo seu notável desempenho em comparação com vários outros AE em uma ampla variedade de problemas, inclusive mantendo esse bom desempenho em problemas de grande porte, diferentemente de outros AE que utilizam codificação real [8].
Desde sua proposição, diversos AE baseados em ED para problemas multiobjetivos foram propostos [9]. Adota-se aqui, seguindo a sugestão de Zavala et al. [1], o algoritmo GDE3 proposto por Kukkonen e Lampinen [5].
Nos problemas de OE multiobjetivo de treliças sem restrições, o GDE3 funciona da seguinte maneira:
- 1.
Uma população inicial P0 de POP soluções candidatas é criada aleatoriamente (P0={x1, …, xPOP}).
- 2.
Cada solução candidata x∈P0 gera uma nova u através do Algoritmo1, onde F∈ℝ e CR∈[0, 1] são parâmetros definidos pelo usuário.
- 3.
O conjunto R0 recebe, entre as soluções candidatas x e u, aquela que dominar a outra. Caso as 2 sejam não-dominadas entre si, R0 recebe as 2.
A próxima geração da população P1 será composta pelas POP melhores soluções candidatas de R0, conforme posição na Ordenação de Pareto e valor do indicador de densidade de soluções, crowding distance (CD), segundo esquemas propostos por Deb et al. [10].
O esquema de Ordenação de Pareto consiste em classificar o conjunto R0 em d subconjuntos tais que F1={elementos não-dominados de R0} (posto 1), F2={elementos não-dominados de R0\{F1}} (posto 2), F3={elementos não-dominados de R0\{F1∪F2}} (posto 3), …, Fd={elementos não-dominados de R0\{F1∪F2∪…∪Fd−1}} (posto d), onde R0={F1∪F2∪…∪Fd}}.
Para o Problema 1, o valor do CD de cada solução candidata é o semi-perímetro do retângulo cujos vértices são as imagens vizinhas mais próximas da sua, dentre todas as imagens das soluções candidatas de mesmo posto. Quanto mais distante a imagem de uma solução candidata se encontra dessas imagens vizinhas, maior é o seu valor de CD (menor densidade de soluções com imagens nesta região). Se uma solução candidata tem uma das funções objetivo como a melhor do seu posto, seu valor de CD é tomado como infinito.
Assim, a próxima geração da população P1 será composta pelas soluções candidatas de R0 que estiverem nos subconjuntos com postos menores. Caso exista algum posto di tal que F1∪F2∪…∪Fdi tenha mais que POP elementos e F1∪F2∪…∪Fdi−1 tenha menos que POP elementos, deve-se excluir os elementos de Fdi com menores valores de CD até que se tenha F1∪F2∪…∪Fdi com POP elementos. A próxima população será P1=F1∪F2∪…∪Fdi.
Nesse procedimento, após a exclusão de uma solução candidata de Fdi, todos os valores de CD das restantes são recalculados. Isso pode fornecer uma melhoria na diversidade da população sem a introdução de um novo parâmetro [5].
Algorithm 1 Geração de uma nova solução candidata u no GDE3. 1:Seja x∈ população. 2: Sorteiam-se 3 soluções candidatas xr1, xr2 e xr3 da população. 3:Irand← inteiro entre 1 e N escolhido aleatoriamente. 4:parai=1:Nfaça 5:rand← real entre 0 - 1 escolhido aleatoriamente. 6:serand<CR ou i=Irandentão 7:u(i)←xr1(i)+F(xr2(i)−xr3(i)). 8:senão 9:u(i)←x(i). 10:fim se 11:fim para
Para transformar um problema com restrições em um problema sem restrições, tanto Angelo et al. [2] quanto Silva et al. [4], adotaram a APM proposta por Barbosa e Lemonge [3].
Originalmente, a técnica APM foi aplicada em problemas de otimização mono-objetivo com restrições, obtendo resultados competitivos. Entre as suas vantagens estão o tratamento de restrições de igualdade e desigualdade, a não necessidade de que as restrições sejam funções explícitas das variáveis de projeto, a ausência de parâmetros a serem definidos pelo usuário e a facilidade de implementação computacional.
Apesar da sua proposição inicial ser para problemas mono-objetivos, a técnica APM pode ser adaptada para problemas multiobjetivos facilmente, apenas repetindo seu procedimento para cada função objetivo separadamente, como foi feito por Angelo et al. [2].
Para a função objetivo f1 da Equação 1, a técnica APM funciona da seguinte maneira: conhecidos os valores para f1 de todas as POP soluções candidatas de PG (população na geração G) e supondo Nc o número total de restrições, calcula-se para cada x∈PG os valores de F1(x) pela fórmula
ondesendo 〈f1(x)〉 a média dos valores de f1(x) de todas as POP soluções candidatas.A função δm é dada por δm(x)=max(|sm|−sadm, 0) e o coeficiente de penalização kj da j-ésima restrição é definido por
Esse procedimento se repete para a segunda função objetivo, obtendo-se F2(x) para cada x∈PG a partir dos valores de f2. O APM foi projetado de tal forma que os valores dos coeficientes de penalização correspondentes às restrições mais difíceis de serem atendidas sejam maiores.
5Algoritmo propostoA proposta do algoritmo GDE3 acoplado à técnica APM usada nos experimentos numéricos consiste em substituir o uso de f1 e f2 no esquema de seleção da nova geração pelo uso dos valores de F1 e F2. Isto significa que a avaliação da dominância do vetor u sobre o vetor x, o processo de Ordenação de Pareto do conjunto Rt e o cálculo dos valores de CD de cada posto foram realizados considerando os valores de F1 e F2. Além disso, como em Angelo et al. [2] foi definido que o SPO de cada algoritmo corresponde a todas as soluções candidatas não-dominadas factíveis obtidas ao longo de toda sua execução, isso também foi adotado aqui. O detalhamento da proposta pode ser visto no Algoritmo2.
Algorithm 2 GDE3+APM. 1: Defina os parâmetros CR, F e GEN ▷ GEN é o numero máximo de gerações. 2:P0← população inicial criada aleatoriamente de POP soluções candidatas x∈[1, P]N. 3:Arq←P0 ▷ Arquivo externo que vai armazenar todas as soluções candidatas encontradas durante toda a execução do algoritmo. 4:f1, f2← funções objetivo de cada solução candidata de P0. 5:G←0 contador de gerações. 6:enquantoG≤GENfaça 7:F1, F2← funções objetivo de cada solução candidata de PG modificadas pela técnica APM. 8:parai=1:POPfaça 9:u← criado a partir de xi∈PG através do Algoritmo1. 10:Obtenha f1(u) e f2(u). 11:Obtenha F1(u) e F2(u) modificadas pela técnica APM com os mesmos valores dos coeficientes de penalização usados na linha 7. 12:seu domina xientão 13:RG←u. 14:senão 15:sexi domina uentão 16:RG←xi. 17:senão 18:RG←xi, u. 19:fim se 20:fim se 21:fim para 22:seRG tem mais de POP soluções candidatasentão 23:Classifique RG em d postos pelo processo de Ordenação de Pareto. 24:PG+1←∅. 25:γ←1. 26:enquanto Quantidade de soluções candidatas em PG+1<POPfaça 27:PG+1←PG+1∪ soluções candidatas do posto γ. 28:γ←γ+1. 29:fim enquanto 30:enquanto Quantidade de soluções candidatas em PG+1>POPfaça 31:Calcule CD para todos as soluções candidatas de posto γ−1. 32:Exclua de PG+1 a solução candidata de posto γ−1 com menor valor de CD. 33:fim enquanto 34:senão 35:PG+1←RG. 36:fim se 37:Arq←Arq∪PG+1 38:fim enquanto 39:SPO← soluções candidatas não-dominadas e factíveis de Arq. 40: Retorne SPO.
As descrições dos problemas, os parâmetros e as métricas de desempenho adotadas aqui são idênticas àquelas utilizados por Angelo et al. [2]. Cada algoritmo foi executado 100 vezes com tamanho da população de 50 soluções candidatas e 1.000 gerações, perfazendo um total de 50.000 avaliações de cada uma das funções objetivo. Da mesma forma, os parâmetros do GDE3 adotados em todos os problemas são os mesmos utilizados por Kukkonen e Lampinen [11] para problemas com restrições: CR=0, 4 e F=0, 3.
As métricas de desempenho adotadas foram o Hipervolume, proposta por Zitzler e Thiele [12], e a métrica Empirical Attainment Function, proposta por Fonseca e Fleming [13].
No caso de 2 funções objetivo, a métrica Hipervolume fornece o valor de H(área do polígono limitado pela Frente de Pareto da SPO e um dado ponto de referência). O algoritmo que gerou a SPO que obteve o maior valor de H será o melhor.
A métrica Empirical Attainment Function (EAF) atua como uma distribuição de probabilidade. Dada uma probabilidade α%, com 0<α<100, o EAF é um conjunto de pontos não-dominados entre si de tal forma que qualquer solução arbitrária desse algoritmo obtida por qualquer execução tem 100−α% de chance de dominar pelo menos um desses pontos. Quando α=0, o EAF é um conjunto de pontos não-dominados entre si de tal forma que qualquer solução arbitrária desse algoritmo obtida por qualquer execução tem 0% de chance de ser dominada por algum desses pontos. Já quando α=100, o EAF é o conjunto de todos os pontos não-dominados entre si obtidos em todas as execuções. O algoritmo cujo EAF tem maior hipervolume é o melhor algoritmo. Uma discussão mais detalhada sobre a obtenção do EAF pode ser encontrada em [13].
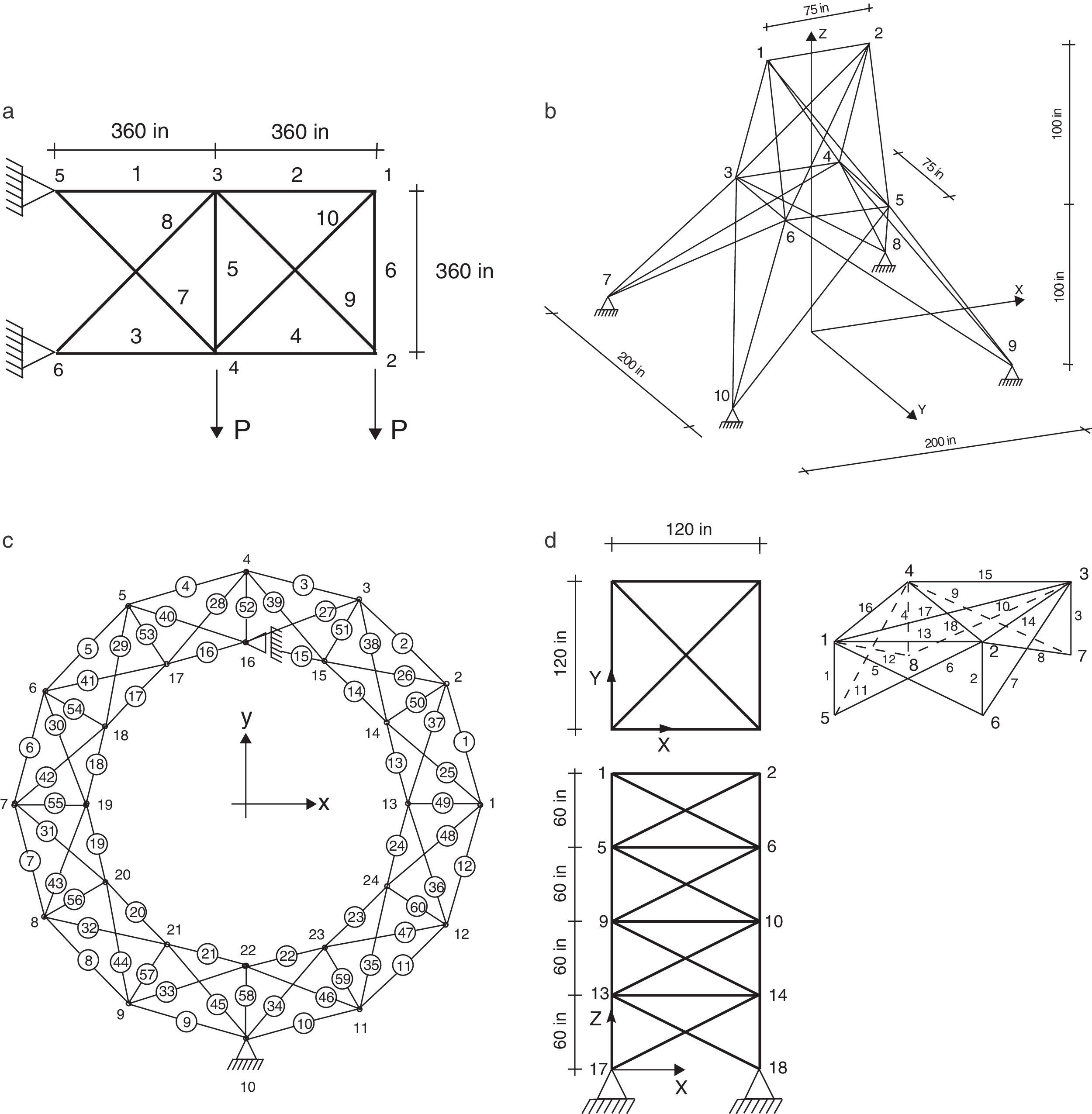
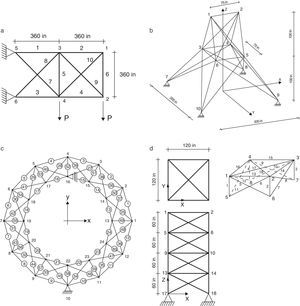
6.1Problemas6.1.1Treliça de 10 barrasO primeiro problema analisado é a treliça clássica de 10 barras, ilustrado pela figura 1a. A versão mono-objetivo é amplamente estudada [14,4] e trabalhos sobre sua versão multiobjetivo podem ser encontrados em [15–18,2].
A densidade do material é ρ=0, 1lb/in3, a tensão normal máxima é limitada em ±25ksi, o Módulo de Young E=104ksi e cargas de 100kips são aplicadas nos nós 2 e 4 na direção y (representadas na figura 1a por P).
O conjunto das áreas possíveis é (em (in2)): AP={1,62; 1,80; 1,99; 2,13; 2,38; 2,62; 2,63; 2,88; 2,93; 3,09; 3,13; 3,38; 3,47; 3,55; 3,63; 3,84; 3,87; 3,88; 4,18; 4,22; 4,49; 4,59; 4,80; 4,97; 5,12; 5,74; 7,22; 7,97; 11,50; 13,50; 13,90; 14,20; 15,50; 16,00; 16,90; 18,80; 19,90; 22,00; 22,90; 26,50; 30,00; 33,50}, definindo P=42.
6.1.2Treliça de 25 barrasO segundo problema analisado é a treliça de 25 barras, ilustrado pela figura 1b. Da mesma forma que a treliça de 10 barras, a versão mono-objetivo também é amplamente estudada [14,4] e trabalhos sobre sua versão multiobjetivo podem ser encontrados em [19,17,20,21,2].
A densidade do material é ρ=0, 1lb/in3, a tensão normal máxima é limitada em ±40ksi e o Módulo de Young E=104ksi. O conjunto das áreas possíveis é (em (in2)): AP={0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1,0; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2,0; 2,1; 2,2; 2,3; 2,4; 2,5; 2,6; 2,8; 3,0; 3,2; 3,4}, definindo P=30.
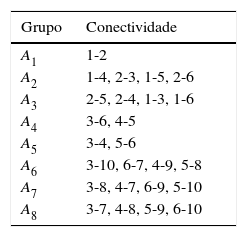
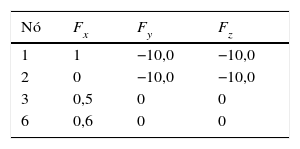
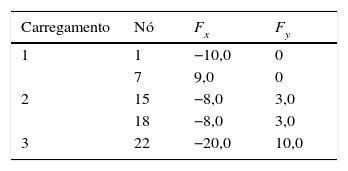
As barras da treliça são agrupadas e cada grupo possui uma única área A, a fim de manter a simetria da estrutura. O agrupamento das barras é mostrado na tabela 1 e o carregamento aplicado sobre a estrutura é mostrado na tabela 2.
O terceiro problema analisado foi o da treliça de 60 barras em formato de anel, proposto em [22] e ilustrado pela figura 1c. A versão mono-objetivo pode ser encontrada em [23,4] e somente em [2] foi encontrada a versão multiobjetivo desse problema.
A densidade do material é ρ=0, 1lb/in3, a tensão normal máxima é limitada em ±10ksi e o Módulo de Young E=104ksi. O raio externo do anel dessa treliça mede 100in e o raio interno 90in. O conjunto das áreas possíveis é (em (in2)): AP={0,5; 0,6; 0,7; …; 4,7; 4,8; 4,9}, definindo P=45.
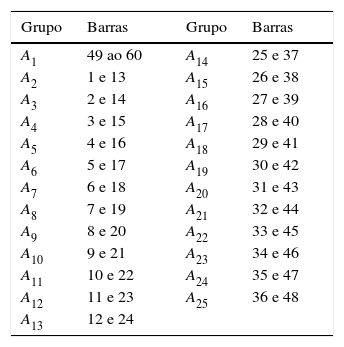
A treliça é submetida a 3 casos de carregamento, observados na tabela 4, totalizando 180 restrições. As barras são agrupadas conforme dados da tabela 3.
Agrupamento para a treliça de 60 barras.
| Grupo | Barras | Grupo | Barras |
|---|---|---|---|
| A1 | 49 ao 60 | A14 | 25 e 37 |
| A2 | 1 e 13 | A15 | 26 e 38 |
| A3 | 2 e 14 | A16 | 27 e 39 |
| A4 | 3 e 15 | A17 | 28 e 40 |
| A5 | 4 e 16 | A18 | 29 e 41 |
| A6 | 5 e 17 | A19 | 30 e 42 |
| A7 | 6 e 18 | A20 | 31 e 43 |
| A8 | 7 e 19 | A21 | 32 e 44 |
| A9 | 8 e 20 | A22 | 33 e 45 |
| A10 | 9 e 21 | A23 | 34 e 46 |
| A11 | 10 e 22 | A24 | 35 e 47 |
| A12 | 11 e 23 | A25 | 36 e 48 |
| A13 | 12 e 24 |
O quarto problema analisado foi o da treliça de 72 barras, ilustrado pela figura 1d. A versão mono-objetivo pode ser encontrada em [14,23,4] e a versão multiobjetivo foi encontrada somente em [2].
A densidade do material é ρ=0, 1lb/in3, a tensão normal máxima é limitada em ±25ksi e o Módulo de Young E=104ksi. O conjunto das áreas possíveis é (em (in2)): AP={0,1; 0,2; 0,3;…; 2,4; 2,5}, definindo P=25.
A treliça é submetida a 2 casos de carregamento, observados na tabela 6, totalizando 60 restrições de tensão. As barras são agrupadas conforme tabela 5.
Agrupamento para a treliça de 72 barras.
| Grupo | Barras |
|---|---|
| A1 | 1, 2, 3 e 4 |
| A2 | 5, 6, 7, 8, 9, 10, 11 e 12 |
| A3 | 13, 14, 15 e 16 |
| A4 | 17 e 18 |
| A5 | 19, 20, 21 e 22 |
| A6 | 23, 24, 25, 26, 27, 28, 29 e 30 |
| A7 | 31, 32, 33 e 34 |
| A8 | 35 e 36 |
| A9 | 37, 38, 39 e 40 |
| A10 | 41, 42, 43, 44, 45, 46, 47 e 48 |
| A11 | 49, 50, 51 e 52 |
| A12 | 53 e 54 |
| A13 | 55, 56, 57 e 58 |
| A14 | 59, 60, 61, 62, 63, 64, 65 e 66 |
| A15 | 67, 68, 69 e 70 |
| A16 | 71 e 72 |
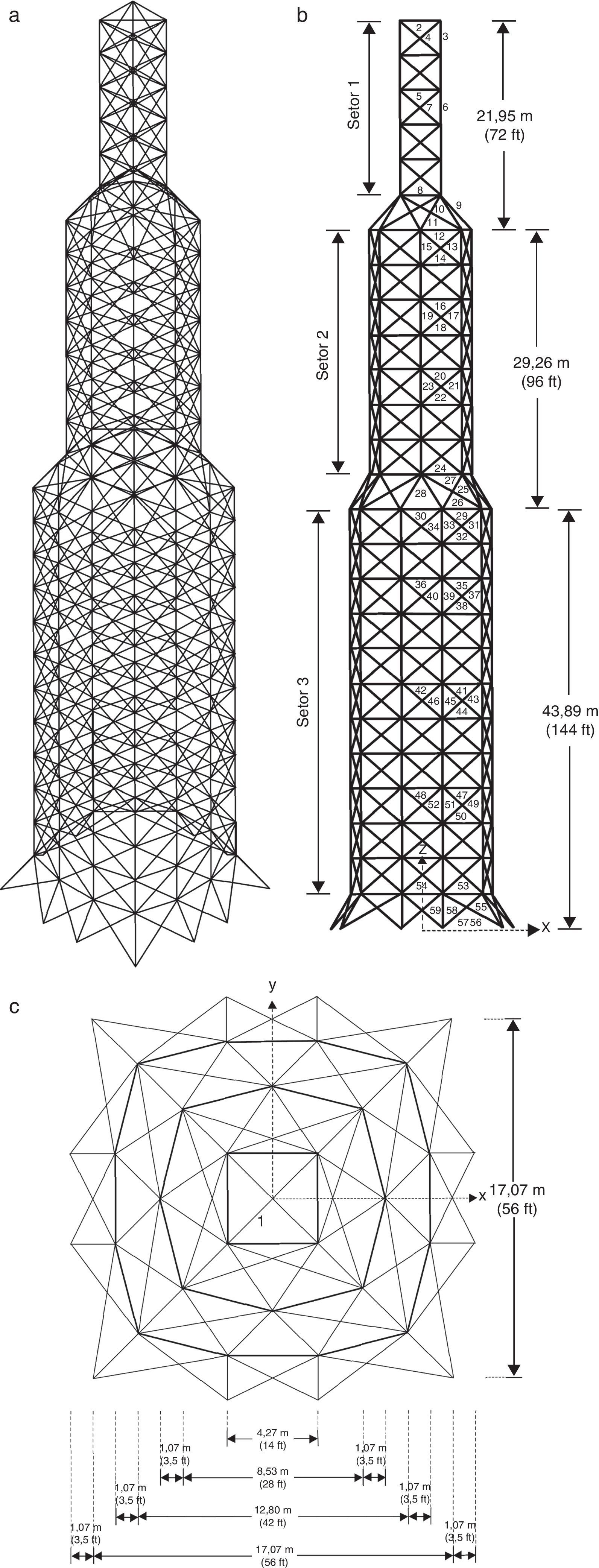
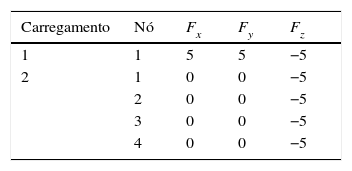
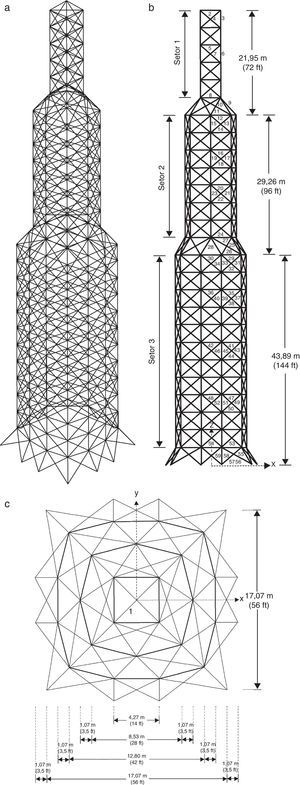
O último problema analisado aqui foi a treliça de 942 barras, ilustrada pela figura 2. As 942 barras são agrupadas em 59 variáveis de projeto e considera-se um caso de carregamento que consiste em cargas horizontais e verticais da seguinte forma: cargas verticais na direção z de −3kips, −6kips e −9kips em cada nó no primeiro, segundo e terceiro setores, respectivamente; cargas laterais na direção y de 1kips em todos os nós da torre; e cargas laterais na direção x de 1, 5kips e 1kips em cada nó à esquerda e à direita da torre, respectivamente. As variáveis de projeto são valores inteiros no intervalo de [1, 200]in2 e as restrições incluem tensão normal máxima limitada em ±25ksi para todas as barras. O Módulo de Young é E=104ksi e a densidade do material é de ρ=0, 1lb/in3. A versão mono-objetivo pode ser encontrada em [24–27] e a versão multiobjetivo foi encontrada somente em [2].
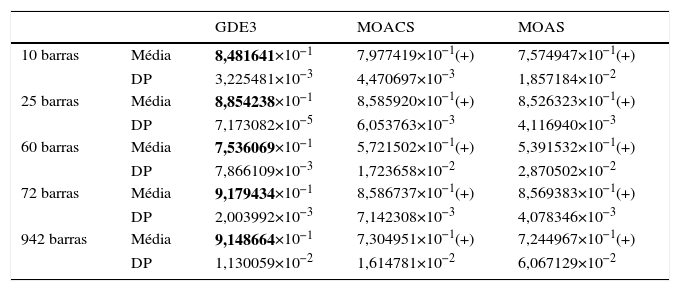
6.2Discussão dos resultadosA tabela 7 mostra as médias e os desvios padrão (DP) dos resultados da métrica Hipervolume, calculados para cada uma das 100 execuções realizadas. Para o cálculo de H, optou-se pela normalização de todos os SPO, mapeando cada função objetivo no intervalo de [0, 1] de tal forma que o valor mínimo correspondesse ao 0 e o valor máximo ao 1. O ponto de referência é dado pelos melhores valores extremos de todos os SPO gerados por todos os algoritmos em um dado problema, o qual normalizado fica [1, 1].
Média e Desvio Padrão (DP) dos Resultados de H.
| GDE3 | MOACS | MOAS | ||
|---|---|---|---|---|
| 10 barras | Média | 8,481641×10−1 | 7,977419×10−1(+) | 7,574947×10−1(+) |
| DP | 3,225481×10−3 | 4,470697×10−3 | 1,857184×10−2 | |
| 25 barras | Média | 8,854238×10−1 | 8,585920×10−1(+) | 8,526323×10−1(+) |
| DP | 7,173082×10−5 | 6,053763×10−3 | 4,116940×10−3 | |
| 60 barras | Média | 7,536069×10−1 | 5,721502×10−1(+) | 5,391532×10−1(+) |
| DP | 7,866109×10−3 | 1,723658×10−2 | 2,870502×10−2 | |
| 72 barras | Média | 9,179434×10−1 | 8,586737×10−1(+) | 8,569383×10−1(+) |
| DP | 2,003992×10−3 | 7,142308×10−3 | 4,078346×10−3 | |
| 942 barras | Média | 9,148664×10−1 | 7,304951×10−1(+) | 7,244967×10−1(+) |
| DP | 1,130059×10−2 | 1,614781×10−2 | 6,067129×10−2 | |
O sinal (+) indica que a diferença entre os 100 resultados obtidos naquela métrica é estatisticamente significante (p-valor ≤0, 05), conforme o teste não-paramétrico de Wilcoxon calculado através da função ranksum do MATLAB®. Para cada problema, o melhor resultado em cada métrica está marcado em negrito.
Pelos resultados exibidos na tabela 7 pode-se observar que o desempenho do GDE3 é melhor do que o dos algoritmos MOAS e MOACS na métrica Hipervolume. A média dos valores de H dos SPOs obtidos pelo GDE3 é maior do que a média dos valores de H dos SPO obtidos pelo MOAS e pelo MOACS em todos os problemas, com diferença estatisticamente significante. Além disso, o desvio padrão dos 100 valores de H obtidos pelo GDE3 é o menor.
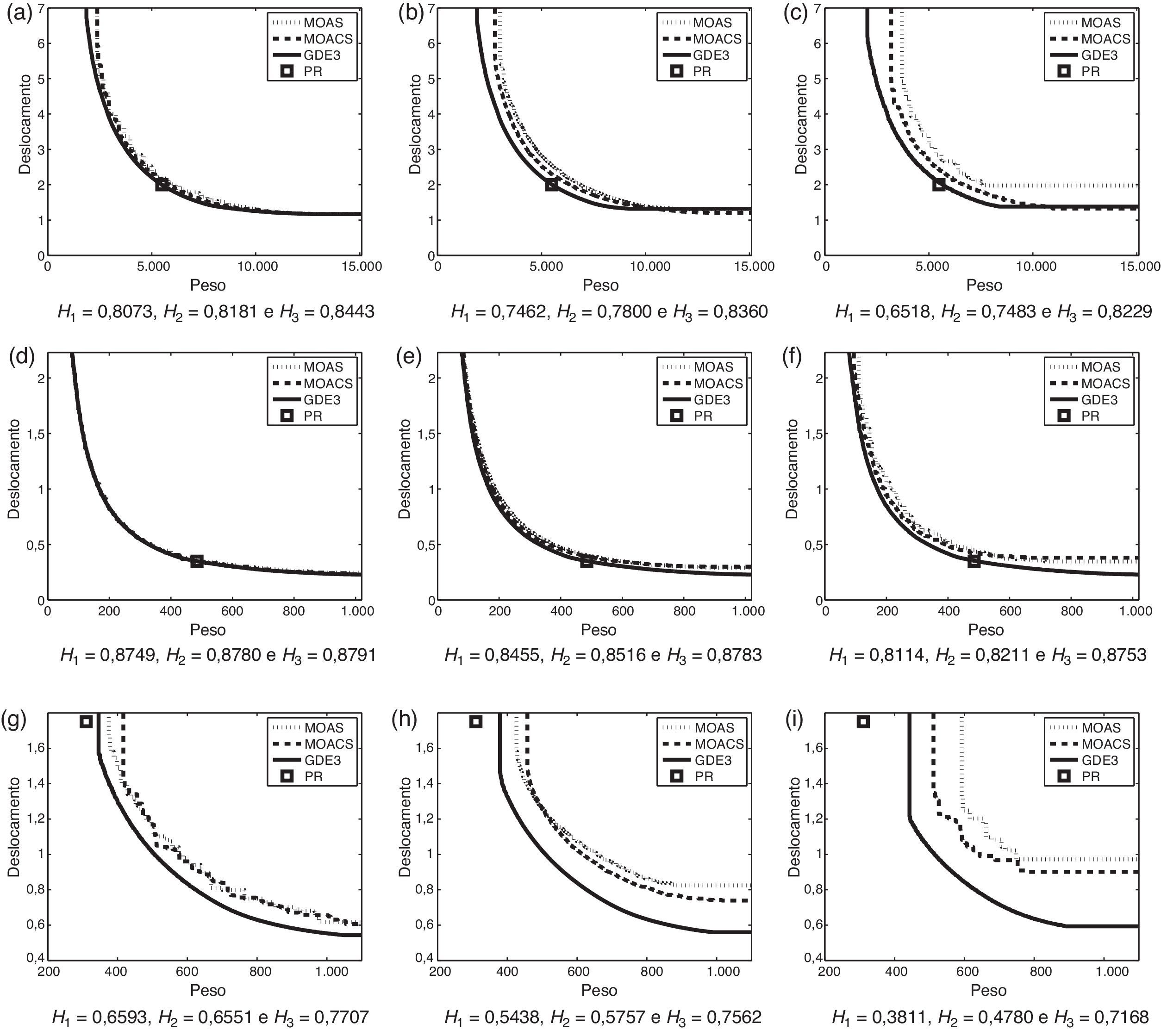
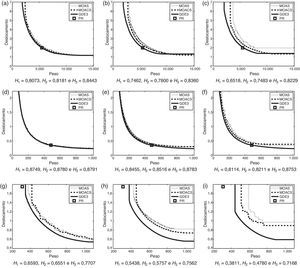
Em relação à métrica Empirical Attainment Function, foi definida as probabilidades de 100, 50 e 0%. Os conjuntos EAFs foram gerados pelo pacote EAF Tools1. Os gráficos das figuras 3, 4 e 5 referem-se às curvas formadas pelos pontos dos conjuntos EAF para os problemas adotados. Os valores dos hipervolumes normalizados de cada uma dessas curvas estão indicadas na própria figura por H1, H2 e H3 referindo-se aos algoritmos MOAS, MOACS e GDE3, respectivamente.
Curvas dos conjuntos EAF referentes aos problemas das treliças de 10 (3a,3b,3c), 25 (3d,3e,3f) e 60 (3g,3h,3i) barras com probabilidades de 100% (3a,3d,3g), 50% (3b,3e,3h) e 0% (3c,3f,3i). Os valores dos hipervolumes normalizados de cada curva dos algoritmos MOAS, MOACS e GDE3 estão indicadas por H1, H2 e H3, respectivamente.
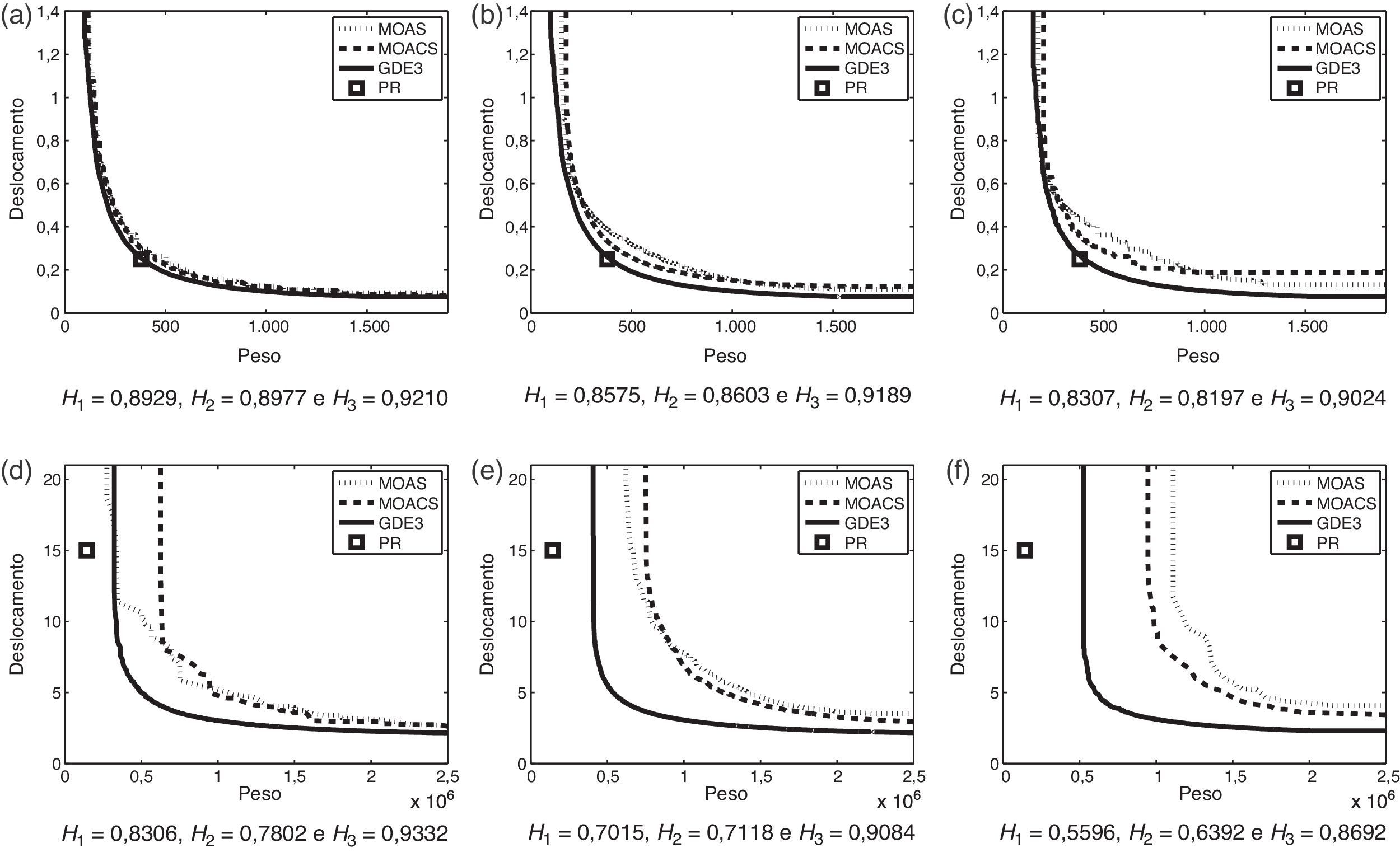
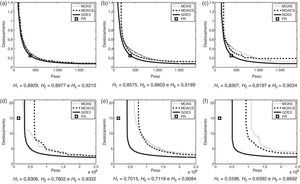
Curvas dos conjuntos EAF referentes aos problemas das treliças de 72 (4a,4b,4c) e 942 (4d,4e,4f) barras com probabilidades de 100% (4a,4d), 50% (4b,4e) e 0% (4c,4f). Os valores dos hipervolumes normalizados de cada curva dos algoritmos MOAS, MOACS e GDE3 estão indicadas por H1, H2 e H3, respectivamente.
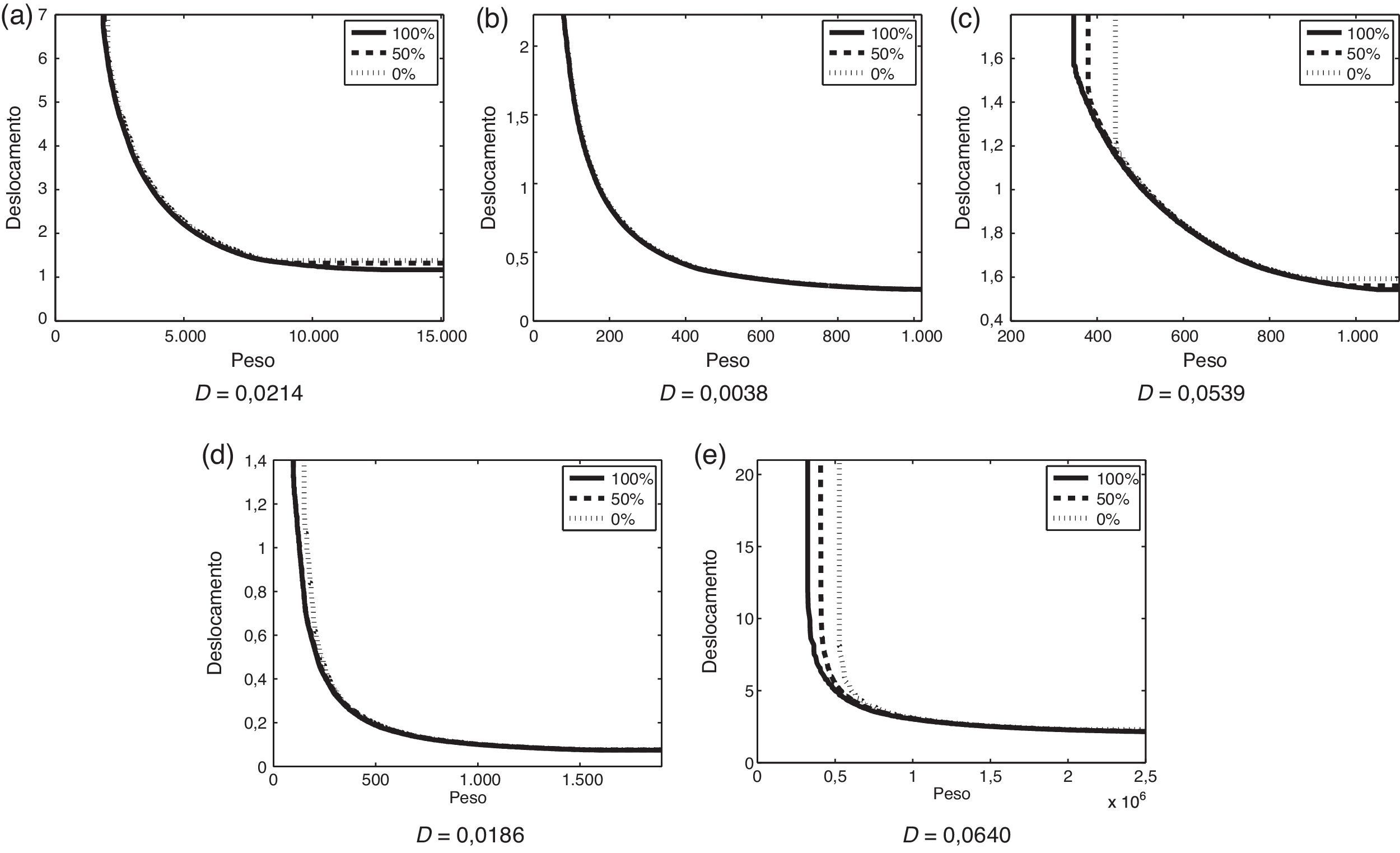
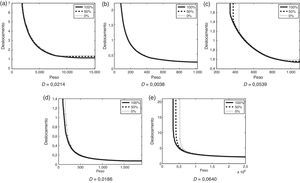
Curvas dos conjuntos EAF do algoritmo GDE3 com probabilidades de 100, 50 e 0% referentes aos problemas das treliças de 10 (5a), 25 (5b), 60 (5c), 72 (5d) e 942 (5e) barras. A diferença entre os valores dos hipervolumes normalizados das curvas correspondentes às probabilidades de 100 e 0% estão indicadas por D.
Esses gráficos também apresentam a imagem da melhor solução do problema mono-objetivo como um ponto de referência (f1;f2). São eles (5.490,70; 2) para a treliça de 10 barras, (484, 85;0, 35) para a treliça de 25 barras, (309, 44;1, 75) para a treliça de 60 barras e (379, 667;0, 25) para a treliça de 72 barras, todos encontrados em [4]. O ponto de referência para a treliça de 942 barras é (142.295,75; 15), solução da versão mono-objetivo do problema encontrado em [26]. Isso mostra que a qualidade das soluções é mantida na versão multiobjetivo, visto que a Frente de Pareto se encontra bastante próxima desses pontos de referência.
Observando-se os gráficos das figuras 3, 4 e 5, percebe-se que a curva do conjunto EAF do algoritmo GDE3 domina, no geral, uma área muito maior do que os demais em todos os problemas e em todas as probabilidades. Nos problemas da treliça de 10 e 942 barras, o algoritmo GDE3 apresenta apenas uma parte dessa curva ligeiramente dominada por pelo menos um dos outros algoritmos. Nos demais problemas, os algoritmos MOAS e MOACS apresentam, no máximo, pequenas partes da curva coincidentes com a do algoritmo GDE3.
No problema da treliça de 60 barras, as curvas dos algoritmos MOAS e MOACS ficaram totalmente dominadas pela do algoritmo GDE3 em todas as probabilidades. Em todos os problemas foram encontradas soluções cujas imagens são muito próximas ao ponto de referência pelo algoritmo GDE3. Além disso, as imagens das soluções obtidas pelo algoritmo GDE3 estão mais próximas do ponto de referência do que as imagens das soluções obtidas pelos algoritmos MOAS e MOACS.
Os gráficos das 3 curvas dos conjuntos EAF do algoritmo GDE3 apresentado na figura indicam ainda que ele é mais estável do que os demais, uma vez que a área entre as curvas relativas às probabilidades de 0 e 100% é bem menor quando comparada aos algoritmos MOAS e MOACS. Essa diferença está indicada por D em cada figura, que é dado pela diferença entre os valores dos hipervolumes normalizados das curvas correspondentes às probabilidades de 100 e 0%. Além disso, as curvas do algoritmo GDE3 relativas às probabilidades de 50 e 100% são muito próximas em todos os problemas, indicando que a maioria das soluções obtidas por ele tem imagens próximas das melhores.
7ConclusõesNeste trabalho foi analisado o desempenho do algoritmo GDE3 combinado com a APM em 5 problemas de OE de treliças com codificação real para as variáveis de projeto, as quais pertencem a um espaço de busca discreto. Esses problemas foram resolvidos por Angelo et al. [2] utilizando 2 algoritmos baseados em colônia de formigas: MOAS e MOACS. Compararam-se aqui os resultados obtidos pelos algoritmos GDE3, MOAS e MOACS em 2 métricas: Hipervolume e Empirical Attainment Function.
A versão mono-objetivo de 4 desses problemas foram resolvidos via ED por Silva et al. [4] também com codificação real para as variáveis de projeto. A mesma técnica de tratamento de restrições APM foi utilizada em [2] e [4].
A comparação dos resultados indica que o GDE3 apresentou desempenho significantemente superior aos demais algoritmos nas 2 métricas. Na métrica Hipervolume, a média dos valores de H dos SPO obtidos pelo GDE3 é maior do que a média dos valores de H dos SPO obtidos pelo MOAS e MOACS em todos os problemas, com diferença estatisticamente significante entre todos os resultados. Além disso, um menor desvio padrão dos valores de H relativos ao GDE3 foi observado em todos os problemas quando comparado ao desvio padrão dos valores de H relativos ao MOAS e ao MOACS.
Na métrica Empirical Attainment Function, o conjunto EAF do algoritmo GDE3 domina, em geral, uma área bem maior do que a dominada pelos conjuntos EAF dos algoritmos MOAS e MOACS em todos os problemas e em todas as probabilidades consideradas aqui (0, 50 e 100%). A área entre as curvas EAF relativas às probabilidades de 0 e 100% do algoritmo GDE3 é bem menor quando comparada à área entre as curvas EAF relativas às mesmas probabilidades dos algoritmos MOAS e MOACS. Em alguns casos, as curvas EAF relativas às probabilidades de 0 e 100% do algoritmo GDE3 foram quase coincidentes, indicando que ele é o algoritmo mais estável entre todos os analisados.
Também observou-se nos experimentos que em todos os problemas foram encontradas soluções cujas imagens são muito próximas ao ponto de referência pelo algoritmo GDE3, sendo essas mais próximas do ponto de referência do que as obtidas pelos algoritmos MOAS e MOACS. Isso indica que não há perda significativa da qualidade das soluções obtidas pelo GDE3 em relação aos resultados da versão mono-objetivo desses problemas.
Como Zavala et al. [1] também aponta a carência de trabalhos envolvendo a incorporação de preferências do usuário nos AE aplicados a OE multiobjetivo, para trabalhos futuros está previsto experimentos com essa característica. Isso pode permitir a busca por soluções cujas imagens estão em uma região específica da Frente de Pareto, melhorando a qualidade das soluções a serem apresentadas ao(s) tomador(es) de decisão.
Os autores agradecem às agências de fomento pelos seguintes apoios CNPq (306815/2011- 7) e FAPEMIG (TEC PPM 528/11 e TEC PPM 388/14).