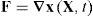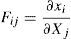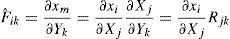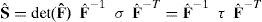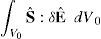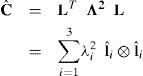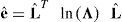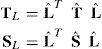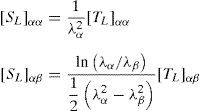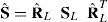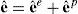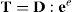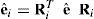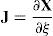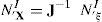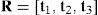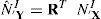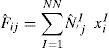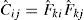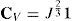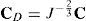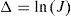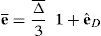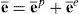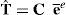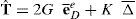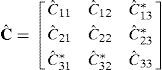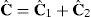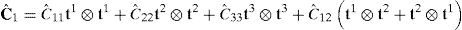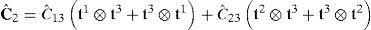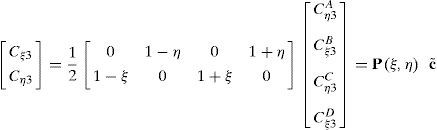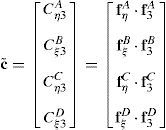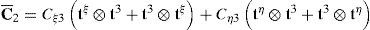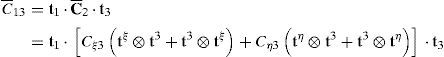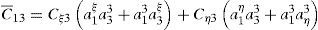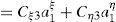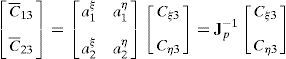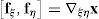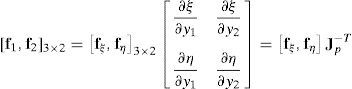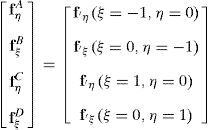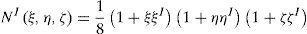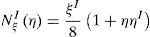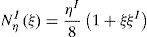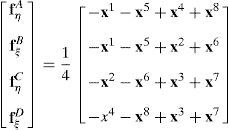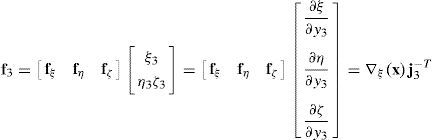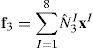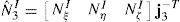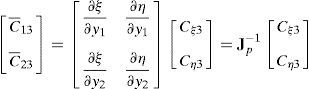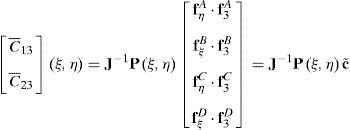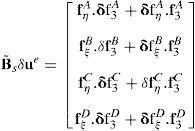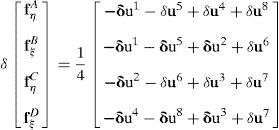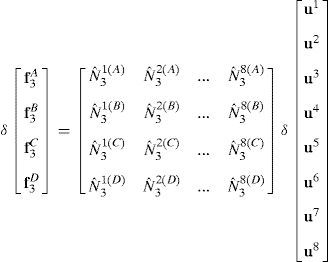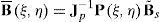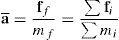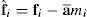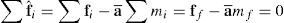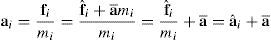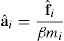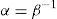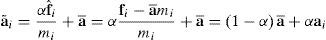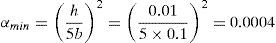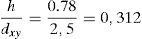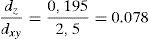Un elemento de sólido con una mejora en el comportamiento del corte transversal para el tratamiento de láminas

Resumen

Este trabajo combina un elemento de sólido basado en una formulación lagrangeana total que utiliza deformaciones logarítmicas con una aproximación clásica de deformaciones transversales impuestas para láminas gruesas. El objetivo es poder utilizar el elemento para la simulación de láminas sin que bloquee por cortante. Se resume la técnica de escalamiento selectivo de masa utilizada a los fines de que la discretización en el espesor no condicione el tiempo crítico en códigos con integración explícita de las ecuaciones de movimiento. Se presentan varios ejemplos que muestran el comportamiento libre de bloqueo por corte del elemento, la influencia del escalamiento de masa y las posibilidades del elemento para el análisis de laminados en régimen no lineal material.

Abstract

In this work a solid finite element based on a Total Lagrangian Formulation using logarithmic strains is combined with a classical assumed strain approach of the transverse strains for thick shells. The target is to use the element for shell simulations without shear locking. The selective mass scaling technique used to avoid that the discretization across the thickness reduce the critical time in codes with explicit integration of the momentum equations is summarized. Several examples are presented showing that the element is shear-locking free, the consequences of the selective mass scaling and the possibilities of the element for the analysis of composites laminates in non-linear material regime.

1

Introducción

En el área de la mecánica de los sólidos, para la simulación de problemas de láminas (i.e. cuando una de las dimensiones del sólido es mucho menor que la otra), se prefiere la utilización de elementos finitos que utilicen hipótesis plausibles respecto al comportamiento de la normal a la lámina (hipótesis de Kirchhoff-Love o Reissner-Mindlin) lo que conduce a elementos donde el comportamiento cinemático queda descripto por el movimiento de la superficie media con una importante economía de recursos, tanto en memoria como en tiempo de proceso.

Sin embargo, la utilización de elementos de sólidos para simular láminas ha crecido notoriamente en el último tiempo auspiciado en parte por la continua mejora en las facilidades de procesamiento y también por la necesidad de mejorar distintos aspectos de los modelos a los fines de lograr simulaciones más fieles. Algunas de las ventajas que se obtienen de utilizar elementos de sólido en vez de elementos de lámina son: a) la posibilidad de utilizar relaciones constitutivas efectivamente tridimensionales y no restringirse a modelos de tensión plana; b) incluir el efecto del contacto correctamente, en particular cuando hay fricción; c) tratar grandes deformaciones de corte transversal o discontinuidades en las deformaciones a través del espesor; d) evitar elementos especiales de transición entre mallas de elementos de sólidos y de elementos de láminas; e) tratar correctamente contornos no paralelos a la normal a la lámina o campo director; f) deshacerse de los grados de libertad rotacionales que son en general costosos y dificultosos de parametrizar y actualizar.

Los elementos de sólido estándar de 8 nudos integrados con 8 puntos cuando se utilizan para simular láminas adolecen (al igual que un elemento de lámina deformable por corte) del problema de bloqueo por cortante en forma pronunciada. Este problema se agudiza cuando la esbeltez de la lámina aumenta y si el comportamiento es predominantemente de flexión. Por otro lado al tratar materiales elásticos quasi-incompresibles o materiales elasto-plásticos con flujo plástico isócoro (típico de los metales) se generan problemas de bloqueo volumétrico. El uso de un solo elemento de sólido en el espesor de la lámina hace evidente la imposibilidad del elemento de adecuarse al efecto de Poisson en todo el espesor. Finalmente en modelos de láminas curvas donde el comportamiento es principalmente de flexión sin estiramiento de la superficie media es común la aparición de bloqueo membranal. Estos bloqueos numéricos indican la incapacidad de las funciones de interpolación utilizadas (y sus gradientes) de amoldarse al comportamiento del sólido que muchas veces invalidan las soluciones obtenidas.

Los avances en el desarrollo de elementos de sólidos a los fines de evitar los diferentes bloqueos indicados son numerosos. En muchos casos el objetivo es lograr modelos que requieran un solo elemento en el espesor, estos elementos se denominan de «sólido-lámina» y en general utilizan formulaciones en deformaciones naturales impuestas «ANS» y deformaciones impuestas mejoradas «EAS» (de sus acrónimos en inglés) con la inclusión de distintos grados de libertad internos que se condensan localmente. Para solucionar el problema de bloqueo por corte transversal la ya clásica aproximación de Dvorkin y Bathe[5] es la más utilizada cuando se realiza integración completa (ver por ejemplo [10,18]) y una variación de la misma cuando se realiza integración reducida (ver por ejemplo [3]). Para solucionar el bloqueo membranal se han desarrollado elementos con ambos tipos de formulación. Para evitar el bloqueo debido al efecto de Poisson se suelen combinar ambas técnicas. El bloqueo volumétrico se soluciona habitualmente usando integración reducida selectiva (SRI del acrónimo en inglés) o promediando la dilatación sobre todo el elemento. En el plano de la lámina se utiliza 1 o 4 puntos de integración (en el primer caso se requiere estabilización para evitar los modos de «hourglass»), en tanto que en el espesor de la lámina se utilizan por lo menos dos puntos (a veces hasta 7 en problemas elasto-plásticos) para captar los efectos de flexión. La implementación es más compleja que los elementos de sólido estándar y pueden presentar algunas inestabilidades cuando se utiliza integración reducida debido a los modos de «hourglass» o en grandes deformaciones cuando se utiliza la técnica EAS. En la referencia [16] se indica un detallado estado del arte de este tipo de elementos. A pesar de las mejoras, si se utiliza un solo elemento en el espesor estos elementos de «sólido-lámina» no pueden modelar discontinuidades en el espesor como las que aparecen en materiales composites y deben aumentar la discretización en el espesor para captar estos detalles, lo cual hace que pierdan algunas de sus ventajas. Como alternativa a la integración completa con 8 puntos Liu et al. [11] proponen la utilización de 4 puntos de integración lo que representa una economía importante y un mejor seguimiento del comportamiento elastoplástico cuando se lo compara con los elementos con un punto de integración en el plano de la lámina. Esto a expensas de una posible dependencia de la malla.

En el caso de simulaciones a gran escala con fuertes no-linealidades asociadas a inestabilidades geométricas, modelos constitutivos complejos, contacto friccional, es común utilizar algoritmos explícitos que son condicionalmente estables. Al simular láminas discretizadas con varios elementos de sólido en el espesor el tiempo de avance crítico puede resultar prohibitivamente pequeño. Para este tipo de modelos Olovsson[14] propuso una estrategia de escalamiento selectivo de masa que permite que el tiempo crítico no dependa de la discretización en el espesor.

Una de las motivaciones principales de este trabajo es la simulación de materiales laminados en régimen no lineal material que requiere incluir varios elementos en el espesor de la lámina. Por ello en lo que aquí se presenta solo se intenta aliviar el problema de bloqueo volumétrico (cuando se tratan problemas de flujo plástico) y por cortante transversal en problemas dominados por la flexión, pero no se considera bloqueo membranal de láminas inicialmente curvas o mejorar el comportamiento en flexión frente al efecto «Poisson» debido a una pobre interpolación en la dirección transversal. Para ello propondremos algo similar a lo que se usa en los elementos de lámina cuadrilátero [5], es decir, que en la dirección local normal a la lámina utilizaremos para el cálculo de algunas componentes del tensor métrico una aproximación del tipo ANS. El objetivo final es tener un elemento sencillo, que no requiera estabilización alguna, no presente inestabilidades en grandes deformaciones y sea adecuado para problemas con contacto.

Un la siguiente sección se resumen las ecuaciones de la mecánica de sólidos más relevantes para este trabajo. En la sección 3 se presenta la formulación del elemento de sólido. A continuación se muestra como tratar el corte transversal cuando se simulan láminas. En la sección 5 se resume una técnica de escalamiento selectivo de masa usada para disminuir los tiempos de CPU. En la sección 6 se presentan varios ejemplos mostrando el buen comportamiento del elemento y finalmente se resumen algunas conclusiones.

2

Expresiones relevantes de la mecánica de los sólidos

Referidos a un sistema cartesiano global arbitrario denotamos con X la posición original de los puntos materiales del sólido, con R(X)=t1,t2,t3: la terna ortogonal respecto a la cual se caracteriza el material en cada punto del sólido indeformado (sistema local) y con Y: a las coordenadas originales referidas al sistema local

La posición de los puntos materiales del sólidos en un instante cualquiera t se escriben como xx,t. Denominando con F al gradiente de la deformación

que puede referirse al sistema local (indicaremos con un sombrero superpuesto _ˆ, las variables referidas al sistema local cuando sea necesario)

El cual permite evaluar el tensor derecho de Cauchy-Green y las deformaciones de Green-Lagrange

La medida de tensión asociada (a través del principio de trabajos virtuales) es el segundo tensor de tensiones de Piola Kirchhoff Sˆ que se relaciona con el tensor de tensiones (reales) de Cauchy σ o con el de Kirchhoff (τ) por:

lo que permite escribir el trabajo virtual interno como

donde V₀ es el volumen original indeformado del sólido.

Este par conjugado tensión-deformación presenta algunas dificultades para el tratamiento de relaciones constitutivas elasto-plásticas en grandes deformaciones, por lo cual introduciremos la deformación de Hencky, lo cual requiere la descomposición espectral de Cˆ

donde Λ² es la matriz diagonal que agrupa a los autovalores λi2 de C y lˆi son los autovectores (unitarios) asociados. Entonces es posible escribir las deformaciones como

Esta medida de deformación es una extensión adecuada de la deformación logarítmica (natural) unidimensional y es lagrangeana, es decir, que mide deformaciones respecto a la terna original. Denominaremos con Tˆ a la medida de tensión asociada, que puede relacionarse con Sˆ a través de las expresiones siguientes: definiendo los tensores rotados

la relación entre el 2.^o tensor de Piola Kirchhoff y la tensión de Hencky es (ver por ejemplo la referencia [4]):

finalmente

El objetivo de calcular Sˆ es que las condiciones de equilibrio se expresan a partir de la expresión (8) debido a la complejidad computacional que representa obtener la variación de la deformación de Hencky (expresión (10)).

A los fines de considerar comportamiento inelástico se supondrá que las deformaciones elásticas son pequeñas y que es admisible descomponer en forma aditiva al tensor de deformación de Hencky en una componente elástica y una componente plástica

Para el caso de materiales isótropos se supondrá además que existe una relación lineal entre la medida de tensión de Hencky T y la componente elástica del tensor de deformaciones e^e.

En el caso de materiales composites existen diferentes formas de tratarlo. Una posibilidad es considerarlo como un único material equivalente, en tal caso se aplica directamente la expresión anterior, esta aproximación en general es válida solo en el rango elástico lineal o el tratamiento plástico resulta muy complejo. Una segunda posibilidad, de mayor generalidad pero más costosa computacionalmente, es analizar separadamente el comportamiento de cada componente cuando corresponda (comportamiento en paralelo en la dirección de las fibras) y su interacción (comportamiento en serie en la dirección transversal al las fibras)[15,13]. En este caso resulta conveniente expresar al tensor de deformaciones e¯ en las direcciones principales de ortotropía de cada componente

donde Ri=t1i,t2i,t3i son las direcciones principales de ortotropía de la componente i referidas al sistema local R. La teoría de mezclas permite tratar separadamente la evolución de cada componente, evaluando su estado tensional y luego calcular el estado tensional equivalente en función de la fracción de volumen de cada componente dentro del compuesto.

3

Elemento finito de sólido

La cinemática descripta se ha implementado en un elemento sólido en 3 dimensiones [6]. Se han considerado un elemento hexaédrico de 8 nudos. Las geometrías inicial y deformada del elemento están descriptas por las aproximaciones isoparamétricas estándar [19].

donde X^I, x^I, y u^I son respectivamente las coordenadas originales, coordenadas actuales y desplazamientos del nudo I. Las funciones de forma NIξ son las habituales funciones de forma Lagrangeanas en función de las coordenadas locales ξ del elemento maestro correspondiente.

La evaluación de las derivadas cartesianas se realiza en forma estándar, definiendo la matriz jacobiana en cada punto de integración

En cada elemento se define un sistema cartesiano local coincidente con las direcciones principales de ortotropía del material constitutivo

de tal forma que las derivadas cartesianas referidas a este sistema (Y) resultan

lo que permite evaluar el gradiente de deformación Fˆ en función de las coordenadas actuales de los nudos

y las componentes del tensor Cˆ

Para la descomposición espectral de Cˆ en 3 dimensiones (9) es necesario un cierto cuidado para deformaciones muy pequeñas o para autovalores casi-coincidentes para evitar problemas de precisión en la obtención de los autovectores correspondientes [17].

Para evitar problemas de bloqueo debido al flujo plástico incompresible el tensor derecho de Cauchy-Green se descompone multiplicativamente en sus componentes volumétrica y desviadora.

La componente volumétrica resulta del determinante J del gradiente de la deformación F

que se promedia sobre todo el elemento (Δ¯), con lo cual se obtiene un valor corregido del tensor de deformaciones en cada punto de integración

Aceptando la hipótesis de aditividad de componentes elástica y plástica del tensor de deformaciones éste se escribe:

Para el caso de materiales donde la ley de fluencia es independiente de la componente volumétrica, la componente plástica tiene traza nula y Δ¯ es puramente elástica. El tensor de tensiones asociado se obtiene de suponer una ley constitutiva hiperelástica, lineal entre tensiones y componentes elásticas del tensor de deformaciones

Para el caso de un material isótropo con deformación plástica incompresible, lo anterior puede escribirse

Si se utiliza el criterio de von Mises o el criterio de Hill es posible trabajar con las componentes desviadoras de tensiones y deformaciones, lo que facilita y hace más económica la integración de las ecuaciones constitutivas.

Como alternativa a la utilización de la deformación logarítmica la descomposición espectral (9) permite considerar en forma sencilla materiales hiper-elásticos en grandes deformaciones (elastómeros), utilizando modelos tales como los de Ogden, Mooney-Rivlin, neohookeanos, etc. que habitualmente se definen en función de la energía interna de deformación a partir de los estiramientos principales.

4

Tratamiento del corte transversal

En lo que aquí se presenta solo se intenta aliviar el problema de bloqueo por cortante transversal en problemas dominados por la flexión, pero no se considera bloqueo membranal o mejorar el comportamiento en flexión frente al efecto «Poisson» debido a una pobre interpolación en la dirección transversal.

Normalmente la discretización de una lámina con elementos de sólido de 8 nudos implica dos pasos: a) una discretización de la superficie de la lámina con cuadriláteros de 4 nudos, y b) un discretización del espesor de la lámina con uno o más elementos de sólido en base al cuadrilátero definido sobre la superficie media.

En base a lo anterior supondremos que las conectividades del elemento de 8 nudos se introducen con los nudos locales 1 a 4 y 5 a 8 asociados con superficies paralelas a la superficie media i.e. que las conectividades del elemento de sólido son tales que los últimos cuatro nudos están por encima de los cuatro primeros en la dirección del espesor a una distancia igual al espesor de la capa (lo habitual en elementos de sólido-lámina). De esta forma la dirección normal a la superficie media (y₃ local) coincide con la variable natural local ζ, llegado el caso se pueden modificar internamente las conectividades para que estas direcciones coincidan.

El sistema de coordenadas cartesiano local (t₁, t₂, t₃) se define en cada punto de integración y en cada punto de muestreo en forma independiente, pero con un criterio similar de tal forma que haya una continuidad del mismo. Las condiciones sobre este sistema son que:

• •

  el plano y₁ − y₂ local es el mismo que el plano tangente local definido por la coordenadas locales ξ − η. La elección final de la dirección t₁ es arbitraria, pero es conveniente un criterio que permita un suavisado sencillo de los esfuerzos y/o deformaciones a los fines de visualización. Por otro lado, al tratar materiales ortótropos resulta conveniente que las direcciones t₁ y t₂ coincidan con las direcciones principales de ortotropía;

• •

  la dirección y₃ resulta naturalmente normal al plano y₁ − y₂ y, si no hay distorsión inicial asociada a la dirección del espesor, coincidirá con la dirección local ζ.

La formulación del elemento de sólido de la sección anterior se basa en el tensor derecho de Cauchy-Green, por lo cual una posibilidad interesante es plantear una formulación basada en modificar las componentes de Cˆ directamente asociadas al corte transversal

donde las componentes indicadas con un * son las que tienen directa influencia en el corte transversal. Esto permite separar el tensor en dos partes

A los efectos de aproximar las componentes más relevantes para el corte transversal consideremos el elemento maestro correspondiente al cuadrilátero asociado a las coordenadas naturales (ξ, η), es decir, un cuadrado de lado dos. En este elemento impondremos la siguiente interpolación [5] para las componentes de corte transversal (en todos los casos para ζ = 0, es decir, sobre la superficie media):

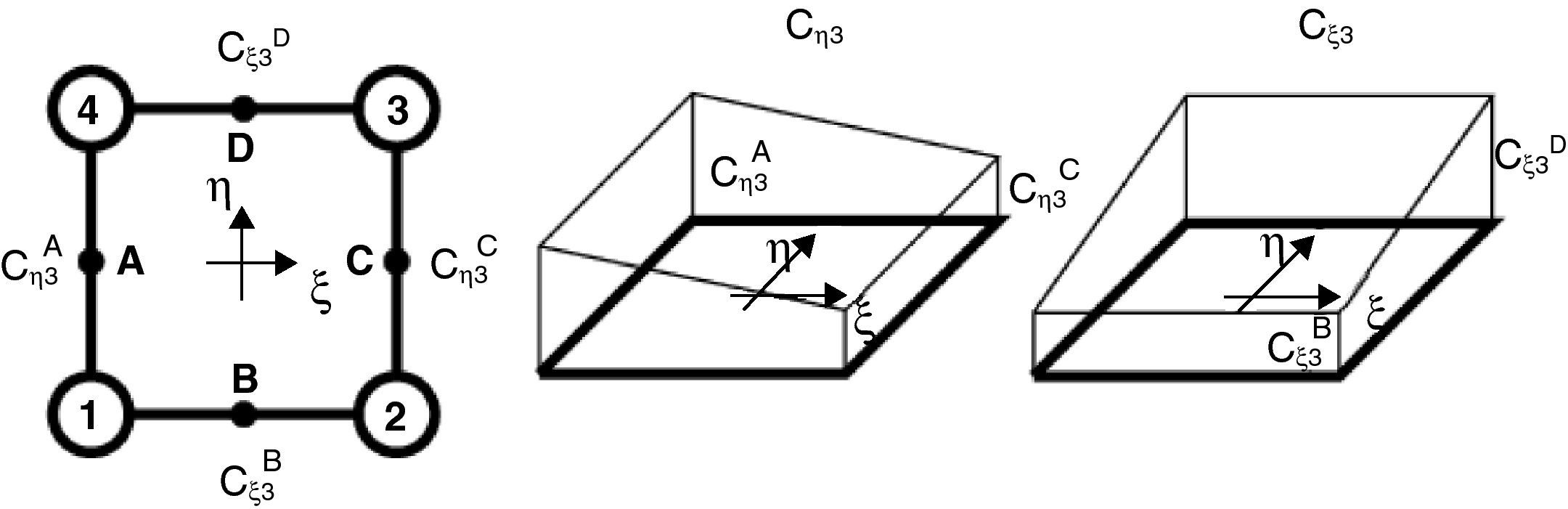
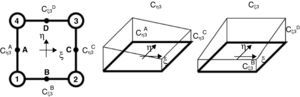
donde las componentes de corte transversal han sido definidas en un sistema mixto, i.e. que incluye las coordenadas naturales en el plano y la coordenada espacial en la dirección transversal (ξ, η, y₃). Las componentes de interés se calculan en función del gradiente tangencial al contorno y el gradiente en la dirección normal t₃ en cuatro puntos indicados como Aξ=−1,η=0, Bξ=0,η=−1, Cξ=1,η=0 y Dξ=0,η=1 (ver fig. 1). Según se ve en (36) cada componente del gradiente se mantiene constante en una dirección y varía linealmente en la otra.

Figura 1.

Puntos de evaluación de las componentes transversales en cuadriláteros.

Las componentes mixtas evaluadas en los puntos de muestreo son:

donde las fiK son las derivadas de la configuración respecto a las coordenadas indicadas con un subíndice en cada punto de muestreo, lo cual permite evaluar alternativamente (se indica con una barra superpuesta las componentes modificadas)

y de allí calcular las componentes cartesianas modificadas:

y similarmente para la otra componente de interés. Luego usando la condición aij=δij resulta

donde Jp−1 es la inversa del jacobiano de la interpolación isoparamétrica restringido al plano tangente a la superficie media. Notar que debido a la forma en que se ha definido a los sistemas locales las componentes son nulas en la configuración de referencia.

Para la evaluación de (37), se expresan las componentes del gradiente en el plano tangente respecto al sistema coordenado natural:

en tanto que el gradiente de las deformaciones respecto al sistema cartesiano resulta:

Las componentes de interés del gradiente de la deformación en el sistema natural en los puntos de muestreo (A,B,C y D) se obtienen valuando las derivadas de las funciones de forma

Recordando las funciones de forma del elemento de sólido de 8 nudos

que derivadas respecto a las componentes en el plano y valuadas en la superficie media (ζ = 0)

Evaluando en los puntos de muestreo resultan

Hasta aquí se ha escrito los gradientes (coordenadas naturales) de x en los puntos de muestreo en función de las coordenadas nodales. Los gradientes en la dirección transversal se expresan como

donde (∂∂y3) son las componentes en la dirección y₃ de la inversa del jacobiano (la tercera columna o j3−1) o también

con

Obtenidas las componentes de corte transversal, estas se pueden pasar al sistema cartesiano en la misma forma que el gradiente

Las componentes de corte transversal del tensor modificado C¯2 respecto al sistema cartesiano resultan entonces de reemplazar las (37) en las (36) y éstas en las (42)

La matriz que relaciona el incremento de desplazamientos con el incremento de deformaciones B¯, resulta de primero evaluar en los puntos de muestreo

donde (con δx^e = δu^e)

y

luego interpolar a los puntos de integración usando (36) y finalmente pasar al sistema cartesiano

5

Sobre el escalamiento selectivo de masa

La utilización de elementos de sólido para simular láminas delgadas dentro de códigos con integración explícita de las ecuaciones de movimiento tiene una importante desventaja debido a la penalización que se introduce en el incremento de tiempo crítico. Mientras que cuando se usa elementos de lámina el tiempo crítico depende de la mínima dimensión de la malla en la discretización de la superficie, cuando se usan elementos de sólidos el tiempo crítico depende de la mínima distancia en la dirección del espesor, la que puede ser muy baja para láminas delgadas, lo cual se agrava aun más al utilizar varios elementos en el espesor. Para alivianar este problema Olovsson [14] presentó un método sencillo orientado específicamente a mejorar el tiempo crítico en láminas discretizadas con varios elementos de sólido en el espesor de la lámina, que se describe a continuación en una forma diferente a la referencia original.

La idea básica en dicha estrategia es distinguir entre las aceleraciones de la superficie media, i.e. del conjunto de nudos sobre una fibra normal a la lámina, y las aceleraciones relativas a esta. Para ello se define una aceleración promedio del conjunto de los nudos sobre la fibra normal a¯ que se interpreta como la aceleración de la superficie media

donde las sumatorias incluyen a los nudos ubicados sobre la fibra y f_i y m_i son la fuerza nodal equivalente y la masa nodal respectivamente de cada uno de los nudos sobre la fibra normal. En cada nudo queda entonces una fuerza nodal equivalente que no ha sido considerada dentro de este promedio

cuya suma sobre cada fibra es nula

La aceleración de la estrategia explícita estándar es

Donde se ha separado la aceleración en la aceleración promedio de los nudos sobre la fibra (a¯) y una aceleración «relativa» de cada nudo (aˆi). Es en esta expresión donde se introduce la noción de escalamiento selectivo de la masa, modificando la aceleración relativa de cada nudo individual en la forma:

donde se ha introducido un factor β > 1 que escala la masa de cada nudo i solo a los fines de evaluar la aceleración relativa pero no la del conjunto de nudos sobre una fibra. El efecto de este factor es disminuir la velocidad de propagación de las ondas en la dirección transversal de la lámina. El factor β disminuye entonces las aceleraciones relativas entre los nudos de una misma fibra y permite aumentar el tiempo crítico.

Por otro lado denominando con α a la inversa del factor de escalamiento β

la aceleración del nudo modificada a˜i se puede escribir

con lo cual puede interpretarse al factor α de forma independiente de β. Es decir, que la aceleración modificada resulta de la suma de la aceleración promedio (a¯) escalada por un valor ligeramente menor que uno (1 − α) como valor principal y la aceleración estándar (a_i) escalada por α.

Esta técnica modifica el comportamiento dinámico del modelo cuando se utilizan valores muy bajos de α (incrementa los períodos naturales al modificar la masa), por lo cual solo puede usarse en forma totalmente confiable para problemas pseudo-estáticos, donde no importe los detalles de la respuesta dinámica.

6

Ejemplos

En el conjunto de ejemplos presentados abajo se denota por «sólido estándar» al elemento descripto en el apartado 3 y se lo denota por «SOLID» en tanto que al elemento en el que se incorpora la técnica de deformaciones impuestas para el tratamiento del corte transversal se lo designa como la versión «shell» del elemento y se lo denota por «SOL-SHE». Para materiales isótropos se realiza la descomposición de las deformaciones en partes esférica y desviadora, usando un punto de integración para la componente volumétrica y cuatro puntos de integración para la parte desviadora como se propone en [11]. Para materiales ortótropos, que no tienen flujo plástico isócoro, no se realiza la descomposición de las deformaciones y la integración de las fuerzas residuales se realiza con cuatro puntos.

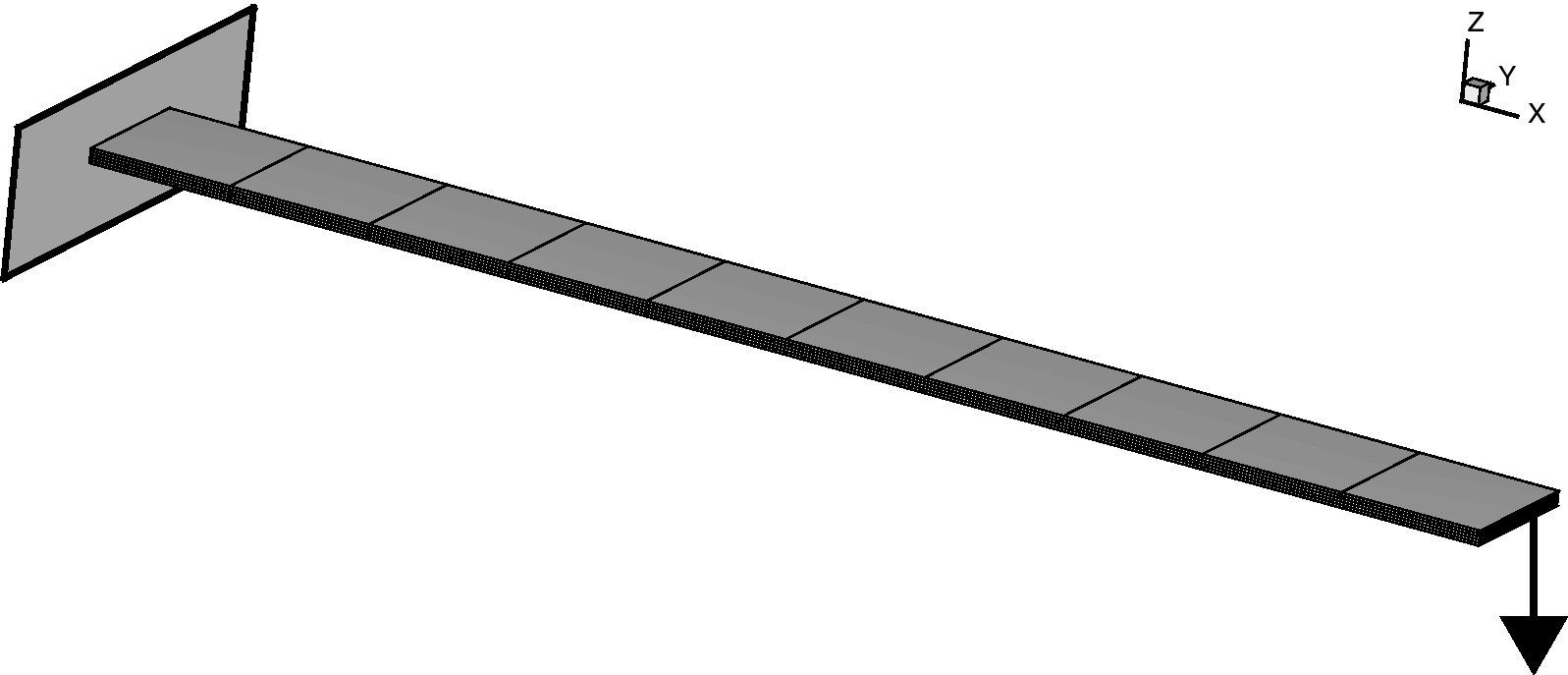
6.1

Viga en voladizo con carga puntual

En este primer ejemplo (tomado de [14]) se considera una viga en voladizo de longitud, ancho y espesor L = 1, b = 0.1 y h = 0.01 (ver figura 2). Las propiedades mecánicas son módulo de Young E = 1 × 10¹¹Pa, relación de Poisson ν = 0 y densidad δ = 1.000 kg/m³. La carga puntual tiene un valor de 100 N.

Figura 2.

Viga en voladizo bajo carga puntual.

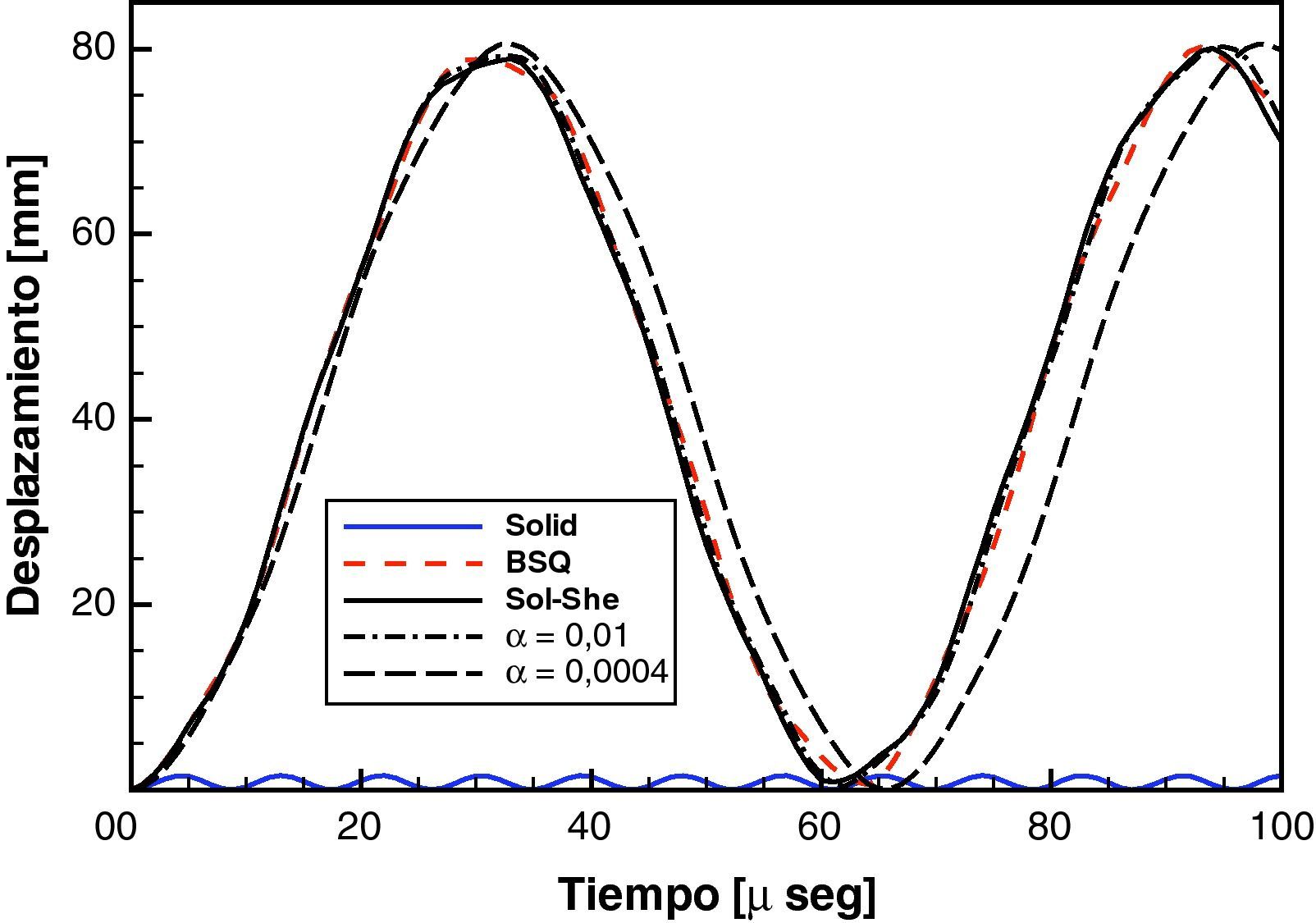
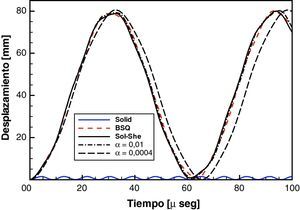
Con el elemento sólido estándar se obtiene un bloqueo por cortante que invalida totalmente el resultado. En la figura 3 se puede ver que este desplazamiento (indicado como SOLID) apenas supera el 2% del desplazamiento correcto. En dicha figura se incluye los desplazamientos obtenidos con el elemento de lámina clásico (Love-Kirchhoff) cuadrilátero sin rotaciones BSQ[7] y con la versión SOL-SHE que son practicamente coincidentes. La discretización incluye 10 elementos a lo largo del eje de la viga y 5 en el espesor.

Figura 3.

Viga en voladizo bajo carga puntual. Resultados.

Por otro lado a los efectos de ilustrar el comportamiento de la estrategia de escalamiento selectivo de masa se incluyen resultados obtenidos con dos valores del factor α, un primer valor de 0,01 que permite aumentar el incremento de tiempo 10 veces y un segundo valor (el mínimo para este modelo) de 0,0004 que permite aumentar el tiempo crítico hasta 50 veces el de la estrategia estándar. El mínimo valor de α resulta de relacionar el mínimo paso de la malla en la dirección del espesor con el mínimo paso de la malla en el plano de la lámina, en este caso

Puede verse que el primer valor no modifica el período de vibración y que el segundo ya introduce una modificación perceptible en el comportamiento dinámico, lo cual ocurre para valores aún mayores de α cuando la inercia rotacional es mayor (láminas más gruesas).

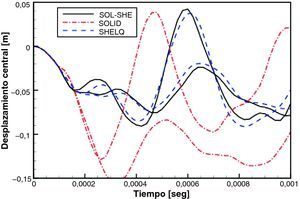
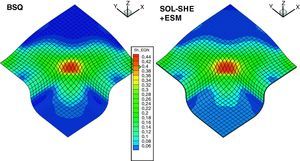
6.2

Casquete esférico bajo carga uniforme

Este es un ejemplo clásico [2] del comportamiento dinámico de láminas tanto en régimen elástico como elasto-plástico y aparece en la mayoría de los manuales de programas de elementos finitos con capacidad no-lineal (ver por ejemplo [1]). Se ha considerado una discretización de 48 elementos sobre un cuarto de la superficie de la lámina y dos elementos en el espesor. Las comparaciones se realizan entre la versión estándar y con el elemento cuadrilátero deformable por corte SHELD[9] que tiene la misma formulación para el tratamiento del corte

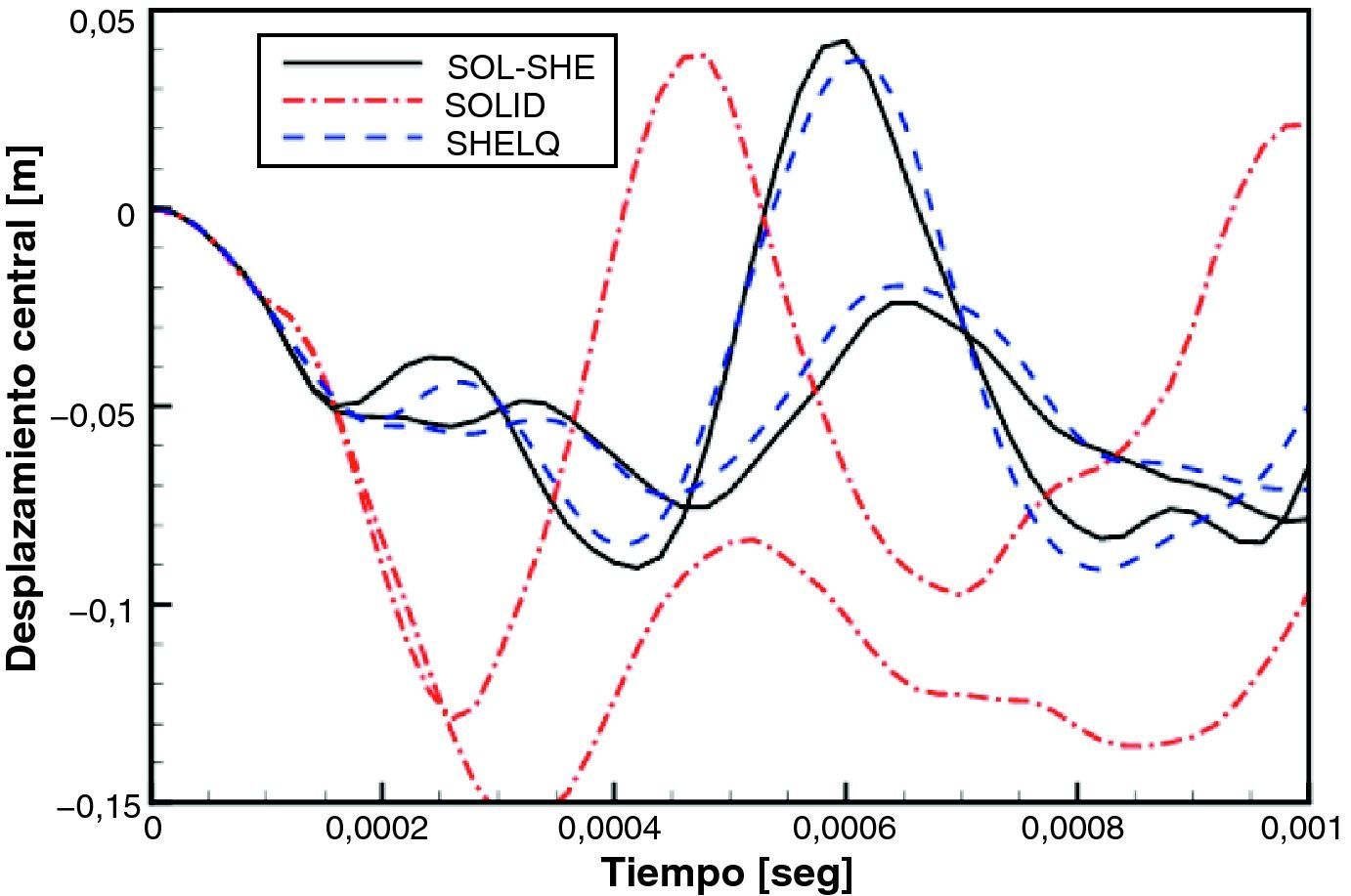
En la figura 4 se incluyen los desplazamientos del ápice del domo para comportamiento elástico (las de mayor rebote) y elasto-plástico (mayor desplazamiento negativo). Los resultados de la versión SHELL del elemento de sólido (SOL-SHE) concuerdan muy bien con el elemento de lámina SHELQ, que a su vez son los resultados habitualmente aceptados para este ejemplo. En tanto que los resultados del elemento estándar muestran una importante diferencia con los del elemento de lámina. El elemento estándar al presentar bloqueo por cortante muestra un comportamiento más rígido en toda la zona externa del casquete y mayores desplazamientos en la zona central.

Figura 4.

Domo esférico con carga uniforme.

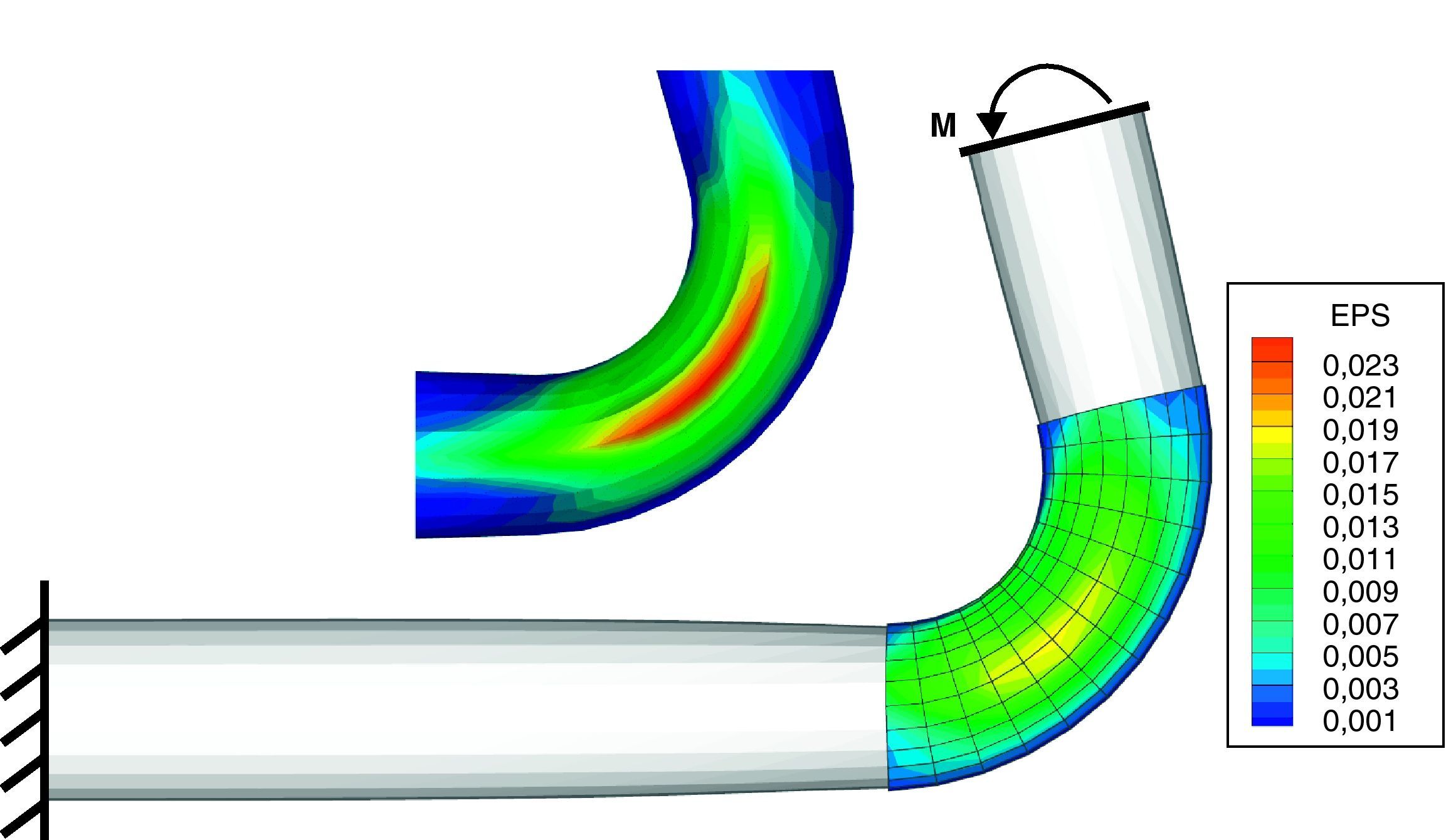
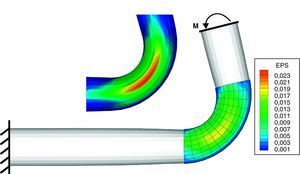
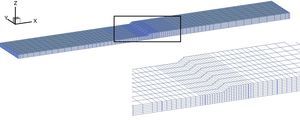
6.3

Ovalamiento de un codo

Un tubo de radio r = 19, 83 cm y espesor t = 1, 041 cm, empotrado en un extremo y formado por un tramo recto de 182, 9 cm un codo a 90^o de radio 60, 95 cm y un segundo tramo recto de 60, 96 cm, está sometido a un giro impuesto en su extremo libre. Este giro se impone sobre todos los nudos de la sección extrema de tal forma que esta se mantiene plana y circular. El tubo puede estar sometido a una presión interna y se consideran entonces dos casos a) p = 0 y b) p = 3, 45 MPa. La flexión produce un ovalamiento principalmente en la zona del codo. Las propiedades mecánicas del material constitutivo son: E = 194GPa, ν = 0.264, δ = 7.800 kg/m³ y plasticidad asociada (von Mises) con endurecimiento isótropo gobernado por la relación σ_y = 5, 71 × 10⁸(e_p + 0, 006)^0,1. Se consideraron dos tipos de modelos uno exclusivamente con elementos de láminas triangulares de 3 nudos (NBST[8]) y otro acoplado donde la zona del codo se modeló con elementos de sólido de 8 nudos. La disctretización utilizada es relativamente gruesa con 672 elementos triangulares sobre la superficie media. Se utilizaron 5 puntos de integración en el espesor de la lámina a los fines de captar razonablemente la flexión elasto-plástica. Para el modelo acoplado con sólidos se utilizaron 3 elementos en el espesor, la relación de aspecto (largo/espesor) de los elementos de sólido varía entre 15 y 30. La figura 5 muestra la geometría final del codo con la malla acoplada y la zona del codo en el modelo puramente de elementos de lámina. Se han graficado los contornos de deformaciones plásticas efectivas sobre el codo. Los valores máximos son del orden de 0,24. Se ha incluido el mismo contorno de deformaciones sobre el modelo con solo elementos de lámina con fines comparativos. En los modelos solo se ha discretizado la mitad del tubo debido a la simetría.

Figura 5.

Codo sometido a flexión. Deformada final (X = 1). Contorno de deformaciones plásticas efectivas sobre la cara externa del codo.

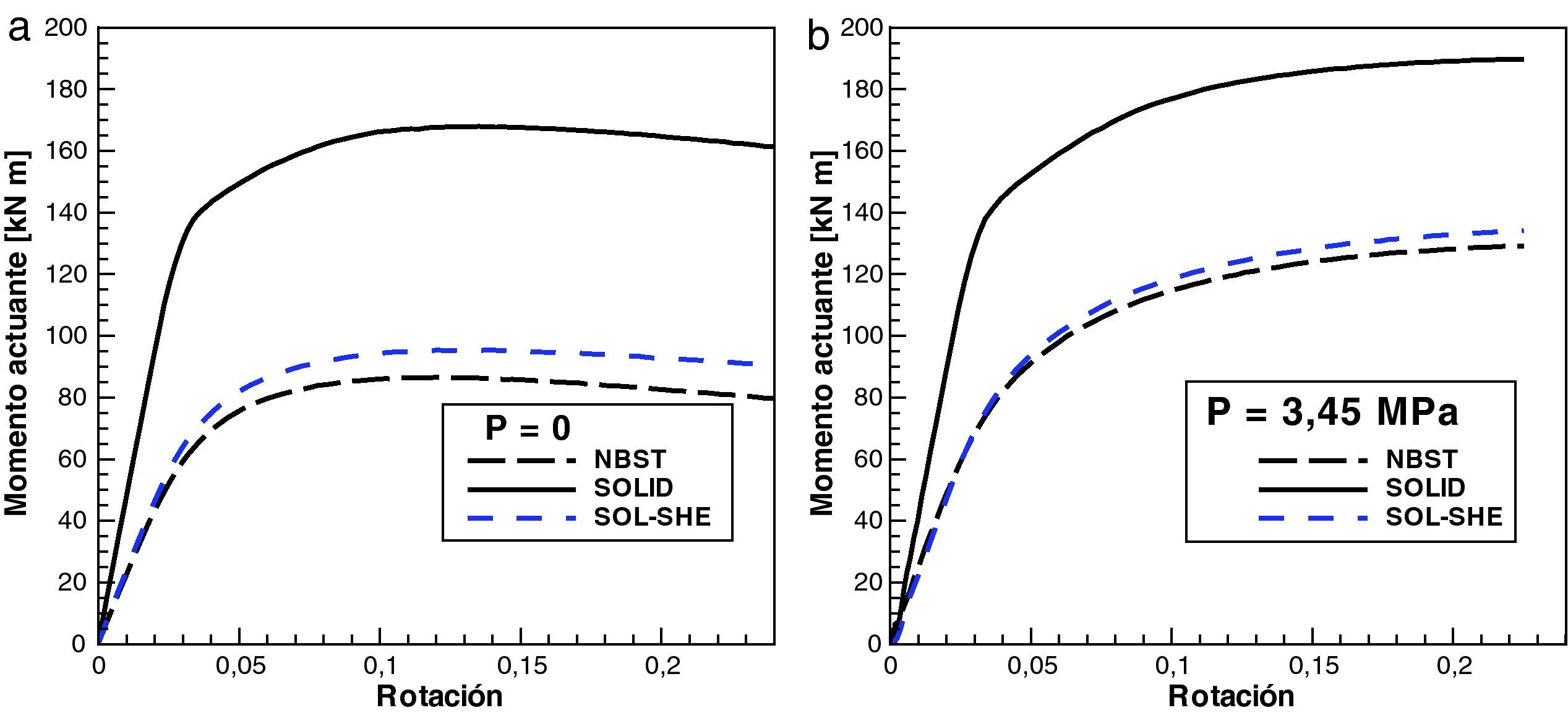
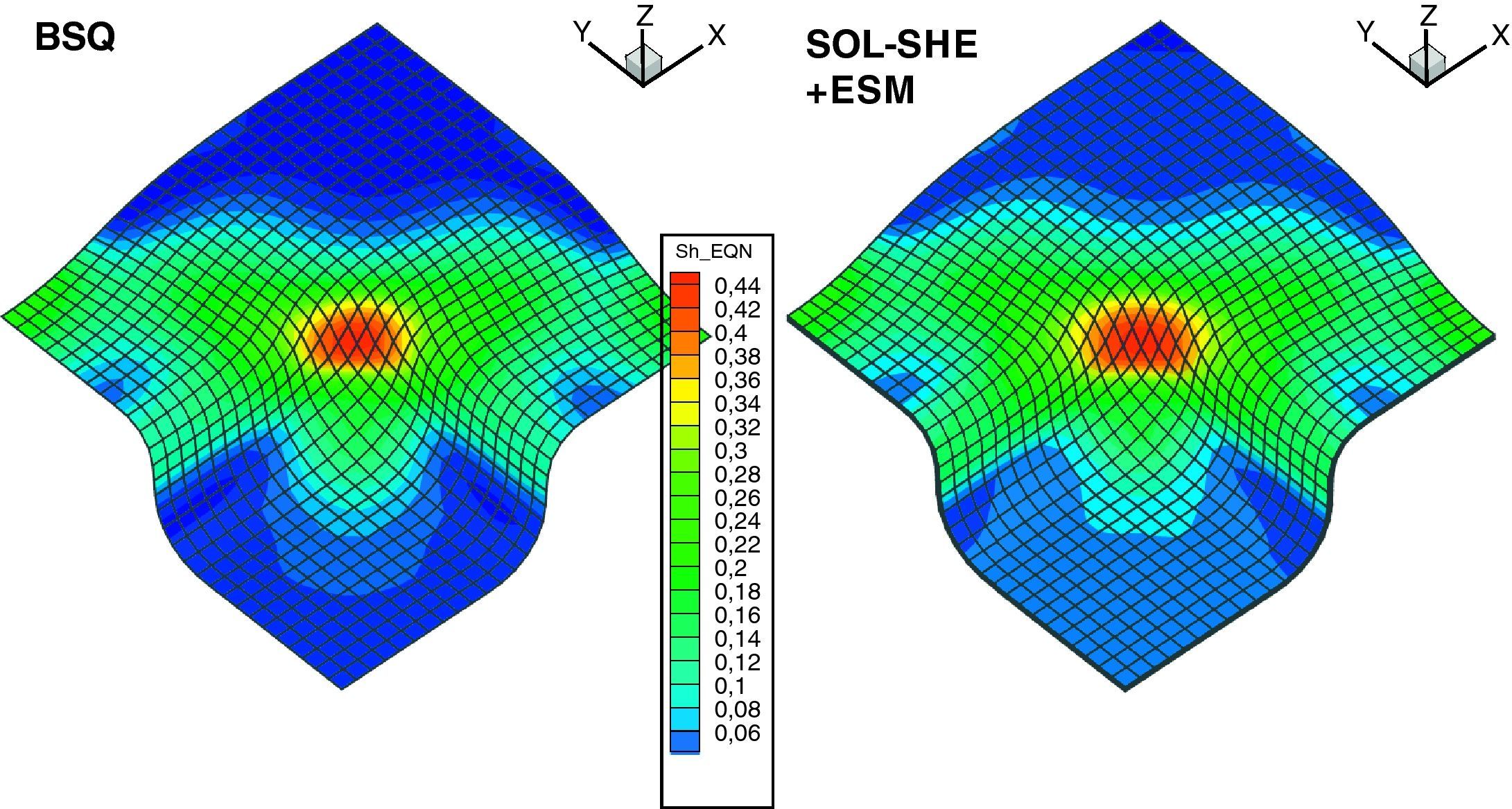
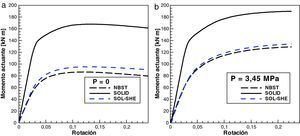
En la figura 6 se ha graficado el momento resistente en función de la rotación impuesta para ambos casos de carga (con y sin presión) y para los dos modelos considerados. Además se distinguen el caso de utilizar la formulación estándar (SOLID) y la formulación en deformaciones impuestas para el corte transversal (SOL-SHE). El modelo con sólidos estándar es notoriamente rígido debido al bloqueo por cortante en tanto que no hay diferencias significativas entre el modelo de lámina y el modelo acoplado cuando se utiliza la formulación en deformaciones impuestas. Las diferencias en este último caso son en parte debido al excelente comportamiento membranal del elemento NBST.

Figura 6.

Codo sometido a flexión. Momento resistente en función de la rotación impuesta. (a) Sin presión interna. (b) Con presión interna.

Debido a la alta relación de aspecto de los elementos de sólido y que se modela el problema como pseudo-estático se ha utilizado el escalamiento selectivo de masa que permite aumentar el tiempo crítico en 14 veces (α = 0.005).

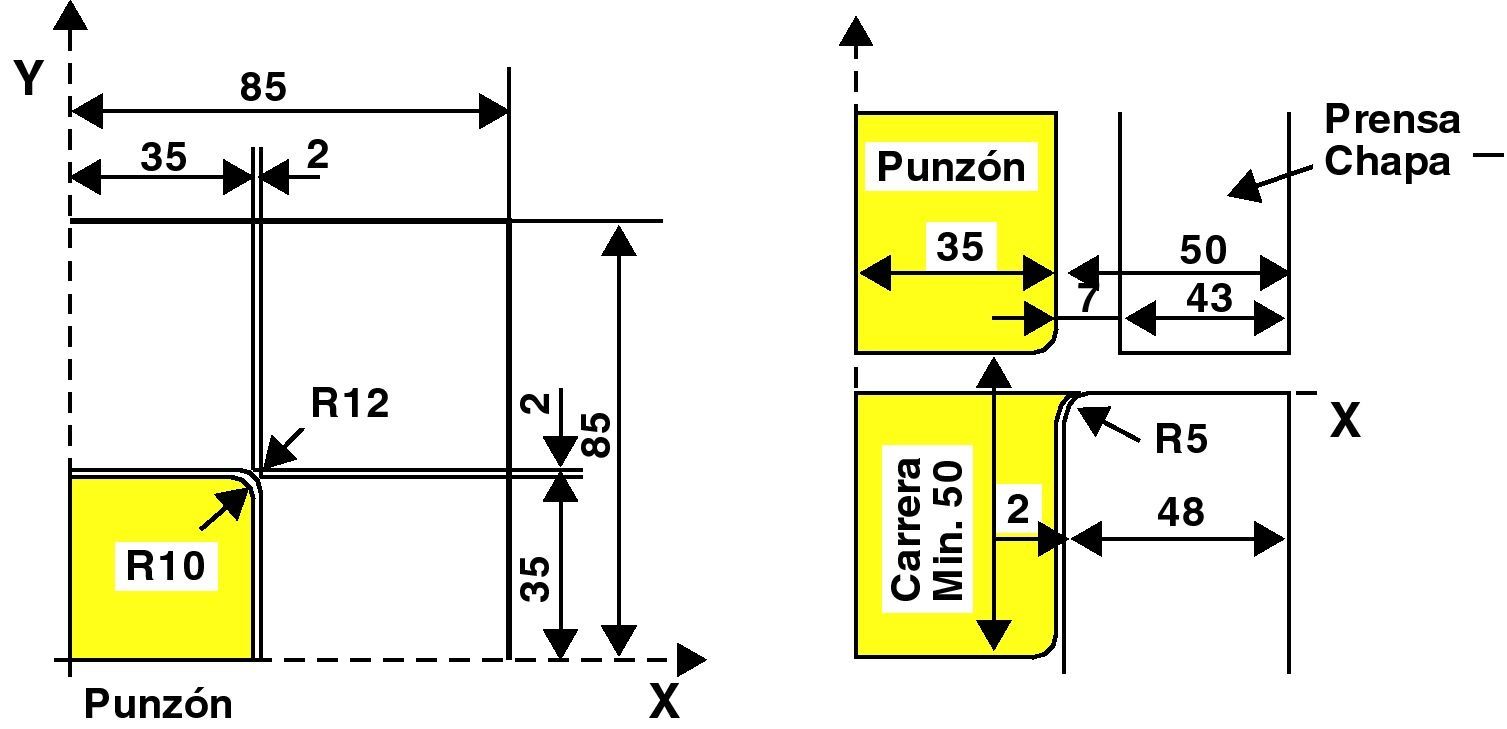
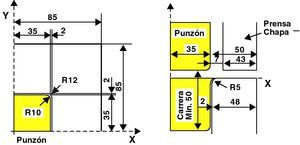
6.4

Embutición de una lámina cuadrada

Como cuarto ejemplo se ha considerado la embutición de una lámina delgada correspondiente a un «benchmark» de NUMISHEET’93 [12], que es un caso donde no interesa el comportamiento dinámico, sino que se intenta simular un problema pseudo estático. En la figura 7 se ve la geometría de las herramientas. La chapa original es cuadrada de 75 mm de lado.

Figura 7.

Geometría de las herramientas (dimensiones en mm) en el «benchmark» de Numisheet ‘93.

Se han considerado condiciones de simetría según los ejes coordenados, por lo que se ha modelado solo un cuarto de la geometría con una discretización en planta de 30 divisiones en cada dirección (900 elementos en el plano) y 4 elementos en la dirección del espesor (3.600 elementos en total). La fuerza sobre el pisador (prensa chapa) es de 19,6 kN y el coeficiente de fricción adoptado es μ = 0.144. Se ha realizado una embutición de 20 mm (carrera del punzón).

La relación entre el espesor h y el paso de la malla d_xy en el plano es

en tanto que la relación entre la mínima dimensión de la malla en el espesor y en el plano es

es decir, que la discretización en el espesor penaliza el incremento de tiempo crítico en un factor 12, 8 respecto a la discretización el espesor.

El coeficiente de escalamiento selectivo adoptado es α = 0.01 (el mínimo efectivo en este caso sería 0, 078² = 0, 006), lo cual permite aumentar el incremento de tiempo crítico 10 veces.

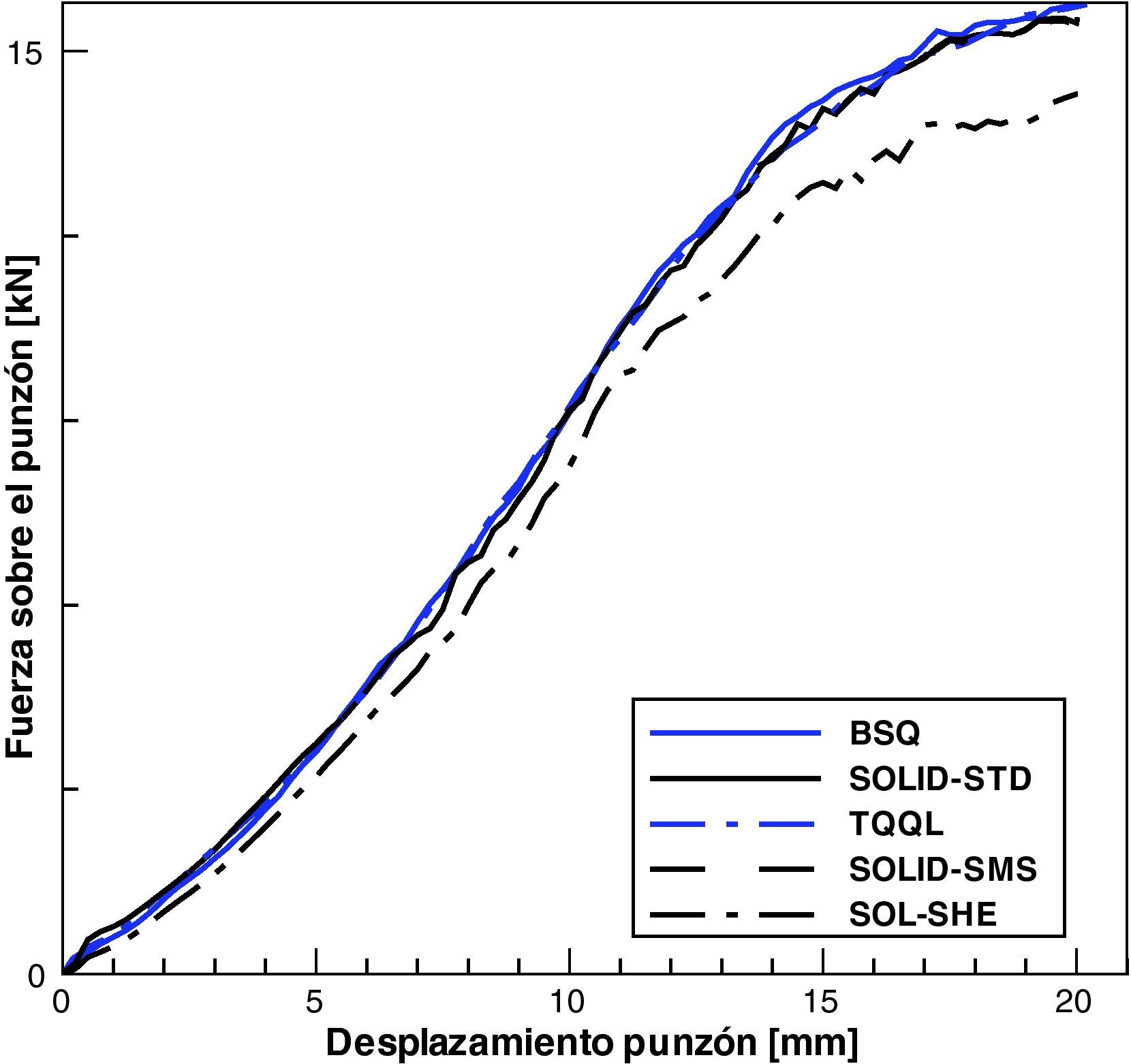
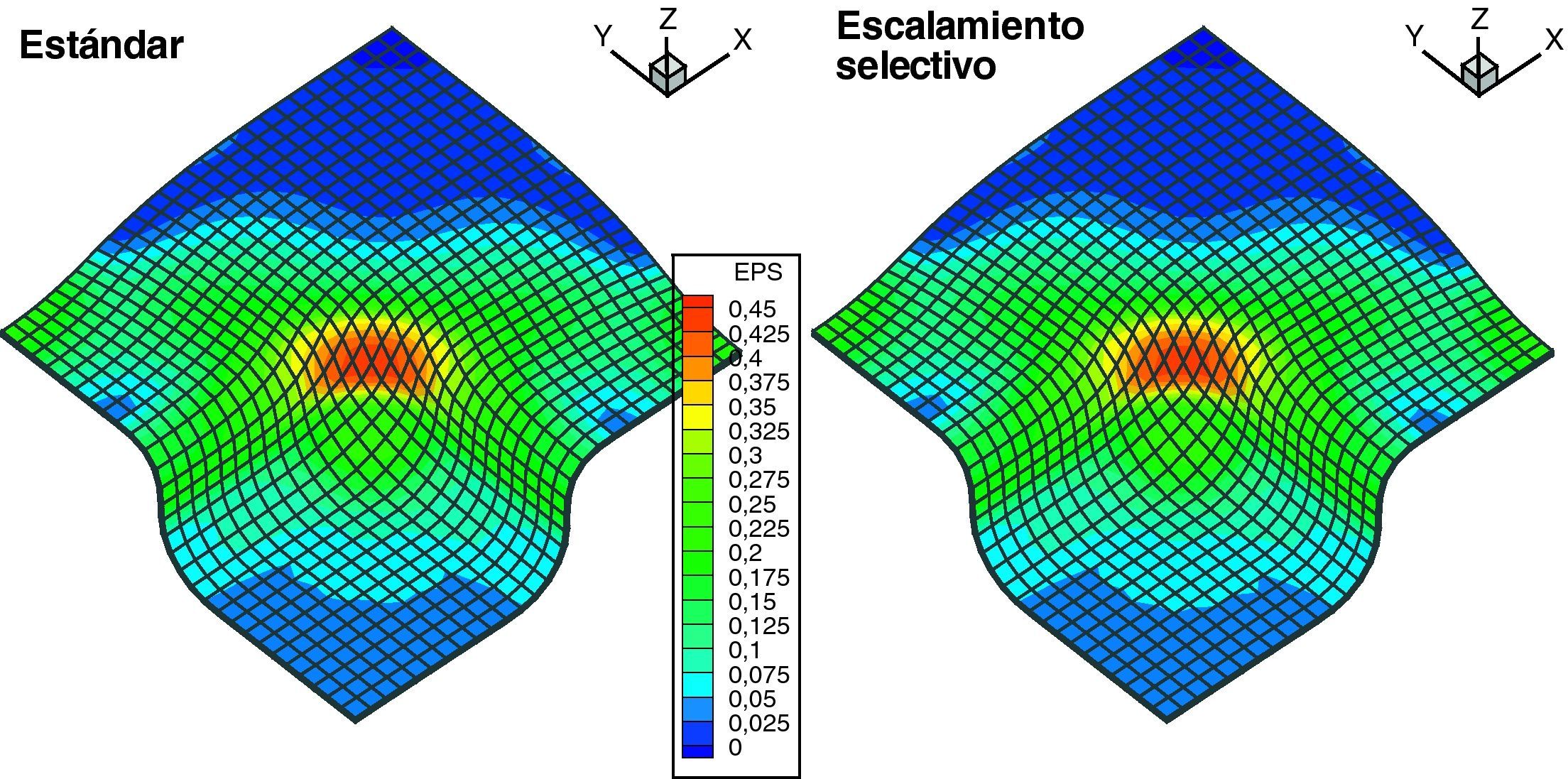
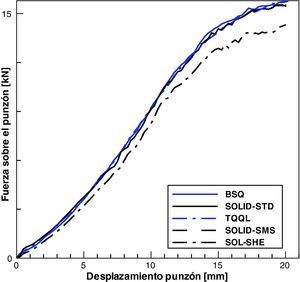
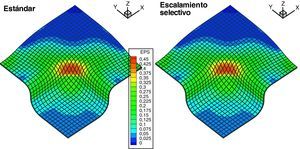
En la figura 8 se muestra la fuerza sobre el punzón en función del avance del mismo. En la figura se han incluido los resultados obtenidos con elementos de lámina triangulares de 6 nudos deformables por corte TQQL[9] y elementos cuadriláteros de lámina clásica de 4 nudos (BSQ) a los fines de la comparación con la formulación con sólidos estándar (SOLID-STD, Δt = 0, 28 × 10⁻⁷seg) y usando escalado selectivo de la masa (SOLID-SMS, Δt = 0, 28 × 10⁻⁶seg). Los incrementos de tiempo indicados son al comenzar el proceso luego decrecen durante la simulación. Puede observarse que los resultados no presentan diferencias significativas. Por otro lado se han incluido los resultados obtenidos con la versión SHELL del elemento de sólido SOLID a los fines de mostrar que el elemento funciona correctamente en grandes deformaciones, aunque es un poco más flexible.

Figura 8.

Fuerza en el punzón en función del avance del mismo.

En la figura 9 se muestra los contornos de deformación plástica efectiva para los modelos de sólido usando la formulación estándar y el escalamiento selectivo de la masa, en tanto que en la figura 10 se muestra el mismo gráfico pero para los modelos con elementos de lámina BSQ y la versión SOLID-SHELL.

Figura 9.

Deformación plástica equivalente para el máximo desplazamiento del punzón.

Figura 10.

Deformación plástica equivalente para el máximo desplazamiento del punzón.

Con el escalamiento en el presente ejemplo se logra disminuir los tiempos de ejecución a practicamente a un 10% de la versión estándar.

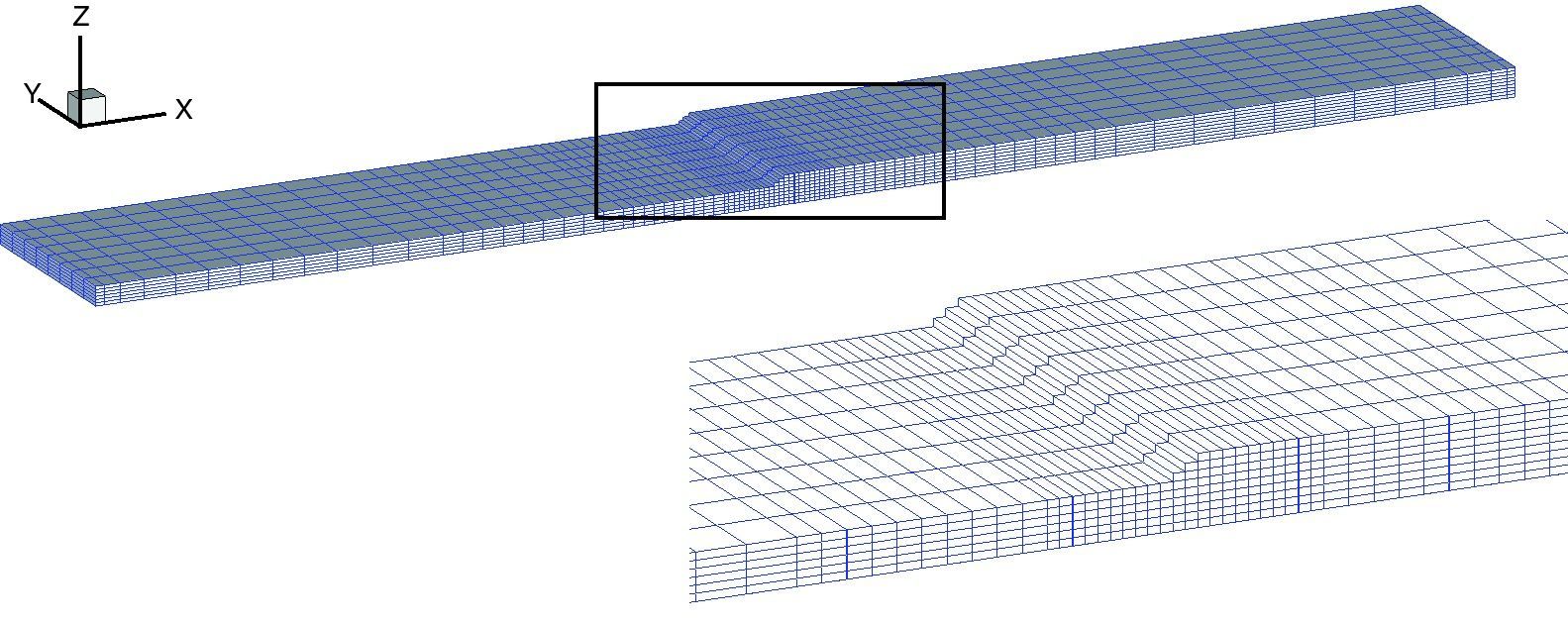
6.5

Delaminación de una probeta de material compuesto

Este último ejemplo intenta mostrar la capacidad del elemento para simular comportamiento no lineal de materiales compuestos. En la figura 11 se muestra la geometría global discretizada con elementos de sólido y un detalle de la zona donde se encuentra una discontinuidad en el espesor. La probeta está compuesta de 18 capas continuas de extremo a extremo y nueve capas discontinuas que se escalonan en la zona de central). La probeta está sometida a tracción axial lo que genera esfuerzos de flexión (corte y momento) concentrados en la zona de la discontinuidad. El esfuerzo de corte provoca la delaminación, es decir, el despegue entre la capa continua superior y la primera de las discontinuas.

Figura 11.

Probeta de material compuesto.

En el presente modelo la discretización es uniforme en la dirección del espesor con 6 elementos en la parte continua y 9 en la parte más gruesa donde cada elemento incluye una combinación de las propiedades de 3 capas. En la dirección transversal se han colocado, también en forma uniforme, 8 elementos. En la dirección axial hay 84 divisiones con elementos concentrados en la zona de discontinuidad lo que hace un total de 5.040 elementos. En este modelo el tamaño de los elementos está condicionado por el escalonado de la parte discontinua, por lo cual la estrategia de escalamiento de masa no representa ventaja y no ha sido utilizada. Por otro lado, la lámina es gruesa y la discretización suficientemente fina como para que no haya bloqueo por cortante, por lo cual se ha considerado solo al elemento estándar.

La simulación del comportamiento de esta probeta es compleja, debido a que al iniciarse el proceso de delaminación, este se autopropaga con una importante liberación de energía en forma dinámica. Esto hace difícil establecer una estrategia implícita estática (debido a que el proceso de delaminación es dinámico) con lo cual las técnicas de continuación usuales no alcanzan convergencia. Por otro lado, un análisis dinámico requiere que: a) si es implícito que el incremento de tiempo disminuya durante la delaminación debido a la velocidad de la misma, y b) si es explícito, la velocidad de estiramiento debe se lo suficientemente lenta como para permitir que se desarrolle el proceso de delaminación. En este trabajo se ha utilizado una integración explícita de las ecuaciones de movimiento pero utilizando una estrategia especial que permite el desarrollo de la delaminación.

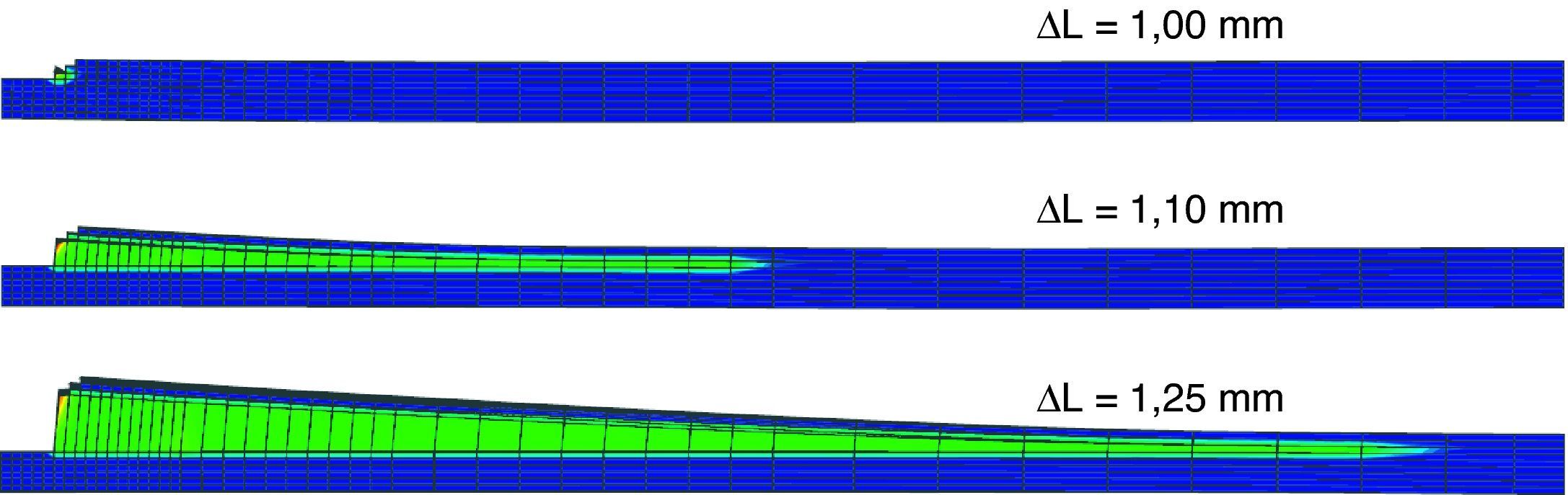
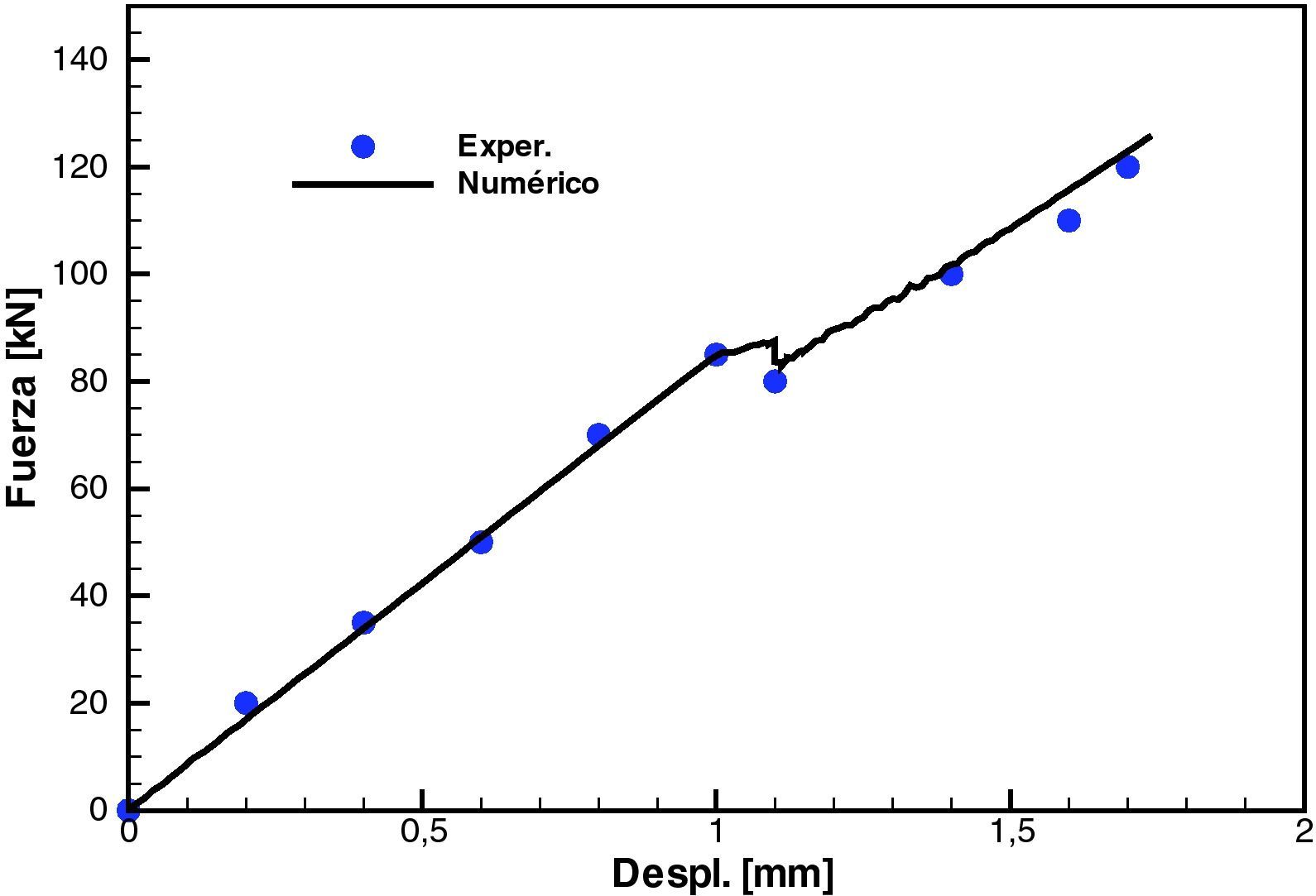
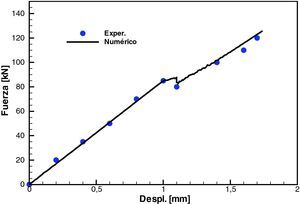
La figura 12 muestra en una vista lateral la evolución de una variable interna asociada al daño en la matriz del compuesto y la geometría deformada para tres valores de estiramiento ΔL. Finalmente en la figura 13 se ha graficado la fuerza sobre la probeta en función del estiramiento. Se incluyen allí resultados experimentales y numéricos con una excelente correlación.

Figura 12.

Probeta de material compuesto. Evolución de la delaminación.

Figura 13.

Probeta de material compuesto. Fuerza vs. estiramiento.

7

Conclusiones

En el presente trabajo se ha extendido la formulación de un elemento de sólido [6] usando una técnica clásica de deformaciones impuestas para evitar el bloqueo por corte transversal al modelar estructuras laminares. La formulación es sencilla y permite efectivamente lograr el objetivo buscado. El comportamiento es excelente para pequeñas deformaciones y resulta a un poco flexible para grandes deformaciones

Se ha reinterpretado una técnica de escalamiento selectivo de masa para aumentar el tiempo crítico de avance en códigos explícitos. Se muestra que dicha técnica es efectiva pero puede modificar las propiedades dinámicas del modelo, por lo cual su utilización debe hacerse con cuidado si es importante el seguimiento detallado en el tiempo. Por otro lado la técnica resulta muy adecuada para ser utilizadas en modelos pseudo-estáticos donde el tiempo es solo una variable auxiliar.

La formulación del elemento combinada con modelos constitutivos para materiales compuestos basados en teoría de mezclas permite modelar, con un costo razonable, el comportamiento no lineal material de estructuras de materiales compuestos.

Agradecimientos

El primer autor agradece el apoyo financiero de CONICET (Argentina), de la SeCyT-UNC y del MCyT-Cba.