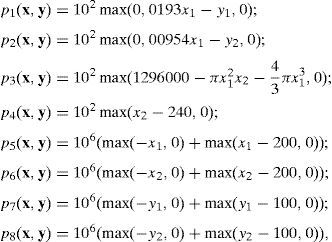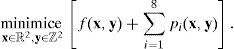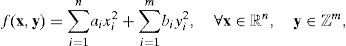Este artículo presenta un algoritmo nuevo basado en una extensión del método algorítmico simplex de Nelder Mead para la identificación de al menos un óptimo local cuando se usa en problemas no lineales enteros mixtos irrestrictos. Este método algorítmico, denominado Algoritmo Simplex Entero Mixto (ASEM) por el autor, se basa en una doble estructura de símpleces que está compuesta por una estructura simplex real de dimensión n (simplex real) y otra estructura simplex entera de igual dimensión n (simplex entero). Las operaciones propuestas originalmente por Nelder Mead se ejecutan sobre el simplex real. Por otra parte, un grupo de nuevas operaciones presentadas en este artículo se emplean en el simplex entero. Este conjunto de nuevas operaciones junto con las operaciones originales del método de Nelder Mead garantizan que en cada iteración del ASEM se arroje un nuevo punto de prueba definido en el campo numérico de dimensión 2n enteros mixtos ℝn×ℤn, con el objetivo de garantizar la identificación del óptimo local entero mixto, sin convertir las variables enteras en variables reales.
This article presents a new algorithm based on the Nelder-Mead simplex algorithmic method for identifying a local optimum, at least on unconstrained nonlinear mixed-integer problems. The algorithmic method, Integer Mixed Simplex Algorithm (IMSA), so called by the author, is based on a double simplex structure, which is composed of a real n-dimensional simplex structure (real simplex) and an integer n-dimensional simplex structure (integer simplex). The original Nelder-Mead operations are applied on the real simplex. Meanwhile, a novel group of operations are applied on the integer simplex. This new set of operations, together with the original Nelder-Mead operations, guarantee a new trail point at each IMSA iteration in the search of the local optimum in the integer real mixed 2n-dimensional numerical field ℝn×ℤn without the need of integer to real conversions.
El desarrollo de métodos de optimización para su empleo en la búsqueda de soluciones a problemas enteros mixtos ocupa un lugar importante en diversos campos de la ingeniería, debido a las amplias posibilidades de aplicación en problemas de diseño óptimo, cuando en este tipo de problemas las variables enteras no pueden ser relajadas a variables reales, que suelen ser abordados con el propósito de emplear algún método algorítmico de optimización desarrollado para variables reales. Además, esta situación de inconvertibilidad de las variables enteras a variables reales se presenta con frecuencia cuando la función objetivo del problema de optimización es representada mediante la función de desempeño del sistema bajo estudio, la cual es medida mediante algún modelo de simulación que depende tanto de variables reales como de variables enteras. Bajo estas circunstancias es inconveniente transformar el problema de optimización entero mixto (OEM) a un problema de optimización de variables reales, debido al hecho de que existen variables de decisión que no pueden ser tratadas como variables reales. Como ejemplo de sistemas que son definidos por variables enteras mixtas se tienen: el número de cajeros en un supermercado y su respectiva tasa de atención; la capacidad de clientes que pueden aguardar a ser atendidos en cada cola correspondiente a su taquilla de una agencia bancaria y la tasa de servicio de cada cajero; el número de dientes de cada engranaje que conforman una caja reductora y la dimensión de cada engranaje; el número de etapas de un sistema amplificador de señales y la ganancia de cada etapa de amplificación entre otros.
Es en esta situación donde los métodos de búsqueda directa, llamados así por primera vez por Hooke y Jeeves [1], pueden brindar una solución a este tipo de problemas de optimización, bien sea por no disponer de una expresión matemática de la función objetivo o por no contar con el gradiente de esta, principalmente cuando se requiere optimizar un proceso que depende tanto de variables reales como de variables enteras, lo que exige la aplicación de estrategias de exploración que permitan avanzar a un mejor punto de prueba en cada iteración, con el fin de identificar la solución óptima del problema.
En este artículo se presenta una extensión del método simplex de Nelder Mead (MSNM) [2] a problemas OEM cuando la función objetivo es no lineal y no está sujeta a restricciones. El Algoritmo Simplex Entero Mixto (ASEM), denominado así por el autor debido a que se basa en el patrón de búsqueda conocido como simplex, se fundamenta en las operaciones definidas por el MSNM y en un conjunto de nuevas operaciones propuestas por Brea [3], que son ejecutadas únicamente sobre las variables enteras.
De acuerdo con Brandts et al. [4], puede decirse que un simplex (d-simplex) definido en el espacio euclidiano ℝd, siendo d un entero positivo, es un casco o envoltorio convexo de d+1 puntos, los cuales no todos pertenecen al mismo hiperplano definido en el espacio ℝd, y cuyos puntos son denominados vértices del simplex.
En consecuencia, un 1-simplex es un segmento de recta en el espacio ℝ1; un 2-simplex es un triángulo en el espacio ℝ2; un 3-simplex es un tetraedro en el espacio ℝ3, y así sucesivamente.
Debido a que los problemas de optimización enteros mixtos son abordados en esta investigación mediante estructuras de simplex, se hace necesario definir 2 símpleces: uno para las variables reales, denominada aquí simplex real y otro que es empleado en el campo entero, denominado en este artículo simplex entero. Sobre estos símpleces es definido un conjunto de operaciones a fin de explorar en el espacio de búsqueda entero mixto y así poder identificar la solución óptima local del problema.
El ASEM ha mostrado ser lo suficientemente eficiente a problemas OEM irrestrictos [3]. No obstante, también ha sido probado con problemas no lineales enteros mixtos bajo restricciones a través de funciones de penalización, lo cual ha permitido comprobar que el ASEM es lo suficientemente eficaz en la identificación de óptimos locales en problemas de OEM bajo restricciones.
Mediante la ejecución de un número importante de ejemplos numéricos, Brea [5] ha comprobado el buen desempeño del MSNM cuando la función objetivo está sujeta a ruido, y además cuando el problema está sujeto a restricciones lineales. Sin embargo, existen condiciones particulares en donde el método algorítmico que él desarrolló [5] converge muy lentamente al óptimo.
Por otra parte, Barton e Ivey [6] y Humphrey y Wilson [7] han estudiado los parámetros que ofrecen el mejor desempeño del MSNM, cuando la función objetivo de un problema de optimización irrestricto está influenciada por ruido.
Estos hechos han motivado al autor a desarrollar un método algorítmico basado en el MSNM en el campo de los números enteros mixtos.
El resto de este artículo está estructurado como sigue: en la sección 2 se describe matemáticamente el tipo de problema de OEM que hay que resolver mediante el ASEM; en la sección 3 se enuncian un conjunto de definiciones preliminares que permitirán exponer claramente las proposiciones que definen las nuevas operaciones que se deben emplear sobre el simplex entero, además de facilitar la explicación del algoritmo; en la sección 4 se enuncian las proposiciones que definen las nuevas operaciones que son aplicadas sobre el simplex entero; en la sección 5 son establecidos los procedimientos empleados en el ASEM; en la sección 6 se ofrece una explicación del ASEM mediante una inédita representación basada en grafo; en la sección 7 se presenta un modo de flexibilizar el ASEM con el propósito de emplearlo en la optimización de problemas, en donde el número de componentes reales es diferente al número de componentes enteras de las variables de decisión; la sintonización o los ajustes de los parámetros del ASEM se muestran en la sección 8; en la sección 9 se muestra un conjunto de experimentos numéricos con el objeto de mostrar la eficacia del ASEM; una comparación del ASEM con otros algoritmos de optimización en el problema de diseño óptimo de un tanque presurizado se presenta en la sección 10; finalmente, se presentan conclusiones y propuestas de futuras investigaciones en la sección 11.
2El problemaProblema 1 Sean x∈ℝn el conjunto de n variables reales independientes e y∈ℤm el conjunto de m variables enteras independientes. Entonces, el problema de minimización irrestricto entero mixto puede ser expresado por:
En esta sección se establecerá un conjunto de definiciones que facilitarán la explicación del método algorítmico desarrollado.
Definición 1Espacio euclidiano entero mixto Se entenderá por espacio euclidiano entero mixto de dimensión n+m el conjunto de puntos definidos por el producto cartesiano ℝn×ℤm, donde ℝ es el conjunto de los números reales y ℤ es el conjunto de los números enteros.
Es importante señalar que, debido a la naturaleza del problema, el espacio de exploración donde deben ejecutarse las operaciones matemáticas es el espacio euclidiano entero mixto ℝn×ℤm, cuya dimensión corresponde a n+m, indicando respectivamente así el número de variables reales y enteras que conforman el problema.
Definición 2Vector precedente Sea una función f(w):W→ℝ y sean a y b 2 vectores cualesquiera definidos en un dominio W. Se dice que a precede o es igualmente precedente a b, y se denota mediante a⪯b, si f(a)≤f(b).
La definición 2 también se puede entender en el sentido estricto, esto es: un vector precede estrictamente a otro si la relación entre los valores de la función es estrictamente menor, es decir, a≺b si f(a)<f(b).
Definición 3Vector subsecuente Sea una función f(w):W→ℝ y sean a y b 2 vectores cualesquiera definidos en un dominio W. Se dice que a es subsecuente o es igualmente subsecuente a b, y se denota como a⪰b, si f(a)≥f(b).
También la definición 3 se puede entender en su sentido estrictamente subsecuente. En este caso se dice que el vector a es estrictamente subsecuente al vector b, y se denota como a≻b, si f(a)>f(b).
Definición 4Vector entero mixto Sean x∈ℝn e y∈ℤm 2 subvectores que conforman un vector v=[xtyt]t. Se dice que el vector v es un vector entero mixto en el espacio euclidiano entero mixto de dimensión n+m, para indicar respectivamente la dimensión de las componentes reales y enteras, si el vector v∈ℝn×ℤm.
Definición 5Subvector real Sea v∈ℝn×ℤm un vector entero mixto. Se dice entonces que x∈ℝn es el subvector real de dimensión n, si sus componentes representan las cantidades reales del vector entero mixto v.
Definición 6Subvector entero Sea v∈ℝn×ℤm un vector entero mixto. Se dice que y∈ℤm es el subvector entero de dimensión m, si sus componentes representan cantidades enteras del vector entero mixto v.
Debido a que el método algorítmico desarrollado para resolver problemas enteros mixtos requiere que las operaciones sobre cada subvector se ejecuten de forma independiente, es decir, que los nuevos puntos sean definidos por operaciones sobre los subvectores reales y sobre los subvectores enteros de forma separada, y que se permita así la coexistencia de ambos conjuntos de subvectores sin que ellos cambien sus condiciones en cuanto al espacio numérico que lo definen, se hacen necesarias las definiciones de operaciones sobre los subvectores pertenecientes a un mismo campo numérico.
Como consecuencia de las exigencias impuestas, se estudiará el caso particular donde n=m, quedando entonces las siguientes definiciones en el espacio euclidiano ℝn×ℤn. No obstante, se propondrá una adecuación a los problemas en el espacio euclidiano entero mixto ℝn×ℤm para cuando n≠m, y de esta forma poder aplicar el algoritmo desarrollado a situaciones en donde el número de variables reales y enteras son distintos.
Definición 7Centroide Sea un conjunto de k puntos pi=(xityit)t definidos en el espacio euclidiano entero mixto ℝn×ℤn para cada i=1, …k. Se dice que el centroide p¯ es el centro de masa de los k puntos, si a cada uno de los puntos se le ha considerado una masa mi. En el caso de que la masa de cada uno de los puntos pi sea igual, el centroide es determinado por
Observación 1 Nótese que el punto p¯ no necesariamente pertenece al espacio euclidiano ℝn×ℤn. Más aún, p¯=(x¯t,y¯t)t, donde
Definición 8Simplex entero mixto Se dice que un q-ésimo simplex entero mixto en el espacio euclidiano entero mixto ℝn×ℤn es un conjunto de diferentes puntos vi=[xityit]t para todo i=1, …, ν, donde xi∈ℝn corresponde al i-ésimo subvector real de dimensión n, yi∈ℤn denota cada i-ésimo subvector entero de dimensión n, ν=n+1 representa el número de vértices del simplex entero mixto, los cuales no todos pertenecen a la misma hipercara definida en el espacio euclidiano ℝn×ℤn, y cada uno es representado por un vector de dimensión n+n. El q-ésimo simplex entero mixto puede entonces ser representado en notación matricial como Sν[q]=[v1[q];v2[q];⋯;vν[q]].
De acuerdo con la definición 8, se establece que
donde Xν[q]∈ℝn×(n+1) e Yν[q]∈ℤn×(n+1) representan respectivamente el simplex real y el simplex entero.Un concepto importante que debe conocerse es el referente al significado de simplex colapsado o degenerado, el cual se identifica cuando todos los vértices del simplex pertenecen a un mismo hiperplano.
Definición 9Menor simplex entero Sea la matriz Yν[q]=[y1[q];y2[q];⋯;yν[q]] un q-ésimo simplex entero. Se dice que Sν[q] es el más pequeño simplex entero no colapsado contenido en ℤn×(n+1), si existe un vértice que equidista de sus otros vértices del simplex entero Sν[q] en 1.
Definición 10Aristas de Sν[q] Una p-ésima matriz de aristas de un q-ésimo simplex entero mixto Sν[q] en el espacio euclidiano entero mixto ℝn×ℤn se define como una matriz de dimensión 2n×n, cuya j-ésima columna representa la arista del simplex entero mixto Sν[q] entre un vértice referencial vp y vj para todo j=1, …, ν y j≠p, es decir,
Nótese que de acuerdo con la definición 10, una matriz Ap[q] representa el conjunto de aristas del q-ésimo simplex entero mixto Sν[q] que comparten un mismo p-ésimo vértice, es decir, son todas las aristas que se intersectan en el p-ésimo vértice del q-ésimo simplex Sν[q].
Definición 11Aristas de Xν[q] Una p-ésima submatriz de aristas de un q-ésimo simplex real Xν[q] en el espacio euclidiano ℝn se define como una matriz de dimensión n×n, cuya j-ésima columna representa la arista del simplex real Xν[q] entre un vértice referencial xp y xj para todo j=1, …, ν y j≠p, es decir,
De igual manera puede ser definida la matriz de aristas del simplex entero, la cual se puede enunciar como:
Definición 12Aristas de Yν[q] Una p-ésima submatriz de aristas de un q-ésimo simplex entera Yν[q] en el espacio euclidiano ℤn, se define como una matriz de dimensión n×n, cuya j-ésima columna representa la arista del simplex entero Yν[q] entre un vértice referencial yp e yj para todo j=1, …, ν y j≠p, es decir,
Observación 2 Nótese que un simplex real Xν[q] es colapsado si la matriz de arista Axp[q] es singular para todo j=1, …, ν. De igual modo se puede afirmar que un simplex entero Yν[q] es colapsado o degenerado si la matriz Ayp[q] es singular para todo j=1, …, ν.
Definición 13Simplex Sν[q] jerarquizado Se dice que un q-ésimo simplex entero mixto Sν[q] es jerarquizado de acuerdo con f(v) si v1⪯v2⪯⋯⪯vν, lo que significa que f(v1)≤f(v2)≤⋯≤f(vν), en el espacio euclidiano entero mixto ℝn×ℤn.
Observación 3 Cuando el simplex no esté jerarquizado según algún criterio, esto se indica con el símbolo tilde, es decir, como Y˜ν[q]. Por otra parte, nótese que cuando un q-ésimo simplex mixto está jerarquizado, tanto su correspondiente simplex real Xν[q] como su simplex entero Yν[q] están jerarquizados de acuerdo con f(v).
Definición 14Función signo de un entero Sea un número entero k∈ℤ. Entonces la función signo entero de k y que es denotada por sgnd(k) adquiere el valor de 1, si k>0; 0, si k=0; o −1, si k<0.
Debido a que el ASEM requiere contar con un conjunto de operaciones que han de ser aplicadas sobre la submatriz de elementos enteros Yν[q], se requiere establecer un conjunto de proposiciones que formarán parte de los operadores que actuarán sobre el simplex entero mixto jerarquizado de acuerdo con f(v), junto con las ya conocidas operaciones de Nelder Mead [2], las cuales son aplicadas sobre el simplex Xν[q].
Proposición 1Punto reflejado entero Sea un q-ésimo simplex entero jerarquizado Yν[q] de acuerdo a f(v), en el espacio euclidiano entero ℤn. Si el punto reflejado entero vr a través del centroide de su hipercara Hν[q]={vi∈Yν[q]|i=1,…,ν−1} opuesta al ν-ésimo vértice vν es calculado por yr es vector definido en el espacio entero ℤn; yr e yν están a sendos lados de la hipercara Hν[q].
Demostración Parte I) Denote (y1,ν, …, yn,ν)t el vértice yν, es decir, yν=(y1,ν, …, yn,ν)t. Entonces, de acuerdo con la ecuación (8), se tiene que
donde ki∈{−1, 0, 1} para todo i=1, …, n debido a la función signo discreta que es aplicada sobre cada elemento del vector. En consecuencia, cada una de las componentes de yr es entera, en virtud de que yi,ν, αe, μ y ki son todos números enteros, y para cada i=1, …, n su operación arroja un número entero.Parte II) Si tanto el vértice yν como el punto yr están ubicados en sendos lados de la hipercara Hν[q], entonces el ángulo entre los vectores formados por yν−y¯ e yr−y¯ debe ser obtuso.
Este hecho se demuestra cuando, al realizar el producto escalar (yν−y¯)t(yr−y¯), este es negativo. De esta manera se tiene que de la ecuación (8) se puede escribir
Entonces, al premultiplicar la ecuación (9) por (yν−y¯)t, se obtiene que
Simplificando la ecuación (10), se tiene que
Si se denota a (yν−y¯)t=(d1,d2,…,dn)t se tiene que
Sustituyendo la ecuación (12) en la ecuación (11) se puede afirmar que
Dado que μ=⌈∥y¯−yν∥⌉≥|di| para todo i=1, …, n, y que αe≥2 se puede asegurar que di2−αeμ|di|<0 para todo i=1, …, n, y en consecuencia (yν−y¯)t(yr−y¯)<0. Solo cuando αe=1 el producto escalar (yν−y¯)t(yr−y¯) puede ser igual a cero, lo cual provocaría el colapso del simplex entero. □
Lema 1 Sean: un vector y=(y1, …, yn)t de componentes enteros definido en el espacio euclidiano ℤn, ξ un número entero positivo, y k˜n=(k1,…,kn)t un vector cuyas componentes ki∈{−1, 0, 1}, para todo i=1, …, n. Entonces, y+ξk˜n también pertenece al espacio euclidiano entero ℤn, y su distancia a y es de ξn−l, donde l≤n es el número de componentes nulas en el vector k˜n.
Demostración. En virtud de que y=(y1,…,yn)t∈ℤn, entonces,
Debido al hecho de que cada i-ésima componente de yk indicada en la ecuación (14), es decir, yi+ξki para todo i=1, …, n es un número entero, puede asegurarse que yk∈ℤn. Por otra parte, la norma euclidiana del vector definido por la diferencia entre yk e y es
en virtud de que para todo i=1, …, n los números escalares ki∈{−1, 0, 1}. La ecuación (15) determina la distancia de y a un punto vecino yk. □Proposición 2Punto expandido entero Sea Yν[q] un q-ésimo simplex entero jerarquizado de acuerdo con f(v), definido exclusivamente en el espacio euclidiano entero ℤn. Si el punto expandido entero ye es definido por ye es un punto en el espacio de los números enteros ℤn; con respecto al vértice yν, ye nunca está más cerca de yν, de lo que está yr de yν.
Demostración. Parte I) Represente yr=(y1,r, …, yn,r)t un punto reflejado producto de la operación definida por la ecuación (8). Entonces
donde ki∈{−1, 0, 1} para todo i=1, …, n debido a la función signo discreta. En consecuencia, cada una de las componentes de ye es entera, debido al hecho de que yi,r, βe y ki son todos números enteros, para cada i=1, …, n su operación arroja un número entero.Parte II) Claramente el vector sgnd(y¯−yν) tiene la misma orientación del vector y¯−yν, y este último va desde el punto yν hasta el punto y¯. Como resultado de esto, el vector sgnd(y¯−yν) tiene como orientación un vector que va desde el punto y¯ hasta un punto que se encuentra en la región discreta entre y¯ e yr, y la norma euclidiana de βesgnd(y¯−yν), según el lema 1, es βen−l≮0, lo cual, al sumarse con yr, se ubica en un punto que no está más cerca de lo que está yr de yν.
Proposición 3Punto contraído entero Sea un q-ésimo simplex entero jerarquizado Yν[q] de acuerdo a f(v), definido únicamente en el espacio euclidiano entero ℤn. Si el punto contraído entero yc es determinado por yc es un punto en el espacio de los números enteros ℤn; con respecto al vértice yν está más cerca, de lo que está yr de yν.
Demostración. Aplicando el mismo método empleado en la demostración de la proposición 2, se demuestra la parte I) y parte II) de la proposición.
Proposición 4Simplex entero encogido Sea un q-ésimo simplex entero jerarquizado Yν[q] de acuerdo a f(v), definido solamente en el espacio euclidiano entero ℤn. Si 0<δe<1 es el coeficiente de encogimiento entero, y además, la matriz formada por
las aristas del simplex Y˜ν[q+1] con respecto al vértice y1[q] nunca son mayores a las aristas del simplex Yν[q] con respecto al vértice y1[q], en consecuencia el nuevo simplex es igual o menor en tamaño.
Demostración. Parte I) Del análisis de la operación definida por la ecuación (19) se puede afirmar que esta arroja como resultado una matriz de dimensión n×n compuesta de elementos enteros, en virtud de que el operador ⌈·⌉ aproxima cada uno de los elementos de la matrix al próximo entero por encima.
Parte II) Para demostrar esta afirmación, se tiene primero que, de acuerdo con la ecuación (20), sendas primeras columnas de Sν[q] y S˜ν[q+1] son iguales al vértice y1[q]. Ahora se deberán estudiar las normas de las aristas de sendos símpleces con respecto al vértice y1[q].
Se tiene que la matriz de aristas del simplex Sν[q] con respecto al vértice y1[q] está definida por
donde ai[q]=(a1i,a2i,…,ani)t para todo i=1, …, n.Por otra parte, la matriz de arista del simplex S˜ν[q+1] con respecto al vértice y1[q+1], de acuerdo a la ecuación (20) viene dada por
Ahora, al comparar la norma euclidiana de cada arista de ambas matrices, es decir, las matrices dadas por las ecuaciones (21) y (22), se tiene que para todo j=1, …, n
Debido al hecho de que 0<δe<1, para cada i=1, …, n y j=1, …, n, siempre se cumple que ⌈δeaij⌉2≤aij2, lo cual permite asegurar que para todo i=1, …, n, la norma euclidiana de cada j-ésima arista del simplex S˜ν[q+1] con respecto al vértice y1[q] nunca es mayor a la norma euclidiana para esa misma j-ésima arista del simplex Sν[q] con respecto al vértice y1[q]. □
Observación 4 La construcción de un nuevo simplex entero encogido mediante la proposición 4 puede producir un simplex entero colapsado S˜ν[q+1]. Como ejemplo, nótese que la proposición 4 aplicada al simplex entero S3[q]=[y1;y2;y3]=123311, con una valor de δe=1/2, arroja como resultado el simplex entero colapsado S˜3[q+1]=122322.
La figura 1 muestra las operaciones de reflexión, expansión, contracción y construcción de un simplex encogido que pueden ser ejecutadas sobre un q-ésimo simplex entero jerarquizado S3[q]=[y1;y2;y3]=131521, definido en el espacio ℤ2, cuando los coeficientes tomaron los valores αe=2, y βe=γe=1, y δe=1/2.
Obsérvese que el punto y¯=(2,72)t claramente no pertenece a los números ℤ2, sin embargo, el resto de los puntos arrojados por las distintas operaciones sobre el simplex entero S3[q] sí pertenecen al espacio de los números ℤ2.
Por último, nótese además que en la figura 1 se muestra el simplex entero encogido, el cual es denotado por S˜3[q+1]=[y1;y´2;y´3]=121543, para lo cual se empleó la proposición 4, la cual podría arrojar un simplex entero colapsado según la observación 4. No obstante, el algoritmo propuesto cuenta con etapas, las cuales deben iniciar con un nuevo simplex entero mixto.
5ProcedimientosEl ASEM se basa, entre otros pasos, en 2 procedimientos principales, que se presentan en esta sección. Es importante señalar que el superíndice [q] es en algunas oportunidades suprimido con el propósito de simplificar la notación, sin que pierda su significado.
El procedimiento mostrado en la figura 2, llamado Procedimiento de Construcción de un Simplex Entero Mixto (CSEM), permite construir un simplex entero mixto basándose, entre otros parámetros, en los valores de Δr y Δe que son definidos inicialmente por el usuario del ASEM a los efectos de tener control de los parámetros del algoritmo. Nótese que en la figura se emplea la notación 02n, la cual representa un vector nulo de dimensión 2n, es decir, un vector de elementos todos nulos.
Otro procedimiento empleado en el ASEM es el Mejoramiento de un Simplex Entero Mixto (MSEM), el cual tiene como propósito redefinir el simplex entero mixto inicial a través de la orientación de sus aristas. Este procedimiento se presenta en la figura 3 con el objetivo de buscar la mejor orientación del simplex construido por el procedimiento CSEM. Los experimentos numéricos realizados por Brea [3] probaron la eficacia del MSEM.
6El algoritmoPara iniciar la búsqueda de un mínimo local del problema 1, el ASEM, mostrado en la figura 4, arranca con sus parámetros definidos por el usuario, el número de la etapa s=1 y un punto de inicio v0∈ℝw×ℤw, donde w=max(n,m). Con el punto de inicio v0 y los parámetros, el algoritmo construye un simplex entero mixto mediante la ejecución del procedimiento CSEM. Si el ASEM es ejecutado bajo la modalidad de selección del mejor simplex entero mixto construido, el cual se indica con m=1, el algoritmo ejecuta el procedimiento MSEM e inicia el contador de iteraciones q en cero.
Una vez construido un simplex entero mixto inicial, el ASEM evalúa la función objetivo para cada uno de los vértices del simplex actual de los que no se conoce su valor, mediante el paso (3) Evaluación. Seguidamente, se determina el orden de precedencia de sus vértices a través del paso (4) Ordenamiento, lo cual permite determinar el punto de prueba reflejado mediante la ejecución del paso (5) Reflexión. Al final de este último paso, el ASEM selecciona uno de los 4 posibles casos, en función de la precedencia del punto de prueba reflejado, denotado por vr con relación a: v1, vν−1 y vν. Si vr≺v1, es decir, si f(vr)<f(v1), el ASEM ejecuta una operación de expansión, para luego decidir si el vértice vν será sustituido por el punto de prueba vr o ve. Por otra parte, si v1⪯vr⪯vν−1, el ASEM reemplaza el vértice vν por el punto de prueba vr. No obstante, si vν−1≺vr≺vν el algoritmo sustituye el vértice vν del simplex actual por el punto de prueba vr para luego ejecutar el paso (7) Contracción. Finalmente, en el caso de que vν⪯vr, el ASEM ejecuta una contracción del simplex actual por medio del paso (7) Contracción.
Después de que el ASEM tome una de las opciones de acuerdo con la precedencia de vr con relación a v1, vν−1 y vν, el algoritmo determina la cualidad del nuevo simplex de acuerdo al diámetro del simplex X, el cual es denotado por ℓx. Este valor de ℓx es comparado con un criterio de parada κx[s] de la s-ésima etapa, el cual adquiere distintos valores según la etapa que se esté ejecutando. Si ℓx≥κx[s], el ASEM ejecuta una nueva iteración. En caso contrario, el algoritmo detiene las iteraciones dentro de la etapa actual para decidir si continúa la búsqueda o no, de acuerdo con el valor de Δ=||vˆ[s]−vˆ[s−1]||. Si Δ≥¿, el ASEM asigna a κx[s]=φκx[s−1]; Δr[s]=ρΔr[s−1] y con v1 va al paso (2) Construcción de un Simplex Entero Mixto a fin de rearrancar una nueva etapa. En caso contrario, el ASEM reporta a vˆ[s]=vˆ1 como el mínimo.
7Flexibilidad del Algoritmo Ximplex Entero MixtoUna característica particular que tiene el ASEM es su flexibilidad con respecto a problemas en donde el número de componentes reales y enteras son diferentes, es decir, problemas del tipo ℝn×ℤm, donde n∈ℕ+ y m∈ℕ+ pueden ser diferentes.
Para tratar este tipo de problemas se debe convertir el problema de ℝn×ℤm a ℝmax(n,m)×ℤmax(n,m), para así permitir definir un simplex entero mixto con igual número de componentes reales y enteras.
Es importante destacar que la función objetivo definida en el espacio ℝn×ℤm es tratada con su número original de variables. No obstante, el simplex es definido con max(n, m)+1 vértices enteros mixtos todos definidos en espacio euclidiano entero mixto ℝmax(n,m)×ℤmax(n,m).
Esta generalización de los problemas enteros mixtos se muestra a través de las funciones de pruebas presentadas en el apéndice A.
8Sintonización del Algoritmo Ximplex Entero MixtoPara el proceso de sintonización del ASEM se consideraron los parámetros obtenidos en la sintonización del Algoritmo Simplex Entero Relajado (ASER) desarrollado por Brea [3], además de los valores recomendados y apoyados en las investigaciones de Brea sobre el MSNM cuando el problema de optimización no lineal está bajo restricciones lineales [5] (tabla 1).
En consecuencia, los parámetros αr, βr, γr y δr indicados en la tabla 1 fueron ajustados de acuerdo a los valores recomendados en Nelder y Mead [2], mientras los parámetros Δe, αe, βe, γe y δe se fijaron de acuerdo con los valores obtenidos en el proceso de sintonización del ASER (véase Brea [3, cap. 5]). Además, los valores de los parámetros φ y kx[1] mostrados en la tabla 1 se obtuvieron mediante pruebas preliminares, las cuales permitieron mostrar un desempeño satisfactorio del ASEM. Finalmente, el parámetro ¿ representa el criterio de comparación de los resultados obtenidos en 2 etapas sucesivas y, en consecuencia, debe ser fijado por el usuario dependiendo del máximo error que espera obtener en la comparación de 2 etapas sucesivas.
Estas consideraciones permitieron simplificar significativamente la experimentación para la obtención de los valores apropiados de ρ y Δr[1]. Es importante señalar que durante la realización de los experimentos, el número máximo de iteraciones que se le permitió ejecutar al ASEM por etapa fue de 15.000, debido a que el ASEM podía quedar en un proceso iterativo, sin encontrar un avance significativo en la minimización de la función objetivo.
La tabla 2 muestra el número de evaluaciones (NE) ejecutadas sobre la función objetivo FCℝℤ[d+d] con ai=bi=1 para todo i=1, …, d, de acuerdo con los valores de ρ y Δr[1] indicados en la tabla.
Resultados obtenidos del experimento a 3 niveles sobre la función FCℝℤ[d+d]
| d=2 | ρ∖Δr[1] | 0,5 | 1,0 | 1,5 |
| 0,7 | 175 (288e-6) | 127 (163e-6) | 133 (169e-6) | |
| 0,8 | 192 (10e-6) | 115 (14e-6) | 146 (19e-6) | |
| 0,9 | 107 (214e-6) | 165 (71e-6) | 169 (2) | |
| d=4 | ρ∖Δr[1] | 0,5 | 1,0 | 1,5 |
| 0,7 | 529 (5e-6) | 457 (1) | 425 (100e-6) | |
| 0,8 | 727 (2e-6) | 435 (174e-6) | 544(107e-6) | |
| 0,9 | 883 (15e-6) | 379 (174e-6) | 544 (3) | |
| d=8 | ρ∖Δr[1] | 0,5 | 1,0 | 1,5 |
| 0,7 | 12498 (0) | 3123 (1e-6) | 5452 (3e-6) | |
| 0,8 | 14192 (0) | 7651 (0) | 4835 (2e-6) | |
| 0,9 | 5686 (0) | 2761 (2) | 3642 (1) | |
| d=14 | ρ∖Δr[1] | 0,5 | 1,0 | 1,5 |
| 0,7 | 57251 (90) | 96558 (0) | 45253 (1) | |
| 0,8 | 17107 (1e-6) | 80936 (0) | 38234 (0) | |
| 0,9 | 5686 (0) | 2761 (2) | 3642 (1) | |
| d=18 | ρ∖Δr[1] | 0,5 | 1,0 | 1,5 |
| 0,7 | 35378 (0) | 270236 (596e-6) | 40550 (3) | |
| 0,8 | 188136 (0) | 72880 (0) | 58245 (2) | |
| 0,9 | 83971 (0) | 146017 (3e-6) | 33041 (5) | |
| d=20 | ρ∖Δr[1] | 0,5 | 1,0 | 1,5 |
| 0,7 | 405221 (3952e-6) | 253326 (1009) | 71239 (2) | |
| 0,8 | 281525 (0) | 161640 (0) | 57712 (1) | |
| 0,9 | 95165 (0) | 160039 (0) | 68075 (4) |
Además, en la tabla 2 se muestra entre paréntesis el mejor valor de la función objetivo para el NE indicado, siendo en todos los casos el punto óptimo en xˆ=0d e yˆ=0d, con un valor de la función objetivo de f(vˆ)=0.
Como ejemplo de lectura de la tabla 2 se tiene que para d=8, ρ=0, 8 y Δr[1]=1 el NE fue igual a 7.651 y el valor mínimo obtenido de la función objetivo fue entre 0 y un valor menor a 10−6, en particular fue igual a 7.67546044785799×10−8.
De la tabla 2 se puede apreciar que unos valores adecuados para ρ y Δr[1] son 0,8 y 1 respectivamente, debido al hecho de que para esos valores el ASEM identificó el punto mínimo de la función objetivo para todos los casos de dimensión entera mixta considerados.
Es importante destacar que estos valores de sintonización del ASEM son referenciales y que no deben tomarse como valores que deben satisfacer la totalidad de los casos de estudio, puesto que fueron obtenidos de casos particulares.
9Experimentos numéricosLa tabla 3 muestra los valores mínimos obtenidos por el ASEM, el mínimo teórico y el orden O de magnitud del error e, definido como
donde f˜(vˆ) representa el valor mínimo determinado por el ASEM f(vˆ) representa el valor mínimo teórico para cada una de las funciones de prueba definidas en el Apéndice A.Experimentos numéricos del ASEM sobre diversas funciones objetivo
| Problema | Condiciones | Mínimo | Total | |||||
| ρ | x0 | y0 | ASEM | Teórico | O(e) | NE | NI | |
| FCℝℤ[5+10] | 0, 85 | 10·15 | 10·110 | 3, 85399595970641×10−17 | 0 | 10−16 | 2.687 | 1.525 |
| FCℝℤ[10+5] | 0, 85 | 10·110 | 10·15 | 3, 19278384117684×10−7 | 0 | 10−6 | 22.718 | 14.854 |
| FCℝℤ[10+10] | 0, 85 | 10·110 | 10·110 | 3, 2938056148257×10−11 | 0 | 10−10 | 27.550 | 18.956 |
| FCℝℤ[20+20] | 0, 85 | 10·120 | 10·120 | 1, 42023676961727×10−9 | 0 | 10−8 | 156.785 | 121.154 |
| FCDℝℤ[5+10] | 0, 85 | 10·15 | 10·110 | 0,777777777837533 | 79 | 10−9 | 15.428 | 10.553 |
| FCDℝℤ[10+5] | 0, 85 | 10·110 | 10·15 | 0,444444465663501 | 49 | 10−7 | 5.511 | 3.551 |
| FCDℝℤ[10+10] | 0, 85 | 10·110 | 10·110 | 0,777777777837533 | 79 | 10−9 | 15.428 | 10.553 |
| FCDℝℤ[20+20] | 0, 85 | 10·120 | 10·120 | 1, 55555555557834 | 149 | 10−10 | 68.884 | 53.399 |
| FGMℝℤ[5+10] | 0, 85 | 10·15 | 10·110 | 3, 1137516964225 | - | - | 1.639 | 863 |
| FGMℝℤ[10+5] | 0, 85 | 10·110 | 10·15 | −0, 9998056161237 | - | - | 3.036 | 1.942 |
| FGMℝℤ[10+10] | 0, 85 | 10·110 | 10·110 | 3, 91853917817428 | - | - | 2.982 | 1.703 |
| FGMℝℤ[20+20] | 0, 85 | 10·120 | 10·120 | 0, 995491554751617 | - | - | 55.667 | 43.607 |
| FPMℝℤ[5+5] | 0, 85 | 10·15 | 10·15 | 1, 91104307081247×10−5 | 0 | 10−4 | 1.276 | 371 |
| FPMℝℤ[10+10] | 0, 85 | 10·110 | 10·110 | 0, 00596898501698284 | 0 | 10−2 | 2.172 | 927 |
| FPMℝℤ[20+20] | 0, 85 | 10·120 | 10·120 | 3, 07×10−5 | 0 | 10−4 | 27.897 | 17.457 |
| FRℝℤ[10+10] | 0, 99 | 5·110 | 5·110 | 6, 1531×10−13 | 0 | 10−12 | 10.213 | 6.677 |
| FRℝℤ[20+20] | 0, 99 | 5·120 | 5·120 | 4, 75×10−6 | 0 | 10−5 | 48.777 | 36.038 |
| FADℝℤ[2+1] | 0, 85 | 10·12 | 10·11 | −13, 9942 | -14 | 10−2 | 272 | 67 |
Adicionalmente, la tabla 3 presenta el número de evaluaciones (NE) de la función objetivo y el número de iteraciones (NI) totales ejecutadas por el ASEM, para las funciones de prueba. La tabla también suministra las condiciones con que fue ejecutado el ASEM, tales como el factor ρ que significa la tasa de reducción del paso de cada simplex de arranque por etapa, así como el punto inicial v0, donde 1d es el vector unitario de dimensión d. Además, el resto de los parámetros fueron ajustados de acuerdo con los valores indicados en la tabla 1.
Nótese que para los tipos de problemas denotados como FGMℝℤ[n+m] no se especificó el valor teórico debido a que esos tipos de problemas presentan múltiples mínimos locales y se ha supuesto que el mínimo identificado por el ASEM es un mínimo local al problema, mas no el mínimo global.
Para los casos en donde fue considerado un punto de inicio v0 con componentes todas iguales a 10, se puede inferir que, de haberse identificado sus respectivos mínimos por búsqueda exhaustiva, solo por las variables enteras, se hubiesen requerido 1020 evaluaciones, es decir, 100×106 T evaluaciones de la función objetivo, lo cual permite inferir la alta eficiencia que posee el ASEM desde el punto de vista del NE, en el caso de funciones objetivo convexas.
La figura 5 muestra la gráfica de f(v1[q]) del problema FCℝℤ[5+10] en función de la iteración q del ASEM, para un valor de ρ=0, 8, dejando ajustado el resto de los parámetros según lo indicado en la tabla 1, y punto v0t=(10·15t,10·110t). La figura muestra al final de cada s-ésima etapa, sobre la escala denotada por q, el valor alcanzado del número de iteraciones q. Por otro lado, en la parte inferior de la figura se muestra la escala correspondiente al número de la etapa s del ASEM, y es denotada por s. Nótese además que en la figura se representa el valor de f(v1[1]), es decir, al final de la primera iteración, cuyo valor fue de 1462.
Por otra parte, la tabla 4 presenta un resumen por etapa del ASEM, cuando este fue aplicado al problema FCℝℤ[5+10] bajo las mismas condiciones con que fue reportada la figura 5. Nótese que los datos numéricos que se muestran en la columna q corresponden al número máximo de iteraciones empleadas por el ASEM en cada etapa, así como el NE de la función objetivo.
10Comparación con otros métodosEl problema del diseño óptimo de un tanque presurizado ha servido de ejemplo de aplicación y comparación de diversos métodos algorítmicos de optimización, entre los cuales se pueden señalar los métodos de optimización estudiados por Zahara y Kao [8] y por Tahera et al. [9].
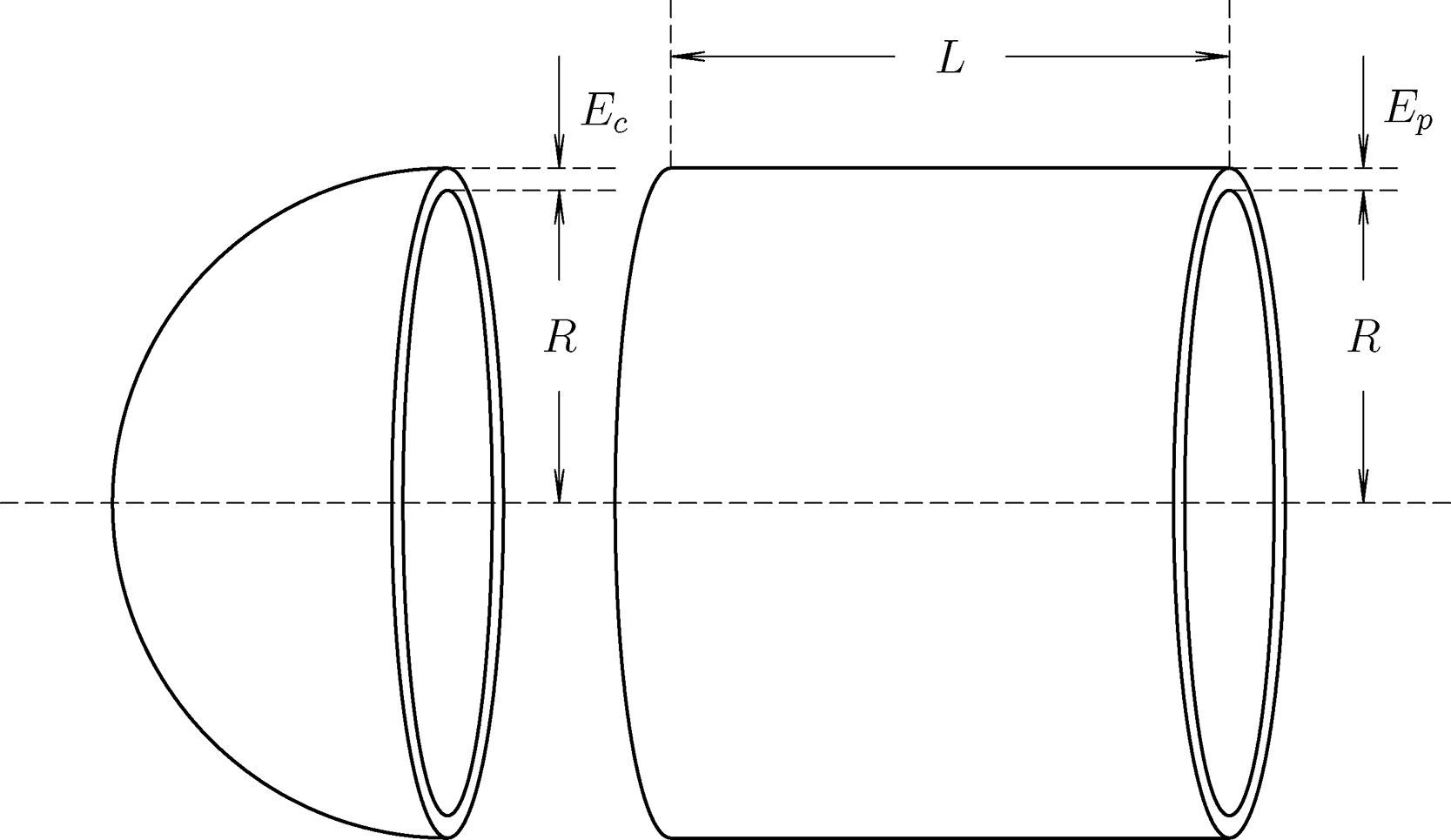
La figura 6 muestra la concha semiesférica izquierda y el cilindro de un tanque presurizado, mas no la concha semiesférica derecha que es también parte de la estructura del tanque. La gráfica presenta la geometría del tanque que hay que diseñar junto a las variables de decisión: R (x1∈ℝ, radio interno del cilindro y de las conchas semiesféricas medido en pulgadas); L (x2∈ℝ, longitud del cilindro en pulgadas); Ep (y1∈ℤ, espesor de la pared del cilindro en cantidades enteras de la fracción 116 pulgadas, debido a los distintos calibres con que es fabricado el material) y Ec (y2∈ℤ, espesor de la pared de las conchas semiesféricas en cantidades enteras de la fracción 116 pulgadas).
El problema en términos matemáticos presentado por Zahara y Kao [8,9], que expresa en dólares americanos el costo de producir un tanque cilíndrico presurizado en el que se adecuan las variables a la notación empleada en esta investigación, viene dada por
donde para todo x∈ℝ2 e y∈ℤ2,sujeto a:Con el propósito de redefinir el problema como un problema de minimización irrestricto, se definieron las siguientes funciones de penalización:
lo que permitió redefinir el problema a través de las funciones de penalización dadas por la ecuación (27) como:Para la identificación del mínimo se empleó el ASEM con sus parámetros ajustados de acuerdo con lo especificado por la tabla 1 y con valores de ρ=0, 8 y Δr[1]=1, y como punto de inicio se fijaron todas las componentes en 10.
El resultado obtenido a través del ASEM se comparó con los resultados de otros métodos tales como: el GADYM, acrónimo del inglés Gender-Age structure DYnamic parameter tuning and Mandatory self perfection scheme, propuesto por Tahera et al. [9]; el GRTA, del inglés Generalized Random Tunneling Algorithm, desarrollado por Kitayama y Yamazaki [10]; el NM-PSO, acrónimo del inglés Nelder-Mead simplex search method and Particle Swarm Optimization, de Zahara y Kao [8] y el GRG, conocido del inglés Generalised Reduced Gradient, reportado también en Tahera et al. [9], los cuales son indicados en la tabla 5.
Resultados comparativos en el problema del diseño óptimo de un envase presurizado
| Variables medidas en pulgadas [in] | ||||||
| Algoritmo | f(x, y) | S(L, R)[in2] | R(x1) | L(x2) | Ep(y1) | Ec(y2) |
| GADYM | 6.062,65 | 69.026,731 | 42,098 | 176,769 | 0,4357 | 0,8125 |
| GRTA | 6.059,58 | 68.992,022 | 42,098 | 176,634 | 0,4375 | 0,8125 |
| NM-PSO | 5.930,31 | 69.511,951 | 41,639 | 182,412 | 0,3972 | 0,8036 |
| GRG | 9.664,09 | 74.691,075 | 37,692 | 240,000 | 1 (116) | 1 (116) |
| ASEM | 8.796,92 | 60.623,882 | 51,807 | 84,627 | 1 (116) | 1 (116) |
La tabla 5 muestra los valores obtenidos de la función objetivo y sus correspondientes valores de las variables de decisión para el mejor punto identificado por cada algoritmo. Además, incluye el valor de la superficie, S(L, R)=2πRL+4πR2, de material requerido para la construcción del envase presurizado, puesto que la comparación debe hacerse según la superficie de material requerido, en virtud de que únicamente el GRG y el ASEM tomaron en cuenta la naturaleza entera de las variables Ec y Ep, las cuales están indicadas en la tabla mediante el número de fracciones de 116 pulgadas. El hecho de no poder asignar valores reales a las variables Ec y Ep produce un aumento en la función objetivo con relación a los valores que hubieran tomado Ec y Ep, en caso de haberse considerado variables reales. Nótese que de acuerdo con los resultados mostrados en la tabla 5, el ASEM alcanzó a identificar la menor superficie de material para la fabricación del envase presurizado, con sólo 440 NE, mientras que el resto de los algoritmos emplearon decenas de miles de evaluaciones de la función objetivo.
Más aún, el ASEM identificó un mejor resultado en comparación al algoritmo GRG, el cual es un algoritmo para problemas de OEM.
11ConclusionesComo conclusiones de este trabajo de investigación se tiene que:
- a)
El empleo de la estructura del simplex dentro del campo de los números enteros, junto a las redefinidas operaciones de reflexión, extensión, contracción y encogimiento, result’0 muy apropiado para definir una estrategia de identificación de óptimos de problemas enteros mixtos irrestrictos, sin el relajamiento de las variables enteras de decisión.
- b)
La principal característica que tienen los problemas de variables enteras mixtas en cuanto a la derivabilidad de sus funciones objetivo es que estas no cuentan con expresiones de derivadas con respecto a las variables enteras, desde el punto de vista estricto de la definición de derivada. Este hecho ha llevado a desarrollar un método libre de derivadas, además de haber desarrollado métodos algorítmicos que requieren un relativo bajo número de evaluaciones de la función objetivo.
Por otra parte, el desarrollo de otros enfoques para la identificación de óptimos así como de estructuras teóricas son temas de investigación que podrían constituir interesantes investigaciones, debido al reto que imponen. En específico, se pueden sugerir como temas de investigación:
- a)
El estudio teórico de las condiciones de optimalidad dentro de la programación no lineal entera mixta.
- b)
El desarrollo de funciones de penalización para el empleo del ASEM con problemas bajo restricciones. Este último puede constituir un importante trabajo de investigación, debido a las innumerables aplicaciones que tiene este tipo de problemas dentro de la ingeniería.
El autor desea expresar su gratitud al Consejo de Desarrollo Científico y Humanístico de la Universidad Central de Venezuela por la financiación de esta investigación a través del proyecto PI-08-7506-2009/1. Él desea realmente agradecer también a los árbitros por sus valiosos comentarios y sugerencias, los cuales permitieron mejorar el artículo.
En este apartado son mostrados los problemas enteros mixtos empleados en los experimentos numéricos, para lo cual se empleó una notación que permite definir la dimensión del problema de optimización. Además, para cada uno de los problemas mostrados se establece su respectiva solución óptima.
Para el caso particular de los experimentos numéricos ejecutados, se consideró ai=1 y x0i=i/3 para todo i=1, …, n, bi=1 y y0i=i/3 para todo i=1, …, m.
Solución. El mínimo global está ubicado en xˆt=(x01,x02,…,x0n¿n) e yˆt=(yˆ1,yˆ2,…,yˆm¿m), donde
con un valor de f(vˆ)=∑i=1mbiyˆi−y0i2.El problema original de [11] es:
sujeto a:dondey las funciones g(x1, x2) y h(x1, x2) para todo x∈ℝ2 vienen dadas porEl planteamiento del problema, empleando el concepto de función de penalización, queda entonces de la siguiente forma:
donde para todo x1∈ℝ; x2∈ℝ; y1∈ℤ y k=103Solución. El mínimo global está ubicado en el punto xˆt=(−2,−2) e yˆ=(0) con un valor de f(vˆ)=−14.
Una versión modificada en el campo de los números enteros mixtos al problema de optimización de la función de Griewank presentada por Fu et al. [12] se muestra a continuación:
















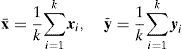
















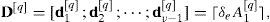
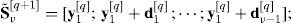
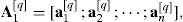






![Evolución de la función objetivo para el Problema FCℝℤ[5+10], para el caso cuando ρ=0, 8. Evolución de la función objetivo para el Problema FCℝℤ[5+10], para el caso cuando ρ=0, 8.](https://static.elsevier.es/multimedia/02131315/0000002900000003/v1_201309070038/S0213131513000345/v1_201309070038/es/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)