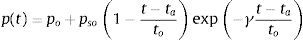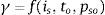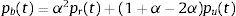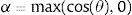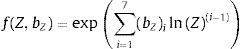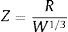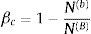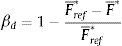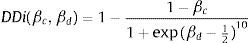En este artículo se describe una nueva metodología para evaluar el efecto de las explosiones a cielo abierto sobre estructuras equivalentes a las fachadas de los edificios. El daño sufrido por la estructura se define mediante superficies de vulnerabilidad que son función de la magnitud de la explosión, la distancia de esta a la estructura y del índice de daño por detonación desarrollado en este artículo. El índice propuesto considera la degradación de la capacidad de carga de la estructura, la fracturación y la perdida de material debido a la explosión. Para ello, la estructura se modela mediante elementos discretos (DEM) los cuales permiten representar adecuadamente estados de multifractura. La capacidad de carga de la estructura se cuantifica mediante un ensayo virtual sobre la estructura dañada. Las fuerzas provocadas sobre la estructura por la explosión se modelan utilizando una metodología semiempírica, lo que permite obviar el análisis con base en la dinámica de fluidos reduciendo el tiempo de cálculo.
In this paper, a new methodology is described to evaluate the effect of open air explosions on equivalent structures to the facades of buildings. The structural damage is defined by vulnerability surfaces that are a function of the explosion magnitude, the distance to the structure and the detonation damage index developed in this article. The proposed index considers the structural load capacity degradation, the fracturing and the loss material due to the explosion. The structure is modeled by means of discrete elements (DEM) which allows describing the multifracturing state. The load capacity of the structure is quantified by a virtual compression test on the damaged structure. The forces on the structure caused by the explosion are modeled by a semi-empirical methodology, which avoids the fluid-dynamic analysis and reduces the computation time.
La seguridad es un aspecto esencial en la gestión urbana, de manera que los métodos de detección de riesgos y cuantificación de daños juegan un papel fundamental en el diseño, planificación y operatividad de cualquier ciudad. Por desgracia, la actividad humana es en sí misma un riesgo potencial, ya sea de forma involuntaria, o premeditada. En los últimos años algunas de las áreas urbanas más importantes en el mundo han sido objeto de amenazas terroristas: El WTC de Nueva York, la estación de trenes de Atocha, el maratón de Boston, etc. Por otra parte, también es necesario considerar explosiones de origen no intencionado, provocados por desastres naturales, incendios, tornados, etc., así como accidentes. Por tales razones, en este artículo se propone una metodología para analizar los daños en los edificios causados por detonaciones.
Debido a la vulnerabilidad de las ciudades, las agencias gubernamentales están buscando estrategias para mantener niveles aceptables de seguridad [1–3] así como herramientas para gestionar el riesgo [4,5], con el objeto de estar siempre por delante de las amenazas. Estas acciones intentan reducir los daños materiales, las pérdidas humanas y mejorar la resiliencia [6].
Las detonaciones pueden ser un riesgo importante que afecta a las zonas urbanas, por ejemplo, cuando se transportan productos inflamables para ser procesados o distribuidos, cuando existen amenazas terroristas o cuando son producidas a consecuencia de un desastre natural. Bajo estas consideraciones, la planificación y la gestión urbana debe considerar dicho riesgo. Algunos autores proponen mitigar el impacto de la onda explosiva utilizando meta-materiales elásticos [7], pero esta solución es demasiado cara para ser implementada de forma generalizada en una zona urbana. En lugar de ello, la planificación de la capacidad de recuperación es más asequible y útil, lo que permite clasificar las ciudades en función de su resiliencia [8].
El efecto mecánico de una explosión se debe a la interacción de la onda de choque generada por la explosión contra una estructura. Por ello es necesario caracterizar adecuadamente el comportamiento de las ondas de choque existiendo varias estrategias. En particular Strehlow et al. [9] proponen un modelo simplificado basado en llamas de velocidad constante. Kim et al. [10] simulan la propagación de la onda expansiva en un tubo utilizando una formulación totalmente conservadora, teniendo en cuenta las propiedades termodinámicas y los parámetros químicos de detonación. Kong et al. [11] estudiaron el mecanismo de las explosiones utilizando la hidrodinámica de partículas y el método de los elementos finitos (MEF) validando sus resultados numéricos con pruebas experimentales.
Todos estos enfoques son excesivamente costosos desde el punto de vista computacional cuando el problema a resolver es la evaluación del comportamiento de un edificio sometido a una explosión. Algunos autores abordan este inconveniente incorporando funciones de onda [12,13]. Kingery desarrolla una función de ondas de choque semiempírica, utilizando la conocida escala Hopkinson o ley de la “ raíz cúbica” para escalar el efecto de la explosión [14,15]. El modelo tiene en cuenta el ángulo de incidencia de la onda de explosión, pero no considera la mitigación por objetos interpuestos entre la onda y el edificio, así como las condiciones de confinamiento.
En los últimos años, se han realizado simulaciones numéricas considerando el efecto del chorro de aire provocado por la explosión mediante el MEF, para estudiar el comportamiento de las estructuras fabricadas por diferentes materiales compuestos como el hormigón armado [16–18], fibras de alto rendimiento [19], paneles sándwich de aluminio corrugado [20,21]. Sin embargo, estos estudios no cuantifican el daño estructural, ni la vulnerabilidad de las edificaciones así como la metralla generada por la explosión. El método desarrollado por Cizelj et al. [22] predice la respuesta inelástica y la fractura de elementos subestructurales sometidos a la explosión y proporciona una evaluación rápida de la vulnerabilidad, sin embargo no mide el material desprendido del edificio y su capacidad de carga remanente. Aunque el fenómeno de la explosión está bien analizado numéricamente, las incertidumbres en el modelo tienen un efecto importante en los resultados de la simulación [23–26].
En este artículo se propone una metodología para evaluar los efectos producidos en una estructura por una explosión. Para ello se hace uso de metodologias bien probadas y experimentadas. El aspecto novedoso es su uso en situación de riesgo ante explosiones, definiendo un experimento virtual que permite cuantificar el daño mediante un nuevo índice de daño definido a partir de las simulaciones numéricas. Dichas simulaciones caracterizan adecuadamente las fuerzas de presión sobre la estructura debidas a la onda de choque [16,27,28]. La estructura se discretiza mediente el método de los elementos discretos (DEM) [29] el cual ha sido ampliamente estudiado [30–33] y en especial bajo el efecto de las explosiones [28,34–36]. Posteriormente, mediante la simuación de un ensayo de compresión, se evalúa la capacidad resistente remanente a fin de obtener la correspondiente superficie de daño o de vulnerabilidad similar a la que ha sido desarrollada en el caso de la amenaza sísmica [37–39]. Se muestra un ejemplo completo que ilustra la metodología propuesta del efecto de las explosiones sobre las estructuras. El resultado más importante es la superficie de vulnerabilidad. Cabe mencionar que la finalidad última es la de diseñar una herramienta computacional que facilite la interpretación del efecto causado por explosiones en zonas urbanas.
2El método de los elementos discretosEl método de los elementos discretos (DEM) es una técnica numérica eficaz y potente para reproducir el comportamiento del material granular. En los últimos años el DEM también se ha aplicado de manera efectiva al estudio de múltiples fracturas en sólidos formados por geomateriales (suelos y rocas), hormigón, mampostería y materiales cerámicos, entre otros.
Muy diversos trabajos de investigación sobre el DEM se han realizado en las últimas décadas ya que las primeras ideas fueron presentadas por Cundall [29]. Algunos acontecimientos clave, incluyendo las contribuciones del equipo del autor, se pueden encontrar en [29,31,32,40–60].
El análisis de materiales sólidos cohesivos con el DEM plantea una serie de dificultades para reproducir el comportamiento constitutivo de un material bajo las hipótesis del comportamiento elástico lineal y/o no lineal. Dentro del análisis de los sólidos mediante el DEM el material se representa típicamente como una colección de partículas rígidas (esferas en tres dimensiones (3D) y discos en dos dimensiones (2D)) de diámetro variable y que interactúan entre sí en las direcciones normal y tangencial. Aunque el método no se limita únicamente al uso de partículas esféricas, existiendo también el uso de polígonos (2D) y poliedros (3D). Dado que no existe una ventaja significativa para definir un continuo mediante esferas o poliedros [61], se ha optado por el uso de las primeras debido a la eficiencia y simplicidad de los algoritmos de contacto necesarios.
Respecto al diámetro de las esferas y su distribución, se requiere que sea aleatoria, siguiendo una ley de distribución normal sobre un radio medio y ordenando los elementos de forma que logre la máxima compacidad dado el dominio a discretizar. Adicionalmente es requerido que el número de coordinación medio sea superior a nueve con el fin de que las propiedades macroscópicas sean correctamente capturadas [31,34,50,62].
Dichas propiedades son función de las leyes de contacto entre las partículas, por lo que puede verse como la formulación del modelo de material del continuo subyacente a nivel microscópico. Para materiales friccionantes la ley de contactos debe tomar en cuenta la cohesión entre las partículas rígidas. Dichas uniones cohesivas pueden romperse, permitiendo así simular la fractura del material y su propagación.
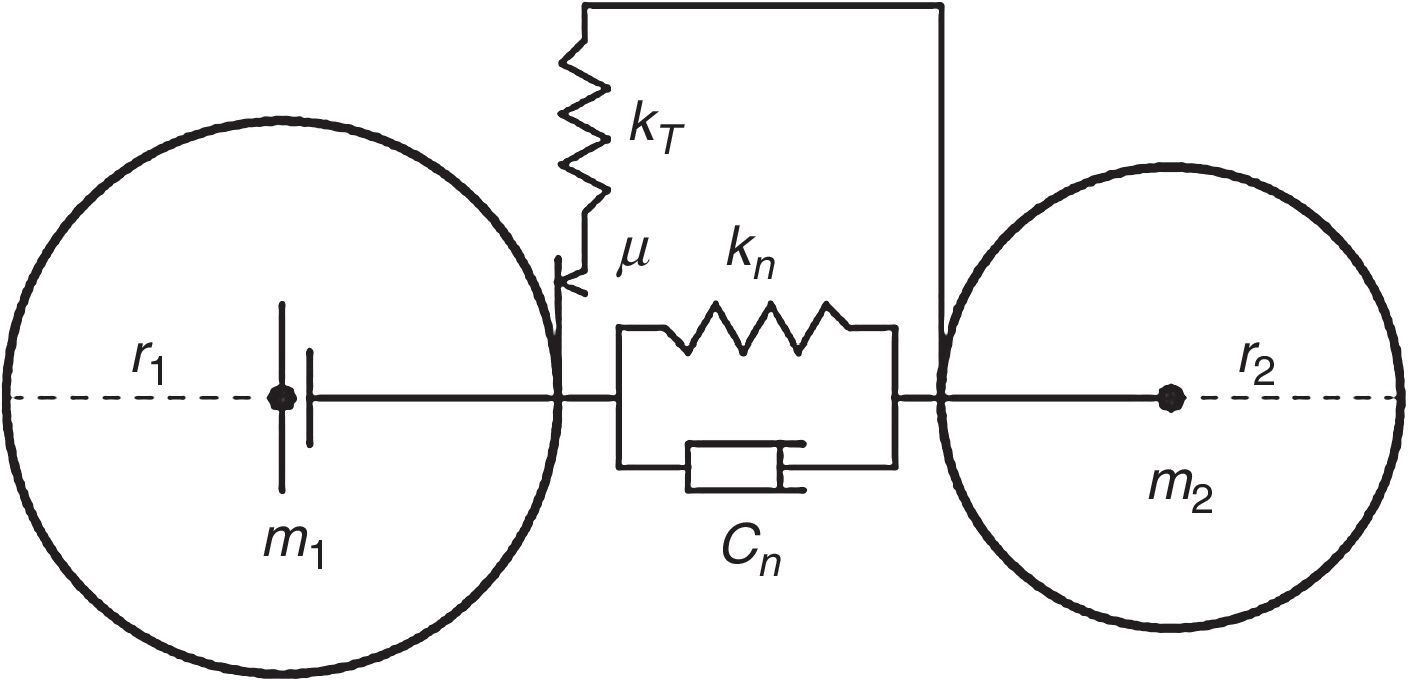
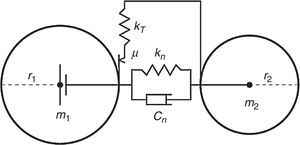
El modelo que define el contacto entre dos esferas rígidas se emplea para calcular las fuerzas de interacción entre ellas (normal y tangenciales). Este modelo se ilustra en la figura 1 y se caracteriza por la rigidez normal, kn, la rigidez tangencial, kT, el coeficiente de fricción de Coulomb, μ, y el coeficiente de amortiguamiento, cn. que disipa la energía cinética y contribuye a la fuerza de contacto normal.
Existen dos enfoques diferentes que pueden seguirse para determinar los parámetros constitutivos DEM para un material cohesivo, a saber, el enfoque global y el enfoque local [63]. El enfoque local asume que los parámetros DEM dependen de las propiedades locales de las partículas de interacción, es decir, sus radios y los parámetros continuos en cada punto de interacción [63]. En el enfoque global se asumen las propiedades del modelo de contacto de manera uniforme para todo el conjunto de elementos discretos. Los valores de los parámetros a usar en el DEM se pueden encontrar a través de diferentes procedimientos. Algunos autores [47,48] han utilizado experimentos numéricos para determinar las relaciones entre los parámetros DEM y continuos expresados en forma adimensional. Este método ha sido utilizado por los autores en trabajos anteriores [31,32,50–52,54,55] y en él se basa la determinación de los parámetros en este trabajo.
La dinámica de una estrucutra discretizada mediante el DEM se basa en la evaluación de las fuerzas de cohesión así como las externas provocando el movimento de las esferas de acuerdo con las leyes de newton por lo que se utiliza un esquema de integración explícito (Euler) de paso medio.
3Fuerzas por detonaciónEn lugar de realizar la simulación del movimiento en el aire de la onda de choque provocada por la explosión, se utiliza un modelo semi-empírico basado en la ecuación de Friedlander [16,27] para evaluar la presión generada por esta a fin de reducir el esfuerzo computacional.
Si bien esta formulación se basa en las implementaciones de Hyde en el programa CONWEP [64] en este trabajo se ha utilizado el modelo propuesto por Swisdak [65] el cual está basado en las consideraciones realizadas por Kingery et al. [15], siendo hoy en día una de las formas más aproximadas para el cálculo de la presión debido a una explosión [66] Aunque la exactitud de la metodología usada puede ser superada por un análisis fluido dinámico mediante elementos finitos, el tiempo de cálculo necesario por dicho análisis lo vuelve inviable para obtener las curvas de vulnerabilidad ya que se requiere calcular un gran número de explosiones variando la magnitud de esta así como la distancia entre la detonación y la estructura.
Por otra parte, considerando la dificultad inherente a la realización de experimentos con la finalidad de validar la formulación utilizada, se ha decidido utilizar una metodología suficientemente probada y documentada, a efectos de contar con la certeza de evaluar correctamente los efectos de una explosión a cielo abierto [15,64,66–68]
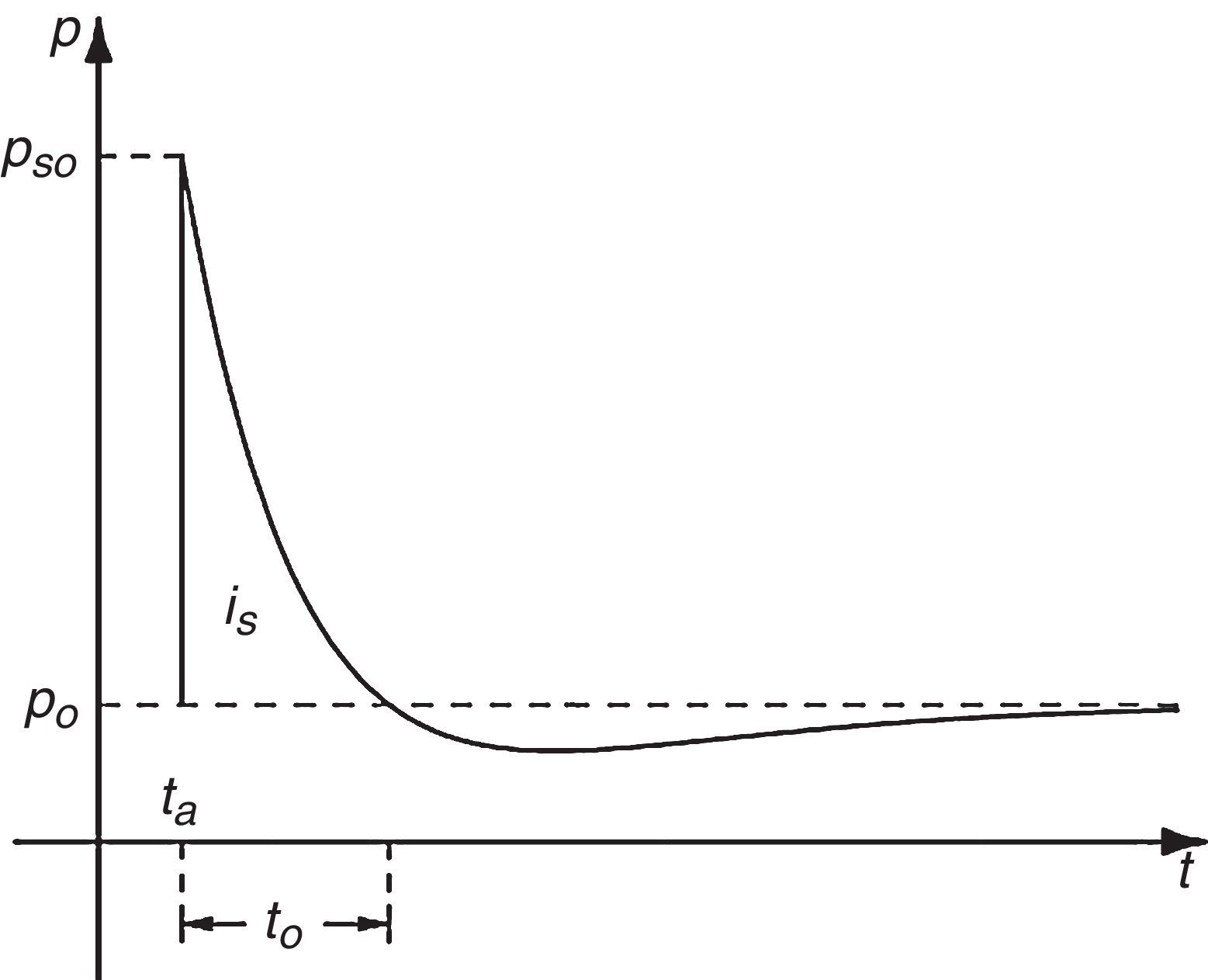
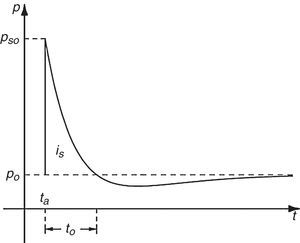
3.1Ondas de choqueLas fuerzas actuantes sobre un objeto, debido a una explosión, se debe a la onda de choque, que se caracteriza como un aumento instantáneo de la presión, respecto la presión de referencia, Po, hasta llegar a un valor máximo de sobrepresión, definido por pso como se puede ver en la figura 2 que ilustra la distribución de la presión de la ecuación de Friedlander. Este valor máximo decae exponencialmente hasta alcanzar de nuevo la presión de referencia. El área bajo la curva por encima de la presión de referencia se conoce como fase positiva y se denota como iS. El tiempo de llegada de la onda se denota por ta y la duración del pico de presión en la fase positiva es to. La fase negativa (p<Po) se produce indirectamente por el decaimiento de la función controlada por el parámetro γ en la ecuación de Friedlander (1)
conEl coeficiente de decrecimiento γ juega un papel importante en la predicción de la distribución de la presión. Para calcular este parámetro se utiliza el método iterativo de Randers et al. [69], que tiene en cuenta la fase positiva, su duración y la sobrepresión [65].
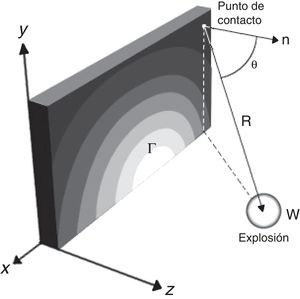
La presión provocada por la onda de choque sobre una superficie Γ (fig. 3) se define como pb(t), y es una combinación de dos funciones de presión: La presión incidente, pu(t), y la presión reflejada, pr(t), pues se considera que la explosión ocurre a nivel del suelo.
La onda de presión incidente es provocada directamente por la detonación, mientras que la onda de presión reflejada se debe a la reflexión de la onda incidente sobre suelo, él cual es considerado infinitamente rígido. Ambas funciones son dadas por la ecuación de Friedlander y se pueden combinar con la formulación propuesta por Randers et al. [69]
donde α está relacionada con el ángulo de incidencia de la onda de choque medianteEn esta ecuación, θ es el ángulo entre el vector normal a la superficie Γ y el vector que apunta hacia la fuente de la detonación desde el centroide del elemento i, como se muestra en la figura 3.
La estimación de los parámetros correspondientes a las ecuaciones (3), (1) y (2) se realiza mediante la función f(Z, bZ)
en donde bZ es un conjunto de siete coeficientes calibrados experimentalmente [42] y asociados a cada uno de los seis parámetros necesarios para calcular el valor de pb(t). Z corresponde a la distancia escalada definida pordonde R es la distancia entre la detonación y el punto analizado (3) y W corresponde a la masa explosiva expresada en kg equivalentes de TNT [64]. Mas detalles de la implementación de esta formulación sobre el DEM se pueden encontrar en el trabajo de Neri [28].4Índices de daño4.1βc: Índice de enlaces cohesivos rotosEl método de los elementos discretos permite obtener un indicador indirecto del volumen de material dañado si consideramos que el número de enlaces para una esfera cualquiera es constante (número de coordinación) y el radio de todas estas es similar. Esta condición se da y es necesaria en los análisis realizados mediante elementos discretos para la modelización de un continuo, de manera que se define el índice de enlaces cohesivos rotos como
βc se puede interpretar como un indicador global sobre el volumen de material dañado y/o desprendido de la estructura. En dicha expresión N(b) es la suma de las uniones cohesivas que se han roto después de la explosión y N(B) es la totalidad de las uniones cohesivas iniciales. βc toma valores entre cero y uno. Cuando βc es igual a cero, la estructura está intacta y cuando βc es igual a uno, la estructura está completamente pulverizada, es decir, todas las uniones cohesivas de los elementos se han roto.4.2βd: Índice de la capacidad remanenteEs obvio que si la capacidad de carga de una estructura disminuye, su estabilidad queda comprometida, esta información queda reflejada por el índice de la capacidad remanente, que es la relación entre la fuerza de compresión máxima que soporta la estructura afectada por la detonación, F¯*, y F¯ref* la correspondiente para la estructura sin daño alguno
el índice βd también toma valores entre cero y uno. Cuando βd es igual a cero, la estructura está intacta y cuando βd es igual a uno la estructura es incapaz de soportar carga alguna.La capacidad de carga máxima de la estructura es evaluada de forma global mediante un ensayo virtual de compresión de manera análoga a las pruebas de compresión de cilindros de hormigón. Es obvio que este experimento es irreproducible en la realidad, sin embargo, el uso de técnicas numéricas permite extraer información de gran utilidad como se detalla en el apartado 6.
4.3DDi: Índice de daño por detonaciónEl índice de daño por detonación (DDi) combina la información proporcionada por los índices globales de la estructura βc y βd. Este nuevo índice está inspirado en los propuestos para el análisis de riesgos sísmicos y de desastres [38,70–73].
Tanto βd como βc presentan un comportamiento sigmoidal en función del número de kg de TNT y de la distancia considerada, sin embargo βd crece de forma más rápida que βc, por esta razón, βc puede ser aproximada por una función lineal en el mismo dominio en el que βd se describe como sigmoidal. Por este motivo, la variable βd modula el comportamiento sigmoidal que da forma a la curva del DDi, pues se considera que es más representativa del daño que la variable βc. De esta forma, el índice de daño por detonación se define como
con la ventaja de que también está acotado ente cero y uno, y se interpreta de la misma forma que los indicadores βc y βd. Esta idea fue utilizada por Carreño et al. [74] al proponer un índice de gestión de riesgos.Obsérvese que la ecuación (9) también actúa como un operador lógico suavizado tipo “OR”, ya que si βc o βd son iguales a uno, el DDi también lo será, pero si βc o βd es igual a cero, el índice DDi lo será igualmente. Esto permite evaluar una amplia gama de escenarios, como el caso extremo donde βc es muy cercano de uno y βd es muy cercano a cero, lo que implica que la detonación desplaza la fachada de la verticalidad (rompiendo pocos enlaces cohesivos) y provocando su colapso por flexión. Como es de esperar, en este caso el DDi indica un daño grave aunque este no sea capturado por la variable βc.
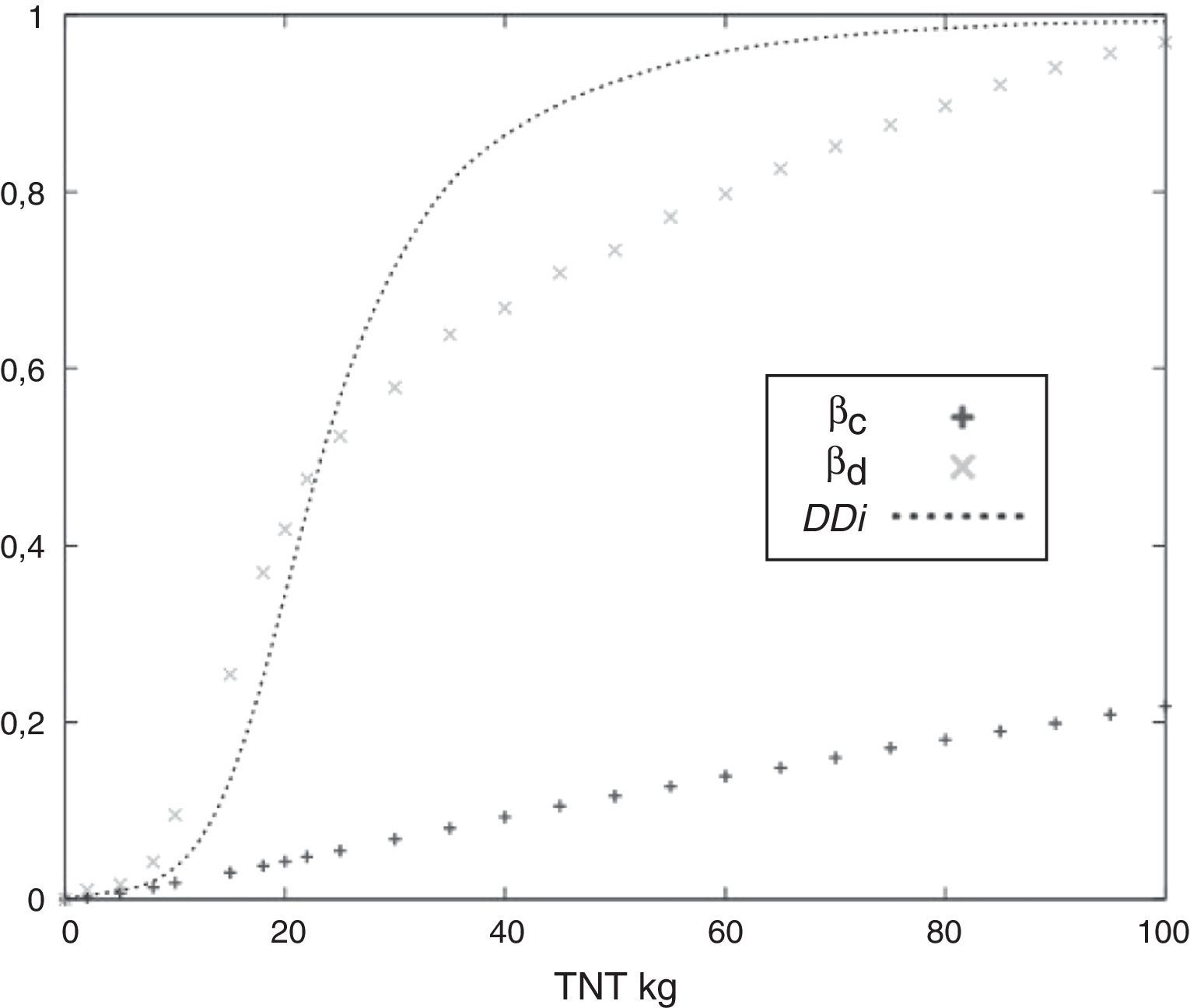
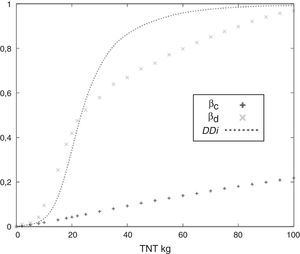
5Curvas de vulnerabilidadUna curva de vulnerabilidad es una función que representa el daño como una variable acotada entre 0 y 1 en función de la magnitud de la acción que provoca dicho daño. Para desarrollar curvas de vulnerabilidad en función del DDi es necesario calcular los índices βd y βc para distintas cargas de TNT ubicadas a la misma distancia de la estructura. Los valores intermedios se interpolan para estimar todo el rango de valores de la carga de TNT. A manera de ejemplo, la figura 4 muestra la curva de vulnerabilidad y los índices βd y βc obtenidos a partir de 24 simulaciones numéricas, variando la magnitud de la explosión a una distancia de 1m respecto a la estructura.
Un conjunto de curvas de vulnerabilidad forman una superficie de vulnerabilidad con dos variables independientes: la energía de la explosión en kg de TNT y la distancia en m de esta a la estructura. De la misma forma que en el caso de las curvas de vulnerabilidad, los valores intermedios se generan por interpolación. Las superficies de vulnerabilidad resultan útiles para estimar el valor de índice de daño de la fachada de un edificio sin la necesidad de realizar una simulación numérica.
Con base en la evaluación de la vulnerabilidad propuesto por Cizelj et al. [22] y el análisis de la vulnerabilidad sísmica realizado por Barbat et al. [70,75], se presenta una interpretación práctica de los valores proporcionados por DDi y definidos en la tabla 1.
Rangos propuestos para la interpretación del DDi
| DDi | Consecuencias esperadas |
|---|---|
| [0, 0.1] | No hay un daño considerable y podría ser ignorado en la mayoría de los casos. |
| (0.1, 0.45] | La estructura debe ser inspeccionada con cautela, debido a que el daño podría afectar seriamente su capacidad de carga. |
| (0.45, 0.8] | La estructura se derrumbó total o parcialmente y debe ser reconstruida. |
| (0.8, 1] | La estructura ha desaparecido. |
Cuando las explosiones ocurren fuera de un edificio, por lo general suelen suceder a nivel del suelo; por lo tanto, las fuerzas ejercidas por la onda de choque son considerablemente mayores en la fachada del edificio que en el resto de sus elementos estructurales y ornamentales. De esta manera el daño de toda la estructura se puede estimar de forma razonable tomando en cuenta únicamente el daño sobre la fachada, lo que reduce drásticamente el tiempo de cálculo, pudiendo simular una amplia gama de posibles situaciones de peligro. En aras de la simplicidad, las fachadas son modelizadas mediante paredes con un marco fijo utilizando elementos discretos.
Otro aspecto a tomar en cuenta es la gran diversidad de configuraciones de elementos resistentes en una estructura, existiendo muros portantes o de cerramiento. En este estudio, el considerar una pared con un marco fijo cumple dos funciones: Conocer en cierta medida la metralla provocada por la explosión y simplificar la modelización de los elementos resistentes de un edificio, pensando principalmente en la generalización de los efectos de una explosión en un entorno urbano. quedando fuera de esta consideración los edificios singulares que por su arquitectura, historia o dimensión no pueden apegarse a esta hipótesis simplificativa.
La figura 5 muestra cómo se modelizan las fachadas para capturar las fuerzas de choque usadas en el análisis de vulnerabilidad propuesto. La simulación numérica propuesta se realiza en dos fases consecutivas. La primera de ellas corresponde a la simulación de la explosión, donde las fuerzas de la detonación actúan sobre la estructura y son evaluadas en cada paso de tiempo. Esta fase tiene en promedio una duración de 0.03s. La segunda fase corresponde a un ensayo de la capacidad resistente de la estructura, utilizando un control de desplazamientos para mover una prensa a velocidad constante de 0.07m/s y que carga verticalmente la estructura hasta su colapso. La fuerza resultante sobre la prensa permite evaluar la capacidad resistente de la estructura.
A efectos de referencia, se realiza también un ensayo de control que simula únicamente la segunda fase, con la finalidad de determinar la capacidad estructural sin daño alguno.
La estructura analizada es un panel de 3m de ancho, 2.5m de altura y 0.15m de espesor. La rigidez del material que forma el panel tiene un módulo de Young de 6.2MPa, un coeficiente de Poisson de 0.25 y una densidad de 3,780kg/m3 La tensión máxima admisible es de 10MPa. Valores equivalentes a la fachada de un edificio habitacional de tres a cuatro plantas con estrucutra de hormigón reforzado. El panel se ha discretizado utilizando 44,328 elementos y 110,389 uniones cohesivas, con un promedio de 9.3 uniones por elemento. Los radios de los elementos se distribuyen aleatoriamente entre 9 y 16mm. Se realizaron 160 simulaciones numéricas variando la masa explosiva entre 1 y 600kg de TNT y la distancia de esta a la estructura en un rango comprendido entre 1 y 6m.
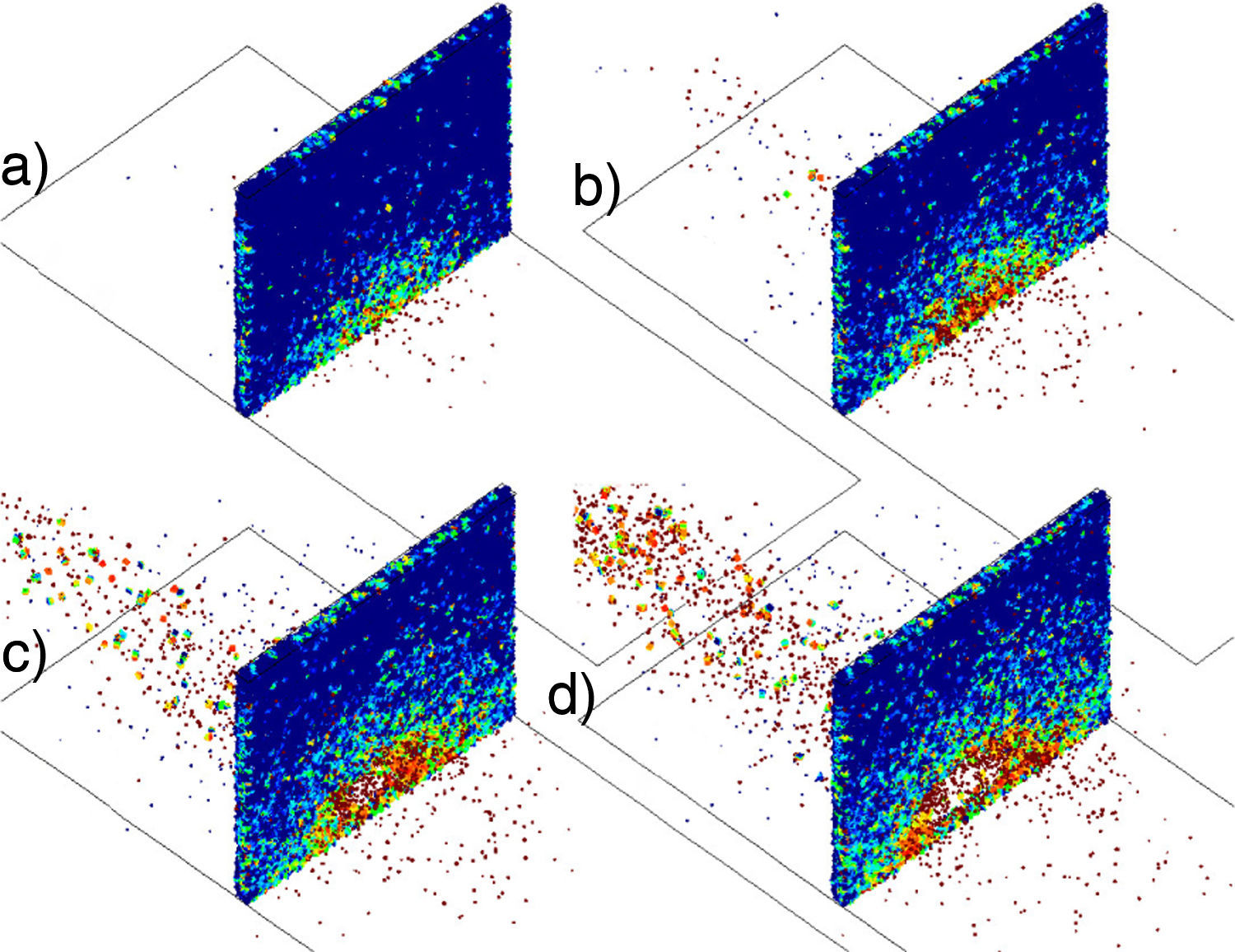
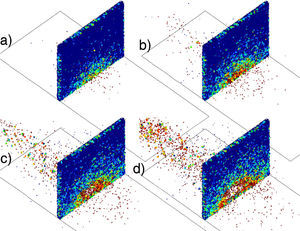
La figura 6 muestra una secuencia de imágenes ilustrando los daños causados por distintas cantidades de kg de TNT a una distancia de un metro. Cualitativamente, se observa cómo el número de enlaces cohesivos rotos aumentan conforme se incrementa la carga de TNT. La última detonación (100kg de TNT) produce un gran agujero en la pared y proyecta miles de elementos equivalentes a la metralla de un caso real.
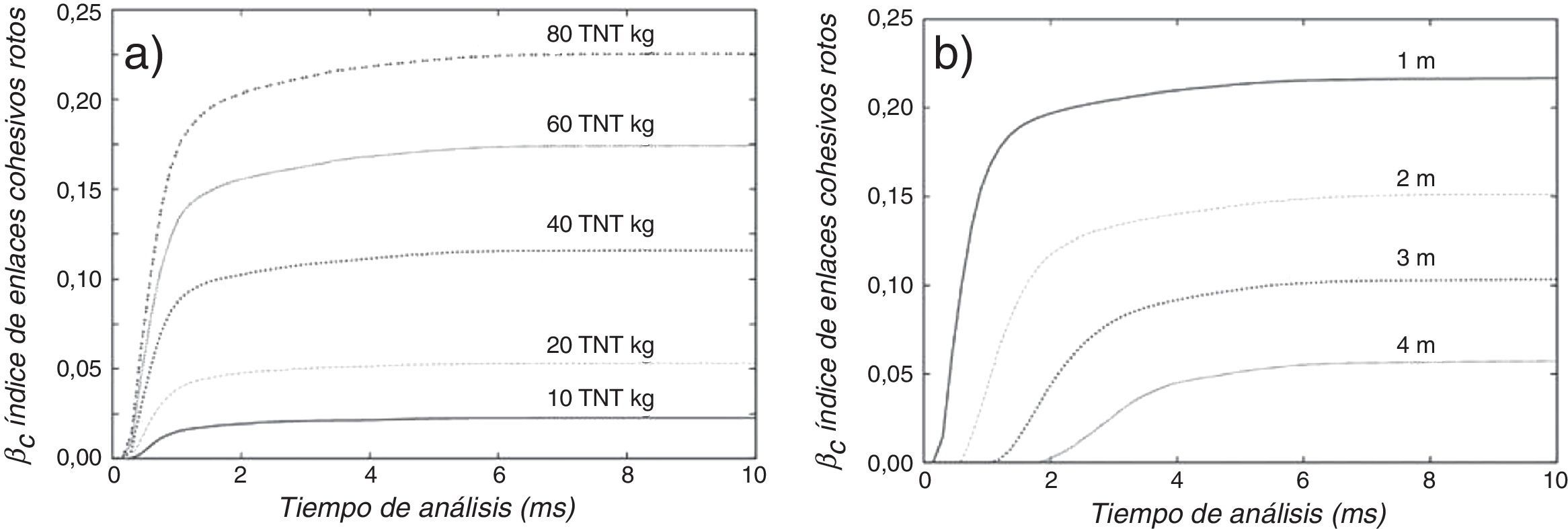
La figura 7a muestra el comportamiento del índice βc después de la explosión producida a 1m de la pared para distintas cargas de TNT. La figura 7b es similar a la anterior, pero en este caso se varía la distancia de la explosión mientras que el valor de la carga de 100kg de TNT es constante. Ambas figuras ponen de manifiesto la utilidad del índice βc como parte del DDi.
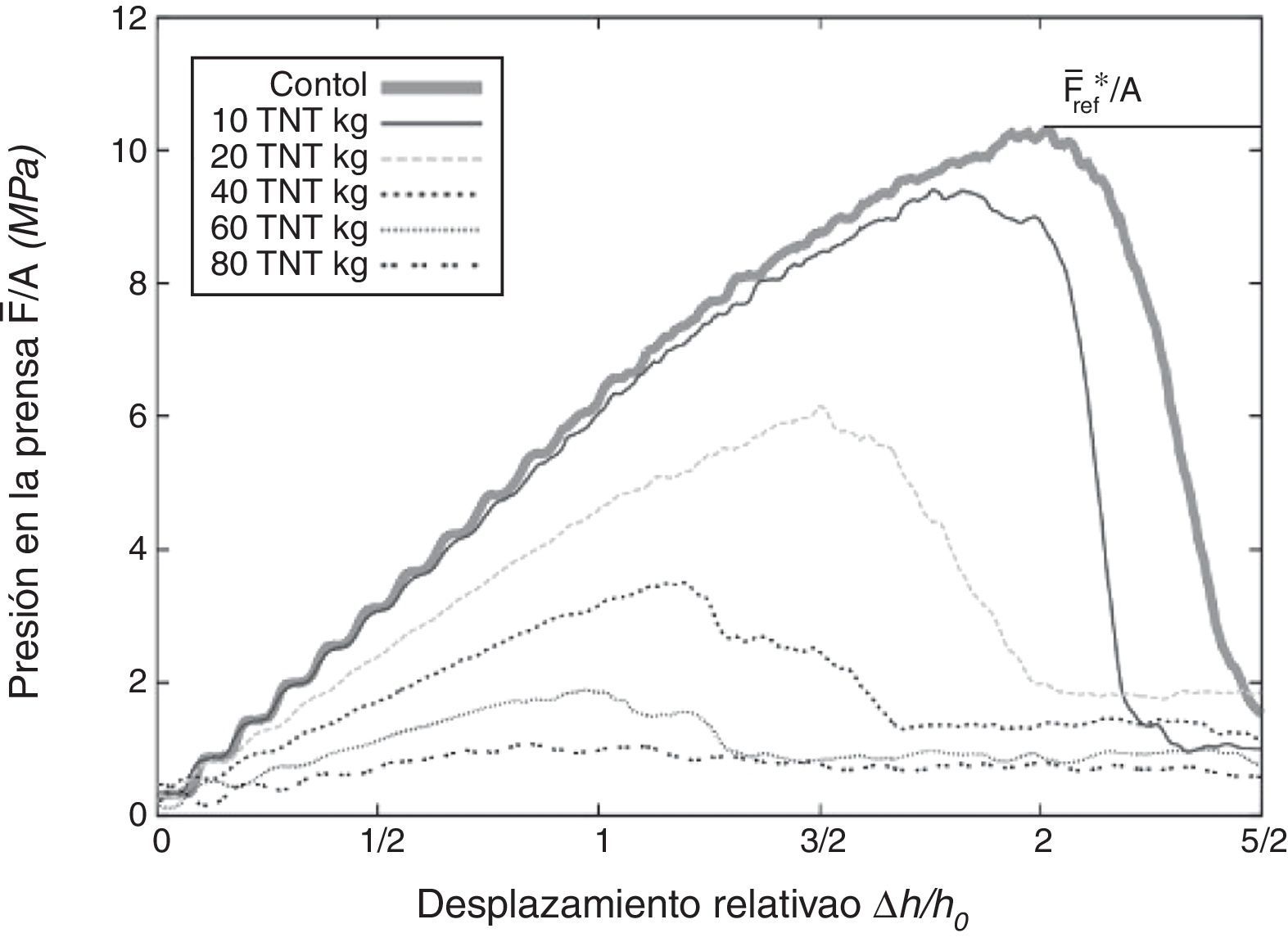
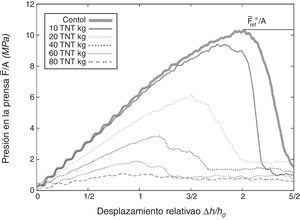
La capacidad remanente de la estructura después de la detonación se evalúa en el ensayo de compresión y es función de la relación entre la presión máxima ejercida por la prensa y el desplazamiento relativo de esta. La figura 8 muestra dicha relación cuando la estructura es afectada por varias explosiones de distinta magnitud a una distancia constante de 1m. Como era de esperar, a mayor carga menor es la capacidad resistente. En dicha figura, Δh es el desplazamiento vertical de la prensa, hO es la altura inicial de la estructura, F¯ es la fuerza media en la superficie de prensa, F¯ref* es la fuerza máxima aplicada por la prensa durante la prueba de control que en este ejemplo es de 4.7489 MN y A es el área de contacto entre la prensa y la estructura.
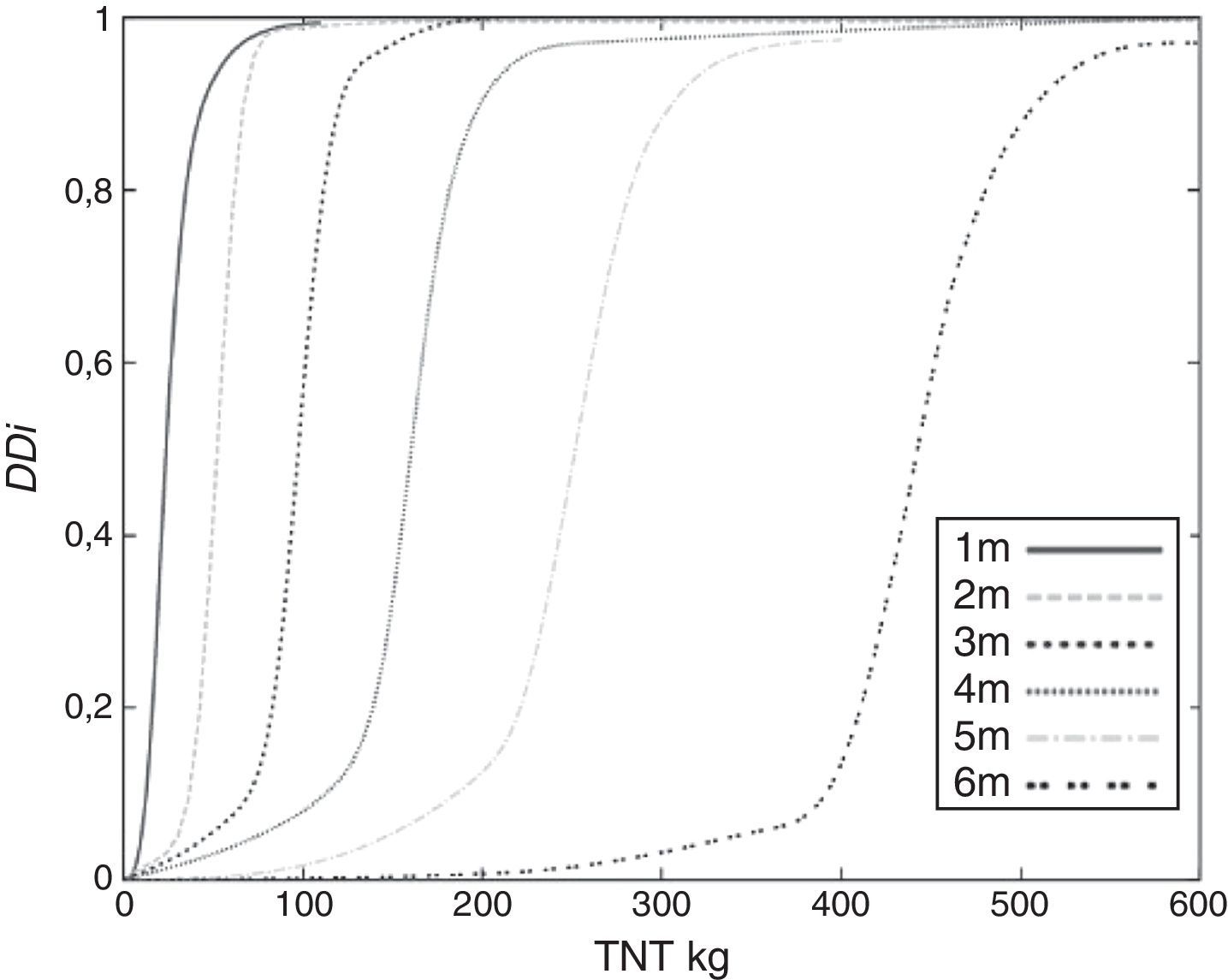
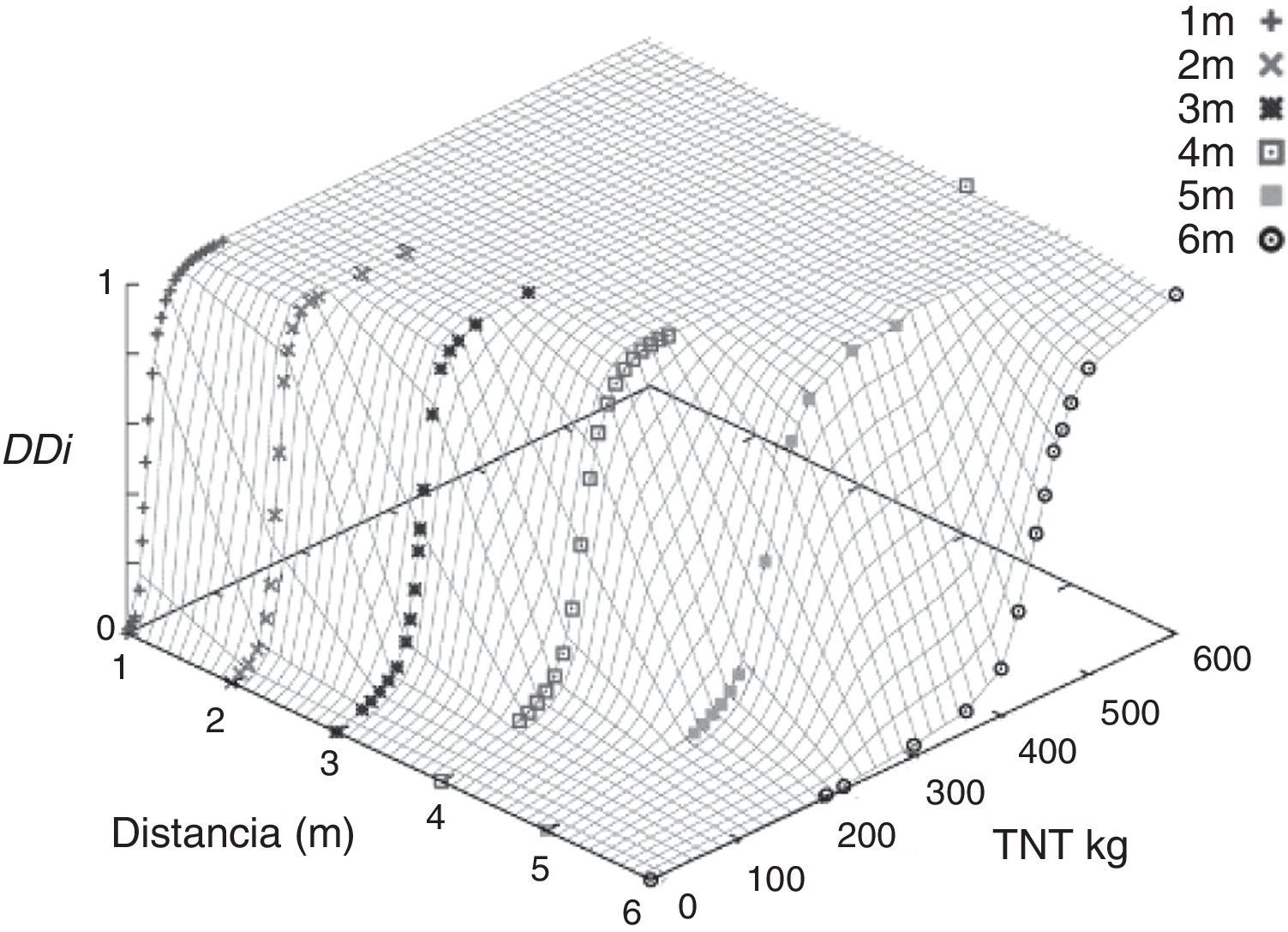
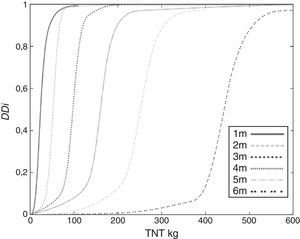
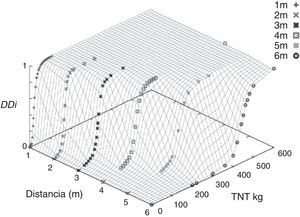
Una vez obtenidos los índices βc y βd se obtiene el índice DDi de manera que es posible describir las curvas de vulnerabilidad de la estructura analizada mediante el procedimiento descrito en el apartado 5. La figura 9 muestra las curvas de vulnerabilidad para seis distancias (ente la fachada y la explosión). Como se ha observado a lo largo de este ejemplo, el daño en un edificio es función de la carga y la distancia, por lo que la representación geométrica del daño viene dado por superficies de vulnerabilidad tal y como se muestra en la figura 10.
La importancia de este modelo radica en que puede ser replicado para los edificios de una zona urbana, lo que permite elaborar de forma sencilla y práctica, mapas de vulnerabilidad a nivel ciudad.
7ConclusionesDebido a la falta de una metodología de evaluación del daño ocasionado por una explosión sobre edificaciones, en este artículo se propone la evaluación del riesgo mediante superficies de vulnerabilidad. Dichas superficies son obtenidas mediante el índice de daño por detonación, DDi, relacionado exprofeso al ensayo de capacidad remanente propuesto. Para dicho ensayo se ha hecho uso de los elementos discretos para definir la estructura y funciones de onda semiempíricas para estimar el impacto de la explosión.
La ventaja principal de evaluar el daño mediante superficies de vulnerabilidad radica en poder llevar de forma eficiente, a una escala urbana, el análisis de riesgo, en donde los edificios son agrupadas por tipologías estructurales con la misma superficie de vulnerabilidad. Esto conlleva a la obtención de mapas de riesgo por explosiones dentro de un núcleo urbano, información necesaria y fundamental para la gestión del riesgo a nivel urbano, la toma de decisiones y el diseño de políticas y planes de crecimiento, contención y emergencia.
Los autores agradecen el apoyo de los proyectos Designing Safer Urban Spaces (DESURBS) y la Alianza Tricontinental en Métodos Numéricos Aplicados a los Desastres Naturales (TCAiNMaND), auspiciados por la Unión Europea y el Programa de intercambio internacional de personal investigador (IRSES), respectivamente. También agradecen el apoyo del Ministerio de Educación y Ciencia de España, dentro del proyecto “Enfoque integral y probabilista para La evaluación del riesgo sísmico en España, CoPASRE” (CGL2011-29063).