En los últimos años los materiales de cerámica altamente resistentes han experimentado una mejora sustancial para poder ser utilizados en restauraciones dentales, y los estudios clínicos de seguimiento realizados durante unos períodos de observación relativamente cortos han arrojado resultados prometedores en el tratamiento que incluyen prótesis parciales fijas (PPF) totalmente cerámicas, incluso sobre los dientes posteriores1. Al margen de los estudios de seguimiento in vivo, existen otros métodos de prueba conocidos para investigar la longevidad, la resistencia a la fractura y las fuerzas en las restauraciones dentales. En la mayor parte de los estudios, se realiza una simulación in vitro de la situación in vivo, pero hasta el momento no se ha desarrollado ningún procedimiento estándar para las pruebas in vitro para las PPF. Una revisión de la literatura revela que las bases del modelo en yeso utilizadas para sostener las PPF, por ejemplo, tienen un diseño distinto hasta el punto que parece cuestionable la comparabilidad de los resultados. Al margen de los dientes naturales2,3, se utilizaron dientes modelados en yeso y fabricados con aleaciones4,5 y polímeros6 como dientes pilares para las PPF. Más aún, los dientes del modelo en yeso fueron o bien fijados7,8 o insertados de forma elástica9-13 en sus respectivos alvéolos. Con objeto de simular elasticidad periodontal, las raíces suelen cubrirse, por lo general, con materiales que van desde material de poliéter9 hasta la goma a base de resina10,11. Kohorst y cols.12,13 investigaron la capacidad de las PPF de 4 unidades totalmente cerámicas para soportar una carga en relación con el tipo de estructura de zirconia y la fatiga cíclica en el agua. En ambos estudios, los autores utilizaron dientes modelados en poliuretano (PUR) cubiertos con una fina capa de látex en el área de la raíz para simular el ligamento periodontal (LPD). Estos dientes se sumergieron en un lecho de PUR para similar el soporte óseo. El segundo método establecido para analizar las PPF es el análisis de elemento finito (EF). Inicialmente, se crearon modelos de EF con ejes simétricos, que analizaban la distribución de las fuerzas en las coronas molares con diferentes tipos de preparaciones14,15. No se modeló la raíz, o tan sólo una pequeña parte de la misma, presumiblemente debido a la falta de conocimiento sobre la elasticidad periodontal. En los últimos años, se crearon modelos EF bidimensionales con una raíz simulada y LPD16-18. Con los continuos avances de la tecnología, se han desarrollado modelos tridimensionales (3D) más complejos; algunos de ellos tienen en cuenta las raíces y la elasticidad periodontal19 y otros, ninguno de estos parámetros20-23.
El objetivo de este estudio fue calcular las fuerzas que actúan en una PPF de 4 unidades totalmente cerámicas bajo una carga de prueba in vitro mediante el análisis de EF y revelar la influencia de los distintos parámetros sobre la distribución de fuerzas resultante. Tuvieron que considerarse dos factores: la elección del material para el alvéolo y los dientes pilares sobre los que se apoyaría la PPF en el experimento, y el método de inserción de los dientes pilares en el alvéolo (es decir, de forma rígida o elástica). Finalmente, se compararían los resultados de las fuerzas respectivas con las obtenidas utilizando el modelo de EF que se aproximara a una posible situación in vivo.
Materiales y métodos
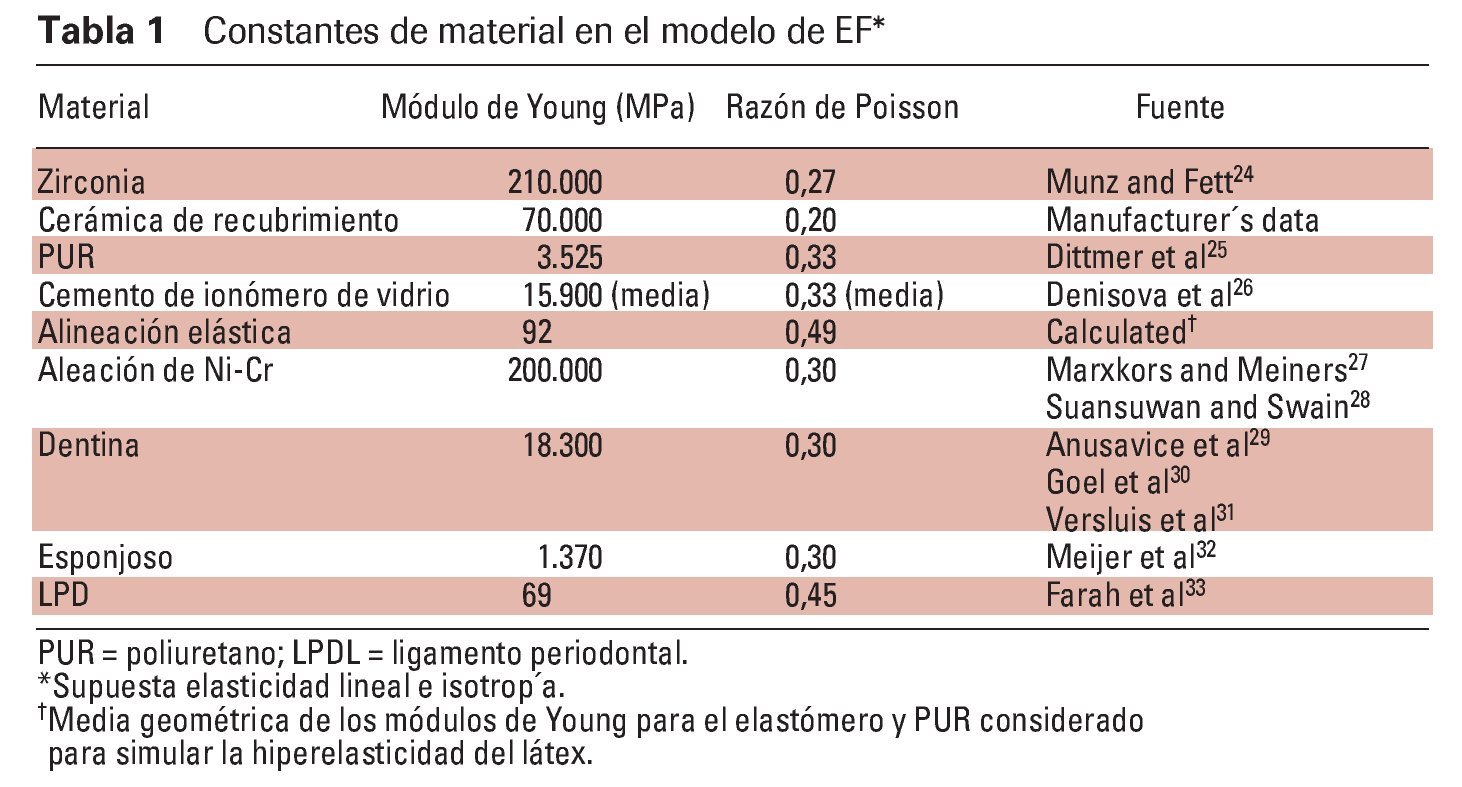
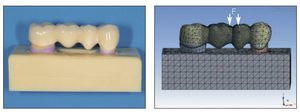
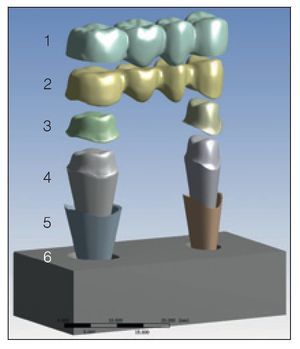
Para construir el modelo virtual se utilizó un modelo maestro de PPF de 4 unidades totalmente cerámico que abarcaba desde el primer premolar izquierdo superior hasta el segundo molar, tal como se había utilizado en estudios experimentales anteriores para determinar la capacidad de resistencia a la carga12,13. La PPF se escaneó opticamente (ATOS II SO, GOM) tanto antes como después de colocar el recubrimiento y se determinaron las coordenadas de la superficie mediante triangulación. Antes de proceder al escaneado, se aplicó una fina capa de material antirreflejante a base de una suspensión especial con un tamaño de granulado de aproximadamente 1 μm aplicado con un sistema de cepillo de aire. Posteriormente, las mallas polígonales resultantes fueron transferidas a modelos con volumen en 3D mediante ingeniería inversa utilizando un programa informático específico (Point-Master, Knotenpunkt). A continuación, se sustrajo virtualmente la estructura de la PPF de recubrimiento para obtener un modelo separado de la capa de recubrimiento (Cerconceram S, Degudent). Se trazaron elípticamente secciones transversales del conector de la estructura, con áreas de (de mesial a distal) 12,5 mm2, 15,6 mm2 y 11,6 mm2, respectivamente. El tramo entre ambos dientes pilares era de 14,5 mm. Se crearon los dientes modelo con capas de cemento de unión (de aproximadamente 100 μm de grosor) y siempre que se pudo, se aplicó una fina capa de 300 μm de grosor en el área de la raíz para simular la elasticidad tanto del LPD como de la capa de látex (DesignModeler, ANSYS) y se insertó virtualmente en un bloque de PUR, de acuerdo con el estudio experimental mencionado anteriormente (figura 1)12,13. La imagen ampliada que ofrece la figura 2 muestra los componentes del modelo virtual.
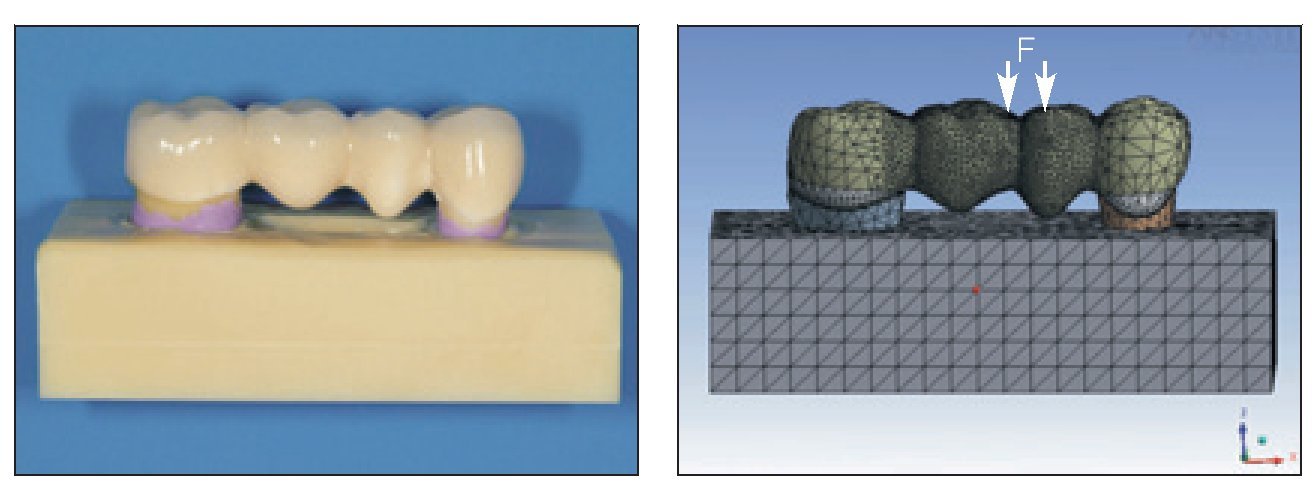
Figura 1 (arriba) (izquierda) Modelo in vitro cast y (derecha) modelo virtual (mallas) de la PPF con aplicación de una carga (F) en la dirección de las flechas.
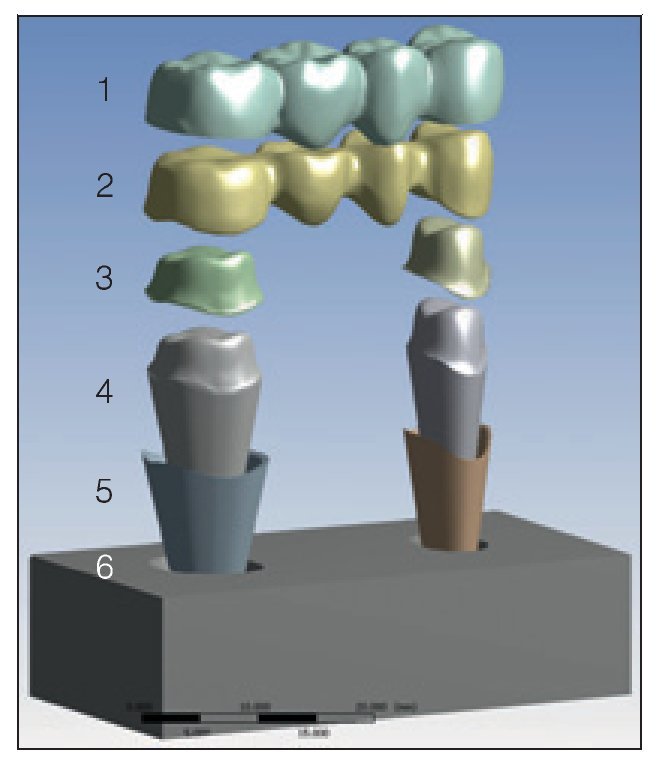
Figura 2 (derecha) Visión ampliada del modelo de PPF: (1) capa de recubrimiento, (2) estructura de zirconia, (3) capa de cemento, (4) diente modelo, (5) capa de interfase elástica y (6) alvéolo.
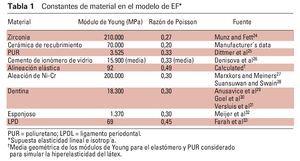
Se creó un modelo de EF en 3D que comprendía 110.380 elementos hexaédricos y tetraédricos con la ayuda de una herramienta para la creación de mallas integrada en el programa informático (DesignSpace, ANSYS), cuyo tamaño del elemento preseleccionado para la estructura y la capa de recubrimiento para el área del conector era de 0,5 mm. Todas las constantes del material excepto una se tomaron de la literatura; el módulo de Poisson y el módulo de Young del PUR reforzado (AlphaDie Top, Schütz Dental) se determinaron a partir de una prueba tensil preliminar. Una vez asignadas las propiedades elásticas apropiadas a las distintas partes de los modelos, se construyeron 4 versiones del modelo. En la primera versión, el alvéolo y los dientes pilares rígidamente fijados se habían elaborado a partir de una aleación de níquel-cromo (Ni-Cr). La segunda versión era parecida a la primera, pero la capa sobre el área radicular se optó porque fuera elástica y flexible, en este caso, de látex. La tercera versión se elaboró de acuerdo con un estudio in vitro, con el alvéolo y los dientes pilares insertados de forma elástica, fabricados con PUR. La cuarta versión se acercaba a la situación in vivo con el alvéolo y consistió en sustancia esponjosa, y los dientes pilares, de dentina y un LPD simulado.
Existe una relación de todas las constantes de los materiales en la tabla 1. La alineación flexible de las raíces dentales en el alvéolo de PUR para simular el LPD no se comporta linealmente y se vuelve más rígida cuanto mayor es la carga aplicada (hiperelasticidad).
Dada la limitación de cálculo derivada del propio programa informático para el cálculo lineal elástico, la hiperelasticidad únicamente pudo determinarse de forma aproximada asignando un módulo de elasticidad efectivo a partir de una media geométrica en el módulo del elastómero y del PUR. Al aplicar una fuerza oclusal de 1.630 N de manera uniforme sobre dos áreas circulares de la superficie oclusal cerca del conector entre el segundo premolar superior izquierdo y el primer molar, las condiciones de carga se ajustaron de acuerdo con el estudio in vitro comentado anteriormente (figura 1)12,13,34. En el experimento, la fuerza de 1.630 N provocó el fracaso en un 63,2 % de las PPF (análisis de Weibull). En todos los casos simulados, el alvéolo de PUR se fijó virtualmente al suelo para prevenir cualquier posible desplazamiento.
Las conexiones entre las diferentes partes del modelo se definieron como si hubieran sido soldadas. Anteriormente, en una serie de modelos de EF con un aumento en la densidad de la malla descrita en otro artículo25, se habían verificado los resultados de la convergencia de las fuerzas, y se había seleccionado el modelo que ofrecía la rigurosidad y precisión mejores con el mínimo esfuerzo informático posible para ser utilizado en este y en otros estudios.
Resultados
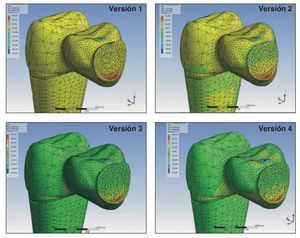
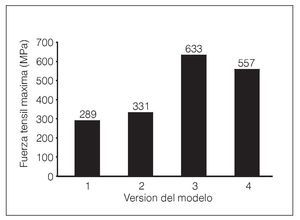
En todas las diferentes versiones del modelo (del primero al cuarto) las fuerzas tensiles más intensas dentro de toda la estructura se produjeron cerca de la superficie de la misma, sobre el conector abrazadera gingival, entre los premolares y los molares (figura 3). Por lo general, la fuerza tensil pico (máxima) era más elevada cuanto más elástico era el soporte de las PPF, ya sea introduciendo un LPD simulado o por haber elegido un material menos rígido para los dientes pilares y el alvéolo (figura 4).
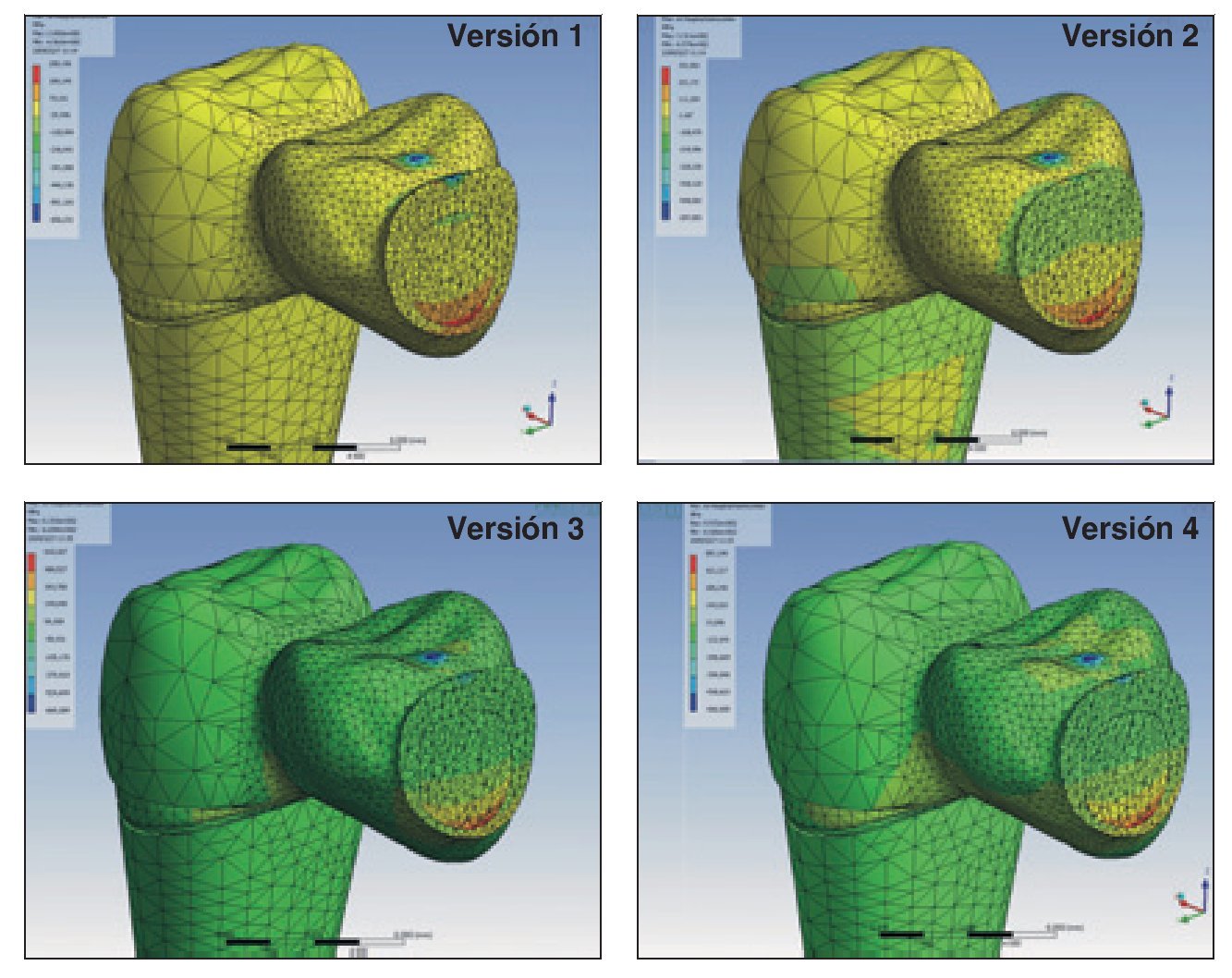
Figura 3 Visión general de la distribución de las fuerzas sobre las superficies de la estructura, la capa elástica, y sección transversal a través del área del conector entre el segundo premolar superior izquierdo y el primer molar en las cuatro versiones. Nótese, que el bloque de PUR se ha dejado fuera de la imagen para mayor claridad.
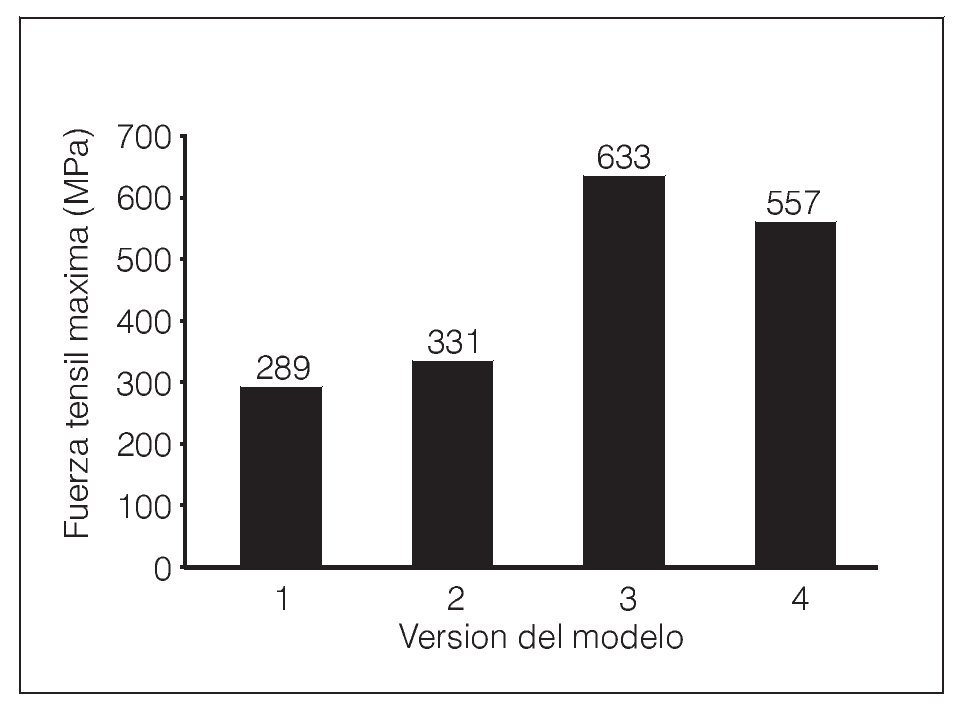
Figura 4 Principal fuerza máxima más elevada en las diferentes versiones del modelo.
Las fuerzas tensiles máximas en el área del conector que abarcaba del segundo premolar al primer molar iban de 289 MPa para la primera versión, pasando por 331 MPa en la segunda versión, alcanzaron los 633 MPa en la tercera versión para disminuir a 557 MPa en la cuarta versión. En todas estas versiones, los desplazamientos máximos se observaron en la región del puente, cerca del punto en el que se aplicó la fuerza, principalmente en la dirección de la aplicación de la misma, con una ligera inclinación hacia la cara vestibular. El desplazamiento aumentó de la primera a la tercera versión, alcanzando las 22 μm en la primera versión, 36 μm en la segunda y 115 μm, en la tercera, que simulaba el modelo in vitro de Kohorst y cols.12,13 La cuarta versión, que simulaba el LPD in vivo, reveló un desplazamiento máximo de 104 μm en la región del puente y, al mismo tiempo, una intrusion axial del diente pilar de 110 μm aproximadamente. Tal como se desprende de la imagen transversal de la distribución de las fuerzas en el conector entre el segundo premolar al primer molar, el gradiente de la fuerza dentro de la estructura se desplazó prácticamente en vertical desde la cara basal a la cara oclusal (figura 3). El intervalo de las fuerzas principales máximas era de 633 MPa (tensión, cara basal) hasta -669 MPa (compresión, cara oclusal). Sin tener en cuenta la capa de recubrimiento, las fuerzas compresivas máximas se registraron en la primera y la segunda versión, sobre el área de la dentina distocervical del premolar, mientras que en la tercera y en la cuarta versión aparecían cerca del punto de aplicación de la fuerza, en el área del conector entre ambos puentes (figura 3).
Discusión
En todos los análisis de EF llevados a cabo con PPF descritos anteriormente se identificaba el área del conector como la parte en la que se registraban las mayores concentraciones de fuerzas dentro de la estructura17,22,23,35,36. Estos resultados no son inferiores a los obtenidos en el presente estudio. En las cuatro versiones, la localización de las fuerzas tensiles máximas se situaba en la estructura, cerca de la superficie en la abrazadera gingival del conector, entre los premolares y los molares (figura 3). En la primera y la segunda versión, las fuerzas compresivas máximas se hallaban en el área cervical de la dentina, cerca de la cresta residual. Este hecho concuerda con los resultados obtenidos de los estudios llevados a cabo por Oruc y cols.37 y Yang y cols.17 quienes también habían observado una concentración de fuerzas en esa región. Adicionalmente, la intrusión axial de los dientes pilares de 10 μm (cuarta versión) se corresponde en buena parte con la movilidad fisiológica del diente, cuyo límite superior es del orden de las 150 μm38. Tal como se muestra en la figura 4, se observó un aumento de las fuerzas tensiles máximas cuando el soporte de la PPF se suponía más elástico. El uso de una capa de elastómero en comparación con un pilar dental rígido indujo un aumento del 14,5 % de las fuerzas tensiles (primera y segunda versión). El riesgo de fracaso aumenta al incrementar las fuerzas, y en particular las fuerzas tensiles pueden influir en el hecho de que aumenten positivamente las fisuras en los materiales cerámicos. Como resultado de estos hallazgos, podemos llegar a la conclusión de que las PPF fracasarán antes in vivo si el soporte es más elástico. Yang y cols.17 investigaron la necesidad de modelar las estructuras de soporte y simularon una situación de pérdida ósea, que tuvo como resultado un aumento en la movilidad de los dientes pilares. Llegaron a la conclusión de que la pérdida ósea aumenta las fuerzas generadas en las estructuras. Esta movilidad y elasticidad de los dientes pilares influye de manera significativa en las fuerzas, lo que concuerda con los resultados obtenidos en el estudio actual (figura 4). Molin y cols.39 demostraron mediante un análisis de EF de una PPF de 3 unidades que un LPD simulado induce valores de fuerzas un 40 % más elevadas que un modelo sin ligamento, hecho que corroboran estos resultados. Rees40 halló variaciones en las fuerzas mucho más elevadas cuando se variaban las estructuras de soporte y señaló la necesidad de modelar tanto el LPD como el hueso alveolar cuando se pretendiera llevar a cabo un análisis de EF de los dientes. Sin embargo, también se ha mencionado el hecho de que estos dos estudios citados simulaban situaciones in vivo y no in vitro.
Otros estudios in vitro distintos también se han centrado en la investigación de la influencia de la elasticidad de los dientes pilares sobre la capacidad de soportar la carga de la PPF. Parece obvio que existan diferencias entre los materiales utilizados para simular la capa elástica. En dos estudios se empleó una capa de poliéter41,42, mientras que en otros dos43,44 se utilizó un material con una base de silicona. En los cuatro estudios se llegó a la conclusión de que la capacidad para soportar la carga es considerablemente inferior cuando el apoyo es más elástico. Esto apoya claramente los resultados de este estudio. Únicamente Kern y cols.10 constataron que un apoyo más elástico no influía en la capacidad para soportar la carga de la PPF.
Otro aspecto más que se evaluó en el presente trabajo fue la influencia del material del diente pilar sobre la distribución de las fuerzas en las PPF. Como puede observarse en la figura 4, el uso de hueso, la dentina y las constantes del material del LPD en la cuarta versión provocó un aumento del 68,3 % de las fuerzas respecto a la simulación con dientes pilares elaborados a base de una aleación de Cr-Ni y una capa de elastómero (segunda versión). En consecuencia, parece ser que el material del diente pilar ejerce una enorme influencia en las fuerzas de las PPF cargadas, de manera que es de vital importancia tenerlo en consideración cuando se pretende realizar una simulación experimental de una situación in vivo. Existen ciertos inconvenientes a la hora de utilizar dientes pilares naturales por las restricciones existentes al reproducir y comparar entre varias muestras. Con objeto de evitar estos inconvenientes Kohorst y cols.12,13 crearon un modelo con dientes pilares artificiales fabricados a base de PUR reforzado, cuyo módulo elástico es inferior al de la dentina pero similar al del hueso. Esta situación experimental fijó las directrices para la tercera versión del modelo de EF presentado en este estudio. Tal como se muestra en la figura 4, las fuerzas tensiles máximas desarrolladas en la tercera versión tan sólo fueron comparativamente un 14 % superiores a la cuarta versión, que simulaba la situación in vivo. Por ello, se considera que la tercera versión se aproxima de forma aceptable a la situación in vitro. Por el contrario, la segunda versión, para la que se utilizó un material para los dientes pilares y el alvéolo con un módulo superior, se desvía más de la situación in vivo en cuanto a las fuerzas sobre la estructura se refiere. Esto nos llega a sugerir que se debería utilizar un material moderadamente rígido (PUR) para los modelos de los dientes y los alvéolos in vitro en las pruebas de carga con PPF. Esto proporciona adicionalmente un 10 % de margen de seguridad al generar fuerzas más elevadas en las PPF, lo que resulta en la correspondiente disminución de la capacidad de soportar las cargas obtenida en el experimento si se compara con la situación in vivo.
Otro factor importante que afecta a la distribución de las fuerzas, y consecuentemente, a la capacidad de soportar la carga, es el método de carga de la PPF25,45. Mientras que la distribución uniforme de las fuerzas oclusales se consideraría un caso ideal, las fuerzas más o menos concentradas aplicadas a los bordes adyacentes de los puentes en los experimentos in vitro llevados a cabo por Kohorst y cols.12,13 así como en los análisis de EF de este estudio, constituyen la peor situación posible, con fuerzas más elevadas en las PPF que en condiciones clínicas de carga habituales. El análisis de EF es un método aproximado para simular el comportamiento de estructuras en condiciones de carga. Como es natural, el modelo sólo podía consistir en un número finito de elementos. El supuesto de un comportamiento elástico lineal en el caso del látex constituye una aproximación adicional, que al menos estuvo compensada en parte con la introducción de un módulo estático efectivo. Finalmente, las fuerzas residuales generadas por una carga térmica durante el recubrimiento no se han tenido en consideración. Estas fuerzas son del orden de 80 al 110 MPa46 y se habrían superpuesto a las generadas por la carga mecánica. No obstante, es posible efectuar una comparativa entre los resultados de la fuerza obtenida para las diferentes versiones del modelo bajo condiciones equivalentes, lo que permite realizar una valoración de la influencia de las estructuras de soporte sobre la capacidad de resistir la carga.
Conclusiones
Basándonos en los resultados de este estudio, podemos concluir que el material del diente pilar y del alvéolo, así como el tipo de soporte dental, ejercen una influencia significativa sobre las fuerzas generadas en las PPF durante las pruebas de carga in vitro. Para producir fuerzas en las PPF lo más parecidas posible a las generadas en una caso de carga in vivo, es particularmente importante emplear dientes pilares insertados de forma elástica y fabricados con un material moderadamente rígido (por ejemplo, PUR reforzado) para soportar las muestras. El hecho de transferir estos resultados a una situación in vivo significa que probablemente aumente el riesgo de fracaso de una PPF, al aumentar la elasticidad de los dientes pilares, especialmente si los contactos oclusales son dirigidos sobre el puente/región del conector más que distribuidos sobre los retenedores.
Agradecimientos
Este estudio obtuvo el apoyo de GOM, Braunschweig, Alemania, y Knotenpunkt, Balingen, Alemania, a quienes se les agradece encarecidamente su ayuda.
Correspondencia: Dr Marc Philipp Dittmer,
Hannover Medical School, Department of Prosthetic Dentistry and Biomedical Materials Science, Carl-Neuberg-Str. 1, 30625 Hannover, Germany.
Fax: 49 (0) 511 532 4790.
e-mail: Dittmer.Marc@mh-hannover.de
Este artículo fue presentado en la sesión general de la International Association for Dental Research, Toronto, Ontario, Canada, en julio de 2008.