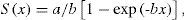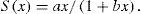Using empirical field data of aquatic insects to infer a cut-off slope value in asymptotic models to assess inventories completeness

Abstract

The selection of the most appropriate model is essential to predict the potential species richness of a site or landscape. Species accumulation curves have been used as a basic tool for comparing richness when different sampling protocols have been applied. Among the parameters generated by these models the slope has been cited as an indicator of completeness without regard to a defined cut-off value. In this work, we fit 12 field data sets of aquatic Coleoptera (Hidalgo) and Odonata larvae (Michoacán) to 2 asymptotic models (Clench and Linear Dependence) in order to calculate the slopes at the maximum effort and relate them with efficiency. Then, the theoretical effort needed to achieve the 95% of the lists was calculated for each data set in order to get the theoretical slopes. The average slope value found was 0.01 with a variance of <0.001, so we propose this value as indicative of a list reaching 95% of completeness for data obtained from similar sampling protocols. Additionally, we propose the use of number of rare species as an additional criterion to evaluate the inventories completeness. The effect of different sampling intensity on fitted models and estimation of parameters and the importance of a cut-off slope value in asymptotic models as a criterion to evaluate completeness of biological inventories are discussed.

Resumen

La selección del modelo más adecuado es esencial para predecir la riqueza potencial de especies de un sitio o paisaje. Las curvas de acumulación de especies se han utilizado como una herramienta básica para la comparación de la riqueza cuando se han aplicado diferentes protocolos de muestreo. Entre los parámetros generados por estos modelos, la pendiente se ha citado como un indicador de completitud sin tener en cuenta un valor de corte definido. En este trabajo, ajustamos 12 conjuntos de datos de campo de coleópteros acuáticos y larvas de odonatos de Zimapán (Hidalgo) y Coalcomán (Michoacán) a 2 modelos asintóticos (Clench y Dependencia Lineal), con la finalidad de calcular las pendientes al máximo esfuerzo realizado y relacionarlas luego con la eficiencia del muestreo. Después, calculamos el esfuerzo teórico necesario para conseguir el 95% de las listas y calculamos las pendientes teóricas. El valor promedio de la pendiente teórica fue de 0.01, con una varianza de <0.001, por lo que proponemos este valor como indicativo de una lista que ha alcanzado el 95% de completitud para datos obtenidos de protocolos de muestreo similares. Además, se propone el uso del número de especies raras como un criterio adicional para evaluar la completitud de los inventarios. Se discute el efecto de la intensidad de muestreo en los modelos ajustados y la estimación de los parámetros, así como la importancia de contar con un valor de corte de la pendiente en modelos asintóticos como criterio para evaluar la completitud de los inventarios biológicos.

Introduction

Biodiversity inventories are central to most conservation and planning efforts (Cutko, 2009). Inventories, however, are encumbering endeavors that often suffer from limited sampling efforts, either because resources are limited or the necessary sampling effort is unknown (Silveira et al., 2010). Assessment of biodiversity often relies on statistical techniques to estimate total diversity and inventory completeness (Colwell and Coddington, 1994; Hortal and Lobo, 2005). The rapid pace of global change and severe treats to global biodiversity increases the value of approximate methods to assess species richness and diversity. Therefore, it is urgent that we attempt our understanding of these methods and their limitations.

The use of randomized sample accumulation curves, or species accumulation curves, has been a preferred technique when assessing biodiversity. This technique has been applied with variable degrees of success to field inventories using standardized sampling (e.g. Soberón and Llorente, 1993; Colwell and Coddington, 1994; Moreno and Halffter, 2000; Summerville et al., 2001; Noguera et al., 2002) and also to non-standardized samplings, like museum collections or faunal databases (Soberón et al., 2000; Hortal and Lobo, 2001; Martín-Piera and Lobo, 2003; Petersen et al., 2003; Rosenzweig et al., 2003; Hortal et al., 2004; Baselga and Novoa, 2008). Species accumulation curves are attractive because they allow for the estimation of the total number of species present in an area by extrapolating the function to its asymptote. Although the validity of this extrapolation is still source of controversy, it is a commonly used technique (Colwell and Coddington, 1994; Gotelli and Colwell, 2001; Willott, 2001; Hortal et al., 2004; Hortal et al., 2006).

Species accumulation curves are also useful at describing the rate of new species additions to inventories (Soberón and Llorente, 1993; Hortal and Lobo, 2005; Soberón et al., 2007). In asymptotic models the slope of the species accumulation curve describes such rate, and can be used as a measure of survey completeness (Hortal et al., 2004; Hortal and Lobo, 2005; Delgado et al., 2012): the higher the slope value the greater the sampling effort needed for a complete inventory. Conversely, small slope values indicate more complete surveys, since additional samples add little to the number of species in the inventory. If the slope is small, but not zero, it can be assumed that the species missing from current inventory are locally rare or vagrants (see Moreno and Halffter 2000). Thus the inventory can be considered reliable, though incomplete. The slope can be easily calculated from the fitted function, for it is the first derivative of such function. Many functions have been proposed to describe the relationship between sampling effort and species diversity (Soberón and Llorente, 1993; Colwell and Coddington, 1994; Moreno and Halffter, 2000; Thompson, 2003). Among them, Clench´s equation is one of the best options, as it avoids problems of overfitting and critical richness underestimation, providing a good description of the inventory process (Hortal et al., 2004; Hortal and Lobo, 2005). Once the function has been fitted, its slope becomes a simple, yet powerful, measure of inventory completeness at current sampling-effort levels. Although no studies have explored which is the most adequate slope cut-off to identify a reliable inventory, the use of intuitive thresholds of 0.05 or lower has been proposed (Hortal and Lobo, 2005).

The use of species accumulation curves generated by asymptotic models has been widely used with different faunal groups (Moreno and Halffter, 2000; Alcázar-Ruiz et al., 2003; Thompson et al., 2003; González and Baselga, 2007; González-Oreja et al., 2010; Pedraza et al., 2010). However, in very few papers the slope value has been calculated and reported, and it has been much less used as criteria to assess the completeness of inventories (León-Cortés et al., 1998; Novelo-Gutiérrez and Gómez-Anaya, 2009; Pedraza et al., 2010; Gómez-Anaya et al., 2011;). Likewise, very few authors have considered intuitively the slope value in relation to obtain a nominated percentage (e.g. 95%) of completeness of their inventory (Delgado et al., 2012) without considering a cut-off value as indicative of completeness.

In this work, we compare the relative fit of 2 asymptotic models (Clench and Linear Dependence) when applied to aquatic Coleptera and Odonata larval assemblages (habitat scale), and their combined assemblages for each group (landscape scale). The main purpose of this work is to recommend an appropriate cut-off slope value as indicative of inventories at 95% of completeness. We hypothesize that: (1) slopes of cumulative species curves will decrease with increasing sampling effort, (2) species richness will increase with sampling effort, 3) few rare species (singletons, doubletons, unique and duplicates) will be found where slopes are small and higher effort was applied, because oversampling reduces their presence in inventories.

Materials and methods

Study area

Analyzed data come from the hydroelectric dam Zimapán, Hidalgo (20°39’-20°52’ N, 99°27’-99°32’ W) and from Coalcomán Mountain Range, Michoacán (18°35’-19°00’ N, 102°28’-103°40’ W). Details on sampled sites have been published by Arce-Pérez et al. (2010, Hidalgo) and Novelo-Gutiérrez and Gómez- Anaya (2009, Michoacán). Herein nomenclature used for the water bodies is as follows: Hidalgo State: San Francisco River (SF), El Saucillo stream (ES), San Juan River (RJ), Tula River (TL), the entire area of influence of the Zimapán dam (ZHP); Michoacán State: streams El Ticuiz (TZ), Estanzuela (EZ), Pinolapa (RP), Colorín (CL), Chichihua (CH), and the whole Coalcomán Mountain Range (CMR).

Sampling size and intensity

Sampling effort was monthly in all water bodies but with different intensity and size. In SF sampling was monthly throughout the year with an average of 36 D-net samples in each occasion while in ES was also monthly but with an average of 12 D-net samples each month; in SJ sampling was only during 6 months with an average of 10 D-net samples each month and in TL just 1 monthly big sample (about 10 D-net size) was taken during 10 months. In all the Michoacán water bodies 8 sampling trips were performed using a D-net frame, number of samples were also variable (Table 1).

Table 1.

Summary of sites and parameters of 2 asymptotic models fitted for aquatic Coleoptera and Odonata larval assemblages from Zimapán, Hidalgo, and Coalcomán, Michoacán. S_obs= observed number of species during sampling; N_95%= theoretical effort required to achieve 95% of the list; SL_N95%= theoretical slope using N_95%

Site	Group	Coverage	Sobs		Clench								Linear Dependence
				N	a	b	a/b	R2^+	eff%	Sl	N95%	SlN95%	a	b	a/b	R2^+	eff%	Sl	N95%	SlN95%
Zimapán, Hgo.	Col. Imagos	Landscape	66	633	2.14	0.03	67	0.9850	98.8	0.005	594	0.005	1.24	0.02	65.16	0.9200	101.29	0.007	1000	7E-09
San Francisco, Hgo.	Col. Imagos	Local	49	427	1.75	0.03	52	0.9469	94.2	0.007	565	0.004	1.10	0.02	46.73	0.9717	104.86	0.009	808	6E-09
Saucillo, Hgo.	Col. Imagos	Local	46	137	3.92	0.08	48	0.9703	95.7	0.026	233	0.010	2.84	0.07	42.51	0.9310	108.20	0.028	284	2E-08
San Juan, Hgo.	Col. Imagos	Local	30	59	2.36	0.06	36	0.9839	82.2	0.102	293	0.006	1.90	0.07	28.46	0.9740	105.40	0.078	284	1E-08
Tula, Hgo.	Col. Imagos	Local	26	10	6.18	0.14	45	0.9980	57.6	1.101	139	0.015	5.65	0.184	30.73	0.9980	84.60	0.701	103	3E-08
Coalcomán, Mich.	Odon. larvae	Landscape	75	243	2.39	0.03	82	0.9838	91.4	0.037	652	0.006	1.69	0.02	70.48	0.9368	106.41	0.005	793	9E-09
Chichihua, Mich.	Odon. larvae	Local	30	54	2.48	0.07	37	0.9971	80.7	0.117	285	0.006	1.95	0.07	29.22	0.9739	102.67	0.053	285	1E-08
Estanzuela, Mich.	Odon. larvae	Local	25	65	3.01	0.11	27	0.9776	92.3	0.045	171	0.008	2.05	0.09	23.06	0.9236	108.40	0.006	214	1E-08
Colorín, Mich.	Odon. larvae	Local	18	49	1.87	0.09	21	0.9845	85.3	0.066	215	0.005	1.40	0.08	17.02	0.9566	105.74	0.025	231	8E-09
Ticuiz, Mich.	Odon. larvae	Local	36	38	3.00	0.06	50	0.9935	71.3	0.283	320	0.007	2.55	0.069	37.19	0.9849	96.80	0.188	277	1E-08
Río Pinolapa, Mich.	Odon. larvae	Local	28	42	3.86	0.12	31	0.9573	90.4	0.099	152	0.010	2.75	0.107	25.62	0.8997	109.29	0.030	177	2E-08
San Francisco, Hgo.	Odon. larvae	Local	29	409	1.21	0.04	29	0.9490	98.9	0.004	460	0.003	0.71	0.027	26.64	0.8212	108.85	0.000	716	4E-09

a, Slope at the beginning of sampling; b, a parameter related to the mode of accumulation of new species during sampling; N, sampling effort; a/b, asymptote; R2, coefficient of determination; Sl, slope; eff%, percentage of efficiency. The slope was estimated by the first derivative of Clench’s function [a/(1+b *n)²], and the first derivative of linear dependence [a * exp(-b* n)]. Note: the number of theoretical species (asymptote) is set to integers, however, several decimals have been used in the calculation of the efficiency which might seem a miscalculation in the table (see last line San Francisco).

Data analysis

Curves of aquatic Coleoptera and Odonata larval species accumulation were generated versus sampling effort for each of the 9 streams (local) separately, and for ZHP and CMR (landscape). To assess inventory completeness relative to sampling effort, and to construct species accumulation curves, we fitted 2 asymptotic models (Soberón and Llorente, 1993) to our data using EstimateS 8.0 software (Colwell, 2009; Longino and Colwell, 1997), a Linear Dependence Model (LDM) and the Clench Model (CM). LDM assumes that as the species list increases the probability of adding new species diminishes exponentially and is a model that is ideal for the study of small areas and known taxa (León-Cortés 1994, León-Cortés et al. 1998). Equation of LDM is:

where x is a measure of sampling effort, S(x) is the predicted number of species at x effort, a represents the rate of increase at the beginning of the sampling, b is a parameter related to the mode of accumulation of new species during sampling a/b is the asymptote. CM assumes that the probability of adding species to the list decreases with the number of species already recorded, but increases over time. This model is commonly used in diversity inventory assessment and is an adequate function for a relatively small-intermediate number of samples (Colwell and Coddington, 1994; Colwell, 2009).The model is:

To adjust the models, the mean number of species per sample was used from the results provided by EstimateS to obtain the ideal curve or statistical average of species added with increased effort (Jiménez-Valverde and Hortal, 2003). This was accomplished using the non-linear estimation module in STATISTICA (StatSoft, 2006), and applying the Simplex and Quasi-Newton methods for parameter estimation.

We used the first derivative of each model to calculate the slope of the species accumulation curve. The first derivative of LDM function is [a exp(-bx)] and the first derivative of CM function is [a/(1+bx)²] (Jiménez-Valverde and Hortal, 2003). We then used the slope evaluated at maximum effort as a measure of inventory completeness according to Jiménez-Valverde and Hortal (2003) and Hortal and Lobo (2005). Since no studies have explored this issue, and as a starting point, we arbitrarily considered slopes under 0.05 as evidence of a sufficiently complete inventory, following Hortal and Lobo (2005). Also, the theoretical effort required (n_q), in this case n_0.95, to reach 95% of each inventory was calculated, according to Jiménez-Valverde and Hortal (2003) by the equation [n_q = q/[b·(1-q)] where q = the relative proportion of the list of species to be detected.

Finally, Sperman rank coefficients (r_s) were calculated between sampling effort and slope, asymptote, and between slope and efficiency and number of rare species over all sites. Rare species, singletons and doubletons such as species registered in just numbers of 1 and 2 individuals, and unique and duplicates species, as those registered in just 1 and 2 samples, were calculated by the EstimateS 8.0 (Colwell, 2009).

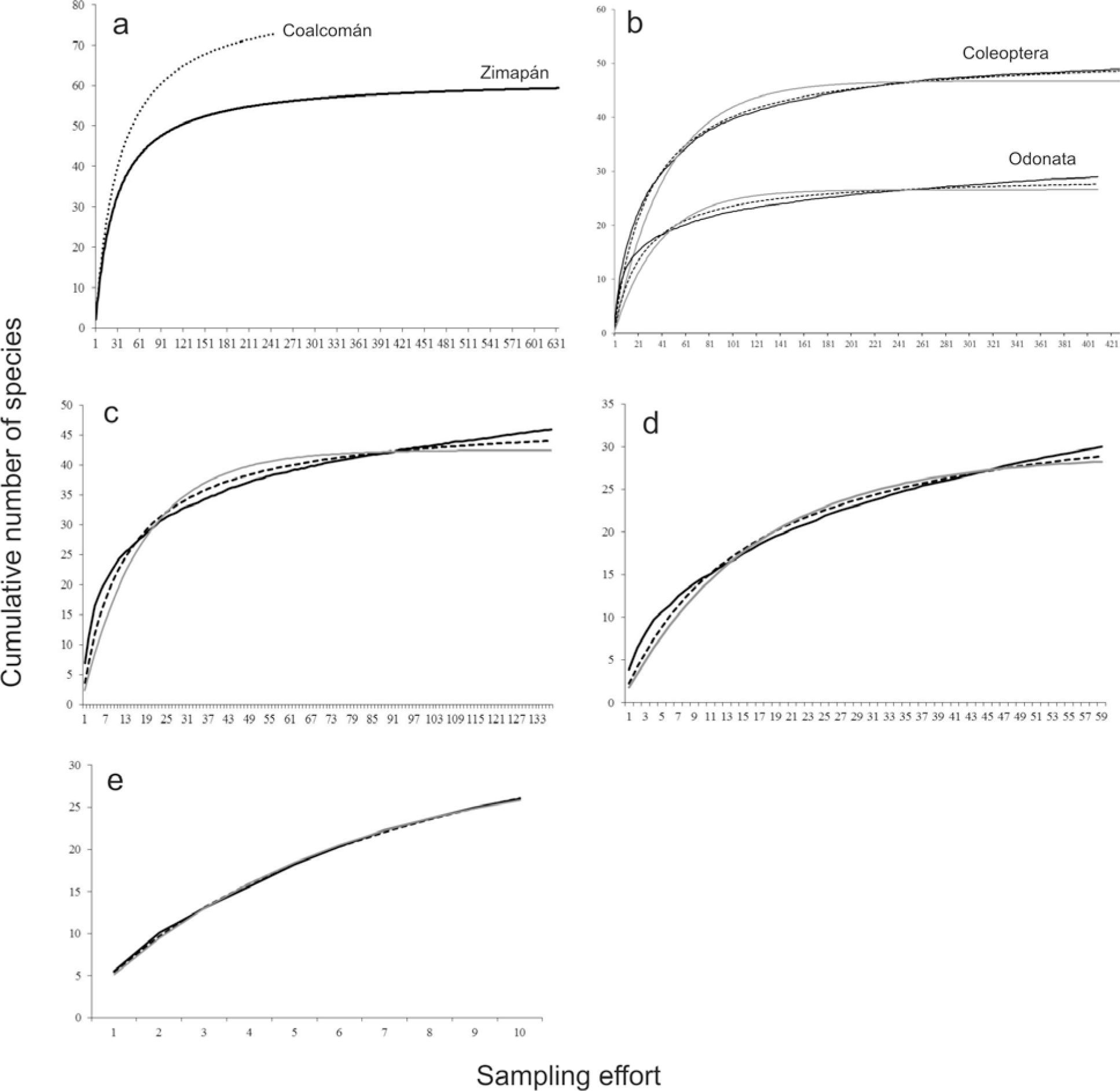
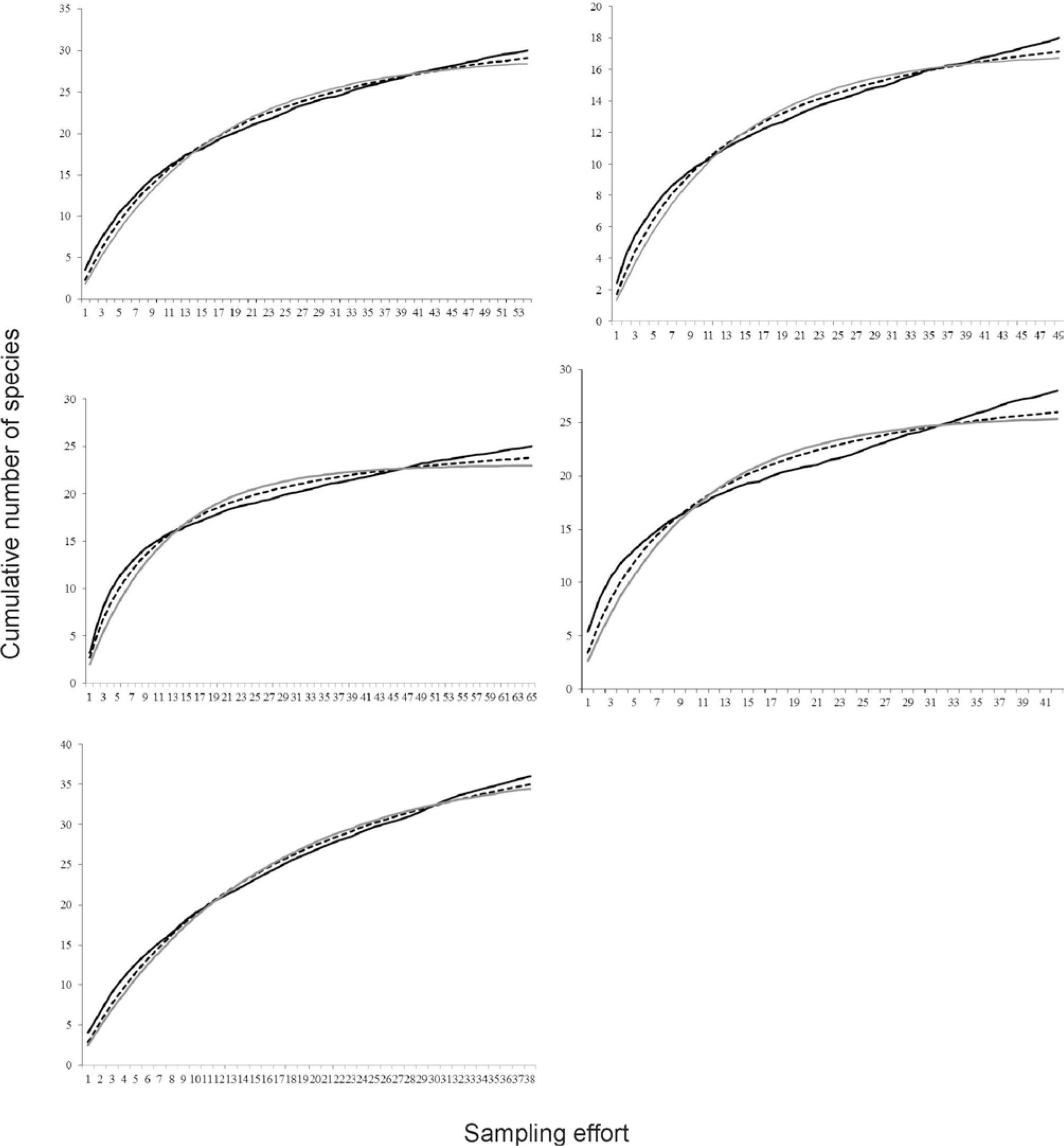
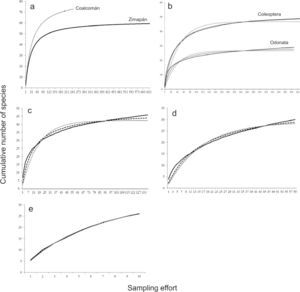
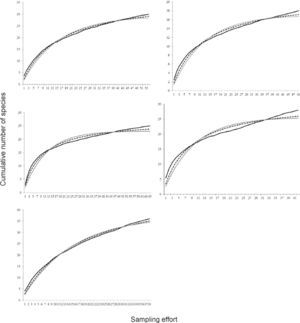
Results

Our data provided a good fit for both the Clench and Linear Dependence models (Table 1, Figs. 1, 2). However, the CM resulted in larger R2 values (range: 0.9469-0.9980) than LDM (range: 0.8212-0.9980, Table 1). In addition, LDM provided consistent overestimations of the theoretical number of species (see sampling efficiency in Table 1). The 2 sites where the largest sampling effort was conducted (San Francisco for both groups and El Saucillo for Coleoptera) showed low slope values, indicating more complete inventories (Table 1). The efficiency was higher in Zimapán (ZHP) than in Coalcomán Range landscape (CMR) perhaps due to the overall effort was also higher in ZHP, however, both slopes showed complete inventories.

Figure 1.

a), Landscape cumulative species curves for Odonata larval assemblage from Coalcomán and aquatic Coleoptera assemblage from Zimapán generated by the Clench model; b), site cumulative curves of Coleoptera and Odonata larvae from Rio San Francisco; site cumulative curves of aquatic Coleoptera from c) El Saucillo, d) San Juan and e) Tula river. From b-e observed data (full black line), Clench model (dashed line) and linear dependence model (grey full line).

Figure 2.

Cumulative species curves of Odonata larval assemblages in Coalcomán. a), Chichihua; b), Colorín; c), Estanzuela; d), Pinolapa, and e), Ticuiz. Observed data (full black line), Clench model (dashed line) and linear dependence model (grey full line).

Theoretical number of missing species among streams varied from 0 (SF Odonata larvae) to 19(TZ), while only 1 missing species was theorized to ZHP and 7 to CMR. Few species were missing in some local assemblages as ES (2 spp. Coleoptera) and EZ (2 spp. Odonata).

The theoretical number of samples needed to reach local inventories at 95% (N_95% in Table 1) varied from 139 (TL) to 652 (SF). Few samples were needed at CMR (51 Odonata larvae) and many more in CMR (409) to reach 95% inventories, while it was surpassed with only 39 samples in ZHP. The new slopes calculated with N_95% varied between 0.003 for SF (Odonata larvae) and 0.015 for TL. Average and variance of all the slopes were 0.0071 and 0.00001, respectively. In summary, the slope as indicative of an inventory at 95% of completeness is practically 0.01.

Number of singletons varied from 0 (ZHP) to 14 (CMR), doubletons from 1 (ZHP, SF Odonata) to 6 (TL, CMR), uniques from 3 (SF) to 19 (CMR), and duplicates from 0 (ZHP) to 7 (TL, CMR). The number of singletons varied from 0 (ZHP) to 14 (CMR), doubletons from 1 (ZHP and SF) to 6 (TL and CMR), uniques from 3 (SF) to 19 (CMR) and duplicates from 0 (ZHP) to 7 (CMR and TL, Table 2). The number of rare species, singletons and doubletons, for aquatic Coleoptera assemblages were lower for 1 landscape (ZHP) and 1 site (SF), both considered oversampled.

Table 2.

Number of rare species at each sampling site. The order of groups is the same as indicated in Table 1

	Singletons	Doubletons	Uniques	Duplicates
Zimapán, Hgo.	0	1	8	0
San Francisco, Hgo.	2	1	3	3
Saucillo, Hgo.	7	3	9	4
San Juan, Hgo.	9	5	12	3
Tula, Hgo.	6	6	10	7
Coalcomán, Mich.	14	6	19	7
Chichihua, Mich.	5	2	10	3
Estanzuela, Mich.	3	4	7	3
Colorín, Mich.	6	3	7	3
Ticuiz, Mich.	10	5	16	5
Río Pinolapa, Mich.	3	2	11	3
San Francisco, Hgo.	4	1	5	3

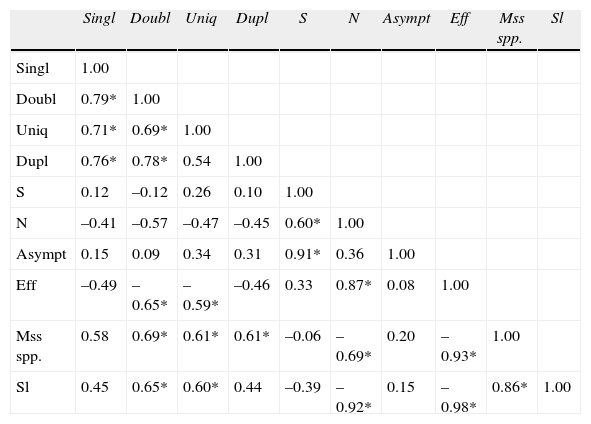
Slope was positively and significantly correlated with doubletons (Table 3, r_s= 0.65, p< 0.05) and uniques (r_s= 0.60, p< 0.05), and negatively correlated with efficiency (r_s= -0.98, p< 0.05) and maximum sampling effort (r_s= -0.92, p< 0.05). Efficiency was negatively correlated with doubletons (r_s= -0.65, p< 0.05) and uniques (r= -0.59, p< 0.05), and positively with sampling effort (r_s= 0.87, p< 0.05). Observed and theoretical number of species were positively correlated (r_s= 0.91, p< 0.05) and maximum effort was positively correlated with observed number of species (r_s= 0.60, p< 0.05, see Table 3).

Table 3.

Sperman rank coefficients among rare species and observed number of species (S), maximum sampling effort (N), theoretical number of species (Asympt), efficiency (Eff), missing species (Mss spp.) and slope (Sl) at the maximum sampling effort. N= 12 for all the cases. Significant correlations with p< 0.05 are marked with *

	Singl	Doubl	Uniq	Dupl	S	N	Asympt	Eff	Mss spp.	Sl
Singl	1.00
Doubl	0.79*	1.00
Uniq	0.71*	0.69*	1.00
Dupl	0.76*	0.78*	0.54	1.00
S	0.12	–0.12	0.26	0.10	1.00
N	–0.41	–0.57	–0.47	–0.45	0.60*	1.00
Asympt	0.15	0.09	0.34	0.31	0.91*	0.36	1.00
Eff	–0.49	–0.65*	–0.59*	–0.46	0.33	0.87*	0.08	1.00
Mss spp.	0.58	0.69*	0.61*	0.61*	–0.06	–0.69*	0.20	–0.93*	1.00
Sl	0.45	0.65*	0.60*	0.44	–0.39	–0.92*	0.15	–0.98*	0.86*	1.00

Discussion

According to the slope analyses at the maximum sampling effort (N), the best surveyed sites were SF in both, Odonata and Coleoptera assemblages, and ZHP landscape for Coleoptera assemblage (slope < 0.001; Table 1). The remaining sites still had a high number of species to be recorded (e.g. sites with high slopes). This result supports our hypothesis 1, and these observations are also important in planning future sampling efforts in water bodies such as TL, TZ, CH and RJ. In addition, more species were recorded where more sampling effort was applied, thus supporting hypothesis 2 and the number of missing species were negatively correlated with effort and efficiency, in other words, few species are missing where high sampling effort was conducted, also obtaining a greater sampling efficiency (Table 1).

On the other hand, estimations of sample size to reach 95% of the species lists for each site and landscape were variable. In some cases we found clear oversampling and in others undersampling was evident. RJ and TL were undersampled in Zimpán with a deficit of 234 and 129 samples, respectively, representing the 2 water bodies with more missing species and higher rates of species addition at the end of the sampling period. Along with this, the Coalcomán landscape, and TZ and CH sites, resulted in deficiently sampled sites, with higher slopes and more missing species. Thus, it becomes evident the effect of the performed sampling intensity: in the Tula river (TL) the sampling units were months instead of D-nets, while in all other streams from Zimapán and Coalcomán D-nets were the standard units (Fig. 1). Achieved efficiency in each stream must be related to the intrinsic characteristics of each site to whereby a sample size (N) should be required.

When the achieved efficiency in each site or landscape was analyzed, we found that Zimapán landscape (ZHP), and ES and SF streams (Odonata) were oversampled (efficiency exceeded the 95%), then we calculated the theoretical effort required to reach only 95% of the list, according to the formula proposed by Jiménez-Valverde and Hortal (2003), resulting in a fewer number of samples required for Zimapán landscape (from 633 down to 594), however, surprisingly higher number of samples were required for SF and ES sites to reach lists at 95%. As a result we suggest caution in estimating the required sampling effort to obtain a nominated percentage of inventory using this procedure. From the obtained model, at maximum effort, a lesser size effort can be obtained to detect a nominated percentage of the list by interpolation, and doing the opposite (extrapolating), a higher efficiency should get the maximum initial effort. However, this discrepancy can be seen only when it has exceeded the 95% of the lists for any of our assemblages, although probably also occurs with the other assemblages which did not reach 95% of efficiency.

The species accumulation is not a gradual and proportional process to sampling effort. For example, it is not possible to say that 1 species is added on average every 20 samples. Sometimes several species are added from small sample groups, while no species are added in other large groups of samples. The analysis of the Clench’s curve for ZHP shows a high rate of species accumulation between 1 to 15 samples. In this part of the curve, the slope varied between 2.01 and 1.02, showing a high rate of increase in the inventory list. The slope becomes lower than 0.1 at a sampling effort of 117 samples, when the size of the inventory list was of 52 species (77.61% of the total list). However, 95% of the total species list is reached with a sampling effort of 500 samples and this gives a slope of 0.01. This basically indicates that 382 samples are needed to add 12 species to the list. Within these 382 samples a proportional increasing species-effort was not observed (e.g. 8 samples are needed to pass from 51 to 52 species, 17 samples to pass from 56 to 57 species, 41 samples to pass from 60 to 61 species, and 125 samples to pass from 63 to 64 species). Similarly, despite the significance in the negative correlation, there does not seem to be a proportional relationship between slope and efficiency. We observed that, when sampling effort is 164 the slope reaches 0.05 and efficiency is then 85%; when sampling effort is 342 the slope reaches 0.01 and efficiency is 92%, but the 95% of efficiency is reached at 500 samples when slope is also 0.01. Both, the slope and efficiency, are independent criterions to assess completeness but we may first reach 95% of the list or a slope of 0.01, but they do not necessarily go hand in hand.

Cut-off slope value

The completeness of an inventory is a relative measure to the effort and the need to know which species are present. For megadiverse groups the need and the effort can be large, although large efforts may make evident only a fraction of which species exist. For groups less diverse and taxonomically well-known, the need to know can be satisfied with less effort and greater accuracy.

The average value of the slope based on our 12 data sets yielded 0.01 and a variance less than 0.001. This is the theoretical value we proposed as indicative when a list has reached 95% of completeness. Our results are in agreement with the slope valuesreported by Delgado et al., (2012) for local inventories of beetles in Montebello Chiapas with values of less than 0.01. The authors argue high completeness of their inventories judging only by the obtained slope values, but without any proposal of cut-off slope value. Also, our results agree well with the intuitive theoretical cut-off slope value proposed by Hortal and Lobo (2005), of less than 0.05, although these authors do not specify a nominated percentage of the fauna that would be covered by this value.

Rare species

Rare species have a low propensity for being recorded or caught, and sites with high species evenness had a high proportion of species with a similar propensity for being caught (Thompson et al., 2003). In the biological context, rareness can be defined as species that are: i) broad ranging but generally sparsely distributed; ii) locally dense but with a very restricted range, and iii) locally sparse with a very restricted range. Because the proportion of rare species at a given site affects the species accumulation curve, their presence plays an important role in some non-parametric estimators (Chao1, Chao2, Jack1 and Jack2, Smith and Belle, 1984), as they tend to increase the theoretical number of species based on rare species. Thus, if the number of rare species decreases, the theoretical richness estimation will be almost equal to the observed number of species. Unfortunately, these non-parametric richness estimators only work well if the number of rare species is low (Smith and Belle, 1984). Oversampling reduces the number of rare species (hypothesis 3) as this occurred particularly in SF where the number of rare species was the lowest, and also at ZHP landscape. On the other hand, the property of being rare (singleton, doubleton, unique or duplicate) varies according to the scale of sampling. For example, few species maintained their rare condition at both habitat and landscape scale in ZHP: Agabus americanus (ES), Berosus mexicanus (ES), Hemiosus exilis (ES), Microsporus sp. (SF), and Neoelmis sp. (SF).

Rare species numbers, mainly doubletons and duplicates, could be also used as additional indicative criterion of completeness as its number is reduced significantly when efficiency increases and slope is reduced.

Implications for conservation

In studies for biodiversity assessment, species accumulation curves are powerful tools for evaluating the sampling efficiency, for planning and to distribute additional efforts, and for assessing the completeness of inventory lists. The slope of the curve can be particularly useful in the assessment of inventory completeness, being a small slope value indicative of a small rate of species addition, and a complete inventory, as was already mentioned. However, although the sampling efficiency may be high, the slope very small, and the number of rare species low, all of them are indicative that few potential species may exist in a determined area (e.g. Zimapán), so care must be taken beforehand to conclude there do not exist more species to be recorded in a landscape, as evidenced by observations of the last author of this work, who has recorded at least 3 more species of aquatic Coleoptera in other internal points of the Zimapán influence area, Hydrophilus insularis, H. triangularis and Paracymus regularis at the nearby El Epazote (an intermediate small stream). Some species require some specific ecological conditions as larvae, so if requirements exist at specific points within the landscape, there is also the chance of adding more species to the inventory list.

The herein proposed cut-off slope value comes from data sets gathered under a similar sampling protocol applied to 2 different scales (sites and landscapes), of 2 taxonomically well-known groups of aquatic insects, providing ecological matrices with similar characteristics: many columns (samples) and few rows (species) (horizontally extended matrix). Particularly, the data set from TL was different from the rest of the assemblages because we used the collecting dates instead of D-nets as sampling units. This resulted in a vertical extended matrix or approximately square matrix (as many columns as rows). In this latter special form of matrix, species accumulate in large numbers as effort increases, and almost all samples contribute to add species, unlike long and narrow matrices in which there are groups of samples which do not add species to the list. Apparently, the sample size influences the estimated value of the slope with a tendency to be slightly higher. We assume that when collection dates are used as sampling units the estimated value of the slope as an indicator of 95% of inventory will be greater than 0.01.

Acknowledgements

Thanks to two anonymous reviewers for their criticism and suggestions that improved the final version.