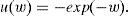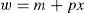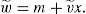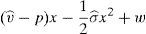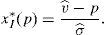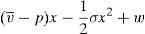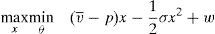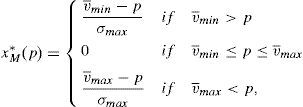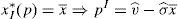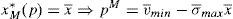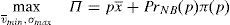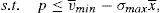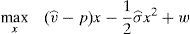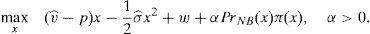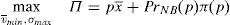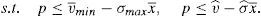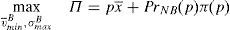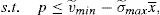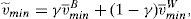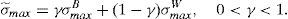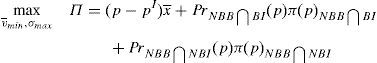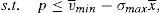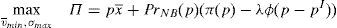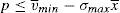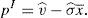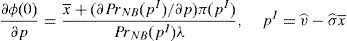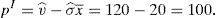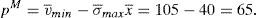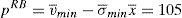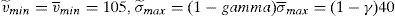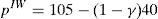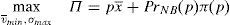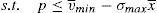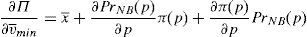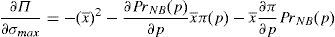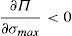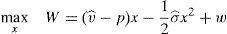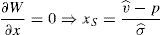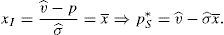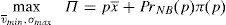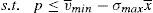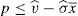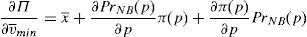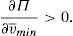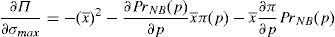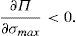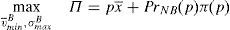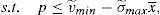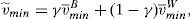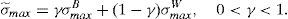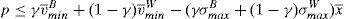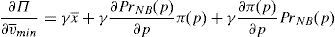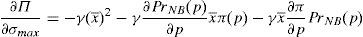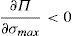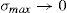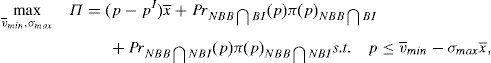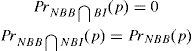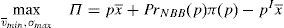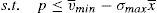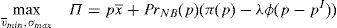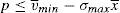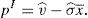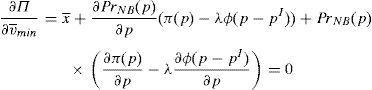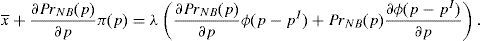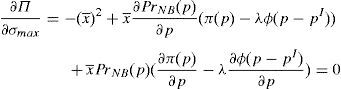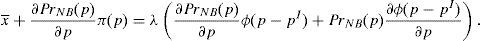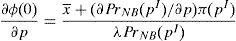This paper analyzes the conflict of interest that exists when a financial institution issues and places a financial asset with credit risk among retail investors. Four regulatory measures are presented and analyzed in order to improve retail investors protection. Theoretically, it is shown that two of these measures, setting a price cap to the issue and an adequate enforcement could implement a first best social optimum.
According to the Spanish Survey of Household Finance, in 2005, the 87.6 percent of households held neither stocks nor bonds. Such retail investors behavior is not exclusive of Spain. For example, in the period 1982–1995, according to the U.S. Consumer Expenditure Survey, the percentage of retail investors that held neither stocks nor bonds was more than two-thirds (cited in Paiella, 2007).1 This behavior is inconsistent with the classic models of optimal portfolio choice (see Merton, 1969 or Samuelson, 1969). Therefore, a large body of literature has been developed to explain this limited participation puzzle of the retail investors.
There are two main theories to explain this puzzle: the first theory states that the retail investor limited participation is due to the high cost of participating in the financial markets (see Vissing-Jorgenson, 2002 or Guiso et al., 2003). Although, participation costs are an important factor for retail investors, the empirical evidence points out that this can only be a partial explanation. Gouskova et al. (2004) showed that “costs are not a major consideration to participate in the stock market”. The other theory argues that the low participation of retail investors is because retail investors are ambiguity averse.
Ambiguity aversion arises in optimal portfolio choice when the investors take into account risk and ambiguity (uncertainty) in their decision making. Knight (1921) was the first to distinguish between known odds (risk) and ambiguity odds (uncertainty) in individuals decisions. Ambiguity aversion is often attributed to naive investors who do not have sufficient skills to form priors over the occurrence of particular states of the world. So, if naive investors believe ambiguity to be too great, they choose not to participate in the market. Given this framework, Easly and O’Hara (2009) showed that the ambiguity aversion is a sensible explanation of the retail investors low participation in the financial markets.2 According to this theory, the retail investors participation could only be higher if the prices of financial assets were sufficiently low to compensate them for their ambiguity-aversion.
Despite the predictions of the ambiguity-aversion theory, it is a fact that financial institutions are sometimes able to sell complex financial assets among retail investors. In particular, they manage to place among their retail clients their own preferred stocks and other funding instruments. This puzzling behavior of the retail investors could be explained by one special characteristic of this type of placements: the issuer and the retail broker belong to the same financial group. Such a characteristic could imply the existence of a conflict of interest between the retail brokers and the investors.
The retail brokers advise investors on the characteristics of any financial products. In theory, the information investors receive from retail brokers allows to reduce the asymmetric information between issuers and retail investors. Thus, the relationship that is established between a retail broker and their investors could be put on the same level as the relationship between a medical doctor and their patients.
In principle, this relationship would make both parts win. Retail investors could allocate more efficiently their resources in financial assets and brokers would earn the fees for their advices. However, the incentives of the retail brokers and their investors are not always lined up. In the case this paper analyzes, the retail broker faces a trade off. On the one hand, as the issuer belongs to the same financial institution, the retail broker has incentives to place the issue at the highest possible price through advices that tend to minimize the risks of the issue. On the other hand, if retail brokers advise their investors wrongly, they could suffer a reputational cost that will be translated in a reduction of future profits. If there are conditions for the first of the two forces to be stronger, there could be a conflict of interest in the relationship between the retail brokers and their investors.
Despite the fact that the possible conflict of interest analyzed in this paper has not been explicitly studied by the academic literature, a similar conflict, the relationships between stocks analysts and investors, has been studied in several academic papers. In Malmendier and Shanthikumar (2007), the authors found empirical evidence that there exists a conflict of interest in this context. They found that stocks analysts have incentives to bias stocks recommendations upwards, specially if they belong to the same financial institution as the underwriter. However, the behavior of institutional and retail investors differ when they face stock recommendations. Institutional investors adjust downwards their demand for stocks when they are advised to buy. Instead, retail investors follow the recommendation literally.
Mehran and Stulz (2007) argued that a conflict of interest of this type can be avoided if at least one of the following two conditions between the sell and buy side of the relationship is met. The first condition is that the sell side bears a reputational cost if it does not place the best possible product to their investors. The other condition is that investors are sufficiently rational to be able to adjust their investment decision to the possible sell side's conflict of interest. An example of this behavior is described previously in the description of the paper by Malmendier and Shanthikumar (2007).
The possible conflict of interest that could arise when financial products are issued and placed by the same financial institution has not gone unnoticed to regulators. IOSCO (2007) presented a list of regulatory measures that the members of this international standard setter must put in place in case a conflict of interest is detected. In the European Union, the Directive 2004/39/CE of the European Parliament and the Council known as MiFID and the Directive 2006/73/CE of the Commission established the regulation applied within the European Union to remedy these conflicts of interest.
The aim of this paper is to study if a conflict of interest exists when a broker that belongs to the same financial institution as the issuer places a financial asset with high credit risk exclusively among retail investors. As far as the author is concerned, this is the first paper that analyzes this problem taking into account retail investors financial behavior. Financial literature has always approached this conflict of interest from a perspective where investors were only risk averse. Finally, in this paper several regulations are also presented and analyzed against this conflict of interest.
The remainder of the paper is organized as follows. Section 2 describes what ambiguity aversion is and how this type of aversion fits retail investors behavior when they make investment decisions. Section 3 presents the model and describes retail investors, issuers and retail brokers. Section 4 analyzes the outcomes of the model presented in the previous section. Section 5 compares the private outcome from the model with the social welfare optima. Section 6 proposes four regulatory solutions to approximate as much as possible the private outcome to the first best social welfare optimum. Section 7 provides a numerical example where the four analyzed regulatory measures are compared. Finally, Section 8 lays out the conclusions.
2Expected utility and ambiguityIn the expected utility theory, decision makers have preferences over, and make decisions between, objective payoff distributions. The application of this theory to financial assets markets assumes that distributions of portfolio payoffs of financial assets are known by the investors. This assumption is usually justified under the rational expectations hypothesis. For some assets and some investors, this could be a reasonable assumption. However, for other investors and assets, it may not be reasonable.
The generalization of the expected utility theory by Savage gave a Bayesian approach to subjective uncertainty about payoff distributions. In this approach, individuals’ subjective distribution of payoffs derives from their preferences over stochastic consumption streams. The Savage's approach allows similarly informed investors to disagree on the predicted distribution of payoffs on portfolios. But it does imply that each investor acts as if he or she had some subjective distribution. This could seem reasonable in many cases; in others, however, such as with the example of a new type of asset, it is much less plausible.
In this paper, some of the investors are modeled as Savage expected utility maximizers. It is assumed that these investors are sophisticated and can know the payoff distribution for each asset. The rational expectation assumption for expected utility traders is strong, but standard in the literature. The other investors are aware of the possible payoffs distributions, but they are unable to set a prior over them. These naive investors are what is called in the literature as ambiguity-averse and could be assimilated to retail investors.
There are two reasons for considering some investors ambiguity-averse. In the case of many investors, the expected utility theory yields optimal portfolios that are different from the actual ones. In the case of retail investors, the expected utility theory predicts diversified portfolios, while this kind of investors hold portfolios that prioritize some kinds of assets.3 The other reason is that there is evidence that some individuals and by extension, some investors, do not act as if they had a rational prior. One of the most famous examples of this behavior is the Ellsberg paradox (Ellsberg, 1961). In the simple version of the Ellsberg experiment, an individual bets on the draw of a ball from one of two urns. In one of the urns, there are fifty black balls and fifty red balls. In the other urn, there are one hundred balls, which are an unknown mix of black and red. Two gambles are proposed and the individual has to choose one of them. In the first gamble, if a red ball is drawn from urn one, the individual wins one euro and zero euros if a black ball is drawn. In the second gamble, if a red ball is drawn from urn two, the individual wins one euro and zero euros if a black ball is drawn. If the individual chooses the first of the gambles, it could be interpreted as if he had set a prior on urn two where he has predicted that there is less than 50 percent of red balls.
Next, the same individuals are offered to choose between two new gambles over the same two urns. In the first gamble, if a black ball is drawn from urn one, the individual wins one euro and zero euros if a red ball is drawn. In the second gamble, if a black ball is drawn from urn two, the individual wins one euro and zero euros if a red ball is drawn. Ellsberg proved through this experiment that most of the individuals choose the first of the gambles again. This means that the same individuals predicted that there were less than 50 percent of black balls. Individuals do not behave rationally since the priors that they have set over the percentage of the red balls in the first of the experiments and over the percentage of the black balls in the second experiment do not sum up to 100 percent.
Results of experiments as the one described have been proved consistent by the literature. Given this evidence, Gilboa and Schmeidler (1989) relaxed the Savage axioms in order to develop a decision theory consistent with the behavior observed in the Ellsberg's experiment.4 To do so, they presented a utility function payoffs that did not depend on a prior, instead, the individuals utility function payoffs depended on a set of priors. Under their axiomatic approach, they proved that individuals behaved in a pessimistic manner. Given individuals’ set of priors, they evaluated any option according to the minimum possible payoff. So, when these individuals tried to make a decision, they decided on the option that maximized the minimum expected utility.
In this paper, the modelization of ambiguity averse naive investors follows Easly and O’Hara (2009). Despite the fact, that there are two alternative ways of modeling ambiguity aversion in decision making (Ghirardato et al., 2004; Klibanoff et al., 2005), Easly and O’Hara chose to adapt the Gilboa and Shmeidler model to illustrate their ideas in a very tractable way.
3The model3.1Modeling investorsThe model is an extension of the model by Easly and O’Hara (2009). In this economy, there are two assets: money, which has a constant price of one and is in zero net supply, and another risky financial asset with normally distributed payoffs v. This risky asset is supposed to be bought only in the primary market and can be interpreted as junior bonds or preferred shares.
Investors know that the payoffs of the risky asset follow a normal distribution. The set of possible payoffs is v¯1,…,v¯N and the set of possible variances is σ1, …, σN. All possible pairs of mean and variance are possible and let Θ=θ1, …, θn, with n=N2 elements, be the set of possible pairs of parameters.5
The number of investors is normalized to one. All investors utility function for wealth is CARA with the risk aversion parameter set to one6:
In this economy, there are two types of investors: sophisticated investors, S and naive investors, U. The sophisticated investors are expected utility maximizers with rational expectations about payoffs. Let (vˆ,σˆ) denote the true mean payoffs and variance for the risky asset. Since the sophisticated investors have rational expectations, they know (vˆ,σˆ). This kind of investors can be interpreted as institutional investors.
The naive investors also care about means and variances, but they differ from sophisticated investors in that they cannot know the true parameters.7 Instead, they consider each normal distribution payoff, N(θ), as a possible payoffs distribution. Following Gilboa and Schmeidler (1989) axioms for ambiguity aversion, it is assumed that naive investors consider as possible mean payoff above and below vˆ and variances above and below σˆ. In other words, the true parameter values are convex combinations of the extreme values considered as possible by the naive traders. These naive investors can be interpreted as retail investors.
The amount of the issue of the risky asset is x¯≥1.8 This amount comes out from a previous maximization problem where the issuer has decided the optimal mix of products; deposits, bonds, share,.. etc to finance his activity.
In this model, a typical investor's wealth is denoted by w. Thus, the investor's budget constraint is:
where m is the quantity of money, p and x are the quantity and the price of risky asset. Investors are allowed to go long or short in each of the assets. If an investor chooses portfolio (m, x), his random next period wealth will be:In the economy, there are no arbitrage opportunities. This means that for any price p of the financial asset, there is a unique pair (v¯,σ) that supports it.
The primary market for the risky asset is modeled as the result of the following game:
- 1.
An issuer launches an issue of the risky asset. This issuer decides to place it exclusively among retail investors and the price of the issue.9
- 2.
Given the price and the characteristics of the issue, the retail broker of the issue advises investors about the characteristics of the issue. In particular, the broker helps investors to estimate the mean and the variance of the issue.
- 3.
Given the price and the characteristics of the issue that investors perceive, they decide the amount of the risky asset they want to hold in their portfolio.
The model is conceived as a two periods model where both the issuer and the broker try to maximize their profit. In the first period, the issuer lives for sure. In the second period the issuer can go bankrupt with a positive probability that is denoted by PrB. In that case, the issuer would stop paying the promised payments of the issue and would earn zero profits. It is finally assumed that retail investors fully trust the advice of the broker when placing them the issue.
3.2Investors demands and market pricesThe demand of institutional and retail investors are figured out given the price and the advice given by the retail broker of the issue. The demand of the institutional investors is figured in order to provide a benchmark to compare the outcomes in the retail market with what would happen in case the issue were for institutional investors. So, for an institutional investor with CARA utility function and expected payoff parameters (vˆ,σˆ), the expected utility of this random wealth is a strictly increasing transformation of:
Working out the institutional investor maximization problem, the institutional investor's demand function for the risky asset is found out:
A retail investor evaluates the expected utility of wealth for each parameter vector and chooses the portfolio that maximizes the minimum of these expected utilities. Thus, a retail investor tries to avoid the worst case outcomes, and so, they choose a portfolio that explicitly limits their exposure to such adverse outcomes. The expected utility of the random wealth, given parameters θ=(v¯,σ), is a strictly increasing transformation of:
Thus, following Gilboa and Schmeidler (1989), the retail investor's decision problem can be written as:
This maximum problem reveals that for any considered portfolio the minimum possible payoff is considered at the maximum possible variance for the risky asset. Denote this variance by σmax. Whether the maximum or minimum payoff is considered by the retail investor depends on his net position in the risky asset. When the retail investor is long, he considers the minimum possible payoff, which is denoted by v¯min. Instead, when the retail investor is short, he considers the maximum possible payoff, v¯max.10 If the retail investor's decision problem is solved, it is found out that:
Lemma 1Easly and O’Hara (2009) The retail investor's demand function for the risky asset is:
Proof See Appendix A and Easly and O’Hara (2009). □
This demand function has important properties. The most important one is that for a wide range of prices, the retail investor neither buys nor sells the risky asset. This means that when the price is set between the minimum and maximum possible payoff, the retail investors do not participate in the market of the risky asset. Only if the retail investor decides to hold the risky asset, the variance of the asset matters.
As a consequence of the behavior of the retail investors, their risky asset demand is not continuous as it is in the case of institutional investors. The retail demand function has kinks at v¯min and v¯max. The other consequence of the retail investors behavior is that their demand is always lower in absolute values than the demand of the institutional investors when they hold a long and short position. In other words, retail investors always require a better compensation than the institutional ones in order to hold the risky asset. This results in:
By simple inspection, it is easy to observe that the price required by institutional investors is higher than the one required by retail investors. This difference in the prices at which the issue is placed is due to the compensation that retail investors require because of their ambiguity aversion.
Thus, if there is no advice about the characteristics of the issue to retail investors (in terms of the model, which are the value of its mean, v, and its variance, σ) the prices of the issue for retail investors should be lower than the prices of the issue for institutional investors. However, this is not what has been observed in Spain in the last years.
4The incentives of the retail broker when it places an issue for retail investorsIn most issues placed only among retail investors, the issuer and the retail broker belong to the same financial institution.11 So, in terms of the model, the financial institution solves at the same time the decisions of stages one and two of the game. The same institution has to decide the price of the issue and the mean and the variance the retail broker advises as true to the investors. It is good to point out that in this case, given that the amount of issue, x¯ was decided previously*, the main goal of the financial institution is to place the issue to the lowest possible price.
In general terms, retail investors have a relationship with their brokers that resembles that between a doctor and a patient. In this kind of relationships, the advised part fully trusts the information received from the retail broker that acts as adviser. Thus, in this paper, it is assumed that investors fully trust the information they receive from the retail broker about the characteristics of the issue it is trying to place.
Therefore, the financial institution only has to decide the mean and variance that the retail broker will advise as true to the retail investors in order to set the price the financial institution finds optimum.
The financial institution solves the following maximization problem:
where π(p) are the profits of the financial institution in case it does not go bankrupt in the period that follows the issue. In case the financial institution goes bankrupt, it is assumed that its profits are zero. It is assumed that the cost of the issuance and brokerage is normalized to zero. The profit function is made up of two parts that depend on the final price of the issue. The first part reflects the direct income from the placement of the issue. The second part reflects the influence of the placement in the financial institution's future profits. The second part is the multiplication of the probability that the institution survives in the next periods by the profits that the financial institution will earn in case it survives. Both elements are influenced by the price at which the issue was placed. In principle, it is assumed that the higher the price, the higher the probability to survive.For simplicity, it is considered that the future profits are not influenced by the price of the placement. At first, one could think that if the issue is placed at a very high price and the investors are aware of it, the financial institution could suffer a damage to their reputation. However, it is difficult that this cause-effect arises in reality. If the financial institution is alive in the period posterior to the placement, for sure it will be able to make the promised payments to investors. Moreover, the kind of placement that is analyzed in this paper is usually sold to investors with strong links with the issuer.
The next proposition follows from the solution to the financial institution maximization problem:
Proposition 2 The retail broker places the issue as if it had the mean and the variance of a deposit.
Proof See Appendix A. □
Given that the investors fully trust in their retail broker advice, the financial institution has the incentives to tell investors that the issue has the minimum possible variance. If these characteristics are translated into one of the available products for retail investors, the issue is placed to investors as if it were a deposit.
Therefore, as the retail investors believe that the issue has a lower variance than the actual one, they are willing to buy the issue at a higher price than the institutional investors would do. This means that the issuer always places this type of issues among retail investors. Thus, the conflict of interest between the financial institution and the retail investors exists.12 The financial institution damages retail investors advising them wrongly to profit from them.
It is important to point out the role that the advising from the retail broker plays. Without it, and given their ambiguity aversion, the retail investors would demand lower prices in order to buy the issue or they even would not buy the issue at any price. Thus, it is difficult to think that this type of issues can be placed without the advice from the retail brokers.
5The social optimum benchmarkGiven the results from the previous section, it could be interesting to compare them with the social optimum. To do so, it should first be defined the social welfare function that the regulator optimizes. In the context of current financial regulation and given the problem the regulator has to tackle, there are two possibilities. In the first possibility, the regulator takes into account investors welfare and financial stability. This possibility stays closer to the idea of one sole financial regulator.13 The second possibility comes from the twin peaks regulatory framework. In that regulatory framework, one of the legs is devoted to regulate and supervise the financial markets and the rules of conduct. So, it can be considered in this context that the regulator takes into account only the investors welfare in its social welfare function.14
Thus, if the twin peaks regulatory framework is at work, the regulator solves the following maximization problem:
It is assumed that the regulator is able to know the real characteristics of the issue, vˆ and σˆ. If the regulator maximization problem is solved and the market clearing condition is applied, it is found out that:
Proposition 3 The social optimum price ispS*=vˆ−σˆx¯.
Proof See Appendix A. □
The price that maximizes social welfare is the same as the price that an institutional investor would pay if the same issue were placed only among them. This result is not surprising as it was assumed that institutional investors and the regulator share the same information.
If the other type of regulator is considered, then the regulator solves the following maximization problem:
Considering that the issuer places securities that improve its solvency, it could be assumed that there are no reputational costs in the future while the issuer is in business, and the social welfare optimum price is lower than the other type of regulatory framework. Given a price for the issue, the optimal demand is higher as the regulator internalizes that issuer solvency increases as the sold issuance is higher.
In any case, the social welfare optimum prices are lower in general than prices observed when an issuer places securities to retail investors through its retail banking branches. This means that the conflict of interest decreases social welfare. Only in the type of regulatory framework where there is one sole financial regulator, the price of the placement could be close to the social optimum. This would happen when the weight given by the regulator to the financial stability is high and the issue improves the solvency of the issuer in a significant way.
One important implication of the social optimum price under the twin peaks regulation is that it cannot be implemented without the help of a broker that advises retail investors on the characteristics of the issue. Without such advice, retail investors would demand lower prices in order to buy the issue. Therefore, the implementation of the social optima requires the advice from the broker of the issue, but this advice must reflect its real characteristics and not the ones that maximize issuer's profits.
For the remainder of the paper, it is assumed that the regulatory framework at work is the twin peaks option. Some regulatory solution will be explored in order to implement an outcome as close as possible to the twin peaks regulatory optimum.
6Regulatory solutionsAs it has been shown, some issues have been placed at prices that are far from what is sociably desirable. Although this kind of placements is regulated within the European Union, these examples could mean that the current regulations are not enough.15 In principle, these regulations advocate for two complementary vias to avoid the conflict of interest between the financial institution and their investors in this type of issues. The first of these vias is the obligation that the retail broker has to inform investors about the characteristics of the financial asset through documentation. The other via, which was the real novelty of these regulations, is that the retail broker must test before the financial asset is sold to any investor that the financial asset is really adequate to the investor profile. If the retail investor passes either the suitability test or the appropriateness test, he can invest in complex financial assets (e.g. preferred stocks). If the investor passes none of the tests, the retail broker should recommend the investor that they give up investing in the complex financial product. With these tests, the regulator prevents that retail investors without the adequate investor profile buy complex financial assets.
However, these regulations could not achieve their final goal of avoiding the conflict of interest. One possible reason could be that the retail investors do not make an adequate use of the documentation on the characteristics of the financial asset. The only information that retail investors consider useful comes from the broker. Under this assumption, this regulation would not solve the conflict of interest.
The other reason could be that the tests of suitability and appropriateness do not achieve their final goal of avoiding that investors without the adequate investor profile buy complex financial assets. In the case of the appropriateness test, the investor is not obliged to pay attention to the test result and it could buy the financial asset anyhow. The only condition is that the retail broker must inform the investor documentarily that it has not passed the appropriateness test. Thus, if the retail broker had enough influence on their investors, it could place a complex product among them despite the fact that the complex financial asset does not fit the investors profile by means of this procedure.
Therefore, the current regulation of the European Union on conflicts of interest could be insufficient to prevent the one studied in this paper. In the following subsections, several regulatory proposals will be analyzed in order to implement an scenario where the outcome from the interaction between retail broker and investors is closer to the social optimum.
6.1The supervisor sets a price cap for the issueThe main objective of the issuer is to try to sell the issue at the highest possible price. As it was shown in the previous section, this is not optimum from a social welfare point of view. One of the classic solutions of the economic theory to this problem is that a supervisor sets the price that maximizes social welfare.16
One way of implementing the supervisor's price could be through the use of a price cap.17 The following question that arises is the value of the cap. As the price to implement is the institutional price, this price should be the cap that the financial institution that issues and brokers the financial asset faces when it places the issue among the retail investors. So, the maximization problem of the financial institution would be:
As the new constraint binds in equilibrium, it can be concluded that:
Proposition 4 If a price cap, p≤vˆ−σˆx¯, is imposed to the financial institution that issues and places the financial asset, the social welfare optimum is implemented.
Proof See Appendix A. □
The price cap constraint makes the financial institution set the institutional price for the issue. Given the behavior of the retail investors, the retail broker has the incentive to advise the retail investors rightly. They tell investors a minimum mean and a maximum variance which coincide with the priors about those parameters that institutional investors would have.
One important question that has not been discussed so far is how a supervisor can know which the institutional price of the issue is. Currently, one may think that a supervisor does not have access to the technology to form its own priors about the characteristics of an issue. However, the supervisor has access to the information about prices of issues that can be considered very close to the one the issuers try to place only among retail investors. So, although the prices of other issues are always an imperfect estimator of a new issue, they can be considered a good proxy to the institutional price of a new issue.
Other way to implement this solution is to force issuers to include an institutional tranche in the issue. This institutional tranche would be priced first and it would be used as a price cap for the retail tranche. Under this regulatory solution, the retail investors could profit from the information that institutional investors have about the issue.
In case, there are no comparable issues in the institutional market, the supervisor could use other procedure at the cost of a higher error in estimating the price of a new issue for retail investors. The supervisor could use, for example, a mark to model to estimate it or he could turn to an independent expert. However, it should be taken into account that if a comparable institutional price is not available for the supervisor, he can achieve at most a second best social optimum.
6.2Informational warnings about the characteristics of the issueIn practice, a popular regulatory solution to the conflict of interest between an issuer that places a financial asset with credit risk and its retail investors is to inform retail investors about the possible risk of the issue. The supervisor usually issues an informational warning included in the leaflet used by the retail broker to place the financial asset.
The informational warning can be interpreted as a constraint imposed to the retail broker. The constraint that the retail broker faces depends on how much the investors actually trust in their advice. So, in one extreme, if retail investors only trust in their broker's advice, they ignore the informational warning. In the other extreme, if retail investors do not trust their broker's advice at all, they fully trust the informational warning. In general, retail investors do not behave so extremely. In order to pick up this fact, it is assumed that they form their beliefs about the characteristics of the issue as a weighted average of the broker's advice and the informational warning.
In terms of the model, the important information for retail investors is the worst scenario that the issue can face in the future. This means that the retail investors build up their beliefs about the worst scenario of the issue as v˜;min=γv¯minB+(1−γ)v¯minW and σ˜;max=γσmaxB+(1−γ)σmaxW, where v¯minW and σmaxW are the parameters derived from the informational warning, while v¯minB and σmaxB are derived from the retail broker's advice and γ is the weight the retail investors put on the information that comes from their broker.
Then, if the supervisor decides to set an informational warning, the financial institution faces the following maximization problem:
If the maximization problem is worked out, it is found out that:
Proposition 5 If the supervisor decides to set an informational warning to the issue, the retail broker advises about the characteristics of the issue as if it were a deposit.
Proof See Appendix A. □
Despite the informational warning, retail brokers have the incentives to behave as if the informational warning were not set. This is the way brokers have to make sure that the issue is placed at the lowest possible price.
Although it is assumed that the informational warning informs investors perfectly of the worst possible mean and variance of the issue, only a second best outcome can be implemented.18 However, under this regulation, the price that results from the placement could be lower or higher than the price that implements the social optimum. The final equilibrium price depends crucially on the value of parameter γ.
If γ→0, the retail broker's advice is not taken into account by the investors. They form their beliefs from the informational warning that appears in the issue leaflet, as v¯minB
Under this regulation the price enjoyed by investors is always lower, but this does not mean that the social welfare is always higher than when there is not any regulation at work. If γ→0, it could happen that the price is so low than the distance of this price to the optimum is higher than the distance from the price without regulation to the optimum.19
In this analysis, it has been assumed that the issue is always placed to investors independently of the price needed to do so. However, in reality, if the price is lower than the price the issue could have in an institutional market, the rational decision of the issuer would be to switch the placement of the issue from the retail market to an institutional market or to give up issuing the financial asset.
6.3Obligation of brokerage through a financial institution different from the issuerPreviously, it was proved that in an issue, there is a conflict of interest between a financial institution and the investors when a financial institution plays the role of issuer and retail broker. One possible regulatory remedy could be to split out the two activities among two different financial institutions. This type of regulatory remedy is well known as a source of solution to conflicts of interest in financial institutions. Two examples of this type of regulation are the Glass–Steagall Act, which promoted the separation between the investment and the depositary banks and the recent European Union Regulation on Credit Rating Agencies, which has obliged them to provide only credit ratings and has forbidden them to run consultancy firms.20
As it is considered that the issuing and the retail brokerage activities are made by different financial institutions, the financial institution that is in charge of brokerage the issue solves the following maximization problem when placing an issue with credit risk:
where pI is the price that the broker pays to the issuer for the financial asset.21 The other two latter parts of the profit function are the future profits of the retail broker in case the issuer goes into bankruptcy and the future profits of the retail broker in case the issuer does not go into bankruptcy.Proposition 6 If the probability of the issuer and the retail broker going bankrupt at the same time is one, the retail broker behaves with their investors as if the issuer and the retail broker were integrated in the same financial institution.
Proof See Appendix A. □
This proposition shows the limitation that this regulatory measure can have in practice. This measure could only be effective if two conditions are met. Firstly, the joint probability of the issuer and the retail broker going bankrupt at the same time is close to zero. Secondly, it would also be necessary that the profit of the retail broker decreases when the price of placement increases. This behavior could happen in reality due to the reputational cost the retail broker could bear when the issuer goes bankrupt. Under an issuer bankruptcy, retail investors could realize that the financial asset they bought has different characteristics from the ones the retail broker told them.
Only under these two conditions, this regulatory measure could result in a superior outcome from the social welfare point of view. In theory, if the probability that the retail broker survives when the issuer goes bankrupt is close to one and the reputational cost in the case the broker sells the issue to a higher price than the institutional one is sufficiently large, then an outcome close to the first best social optimum can be implemented. However, these two hypotheses are not very likely to happen at the same time in reality.
This section and the result of its proposition can also help to discuss another very popular regulatory remedy to avoid conflicts of interest. This remedy consists in isolating the different business lines. Under this remedy, the financial institution runs its businesses as if they were owned by different institutions. This remedy is usually implemented through the use of Chinese walls and by separating physically the departments.22
Nevertheless, this remedy could not be effective when placing among retail investors the kind of issues that are being analyzed in this paper. One of the key parameters to implement a superior social welfare outcome by using this remedy is that the broker has a probability of survival conditional on the default of the issuer being close to one. It is rather clear that this condition is not very likely in this context, as both, the issuers and the broker belong to the same financial institution.
6.4EnforcementThe measures considered in this section are possible improvements in the capacity of the supervisory agency to enforce the regulation to avoid conflicts of interest. In particular, the improvements could be based on the capacity of the supervisor to detect breaches in the conduct of the financial institutions and on the deterrence impact of penalties, or on a combinations of both.
Enforcing the law in this case means to detect and penalize the behavior of financial institutions when it can be considered that there is a conflict of interest.23 Thus, if an institution is supervised, the financial institution maximizes the following problem:
where λ is the probability of the financial institution to carry on a behavior that can be considered as a conflict of interest and it is detected and penalized by the supervisor. The function φ(p−pI) gives the penalty that the supervisor imposes to the financial institution when the behavior is against its investors and is detected. This function is increasing in the difference between the price at what the financial asset is sold to retail investors and the price of the financial asset in an institutional market, furthermore φ(0)=0.Under this approach and given the regulatory framework, the supervisor decides how much effort it wants to do in order to detect behaviors that can be considered conflict of interest where retail investors are damaged. This decision is picked up by the probability λ. Moreover, the regulator also decides which is the exact functional form of the function φ(p−pI). Given the decisions of the supervisor and the regulator about the parameter λ and φ(p−pI) respectively, the financial institution decides which v¯min,σmax maximizes its profits.
Proposition 7 Under the following relationship betweenλand the penalty functionφ(p−pI):
Proof See Appendix A. □
Theoretically, a first best social optimum can be implemented. Moreover, there is not a unique way of implementing it, but there are infinite ways. The probability of detecting a financial institution incurring a conflict of interest could be lower (and therefore the supervision effort to detect that behavior) at a cost of imposing a higher penalty when the financial institution places the asset at a higher price than the institutional one.
However, when one looks to reality, it is difficult to think that there are the necessary conditions to implement the first best social optimum in European countries. Currently, the probability of detecting financial institutions’ misconduct regarding the sale of financial products to retail investors is still low. So, the optimal penalty that allows to implement the first best social optimum should be very high. Only a more realistic, lower penalty that could be paid by the financial institution could be imposed. This means that under the current regulatory and supervisory regime only a second best social optimum could be implemented. If the regulator wanted to implement an outcome closer to the social optimum, it could achieve this aim through the reform of the regulatory and the supervisory framework in order to increase the probability that a financial institution is detected and penalized when it conducts a behavior against its investors.
7A numerical comparison among the proposed regulatory measuresBy means of this example, it can be easily compared the outcomes of the four regulatory alternatives that have been analyzed in this paper. In this example, it is considered a risky asset with a mean, vˆ=20, and a variance σˆ=20 and the size of the issue is x¯=1. Moreover, the set of possible means is v∈[5,30] and the set of possible variances is σ∈[0, 40]. So, the institutional price of this issue would be:
According to this paper's model, without any advice from a broker, the price if the issue is only placed in the retail market would be:
and the price if the issue is only placed in the retail market and it is issued and placed by the same financial institution would be:Without any regulatory intervention, two cases should be only observed: an issue is placed in the institutional market at a price of 100 or it is placed in the retail market by a financial institution which issues and brokers the issue at a price of 105.
From the discussion of the four regulatory measures analyzed, it is known that by setting a price cap equals to the institutional price and by setting the optimal level of enforcement, a first best social optimum could be attainted. The issue could be placed in the retail market at a price of 100. However, with the other two measures: setting an informational warning about the characteristics of the issue and setting the obligation of brokerage through a financial institution different from the issuer only a second best social optimum could be attained.
In order to figure out a numerical example for the case of informational warning, it should be noted that the price finally set in the market crucially depends on the degree up to which retail investors trust their brokers advice which is represented by γ. So, in equilibrium, the mean and variance retail investor perceive are:
Therefore, the price if this measure is implemented would be:
It is important to notice that when γ→1, retail investors fully trust their broker advice, this price converges to the equilibrium price when there is not regulatory intervention. In this example, the issue is placed among retail investors only when γ∈[7/8, 1]. When γ is lower than 7/8, the equilibrium price in the retail market would be lower than in the institutional one.
For the fourth regulatory measure, setting the obligation of brokerage issue for the retail market through a financial institution different from the issuer, further assumptions are needed. Specifying how the placement of the issue could influence in the future profits. In particular, in this example, it is assumed that the broker profits are a constant π when neither issuer nor broker defaults after the issue is placed. When issuer defaults after the placement and the broker does not, the broker profits are π−δ(p−pI), where δ=10. Finally, it is also necessary to figure out which the default correlation between the broker and the issuer. One interesting case is to assume that this default correlation is 0, Pr(BB⋂BI)=0.
Under these assumptions, the equilibrium price of the issue in the retail market is 102, which improves the price when there is not regulatory intervention but is higher than the social optimum price, 100.
In this example, it can be easily seen that setting an informational warning does not always provide better outcomes from a social point view. Depending on how much retail investors trust their broker, this regulatory measures could be superior to the obligation of brokerage the issue through a different financial institution. So, if γ∈[7/8, 37/40], the informational warning is superior from a social point of view.
8ConclusionsThere is a puzzle in the financial markets. The percentage of retail investors who hold risky financial assets is very low. This could be mostly due to the ambiguity aversion that retail investors have when they face the possibility of buying a risky financial asset. However, certain complex assets with credit risk are placed successfully among retail investors, for example, preferred shares.
In most of the retail placements, the issuer and the retail broker of the financial asset belong to the same financial institution. This characteristic could make the conflict of interest in this kind of placements possible. In this paper, it has been proved that there are incentives for the financial institution to incur a conflict of interest. The conflict of interest consists in the retail broker selling the financial asset with high credit risk to the investors as if it were a deposit. This allows the financial institution to set a high price for the placement.
It has also been proved that this conflict of interest is not desirable from a social welfare point of view. The social optimum is reached when the financial asset is placed at the price it would have if the placement were only for institutional investors. At that price, the retail broker advises correctly retail investors and informs them on the actual characteristics of the issue. These advices make that the retail investors can internalize the information of the broker and behave as if they were institutional investors.
As current regulation could be insufficient to tackle this conflict of interest, four possible regulatory measures were analyzed in order to implement an outcome closer to the social welfare optimum: setting of a price cap for the issue by a supervisor, setting of an informational warning about the characteristics of the issue by a supervisor, obligation of brokerage through a financial institution different to the issuer and finally, a better enforcement of the rules against the misconducts of the financial institutions that issue and broker financial assets exclusively for retail investors.
Under the first of the proposed regulatory measures, the first best social welfare outcome can be implemented. A cap equal to the price that would be set if the issue were placed to institutional investors would force the retail broker to tell the retail investors the actual characteristics of the issue. By extension, the retail broker would set a price to the retail investors equal to the price for institutional investors.
Under the other three proposed regulatory measures, a second best social welfare outcome could be implemented at most. So, if an informational warning is published, the impact on the price paid by the retail investors depends on how much they trust the warning and how much they trust their broker. If they trust mainly their broker, this measure manages to lower the price for the retail placement. The more retail investors trust the informational warning, the closer to the first best social outcome. However, this dynamic has a limit in improving social welfare. Given the retail investors ambiguity aversion, if the retail investors mainly trust the informational warning, they could ask for a price that is lower than the institutional one as they want to protect themselves against the event the issuer might go bankrupt. In this case, the issuer would switch the issue from the retail market to an institutional market in order to be able to sell the issue at the higher possible price, or even he could give up issuing the financial asset.
The measure based on splitting the activities of issuing and retail brokerage between two different financial institutions will make social welfare higher the closer to zero is the default correlation between the issuer and the retail broker. If the issuer goes bankrupt, the retail investors could realize whether the retail broker did advise them correctly. If the retail broker did not advise them correctly, it would suffer a reputation loss and consequently a profit loss. However, episodes of financial scandals where financial institutions have placed financial assets from other institution that has gone bankrupt have shown that these losses are not large enough to implement a first best social optimum.
Finally, under the option of better enforcement of the conduct of business rules, although theoretically it could be implemented as a first best social optimum, in practice it is not realistic. Currently, the probability that a financial institution that incurs conflict of interest is detected and penalized seems to be low in European countries. If the regulator wanted to implement a first best social optimum, he would need to impose such high penalties to the detected and penalized financial institutions that they would not be able to pay them. Thus, the regulator can only implement a second best social optimum via enforcement.
One important issue, out of the scope of this paper, is which of the regulatory measures that implement second best social optimum gives the highest social welfare. In principle, they are imperfect substitutes and a superiority of a particular measure must be checked on a case by case basis. Moreover, some of the measures are not mutually exclusive and could be applied at the same time. An example of a regulation that combines two of the analyzed solutions is currently implemented by the CNMV. This institution requires independent experts to value the financial assets with credit risk that are placed among retail investors. Under these well-founded opinions about the price of the issue, if there is a significant divergence between the independent expert price and the issuer price, the supervisor could set a warning to inform retail investors.
I gratefully acknowledge the suggestions and comments from two anonymous referees. I also thank the comments from Raquel de Julian, Elisa Muñoz, Julian Baranda, Elias Lopez and the participants in the seminar at the CNMV, XIX Foro de Finanzas and XXXVII Simposio de analisis economico. The usual disclaimer applies.
It is straightforward to derive the lemma following Easly and O’Hara (2009), pages 1823–1825 under the assumption that ν=0.
The financial institution maximizes the following maximization problem:
In equilibrium the constraint is binding. If the first order condition over the objective function is taken, it is found out that:
As it is assumed that ∂π(p)∂p→0, that assumption implies that:
Regarding the variance:
As it is assumed that ∂π(p)∂p→0, that assumption implies that:
Given that there is sufficient competition to avoid arbitrage opportunities in the retail markets and that |∂Π∂v¯min|<|∂Π∂σmax| as x¯≥1, the solution for the financial institution is to advise retail investors that the financial asset has the following characteristics:
and the a v¯min that equals the one of the deposits.If the twin peaks regulatory framework is at work, the regulator solves the following maximization problem:
If the first order condition over the regulator objective function is taken:
The second order condition for being xS a maximum of the welfare function trivially holds. Then, the market clearing price must hold the following condition:
As the regulator has imposed a price cap equal to the institutional price, the financial institution maximizes the following optimization problem:
As for proposition 2, the first constraint of the problem is binding. Then, if the first order condition over the objective function is taken, it is found out that:
As it is assumed that ∂π(p)∂p→0, that assumption implies that:
Regarding the variance:
As it is assumed that ∂π(p)∂p→0, that assumption implies that:
The two first order conditions mean that the second constraint is also binding. So, given that there are no arbitrage opportunities in the retail markets, the retail broker has no incentives to cheat investors and advises v¯min=vˆ and σmax=σˆ to them. Thus, the first best social optimum is implemented.
If the regulator decides to set an informational warning, the financial institution faces the following maximization problem:
If the second and the third constraints are substituted into the first constraint:
In equilibrium the constraint is binding. If the first order condition over the objective function is taken, it is found out that:
As it is assumed that ∂π(p)∂p→0, that assumption implies that:
Regarding the variance:
As it is assumed that ∂π(p)∂p→0, that assumption implies that:
Given that there is sufficient competition to avoid arbitrage opportunities in the retail markets and that |∂Π∂v¯min|<|∂Π∂σmax| as x¯≥1, the solution for the financial institution is to advise retail investors that the financial asset has the following characteristics:
and the a v¯min that equals the one of the deposits.The financial institution that is in charge of brokering the issue solves the following maximization problem:
where pI is the price that the broker pays to the issuer for the financial asset. If the probability that the issuer and the retail broker go bankrupt at the same time is 1, then:If the retail broker maximization problem is rewritten, it is found out that:
As, the retail broker problem is the same as in the case of an integrated financial institution that issues and brokers but for one constant, the solution must be the same. Thus, under the condition pointed out above, the behavior of a financial institution that only brokers an issue is the same as in the case of an integrated financial institution issuing and brokering the same issue.
The financial institution maximizes the following problem:
where λ is the probability that the financial institution carries on a behavior that can be considered conflict of interest and it is detected and penalized by the supervisor. The function φ(p−pI) gives the penalty that the supervisor imposes to the financial institution when its behavior is against its investors and is detected.The second constraint is binding in equilibrium. As it is assumed that there is not arbitrage free opportunities in the retail markets, the objective of the regulator and the supervisor is to find out the λ and φ(p−pI) that implement the first best social optimum. In equilibrium, the first constraint of the financial maximization problem is binding. So, if the first order condition of the financial institution objective function with respect to v¯min and σmax is taken:
As it is assumed that ∂π(p)∂p→0, that assumption implies that:
Regarding the variance:
As it assumed that ∂π(p)∂p→0, that assumption implies that:
As the two first order conditions are identical, the system of equation are undetermined compatible and has infinite solutions. All combinations of λ and φ(p−pI) that hold the following condition implement the first best social optimum under the assumptions that there are no arbitrage opportunities in the retail markets and the φ(p−pI) is sufficiently concave to hold the second order conditions of the financial institution maximization problem:
Anyhow, this first best social optimum is only implemented as far as the financial institution has enough profit to be able to pay the penalty in case it deviates from the social optimum. So, the condition that the profit of the financial institution is greater of equal to zero is needed in case it deviates and behaves against its retail investors.
See Guiso et al. (2003) for participation rates in Europe.
Other papers, as for example Dow and Werlang (1992) or Epstein and Wang (1994), also proved that ambiguity aversion leads investors with that aversion to avoid participating in a market.
The axiom they weakened is the Independence axiom.
As will become apparent, only the minimum and maximum mean payoff and maximum variance affect decisions made by naive traders. So changes to the set Θ that leave these values unchanged have no impact on the market. In particular, Θ can be a continuum.
CARA is the acronym of Constant Absolute Risk Aversion.
These investors can be thought of as inexperienced investors, who do not have enough experience in financial markets to reliably access payoff functions. Perhaps they have not yet participated in the asset market, and although they can imagine many possible payoff distributions, they are unable to place a prior on this set of distributions. They know that holding cash is safe, but are just not sure what to think about risky assets.
Notice that the naive and sophisticated investors have their risk aversion parameter set to one.
In equilibrium, under the assumptions of the model this decision is consistent only when the price of the issue in the retail market is higher than in the institutional market.
Although theoretically retail investors can take a short position in a risky asset in practice, it is unusual that retail investors take such kind of positions.
In 2009, in Spain, the 89.2 percent of the total amount was placed exclusively to retail investors through the issuer's retail banking branches.
The behavior of the retail broker when it maximizes profits can be consider as the result of a conflict of interest that is against recital 19 of the European Union 2004/39/CE of the European Parliament and the Council (MiFID).
Examples of countries that have implemented the one sole financial regulator are Germany and Sweden.
Examples of countries that have implemented the twin peaks regulatory framework are Australia and the Netherlands.
The current European Union regulation is contained in the Directive 2004/39/CE of the European Parliament and the Council known as MiFID and the Directive 2006/73/CE of the Commission.
See for example Laffont and Tirole (1993).
A similar way of implementing regulatory prices can be found in the telecommunications industries. In these industries, regulatory prices are very often implemented through price caps. For a complete description of the price cap regulation, see Vickers and Yarrow (1988).
In general, as σmaxB<σˆ and σmaxW>σˆ, there exists a unique γ that makes the placement price equals the institutional price.
This result is in line with Paredes (2003), who argues that information can be damaged for retail investors.
This measure of the Glass–Steagall Act of 1933 was taken to avoid the conflict of interest that could exist when an entity can have deposits and at the same time can make investment banking. An integrated bank could grant credit to the investment banking division and use that credit to invest in their own profit. The measure in Regulation 1060/2009 of the European Parliament and the Council was taken to avoid the conflict of interest that could happen when a credit rating agency is in charge of advising about how to structure an issue and at the same time it brings in a credit rating on the same issue.
For simplicity, it is assumed that the retail broker also underwrites the issue. It is straightforward that by solving backwards, in equilibrium, pI is equal to the price for institutional investors, pI=vˆ−σˆx¯.
An example of this kind of regulation remedy is what was called “Global Settlement”. The Global Settlement was an enforcement agreement reached on April 28, 2003 between the SEC, the NASD, the NYSE, and ten of the Unites States’ largest investment firms to address issues of conflict of interest within their businesses.
It exists an economic literature about this topic. The seminal paper about this literature is Becker (1968). In this paper, the author proves that a behavior that come be considered against society can be corrected by an adequate penalty.