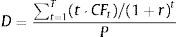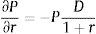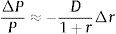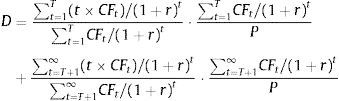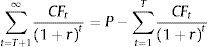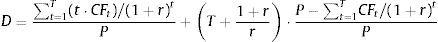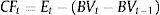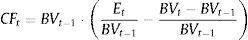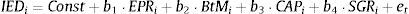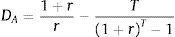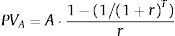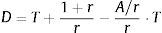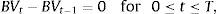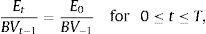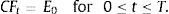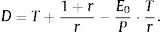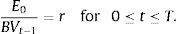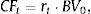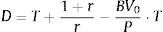The implied equity duration for the Spanish listed firms

Abstract

In this paper, we compute the implied equity duration (IED) for the non-financial companies listed in the Spanish stock market for the first time, to the best of our knowledge. This measure of risk adapts the traditional expression of the duration of a bond to the stock context. We also conduct a sector analysis and a size analysis using the Ibex indices composition. The results are then compared with those from the U.S. stock market and related to other proxies of equity risk. This analysis shows that there is a significant relation between the IED and the earnings to price ratio, the book to market ratio and the sales growth rate, but not to capitalisation, thus excluding the presence of a size effect. The results support the relation of the IED with the high minus low factor, thereby suggesting that the latter is subsumed in this measure.

1

Introduction

The interest rate risk analysis in the fixed income context is built on a rigorous methodological approach based on discounting the cash flows promised by the issuer. The central concept in this framework is the duration, a risk measure commonly accepted and used by both academia and practitioners. This concept, first presented by Macaulay (1938), is defined as the weighted average of the times at which bondholders receive the cash flows from a bond, where the weights are equal to the present values of the payments normalised with respect to the price of the bond. The Macaulay duration effectively measures the sensitivity of a bond to changes in the discount rate in the fixed cash flow model, i.e., the yield to maturity.

However, the interest rate risk analysis for equities does not have a unique framework. Thus, we find from analysis based on simple models of stock valuation (Leibowitz, 1986) to others based on an empirical linear relation between the variations in stock prices and the variations in market interest rates a compromise solution. Despite the efforts of researchers, reaching up prepend the need of results to the rigour of the analysis, none of these methodologies has provided the necessary results to become a reference methodology.

In this context, Dechow et al. (2004) bridge the gap between techniques used in the analyses of bonds and equities, thus developing a measure of implied equity duration (IED) based on the Macaulay duration for a bond. Their methodology also combines, in the equity context, the two aforementioned approaches as they used an analytical model of stock valuation based on the discounted cash flows that matches the market quote by adjusting the terminal cash flow scheme.

Thus, implementing the IED requires estimating in advance the expected cash flows by the equity, in which a two-step process is used. First, using a simple model based on historic financial data, cash flows are estimated for a finite prediction horizon. It is then assumed that the rest of the equity market price is distributed as a perpetual start on the finite prediction horizon. Accordingly, applying the Macaulay duration formula to these cash flows leads to the IED.

Dechow et al. (2004) compute the IED for each of the companies using the available data from the NYSE, AMEX and NASDAQ, between 1963 and 1998, and obtain an IED average of 15.13 years, with a standard deviation of 4.09. The results of their empirical tests show that the IED explains the risk characteristics for the stock returns, resulting in a positive and significant relationship with the volatility of the stock returns and their betas, and that the IED provides more prediction power of these variables than does its own lagged variables. Furthermore, the IED captures a strong common factor in the profitability of the shares that encompass the common factor related to the book-to-market ratio (BtM) whose empirical properties were revealed by Fama and French (1993).

In this context, the objective of this paper is to compute the IED for the listed firms in the Spanish stock market with the data available at the end of 2011, compare the results with those obtained in Dechow et al. (2004) for the U.S. market, perform sector and size analyses and search for the relationship of the IED with other commonly used variables as risk proxies to find evidence of the relationship between the IED and the company growth options as well as the size and effects of the IED as gathered by the Fama and French factors.

The latter analysis links this work within the empirical literature that relates the systematic risk of stock with the premium value by breaking down the betas for assets in cash flow betas and discount-rate betas. In this context, Campbell and Mei (1993) find that the discount-rate betas represent the large part of the total beta of the companies, and based on that, Cornell (1999) suggests that the high betas for growth stocks are a consequence of a greater weight of the cash flows removed in time, or equivalently, of growth stocks longer duration. Campbell et al. (2009) show that the value premium is a consequence of the differences in the timed schedule of the expected cash flows by the shareholder represented by the duration. At the same time, Da (2009) shows how cross-sectional differences in the duration of companies could explain an important part of the stock returns. In summary, as Santa-Clara (2004) has noted, the IED “is an interesting new approach to measuring stock risk”.

This paper is organised as follows. In the next section, we derive the measure of interest rate risk of the equity, the IED. Section 3 describes the data selection process. Section 4 presents the results: (i) the results of computing the IED for each company and the main statistics for the entire sample; (ii) the results of the sectorial and size analyses carried out using the stock market activity classification and size indices; and (iii) the results related to the relationship of the IED with other variables used as risk proxies, which include the earnings-to-price ratio (EPR), the BtM, the sales-growth-rate (SGR) and the capitalisation (CAP). Finally, Section 5 summarises the results and states the main conclusions.

2

Implied equity duration

Macaulay (1938) first introduced the duration concept as the weighted average of the times until fixed bond cash flows are received. Hicks (1939) further showed that the duration is essentially a measure of the elasticity of bonds to interest rates. From the bond price formula, it is straightforward to note that bond prices are inversely related to their yield to maturity as a unique risk factor.¹

However, in the equity valuation, there are many factors, including interest rate, that affect cash flows beyond the discount rate used to compute their present values. Lintner (1971), Boquist et al. (1975) and Livingston (1978) initially proposed the concept of stock duration, and then in the works of Leibowitz (1986) and Leibowitz et al. (1989), it was first computed for individual firms. More recent studies in this line are Cohen (2002), Hamelink et al. (2002)Lewin et al. (2007), Shaffer (2007) and Leibowitz et al. (2010).

In Boquist et al. (1975), the stock duration measure is built on the dividend discount model. However, Leibowitz (1986) used market quotes to develop an alternative measure. But, as Leibowitz and Kogelman (1993) noted, the values for both measures are significantly different, even when the compensation between price risk and reinvestment risk is taken into account as proposed by Johnson (1989). These differences determine the so-called duration paradox and give rise to works, such as Leibowitz and Kogelman (1993) and Hurley and Johnson (1995), that attempt, though unsuccessfully, to conciliate the two measures.

In this paper, we use an alternative stock duration measure proposed by Dechow et al. (2004) that is based on the Macaulay's duration for a bond (one time period before the first future cash flow):

where CF_t are the bond cash flows; r is the bond yield to maturity; and P is the actual price of the bond.

As previously mentioned, the bond duration is a weighted average of the maturities of T-cash flows, where the weights are the relative contribution of each cash flow to the actual bond price. The main role of the bond duration in the fixed income analysis is as a measure of the bond's price sensitivity to changes of bond yield to maturity.

Differentiating the bond price expression with respect to its yield to maturity, we obtain the relationship between changes in the price of a bond and changes in its yield to maturity as a function of the duration:

We can rewrite this relationship and express it in discrete form to obtain the following relation between the relative bond price changes and the discrete changes in its yield to maturity as a function of [D/(1 + r)], the so-called modified duration,

Extending the duration concept to equities introduces one drawback. That is, while the amount and timing of bond cash flows are usually fixed in advance so the bondholder has little uncertainty, the cash flows of equities are not specified in advance and may be subject to great uncertainty.

If we decompose the duration formula shown in Eq. (1) into two parts, one with a finite horizon up to T and another with an infinite horizon from T, we obtain Eq. (4), which expresses the equity duration as a sum of the weighted values of the duration of the cash flows for the finite horizon and the duration of terminal cash flows.

where P is the market firm capitalisation; CF_t are the predicted firm pay outs to the stockholders; and r represents the expected return on firm equity.

If we also assume that the terminal cash flows are a perpetual with an actual value equal to the difference between the market capitalisation and the present value of the predicted cash flows for the finite period, then:

As the duration of the perpetual that begins in T periods is [T + (1 + r)/r], substituting (5) into (4), we obtain the following expression for the IED:

To compute Eq. (6), we need predictions of firm cash flows for the finite period (0, T]. In this sense, Dechow et al. (2004) used a cash flows prediction model based on previous results that relate accounting measures with future cash flows (Nissim and Penman, 2001). Thus, from the accounting identity of the flows distributed to shareholders from the firm earnings and their book value, we have the following:

where E_t is the firm earnings at the end of period t; and BV_t represents the firm book value at the end of period t.

Rewriting the right term of Eq. (7), we obtain:

Thus, a cash flow forecast for period t can be computed with (i) the return on equity (ROE) in period t, i.e., E_t/BV_t−1; and (ii) the growth rate of equity in period t, i.e., (BV_t − BV_t−1)/BV_t−1.

Dechow et al. (2004) modelled ROE as a first-order autoregressive process with an autocorrelation coefficient based on the reversion rate of a mean reversion process of ROE with a mean equal to the historical cost of equity. It is generally accepted that the ROE follows a mean reverting process (Stigler, 1963; Penman, 1991). Further, the economic intuition and the empirical evidence (Nissim and Penman, 2001) suggest that the mean that reverses the ROE approximates the cost of equity.

The results of Nissim and Penman (2001) also show that sales growth rate is the best proxy of the future growth rate of the equity. Accordingly, Dechow et al. (2004) modelled the growth rate of equity as a first-order autoregressive process with an autocorrelation coefficient equal to the reversion rate of the mean reversion process of the sales growth rate and a mean equal to the long-term macroeconomic growth rate.

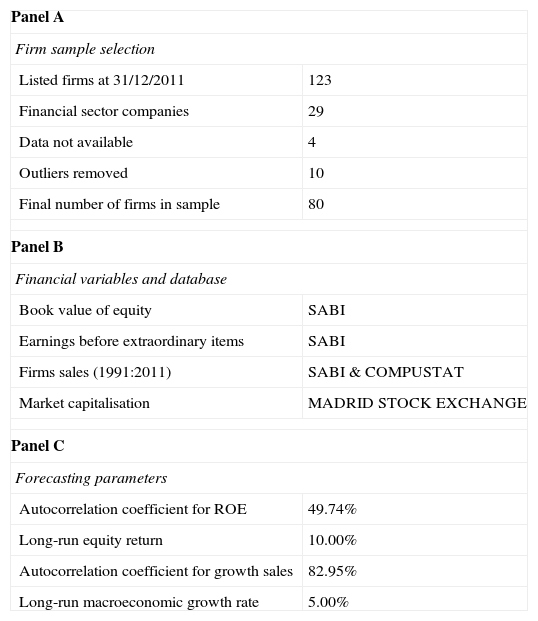
3

Data

Computing the IED from Eq. (6) requires year-end data on four financial variables and four parameters. The financial variables are the firm book value (both current and lagged one year), the firm sales (both current and lagged one year), the firm earnings (current) and the market firm capitalisation (current). The four parameters are the autocorrelation coefficient for the ROE, the autocorrelation coefficient for sales growth, the cost of equity and the long-term growth rate of the economy.

From the SABI database, we obtain the three accounting variables at the end of year 2011 and 2010. SABI includes the annual accounting statements for Spanish and Portuguese firms. We select the non-financial firms listed on the Spanish stock market, of which there are 90.² Then, we eliminate the influence of outside atypical values. In our case, this is achieved by removing the 5% extreme values of the sales growth rate, thus reducing the final sample to eighty firms.

From the Madrid Stock Exchange, we obtain the market variable, capitalisation, the sectorial firms classification and the Ibex indices classification. Non-financial firms are grouped into five sectors with their corresponding numbers, as summarised in Table 1, panel D: Oil & Energy; Commodities, Industry and Construction; Consumer Goods; Consumer Services; and Technology and Communications. Most non-financial firms are present on December 31, 2011, in three Ibex indices according to their size: Ibex 35, Ibex Medium Cap and Ibex Small Cap, as summarised in Table 1, panel D.

Table 1.

Summary of firm sample selection, financial variables and parameters used in the estimation of implied equity duration.

Panel A
Firm sample selection
Listed firms at 31/12/2011	123
Financial sector companies	29
Data not available	4
Outliers removed	10
Final number of firms in sample	80
Panel B
Financial variables and database
Book value of equity	SABI
Earnings before extraordinary items	SABI
Firms sales (1991:2011)	SABI & COMPUSTAT
Market capitalisation	MADRID STOCK EXCHANGE
Panel C
Forecasting parameters
Autocorrelation coefficient for ROE	49.74%
Long-run equity return	10.00%
Autocorrelation coefficient for growth sales	82.95%
Long-run macroeconomic growth rate	5.00%

Sectors	#	IBEX35	IBEX MC	IBEX SC
Panel D: summary of sample companies by index and sector
Oil & Energy	8	6	0	1
Commodities	23	8	5	6
Consumer Goods	27	3	5	10
Consumer Services	17	3	4	4
Technology	5	3	1	0
Totals	80	23	15	21

Data have been obtained from the database for Spanish and Portuguese companies SABI (Bureau Van Dijk Group), from Compustat Global (Standard & Poor's), which includes 145 companies for the Spanish Market that compose 100% of the listed companies, and from the Madrid Stock Exchange (www.bolsamadrid.es). For a long-run growth rate, we used the long-term average for the time series of the GDP, obtained from the Spanish National Statistics Institute (www.ine.es). In Panel D, activity sectors and indices appear according to the Madrid Stock Exchange classifications.

Regarding the parameters, the long-term average cost of equity and the long-term growth rate of the economy are based on long-term historical averages that approximate the parameters to 10% and 5%, respectively, as listed in Table 1, panel C. As in Dechow et al. (2004), we use a constant cross-section forecast of the cost of equity to ensure that each firm's IED differs only by the different distribution of the expected cash flows. Both the ROE autocorrelation coefficient and the sales growth rate autocorrelation coefficient are estimated as the mean of firm values computed using SABI and COMPUSTAT data for sample companies with at least 10 years of available data. Their values, 0.4974 and 0.8295, respectively, as listed in Table 1 – panel C, are applied to all firms as market variables.

4

Results

4.1

The IED for the sample firms

For the IED computation thought Eq. (6), we use a finite prediction horizon of 10 years, as in Dechow et al. (2004), after checking that the mean reversion, both for the SGR and the ROE, are completed before this time. Table 2 shows the IED for the sample firms at the end of year 2011. In this table, we also show the others variables that are usually used as risk proxies (EPR, BtM, CAP, SGR) on the same date.

Table 2.

Implied equity duration, earning-to-price ratio, book-to-market, market capitalisation and sales growth rate.

TICKER	IED	EPR	BtM	CAP	SGR
ABG	18.59	0.12	1.16	1.484	0.13
ABE	15.66	0.11	0.46	9.576	−0.04
ANA	15.17	0.04	1.33	4.241	0.06
ACX	16.56	0.05	0.76	2.471	0.04
ADZ	−2.26	−0.10	2.79	47	−0.07
ALM	9.26	0.10	0.97	882	−0.13
AMS	18.86	0.08	0.23	5.610	0.07
A3TV	17.53	0.10	0.30	982	0.00
CAF	18.21	0.10	0.51	1.320	0.09
AZK	−0.03	0.63	2.74	28	0.06
RIO	16.82	0.03	0.94	27	0.06
BDL	14.02	0.04	0.80	224	−0.04
BIO	15.29	−0.40	1.07	23	−0.14
CFG	15.77	−0.04	0.91	657	0.00
CIE	20.46	0.13	0.86	638	0.16
CLEO	3.37	−0.42	1.88	21	−0.21
CBAV	19.14	0.05	0.22	106	0.04
CDR	21.94	0.11	0.50	336	0.22
DERM	47.48	−2.27	0.69	12	−0.13
CUN	17.38	0.02	0.50	214	0.00
MDF	16.75	0.13	0.36	810	0.00
OLE	5.95	−0.04	1.85	440	−0.06
DIA	20.12	0.04	0.04	2.374	0.02
EBRO	17.43	0.07	0.72	2.208	0.07
ENO	15.73	0.14	0.72	868	0.05
ENG	19.30	0.11	0.62	3.412	0.14
ENC	8.30	0.09	1.60	450	−0.02
ELE	11.57	0.18	1.49	16.781	0.05
EGPW	20.45	0.00	0.07	7.910	−0.01
ECR	20.44	−0.01	2.80	68	0.13
FAE	14.27	0.06	0.65	257	−0.07
FCC	11.63	0.01	1.21	2.551	−0.03
FDR	14.81	0.08	1.52	215	0.07
FUN	7.57	0.17	3.30	99	0.07
GSJ	−2.06	−0.28	2.59	135	−0.12
GAM	17.35	0.07	2.13	794	0.11
GAS	19.06	0.12	0.00	13.155	0.07
GRF	16.67	0.00	0.40	2.770	−0.13
TVX	8.76	−0.27	4.54	36	0.06
IBE	12.05	0.01	0.91	28.465	−0.10
IBG	10.64	0.16	1.51	147	0.03
ITX	20.38	0.03	0.06	39.444	0.07
IDR	16.64	0.11	0.68	1.615	0.06
IAG	14.61	0.18	0.34	3.228	−0.13
JAZ	19.78	0.01	0.10	916	−0.15
SED	26.33	−0.28	1.04	185	0.14
ROVI	18.45	0.07	0.52	255	0.08
LGT	15.50	0.13	1.23	28	0.08
TL5	22.26	0.06	0.79	1.794	0.18
MEL	14.57	0.06	1.59	720	0.07
MCM	16.65	0.10	0.77	233	0.07
NAT	1.72	0.38	3.09	43	0.05
NTC	−5.54	0.31	1.69	51	−0.24
NHH	20.67	0.02	0.00	538	0.05
OHL	11.10	0.18	1.07	1.933	0.00
PVA	14.63	0.10	1.28	501	0.06
PRM	10.85	0.13	1.04	69	−0.04
PRS	−6.43	−0.99	5.57	399	−0.03
PSG	19.03	0.08	0.32	2.085	0.10
REE	20.22	0.10	0.50	4.473	0.17
RDM	14.27	−0.02	1.11	36	0.00
REP	17.93	0.09	0.94	28.977	0.10
SYV	0.52	0.17	1.56	1.678	−0.16
SPS	30.65	−1.00	1.91	40	0.06
SNC	19.80	0.09	1.51	75	0.14
SLR	1.22	−0.43	1.94	96	−0.25
TRE	30.30	0.09	0.89	268	0.30
TEC	19.76	0.04	1.67	105	0.13
TEF	16.99	0.10	0.45	61.089	0.03
TUB	36.77	0.01	0.97	248	0.34
TRG	30.30	0.09	0.89	268	0.30
UPL	12.98	−0.06	1.11	147	−0.04
URA	13.64	−0.09	1.36	309	0.00
VER	64.79	−0.76	2.49	46	0.29
VID	17.12	0.10	0.70	456	0.07
VIS	18.35	0.08	0.34	1.336	0.05
VOC	7.79	−0.25	2.20	194	−0.04
VLG	14.05	0.09	2.09	116	0.08
ZOT	19.70	0.05	0.06	3.889	−0.05
ZEL	20.92	0.00	0.10	382	0.11

For each firm, this table shows: IED at year-end 2011; 2011 year-end earning-to-price ratio as annual earnings over market capitalisation; BtM: book-to-market ratio calculated as year-end 2011 book value of equity over market capitalisation; market capitalisation at year-end 2011 in millions of euros; and sales growth rate as sales annual difference over the previous period sales [(Sales_t − Sales_t−1)/Sales_t−1].

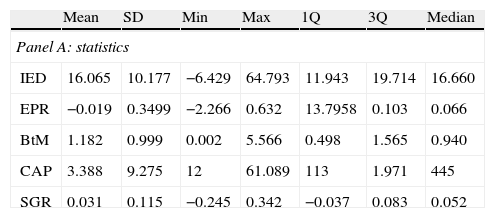
In Table 3, panel A, we summarise the main statistics for all these variables. The average for the IED is 16.07 years with a standard deviation of 10.18 years. The value that defines the lowest quartile is 11.94, while the value that defines the superior quartile is 19.71. Thus, for most firms, the IED is below 21 years, the IED corresponding to terminal cash flows. Therefore, for these firms, only a small portion of the time distribution of their actual value is explained by discounted cash flows for the 10-year finite period. The minimum value of the IED is −6.43 years,³ and the maximum value is 64.79 years. In Table 3, panel B, we show correlations between all the variables included in the analysis. The correlations between the IED and the other variables are generally related to intensity and the expected signs.

Table 3.

Descriptive statistics for implied equity duration and other related measures.

	Mean	SD	Min	Max	1Q	3Q	Median
Panel A: statistics
IED	16.065	10.177	−6.429	64.793	11.943	19.714	16.660
EPR	−0.019	0.3499	−2.266	0.632	13.7958	0.103	0.066
BtM	1.182	0.999	0.002	5.566	0.498	1.565	0.940
CAP	3.388	9.275	12	61.089	113	1.971	445
SGR	0.031	0.115	−0.245	0.342	−0.037	0.083	0.052

	IED	EPR	BtM	CAP	SGR
Panel B: correlations (Pearson/Spearman)
IED	–	−0.122	−0.564	0.192	0.621
EPR	−0.365	–	−0.144	0.283	0.212
BtM	−0.393	−0.231	–	−0.576	−0.038
CAP	0.027	−0.218	0.098	–	0.046
SGR	0.587	−0.051	0.180	−0.004	–

Pearson linear correlation coefficients appear in Panel B below the diagonal and Spearman linear correlation coefficients are above the diagonal. IED: implied equity duration at year-end 2011; EPR: 2011 year-end earning-to-price ratio as annual earnings over market capitalisation; BtM: book-to-market ratio calculated as year-end 2011 book value of equity over market capitalisation; CAP: market capitalisation at year-end 2011 in millions of euros; and SGR: sales growth rate as sales annual difference over the previous period sales [(Sales_t − Sales_t−1)/Sales_t−1].

4.2

Analyses by sectors and Ibex indices

To deepen the characterisation of the sample firms through their IEDs, we conduct a sectorial analysis that groups firms by activity and an analysis by Ibex indices that classifies firms by size. These analyses allow us to perceive evidence of potential firm growth options and size effects. For this, all firms are grouped into five sectors (similar to the Madrid Stock Exchange), and alternatively, into three groups depending on the Ibex index to which each firm belongs, if any.

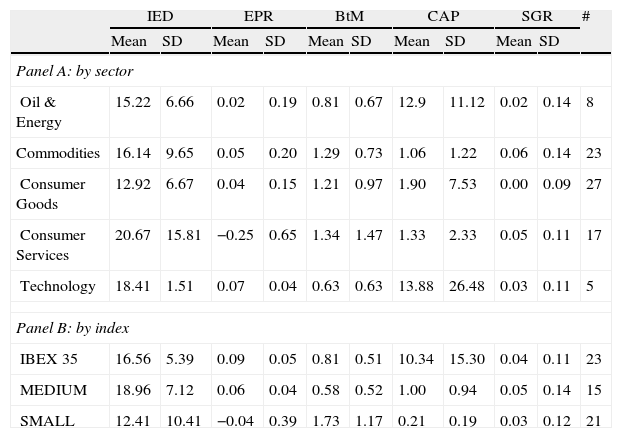
Table 4 shows the main statistics by firm groups of the variables involved in the analysis. By sectors, in panel A, we note that both the IED averages and their standard deviations vary considerably among sectors, in line with the other variables. The Consumer Goods sector has the minimum sectorial IED average at 12.92 years, while the Consumer Services sector has the maximum sectorial IED average at 20.67 years. However, we do not sense from these statistics a clear relation between the IED and any other variable.

Table 4.

Descriptive statistics for measures by sector and index.

	IED		EPR		BtM		CAP		SGR		#
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Panel A: by sector
Oil & Energy	15.22	6.66	0.02	0.19	0.81	0.67	12.9	11.12	0.02	0.14	8
Commodities	16.14	9.65	0.05	0.20	1.29	0.73	1.06	1.22	0.06	0.14	23
Consumer Goods	12.92	6.67	0.04	0.15	1.21	0.97	1.90	7.53	0.00	0.09	27
Consumer Services	20.67	15.81	−0.25	0.65	1.34	1.47	1.33	2.33	0.05	0.11	17
Technology	18.41	1.51	0.07	0.04	0.63	0.63	13.88	26.48	0.03	0.11	5
Panel B: by index
IBEX 35	16.56	5.39	0.09	0.05	0.81	0.51	10.34	15.30	0.04	0.11	23
MEDIUM	18.96	7.12	0.06	0.04	0.58	0.52	1.00	0.94	0.05	0.14	15
SMALL	12.41	10.41	−0.04	0.39	1.73	1.17	0.21	0.19	0.03	0.12	21

Means and standard deviations for each measure by sectors according Madrid Stock Exchange classification in panel A and by Ibex index in panel B (Ibex 35, Ibex Medium Cap and Ibex Small Cap). IED: implied equity duration at year-end 2011; EPR: 2011 year-end earning-to-price ratio as annual earnings over market capitalisation; BtM: book-to-market ratio calculated as year-end 2011 book value of equity over market capitalisation; CAP: market capitalisation at year-end 2011 in millions of euros; and SGR: sales growth rate as sales annual difference over the previous period sales [(Sales_t − Sales_t−1)/Sales_t−1].

The index grouping, in panel B, shows that the average IED variability and the standard deviations are less than that of other variables. Moreover, no relation between the IED and size is found. However, a relation between the IED and the BtM and a relation between the IED and the SGR appear when we group firms by size.

In Table 5, we report the results of different means tests between sectors in panel A and between indices in panel B. We report results for both parametric and non-parametric tests, given the small number of observations included in any of the groups.⁴

Table 5.

Tests of IED means difference and equal variances among groups.

	Oil & Energy	Commodities	Consumer Goods	Consumer Services	Technology
Panel A: between sectors
Oil & Energy 15.224 (6.661)	–	0.400(0.532)	0.006(0.939)	1.106(0.304)	5.557(0.038)
Commodities 16.136 9.646	0.912(0.807)[0.892]	–	1.207(0.277)	1.044(0.313)	3.297(0.081)
Consumer Goods 12.922 (6.668)	2.304(0.397)[0.195]	3.215(0.172)[0.182]	–	3.553(0.066)	3.994(0.055)
Consumer Services 20.672 (15.810)	5.447(0.363)[0.485]	4.536(0.268)[0.389]	7.751(0.070)[0.037]	–	2.422(0.135)
Technology 18.405 (1.507)	3.181(0.230)[0.770]	2.269(0.295)[0.294]	5.486(0.070)[0.040]	2.266(0.756)[0.969]	–

	IBEX35	Medium	Small
Panel B: between size index groups
IBEX35 16.789 (4.811)	–	0.526(0.473)	9.899(0.003)
Medium 18.951 (7.128)	2.402(0.245)0.269	–	3.677(0.064)
Small 13.160 (15.840)	4.144(0.113)[0.226]	6.546(0.032)[0.096]	–

The first column of the table shows the means and standard deviations for the sectors and indices firm groups. In the body of the table, we have collected below the diagonal the mean difference by sectors and indices, respectively, followed by the parametric significance level for the t-statistic in parentheses and asymptotic significance for non-parametric tests in brackets (Mann–Whitney U if one assumes normality and Wilcoxon W otherwise). Above the diagonal we show the results of the Levene test for equality of variances followed by significance in parentheses that determines the test of means difference to use.

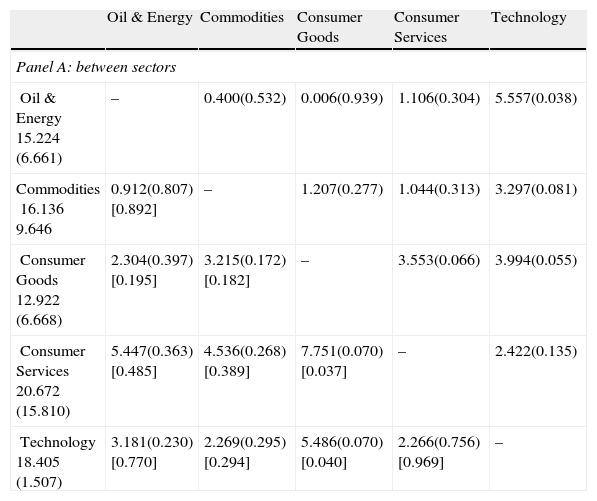
When we analyse the mean differences between sectors, we find two significant differences. In this sense, the parametric and the non-parametric tests have shown very similar results. We note that the mean difference of approximately 7.75 years between the Consumer Goods sector, which has the lowest IED, and the Consumer Services sector, which has the highest sectorial IED, is significant at 10% in the parametric test and at 5% in the non-parametric test. We find an identical result for the mean difference of approximately 6.48 years between the Consumer Goods sector and the Technology and Communications sector, the second largest sectorial IED. These results confirm the relation between the IED and the firm growth options, and they strengthen the relationship between the IED and the BtM.

With respect to the mean differences between the various indices listed in panel B of Table 5, in only one case do we observe significant results, that is, the means difference between the IbexMediumCap index group and IbexSmallCap index group, with a significance level of 5% in the parametric test and a 10% significance level in the non-parametric test. Namely, no significant results for the means difference between index Ibex35 and index IbexSmallCap are found. These results support the argument that the IED does not reflect a size effect, i.e., there is not a relationship between the firm's IED and its size (CAP).

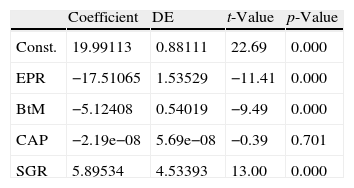
4.3

Cross-sectional regression analysis

Given that the relationship between the IED and the EPR and between the IED and the BtM has been analytically proven by Dechow et al. (2004), as reflected in Appendix A, and given the previous results that (i) confirm empirically these relations in the sample data, (ii) show a relation between the IED and SGR, and (iii) show the usefulness of the size to clarify some of these relationships, we perform a cross-sectional regression analysis between the IED and the EPR, the BtM and the SGR, using CAP as a control variable.⁵

In Table 6, we report the results. As expected, the significance of the EPR and BtM in explaining the IED is clear. The SGR also shows significant explanatory power of the IED as expected due to its important role in forecast firms cash flows. However, the market capitalisation variable has not shown significant results. This is likely because the BtM withdraws its effect, as noted by Chen (2011).

Table 6.

IED cross-sectional regression against the other corporate risk proxies.

	Coefficient	DE	t-Value	p-Value
Const.	19.99113	0.88111	22.69	0.000
EPR	−17.51065	1.53529	−11.41	0.000
BtM	−5.12408	0.54019	−9.49	0.000
CAP	−2.19e−08	5.69e−08	−0.39	0.701
SGR	5.89534	4.53393	13.00	0.000

The coefficients in the table are estimated by linear regression through the equation:

Following is the standard deviation of the t-statistic coefficient and its significance. The F statistic obtained for four degrees of freedom was 79.17, the R-squared of 80.85% and adjusted R-squared of 79.83%. IED: implied equity duration at year-end 2011; EPR: 2011 year-end earning-to-price ratio as annual earnings over market capitalisation; BtM: book-to-market ratio calculated as year-end 2011 book value of equity over market capitalisation; CAP: market capitalisation at year-end 2011 in millions of euros; and SGR: sales growth rate as sales annual difference over the previous period sales [(Sales_t − Sales_t−1)/Sales_t−1].

5

Conclusions

In this paper, we compute for the first time, to the best of our knowledge, the implied duration of equity (IED) for the non-financial listed firms on the Spanish Stock Market, as developed in Dechow et al. (2004). Concretely, the IED is computed for December 31, 2011, for eighty firms. The results are consistent with those presented in Dechow et al. (2004), although the Spanish IED is slightly higher due to the different expected return on equity used in each context.

A further sector and size index analysis enables us to test mean differences between firm groups. The tests implemented across sectors confirm the existence of significant differences between the sectors with the most extreme IED suggesting a relation between IED and firm growth options. The tests for the mean differences between Ibex indices showed that they are, in some cases, significant but without a correlation between firm size and firm IED.

The correlations between the IED and the usual ratios that describe company risk, EPR and BtM are of the expected signs and intensity. A further regression analysis, adding market capitalisation and sales growth rate, confirms the ability of these ratios and sales growth rate to explain the IED. In contrast, capitalisation is not significant, thus removing any possibility of a size effect.

A remarkable result is that the relationship present in the valuation models between the IED and the traditional indicator for value (growth), the BtM, can also be found in the analysed data such that the smaller the BtM, the longer the mean maturity of firm cash flows, and vice versa. This result is consistent with previous results, thus suggesting that the BtM factor from Fama and French could be a simple approximation to a more fundamental cash flow risk factor captured by stock duration in which, according to the results shown herein, it also collects information on the EPR and Sales Growth Rate.

Acknowledgements

The authors thank comments from the editor, Francisco González, and an anonymous referee of the Spanish Review of Financial Economics, from Juan Nave, and from participants in the XVI Applied Economics Meeting (Granada, 2013), and in the internal seminars at Universidad de Castilla – La Mancha, Universidad de Murcia, Universidad de Valencia, Universidad de Huelva and Universidad CEU Cardenal Herrera. They also thank financial support from Gobierno de España (MICINN ECO2009-13616 and MEYC ECO2012-36685) and from Banco Santander (Copernicus UCH-CEU 36/12).