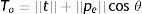To understand why our model may help, a good starting point can be wondering why are the results of a psychological treatment not the same for all patients? This is of course a very complex question because treatment outcome depends on many different variables (see for a review Murphy, Cooper, Hollon, & Fairburn, 2009). Research attempting to identify a universal short list of outcome predictors for psychotherapy has not been very fruitful, and this is an area where there is room for the use of new paradigms. One such paradigm is the dynamical systems paradigm (Hayes, Hope, & Hayes, 2007; Pezard & Nandrino, 2001). For example, in a comprehensive introduction to this approach applied to psychotherapy, Salvatore and Tschacher (2012, p.12) have described it as “a paradigmatic way of looking at phenomena that changes the very agenda of the scientific enterprise”. Essentially, the nonlinear paradigm offers a more holistic approach to science (less reductionistic), while retaining key aspects of the scientific method such as empirical testing of theoretical propositions, formal mathematical modeling, falsifiability and parsimony. This approach involves a broad array of models and methods commonly referred to as: nonlinear dynamical systems theory (NDS; Guastello, Koopmans, & Pincus, 2009).

Models and methods from NDS each have in common a set of basic assumptions. First, most natural phenomena involve nonlinear (disproportionate) causes. One property of linear systems is scaling, which means that “if a given input produces a given output, then doubling the size of the input will double the size of the output, and so on for any arbitrary scaling of the input” (Shelhamer, 2007, p.10). This property does not hold for nonlinear systems. Within psychotherapy, nonlinearity implies that the intensity of intervention (i.e. the input) is often not proportional to therapeutic outcome (i.e., the output)–e.g., many clients show a large improvement following a single key insight or therapeutic intervention. Second, therapeutic changes unfold over time, and timing of interventions serves a critical function. Strictly speaking, this is not an NDS assumption. However, we will show how precise timing can be set depending on our knowledge about the trajectory the emotional system is following in phase space. Third, NDS holds that most natural phenomena involve systemic (multivariate and complex) cause. In psychotherapy, for example, emotional, cognitive, behavioral and emergent relational dynamics are each coupled with one another and interact in complex ways in response to any given intervention.

Within this paradigm, one potential process holds great promise for psychotherapy: emotional inertia. Emotional inertia appears to be a general aspect of personality (Kuppens, Oravecz, & Tuerlinckx, 2010) that is related to psychopathology (Kuppens, Allen, & Sheeber, 2010a), and yet has not been applied to the context of psychotherapy research. In Physics, inertia is formally defined as “the property of matter by which it retains […] its velocity along a straight line so long as it is not acted upon by an external force”. Similarly, emotional inertia would be the property of human emotion by which it retains its course so long as it is not acted upon by an external force. “External” here does not only mean something coming from the environment, but any influence from other closely coupled systems (e.g. physiological or cognitive). Kuppens, Oravecz et al. (2010, p. 985) formally define emotional inertia as: “…resistance to emotional change, formalized as the degree to which a person's current emotional state can be predicted by his or her emotional state at a previous moment (with high predictability reflecting high inertia)”, which leads to the basic operational definition as degrees of autocorrelation in emotional dynamics over time. Using this definition, we will seek to formally describe the dependency of emotional change within psychotherapy on both the force of an intervention and the emotional trajectories of the system at a particular point in time.

What is the need for NDS? The study of treatment outcome in mental health has traditionally followed a linear paradigm where patients are considered as systems that react to environmental influences in a linear and proportional ways. In the case of psychotherapy, generally speaking, more treatment (either more sessions or more intense therapy) is typically expected to produce greater improvement. However, patients’ psychosocial processes are more realistically viewed as dynamical, ever-changing and highly interactive systems that typically do not change proportionally in response to therapeutic interventions (Bell, Koithan, & Pincus, 2012; Hayes, Laurenceau, Feldman, Strauss, & Cadaciotto, 2007). NDS has shown that the behavioral dynamics of complex systems may change suddenly and unexpectedly in response to slight changes in the system's control parameters under certain conditions, while remaining robust against large changes in other circumstances. These sudden changes resemble many clinical phenomena in mental health, such as sudden relapse in recovered substance users (Witkiewitz & Villarroel, 2009), mood instability in bipolar disorder (Bonsall, Wallace-Hadrill, Geddes, Goodwin, & Holmes, 2012), shifts in perceptual dynamics across phases of psychotic breaks (Tschacher & Junghan, 2009), the timing and frequency of compulsive rituals in obsessive-compulsive disorder (Bond & Guastello, 2013; Yaniv, 2008) or the large improvements observed frequently between single sessions in empirically-supported brief therapies (i.e., “sudden gains”, e.g., Tang, DeRubeis, Hollon, Amsterdam, & Shelton, 2007).

Thanks to these, and many other, contributions, researchers have increasingly recognized the inherent nonlinearity of most psychotherapeutic changes (Hayes, Hope et al., 2007; Pincus, 2009; Salvatore & Tschacher, 2012), while the field as a whole has shifted over the last two decades toward an increasing appreciation of processes of change (Crits-Christoph, Connolly Gibbons, & Mukherjee, 2013; Gonçalves, Ribeiro, Mendes, Matos, & Santos, 2011; Nitti, Ciavolino, Salvatore, & Gennaro, 2010; Wampold, 2001). For example, Baldwin, Berkeljon, Atkins, Olsen, and Nielsen (2009) assessed the process of change in a naturalistic study in more than 4,000 individuals who received counseling. In this study, two models of change were compared: the dose-effect model (essentially a linear model) and the good-enough-level model of change (a nonlinear model). This study showed that patients do not change at the same rate, i.e., change does not follow the negatively accelerated curve predicted by the dose-effect model. Patients needing fewer therapy sessions improved more quickly than patients requiring more sessions. Bornas, Gelabert, Llabrés, Balle, and Tortella-Feliu (2011) reported similar results in a study on the treatment of flight phobia.

The study of emotional change within psychotherapy is an obvious place to integrate the efforts of mathematicians, clinicians, and researchers toward a greater understanding of psychotherapy process. The root of the word “emotional” is “mot,” which means “to move.” When emotions are viewed as dynamical systems, therapeutic interventions should be viewed as impacting changing patients. Any well-trained clinician will report that sensitive timing is a key to any therapeutic interventions, accounting for where the client is currently emotionally positioned, as well as the direction and velocity of these emotions. The available evidence suggests that the movement of emotion is an important aspect of personality (Kuppens, Oravecz et al., 2010) and a key process underlying psychopathology (Kuppens, Allen, & Sheeber, 2010). The time has come for psychotherapy process researchers and clinicians alike to begin to account for such emotional movement in a more explicit manner as they consider therapeutic effects.

Nonlinear dynamical systems (NDS) often display very complex, random-looking behaviors. However, NDS shows that apparently erratic behavior of these systems may follow some simple rules, that is, regularities and patterns may be hidden, particularly when using traditional linear statistics (i.e., couched in the general linear model). Discovering such patterns requires the reconstruction of the system's so-called phase or state space. This is an abstract mathematical space used to represent the behavior of a system (i.e., its trajectory), and includes all the instantaneous states that the system may have.

Coordinate axes in phase space represent the variables needed to specify the phase (or state) of the system. For example, on the basis of humidity and temperature meteorologists determine the subjective temperature we are feeling at any particular moment. Humidity has a range of values from 0 to 100%, and temperature in summer (in some locations in the north hemisphere, for example) can vary from 10 to 40°C. If we plot humidity on the x axis of a graph (from low to high) and temperature on the y axis of this graph (also from low to high), any possible state of subjective temperature will be located within the area (i.e., two-dimensional space) of this graph. Attractors are sets or “clouds” of points representing the various possible steady-state conditions to which a dynamical system converges. For instance, after plotting the subjective temperature points from a country in the graph during July and August we could probably see the points grouped as a cloud close to the upper right corner of the graph.

Applied to the field of emotional health, the emotional state of a patient at any moment can be located within the system's phase space where attractors are the emotional states to which the patient converges. Worry, for example, would be an emotional attractor within the phase space of a patient with generalized anxiety disorder as the system, departing from many other emotional states, often converges to worry. Thayer and Lane (2000), in their neurovisceral model of emotion regulation, already proposed that “emotions may represent attractors (preferred configurations) in the state-space (behavioral repertoire) of the organism” (p.203), and Kuppens, Oravecz et al. (2010) have demonstrated that individual differences in affective dynamics are driven by three fundamental processes: affective home base, affective variability, and attractor strength (p.1045).

What we want to stress here is the idea of emotion as a dynamical phenomenon, a trajectory within the phase space, which is followed so long as it is not acted upon by an external force. The persistence of emotional states over time is probably best represented as regions or “clouds” in phase space, and within each of these regions it is empirically feasible to identify and follow the system's trajectory. For example, when someone says “I feel sad” during several consecutive days, his or her sadness can vary in intensity within these days. These changes in sadness severity would be represented by different locations within the sadness attractor/region of the patient's phase space. The next question is: How can we capture emotional trajectories in phase space?

If we know or assume that a time series of emotional scores (e.g. discomfort) depend on specific, measurable variables, then we can proceed as in the subjective temperature example above. For example, Katerndahl and Wang (2007) used a two dimensional phase space in a study on the dynamic covariation of symptoms of anxiety and depression among different diagnostic groups. These authors used the state space grid method (Hollenstein, 2012; Lewis, Lamey, & Douglas, 1999). The x axis was a 1 to 10 anxiety scale and the y axis was a 1 to 10 depression scale, so that the point at (5.5) should be read as the state of the system when the anxiety level was 5 and the depression level was 5. A similar method was introduced by Gonçalves et al. (2011). For an application of this method in a psychotherapy case study see Ribeiro, Bento, Salgado, Stiles, & Gonçalves, 2011.

However, we have often only one time series of self-report data. When this is the case, a technique called “time-delay reconstruction” may be used. As pointed out by Shelhamer (2007, p.47), “time-delay reconstruction is almost absurdly simple yet extremely powerful”. Following this method, we can reconstruct the emotional phase space in two or three dimensions so that emotional trajectories are more clearly appreciated. The “trick” consists of making up delayed copies of the time series collected data, and using these copies as “other” variables. The use of time-delay reconstruction methods requires that two parameters be specified: The time delay and the embedding dimension. The choice of an appropriate delay ensures that successive values in a time series are not too similar. On the other hand, as we wish a reliable representation of the system we have to allow it to fully develop in phase space, and to do so an appropriate number of dimensions should be used. There are specific mathematical procedures to make these calculations, but this is far beyond the scope of this paper (for a comprehensive account see Heath (2000) or Shelhamer, 2007).

Psychotherapies can be understood as impacting ever-changing emotional systems of clients. When we know where the system is going to, or from where it has come, more accurate predictions can be made. The first goal of therapy will be to change the current direction of the system. In other words, treatment should account for emotional inertia with interventions that move the system to healthier regions in its phase space. This first goal is consistent with an initial focus upon remoralization or instilling hope for eventual change, a common process across approaches that helps establish a positive therapeutic alliance (Baldwin, Wampold, & Imel, 2007; Frank & Frank, 1993; Pincus, 2009; Wampold, 2001). The stronger the pull is toward a negative attractor region, or the deeper the hole is to get out of, the more power that is needed to return some flexibility to the system. The effort required to change the direction of the system in a certain moment is proportional to the angle formed by the vector of the client's emotional trajectory in that moment and the vector of treatment (see Figure 1). Therefore, we can predict the effect of the treatment as far as we know the direction of its force and the trajectory of the patient's emotional system.

Figure 1.

A three-dimensional representation phase space of a dynamical system with known equations. Axes correspond to the three variables (x, y, and z) upon which the movement of the system depends.

Note. Plain-line vectors show the trajectory the system is following at moments A, B and C. Dotted-line vectors show the direction the treatment wants the system to reach. The angle between the vectors in A is smaller than in B. Thus, more power is needed to change the trajectory. In C, the trajectory of the system is following an optimal direction and therefore the angle is very small. In this case, we do not need a high energy therapy to alter the course of the trajectory.

(0.1MB).

We have discussed so far that the prediction of improvement (that is a healthier emotional state) requires some knowledge about emotional trajectories. Another required element in the equation of treatment outcome is “treatment energy”, which refers to how powerful our treatment is. With this information, all elements in the equation are now present, and we can represent them as in Figure 2. Consider the model applied to the emotional processes within a single therapy session. By convention, descending vectors mean the problem is getting worse (e.g., the individual feels more afraid every moment); horizontal vectors mean the problem is stabilized at some severity level, and ascending vectors would mean recovery from negative emotion. With this kind of graphical representation we can see the dependency of treatment (vector t) on the system's trajectory as psychotherapy is aimed at moving the system up in this graph.

Figure 2.

Treatment outcome (To) as a result of the interaction between the vector of the system's current trajectory (pe), the vector of the treatment (t), and the angle θ from vector t to vector pe.

(0.05MB).

If pe is the tangent vector of the trajectory (emotional momentum or inertia) and t is the vector of the treatment, and ||t|| the energy of the treatment, then we can estimate the treatment outcome To as

To better understand this formula let us think of two patients, A and B while having in mind Figure 2. The state (e.g. depressive state) of the patients when treatment is applied is the origin point in Figure 2, i.e. where the x axis crosses the y axis, which can be thought of as depressive state. Patient A is feeling worse (in fact Figure 2 would represent this specific instance), so that a force is pulling her down, and this force is represented by vector pe. Treatment, on the other hand, is represented by vector t as it is a force that pulls patient A up to a less depressive state. The direction patient A will take as a result of treatment depends on how strong is the “worsening force”, and this is formally represented by the sum of both vectors t+pe. Treatment outcome (To) is the distance from the initial state (remember this is the origin in Figure 2) to the state achieved by the sum of vectors, and it is calculated by subtracting the distance due to the worsening force pe from the distance ||t|| achieved by the force of treatment. Trigonometry shows us that to calculate the first distance we have to multiply ||pe|| (the length of vector pe) by the cos θ (and as θ>90 degrees, the cos θ will be a negative value). Therefore To=||t||+||pe||cosθ. Patient B, unlike patient A, is not feeling worse. Her current state is the origin in Figure 2. There is no force pulling her down, so that the vector of the “worsening force” would be horizontal (not shown in Figure 2). Then the angle between treatment force t (which is the same than for patient A and pulls her up) and this horizontal vector would equal 90 degrees. In this case, the cosθ=0, so that the distance ||pe|| multiplied by zero is zero and To will equal distance ||t||, the expected result if treatment force has no opposing force or resistance.

To sum up, the greater the angle, the higher the energy of the treatment needed to get the desired outcome. Experienced therapists should recognize these relations between client emotional momentum and the moment-by-moment choices regarding if, when and how forcefully we may choose to intervene. Such choices play out early in treatment, when one is more likely to allow clients to experience their naturally unfolding range of emotional movement using high levels of empathic process, even if their range is quite constrained. While at later points in treatment one may find more opportunities to engage a client's emotional process and exert some energy to shift its momentum, for example by pushing clients to identify a wider range of other emotions for which they are actively avoiding or otherwise relatively unaware, consistent with process-experiential approaches to treatment (Greenberg, 2002). Similar dynamics involving emotional trajectories may be understood to be occurring within the paradoxical procedures of 3rd wave behavioral therapies, which aim to facilitate “radical acceptance” of emotional states and unworkable problems. The goal of these procedures is to help a client enter a state of “creative hopelessness”, where giving up on emotional control and other unworkable struggles paradoxically opens clients’ up to alternative areas upon which to focus attention and energy (Hayes, Follette, & Linehan, 2004). The role of emotional momentum is not included in descriptions of these types of therapeutic eliciting maneuvers, yet it may help to explain each these processes as well as others, which come from very different therapeutic traditions. Essentially, when a therapist helps to create an environment where one allows the natural momentum of negative emotions to reach its limit in downward movement (see Figure 2) then one will find that there is increased leverage for emotional change.

Once the relations between emotional vectors and treatment strength are formalized mathematically, some practical aspects of therapeutic process become clearer. For instance, therapists working with client emotional trajectories essentially have two broad ranges of strategies: a) Increase the force of treatment (e.g., using interpersonal leverage or increasing directiveness with a specific technique); or b) reduce the angle of intervention, which is essentially a question of fit. When the intervention (t) is highly attuned to the emotional vector (pe) then the angle is reduced, and so less force is needed hypothetically. This first set of options is related to developing more effective techniques, often associated with the behavioral traditions within therapy. While the second set of strategies, fit, is a function of the non-specific aspects of therapy (e.g., empathy, congruence, non-judgment, and alliance) most often associated with the humanist-existential traditions. Using the concept of emotional momentum in psychotherapy may allow for a novel explanation of why both factors are necessary and are interdependent on one another for helping to shift the trajectories of client emotion–hypothetically, one can either push harder, or get better leverage, but ideally most therapists will attempt to do both at the same time.

At a longer time-scale (but still related to the first goal of psychotherapy) our criteria for a successful outcome may vary. For example, it may be considered that successful treatments are those that make more patients improve, or those that require shorter periods of therapy to obtain a substantial change. Accordingly, there are “higher” and “lower” energy therapies. “Higher” energy therapies will be more successful when the trajectory that the system is following does not require a great shift, but even if it does, therapy will probably succeed. In contrast, “lower” energy therapies will be successful when only a moderate shift of the trajectory is needed, but will not succeed if the system should be shifted far away from the current trajectory. Treatment energy may be operationally defined in myriad ways depending upon the research context. Psycho-education and self-help would be lower energy than individual therapy interventions. Within cognitive-behavior therapy, activity scheduling would generally be a lower energy intervention than desensitization or cognitive restructuring (c.f., Greenberg, Warwar, & Malcolm, 2008 for some empirical comparisons). The key distinction is the forcefulness of the technique in shifting the emotional momentum of the client.

A crucial point for the outcome of treatment is the moment at which therapy impacts the system. When the impact takes place at the right moment (i.e., the angle of the emotion vector and the treatment vector is small), the final result may be independent of the energy of the treatment. The occasional success of long-lasting yet low energy psychotherapies may be explained because it is likely that during the long course of therapy the emotional system, at some point, takes a path that the therapy is able to impact. Further, in accordance with the theoretical relation between treatment energy, emotional inertia (trajectory) and treatment outcome, more energy should be required to change the trajectory during the first therapy session(s). As the trajectory gets closer to the desired one, lesser energy would be enough to promote further changes, as the angle between the tangent vector of the client's emotional system trajectory and the vector of the therapeutic decreases. Ideally at these later stages, the therapy is simply helping the client to keep the ball rolling toward improvement.

Finally, the model enables one to better understand the complex interactions between common and specific factors in treatment. Recall that the intervention (t) will hypothetically be more effective when it is highly attuned to the emotional vector of the patient (pe), such that the angle between the two is reduced. This simple logic allows for a formal understanding of the interactions between common factors and specific techniques (Norcross & Wampold, 2011). Each of the best known common factors (e.g., empathy, level of client emotional “experiencing,” mindfulness) should serve to increase attunement between an intervention (t) and the patient's emotional vector (pe) by reducing the angle between the two.

Preventing relapse is a major goal of any psychotherapeutic intervention. NDS theory can help us to understand why relapse occurs, and to better prevent relapse. Once psychotherapy has successfully moved the system from the unhealthy attractor to a healthy region of its phase space, the trajectory has been changed but the phase space may remain the same, so that the unhealthy attractor may be still there. It is important to notice that in the future the system can fall into one of these attractors. If accurate, attractors would help to explain kindling effects observed in most psychiatric disorders, such as major depression, schizophrenia, bipolar disorders and most recently post-traumatic stress disorders where risk and severity of future episodes increases with each new incident (McFarlane, 2010). From a NDS perspective, the patient's emotional phase space must be reconfigured to prevent relapse. To show how this can be done we should think of a long time scale (a macroscale from beginning to end of treatment).

This emotional space may be modeled as a landscape with mountains and valleys that represent attractors (anxiety, joy, sadness, anger, and so on) and the system moves continuously on the landscape. If the valleys remain unchanged, it is likely that someday the system falls into one of the negative attractors (emotions), and if the valley is deep enough this can mean a relapse into disease as the system gets stuck. To some extent reconfiguring the emotional phase space of the patient would be like irreversibly changing the core aspects of a client's attitudes, values, beliefs, or life philosophy, which is in fact the deeper goal of nearly all psychological therapies (Baldwin et al., 2007; Frank & Frank, 1993; Pincus, 2009; Wampold, 2001).

Different therapeutic approaches, although equivalent in effectiveness, may be expected to change emotional phase spaces through different techniques. A behavioral approach may aim to strengthen distress tolerance, assertiveness, or other skills that allow a client to intentionally “climb out of” areas that were previously deep emotional attractors. Cognitive approaches (e.g., rational restructuring) may help clients to modify rigid and judgmental belief systems that previously caused acceleration (e.g., spiraling) down into deep negative emotional attractors. Newer mindfulness-based therapies aim to decrease judgment of and struggle against negative emotions, which typically backfire and lead to stuckness, and instead to increase acceptance and a here-and-now perspective, which allow negative emotional states to naturally run their course. Finally, emotion-focused approaches may aim to change clients’ deep dysfunctional emotional attractors by increasing awareness of healthy needs and healthy emotions–‘changing emotion with emotion’ (e.g., assertive anger or healthy grief, Greenberg, 2002). Whatever the particular approach, a critical outcome is an enduring shift in the dynamics of emotion, from rigidity and stuckness, to flexibility and resilience.

Successful therapies may aim early in treatment to help clients to move temporarily away from unhealthy regions of the phase space as soon as possible (e.g., emotional regulation strategies and remoralization); while, long lasting therapeutic effects will be achieved as far as psychotherapy has reconfigured the patient's emotional phase space. On a practical level, this notion of phase-space reconfiguration helps to integrate and empirically ground the great variety of similar concepts, known for example as first- and second-order change from the systemic therapy literature of the 1970's (Nichols & Schwartz, 2005). Initial investigations of sudden gains, abrupt improvements in symptoms that occur following a single session, have indeed produced some compelling initial evidence that such gains involve an irreversible process of change involving systemic reorganization (Lichtwarck-Aschoff, Hasselman, Cox, Pepler, & Granic, 2012). Such gains are not rare, occurring in around 40% of positive psychotherapy outcomes; and when they occur there is a significantly lower risk of relapse (Tang et al., 2007).

Future research may follow three main lines. The first line would be to define which methods of phase space reconstruction can be more helpful when working with self-report data, as these time series are rather limited (N<100).

A second line of research can test the model in Figure 1 directly as it transpires within the moment-by-moment interactions in psychotherapy. This research might rely on coding therapeutic interactions in naturalistic designs, for example the interaction between a client's level of emotional experiencing (Pascual-Leone & Greenberg, 2007) at a particular point in time and the force of necessary intervention to produce impactful session outcomes.

A third line of research would address questions related to the relative energy or power of psychotherapy. In accordance with self-organization principles close to the emotional inertia model (Pincus, 2009), the power of any psychotherapy should be estimated from the changes it induces in the complexity of the system. Therefore, higher energy treatments would show more ability to increase the system's complexity (i.e., toward far-from-equilibrium states) than lower energy treatments.

In summary, as far as patients and their emotions are considered as dynamical phenomena, emotional inertia is, to our view, a helpful conceptual tool to understand the complex processes underlying emotional processes within psychotherapy. Therapists, and approaches to therapy, have always been concerned with emotional stability and change. What we have attempted to add is a formal and empirically testable understanding of emotional change as it pertains to psychotherapy. As such, emotional inertia may become a unifying concept, guiding future psychotherapy process research and serving as an integrating framework for understanding the extant knowledge regarding the combined impact of client factors, specific techniques, and common factors on treatment outcome. In addition, the current model provides some empirically testable theory with which to examine more neglected aspects of the therapeutic process, such as the relative fit and timing of interventions.

It is worthwhile to stress, however, that we do not suggest an alternative theory but an additional theoretical framework to search (and hopefully find) explanations of change. Although experimental studies will be required to test the emotional inertia model presented here, NDS theory, in which the model is embedded, is increasingly proving itself to be a promising tool for the study of change in a great variety of psychological processes.