Las revisiones sistemáticas con metaanálisis son pruebas esenciales para resumir de manera fiable la eficacia de las intervenciones sanitarias. Un metaanálisis basado exclusivamente en un pequeño número de ensayos a menudo no será concluyente o puede aportar resultados positivos falsos. La estimación del tamaño óptimo de la información (OIS) puede reducir el riesgo de obtener resultados falsos positivos y determinar si se requieren ensayos clínicos adicionales. El cálculo del OIS tiene similitudes con el realizado para calcular el tamaño de la muestra de un ensayo clínico. El número requerido de participantes para el metaanálisis debe ser al menos tan grande como un solo ensayo con la potencia adecuada. El concepto del OIS proporciona un marco estadístico en el que la información acumulada es convincente para indicar si se necesitan más ensayos clínicos para abordar los efectos de la intervención.
Systematic reviews with meta-analysis are essential tools to reliably summarize the effectiveness of health interventions. A meta-analysis based exclusively on a small number of trials will often not be conclusive or may yield false positive results. The estimation of the optimal information size (OIS) can reduce the risk of obtaining false positive results and determine if additional clinical trials are required. The estimation of the OIS is very similar to that used to estimate the sample size of a clinical trial. The required number of participants for the meta-analysis should be at least as large as a single trial with adequate power. The OIS concept provides a statistical framework in which the accumulated information is convincing to indicate whether more clinical trials are needed to address the effects of the intervention.
La revisión sistemática (RS) con metaanálisis es una prueba esencial para sintetizar de manera fiable la eficacia de las intervenciones sanitarias1. La RS con metaanálisis (MA) es un trabajo de investigación que identifica el máximo número de estudios, evalúa su calidad y resume sus resultados utilizando una metodología científica rigurosa y explícita. Los cirujanos la utilizan para mantenerse actualizados en su campo y es esencial para desarrollar guías de práctica clínica2. Ciertas agencias estatales de financiación de la investigación solicitan conocer las RS existentes antes de financiar un nuevo proyecto de investigación3.
La RS puede incluir el MA como un método estadístico para resumir los resultados de los ensayos clínicos individuales4. El objetivo principal del MA es proporcionar una estimación más precisa que combine la información numérica de los ensayos clínicos individuales. Sin embargo, un MA basado exclusivamente en un pequeño número de ensayos a menudo no será concluyente5 o puede dar lugar a errores de tipo I, es decir, aceptar que hay una diferencia entre las 2intervenciones evaluadas a pesar de que esa diferencia no existe6. En la literatura hay diversos trabajos en los que se concluye que los resultados de un MA con un amplio número de pacientes son probablemente más válidos que aquellos con un pequeño número de pacientes y eventos (<200 eventos)7-9.
Aunque actualmente se discute e incluso cuestiona si se deben continuar utilizando los valores de significación estadística (valores de p) de manera categórica10, hasta el momento lo más extendido ha sido fijar un valor de riesgo menor o igual al 5% o menor o igual al 1% de cometer un error de tipo I. En este sentido, al menos, ese mismo valor de riesgo es el que se debería preservar en el MA. Actualizar un MA cada vez que aparece un nuevo ensayo clínico (algo habitual) incrementa el riesgo de sobreestimar el efecto observado en el MA y esto está principalmente relacionado con el efecto de multiplicidad estadística, lo que significa que se puede asumir un beneficio cuando realmente no existe tal beneficio. Es decir, cada vez que se incorpora un nuevo ensayo o se analiza un outcome diferente, se irá consumiendo valor de α y el nivel de error tipo I podrá llegar a ser superior a 5%. Se estaría obteniendo un resultado significativo que, en realidad, correspondería a una sobreestimación del efecto real de la intervención. Sin embargo, es probable que un gran número de clínicos e investigadores sean ajenos a estas situaciones y acepten como «definitivos» los resultados de un MA.
El objetivo de este trabajo es describir el concepto del tamaño muestral en el MA, del tamaño óptimo de la información (optimal information size; OIS) de un MA, su cálculo, su interpretación y la influencia del análisis del OIS en la interpretación de la evidencia.
Un tamaño de muestra en el metaanálisisDesde un enfoque estadístico clásico (frecuentista), el cálculo del tamaño muestral es un requisito imprescindible cuando se desarrolla el protocolo de un ensayo clínico. Esto se refleja en el número de pacientes u otras unidades experimentales que deben incluirse en un estudio para responder de manera fiable a la pregunta de investigación11. El tamaño de muestra en el MA puede definirse como el número de participantes y eventos necesarios para detectar o rechazar un efecto de intervención asumido a priori en un MA. Aquí también se podría aplicar un criterio similar al de los ensayos clínicos individuales, asumiendo que si la muestra es demasiado pequeña no será posible detectar un efecto y que una muestra demasiado grande puede representar una pérdida de tiempo y dinero, e incluso plantear problemas éticos12. Esto se explicaría principalmente por el hecho de continuar realizando ensayos clínicos cuando un MA ya hubiera demostrado un resultado a favor o en contra de la intervención de manera sólida y, por ello, se estaría exponiendo a pacientes a una intervención inefectiva o no se estaría ofreciendo a los pacientes una intervención efectiva en el caso de que se hubiera mostrado así en el MA. Entre la comunidad científica y los profesionales asistenciales, se ha podido llegar a extender la idea de que los MA proporcionan un resultado fiable solo por el hecho de ser un MA.
Sin embargo, ¿cuándo puede un MA considerarse una prueba definitiva?, ¿es posible realizar un cálculo del tamaño muestral en el MA al igual que en el ensayo clínico?
Casi en paralelo a los inicios del movimiento de la medicina basada en la evidencia, el número de MA publicados anualmente se ha incrementado de manera casi exponencial. En la actualidad, se estima que se publican alrededor de 8.000 revisiones sistemáticas al año13. Sin embargo, no todos los MA incluyen el número apropiado de pacientes para obtener conclusiones fiables y la falta de un número de pacientes y eventos adecuado es una de las razones de la imprecisión en el efecto estimado14.
Cálculo del tamaño óptimo de la información en el metaanálisisEn un esfuerzo por obtener conclusiones más fiables mediante el MA, la estimación del OIS puede reducir el riesgo de obtener resultados falsos positivos y determinar si se requieren ensayos clínicos adicionales en un área de conocimiento. Concretamente, el OIS puede definirse como la cantidad mínima de información requerida en la literatura para llegar a conclusiones confiables sobre una intervención15. El cálculo del OIS tiene similitudes con el realizado para el tamaño de la muestra de un ensayo clínico. El concepto de OIS para el MA fue inicialmente desarrollado y propuesto por Pogue en el año 199815. Para ejecutar el cálculo del OIS se han propuesto varias opciones. El método más sencillo para calcular este número de pacientes, similar al cálculo del tamaño muestral, es ejecutarlo como si se tratara de un ensayo clínico con potencia adecuada. Esto se puede realizar asumiendo un valor de α (falso positivo o error de tipo I), de β (falso negativo o error de tipo II), una potencia, un tamaño del efecto y una tasa de eventos en el grupo control.
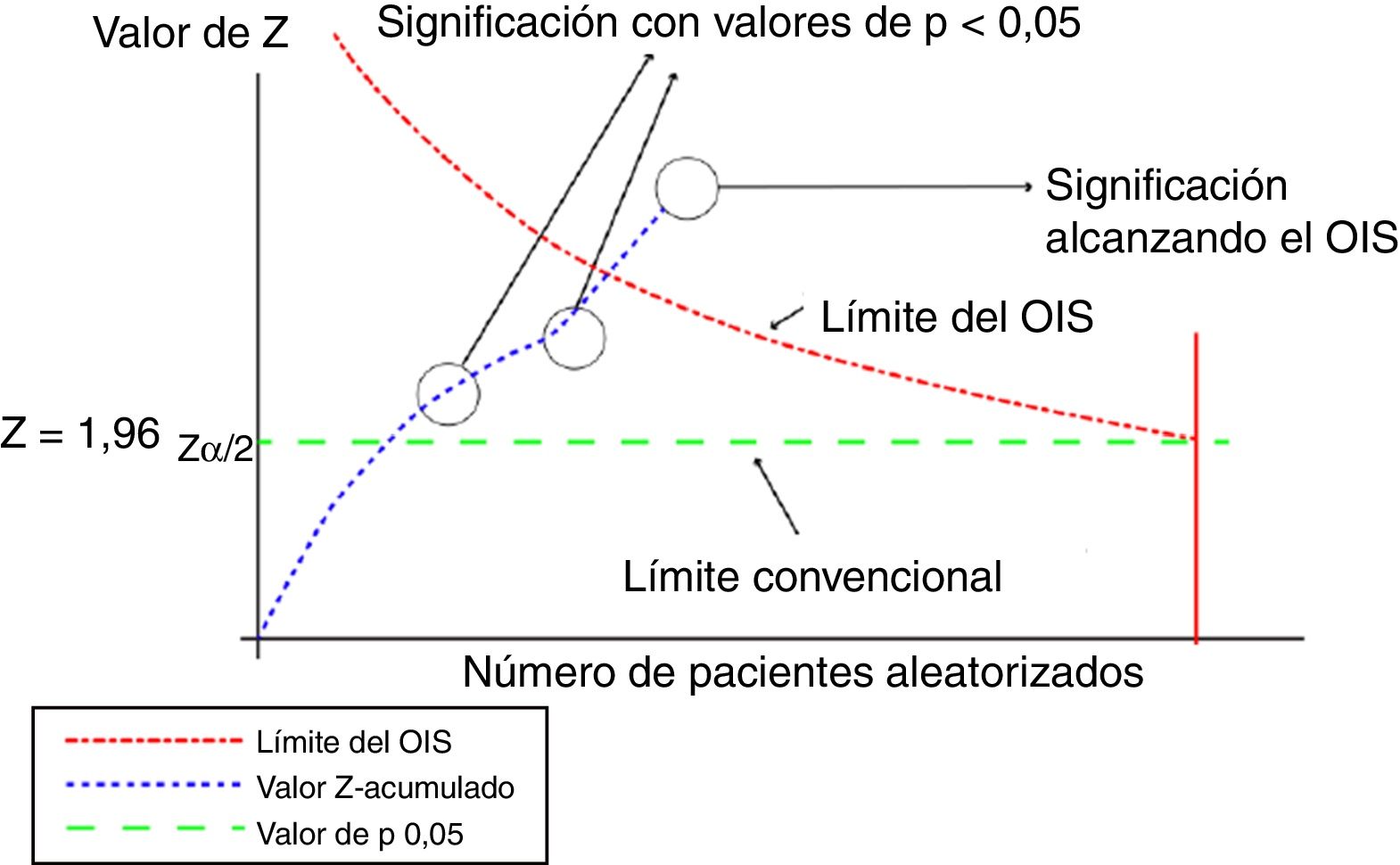
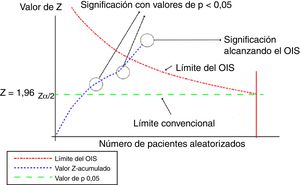
Este análisis se puede representar de forma gráfica, de manera similar a la de los ensayos clínicos secuenciales, según se muestra en la figura 1.
Representación gráfica del análisis secuencial aplicado al metaanálisis. Adaptada con permiso de Imberger et al.22.
En este gráfico la línea del valor Z-acumulado corresponde a la información acumulada a partir de cada uno de los ensayos incluidos en el metaanálisis. En el momento en que la línea del valor Z-acumulado atraviesa la línea de valor p 0,05 (limite convencional), que corresponde al valor tradicional de significación, se obtiene un resultado estadísticamente significativo, pero ello no indica que se haya alcanzado el OIS. Se alcanzará el volumen adecuado de información cuando la línea de valor Z-acumulado atraviese la línea del límite del OIS, tal y como se muestra en el gráfico.
Para hacer este cálculo se puede utilizar un software de cálculo de tamaño de la muestra como, por ejemplo, el de acceso gratuito PS-Power (http://biostat.mc.vanderbilt.edu/wiki/Main/PowerSampleSize). Una década después en el año 2008, Brok et al.16 propusieron incluir la heterogeneidad estadística en la estimación del OIS considerando que es un parámetro esencial en el MA. La heterogeneidad estadística cuantifica la variabilidad entre los resultados de los estudios y esta variabilidad puede ser debida a las diferencias reales de planteamiento y ejecución entre los estudios incluidos o a otras causas. Para la estimación de este OIS, incluyendo la heterogeneidad, se ha diseñado al menos un software específico y de libre acceso que permite el cálculo del OIS asumiendo un valor de heterogeneidad que puede introducirse manualmente o asumirse por defecto según el cálculo realizado por el software (http://www.ctu.dk/tsa/ downloads.aspx).
Tal y como se ha mencionado en unos párrafos previos, en la estimación del OIS un paso clave es decidir qué parámetros incluir en su cálculo y un paso no menos importante pero más controvertido es cómo estimar esos parámetros que se asumirán para el cálculo. Con relación al primer punto, los parámetros necesarios pueden ser el efecto estimado, la tasa de eventos en el grupo control y la heterogeneidad (I2). Hay otros parámetros también necesarios que son el valor de α, el valor de β y la potencia estadística. Para estos 3últimos sí existe un mayor consenso y suelen asumirse los siguientes valores: α = 0,05; β = 95%; potencia = 80%. En el caso del efecto estimado, hay autores que utilizan el efecto estimado en el MA, otros utilizan un valor de 20% expresado como reducción relativa del riesgo. Acerca de la tasa de eventos, principalmente la tasa de eventos en el grupo de control, algún autor propone que la opción más estable es el valor de la mediana de la proporción de eventos en el grupo control17. Respecto a la heterogeneidad, se suele tomar el valor de la heterogeneidad observada en el MA. Wetterslev et al. han propuesto lo que han denominado diversity, expresado como D2, y según los autores parece una mejor alternativa que I2 para considerar la variación del modelo en cualquier MA de efectos aleatorios18. Aunque existen otras opciones quizás más apropiadas, como el uso de valores estimados con distribuciones a priori de la heterogeneidad19,20.
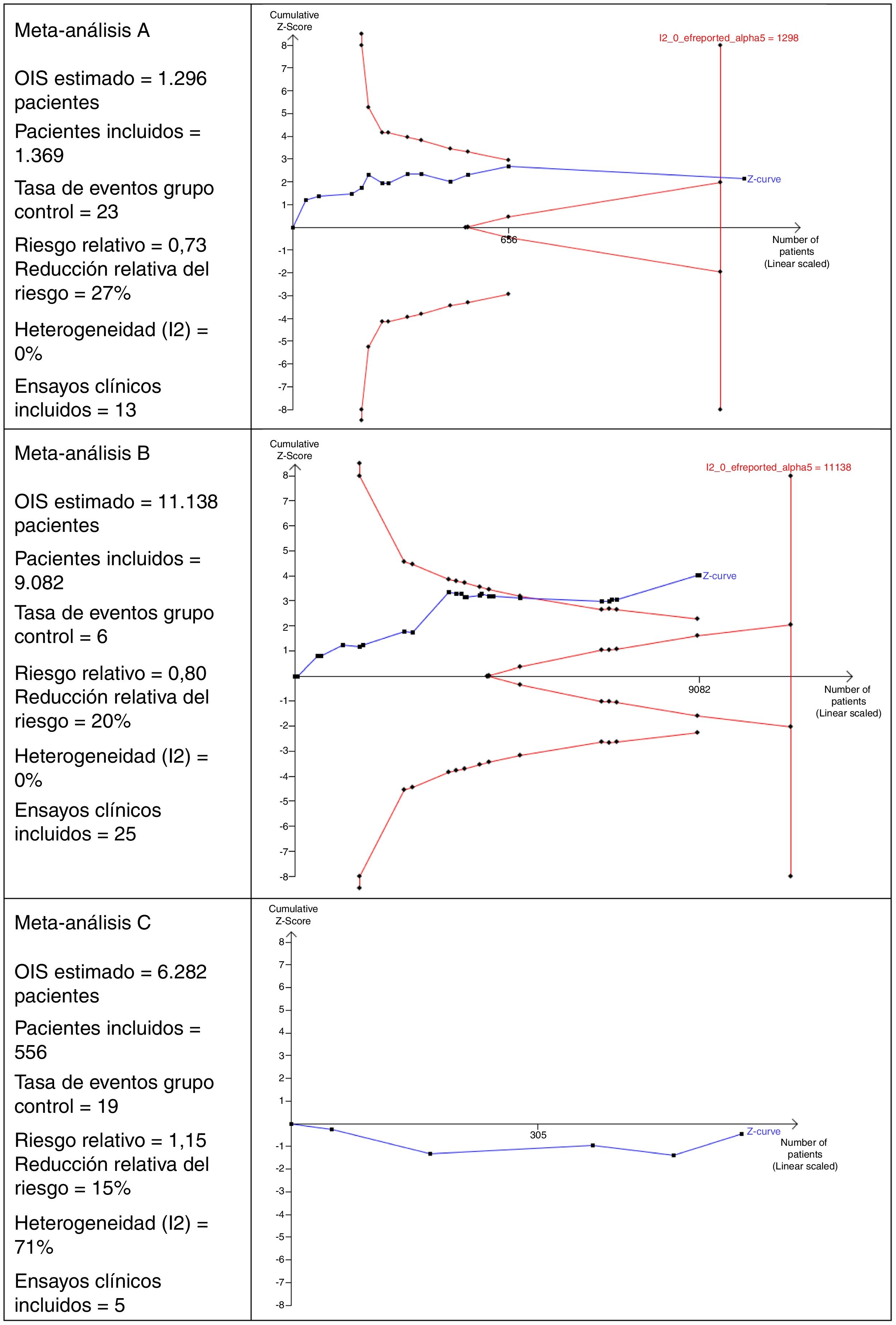
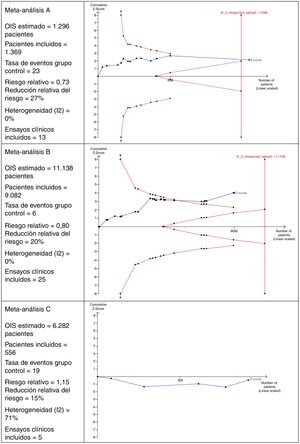
Interpretación del tamaño óptimo de la informaciónEn la figura 2 se muestran 3escenarios diferentes del cálculo del OIS y su interpretación que perfectamente podrían ser aplicables a MA en el ámbito de la cirugía.
En el MA A se observa que incluye 13 ensayos clínicos con un total de 1.369 pacientes. Este número de pacientes es suficiente para alcanzar el OIS de 1.298 pacientes y, por ello, la curva z cruza la línea vertical. Este es un buen ejemplo en el que se alcanza un tamaño muestral suficiente para tener confianza en el resultado obtenido en el MA.
En el MA B se puede observar que hay 25 ensayos clínicos con un total de 9.082 pacientes. Este número es insuficiente para alcanzar el OIS de 11.138 pacientes y, por ello, la curva z no cruza la línea vertical, aunque está cerca de alcanzarla porque, además, se observa la tendencia y cruza la línea de la curva de significación (curva descendente del límite de pacientes que deben incluirse).
En el MA C se puede observar que incluye un total de 5 ensayos clínicos que acumulan 556 pacientes. El OIS estimado es de 6.282 pacientes. Debido a este bajo número de pacientes acumulados, ni siquiera es posible dibujar la curva descendente. Otro detalle interesante de esta figura es que la curva z transcurre por debajo de la línea horizontal debido a que el riesgo relativo observado es >1.
Tamaño óptimo de la información e interpretación de la evidenciaEl concepto de OIS proporciona un marco estadístico en el que la información acumulada aporta fiabilidad para indicar si se necesitan más ensayos clínicos que evalúen los efectos de la intervención en la población general. El cálculo del OIS es una herramienta estadística que permite tener información más precisa sobre la estimación del efecto observado en un MA. También puede informar de si el volumen de información acumulada en el MA, principalmente el número de estudios, bajo ciertas asunciones, es suficiente para responder a la pregunta de investigación. La estimación del OIS ya ha sido considerada como útil por el GRADE working group, que evalúa la calidad de la evidencia y establece el grado de recomendación para una determinada intervención médica o quirúrgica. El sistema GRADE considera esta estimación del OIS un parámetro informativo para evaluar la imprecisión de los resultados obtenidos en un MA. De esta manera, también determina la confianza que aporta el resultado y, con base en ello, establece un grado de recomendación u otro para la intervención estudiada14.
En las revisiones sistemáticas con MA se está haciendo un uso creciente del OIS: ya existen varios MA publicados en el ámbito quirúrgico que incorporan el cálculo del OIS21-23. A pesar de ello, aún está en desarrollo y existe debate sobre cómo debe realizarse la estimación de los parámetros recomendados para el cálculo24. No obstante, y a pesar de sus limitaciones metodológicas, se hace necesario disponer de una herramienta de este tipo que nos permita tener una información más precisa para interpretar la evidencia y evite en más de una ocasión la conocida frase no hay suficiente evidencia para evaluar el efecto de esta intervención. Son necesarios más estudios para investigar su efecto. En el caso de que se deba utilizar esta frase, se podrá indicar con más precisión qué número de pacientes es necesario en dichos estudios para disponer de una información más precisa y fiable.
FinanciaciónLa presente investigación no ha recibido ninguna beca específica de agencias de los sectores público, comercial ni sin ánimo de lucro.
Conflictos de interesesNinguno.