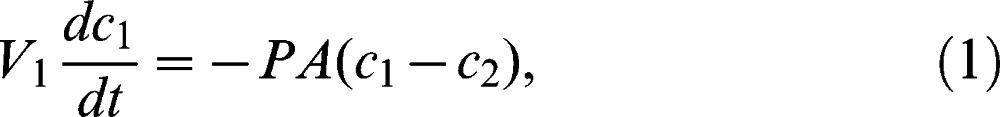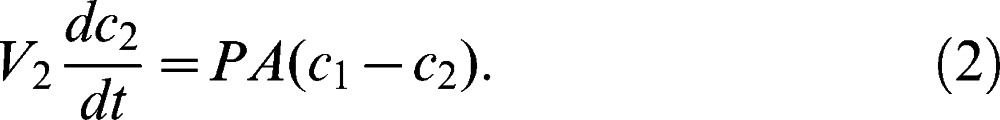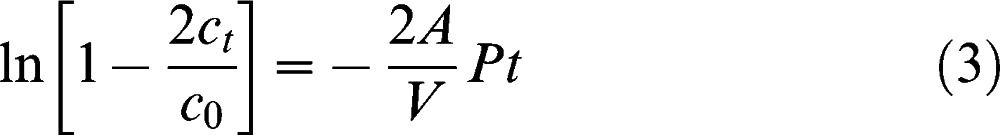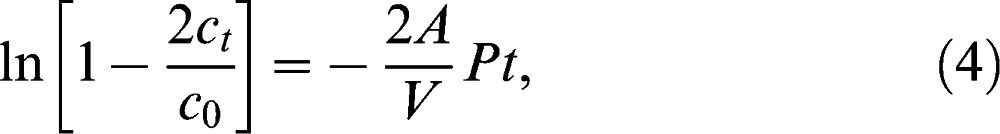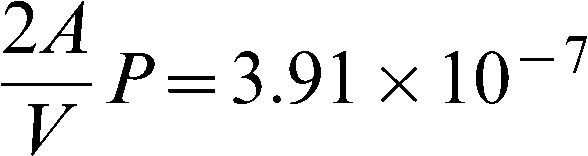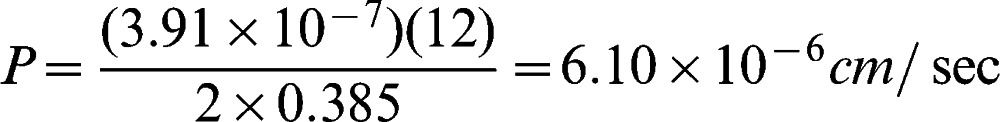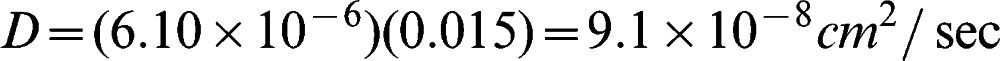Polyvinyl alcohol (PVA) membranes have long been used in many applications, most notably in a number of recent biomedical applications. These applications include the encapsulation of hybrid-type artificial organs,1–3 the controlled release of specific molecules,4,5 targeted drug delivery systems,6,7 enhanced wound dressings,8,9 and myriad other applications that utilize the semi-permeability and high biocompatibility of PVA. Nevertheless, prior to its designation for use as the biomaterial of choice in the design and development processes of artificial tissue fabrication applications, the exact nature of PVA's physiological properties needs to be ascertained. In particular, the permeability and the diffusion coefficient are two important parameters that need to be analyzed. The experimental results can subsequently be used to determine the appropriate fabrication technique and design geometry for the design and development of the required tissue engineering applications.
This study is based on the following presumption: if a researcher could place a semi-permeable membrane at the interface of two chambers (Chambers 1 and 2) that contain different concentrations of the same solution, then the diffusive parameters of the membrane can be measured simply by continuously measuring the changes in solute concentration in the chamber with the lower concentration. If the researcher waits until equilibrium between the two chambers is reached, both of the chambers would then have the same amount of solute (and, therefore, the same concentration of solute). A complete concentration profile will therefore provide the information that is needed to determine (using Fick's Law) the desired parameters of the membrane.
Nevertheless, this procedure is highly impractical, due to the long period of time that is required to record the observations and any related changes. On the other hand, by deriving a model of the underlying diffusion process using Fick's Law, the researcher can predict the diffusive parameters based on the collected data over a relatively short period of time. The derivation of the model begins with constructing materials that are balanced on either side of the membrane. The material balance on the higher-concentration chamber (Chamber 1) can be expressed as
where V1 is the chamber volume, P is the permeability, A is the exposed area of the membrane, c1 is the concentration in Chamber 1, and c2 is the concentration in Chamber 2. Similarly, the material balance in the lower-concentration chamber (Chamber 2) can be expressed as
Assuming the initial conditions of c1 equals c0, and c2 equals zero, the following mathematical model can be derived and used to determine the permeability, P, and thus the diffusion coefficient, D, of the hydrogel membrane.
If the ratio of ct/c0 is sufficiently small (as is the case if the period of the experiment is sufficiently short), then the left-hand side of the equation will be equal to –2ct/c0, according to Taylor's series.5,7 In other words, a linear concentration profile can be expected if the experimental period is sufficiently short, and the permeability and diffusion coefficient can be easily determined thereafter.
The aim of this technical report was to study the fundamental parameters in the design and development of an aqueous PVA hydrogel membrane to be used in generic artificial tissue engineering applications; these parameters included the permeability and diffusion coefficient of the membrane and were measured using dextran-fluorescein isothiocyanate (Dextran-FITC) as the solute of choice.
MATERIALS AND METHODSVarious methods can be used to measure concentration changes. The method that was chosen for the current study utilizes modified dextran molecules that were tagged with a fluorescent material (Dextran-FITC). Next, the fluorescence levels were easily measured using a fluorometer, and the levels were linearly correlated with the concentration of the dextran molecules in the chamber. A standard concentration curve was constructed such that the concentrations could be calculated from the fluorescence levels based on a linear equation that was derived from the curve. The derivations of the permeability and diffusion coefficient values are based on Fick's Law, thus requiring the values of several parameters (including the chamber volume, membrane aperture, and sample times) in addition to the concentrations.
The methods used in this study were divided into two stages: the preparation stage and the running stage. The preparation stage consisted of the preparation of a phosphate-buffered saline (PBS) solution, a Dextran-FITC solution, the PVA hydrogel membrane to be tested, and the experimental chamber apparatus; this stage helped to minimize any foreseeable problems during the experimental runs. In addition, apart from the actual running of the experiment, the running stage also consisted of the calculation of the permeability and diffusion coefficient for the particular hydrogel membrane that was used in the experiment.
PBS solutionsTo prepare a phosphate-buffered saline solution of pH 7.4, approximately 7 g of PBS was dissolved in 1 l of deionized water with continuous stirring. The pH was then measured, and a small amount of PBS was added until the solution pH reached 7.4.
Dextran-FITC solutionsTwo concentrations of Dextran-FITC (100 and 200 μg/ml) were used in this study. The latter concentration was used later in the course of the study to decrease the uncertainties and errors that are associated with using a low concentration of solute. The 100 μg/ml solution was prepared by dissolving 2 mg of Dextran-FITC in 20 ml of deionized water (or PBS). The amount of Dextran-FITC that was dissolved was doubled to produce the 200 μg/ml solution.
Only 12 ml of the solution was used to fill one of the permeation device chambers, and the remaining solution was used for the preparation of the standard Dextran-FITC samples. Each solution was freshly prepared prior to each run of the experiment and was used only once.
PVA hydrogel membranesA 15% w/w PVA solution was prepared from a 30% stock solution. To prepare a 1-ml solution, 0.5 ml of the stock solution was mixed with 0.5 ml of deionized water in a tube. The solution was thoroughly mixed using an electric mixer, and any air bubbles were removed using a vacuum flask in a fume cupboard. The solution was stored at 4°C until use.
A small volume was drawn from the tube using a disposable syringe and injected onto a microscope slide. Two 15-mm-thick cover slips were placed on each end of the slide, and another slide was placed on top of the cover slips to produce a thin membrane of fluid.
A UV spot cure system was used for cross-linking, and the exposure time was set at 100 sec. The separation between the microscope slide arrangement and the tip of the UV system was kept at a distance of approximately 25-30 mm.
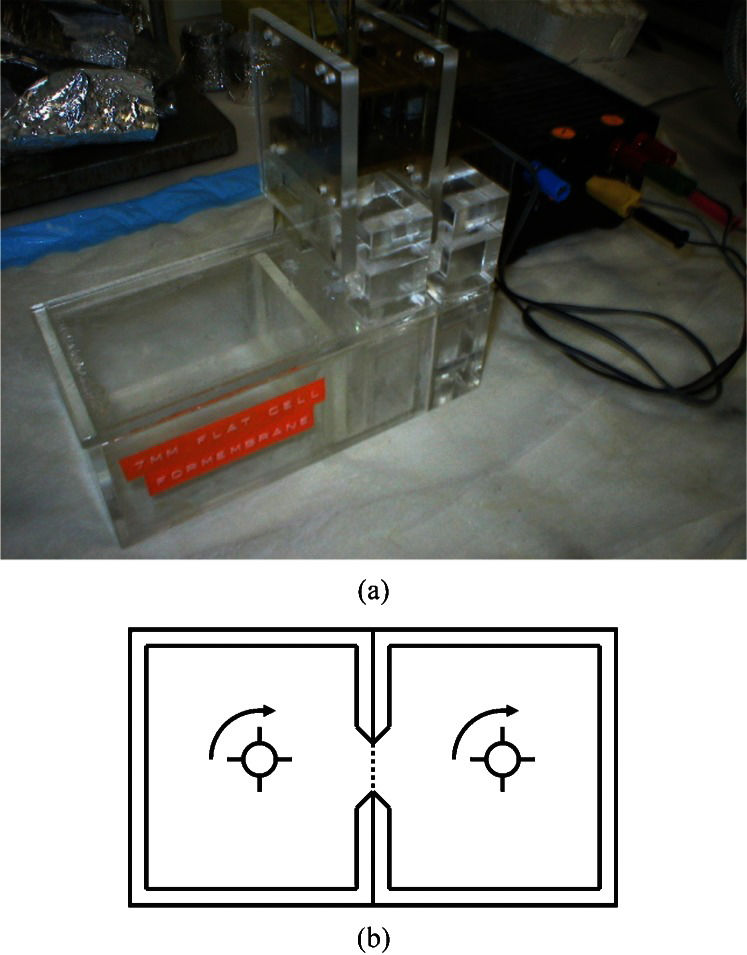
Experimental apparatusA two-chamber device (Figure 1) that was made of Perspex and was previously developed for generic mass transfer studies was used in this study. Because Dextran-FITC was chosen as the solute of choice, the transparent chamber walls needed to be covered with aluminum foil to prevent degradation of the fluorescent marker. A number of openings in the top portion of the chamber were sealed using a sealant to reduce evaporation, which would have greatly affected the concentration of the samples.
The device was thoroughly washed before each experimental run to ensure that no residual Dextran-FITC remained to affect the accuracy of the fluorescence readings.
Permeability studiesEach device component (particularly the surface of the ports where the membrane was clamped) was thoroughly cleaned and dried. Next, the prepared hydrogel membrane was mounted, any folds and creases were removed, and the membrane was clamped and placed into position using four mounting bolts.
Deionized water or PBS (12 ml) was subsequently placed in Chamber 2, and Chamber 1 was filled with 12 ml of Dextran-FITC solution. Both chambers were stirred continuously on the vertical axis, and the ports where the membrane was clamped were chamfered to enhance mixing near the membrane surface. The exposed membrane area was 0.385 cm2 (0.7 cm diameter), and the experiments were conducted at room temperature (22.5±1.5°C) over an average run time of seven hours.
The diffusion of Dextran-FITC (or any solute, for that matter) through the polymer network of the PVA hydrogel follows Fick's Law and can be expressed in the following form:
where ct is the concentration of the solute in Chamber 2 at time t, c0 is the initial concentration of the solute in Chamber 1, t is the diffusion time in seconds, A is the exposed membrane area (0.385 cm2), V is the volume of the chamber (12 ml), and P is the permeability of the hydrogel membrane. The diffusion coefficient is related to the permeability based on the following relationship:
where D is the diffusion coefficient of the membrane, k is the partition coefficient of the solute, and δ is the membrane thickness at the end of the experiment. The partition coefficient of Dextran-FITC is approximately equal to 1.10 Next, the permeability and related diffusion coefficient were calculated by measuring the slope of the linear portion in Equation (1). A strong linear dependence of ln(1 – 2ct/c0) over t was observed when the dextran molecules passed through the PVA hydrogel membrane.
Experimental protocolSamples were taken from Chamber 1 only at the beginning (t0) and the end (tf) of the run, whereas samples were taken from Chamber 2 at t0, tf, and at a number of specified intermediate times. Using a pipette and a clean tip, 1 ml of sample was taken at each specified time point and placed in a microtube; 1 ml of deionized water (or PBS) was subsequently added to the respective chamber using a clean tip to restore the volume.
The microtubes were quickly placed in a rack and stored in the freezer overnight alongside the standard concentration samples. The fluorescence levels of the samples were read on the following day. Three 0.2-ml samples from each microtube was drawn and placed in a fluorescence counting plate. The frequency range of the fluorometer was set at the default setting of 485-538 nm.
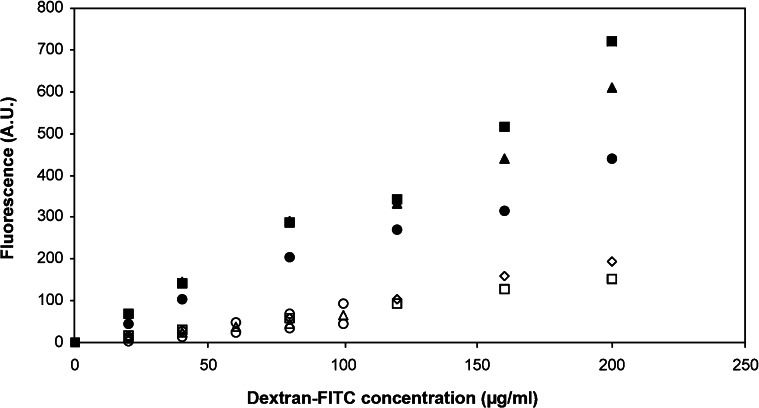
RESULTSThe outcome of the study was entirely dependent on the fluorescence readings of the samples. Thus, it was of the utmost importance that the construction of the standard curve from which the concentrations of the samples were determined yielded consistent and reproducible results. Figure 2 shows the standard curves for both solvents (i.e., water and PBS).
The mean R-squared values when water or PBS was used as the solvent were 0.99±0.0049 and 0.98±0.0022, respectively. Although an R-squared value is merely a measure of the predictability of the next data points (with 0 being impossible to predict and 1 being the most predictable) and is based on the construction of the best-fit linear equation between the two variables, we are of the opinion that it can be used as a measure of linearity to a certain degree. Therefore, for both water and PBS, the relationship between the two variables can be considered linear within the range of these concentrations, and hence this relationship can be used to determine the concentration of the samples.
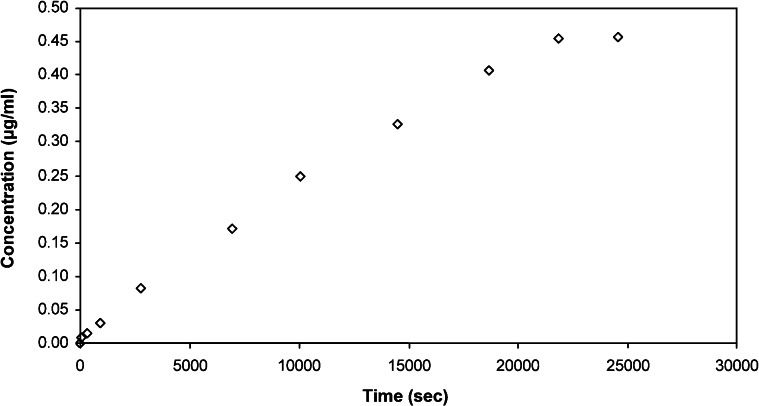
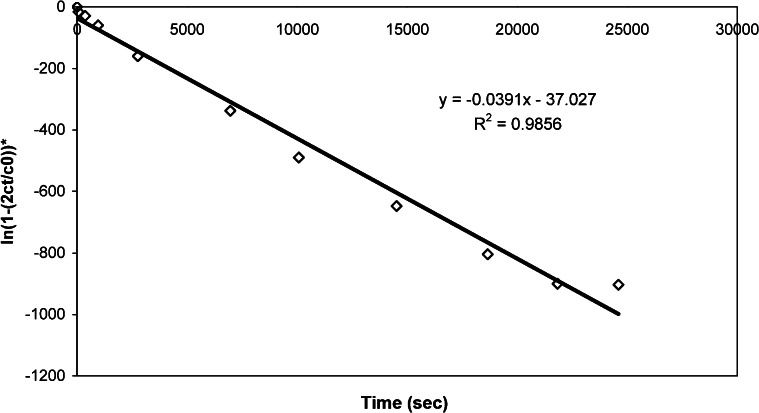
Figure 3 shows an example concentration plot using water as the solvent of choice (from Run 8). Figure 4 shows the plot of ln(1 – 2ct/c0)∗ versus t; this plot was used determine the permeability and diffusion coefficient of the membrane. The asterisk was included to indicate that the value was multiplied by 100,000 to yield a much more precise slope value that was then used to calculate permeability. Next, permeability and thus the diffusion coefficient was calculated using Equations (1) and (2). The calculation for determining P and D is shown below where V was 12 ml, A was 0.385 cm2, and δwater was 0.015 cm.
Equating the m-part of Equation (1) to the slope of the graph in Figure 4 (removing the multiplication factor by multiplying the slope value by 10-5) yields:
Substituting the values of V and A gives the permeability of the hydrogel membrane:
Finally, substituting the values of P and δ in Equation (5) yields the diffusion coefficient of the membrane:
Similar calculation steps and parameter values were used to determining the permeability and diffusion coefficient when PBS was used as the solvent of choice.
Table 1 summarizes the values for a select number of parameters, including the initial and final concentrations in Chamber 1, the final concentrations in Chamber 2, and the permeability and diffusion coefficient values of the hydrogel membrane for each experimental run.
The measured and calculated values for the indicated parameters. Runs 6 through 10 used water as the solvent, and Runs 11 through 13 used PBS. Runs 6 and 8 used 100 μg/ml Dextran-FITC, and the rest of the runs used 200 μg/ml Dextran-FITC.
| Experimentalruns | Chamber 1(μg/ml) | Chamber 2 (μg/ml) | Permeability (10-6 cm/sec) | Diff. coefficient (10-7 cm2/sec) | |
|---|---|---|---|---|---|
| c0 | cf | cf | |||
| 6 | 131.7 | 196.6 | 0.63 | 7.1 | 1.1 |
| 8 | 101.5 | 174.0 | 0.46 | 6.1 | 0.9 |
| 9 | 239.2 | 394.8 | 1.25 | 5.9 | 0.9 |
| 10 | 193.8 | 301.0 | 0.82 | 5.6 | 0.8 |
| Average (±SD) | 6.2 (±0.65) | 0.9 (±0.98) | |||
| 11 | 196.6 | 159.7 | 1.59 | 10.1 | 1.5 |
| 12 | 171.1 | 146.9 | 1.21 | 9.0 | 1.3 |
| 13 | 191.6 | 138.8 | 1.33 | 8.0 | 1.2 |
| Average (±SD) | 9.0 (±1.08) | 1.4 (±0.16) | |||
In accordance with the objectives of this study, the calculated permeability and diffusion coefficient values of the membrane were comparable with the expected values from the literature. As part of their diffusion studies, Hickey and Peppas10 studied the membrane diffusion coefficient of 10 and 15% PVA hydrogel membranes using theophylline and Dextran-FITC that were prepared using the freezing/thawing technique. Their studies yielded a range of values for the diffusion coefficient that was dependent on the degree of crystallinity and the equilibrium swelling ratio. Although the diffusion coefficient ranged from 1.70-5.28 × 10-8 cm2/sec, this range was still within an order of magnitude, and thus the authors believed that these values (which were calculated using water as the solvent) are still relevant as reference values.
As listed in Table 1, the values that were calculated in the present study differed from, but were still within an order of magnitude to, the values that were reported in previous studies,10,11 even though the solute and solvent used in the experiments are exactly the same. There are many differences in the setup of the experiments, and these differences may have affected the outcome of the experiments. For example, the degree of crystallinity and the equilibrium swelling ratio were not determined in the current study, thereby making it difficult to place the calculated value within the range of the previously determined diffusion coefficient values. These diffusion coefficient values seemed to increase non-linearly with an increase in equilibrium swelling ratio, whereas the degree of crystallinity remained relatively constant.
In our opinion, one of the fundamental issues that needed to be considered before the difference in the calculated diffusion coefficient values could be interpreted concerns experimental consistency. As noted in Table 1, there was an increase in the final concentration in Chamber 1 (cf) when water was used as the solvent (Runs 6 to 10). This is counter-intuitive, as the concentration clearly should have dropped with a corresponding increase in the concentration in Chamber 2. Moreover, even when there was a concentration drop in Chamber 1 (when using PBS), this drop did not closely correspond to the concentration increase that was observed in Chamber 2.
There was also a significant difference between the two solvent types that were used with respect to the amount of fluorescence that was obtained from the Dextran-FITC samples (Figure 2). When using water as the solvent, there was a decrease of up to three times the amount of fluorescence that was obtained using PBS as the solvent. Due to time constraints, this phenomenon was not investigated, but it could play a role in explaining the inconsistencies that were found in the results.
In addition, another inconsistency that is worth noting for future studies concerns the thickness of the hydrogel membrane at the conclusion of the experimental runs. On a number of occasions in which the thickness was measured post-experimentally, the thickness changed when using water as the solvent but remained constant when using PBS. When using water, the membrane thickness was almost always increased by up to twofold at the end of the experimental run relative to the start of the experiment. This phenomenon clearly had a large impact on the diffusion dynamics and on the subsequent accuracy of the calculation that was used to determine the permeability and diffusion coefficient such that they could not be ascertained. Due to this fact, the initial membrane thickness was used for our calculations. The initial membrane thickness was similar for all of the membrane types, and we ensured a consistent initial membrane thickness by using a cover slip to separate the microscope slides while preparing the membranes.
CONCLUSIONSAlthough the experimental protocol that was used in these experiments was sufficiently altered to obtain the diffusion coefficient for a given membrane, there remain certain inexplicable aspects of the results that may render the calculated values less useful and relevant. Therefore, these inconsistencies require further investigation, particularly with respect to the design and fabrication of the experimental chambers, before this protocol can be used in any future permeability-related studies. Nevertheless, from these preliminary data, it can be confidently concluded that PVA is suitable for use in the design and development of artificial membranes in various tissue engineering studies.
NAK and RMG would like to thank the University of Malaya (Malaysia) and the Malaysian Public Services Department for the financial grants that contributed to the completion of the postgraduate studies on which this report was based.