En este trabajo se presenta un método no paramétrico general de simulación estocástica conjunta de propiedades petrofísicas utilizando la cópula Bernstein. Este método consiste básicamente generar simulaciones estocásticas de una determinada propiedad petrofísica (variable primaria) modelando la dependencia empírica subyacente con otras propiedades petrofísicas (variables secundarias), mientras también es reproducida la dependencia espacial de la primera.
Este enfoque multivariado provee una herramienta muy flexible para modelar las complejas relaciones de dependencia de las propiedades petrofísicas. Tiene varias ventajas sobre otros métodos tradicionales, ya que no se limita al caso de la dependencia lineal entre las variables, y tampoco requiere de la suposición de normalidad y/o existencia de momentos.
En este trabajo este método es aplicado para simular un perfil de permeabilidad utilizando la porosidad vugular y velocidad de onda de corte (Ondas S) como covariables, en una formación carbonatada de doble porosidad a escala de pozo. Los valores simulados de la permeabilidad muestran un alto grado de precisión en comparación con los valores reales.
This paper introduces a general nonparametric method for joint stochastic simulation of petrophysical properties using the Bernstein copula. This method consists basically in generating stochastic simulations of a given petrophysical property (primary variable) modeling the underlying empirical dependence with other petrophysical properties (secondary variables) while reproducing the spatial dependence of the first one.
This multivariate approach provides a very flexible tool to model the complex dependence relationships of petrophysical properties. It has several advantages over other traditional methods, since it is not restricted to the case of linear dependence among variables, it does not require the assumption of normality and/or existence of moments.
In this paper this method is applied to simulate rock permeability using Vugular Porosity and Shear Wave Velocity (S-Waves) as covariates in a carbonate double-porosity formation at well log scale. Simulated permeability values show a high degree of accuracy compared to the actual values.
Integrated Reservoir Modeling (IRM) is the most accepted way to obtain the spatial distribution of petrophysical properties in oilfields (Cosentino, 2001). An important and common task performed in this method is the estimation of permeability, because it is well known that this petrophysical property is quite informative about the oil flux patterns in a reservoir. However, it is difficult to obtain direct information about permeability, and therefore it is necessary to find models of dependence with another petrophysical property (such as porosity, water saturation, etc.) in order to have an estimation of its profile (Landa et al., 1996).
The linear regression approach is the most common way to model permeability values using other petrophysical properties as covariates (Balan et al., 1995). To meet the requirement of linearity it is common to perform transformations which imply that the final result could be biased when it is back transformed; there are approaches that, in order to fit linear models, apply logarithmic transformations to induce this behavior, for example, to use the Cokriging method it is necessary to have a linear relationship since it requires the linear corregionalization model (Sanjay and Journel 1994).
The main disadvantage of linear dependency models is their lack of ability to capture and model the dependence structure or pattern (Al-Harthy et al. 2005). In other words, traditional methods cannot capture the complex variability of data, in terms of variance or standard deviation; hence, the predicted permeability will not reproduce extreme values of the real data. In other words, these approaches will not be able to represent impermeable barriers or high permeability zones, and from a fluid flow point of view this aspects are the most important characteristics that determine the patterns of fluid movement. In this context, the predicted permeability profile, using linear estimators, will not be an effective approximation due to its oversmoothing nature.
On the other hand, model-free function estimators like artificial neural networks are very flexible tools that have been used to model permeability. However, neural networks have some disadvantages too. First, the training process has to be done with caution and can be a lengthy process. The good results obtained by this technique are reached using a comprehensive training data set, which is not always available. On the other hand, failing in correctly calibrating the network may result in aberrant results. Another point to take into consideration is that the methodology is not yet an “off the shelf” application and requires expertise by the geoscientist (Cosentino, 2001).
Another alternative are Bayesian methods; however, the traditional framework of the Bayesian analysis is based on the multivariate normal distribution where the lower and upper tails are symmetrical. Armstrong et al. (2004) proposed an alternative Bayesian analysis that is based on Archimedean copulas where the joint distribution does not have to be normal and there is flexibility to have a lower tail or upper tail dependence based on the specific type of copula.
Constructing numerical models of the reservoir that honor all available data (core measurements, well logs, seismic and geological interpretations, etc.) having sparse knowledge of rock properties, leads us to consider the stochastic simulation approach (Deutsch, 1992). This is not a new concept (Haldorsen and Damsleth, 1990; Journel and Alabert, 1990), stochastic models of physical systems are used extensively in many disciplines.
Stochastic simulation is the process of building alternate, equally probable models of the spatial distribution of a random function. It is said that a simulation is conditional if the resulting realizations honor the raw data values at their locations. The most straightforward algorithms for generating realizations of a multivariate Gaussian field is provided by Sequential Gaussian Simulation (SGS) and Sequential Indicator Simulation (SIS), which are extensively used to perform permeability simulations (Holden et al. 1995). However despite of their improvements (Journel and Zhu, 1990; Suro-Perez, 1990) these methods are limited to cases when the spatial continuity is characterized by stationary two-point statistics and to data that is defined on the same support (Deutsch, 1992).
A competitive and more systematic method for predicting permeability may be achieved by applying stochastic joint simulations, in which the correct specification of dependence pattern between petrophysical properties is crucial (Deutsch and Cockerham, 1994). According to Deutsch this approach basically consists of an annealing geostatistical cosimulation of porosity-permeability using their empirical joint distribution.
A modification of Deutsch’s methodology was presented by Díaz-Viera and Casar-González, (2005). Here, it was proposed the use of a bivariate t-copula to construct the joint distribution function between porosity and permeability rather than use the joint distribution function of the sample data, the dependence structure was specified by matching concordance measures such as Kendall’s τ and Spearman’s ρ. The above methodology was applied to simulate permeability from the porosity profile in a double porosity carbonate systems, restricted to one-dimensional case at well-log scale (Díaz-Viera et al. 2006).
While Díaz-Viera and Casar-González proposal can reproduce adequately the observed data, and also their extreme values using a t-copula, the critical problem is that the applied copula is parametric, and consequently, it is based on a given distribution function, the student t. In that sense, expecting a single copula family to be able to model any kind of dependency relationship seems to be too restrictive, at least for the petrophysical properties under consideration. It does not mean that parametric copulas have not practical use. It means that petrophysical properties modeling, where dependence structure can be complex or non linear, using parametric copulas could be available but in a very complicated form, Sancetta and Satchell (2004).
The copula approach has been successfully used to model dependence patterns in few areas of oil industry, for example, for field development decision process (Accioly and Chiyoshi 2004) or to model dependence in petroleum decision making (Al-Harthy et al. 2005).
In a recent work we use the copula approach to model the bivariate dependence between petrophysical properties in a complete nonparametric fashion (Hernández-Maldonado et al. 2012), it means we did not impose a priori a parametric joint distribution function to characterize the dependence structure of the sample; instead, we used a bivariate Bernstein copula function to model the intrinsic distribution of data values. In this work we introduce a multivariate method for estimating empirical dependence among several petrophysical properties using a nonparametric copula. The dependency model obtained is then used to stochastically simulate one property (primary variable) given other ones (secondary variables). Here, we apply a method widely used in geostatistics, the Simulated Annealing method, which is a global optimization framework where we can add restrictions to simulation. In this case, in addition of using multivariate dependence by sampling the empirical copula model, a spatial correlation function (a variogram) for the secondary variable is imposed. Additionally, if any raw data of the primary variable is available, it can be exactly honored, that is, the method can be conditional.
In this paper this method is applied to simulate rock permeability using a trivariate copula model where permeability is described by Vugular Porosity and Shear Wave Velocity. It is introduced a two stage simulation method in a multivariate fashion to model stochastically the spatial distribution of permeability at well log scale. Conditional and nonconditional simulations, and the median of simulations are performed in order to show the results that this method provides; also it is established that, as far as more descriptive variables integrate the Bernstein copula it will reproduce permeability values in a very precise form, consequently it will not be necessary to perform many simulations to reduce small scale variability.
Brief introduction to multivariate copulasThe main disadvantage of dependency models based on a linear regression approach is their lack of ability to capture and model more general dependence structure. As an alternative a copula can model the joint distribution of petrophysical properties in better ways. The essence of the copula approach is that a joint distribution of random variables can be expressed as a function of the marginal distributions (Al-Harthy et al., 2005).
According to Sklar’s theorem (Sklar, 1959), the underlying copula associated to a multivariate random vector (X1, X2, ..., Xm) represents a functional link between the joint probability distribution and the univariate marginal distributions F1, F2, ..., FM respectively:
For all x1, x2, ..., xm in the extended real numbers system, where C:[0, 1]m →[0, 1] the underlying copula is unique whenever X1, X2, and Xm are continuous random variables. Therefore, all the information about the dependence between continuous random variables is contained in their corresponding copula. Several properties may be derived for copulas (Nelsen, 2006), and among them we have an immediate corollary from Sklar’s theorem: X1, X2 and Xm are independent continuous random variables if and only if their underlying copula is C(u1,...,un)=u,...,un.
Let S={(x11, x21, ... xm1), ..., (x1n, x2n, ...xmn)} be n observations of a random vector (X1, X2, ..., Xm). We may obtain empirical estimates for the marginal distributions X1, X2, ..., Xm by means of:
where stands for an indicator function which takes value whenever its argument is true, and otherwise. It is well-known (Billingsley, 1995) that the empirical distribution Fˆj is a consistent estimator of Fj that is, Fj that is Fˆj(t)is a converges almost surely to Fj(t) as n →∞ all t.
Similarly, we have the empirical copula (Deheuvels, 1979), a function Cn with domain {1n;i=0,1,…n}n (where n is the sample size) defined as
and its convergence to the true copula has also been proved (Fermanian et al., 2004). The empirical copula is not a copula, since it is only defined on a finite grid, not in the whole unit hypercube [0, 1]n, but by Sklar’s Theorem (Sklar, 1959) may be extended to a copula.Cn may be extended to a copula.
Sklar’s theorem is completely general and a joint distribution function can be constructed using the copula function. The copula separates the marginal distributions from correlation and the copula itself can capture the dependence structure. This is an essential property of copulas.
A general example of a multivariate copula model that describes the relationship of three random variables (a trivariate copula) according to Sklar’s theorem is shown:
There are different classes and families of copulas but, for this study, we will work with the Bernstein copula, which is a nonparametric copula since it is a nonparametric smoothing based on the empirical copula.
Joint stochastic simulation method using a multivariate Bernstein copulaThe method presented here basically consists in generating a stochastic simulation of a primary variable, where the joint distribution function of its covariates is modeled using a nonparametric copula. In other words, the spatial dependence and dependence pattern between variables are decoupled; in this context, the Bernstein copula only models the dependence between variables and the spatial dependence is modeled by a variogram applying the Simulated Annealing method.
Basically this proposal is a two-stage modeling algorithm method; first, the pattern relationship between petrophysical properties under study; and second, the spatial structure. In the first stage it is modeled the dependence structure of petrophysical properties using a multivariate nonparametric copula (the Bernstein copula), then a geostatistical simulation of primary variable is performed using simulated annealing technique, whose objective function is the variogram model (Deutsch and Cockerham, 1994). A detailed description of each step of the algorithm will be described.
Multivariate Bernstein Copula ModelingEach petrophysical property is modeled as an absolutely continuous random variable X with unknown marginal distribution function F. For simulation of continuous random variables, the use of the empirical distribution function (2) is not appropriate since Fˆj is a step function, and therefore discontinuous, so a smoothing technique is needed. Since our main goal is to simulate a primary variable using more than one descriptive variable, it will be better to have a smooth estimation of the marginal quantile function Q(u)=F-1(u)=inf{x:F(x)≥u},0≤u≤1 which is possible by means of Bernstein polynomials as in Munoz-Perez and Fernandez-Palacín (1987).
For a smooth estimation of the underlying copula we make use of the Bernstein copula (Sancetta and Satchell, 2004; Sancetta, 2007):
For every (u1, …, um) in the unit hypercube [0, 1]m, and αv1n1,…,vmnm is the empirical copula, defined in (3).
For example, the trivariate Bernstein copula model derived from (6) is:
Sampling algorithm of a Bernstein copula modelFor a pair of random variables (X1, X2) with joint distribution function H and underlying copula C we need to generate an observation of uniform (0, 1) random variables (U, V) whose joint distribution function is C and then transform those uniform variables as in step 3 of the sampling bivariate algorithm. For generating such pair (u, v) it is used a conditional distribution method, this method needs the conditional distribution function for V given U=u, which we denote as cu (v):
where CˆB is the bivariate Bernstein copula model, obtained by (6).
To simulate replications from the random vector with the dependence structure estimated from the observed data S:={(x11, x21), ..., (x1n, x2n)} it is applied the following algorithm:
Sampling bivariate algorithm- 1
Generate two independent and continuous Uniform (0,1) random variatesu andt
- 2
Setv=cu-1 (t); wherecu is defined in (9).
- 3
The desired pair is (x1,x2)=(Q˜;n(u),R˜;n(v)) where Q˜;n and R˜;n according to (5), are the estimated and smoothed quantile functionsX1 ofX2 and, respectively.
For the multivariate case we must solve equations that represent conditional distribution functions for W given U=u,V=v.
To simulate replications from the random vector with the dependence structure estimated from the observed data S:={(x11, x21, x31), ..., (x1n, x2n, x3n)} it is applied the next algorithm.
Sampling trivariate algorithm- 1
Generate three independent and continuous Uniform (0, 1) random variablesu andt1, t2
- 2
Setv=cu-1 (t1) wherecu is defined in (9).
- 3
Setw=cuv-1 (t2) where
where is the trivariate Bernstein copula model (8).
- 4
The desired vector is (x1,x2,x3)=(Q˜;n(u),R˜;n(v),H˜;n(w)) where Q˜;n(u),R˜;n(v) and, H˜;n(w) according to (5), are the estimated and smoothed quantile functions ofX1,X2, yX3, respectively.
To perform stochastic simulations of a primary variable it is applied a method widely used in geostatistics, the Simulated Annealing method, which is a global optimization framework where we can add restrictions to simulation. In this case, in addition of using multivariate dependence by sampling the copula model, a spatial correlation function (a variogram) for the secondary variable is imposed. Additionally, if any raw data of the primary variable is available, it can be exactly honored, that is, the method can be conditional.
A more detailed explanation of each single step of simulated annealing method, as well as technical terminology, can be found in Dreo et al. (2006), Dafflon et. al., (2009a, 2009b), Dafflon and Barrash (2012), Hernandez-Maldonado et al. (2012), Deutsch (2002). In this work, we will just briefly mention its steps.
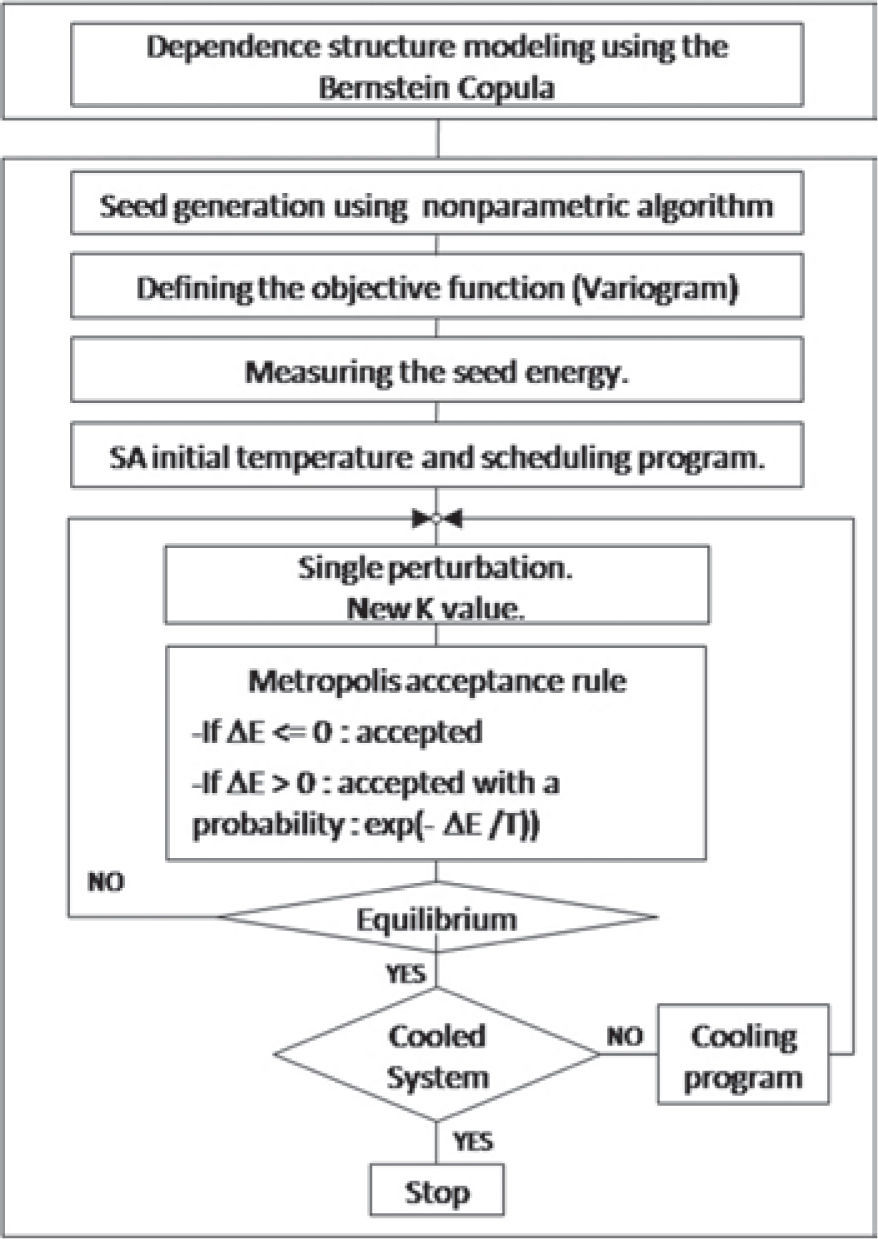
a. Generating an initial configuration, known as “seed”. An initial configuration is the starting point of the simulation, also, it can be considered as a “possible solution” of the spatial disposition of the primary variable. There are some ways of proposing this configuration, see Deutsch (2002), Dréo et al. (2006). One of most popular of them is just proposing random numbers with uniform distribution. We decided to use the multivariate Bernstein copula sampling algorithm (section 3.1.1) to obtain this starting point in order to have a better approximation of the final solution.
b. Defining the objective function. Since we use the Bernstein copula we do not have to include univariate histograms into the objective function because they are reproduced automatically; in the same way, as Bernstein copula models the dependence structure between variables, it is not necessary to include neither a correlation coefficient. In other words, in order to satisfy the spatial distribution of the primary variable, we are able to propose an objective function that consists only in one term (11) the variogram function
Where:
c. Measuring the initial configuration energy. By (12), it is calculated the variogram of the initial configuration and it is compared to the variogram of the real configuration (11), this value is the energy of the starting point, and the main idea is that it must be decreased during the simulation procedure, see Deutsch (2002). This step gives us an idea of the seed´s quality, if we use random numbers to generate it, its measured energy will be very high, however, as long as this method uses a sample given by the Bernstein copula the initial energy is significantly small.
d. Obtaining the initial temperature and the annealing schedule. The initial temperature is obtained by (13):
The annealing schedule is obtained following the procedure proposed by Dréo et al. (2006).
e. Ending up a realization. The simulation ends whenever the objective function error is reached, or an accumulation of 3 stages without change occurs, or when the maximum number of attempted perturbations is reached.
It is shown a diagram of the method to perform multivariate stochastic simulations in, Figure1.
Case studyIt will be modeled the Permeability of double porosity carbonate formations of a South Florida Aquifer in the western Hillsboro Basin of Palm Beach County, Florida. Based in the algorithm described in Section 3, we propose a copula-based approach to model the relationship between permeability, porosity and Shear Wave Velocity (S-waves). The dependency model obtained will be then used to stochastically simulate permeability using Porosity and Shear Wave velocity.
Data descriptionThe characterization of this aquifer for the borehole and field scales is given in Parra et al. (2001), Parra and Hackert (2002), and a hydrogeological situation is described by Bennett et al. (2002). The interpretation of the borehole data, the determination of the matrix and secondary porosity and secondary-pore types (shapes of spheroids approximating secondary pores) were presented by Kazatchenko et al. (2006), where to determine the pore microstructure of aquifer carbonate formations the authors applied the petrophysical inversion technique that consists in minimizing a cost function that includes the sum of weighted square differences between the experimentally measured and theoretically calculated logs as in Kazatchenko et al. (2004).
In this case the following well logs were used for joint simultaneous inversion as input data: resistivity log, transit times of the Pand S-waves (acoustic log), total porosity (neutron log), and formation density (density log). To calculate the theoretical acoustic and resistivity logs the double-porosity model for describing carbonate formations was applied: Kazatchenko et al. (2006).
This model treats carbonate rocks as a composite material that consists of a homogeneous isotropic matrix (solid skeleton and matrix pore system) where the secondary pores of different shapes are embedded. The secondary pores were approximated by spheroids with variable aspect ratios to represent different secondary porosity types: vugs (close-to-sphere shapes), quasi-vugs (oblate spheroids), channels (prolate spheroids), and microfractures (flattened spheroids) Kazatchenko et al. (2006).
We used the results of inversion obtained by Kazatchenko et al. (2006) for carbonate formations of South Florida Aquifer that includes the following petrophysical characteristics: matrix porosity, secondary vugular and crack porosities (Figure 2).
The secondary-porosity system of this formation has complex microstructure and corresponds to a model with two types of pore shapes: cracks (flattened ellipsoids) with the overall porosity of 2% and vugs (close to sphere) with the porosity variations in the range of 10-30%.
Statistical data analysisGiven multivariate data, it is common to start choosing as explanatory variables those who exhibit higher dependence with the variable that is to be explained. We measured the dependence between the petrophysical properties in terms of the dependence index Φ proposed by Hoeffding (1941), which satisfies all desirable properties for a dependence measure for continuous random variables, see Nelsen (2006).
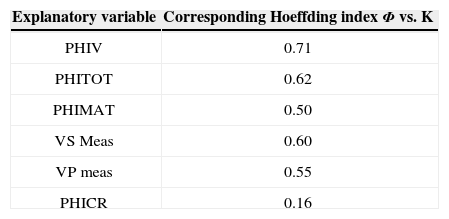
From all possible explanatory variables (PHITOT, PHIMAT, PHICR, PHIV, VS Meas, VP meas) for permeability (K), for the first explanatory random variable it was chosen relative vugular porosity (PHIV) since it exhibited the highest dependence Φ (PHI, K)=0.71 (on a [0,1] scale). In choosing a second explanatory random variable we need, in addition, to have a high dependence with permeability, and the lowest possible dependence with the first explanatory variable (PHIV), otherwise it would mean that it is quite similar to it and it will add no significant information to what the first one already can provide. Under this criteria, the second best choice was Share Wave Velocity (VS meas), with Φ (VS meas, K)=0.60 and Φ (PHIV, VS meas)=0.55
]Table 1 shows all dependence index Φof explanatory variables that are the results of inversion obtained by Kazatchenko et al. (2006); Total porosity (PHITOT), Matrix porosity (PHIMAT), Crack porosity (PHICR), Vugular porosity (PHIV), Share Wave Velocity (VS Meas), P-Wave velocity (VP meas).
Dependence index Φ, Hoeffding (1941), for possible explanatory variables (PHITOT, PHIMAT, PHICR, PHIV, VS Meas, VP meas).
| Explanatory variable | Corresponding Hoeffding index Φ vs. K |
|---|---|
| PHIV | 0.71 |
| PHITOT | 0.62 |
| PHIMAT | 0.50 |
| VS Meas | 0.60 |
| VP meas | 0.55 |
| PHICR | 0.16 |
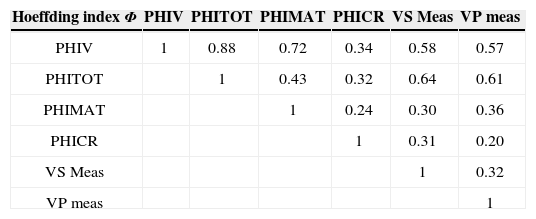
In table 1 explanatory variables are shown, using this information we confirm that PHIV has the highest dependence, but following the order of this table we should use as second explanatory variable PHITOT. We did not make this choice because, as we said before, a second explanatory variable needs to have a high dependence with permeability, and the lowest possible dependence with the first explanatory variable (PHIV). To see this behavior in table two we show the explanatory variables matrix dependence Hoeffding index.
We have chosen PHIV as the first explanatory variable; it means we must pay attention to the first line of table 2, and select the variable with the lowest dependence to PHIV. It should be PHICR but in Table 1 we see that this property offers poor information about K. Finally, we may choose VP meas but, VS Meas explains K in some better way (Table 1).
Hoeffding dependence index Φ matrix, for possible explanatory variables (PHITOT, PHIMAT, PHICR, PHIV, VS Meas, VP meas).
| Hoeffding index Φ | PHIV | PHITOT | PHIMAT | PHICR | VS Meas | VP meas |
|---|---|---|---|---|---|---|
| PHIV | 1 | 0.88 | 0.72 | 0.34 | 0.58 | 0.57 |
| PHITOT | 1 | 0.43 | 0.32 | 0.64 | 0.61 | |
| PHIMAT | 1 | 0.24 | 0.30 | 0.36 | ||
| PHICR | 1 | 0.31 | 0.20 | |||
| VS Meas | 1 | 0.32 | ||||
| VP meas | 1 |
In Figure 3 it is shown a scatter-plot distribution and histograms of PHIV–K sample Explanatory data taken from Kazatchenko et al. (2006), it shows their bivariate distribution. In Figure 4 it is shown a scatter-plot distribution and histograms of VS meas–K data values
Bernstein Copula ModelIt is modeled the trivariate Bernstein Copula using relative vugular porosities (PHIV), Shear Wave Velocity (VS meas=velocity of S-waves measured) and K as absolutely continuous random variables X1, X2 and X3, with unknown theoretical univariate distribution functions F1, F2and F3, see(2). Observations of this random vector were obtained fromKazatchenko et al. (2006).
We use (2) to estimate the empirical distribution function for each variable; however; in order to model them as continuous random variables they should be smoothed using (5), since (2) is not appropriate because Fˆj is a step function and therefore discontinuous. The trivariate Bernstein copula model (8) will be used to sample data to stochastically simulate permeability.
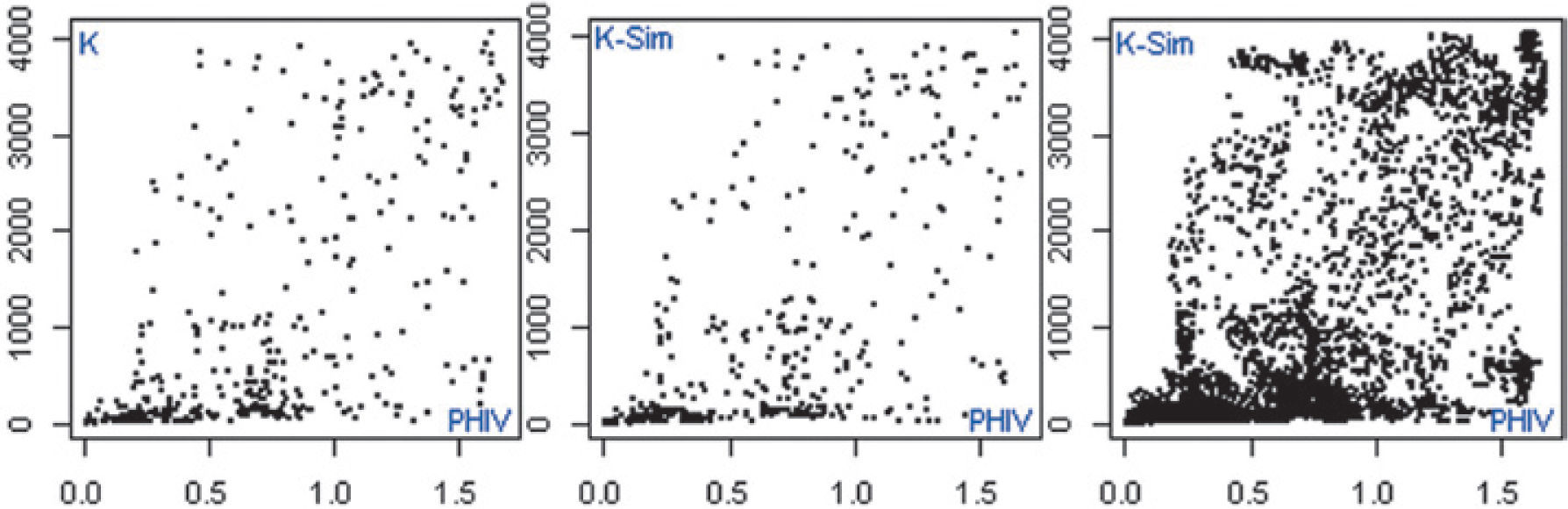
Sampling from Bernstein copulaIn Figure 5 (left side) it is shown a scatterplot distribution and histograms of porosity– permeability real data (sample size of) taken from Kazatchenko et al. (2006). At the center of the same figure, it is shown a trivariate simulation of permeability values using vugular porosity and shear wave velocity as explicative variables. If we do not label these two scatter plots it would be difficult to know which one of them is the original one. In this case the multivariate Bernstein copula provides an acceptable the dependence structure for continuous variables with complex relationship. The right side of Figure 5 shows 3800 simulated values of permeability, according to some analysis, it shows more clearly percolation patterns.
Permeability simulations and discussionIn this section spatial simulation will be performed using simulated annealing technique. Since multivariate dependence is modeled by the Bernstein copula, a spatial correlation function (the variogram) will be used as an objective function in the annealing algorithm.
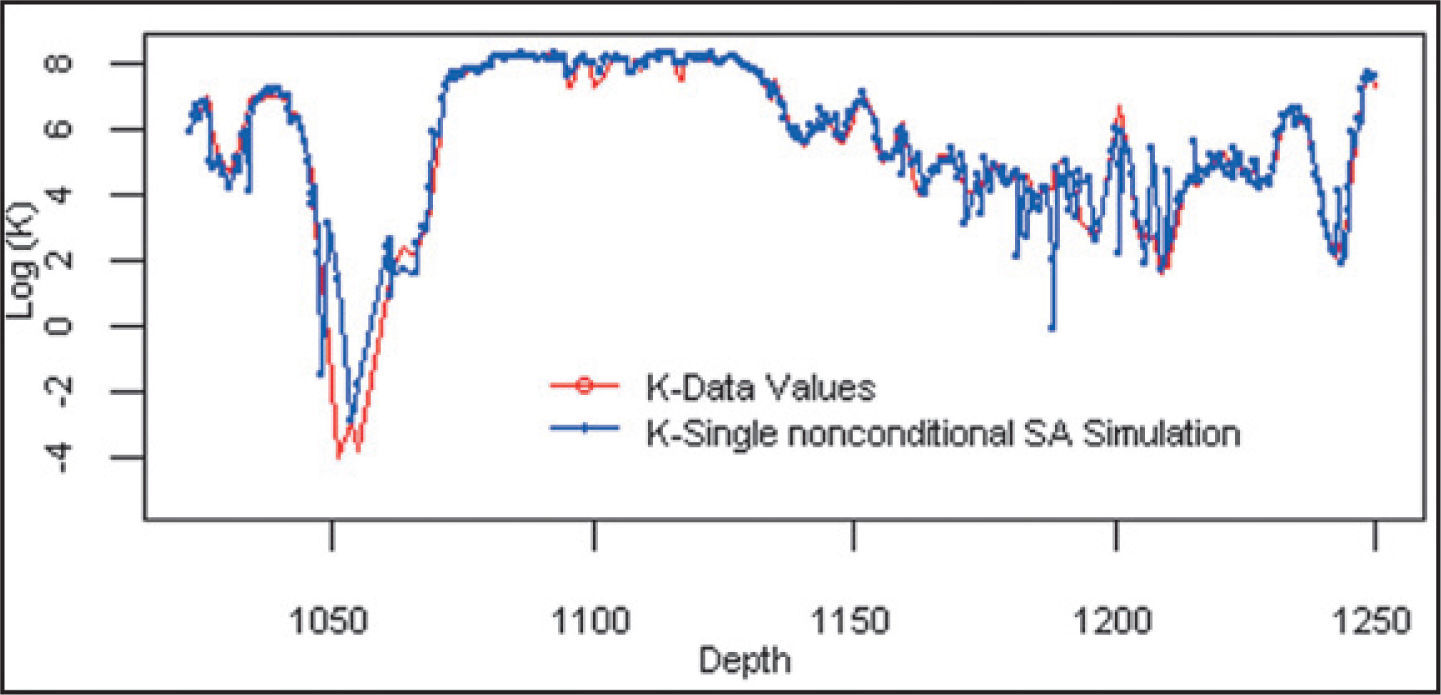
We propose a copula-based nonparametric approach and simulated annealing technique to model the spatial distribution of permeability using as secondary variables, porosity and shear wave velocity (S-waves). In Figure 6 we can see a single nonconditional spatial simulation of permeability (K) in terms of depth. As we note the simulation (blue line) follows very close the real data behavior (red line), this is because we introduce more descriptive information into the Bernstein copula model. However, there is still a small-scale variability which does not exist in the original data values.
As a descriptive measure of the goodness of fit of predicted values of log-permeability (Log K) given values of the explanatory variables PHIV and VS meas, we calculated the Mean Squared Error (MSE) in each case:
where a lower value of MSE represents a better goodness of fit.
The simulated values of log K, given PHIV and VS meas (log K | PHIV, VS meas), show a MSE value of 0.5, which is very low compared to that obtained by Deutsch and Cockerham’s method (1994), which MSE value is 7.76; also it is lower than the obtained one by Díaz-Viera and Casar-González method, where the MSE value is 5.5, details are shown in Hernandez-Maldonado et al., (2012). Finally, the MSE value for the trivariate copula simulation is lower than the MSE value of the bivariate copula simulation (log K | PHIV)(14), consequently it means that trivariate simulation has the best fitted values.
In terms of histograms, scatterplots and variograms, the proposed method shows very good agreement with the original data values. As we are using three variables, the scatterplots of permeability can be seen in terms of K-PHIV (Figure 7) and K-S-waves (Figure 8). The scatterplots of the original data values are shown in Figure 3 and Figure 4 respectively.
The variogram of the simulation (Figure 9) and its fitted model (Table 3), also shows good agreement with respect to real data (Figure 10). We can note that both variograms are almost equal, but in a detailed view, the empirical variogram of the simulated values is a little softer than the original one.
As we could anticipate, the dependence structure between these three petrophysical properties is well represented. The extreme values, and in general, all of most important statistics are quite well reproduced, (Figure 11). In order to reduce small-scale variability seen in Figure 6, a median of 10 nonconditional SA simulations was performed, Figure 12. Once again, the spatial structure, the histograms and the Scatter-plot reproduction shows a very good agreement respecting to real data, see also Figure 13 and Figure 14.
In Figure 12 we can see that for small values of K the simulation is not following real data values too closely, there are two reasons. First, this “behavior” is observed in all simulation methods that were performed in order to compare the simulated values for the bivariate case of this proposal [Hernandez-Maldonado et al., (2012)]. In that work the most accurate results were shown by Bernstein copula. In this particular case is hard to have a simulation that follow too closely the behavior of the real data values, because there is very little information. And second, this is a median value of 10 different simulations, which means that each simulation has different degrees of accuracy, which is normal.
Figure 15 shows the variogram of this simulation and its fitted model. In contrast to Figure 10 (real data values) we can see that this method represents very well, the spatial structure of permeability.
The values of the variogram model for a single simulation and the median of 10 simulations are very close to the real data as well (Table 3). The same happens with their most important statistics (Figure 16).
Using (16) we can see that the MSE values between the real data and these nonconditional simulations are very similar (Table 4). It is an indicative that it is not necessary to perform many simulations to smooth the small-scale variability, and may be unnecessary.
Finally we perform conditional simulations and compare the MSE values in order to study the effect of different percentage of conditioning values. Figure 17 shows the results of the spatial distribution of the permeability in various percentages of conditioning values, from top to bottom order, it is conditioned to 10 percent, 50 percent and 90 percent of the conditioning data values. Note that results are, graphically, very similar to real data and their MSE values as well (see Table 5). This shows that the proposed method in a multivariate fashion does not require big amounts of conditioning data to have consistent results.
The Bernstein copula (8) requires that the empirical copula be ready to be used all the time, hence, it is necessary to propose an efficient and fast algorithm in terms of data storage and computing speed to implement a multidimensional copula. We propose a procedure to efficiently implement a multidimensional empirical copula. Shortly described, this procedure fundamentally solves the two main disadvantages of using nonparametric copulas: it avoids redundant calculation, which increases its speed and just needs to storage the most important values of the generated hypercube.
Of course the method can be extended to more dimensions, but the purpose of the article is to show its application to a well log scale, where we have more control and better data quality. Its application to more dimensions will be the subject of future work.
ConclusionsFrom a methodological point of view, a multivariate copula approach provides a very flexible tool to model complex dependence relationships of petrophysical properties, such as porosity, permeability and shear wave velocity, without imposing strong assumptions of linearity or log-linearity, and/or normality when we are modeling them as random variables.
All the information about the dependence structure is contained in the underlying copula, and its estimation is being used, instead of the extreme information reduction that is done by the use of numerical measures such as the linear correlation coefficient, which under the presence of nonlinear dependence may become useless and/or quite misleading, see Embrechts et al. (1999, 2003). For this reason it is very important to extend the method to higher dimensions, because if we have more than one relevant explanatory variable, we may use this tool to take them into account.
The main advantage of the methodology used in this work is that it represents a straightforward way to perform nonparametric simulations, conditional and nonconditional. As we have said in the results of the application of this method, including more than one explanatory petrophysical property to leads to more accurate results. Consequently, it will not be necessary to perform many simulations (Figure 6 vs. Figure 12) or conditioning with high quantities of data values (Figure 17) to obtain acceptable results (Table 5).
This method has an important improvement with respect to the bivariate case, not only because it provides better results, but also it reduces the number of simulations to decrease the small scale variability. In other words it is not necessary to perform 10 or more simulations. Even more, it is not necessary to have a great number of conditioning values; the conditioned simulations did not show a lot of variation in terms of MSE values.
For future work, we think we can use a Bernstein copula to explore complex relationships between petrophysical properties and then fit, if possible, a semiparametric gluing copula, Siburg and Stoimenov (2008). Also, we consider we may use another optimization method which could give improved results, for example, we can implement genetic algorithms or Estimation of Distribution Algorithms (EDAs). It is very important to remark that the use of multivariate copulas leads to significant serious computational challenges, for this reason it is necessary to propose better ways to calculate them, for example parallel computing.
The present work was partially supported by the two following projects: IN110311 from Programa de Apoyo a Proyectos de Investigación e Innovación Tecnológica (PAPIIT) at Universidad Nacional Autónoma de México, and by 116606 (Y.00102) from Fondo Sectorial CONACYT-SENER-Hidrocarburos.