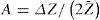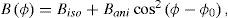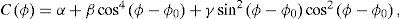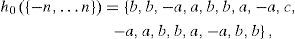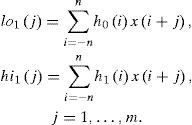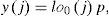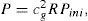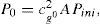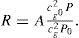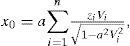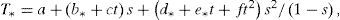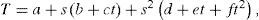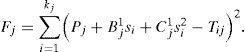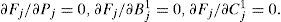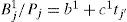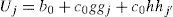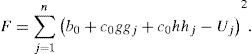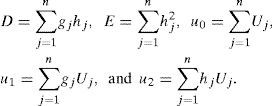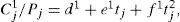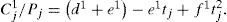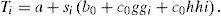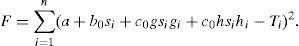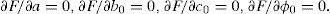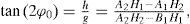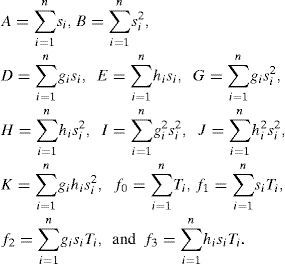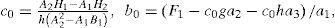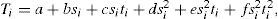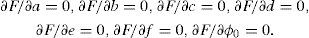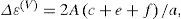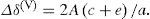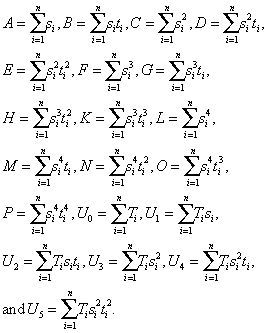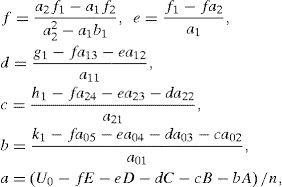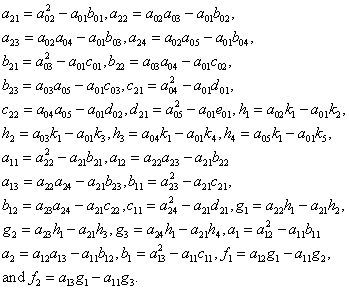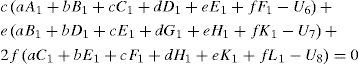AVOA techniques for fracture characterization

Resumen

Se tomaron en consideración distintos aspectos de algunas técnicas computacionales para el análisis AVOA (Amplitud Versus Offset y Azimut), para la composición de fracturas, en particular: utilizando amplitudes en lugar de coeficientes de refección, suavizando los datos sísmicos y el método de la estimación numérica para calcular la dirección. Se estimó un nuevo método de cálculo y se indica un nuevo método suavizado. Se compararan distintos métodos de cálculo en los datos sintéticos de superficie de reflección, con y sin ruido. Se obtuvieron propiedades de los métodos numéricos, dependientes de conjuntos distintos de los azimut y los offset. Se muestra una superioridad del nuevo método.

Abstract

Different aspects of computational techniques for AVOA analysis (Amplitude Versus Offset and Azimuth) for fracture characterization are considered, in particular: using amplitudes instead of reflection coefficients, smoothing seismic data, and numerical methods for estimation of fracture directions. A new computational method and a new filter for smoothing are suggested. The different computational methods are compared in synthetic reflection surface data with noise, and without noise. Properties of the numerical methods in dependence on different sets of azimuths and offsets are obtained. It is shown a superiority of the new method.

Introduction

The analysis of azimuthal variation in reflection coefficients, or AVOA analysis (Amplitude Versus Offset and Azimuth), is widely applied for detecting and mapping highly fractured zones with azimuthally-oriented vertical cracks (Mallik et al., 1998; Jenner, 2002; Sabinin & Chichinina, 2008). The AVOA techniques are based on the Rüger (1998) approximation for the reflection coefficients in HTI medium, and give principal symmetry directions of HTI medium.

Here, the computational aspects of AVOA techniques are considered, namely, applying amplitudes instead of reflection coefficients, smoothing the amplitudes, an incidence angle estimation, methods for obtaining the symmetry-axis angle, synthetic data for testing techniques, and a numerical experiment for investigating properties of the techniques. A new computational method for obtaining the symmetry-axis angle and a new filter for smoothing are suggested. All considered techniques are compared in synthetic anisotropic seismic data with noise, and without noise. The suggested new technique proved better than the others.

Background

The methodology of AVOA analysis is based on the concept of azimuthal anisotropy caused for the most part by parallel vertical fractures. It leads to the azimuthal anisotropy of amplitudes, in particular, to azimuthal variation in reflection coefficients. Let a fractured reservoir be represented by a model of a transversely isotropic medium with horizontal symmetry axis (HTI medium). The PP-wave reflection coefficient R at the interface (or at the reflecting boundary) between weakly anisotropic HTI media (or between an isotropic medium and an anisotropic HTI medium) is defined by the approximate formula (Rüger, 1998):

where θ is the incidence angle, and ϕ is the source-receiver-line azimuth with respect to the coordinate axis x. The term A is the normal-incidence reflection coefficient

where Z≡ρVP‖ is the vertical P-wave impedance, VP‖ is the vertical velocity (or velocity in the isotropy plane) of the P-wave, ρ i s density, Δ denotes the difference between the values of a parameter below and above the reflecting boundary, and the bar … indicates average of these values. VP‖=VP in the isotropic media.

The coefficient B(ϕ) is a so-called AVO gradient, which can be written (Rüger, 1998) as

where ϕ₀ is the angle of the symmetry axis with the x−-axis. The term B_iso is the AVO-gradient isotropic part (equal to the AVO gradient for isotropic media), and B_ani is the anisotropic part of the AVO gradient.

The coefficient C(ϕ) can be written (Rüger, 1998) as,

where α≡ΔVP‖/2V¯P‖,β=12ΔεV, and γ=12ΔδV.

Above, Thomsen-style anisotropy parameters ε^(V), and δ^(V) are negative for HTI media, and they are equal to zero for isotropic media.

The main problem of AVOA analysis is to estimate the symmetry-axis angle ϕ₀ from surface seismic data of amplitudes using numerical techniques.

The techniques of AVOA are based on equations (1) – (4). Note that equation (1) is intended for calculation of reflection coefficients, while in real data, one operates with amplitudes of reflected waves, not with reflection coefficients. This brings some problems which are discussed in the next section.

Using amplitudes instead of reflection coefficients

While the background of AVOA analysis is based on Rüger's equation for the reflection coefficient (1), in real data, AVOA analysis should use signal amplitudes. It is true that the amplitude is not equal to the reflection coefficient. Moreover, no picked instantaneous amplitude (sample) in the signal can be used instead of the reflection coefficient because the signal changes its form during propagation for many reasons. It seems that one should use an integral amplitude characteristic of the signal which adequately corresponds to the reflection coefficient. Let's call this characteristic simply by amplitude and denote it as P.

The estimated value of ϕ₀ is very sensitive to the definition of P, especially for data with noise. I suggest the following procedure for definition of P which gives good and stable results. The procedure calculates an average value of a signal envelope in a time window. In calculating the envelope, the Fourier transform of this signal is used: F = F₊ + F₋, where F is spectrum, F₊ is the part of spectrum corresponding to positive frequencies (ω ≥ 0), and F₋ is the part of negative frequencies. The envelope of the signal is given by the absolute value of inverse Fourier transform of the spectrum with double F₊, and F₋ ≡ 0 (Sheriff & Geldart, 1983).

The sign of envelope is positive; therefore this approach is applicable only to seismograms with the constant sign of reflection coefficient in dependence on offset.

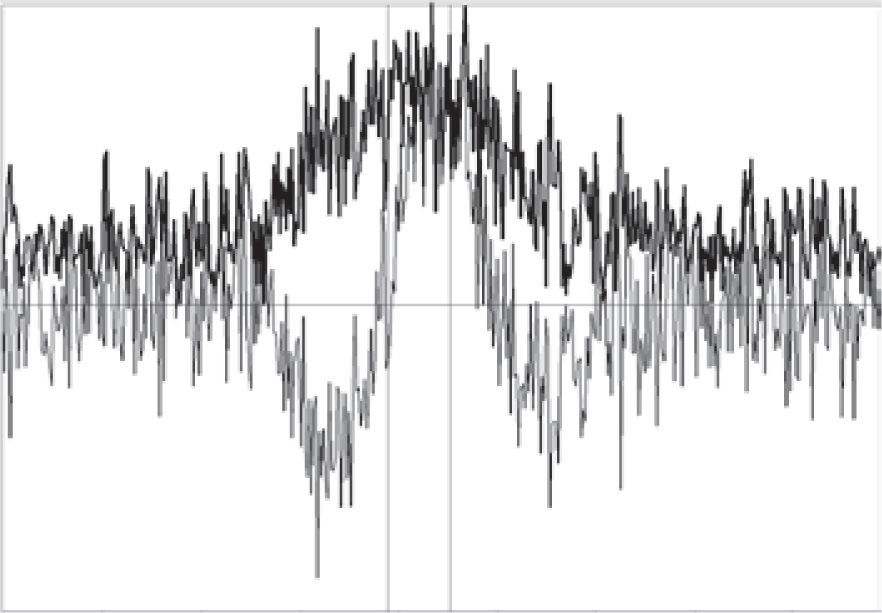
For data with noise, the envelope is noisy, too (see Figure 1). Therefore, smoothing is necessary.

Figure 1.

A signal with noise (thin line) in time, and its envelope.

For smoothing, an algorithm of discrete transformations of wavelet by filters is applied. Four symmetric filters are constructed for it: the low-pass (h₀) end high-pass (h₁) analysis filters, and the low-pass (h₂) and high-pass (h₃) synthesis filters. The right-hand part of h₀ consists from the filter derived by Abdelnour & Selesnick (2004). The left-hand part of h₀ is symmetric to it. That is

where a=M/32,M=2/2,b=4a, and n = 8. The central value is c = 1−M.

The high-pass analysis filter is constructed by formula h₁(i) = (− 1)ⁱh₀ (n − i + 1) for i ≠ 0, and h_l (0) = 0. The synthesis filters are calculated by formula h₂(i) = (− 1)ⁱh₁ (i),h₃ (i) = (− 1)ⁱh₀ (i), see (Abdelnour & Selesnick, 2005). The central values are h₂ (0) = c and h₃(0) = 0.

The smoothed signal is obtained by the decomposition algorithm; see Figure 2 (WSBP, 2012).

Figure 2.

The 3-stage decomposition algorithm.

The input signal is x(j), j = 1,…,m, m > > 2n. It is decomposed into low and high components lo₁(j) and hi₁(j) in the first stage:

In the next stages (s = 2,…, S), the each low component lo_{s - 1}(j) is decomposed by the same analysis filters.

After all stages of decomposition finishing, the stages of applying the synthesis filters are fulfilled in reverse order (s = S, S - 1,…,1):

The output signal y (j) is obtained finally:

where the fitting amplitude coefficient p can be approximately estimated by the formula p = 1+0.057S, where S is the number of stages.

The advantage of this variant of discrete transformation algorithm in comparison with (WSBP, 2012) is the absence of shift functions in it due to applying the fully symmetric filters (i=-n,…,n).

It must be noted that the algorithm gives unsatisfactory results at the edges of the signal because of truncating the filters in 2n edge points. Therefore, it is necessary m >> 2n.

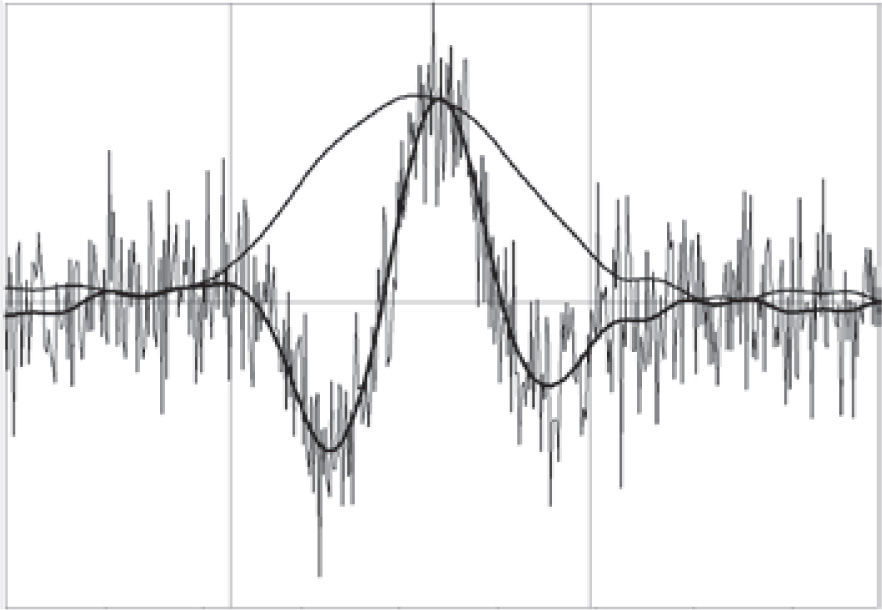
The result of smoothing the signal of Figure 1 by the 3-stage algorithm is presented in Figure 3. The smoothness of resulting curve increases with increasing S. Also with increasing S, the algorithm slightly deforms the resulting impulse in comparison with the parent impulse without noise. Optimum in the smoothness and in the conservation of form is observed at the value S = 3.

Figure 3.

The signal with noise (thin line), the smoothed signal (thick line), and the envelope of smoothed signal.

The limits of time window for calculating P with the help of envelope can be chosen by different ways. I use the following way. From the envelope of signal e(t), the maximum e_m and nearest local minimums, left e_l and right e_r, are calculated. The left limit of the time window is set in the point where e = e_l + 0.15(e_m−e_l), and the right limit – where e = e_r + 0.15(e_m−e_l), see vertical lines in Figures 1, 3. Obviously, this algorithm correctly works only with smoothed signals.

Equation (1) should be rewritten for using the amplitudes. If the source and the receivers are at the earth surface, then the amplitude of reflected PP-wave can be expressed as

where c_g is the coefficient of geometrical spreading (divergence) from source to reflection point for this wave, c_g = c_g (θ, ϕ), P_ini is the amplitude of the source (the initial amplitude), and R is the reflection coefficient, R = R(θ, ϕ) in the equation (1).

The amplitude for the normal-incidence wave can be written as

where c_g0 is the normal-incidence coefficient of geometrical spreading, which does not depend on (θ, ϕ), and A is the normal-incidence reflection coefficient, A = const, see equations (1) - (2). Then the reflection coefficient can be expressed as

Therefore the equation (1) for the reflection coefficient R transforms into the following equation for the amplitude P:

where m = P₀/A, and r_g ≡ (c_g0 / c_g)². This equation should be used in the AVOA techniques instead of (1).

Note that c_g can be expressed as c_g = c(θ, ϕ)/r in 3D space, where r is a half of travel path from source to receiver, and c depends on the direction of wave propagation (for isotropic media, c = const). In assuming a weak anisotropy, one may assume a weak dependence of geometrical spreading on incidence angle: c ≈ const for a given source-to-receiver line with azimuth ϕ. Then, for a homogeneous medium above the reflecting boundary,

where z is the normal-incidence ray path, and c_g0 ≡ c / z. It is the approximate formula for divergent correction.

Also for multilayered media, the expressions for divergence correction can be found from Newman (1973). A practical methodology for the P-wave geometrical-spreading correction in layered azimuthally anisotropic media can be found from Xu & Tsvankin (2004).

The incidence angle estimation

In the case of n isotropic layers above the reflecting boundary, one can obtain the incidence angle θ = θ_n from a solution of the following non-linear equation for a:

where x₀ is the half of offset, z_i is the thickness of i-th layer, V_i is the velocity in i-th layer, and sin (θ_n) = aV_n. For calculating the geometrical spreading, the travel path r=∑i=1nzi1−a2Vi2.

In the case of the reflecting boundary being the lower boundary of anisotropic layer, the problem is more complicated because the last layer is anisotropic, and the velocity V_n depends on θ_n in it and is not known beforehand.

The problem can be solved by Sabinin (2012). An advantage of his method is that the value V_n in the anisotropic layer is unnecessary for calculating angle θ_n and path r. However, it uses additionally the impulse from the upper boundary of anisotropic layer what complicates the technique. It gives results not sufficiently better than the method (8). Therefore, I use the simple method (8) here with setting an approximate value of V_n.

The methods for estimation of symmetry axis angle by AVOA

Usually, 3D seismic data used in AVOA analysis are received from a system of receivers and sources spacing in nodes of a rectangle grid at the surface. The symmetry axis angle is calculated for a small square (for a bin) including a node of the grid, by using seismic traces which have the Common Middle Point (CMP) located in this bin. If such traces are few, then neighbor bins are combined into a superbin, and calculations are made for it. Therefore, a preliminary stage of the estimation is an extraction of seismic traces of the superbin from the seismic data for taking them into consideration.

For numerical methods of estimation of symmetry axis angle, one can use equation (6) as in Rüger's form:

as in the power form:

where T_* = r_gP (θ, ϕ), T = (1−s)T_*, s = sin²θ, t = cos² (ϕ−ϕ₀), a = P₀, b_* = mB_iso, b = b_*−a, c = mB_ani, d_* = mα, d = d_*−b_*, e_* = mΔδ^(V)/2, e = e_*−c, f=mΔε^(V)/2−e_* and m = P₀/A.

The methods vary by simplifying ways applied, and can be separated into Sectored methods (S and SR), Linear methods (L and LR), and General method (G), where the letter ‘R’ denotes that the Ruger's form (9a) is used instead of (9b).

Sectored methods

The method SR was suggested by Mallik et al. (1998) for the case of three azimuths with using equations (1), and (3). It took its perfect form in the work by Sabinin & Chichinina (2008) who used equations (6), (3), and (4). For this method, the traces of superbin are sorted by n azimuthal sectors. It is adopted that all traces of the sector have the same value of azimuth equal to the middle azimuth of the sector. Because of this, sectored methods introduce in ϕ₀ an own error no more than a half of the sector size.

Here, the method S applied to equation (9b) is presented. If in the sector of azimuth ϕ (j = 1, …, n), there are k_j traces with incidence angles θ_j (i = 1,…, k_j) in the last layer above the target boundary, then one can write from (9b) for this sector j:

where T_ij is the value T calculated from the trace i in the sector j. In each sector, Bj1=mjBj,Cj1=mjCj where m_j = P_j/A, and Pj,Bj1,Cj1 are the fitting constants.

Having T_ij and θ_i for all i in the sector j (k_j ≥ 3), one can calculate s_i = sin²θi, and then P_j, Bj1, and Cj1 from (10) by the least-squares method. For this, it is minimized the functional of error for each sector j:

For minimizing F_j, it is necessary to solve the system of three equations:

It gives: Cj1=b1f1−a1g1b12−a1c1,Bj1=f1−Cj1b1/a1, and Pj=u0BCj1−ABj1/kj, where a1=A2−Bkj,b1=AB−Ckj,c1=B2−Dkj,f1=Au0−u1kj,g1=Bu0−u2kj,

These calculations should be made for all sectors.

Then, the unknown value φ₀ can be obtained from the system of equations of type (3), see (9b):

where j = 1, …, n, and t_j = cos²(φ − φ₀). The unknown constants b¹, and c¹ have a sense: b¹A = B_iso − A, and c¹A = B_ani.

Equation (11) is transformed into more convenient form:

where Uj=Bj1/Pj, b₀ = b¹ + 0.5c¹, c₀ = 0.5c¹, g = cos(2φ₀), h = sin(2φ₀), g_j = cos(2φ_j) and h_j = sin(2φ_j).

The system (12) has three unknowns (b₀, c₀, and φ₀), therefore it should be n ≥ 3 for obtaining solution. The system (12) has two solutions (two φ₀ differing in π/2, and two c₀ of opposite signs, correspondently), and is solved by the least-squares method, too. It is minimized the functional of error:

The following system of three equations should be solved:

It gives: tan2ϕ0≡hg=b1f1−a1f2b1f2−c1f1, c₀ = f₁/(ga₁ + hb₁), and b₀ = [u₀ − c₀(Ag + Bh)]/n, where a₁ = A² − Cn, b₁ = AB − Dn, c₁ = B² − En, f₁ = Au₀ − u₁n, f₂ = Bu₀ − u₂n, A=∑j=1ngj,B=∑j=1nhj,C=∑j=1ngj2,

The condition for distinguishing symmetry-axis from fracture-strike directions is derived by Sabinin & Chichinina (2008), and uses equation (4). Here it is presented in more general form.

In terms of equations (9b), (10), and (11), equation (4) can be written as

where j = 1, …, n, d¹ = (α − B_iso)/A, e¹ = (Δδ^(V)/2 − B_ani)/A, and f¹ = (Δε^(V) − Δδ^(V))/(2A).

When substituting the value φ0±π2 instead of φ₀ into equation (14), the sign of the second term e¹t_j switches to the opposite sign, because equation (14) takes the form

The last term of equation (11)c¹t_j switches its sign, too. One can combine Δδ^(V) = 2A(c1 + e¹) from definitions to equations (11), (14), and conclude that the sign of Δδ^(V) is switched, too. For calculating Δδ^(V), it should be solved system (14) which is similar to (10) by the method of solution.

If the HTI layer is situated between isotropic layers then Δδ^(V) must be negative for upper reflecting boundary of the HTI layer, and positive for lower boundary. If the calculated value of Δδ^(V) has this sign then φ₀ is the symmetry-axis angle. In opposite case, it is the fracture-strike direction.

It must be noted that Δε^(V) = 2A(c¹ + e¹ + f¹), and also can be used for distinguishing solutions because ε^(V) and δ^(V) have the same sign.

The formal condition that the second derivative of functional (13) must be positive in the minimum of functional can also be applied. Because of errors in data, it should be used as an additional condition to previous ones, and should have a form ∂2F/∂ϕ02> a small value.

Linear methods

The method LR was suggested by Jenner (2002) for equation (1). It is not needed in sectoring data. All traces of superbin are taken into consideration together.

Here, it is applied to equation (9b), the method L. Equation (9b) is truncated after a line part respecting s. If the superbin has n traces(i = 1, …, n), with incidence angles θ_i at the target boundary, and with azimuthal angles φ_i, then one can write the result of truncation in the form:

where T_i is the value T calculated from the trace i, s_i = sin²θ_i, b₀ = b + 0.5c, c₀ = 0.5c, g = cos(2φ₀), h = sin(2φ₀), g_i = cos(2φ_i), and h_i = sin(2φ_i).

The values s_i, g_i, and h_i are known because they can be calculated from headers of seismograms and parameters of medium. Let us consider the functional of error:

Functional F must be minimized over parameters a, b₀, c₀, and φ₀. For this, it is necessary to solve the system of four equations:

Solution of system (17) gives the equation for obtaining φ₀:

where A1=a1b1−a22,B1=a1c1−a32, A₂ = a₁b₂ − a₂a₃, H₁ = F₂a₁ − F₁a₂, and H₂ = F₃a₁ − F₁a₃ in which a₁ = nB − A², b₁ = nI − D², c₁ = nJ − E², a₂ = nG − AD, b₂ = nK − ED, a₃ = nH − AE, F₁ = nf₁ − Af₀, F₂ = nj₂ − Df₀, and F₃ = nf₃ − Ef₀, and finally:

The other parameters are:

and a = (f₀ − b₀A − c₀gD − c₀hE)/n.

From (18), one can see that the solution φ₀ has a period of π2. This value of the period means that we must use an additional condition for understanding what value φ₀ is the symmetry-axis azimuth. This condition may be B_ani > 0 if V_S / V_P > 0.56 (Chichinina et al., 2003). In general case, it can be the condition ∂2F/∂ϕ02> a small positive value, where F is the functional of error (16).

General method (G)

The method is constructed by analogy with the GM method by Sabinin (2013). It is not needed in sectoring, too. All traces of superbin are taken into consideration together. If the superbin has n traces (i = 1, …, n), with incidence angles θ_i at the target boundary, and with azimuthal angles φ_i, then equation (9b) can be written as:

where T_i is the value T calculated from the trace i, s_i = sin²θ_i, and t_i = cos²(φ_i − φ₀).

Let us consider the functional of error:

Functional F must be minimized over parameters a, b, c, d, e, f, and φ₀. For this, it is necessary to solve the system of seven equations:

The six first equations of system (20) give a line system for deriving expressions for the parameters a, b, c, d, e, and f (for details, see Appendix).

The last equation of (20) can be transformed into a non-linear equation for obtaining φ₀ (for details, see Appendix).

Thus, system (20) is non-linear on φ₀, and is solved by the method of bisecting. It has more than one solution usually. From these local solutions, one chooses that one which gives a minimum for functional (19).

As was observed from calculations, the solutions of system (20) near the symmetry axis angle, and near the fracture strike angle give close values of functional (19). It means that additional criterions are practically needed for separating these directions. For the case of HTI layer situated between isotropic layers, it can be the condition of negative values for calculated ε^(V) and δ^(V) in the anisotropic layer, as above. For this, from definitions to equations (9b) and (2), one can calculate from the solution of (20) at the interface:

In the case of interface between anisotropic layers, it is needed additionally to know the predefined signs of Δε^(V), and Δδ^(V) for comparison.

The additional criterion can also be the maximum of second derivative of functional (19), ∂F/∂φ₀.

Comparing the AVOA techniques

The techniques using the methods above for estimation of symmetry axis angle were compared in ability to give the most precise value of φ₀ for HTI medium. At present, reliable field methods of obtaining φ₀ do not exist. Therefore, I generated synthetic seismograms for an artificial three-layer medium with the anisotropic layer in the middle by applying the technique by Sabinin (2012) of 2D wave modeling. I set φ₀ = 60°, and derived models of the anisotropic layer for different values of φ_j by rotating the stiffness tensor for anisotropic layer (MacBeth, 1999) around z axis relatively to φ₀. Anisotropic parameters e_n = 0.35, and e_t = 0.2 (see MacBeth, 1999) were used in the stiffness tensor.

Host rock velocity V_P in three layers from above had the values 3200, 4000, and 4800 (the other variant was 3200), m/s, V_S was twice less, densities were equal, and thicknesses of two first layers were 1600, and 400 m. A source of explosion type generated one Ricker impulse of frequency 30 Hz. Receivers were spaced over every 100 m beginning from the source, and they measured z-component of velocity. There were 50 offsets, and 50 traces in each seismogram.

There were three goals: to investigate how the techniques behave on different sets of incidence angles, how the techniques are influenced by non-symmetry in φ_j relatively to φ₀, and how the techniques are influenced by noise.

Therefore, for the first goal, I made calculations of φ₀ for different intervals of offsets: from a minimum offset till a maximum offset, provided the minimum offset was fixed at the number one, and the number of maximum offset was changed from number 50 down to 3 in one set of the intervals; and the maximum offset was fixed at the 50-th, and the minimum offset was changed from number 1 to 48 in the other set of the intervals. Naturally, the maximum incidence angle θ_max corresponding to the maximum offset, and the minimum incidence angle θ_min corresponding to the minimum offset was also correspondently changed in these sets of offsets.

For the second goal, I obtained different sets of the synthetic seismograms corresponding to different azimuths, one seismogram for each azimuth. The sets of azimuths were uniform, and differed by symmetry. I did not aim to find the best or the worst set from them. I only supposed that a symmetric set can be better than an asymmetric one. I kept for testing the symmetric set of azimuths φ_j = {−150°, −120°, −90°, −60°, −30°, 0°, 30°, 60°, 90°, 120°, 150°, 180°}, and the asymmetric set φ_j = {85°, 95°, 105°, 115°, 125°, 135°, 145°, 155°, 165°}.

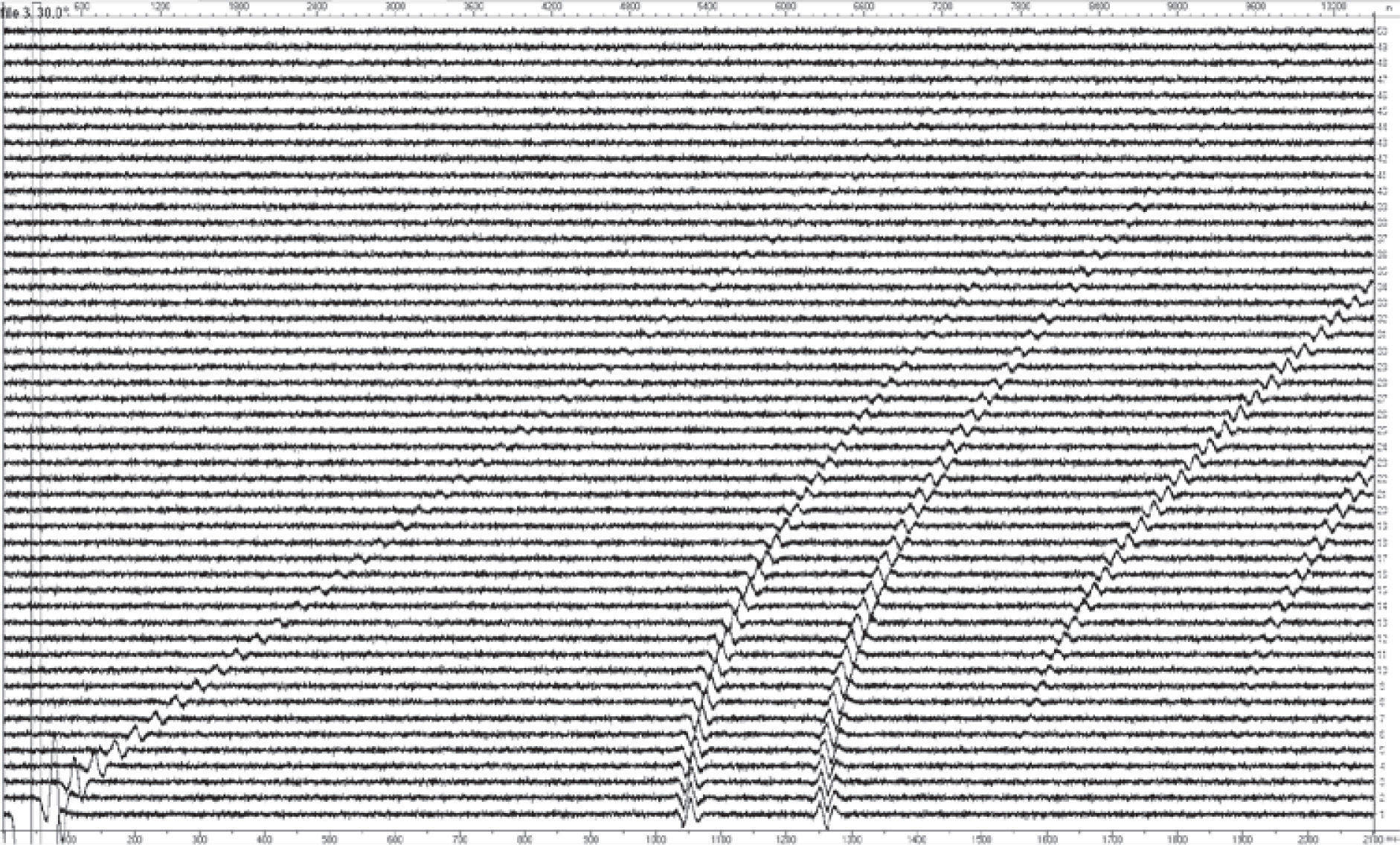
For the third goal, I took the best variant for the symmetric set of seismograms to eliminate the errors as due to the non-symmetry, as due to a finite-difference simulation when applying the artificial noise. The FD simulation by Sabinin (2012) uses PML boundary conditions which give non-visible (see Figure 4) but nonzero waves reflected from the boundaries of area. This slightly distorts the form of some synthetic impulses.

Figure 4.

Synthetic seismogram without noise. Azimuth 5°, V_P3 = 4800. Axis x – time in ms, axis y – numbers of traces. Zero time is origin of the source impulse.

For the synthetic seismic data being quasireal, I added a random Gauss normal noise to the seismograms generated, different for each seismogram. Maximum amplitude of the noise was chosen as 10% of the maximum amplitude of the wave reflected from the top boundary of the anisotropic layer in the first trace of seismogram.

Finally, I added the noise to the seismograms of the asymmetric set.

All seismograms were smoothed by filters (5) in the techniques. High-frequency components of the noise are eliminated well after smoothing, as shown in Figure 3. It is principally impossible to eliminate low frequencies compared with the frequency of signal. Therefore, the signal after smoothing remains slightly deformed. I suppose that just these deformations affect the estimated value of φ₀ in the case of noise.

The same sets of the time windows were used for all the techniques, and for all intervals of offsets.

As illustration, in Figure 4, the seismogram without noise for azimuth 5° is presented for the variant of V_P3 = 4800 m/s; and in Figure 5, the seismogram with noise for azimuth 30° is presented for the variant of V_P3 = 3200 m/s.

Figure 5.

Synthetic seismogram with added 10% noise. Azimuth 30°, V_P3 = 3200. Axis x – time in ms, axis y – numbers of traces.

As one can see from Figure 5, the amplitudes of noise reach really up to 50% of the maximum wave amplitudes in the middle traces, and up to 100% in the far traces.

The techniques were applied as to upper (1050 ms), as to down boundary (1250 ms) of the anisotropic layer.

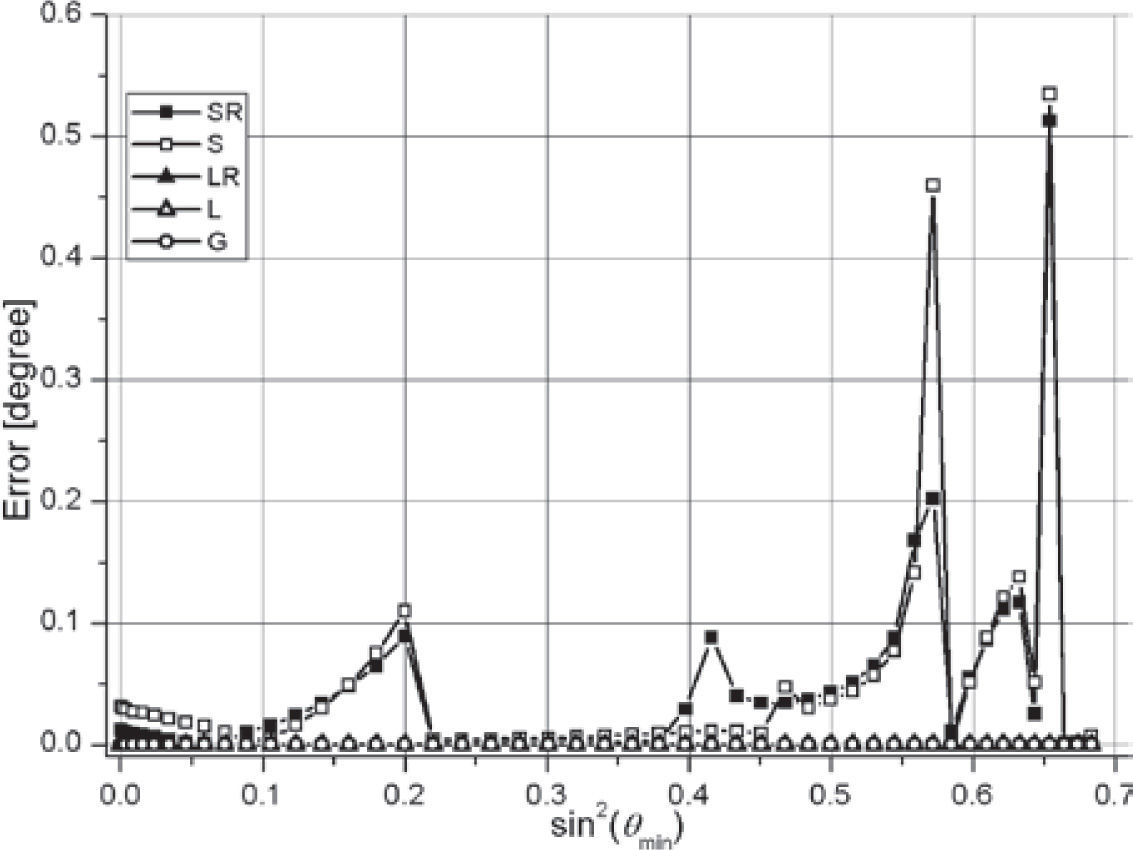
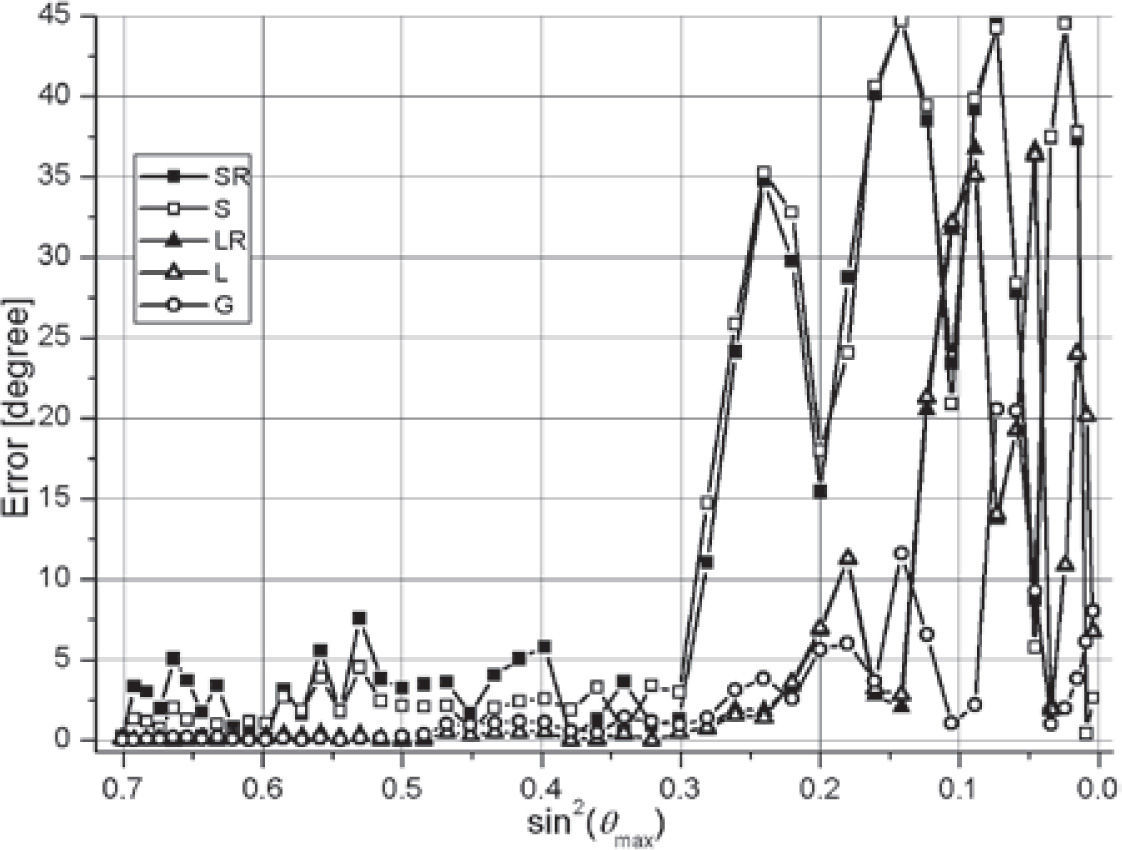
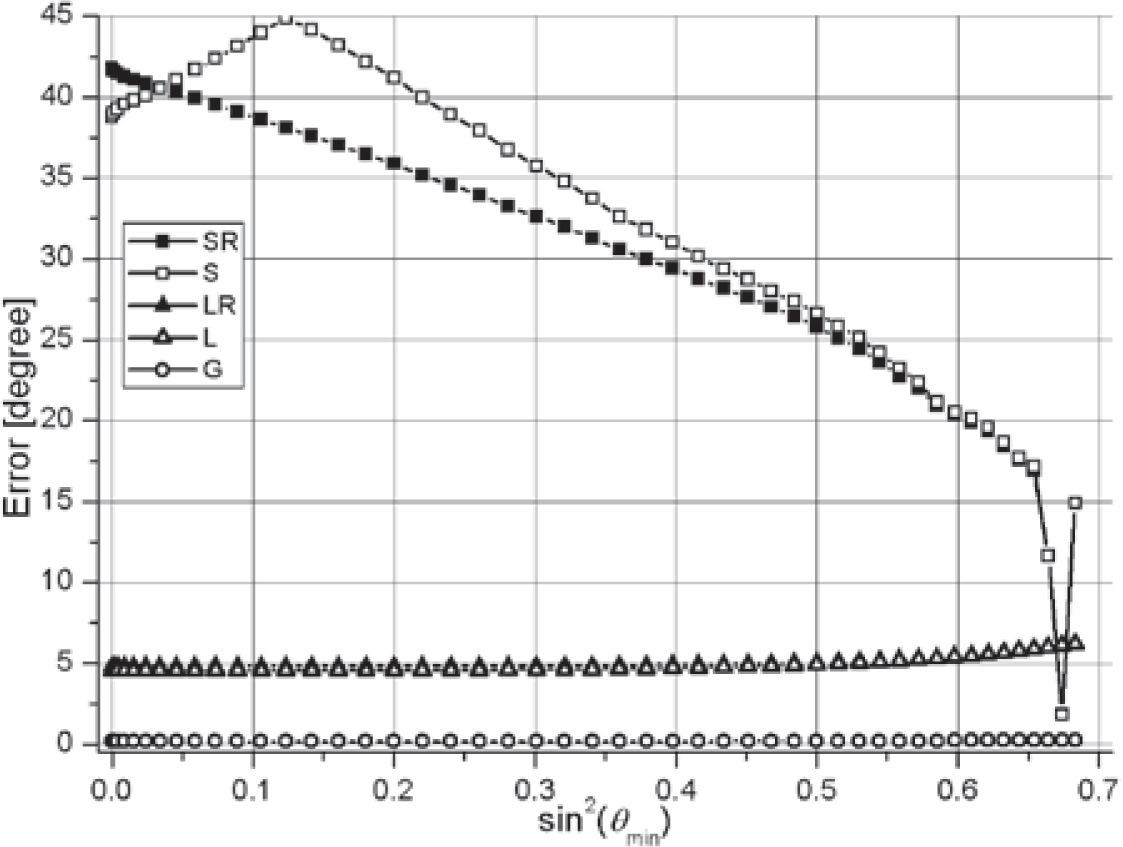
In Figures 6, 7, the error of estimated φ₀ in degrees (difference with the correct value 60°) is presented for the symmetric set of azimuths and the upper boundary, variant V_P3 = 3200. Figure 6 is for fixed θ_min = 0°, and Figure 7 is for fixed θ_max = 56.853°. The sectored methods show some instability for small values of θ_max − θ_min in comparison with the others. All methods increase the error in the case of small θ_max (Figure 6).

Figure 6.

Errors for the symmetric set of azimuths; the upper boundary, and fixed θ_min = 0.

Figure 7.

Errors for the symmetric set of oe azimuths; the upper boundary, and fixed θ_max = 56.853°.

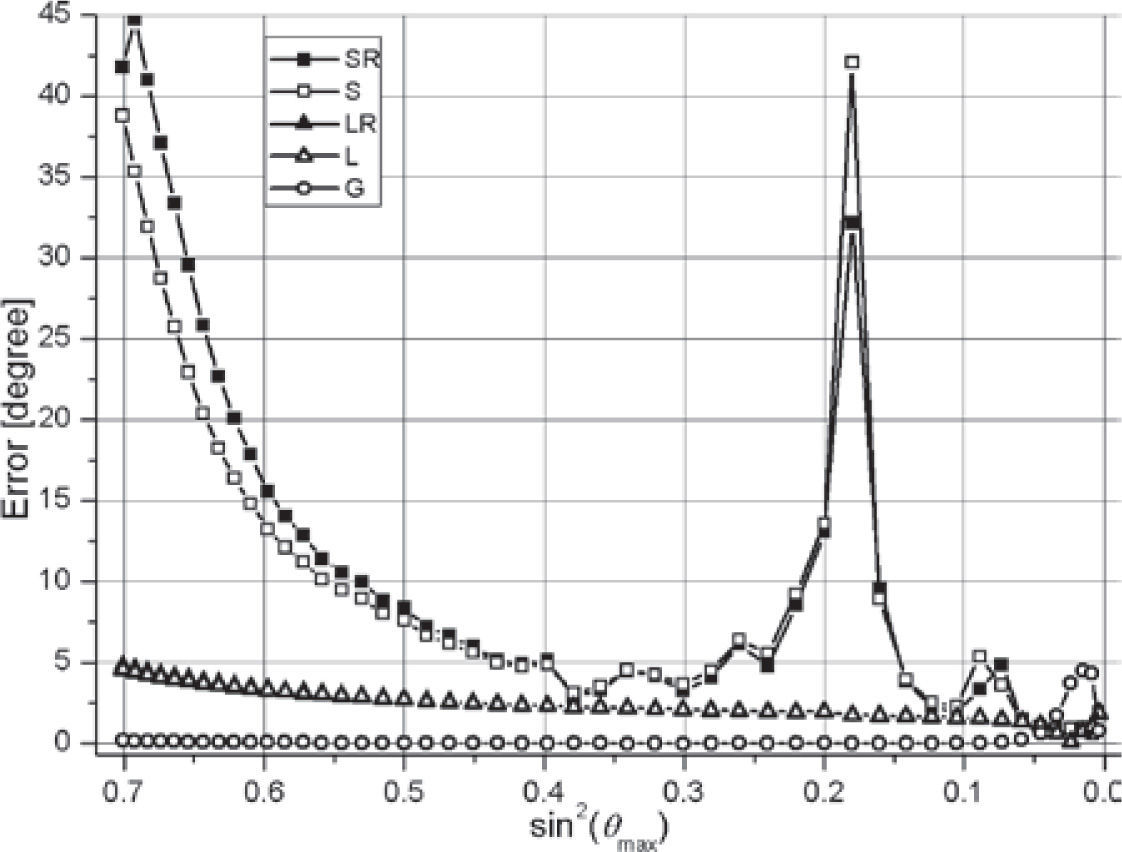
For the lower boundary and in the variant V_P3 = 4800, the general and linear methods also show increasing errors for small θ_max, and small θ_max − θ_min, see Figure 8, and Figure 9. However, the errors of these methods are sufficiently less than of the sectored methods.

Figure 8.

Errors for the symmetric set of azimuths; the lower boundary, variant V_P3 = 4800, and fixed θ_min = 0.

Figure 9.

Errors for the symmetric set of azimuths; the lower boundary, variant V_P3 = 4800, and fixed θ_max = 62.6°.

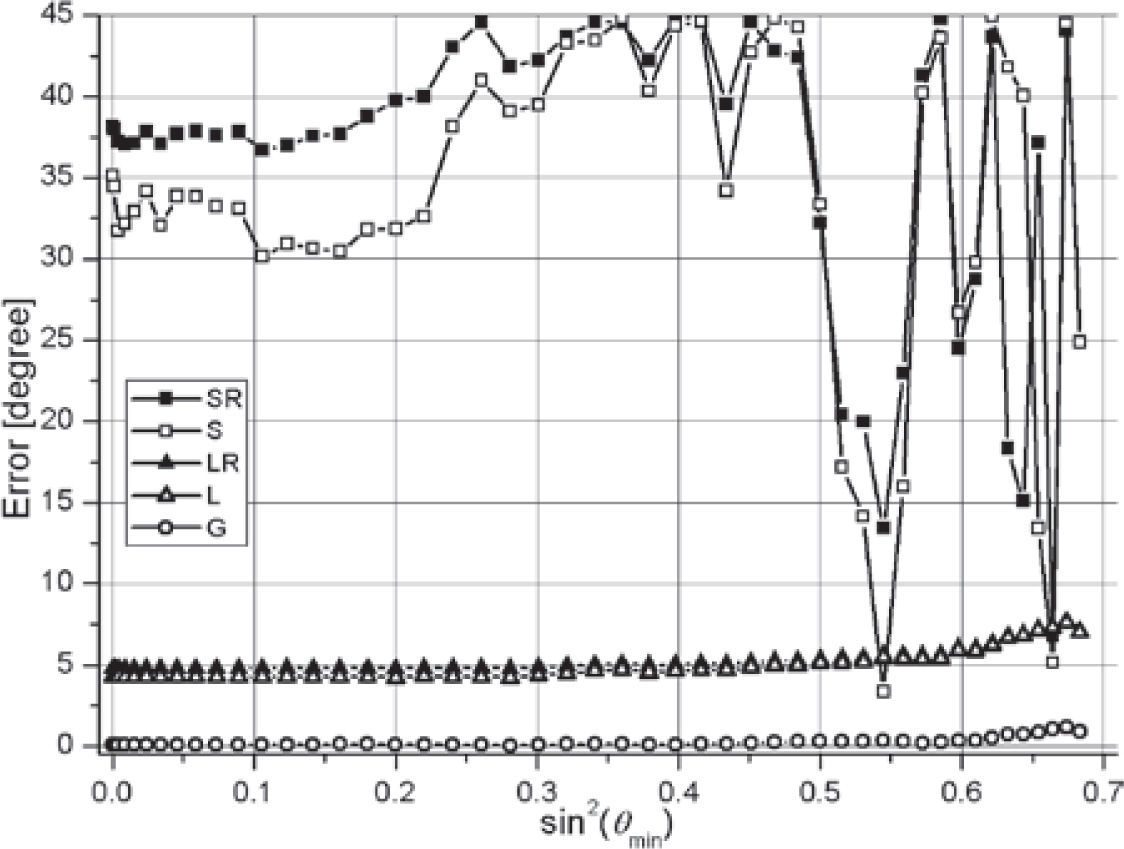
In Figures 10, 11, the variant of Figs. 6, 7 with the added noise is presented. The sectored methods demonstrate so great errors and instability that can not be recommended for applying. The other methods show large errors only for small θ_max (less than 30°).

Figure 10.

Errors for the symmetric set of azimuths; the noise, the upper boundary, V_P3 = 3200, and fixed θ_min = 0.

Figure 11.

Errors for the symmetric set of azimuths; the noise, the upper boundary, V_P3 = 3200, and fixed θ_max = 56.853°.

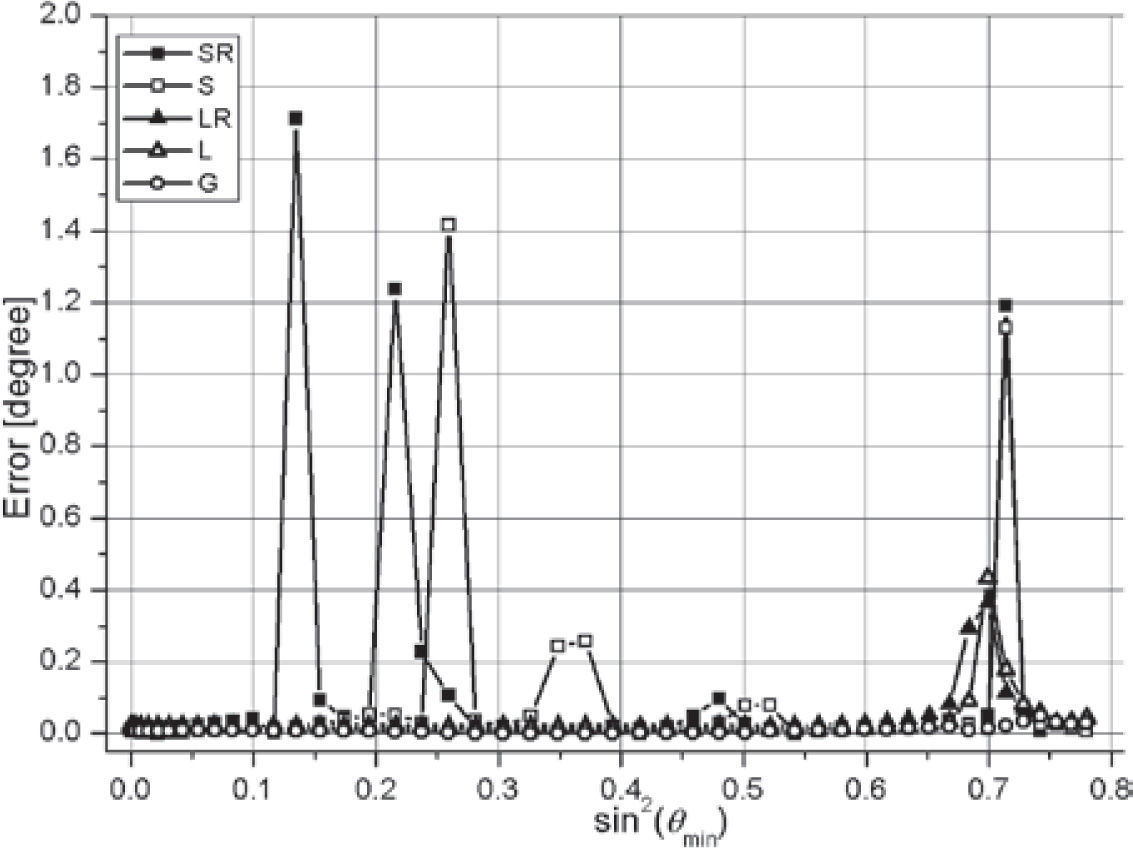
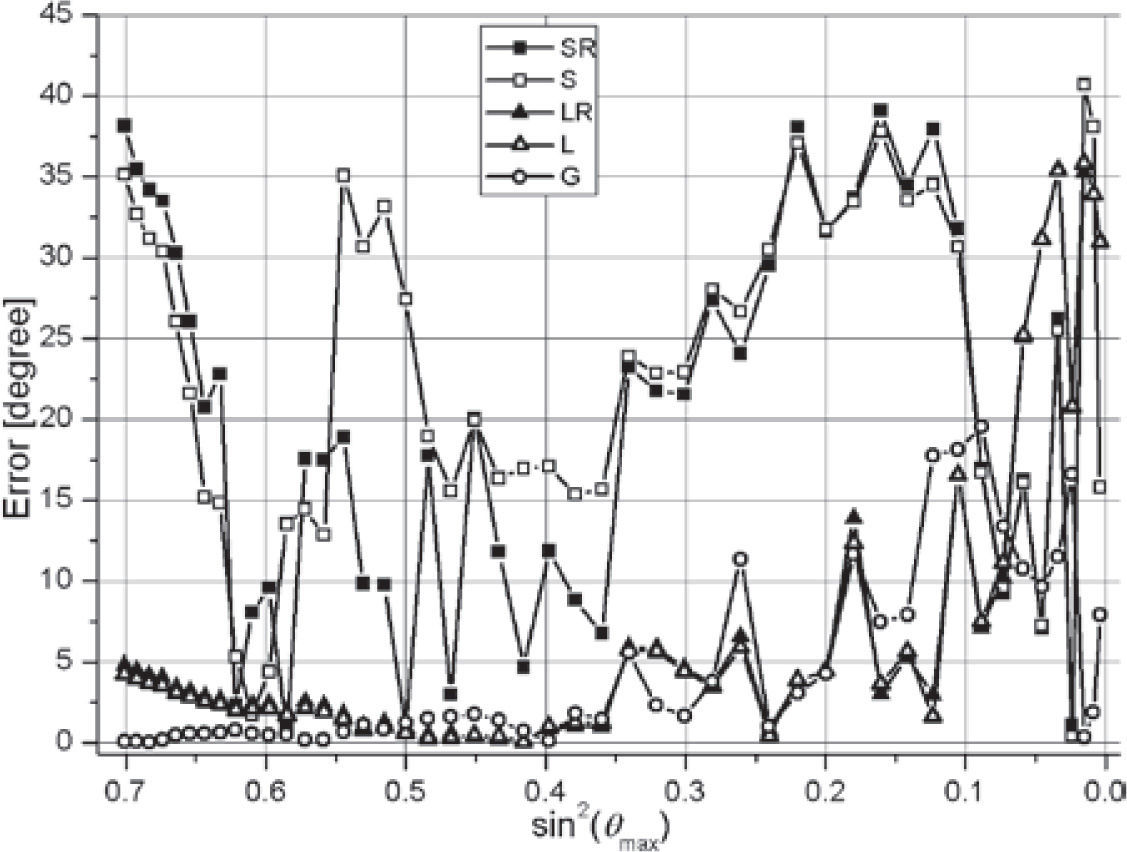
The asymmetric set of azimuths is presented by results in Figures 12–15. The variant of upper boundary and V_P3 = 3200 without noise is presented in Figures 12, 13, and the same with the noise – in Figures 14, 15.

Figure 12.

Errors for the asymmetric set of azimuths; the upper boundary, variant V_P3 = 3200, and fixed θ_min = 0.

Figure 13.

Errors for the asymmetric set of azimuths; the upper boundary, variant V_P3 = 3200, and fixed θ_max = 56.853°.

Figure 14.

Errors for the asymmetric set of azimuths; the noise, the upper boundary, V_P3 = 3200, and fixed θ_min = 0.

Figure 15.

Errors for the asymmetric set of azimuths; the noise, the upper boundary, variant V_P3 = 3200, and fixed θ_max = 56.853°.

Typical peculiarities of the asymmetric set are: great errors of the sectored methods with instability in noised data, and stable large errors of the linear methods (up to 7°). The general method remains of small errors. The noise causes instability of all methods in the interval of θ_max < 36°, provided even the general method (G) gives large errors in this interval.

Discussion and conclusion

Some unexpected results were obtained. The first is that the sectored S and SR methods are failed. They can be used only in seismic data without noise, and for mainly symmetric distributions of azimuths φ in the 3D data (Figures 6–9). This is too ideal conditions.

The second is that the linear L and LR methods have an additional nearly constant error in mainly asymmetric distributions of azimuths φ in the data (Figures 12–15). This error is probably connected with the truncation of high terms in equation (1) of Ruger, because the general method G has not such error. Therefore, the linear methods should be applied to azimuthally symmetric data.

The third is that the smoothing data with noise by simple filters (5) gives relatively stable estimated values of φ₀ in a wide interval of incidence angles θ for the methods L, LR, and G (Figures 10, 11, 14, 15). The interval of instability is near the normal incidence, and has a width of θ_max < 40°, different in different variants (Figures 10, 14). For data without noise, this interval is θ_max < 10° (Figures 6, 8). Presence of the interval of instability is an intrinsic property of the formula (1) in connection with the least-squares method. Errors in amplitudes become relatively more with decreasing θ in definition of φ₀ by equation (1).

The results show a superior of the general method (G). On the whole, its errors are less than of the others. Unfortunately, it has an intrinsic problem of choosing the right solution from the local solutions of non-linear system (20). All criterions described above do not guarantee the correct choosing. It is especially difficult in the interval of instability. All the methods have such problem of distinguishing solutions. The best in this sense is the method L. Its criterions are failed very rarely. Therefore, I recommend applying the method G in a coupling with the method L: after estimation of φ₀ by L, the value φ₀ is defined more precisely by G with expertly taking into consideration the local solutions of (20). The other recommendation is to avoid the interval of instability.

In applying to field data, the techniques can give worse results. The real data have much more interferences of waves than the synthetic data. It is practically impossible to clear each interfered wave of the other by filters. Distorted by this way impulses can lead to unpredictable results.