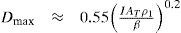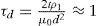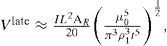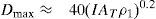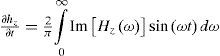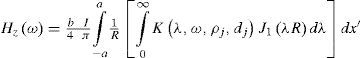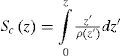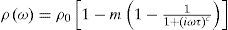Probamos un método propuesto en la literatura para estimar la profundidad máxima de investigación (PMI) de sondeos electromagnéticos transitorios (TEM) de bobina central con datos del transecto Vizcaíno; un perfil de 38 sondeos TEM que cruza la península de Baja California. Se confirma la validez de esta técnica al comparar la PMI con la interfase más profunda de 16 modelos estratificados. En estos sondeos, todos ellos localizados en la cuenca Vizcaíno, los datos medidos no están afectados por polarización inducida. Los modelos indican la presencia de un conductor buzante interpretado como una zona de intrusión salina con una gran extensión lateral de más de 70 km. Los otros 22 sondeos, localizados sobre rocas ígneas y metamórficas, muestran cambios en la polaridad de los voltajes que indican la presencia de efectos de polarización inducida. Los modelos estratificados Cole-Cole de estos sondeos sugieren una disminución importante en la PMI. Esto es confirmado al analizar el comportamiento en profundidad de las densidades de corriente. También se analiza el nivel de ruido de un conjunto de datos que comprende cerca de 2000 voltajes de tiempo tardío de aproximadamente 400 sitios TEM adquiridos en el noroeste de México. No se encontró una diferencia entre los niveles de ruido estacionario de invierno y verano, posiblemente debido a que prácticamente no hay tormentas eléctricas en esta parte de México.
We test an approach proposed in the literature for estimating the maximum depth of investigation (MDI) of in-loop transient electromagnetic soundings (TEM) with data from the Vizcaino transect, a profile of 38 TEM soundings crossing the Baja California peninsula. The validity of this approach is confirmed by comparing the MDI with the deepest interface of 16 stratified models. In these soundings, all located over the Vizcaino basin, the measured data are not affected by induced polarization. The models indicate the presence of a dipping conductor interpreted as a zone of seawater intrusion with a large lateral extension of over 70 km. The remaining 22 soundings, located over igneous and metamorphic rocks, show reversals in the voltage polarity, indicating the presence of induced polarization effects. The layered Cole-Cole models for these soundings suggest a significant decrease in the MDI. This is confirmed by analyzing the depth behavior of the subsurface current densities. We further analyze the noise level of a data set comprising close to 2000 late-time voltages of about 400 TEM sites acquired in northwestern Mexico. No difference was found between the stationary noise levels of winter and summer, presumably because near thunderstorms are practically absent in this part of Mexico.
The transient electromagnetic (TEM) method is based on the induction of electric current in the ground by a transmitter loop. When a DC current injected into the loop is abruptly turned off, an electric field is induced in the ground, which generates the flow of subsurface currents. These currents rapidly vary in time and space, producing a transient magnetic field in the vicinity of the transmitter. The time variation of this field is sensed with the voltage induced in a coil laid on the ground surface. Placing this coil at the center of the loop is known as the in-loop array. The shape and intensity of the measured voltage is a function of the resistivity subsurface distribution. The method has been used extensively in a variety of applications, such as groundwater exploration, mineral and oil prospecting, buriedmetal detection, and geologic mapping.
A frequently asked question during the planning of in-loop transient electromagnetic soundings is, “What is the maximum depth of investigation (MDI) if a square loop of dimensions L by L is used as the transmitting source?” There is no simple answer to this question. Although the MDI does depend on the loop dimensions, it also depends on other parameters. Several estimates of the MDI have been reported in the literature (McNeill, 1980; Fitterman, 1989; Spies, 1989). In this work we adopt and test that proposed by Spies (1989), which is the most clear and complete.
In this paper we start with a brief description of Spies method followed by a presentation of the Vizcaino data and inverted models. Then, we discuss some modifications to Spies expression to be applied to the inverted models. Finally, soundings affected by induced polarization are analyzed.
The maximum depth of investigationBased on the asymptotic behavior of the late-time voltages at the center of a circular loop over a two-layered earth, Spies (1989) proposed the following expression for the MDI,
where I is the current injected into the loop, AT is the area of the loop, ρ1 is the resistivity of the first layer, and β is VN/AR the voltage noise level (VN) over the effective area of the receiving coil (AR). Clearly, this depth not only depends on the size of the transmitting loop, but also on four other parameters; two of them of instrumental character (injected current and area of the receiving coil), a subsurface geophysical parameter (layer resistivity), and an environmental parameter (voltage noise level).
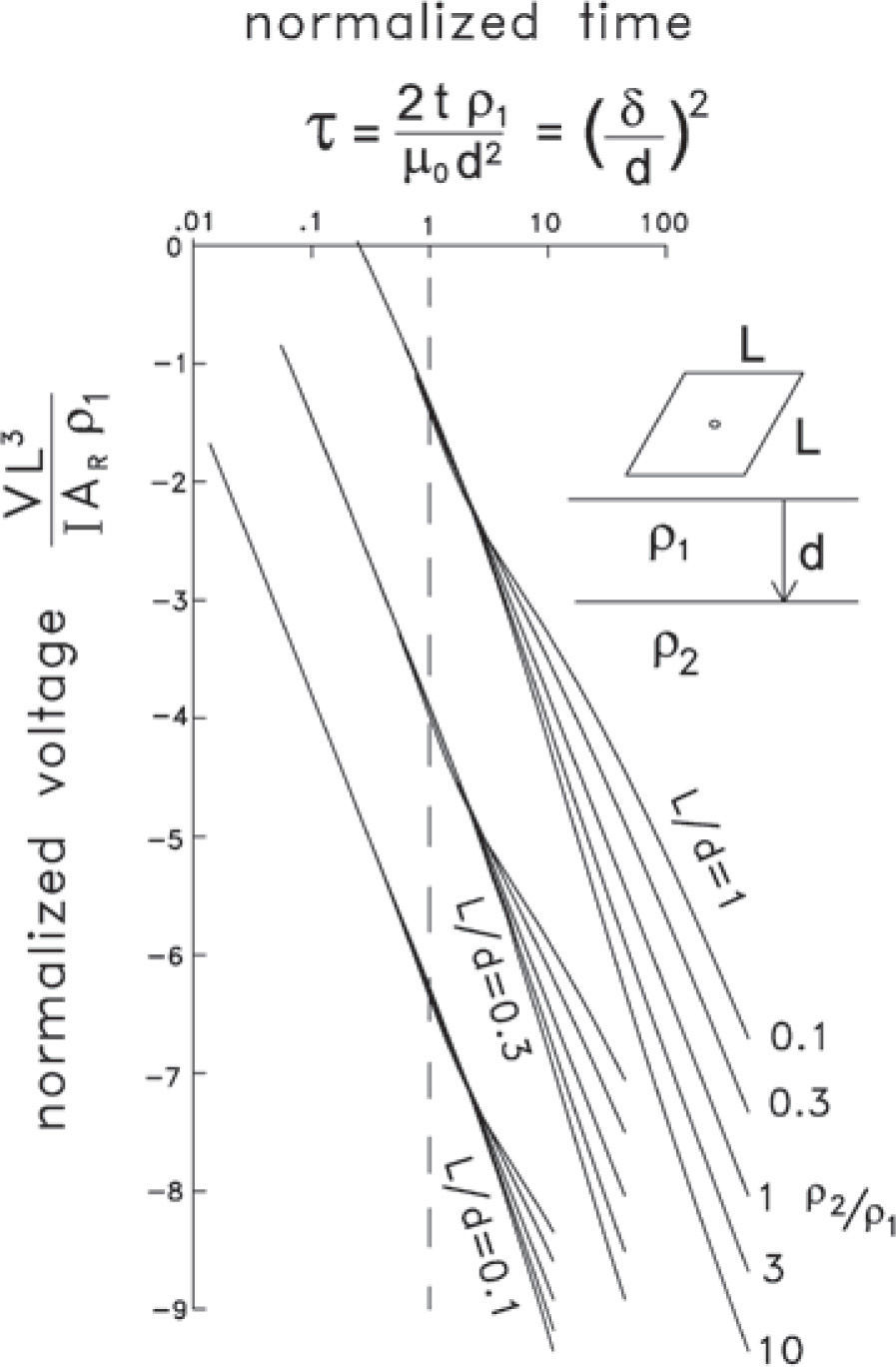
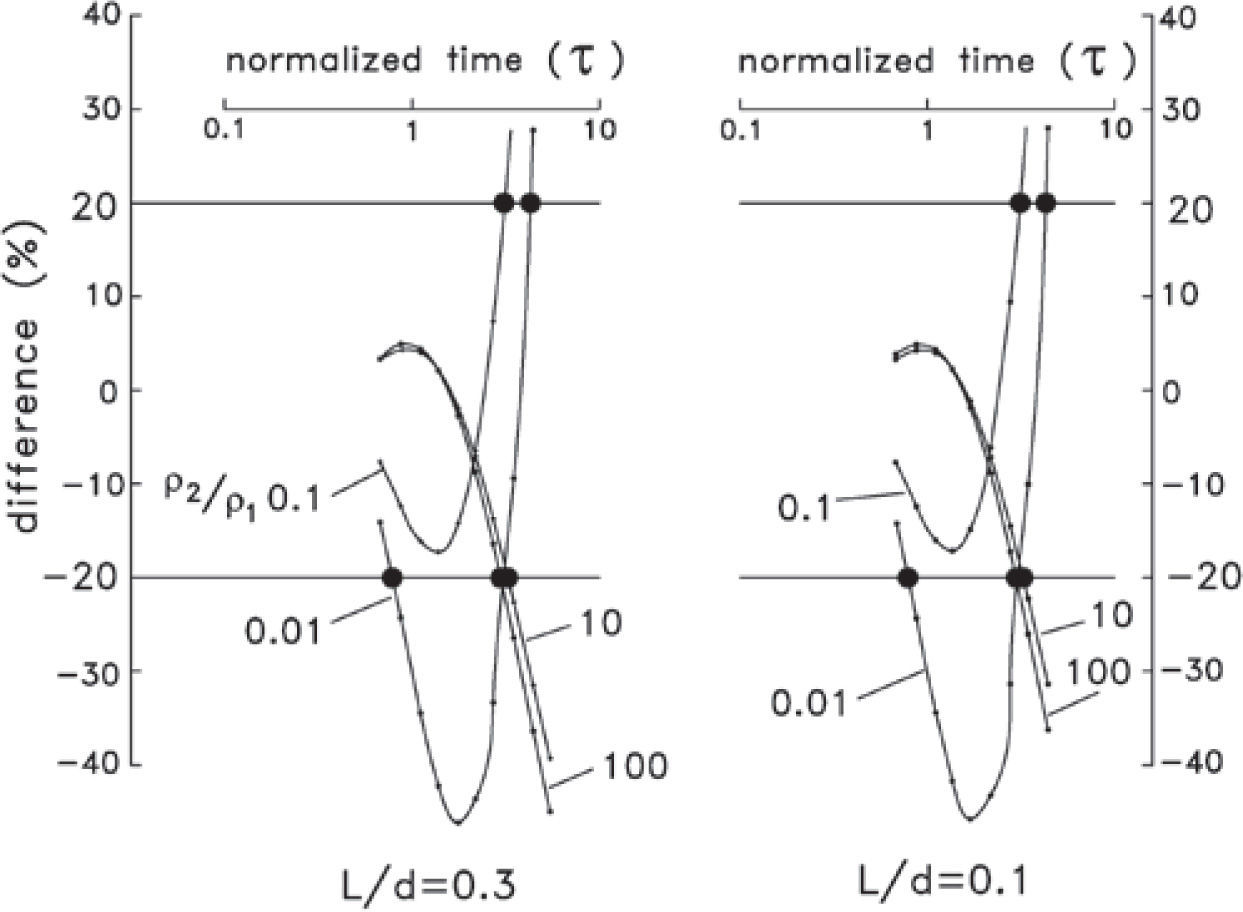
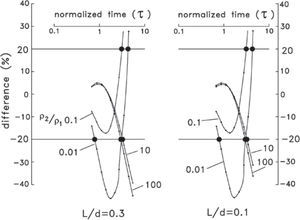
Figure 1 shows the behavior of the normalized voltages induced in a horizontal coil located at the center of an L by L square loop over a two-layer earth for three L/d ratios and five ρ2/ρ1 ratios, where d is the first layer thickness and ρ1 and ρ2 are the layer resistivities. These curves for a square loop are similar to the circular loop responses presented by Spies (1989). Both axes are dimensionless. In the abscissas the variable τ is a normalized time, being the square root of the diffusion depth δ=2tρ/μ0 in the first layer over its thickness. Spies noticed that the time at which the different curves separate at least 20% (denoted as departure time) does not have a strong dependency on the L/d or ρ2/ρ1 ratios, so he approximated it as unity. That is,
By solving for t in (2), substituting it into the late-time asymptotic voltage approximation,
and replacing d by Dmax and Vlate/AR by β, Spies obtained expression (1).
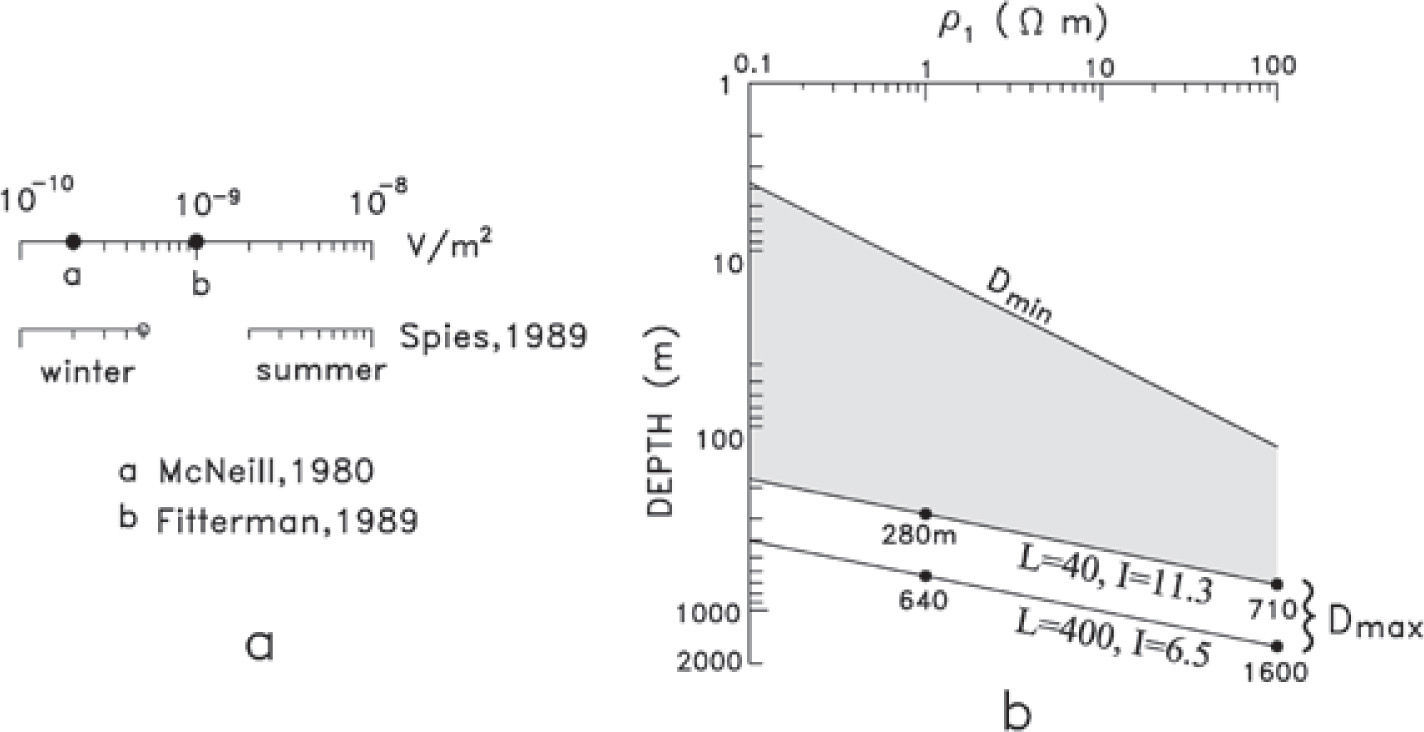
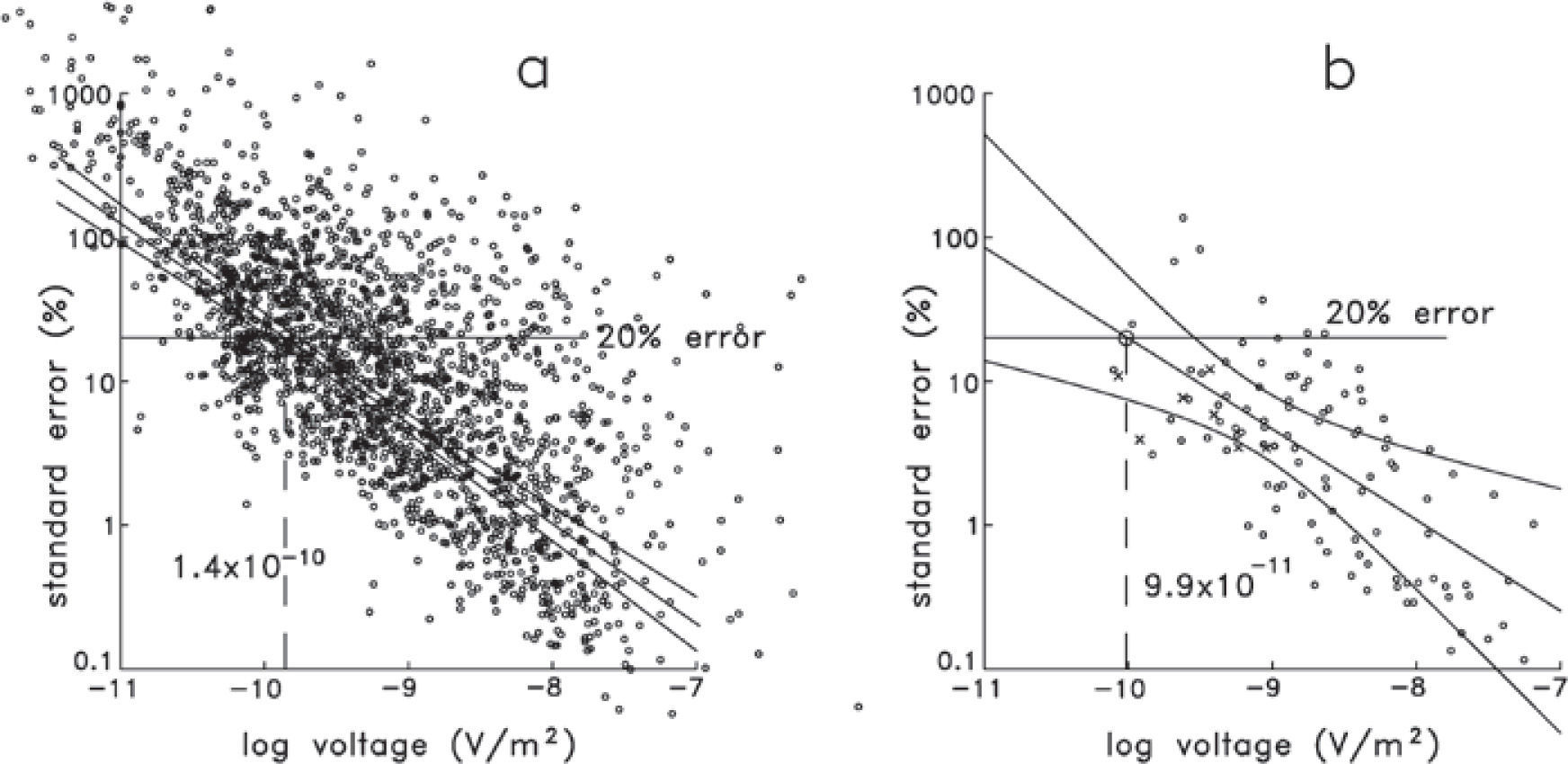
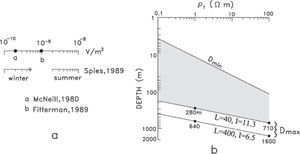
The voltage noise level may have significant variations both in time and space. The main source of natural EM noise affecting TEM soundings are the spherics, which are electromagnetic transients generated by lightning discharges (Ward, 1967). A spheric usually propagates directly to the sounding site if the lightning is nearby or by multiple reflections in the earth-ionosphere waveguide if it occurs at large distances. Several values have been proposed for the natural noise level after the voltages are averaged: 109 (Fitterman, 1989), 2×10−10 (McNeill, 1980), and different ranges for winter (from 1×10−10 to 5×10−10) and summer (from 2×10−9 to 1×10−8) (Spies, 1989), all of them in units of V/m2 (Figure 2a). If we consider a nominal value of 5x10−10 V/m2, the maximum depth of investigation becomes
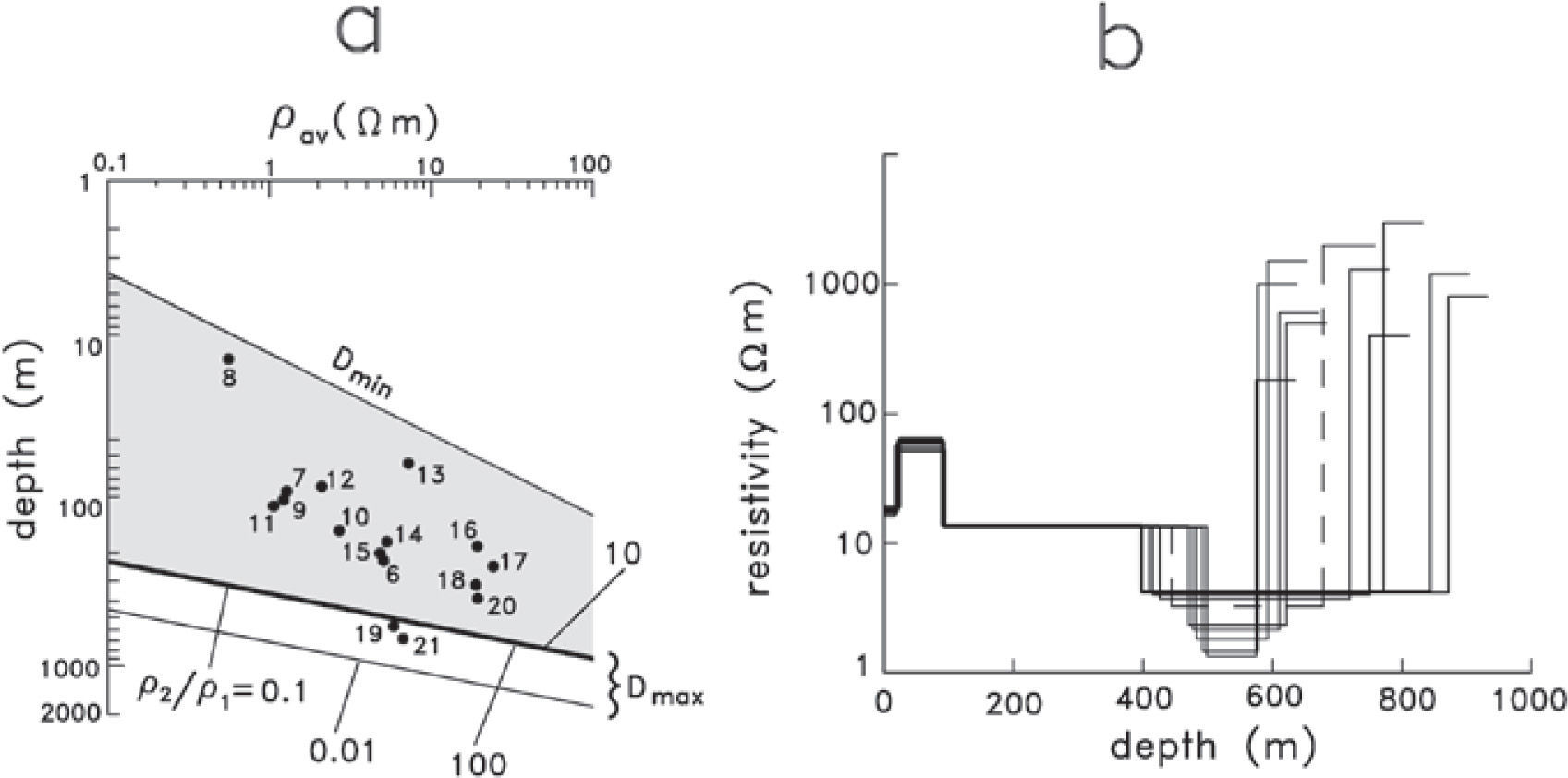
When logarithmic axes for both depth and resistivity of the first layer are used, expression (4) plots as a straight line. This is illustrated in Figure 2b, where the range of depths covered by a sounding with a 40 by 40 m loop and 11.3 A of injected current is shown as the shaded area. The Dmin line indicates the minimum depth of investigation, which depends on the first layer resistivity and the shortest time (tmin) of the particular data acquisition system Dmin=2tminρ1/μ0. The maximum depths of investigation would be 280 or 710 m if the first layer had resistivities of 1 or 100 Ωm, respectively. For a loop of 400 by 400 m and a current of 6.5 A the maximum depth of investigation clearly increases. However, notice that although the size of the loop increased tenfold, the Dmax values (640 and 1600 m) increased only by a factor of about 2.3.
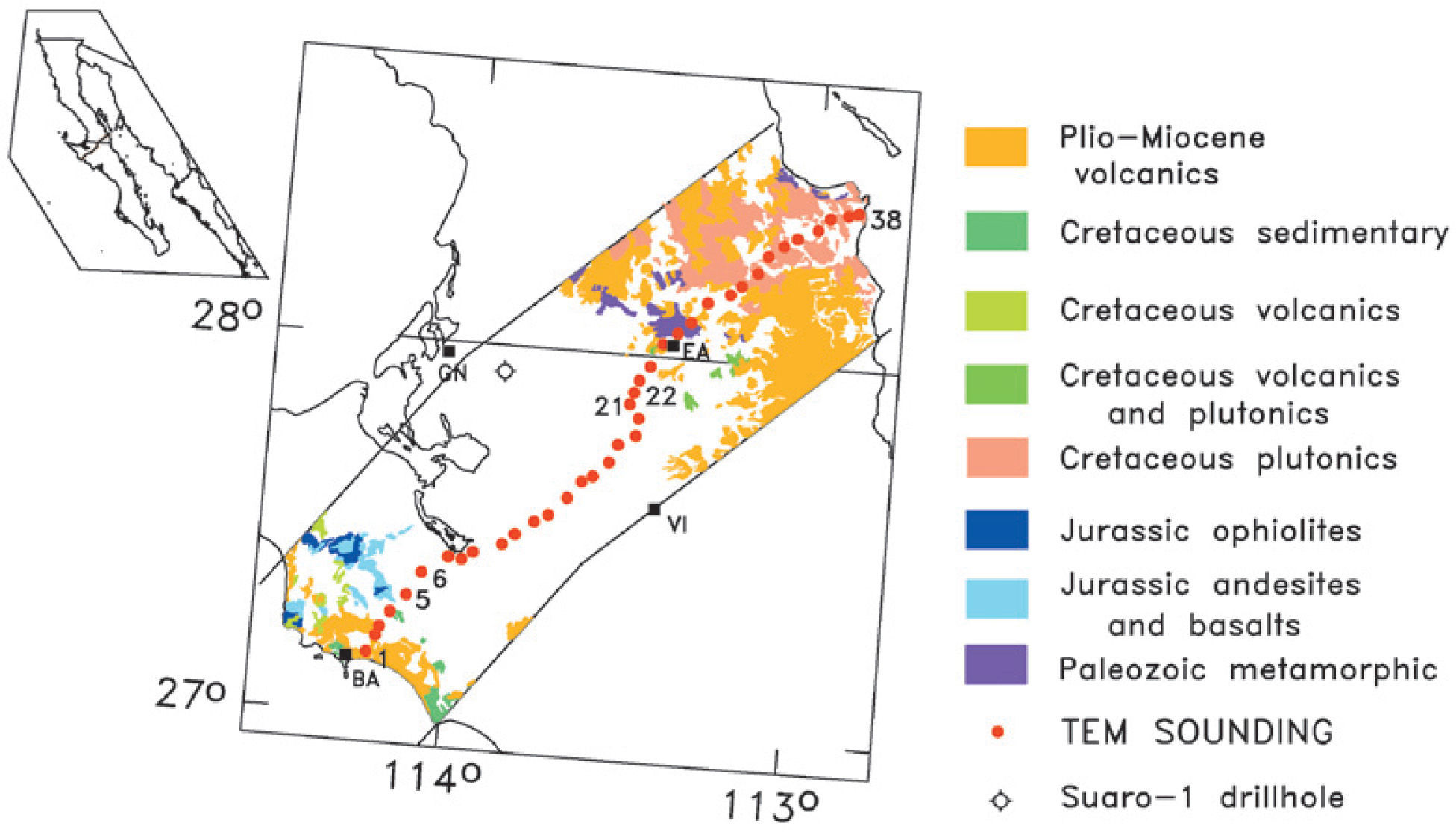
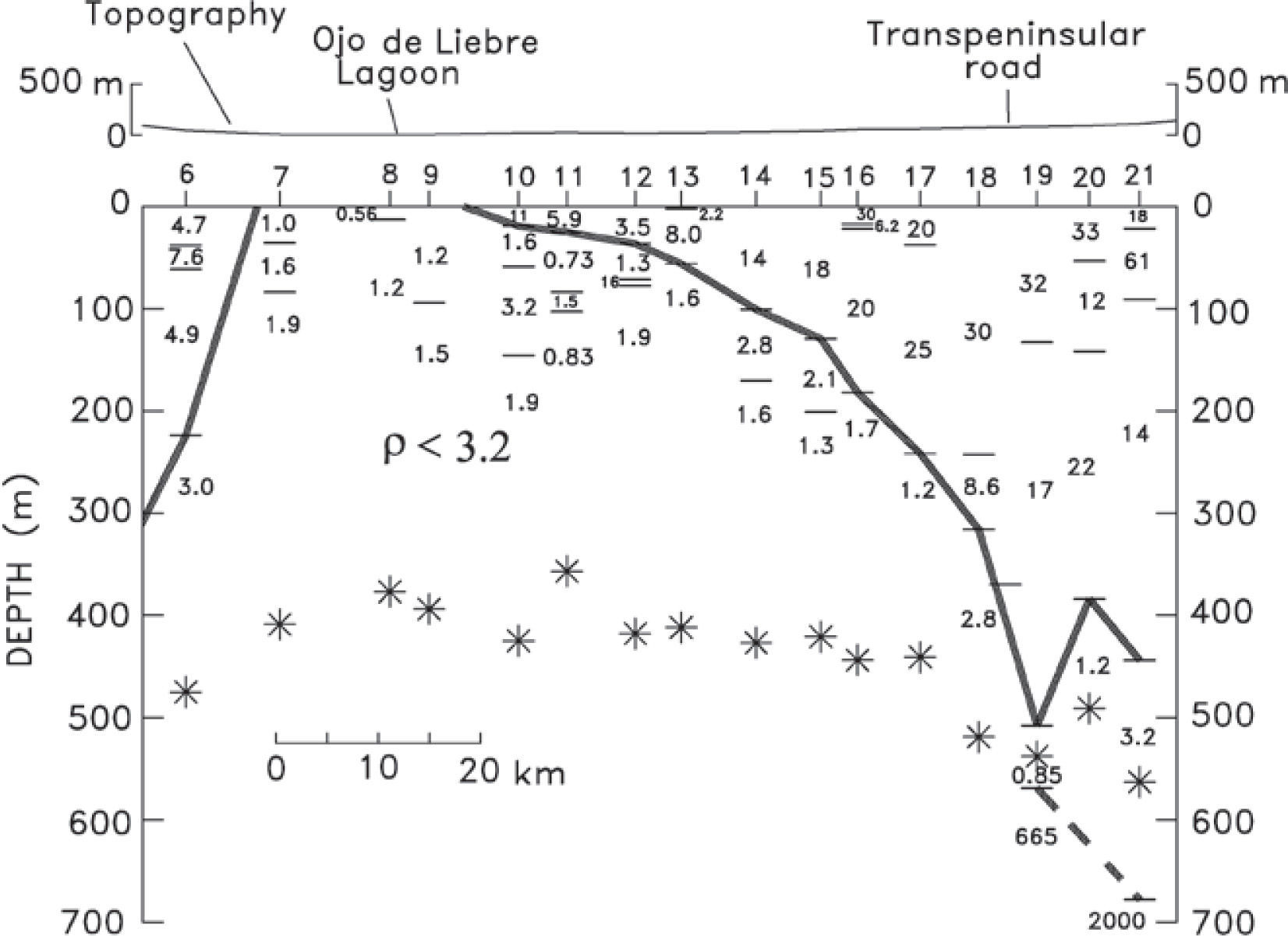
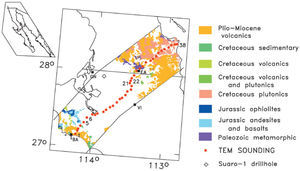
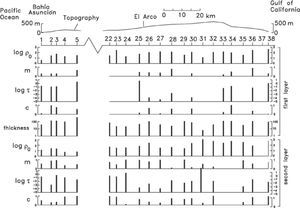
The Vizcaino transectFigure 3 shows the location of the Vizcaino Transect, a profile of 38 TEM soundings running through the Vizcaino desert with a direction approximately perpendicular to the main trend of the Baja California peninsula. These data were originally acquired to apply the static shift correction to the same number of magnetotellu ric soundings (Romo et al., 2001). The sounding sites are approximately 6 km apart. The transect crosses three geologic environments. In the SW part of the profile Mesozoic rocks typical of oceanic crust outcrop. These units belong to the Cochimi terrane (Sedlock et al., 1993). The central part is underlain by the late-Mesozoic-Cenozoic sedimentary rocks of the Vizcaino basin. The geologic column found at the Suaro-1 hole (see location in Figure 3), an exploratory well drilled by Petróleos Mexicanos (García-Domínguez, 1976), gives useful information of the basin lithology. The stratigraphic sequence is, from top to bottom: 60 m of unconsolidated Holocene-Pleistocene sands and soil; 1190 m of fine-grained clastics belonging to the early Paleocene-Eocene Bateque formation; 970 m of interbedded shales, sandstones and some conglomerates of the Late-Cretaceous Valle formation; 355 m of limestones and tuffaceous siltstones of the Early-Cretaceous Alisitos formation. The total depth reached by the Suaro-1 hole was 2640 m. According to the interpretation of the gravity data of the area (García-Abdeslen et al., 2005), the maximum basin thickness is close to 4 km. As a relative gravity high lies close to our TEM traverse, a shallower depth to the basement is expected in its vicinity. In the NE part of the transect subduction-related volcano-plutonic rocks outcrop. This region, defined by Sedlock et al. (1993) as the Yuma terrane, comprise Paleozoic-Mesozoic metamorphic rocks and Cretaceous rocks typical of a volcanic arc. Some areas of the SW and NE portions are covered by Tertiary volcanic rocks of andesitic and basaltic compositions, which form mesas at the topography highs.
Location and generalized geology (after Delgado Argote, 2000) in the vicinity of the Vizcaino transect. Solid dots denote the 38 TEM soundings. Abbreviations: BA Bahía Asunción, GN Guerrero Negro, VI Vizcaino, EA El Arco. The location of the Suaro-1 drillhole is indicated.
All soundings were acquired with a Geonics TEM57 system in the in-loop array, employing 150 by 150 m loops and a 100 m2 effective area circular coil. The currents injected to the loops were close to 8.5 A. The three available repetition frequencies were used (30, 7.5, and 3Hz). The stacking times for these frequencies were 128, 256, and 256 s, respectively, resulting in stacked voltages representing the average of about 7700, 3800, and 1500 individual voltage decays. At least three realizations for each repetition frequency were carried out, from which the final average voltage and standard error were estimated.
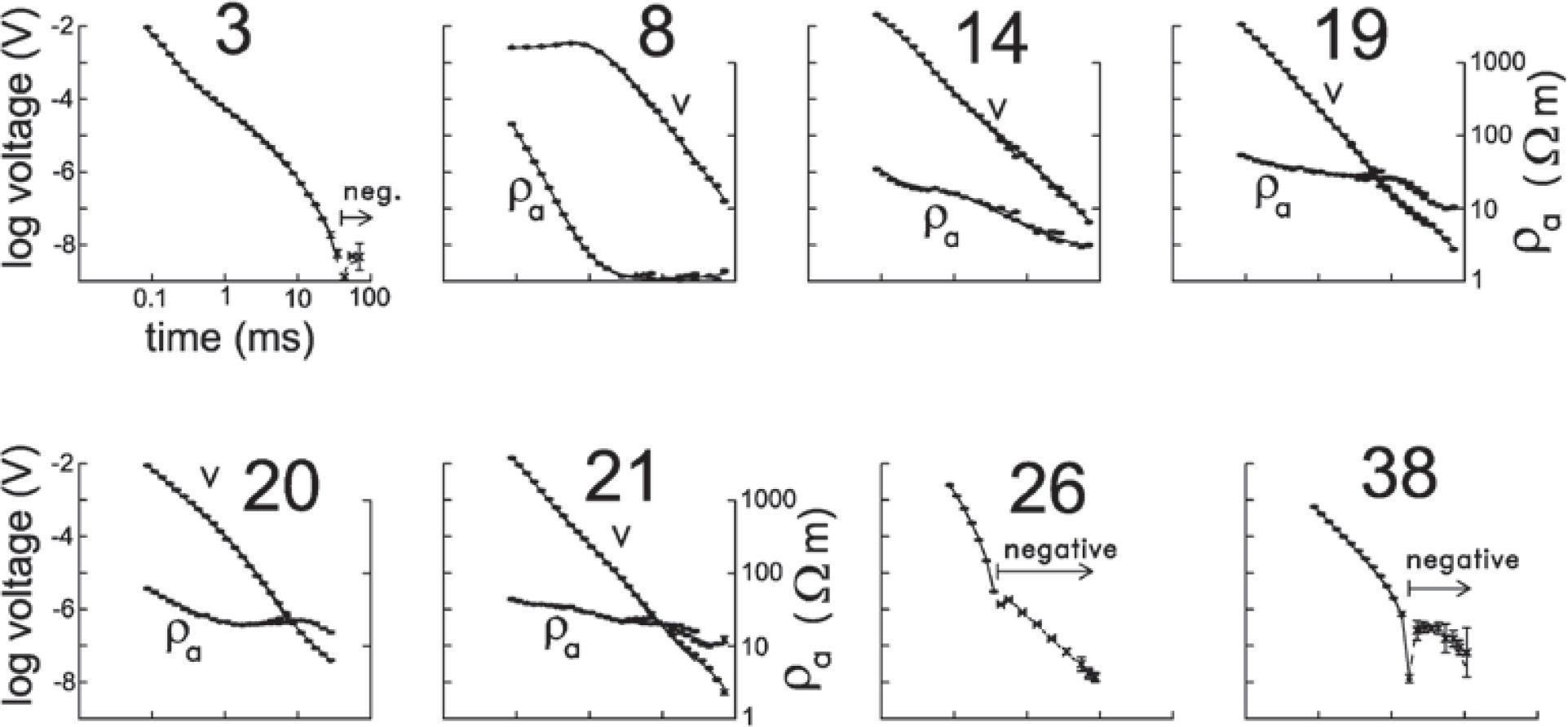
Figure 4 displays the observed data (symbols) and estimated standard deviations (error bars) for a number of selected soundings. The data quality is generally good. All soundings from 1 to 5 and from 22 to 38 have a change of sign in the measured voltages. These sites are located in the southwestern and northeastern portions of the profile, where volcanic, crystalline or metamorphic rocks outcrop. For in-loop soundings the presence of a voltage sign reversal is diagnostic of the presence of a frequency-dependent or dispersive subsurface resistivity (Weidelt, 1982), that is, the presence of Induced Polarization (IP) in the ground. In contrast, the soundings located in the Vizcaino basin, from sites 6 to 21, have positive voltages at all times indicating the presence of a non-polarizable resistivity. Both voltage and apparent resistivity data as a function of time are shown for the non-polarizable soundings (sites 8, 14, 19, 20, and 21 in Figure 4). For those affected by IP the corresponding apparent resistivity data are not displayed because they are undefined when the voltages are negative (sites 3, 26, and 38 of Figure 4). We will discuss first the results for the non-polarizable soundings (6 to 21).
Observed data (symbols) and calculated responses (solid and dashed curves) for selected soundings. Both voltage and apparent resistivities are displayed for the non-dispersive soundings (8, 14, 19, 20, and 21). Only the voltages are shown for soundings affected by Induced Polarization (3, 26, and 38). Negative voltages are indicated.
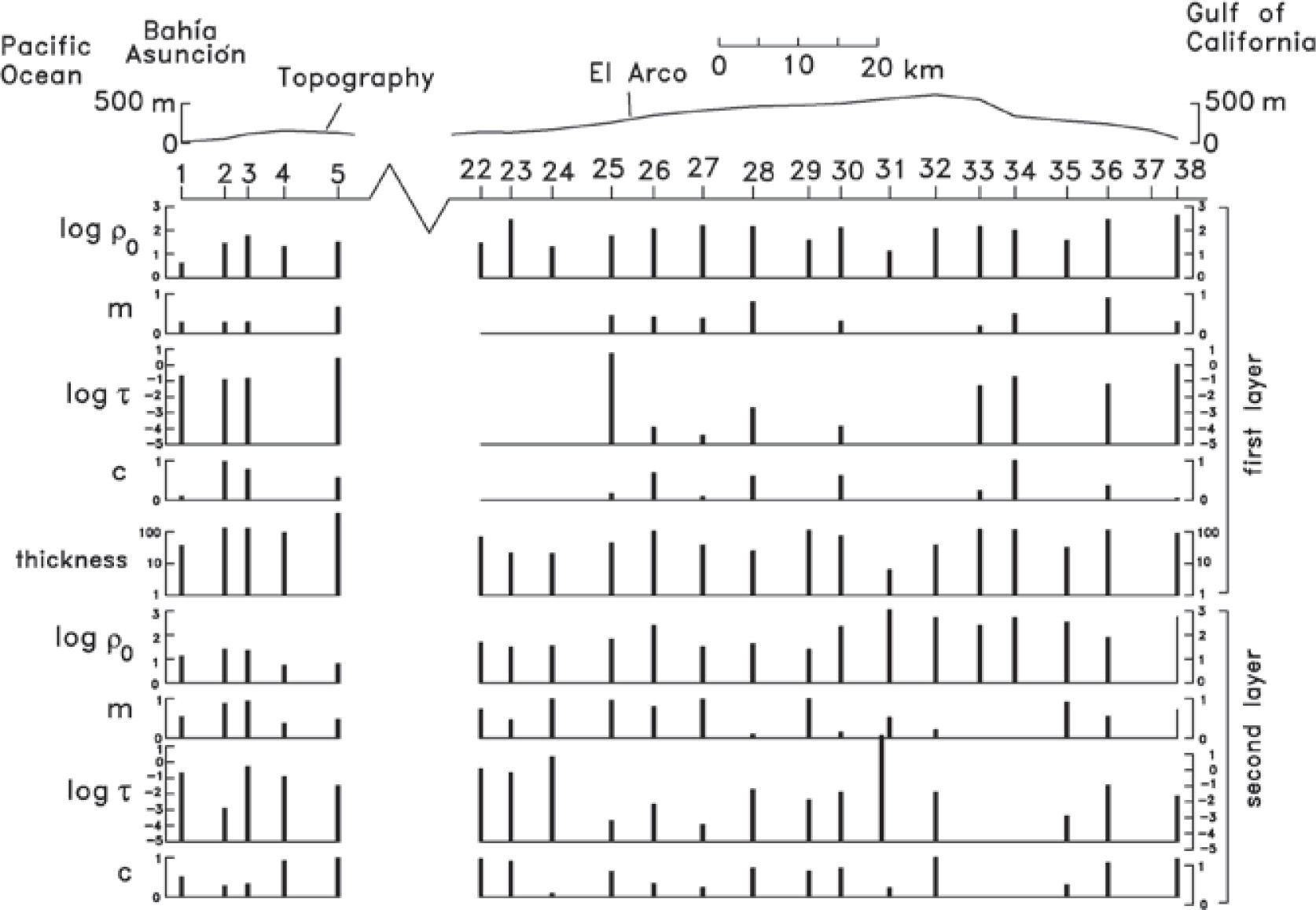
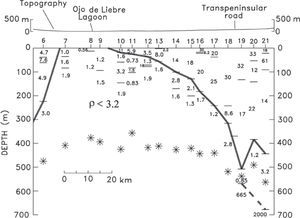
All these soundings were inverted to layered models using a linearized least squares algorithm (Jupp and Vozoff, 1975). The solid lines of Figure 4 correspond to the calculated responses of the inverted models. The fit between observed and calculated responses is good (the average misfit error is 1.4). The layer resistivities and depths are shown in the section of Figure 5, where the maximum depths of investigation (to be discussed below) are also included as stars. Because of the large separation between soundings (about 6 km), it is difficult to carry out lateral correlations between neighboring models. However, an outstanding feature can be noticed; under the thick line shown in Figure 5 all resistivities are less than 3.2 Ωm. This conductive zone outcrops in sites 7, 8, and 9, where a remnant of the highly saline Ojo de Liebre lagoon occurs, and gradually deepens away to the southwest and northeast. These features suggest that this anomalous zone is due to a saline intrusion of large lateral extent (the horizontal distance between sites 8 and 21 is 73 km). This desert area is characterized by a very low rainfall (about 50mm/year). This seawater intrusion could have been produced by natural physical processes, without anthropogenic influence, because there is not groundwater extraction in this Biosphere Reserve Area except in the vicinity of the Vizcaino town (see location in Figure 3). The profile approaches this locality at sounding 17, which is 15 km to the north of this town. We do not see a perturbation in the depth to the conductor in the vicinity of this sounding, which would be an expected feature if groundwater pumping is the driving force of the intrusion.
Before applying the MDI expression to the Vizcaino models, we address three points: a) a more detailed estimation of the departure time, b) the noise level is estimated from the actual field data, and c) the adaptation of expression (1) to multi-layered models.
Instead of approximating the departure time as unity, we estimated it from graphs such as those shown in Figure 1 for different resistivity contrasts and L/d ratios. These responses were calculated with the following procedure. The transient voltage due to an ideal current step turn-off is,
The time derivative of the vertical magnetic field is obtained from the Fourier sine transform (Newman et al., 1986)
The filter weights proposed by Anderson (1979) are used to calculate this transformation from the frequency domain to the time domain. The vertical component H the magnetic field in the frequency domain (Hz (ω)) produced by a rectangular loop requires integrating the field of a horizontal electric dipole along the wire forming the loop. The field at the receiver coil located at P(0, 0, 0) produced by one side of a rectangular loop of dimensions 2a by 2b over a layered earth has the form,
with R=x′2+b212. In this expression ω is the angular frequency, I is the current in the loop, K is the kernel of the Hankel transform and J1(.) is the Bessel function of order 1. The kernel corresponds to the vertical component of the maonetic field produced by a horizontal electric diple on a layered earth (Ward and Hohmann, 1987). It depends on the layer thicknesses dj and the resistivities of each layer ρj. Similar expressions hold for the remaining sides of the loop. This Hankel transform is evaluated with a convolution with the filter proposed by Anderson (1975). The integration along the loop was carried out with a Gauss-Legendre method.
The two graphs shown in Figure 6 are the percentage differences between the two-layered voltages and the homogeneous half-space voltages as a function of normalized time. The solid dots are the departure times, i.e. where the difference is greater than +/− 20%. These departure times have a small dependence on the L/d ratio, but show a larger dependence on the resistivity ratios.
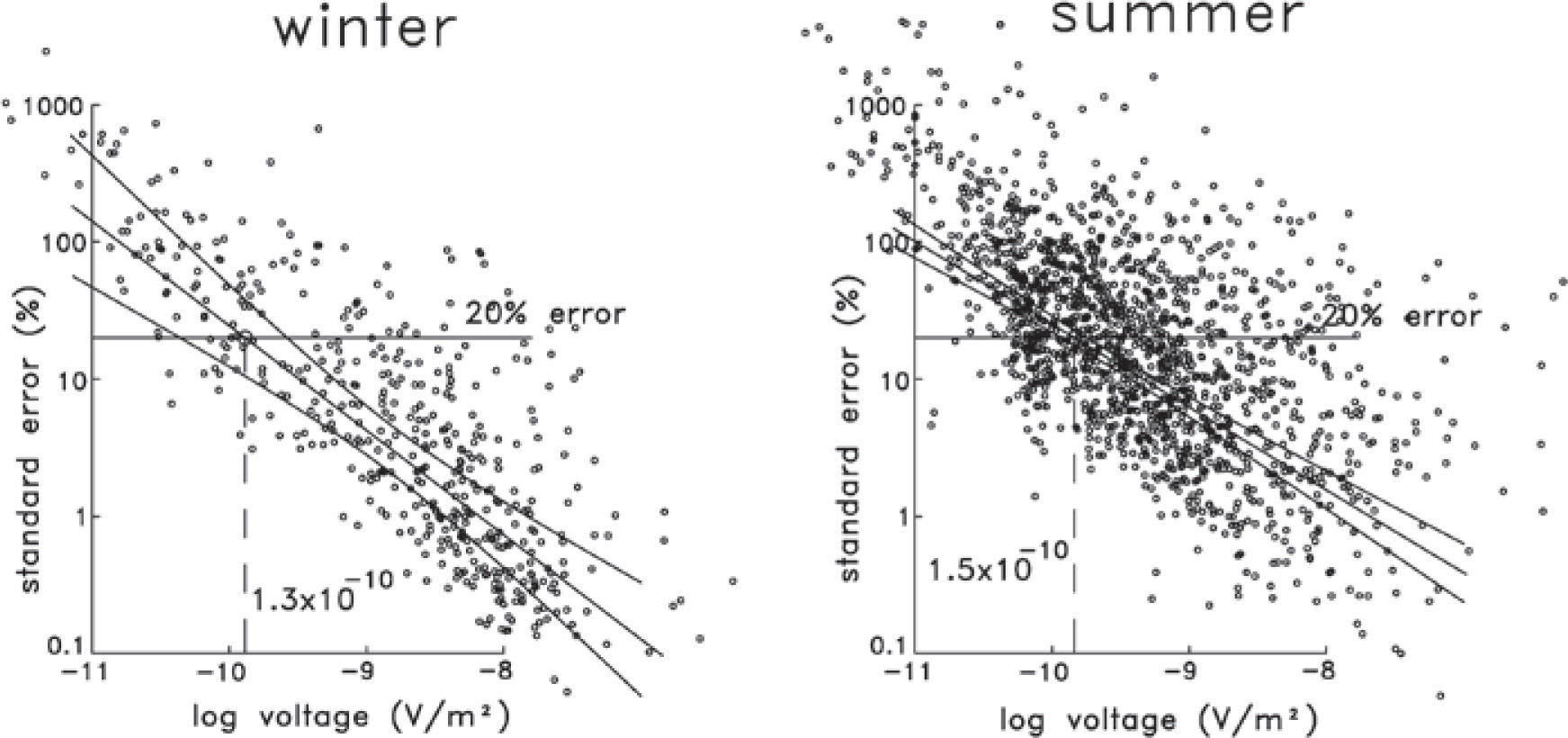
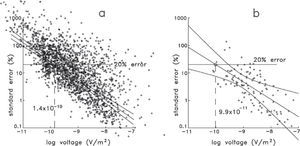
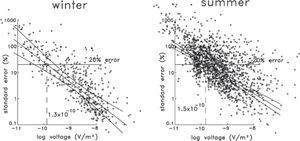
Instead of using any of the noise levels proposed above and depicted in Figure 2a, we estimated it directly from the data. Figure 7a shows a bilogarithmic plot of 1955 late-time measured voltages and their associated percentage standard errors. This data set, denoted here as “NW-Mexico”, was constructed from the voltages of 386 sounding sites acquired during several years in 18 different zones in northwestern Mexico. Although the data set includes a variety of loop sizes, ranging from 10 by 10 m to 400 by 400 m, 84% of the voltages were acquired with loops greater or equal to 150 by 150 m. These voltages are the result of three averaging steps designed to increase the signal to noise ratio: averaging in variable-size time-windows (also known as binning), stacking using the repetitive nature of the source current, and averaging with different realizations, that is, measuring the sounding several times. The standard errors presented in Figure 7 are calculated from the last averaging step, the errors from the first steps are not available in the commercial acquisition systems. This figure shows a clear and expected feature; as the voltage magnitude decreases its standard error increases due to the influence of the ambient electromagnetic noise. We assume the voltage dispersion is the result of the sum of a stationary plus a random process. The stationary component was estimated by a weighted least squares linear fit. A similar assumption was considered by Zhou and Dahlin (2003) for the analysis of dc voltage noise in the resistivity method. To accommodate the variable amount of averaging in these data we assigned error bars to the ordinates (not shown for clarity). The size of the error bars is proportional to 1/N, where N is the total amount of points involved in the average, that is, voltages that consider more averaging values have smaller error bars. The best fitting line for this data set and the predicted voltage with a 20% error (14 × 10−11 V/m2) are shown in Figure 7a. This value is close to 20 × 10−11 V/m2, the value suggested by McNeill (1980) as a typical noise level, shown in Figure 2a. The envelopes around the best fitting line indicate the boundaries of the 95% confidence level (Montgomery and Runger, 1994), that is, we can assert with this confidence level that the true straight line falls within the envelopes. Figure 7b shows the same analysis applied to 114 late-time voltages of the Vizcaino transect, where the estimated 20% error voltage is 9.9 × 10−11 V/m2. This will be the noise value used in expression (1) to estimate the MDI.
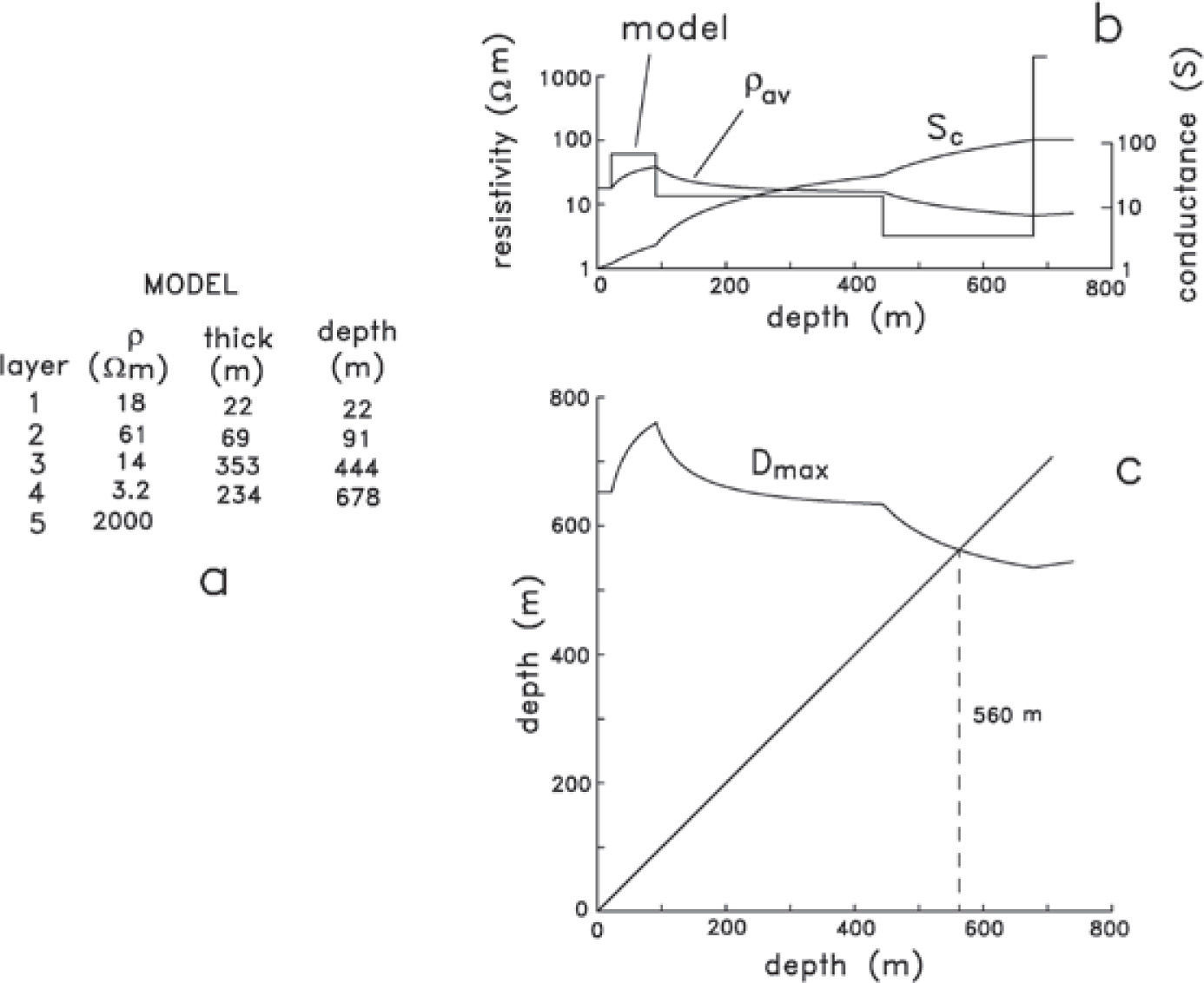
Expression (1) is based on a two-layered earth. The cumulative conductance is used to adapt it to a multilayered subsurface (Spies, 1989). Figure 8 illustrates this for sounding 21. The cumulative conductance at any depth (d) is defined by
where p(z′) are the inverted layer resistivities (Figure 8a). Having determined S c (z), the average resistivity ρav (z) at any depth can be found with ρav (z) = d/Sc (z). The model resistivities, cumulative conductance, and average resistivity as a function of depth are displayed in Figure 8b. Then, the first layer resistivity of expression (1) can be replaced by the average resistivity to obtain an expression of the maximum depth of investigation as a function of depth. For example, by using the average loop moment (1.935×105 Am2), noise level (9.92×10−11 V/m2), and the departure time for a resistivity contrast ρ2/ρ1=100, this expression is Dmax(z) ≈ 366[ρav(z)]0.2. This function is shown in Figure 8c. When Dmax is equal to depth gives the required solution. Graphically, this occurs when the Dmax curve intersects the unit slope line passing through the origin, as shown in Figure 8c. For this stratified model the maximum depth of investigation is 560m.
Figure 9a displays with solid dots the depth to the deepest interface interpreted in the inverted models of the non-dispersive soundings. The minimum (Dmin) and maximum (Dmax) depths of investigation are also shown. The four Dmax lines correspond to the four resistivity contrasts ρ1/ρav of 100, 10, 0.1, and 0.01. These were calculated using the typical current (8.6 Amp), loop size (150 m), estimated noise level (9.92×10−11 V/m2), and the calculated departure times. The shaded area indicates the range of depths explored with these soundings assuming a substratum 100 times more resistive than the average resistivity. The corresponding Dmax values are also shown with stars in the section of Figure 5. In all models the MDI is greater than the deepest interface, except for soundings 19 and 21. Sounding 20 could probably fall in this case, but equipment malfunction prevented recording the latest time voltages. The discrepancy between the MDI and the deepest interface is 120 m for model 21 and 50 m for model 19. This would suggest that either the MDI estimation is not valid or that the deepest interface in these two models is not supported by the data. The latter option seems untrue because a better fit is obtained when the resistive basement is considered. This apparent contradiction is solved when a careful examination of the models for these two soundings indicates that they suffer from an intense equivalence problem in the conductive layer overlying the resistive substratum. This is illustrated in Figure 9b for the model of sounding 21, which shows 11 different models that reproduce the observed voltages with nearly the same misfit error. All these models have practically the same fourth-layer conductance, that is, there are a large number of possible combinations of thickness over resistivity. Then, if we choose a model with the fourth layer about 120 m thinner, keeping its conductance unaltered, the discrepancy between the MDI and the deepest interface no longer exists. Furthermore, the late-time voltage errors for this sounding (shown with crosses in Figure 7b) are systematically lower than the nominal 20% level, which would result in a slightly greater MDI value. A similar situation occurs for sounding 19.
a) Depth versus average resistivity plot for the 16 non-polarizable models. Solid dots are the depths to the deepest layer interface. b) Eleven layered models that reproduce the data of sounding 21 with approximately the same misfit error. The dashed line corresponds to the model of minimum misfit error.
Most of the spheric energy arises in the thunderstorm centers of Central Africa, Central-South America, and Southeastern Asia (Ward, 1967), producing noise that varies diurnally, seasonally, and with latitude. Attenuation of spheric noise is determined by the height of the lower ionosphere and the conductivity of the earth and ionosphere, in such a way that the wave generally propagates more efficiently at night. McCracken et al. (1984) report an increase in spheric noise by a factor of ten from winter to summer and by a further factor of ten from high latitudes (39° S) in southern Australia to low latitudes (12° S) in northern Australia. It is interesting then, to test if our NW-Mexico data set of late-time voltages show a similar difference between the noise level of soundings acquired in winter with those measured in summer. Figure 10 shows the dispersion plots for these seasons with the corresponding weighted linear fits and their 95% confidence level envelopes. In this analysis we considered six-month periods, winter from October to March and summer from April to September. The estimated stationary noise levels are 4.4≤13≤26×10−11 V/m2 in winter and 12≤15≤18×l0−11 V/m2 in summer (the uncertainties are estimated from the 95% confidence envelopes). Although the summer noise level is slightly higher than the winter level, they are not statistically different as their uncertainties overlap. This conclusion is still valid if, instead of considering six-month seasons, we consider three-months (winter from January to March and summer from July to September). Then, our data do not support the difference of one order of magnitude in the seasonal noise level suggested by McCracken et al. (1984). We think the explanation for this unexpected result might reside in the characteristics of the rainy season in northwestern Mexico. The rainy season in this region occurs in winter, not in summer, and the rain episodes are rarely accompanied by lightning.
Polarizable soundingsAs mentioned above, soundings from 1 to 5 and from 22 to 38 were affected by IP. Figure 4 show the negative late-time voltages for three selected soundings, characteristic of the presence of IP. The most common way to represent the IP phenomena is with the Cole-Cole model (Cole and Cole, 1941; Pelton et al., 1978), which describes the frequency dependent resistivity with
where ρ0 is the zero-frequency or direct current resistivity (Ωm), m is the chargeability (dimensionless), τ is the time constant (seconds), and c is the frequency exponent (dimensionless). The four parameters have different ranges of variation. The chargeability and the frequency exponent can vary from 0 to 1. The dc resistivity and the time constant have wide ranges, from 10−2 to 105 Ωm and from 10−5 to 104 s, respectively.
The voltages of these soundings were inverted to layered dispersive models using the linearized least squares algorithm of Jupp and Vozoff (1975). The solution of the forward problem required by the inversion was calculated with the same numerical procedure outlined above in expressions (5) to (7) but with the following four modifications:
- a)
The resistivity in each layer in the kernel of expression (7) is no longer constant, but now depends on the frequency as the Cole-Cole dispersion model (8).
- b)
To circumvent the time-consuming integration along the loop, each loop side is divided into N wire segments of equal length, approximating each segment by an equivalent electric dipole (Stoyer, 1990), considering at least three equivalent dipoles for each loop side.
- c)
Before applying the Fourier transform, the effect of the receiver coil finite bandwidth is incorporated by multiplying the transfer function of the coil by Hz(ω).
- d)
Finally, the effect of the actual current waveform (linear turn-off periodic ramps) is accounted for by using the procedure described by Fitterman and Anderson (1987). This approach requires extrapolating the voltage response beyond the last late-time gate. We fitted an exponential function to the last five voltages to perform this extrapolation, calculating additional voltages points if necessary.
In the inversion process of the sounding voltages we tried to obtain the simplest possible models. We started from a simple polarizable homogeneous subsurface, increasing the model structure by considering a two-layered medium with only one polarizable layer, and so on. This searching process was stopped when a reasonably low misfit error was obtained. Only at one site (sounding 37) we could not obtain any model that reproduced the data. The remaining 21 models resulted of two layers, but in 10 of them one of the layers is not dispersive. The average misfit error for this set of models is higher (2.5) than the corresponding average (1.4) of the non-polarizable models. The four Cole-Cole parameters for each layer and the thickness of the first layer are shown in Figure 11. The following features can be deduced from the behavior of these parameters:
a) The lateral correlation between parameters of contiguous models is quite poor, indicating that the Cole-Cole models are not regional but local. Given the large separation between soundings, this is not surprising.
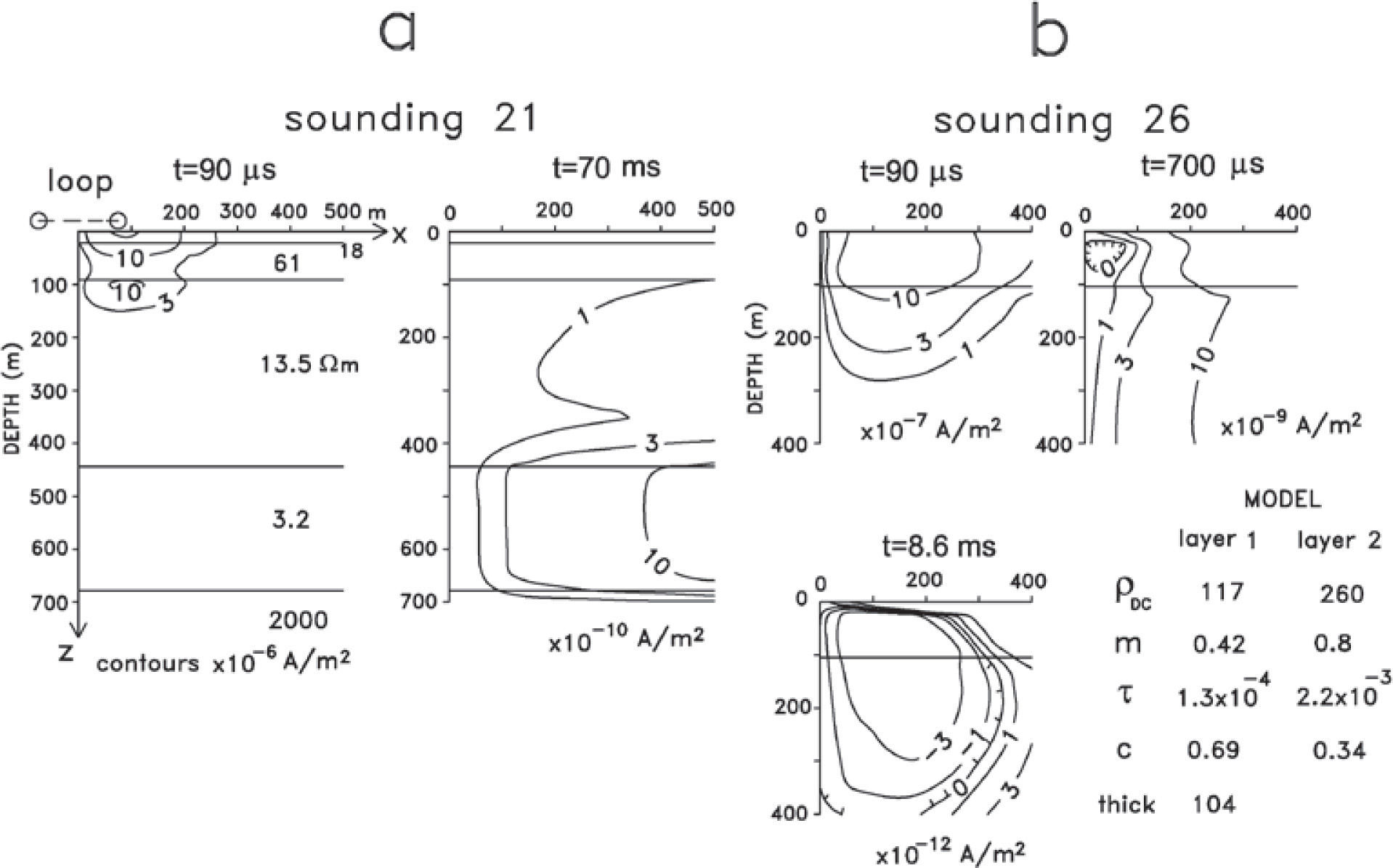
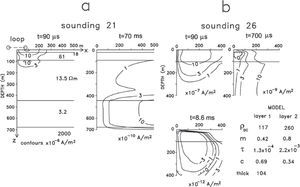
b) The mean depth to the second layer (60 m) is significantly less than the mean depth to the deepest layer in the non-polarizable models (155 m). This suggests that the maximum depth of exploration is significantly reduced when the subsurface is polarizable. For these cases we cannot use expression (1) to estimate the maximum depth, simply because frequency-independent resistivities were employed in its derivation. No similar expression has been proposed in the literature, apparently because the number of possible parameter combinations is too large; for a two layer model, instead of three parameters for the non-polarizable case, there are nine parameters for the polarizable case. To support the argument of a decreased depth of exploration we calculated the subsurface current density at selected times after the current shut-off for a non-polarizable model (sounding 21, Figure 12a) and a polarizable model (sounding 26, Figure 12b). The source in both models is a 150 by 150 m loop located at the origin where a dc current of 1 A is injected. The current density contours are plotted only in the quadrant x≥0, z≥0; in the quadrant x≤0, z≥0 the contours have the same shape but with opposite polarity. As a reference, the measured responses of these models are shown in Figure 4. For the model of sounding 21 (Figure 12a), the two times correspond to the earliest (90 µs) and latest (70 ms) recorded times. At 90 µs the maximum current density is located in the close vicinity of the loop and has a magnitude of close to 30 × 10−6 A/m2. At 70 ms the maximum has migrated down and sideways, while its intensity has decreased substantially to about 10 × 10−10 A/m2. This attenuation and migration of the maximum current density with time was nicknamed as “smoke rings” by Nabighian (1979). Notice that the maximum has been trapped by the conductive layer of resistivity 3.2 Ωm and that little current is flowing in the resistive substratum. This explains why the resistivity of the fifth layer is poorly resolved (Figure 9b).
The eight Cole-Cole parameters and thickness of the first layer for the polarizable model are indicated in Figure 12b. The current densities are shown at three times: earliest (90 µs), intermediate (700 µs) and latest (8.6 ms). Instead of 70 ms as the latest time, we chose 8.6 ms because for later times the voltages flatten, suggesting the noise level has been reached. At 90 us the maximum is in the first layer and has a magnitude of 10 x 107 A/m2. At 700 µs the maximum has attenuated, deepened and moved away from the loop. Notice that close to the loop a zone of negative values, bounded by the zero contour, has developed. Within this contour the current has reversed its direction. This instant corresponds with the time where the voltage changes polarity (see Figure 4). At 8.6 ms the subsurface region with reversed direction has increased in area but its magnitude has also been attenuated. Smith and West (1988) proposed a physical model for the induced current in a polarizable subsurface circuit. The total induced current is the sum of a Fundamental Induced Current (FIC) and a Polarization Current (PC). These two current modes are not separable. The PC always opposes the sense of the FIC. As the FIC usually decays faster than the PC, at late times the PC is greater, producing the negative late-time voltages at the surface. This behavior is similar to the current densities of Figure 12b. At the shortest time the FIC dominates, producing the positive voltages in the receiver. At 700 µs the total current close to the loop has changed its direction because the PC is greater than the FIC, resulting then negative voltages at the receiver. At the latest time the PC clearly dominates the FIC. The end product of these two current modes opposing each other at all times is a diminished depth of investigation.
It is worth mentioning that inverting only the positive voltages of a sounding affected by IP with an algorithm that does not include a polarizable resistivity will give an incorrect result. The opposing Polarization Current is present at all times, not only in late times when the surface voltages have changed sign.
c) The zero-frequency resistivities in the southwestern (SW) group of soundings (6.6 < 16 < 38Ωm) are lower than those of the northeastern (NE) group (36 < 110 < 340Ωm). The +/- one standard deviations in these estimates are not symmetric with respect to the mean because they are defined in a logarithmic scale. The relatively low values in the SW group might be due to membrane polarization associated with the presence of clay in sands (Ward, 1990). In the NE group the likely source of IP is metallic polarization due to mineral grains with electronic conduction, such as sulphides and/or magnetite. In this zone the large El Arco porphyry copper deposit (Coolbaugh et al., 1995) is located, where significant IP anomalies have been measured (Farías, 1978; Flores and Peralta-Ortega, 2009). Other four IP anomalous zones in the vicinity of our traverse were surveyed and associated with the presence of pyrite, magnetite or copper sulphides by Farías (1978).
ConclusionsWe showed the method proposed by Spies (1989) is a reliable technique for estimating the MDI. In 14 out of the 16 non-polarizable soundings the MDI was deeper than the deepest interface estimated from the inversion of the data. In the remaining two models we found the reverse situation, leading to an apparent discrepancy. However, this discrepancy was explained by an equivalence problem associated with a conductive layer and by a lower noise level. Two minor modifications were applied to the Spies expression before using it; a refinement in the departure time by considering different resistivity contrasts, and the estimation of the noise level directly from the field data. The MDI turns out to be a very useful tool for estimating how far beyond the last interface is being explored. An interesting result was obtained in the spatial character of the Vizcaino data; all soundings located on the Vizcaino basin were not affected by induced polarization, but those placed on plutonic, volcanic or metamorphic rocks were affected.
The dipping conductor of resistivities less than 3.2 Ωm was interpreted as the intrusion of saline water in the granular sediments of the Vizcaino basin. Its large lateral extent of more than 70 km is not common. For polarizable soundings the Spies method is not valid. We do not propose an analogous method for this situation but show that the MDI is significantly reduced compared to that of non-polarizable models. The estimated stationary noise level for the NW-Mexico data set was 1.4 × 1010 V/m2, close to the 2 × 1010 V/m2 value reported by McNeill (1980). No difference was found in the noise level between summer and winter in this data set.
This work was funded by CICESE and CONACYT projects. We thank S. Espinoza, H. Benitez, F. Uribe, and J. Parra for their invaluable help during the field work.