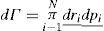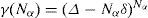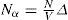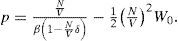Basándonos en los datos experimentales en fluidos encontramos, en referencias Robles-Domínguez et al. (2007) y Robles-Gutiérrez et al. (2010), que en el Campo Electromagnético existen realmente nuevas fuerzas no-aditivas entre 3 o más moléculas; postulamos que también existen nuevas fuerzas no-aditivas en el Campo Gravitacional y al agregarlas a la Ley de Gravitación Universal de Newton éstas dan lugar a la Masa Obscura.
Experimental data in fluids suggest that nonadditive electromagnetic forces between 3 or more molecules account for the existence of critical points, triple states and phase transitions (Robles-Domínguez et al., 2007; Robles-Gutiérrez et al., 2010). Similar nonadditive forces between 3 or more molecules in the gravitational field incorporated into Newton’s universal gravitational law may also explain the existence of dark matter.
Zwicky (1933) interpreted some observations of the Coma Cumulus and concluded that its gravitational mass is several times the luminous mass. He called the difference the dark mass. This work is regarded as the starting point of the Dark Matter problem. Sciama (1993) discussed several theories intended to explain this interesting phenomenon, including the existence of new particles which do not emit electromagnetic radiation but contribute to the gravitational mass, but without experimental confirmation. Other solutions involve a mathematical modification of Newton’s laws but insufficient physical reasons in support of such modification have been presented.
Robles-Domínguez (2007) and Robles-Gutiérrez (2010) proposed new intermolecular forces in field theory that arise from interactions between three and more molecules. We showed that such interactions have not been previously considered, and that such nonadditive electromagnetic forces are needed in order to account for the experimental data on critical points in fluids, triple states, and liquid-solid phase transitions. We call these forces nonadditive because their mathematical form differs from that of binary, or additive, forces. Nonadditive forces are important within relatively short distances. In gases the mean intermolecular distances are large and nonadditive forces are not significant as compared with additive forces. In liquids and solids, however, the density is large and the mean intermolecular distance is very short. In this case the nonadditive forces may overcome the additive forces. We show that the existence of liquid and solid phases is experimental proof for the existence of nonadditive forces.
In Section 2 of this paper we provide a short derivation of the equation of state in fluids from statistical mechanics as provided in greater detail elsewhere (Robles-Domínguez, 2007; Robles-Gutiérrez, 2010). This derivation includes nonadditive forces. In Section 3 we apply the equivalent equation from section 2 to the gravitational field using data from Begeman (1987) on galaxy NGC 3198, and we show how dark mass will arise.
2Nonadditive forces in fluidsMolecules in a fluid interact mainly through the electromagnetic field: the gravitational, weak and strong nuclear fields are irrelevant. We consider a monocomponent fluid that contains N molecules at an absolute temperature T, inside a volume V, which is described in Statistical Mechanics by the canonical partition function Z:
where β=1kBT, kB is Boltzmann’s cons-tant, E is
the Energy of the system, Γ=Γri_;,pi_;,i=1…N is the phase space of the system, ri and pi_; are the vector position and momentum of the ith particle, N is the total number of molecules, V is the volume of the system, and T is the absolute temperature. We may write
where K is the total kinetic energy of the system and Φ is the total potential energy; and
as we are considering a single-component fluid.
Integration of (1) over the momenta is well known (Reichl, 1998) and the result is
where λ = h(2πmkBT)−½ and h is Planck’s Constant.
2.1van der Waals equation of stateEquation (4) considers only the positions of all N molecules in the system. Ornstein and van Kampen (in Reichl, 1998), consider than the molecules interact with the next binary additive potential energy
where hc stands for “hard core”. The subscript 2 denotes binary additive interaction; ri and rj are position of molecules i and j respectively, and it is assumed that the molecules have a hard core of radius a and a smooth attractive binary-additive interaction Φ2 with a very long range. Ornstein and van Kampen assume that the density is high enough and the range of the attractive interaction is wide enough so that many molecules will interact simultaneously. Volume V may be divided in cells of volume ∆ large enough to contain many molecules but small enough so that the attraction between molecules within a given cell is constant regardless of separation in the cell. If the number of molecules in cell α is Nα we may write, from (4) and (5):
where
and δ is the volume of the hard core of one molecule.
The most probable distribution of molecules in V at thermodynamic equilibrium is the uniform distribution
for all α, and defining
for all α.
We use mean field theory and the definition of Helmholtz energy A:
The thermodynamics of the systems is deduced from Helmholtz energy A, ie,: fluids. Pressure p is defined as
Using equations (5) through (11) we obtain van der Waals equation of state
Let us express this equation in terms of fluid density:
where m is the mass of one molecule; and we find
where
In equation (14) the first term of the right-hand side contains the hard core contribution and the second contains all binary-additive interactions. This equation can approximately represent the pressure of the gaseous phase but cannot describe the pressures of the liquid and solid phases in the fluid (Reichl, 1998).
In the van der Waals equation of state (14), we note three important properties:
- 1.
The second term on the right-hand side contains all binary-additive intermolecular interactions;
- 2.
The two terms on the right-hand side are linearly independent in a functional-analysis sense; and
- 3.
This equation cannot reproduce the experimental data in fluids.
Fourier theory (Kolmogorov and Fomin, 1961) may be used to describe a function as a Fourier series. Properties 2 and 3 above mean that the van der Waals equation contains only two terms of the infinite series which we need to reproduce the experimental data of fluids. Property 1 means that the last right-hand terms must be expressed in terms of new forces. Thus in terms of linearly independent nonadditive forces, the third term will contain all third-order nonadditive interactions, the fourth term all fourth-order nonadditive interactions and so on. The total pressure may be written as follows:
where phc contains the hard core interactions, p2
the total scalar additive binary potential energy, p3 the total scalar third-order or triadic nonadditive potential energy, p4 the total scalar fourth-order (or tetradic) nonadditive potential energy, and so on. Thus
Equations (17), (18), etc. constitute an infinite Fourier series of independent linear functions.
The hard core cannot allow the fluid volume to vanish and the density cannot be infinite: thus the Fourier series can converge.
Nonadditive forces in the gravitational fieldIn Robles-Gutiérrez et al. (2010), we postulated the existence of nonadditive gravitational forces in the gravitational field. Before we extend the theory to galaxies let us describe the astronomical observations of galaxy NGC 3198 (Begeman, 1987). Figure 1 shows Begeman’s graph of rotational velocity vs. radius in minutes of arc between the vector from Earth to the object and the vector from Earth to the center of NGC 3198. The distance from Earth to NGC 3198 is 9.2 Mpc. The maximum distances of masses from the center of the galaxy should provide information on the total mass of the galaxy.
Observations of NGC 3198 (From Begeman, 1987).
The galaxy may be likened to a gas inside a jar. The jar exerts a pressure on the gas. In a state of equilibrium the pressure should be constant everywhere in the gas. In the case of a galaxy the peripherical stars plus gas are confined to a galactic volume by a pressure called galactic pressure, which equals gravity per unit area. It is equal to the centripetal force per unit area, and it is not identical at all points of the galaxy.
The centripetal force on an object l is equal to the gravitational force on this object, which is the sum of all gravitational interactions, additive and nonadditive:
where subscript l refers to the peripheral stars or gas clouds observed by Begeman in NGC 3198 galaxy and subscript j refers to the forces. Let j = 2 refer to binary additive forces, j = 3 to ternary nonadditive forces and so on. We omit the hardcore term because m, is far away from the galaxy.
If we divide (21) by the unit of area we obtain the equation of the pressures, as in a fluid:
But a similar expression should obtain for the centripetal and gravitational accelerations, after dividing equation (21) by m which is necessary because the mass m is unknown. Thus the centripetal acceleration equals the gravitational acceleration gl generated by the total galaxy mass including the dark mass, over m, which is the sum of all binary-additive contributions g12 plus all third-order nonadditive accelerations g13, and so on, over ml:
Here the first term of the summand is Newton’s acceleration of gravity:
Written out as
By analogy with the case of a fluid we may write gl, in terms of an infinite density series:
where the density ρl equals the luminous mass Mllum within a sphere of radius rl from the center of the galaxy to ml over the volume of the sphere. Equation (26) may be written
or
If
this term will contribute to dark matter.
The series of equation (28) converges because the density is finite. We may consider only the first and second terms of the series and neglect the small higher terms. Thus
from which
and the terms inside the square brackets are the real mass.
Begeman (1987) obtained the following values of rl =30 kcp, Vc=150 km/s for this galaxy:
From Equations (30), (31) and (32) we find
and by introducing this value in (31) we obtain, for l=30 kcp,
As this value is positive, we fnd that
This result proves that the dark mass must be due to the presence of nonadditive forces.
ConclusionsWhenever nonadditive interactions, that are multi-body terms, are taken into account, Newton’s law of universal gravitation is sufficient to explain the astronomical observations of a “dark mass”. The example of Galaxy NGC 3198 (where substantial amounts of dark matter had been detected) shows that nonadditive terms in Equation (25), a generalization of Newton’s law of gravitation, can provide a satisfying explanation of the difference between luminous and gravitational matter.
The valuable contribution of L.A. Sylvia Robles Gutiérrez is gratefully acknowledged.