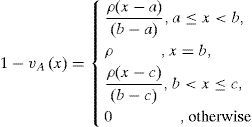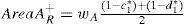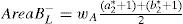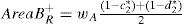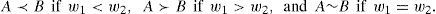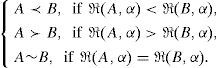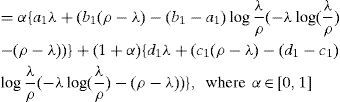The main aim of this paper is to propose a new approach for the ranking of exponential vague sets. The concepts of exponential vague sets and arithmetic operations between two exponential vague sets are introduced. The shortcomings of some existing ranking approaches for the ranking of generalized fuzzy sets and intuitionistic fuzzy numbers are pointed out. The proposed method consider not only the rank but also the decision maker optimistic attitude and it is shown that proposed ranking approach is more intuitive and reasonable as compared to existing ranking approaches. Also the proposed ranking function satisfies the reasonable properties for the ordering of fuzzy quantity. For practical use, proposed ranking approach is applied to decision making problem.
El objetivo principal de este trabajo es proponer un nuevo enfoque para la clasificación de los conjuntos inciertos exponenciales. Se introducen los conceptos de conjuntos inciertos exponenciales y operaciones aritméticas entre dos conjuntos inciertos exponenciales. Se señalan las deficiencias de algunos enfoques de clasificación existentes para la clasificación de los conjuntos difusos generalizados y de los números difusos intuicionistas. El método propuesto toma en cuenta no sólo el rango, sino también el enfoque optimista para toma de decisiones y se muestra que el enfoque de clasificación propuesto es más intuitivo y razonable en comparación con los enfoques de clasificación existentes. Asimismo, la función de clasificación propuesta satisface las propiedades razonables para el ordenamiento de la cantidad difusa. Para usos prácticos, el enfoque de clasificación propuesto se aplica al problema de toma de decisiones.
The theory of fuzzy sets was first introduced by Zadeh [37] in 1965. Since then, the theory of fuzzy sets is applied in many fields such as pattern recognition, control theory, management sciences and picture processing, etc. In the field of fuzzy mathematics many mathematical theory such as fuzzy optimization, fuzzy topology, fuzzy logic, fuzzy analysis and fuzzy algebra etc. are obtained [3, 10, 14, 22, 23, 29, 32, 35]. In many applications of fuzzy set theory to decision making, we are faced with the problem of selecting one from a collection of possible solution, and in general we want to know which one is the best. This selection process may require that we rank or order fuzzy numbers. In order to rank fuzzy numbers, one fuzzy number needs to be evaluated and compared to others but this may not be easy. As known, the real numbers in can be linearly ordered by, however, fuzzy numbers cannot be done in such a way. Since fuzzy numbers are represented by possibility distributions, they can overlap with each other and it is difficult to determine clearly whether one fuzzy number is larger or smaller than the other.
To the task of comparing fuzzy numbers, many authors proposed fuzzy ranking methods [5, 6, 8, 9, 12, 15, 16, 17, 18, 20, 25, 30, 31, 34]. But among all the methods, most of them consider only one point of view on comparing fuzzy quantities in spite of the different demand of the decision maker, so some improved methods have been brought forward which lead to produce different rankings for the same problem. Until now, there have not one unify method to this problem. Fuzzy set theory [37] has been shown to be useful tool to handle the situations, in which the data is imprecise, by attributing a degree to which a certain object belongs to a set. In real life, a person may assume that an object belongs to a set, but it is possible that he is not sure about it. In other words, there may be hesitation or uncertainty thatwhether an object belongs to a set or not. In fuzzy set theory, there is no means to incorporate such type of hesitation or uncertainty. A possible solution is to use intuitionistic fuzzy set [2] and vague set [11]. Bustince and Burillo [4] pointed out that the notion of vague set is the same as that of intuitionistic fuzzy set. Lu and Ng [21] proved that vague sets is more natural than using an intuitionistic fuzzy set. Several authors [19, 24, 27, 28] have proposed different methods for the ranking of intuitionistic fuzzy sets but to the best of our knowledge till now there no method in the literature for the ranking of vague sets.
The main aim of this paper is to propose a new approach for the ranking of exponential vague sets. The concepts of exponential vague sets and arithmetic operations between two exponential vague sets are introduced. The shortcomings of some existing ranking approaches [8, 19] for the ranking of generalized fuzzy sets and intuitionistic fuzzy numbers are pointed out. Also it is shown that proposed ranking approach is more intuitive and reasonable as compared to existing ranking approaches Rest of the paper is organized as follows: In Section 2, some basic definitions related to generalized fuzzy sets, intuitionistic fuzzy sets, vague sets and arithmetic operations between vague sets are presented. In Section 3, a brief review of the existing approach [8] for the ranking of generalized trapezoidal fuzzy numbers and the existing approach [19] for the ranking of intuitionistic fuzzy numbers are presented. In Section 4, the shortcomings of existing approaches [8, 19] are discussed. In Section 5, a new approach is proposed for the ranking of exponential vague sets. In Section 6, it is proved that the proposed ranking function satisfies the reasonable properties for the ordering of fuzzy quantities and results are compared with some existing approached. In Section 7, an application of proposed ranking method to decision making is presented. Section 8 draws the conclusions.
2PreliminariesIn this section some basic definitions related to generalized fuzzy sets, intuitionistic fuzzy sets, vague sets and arithmetic operations between exponential vague sets are presented.
2.1Generalized Fuzzy SetsDefinition 1.[6] A fuzzy set A, defined on the universal set of real numbers R, is said to be a generalized fuzzy number if its membership function has the following characteristics:
- 1.
μA :R→[0,w] is continuous.
- 2.
μA(x) = 0, for all x∈(−∞,a∪d,∞).
- 3.
μA (x)is strictly on[a,b]and strictly decreasing on [c,d].
- 4.
μA (x) = w, for all x ∈ [b,c], where 0<w≤1.
[6] A generalized fuzzy number, denoted as A = (a,b.c,d;w) is said to be a generalized trapezoidal fuzzy number if its membership function is given by
2.2Intuitionisitic Fuzzy SetsDefinition 3.[19] An intuitionistic fuzzy set A = {(x, μa (x),va (x)) | x ∈ X} on the universal setX is characterized by a truth membership function μa(x), μa(x):X→[0,1] and a false membership vA(x),vA(x) :X→ [0,1]. The values μa(x) and vA(x) represents the degree of membership and degree of non-membership of x and always satisfies the condition μA(x) + vA ≤1. The value 1−μA(x) + vA represents the degree of hesitation of x ∈ X.
Definition 4.[19] An intuitionistic fuzzy set A, defined on the universal set of real numbers R, said to be triangular intuitionistic fuzzy number, denoted as A = (a,b,c;w;u), if degree of membership and degree of non-membership are given by:
and
respectively. The values w and u represent the supremum of the degree of membership and the infimum of the degree of non-membership membership, respectively.2.3Vague sets and exponential vague setsDefinition:5.[11] A vague set A = {(x, μA (x),1 - vA (x)) | x ∈ X} on the universal set X is characterized by a truth membership function μa(x), μa(x):X → [0,1] and a false membership vA(x),vA(x) :X → [0,1]. The values μa(x) and vA(x) represents the degree of membership and degree of non-membership of x and always satisfies the condition μA(x) + vA ≤1. The value 1 − μA(x) + vA represents the degree of hesitation of x ∈ X.
Definition 6.[11] A vague set A, defined on the universal set of real numbers R, denoted as A = (a,b,c,d;λ,ρ), where a ≤ b ≤ c ≤ d and λ ≤ ρ, is said to be a triangular vague set if degree of membership, μA(x), and complement of the degree of non-membership, 1−vA(x), are given by
and
Definition 7.A vague set A, defined on the universal set of real numbers R, denoted as A = (a,b,c,d; λ, ρ), where a ≤ b ≤ c ≤ d and λ ≤ ρ, is said to be a exponential vague set if degree of membership, μa(x) , and complement of the degree of non-membership, 1−vA(x), are given by
and
2.4Arithmetic operations between exponential vague setsLet A = (a1,b1,c1,d1;λ1, ρ1) and B = (a2,b2,c2,d2; λ2,ρ2) be two exponential vague sets then
- (i)
A⊕B=(a1+a2,b1+b2,c1+c2,d1+d2;min(λ1,λ2),min(ρ1,ρ2)
- (ii)
AΘB = (a1 − d2,b1 − c2,c1 − b2,d1 − a2;min(λ1, λ2),min(ρ1, ρ2)
- (iii)
αA=(αa1,αb1,αc1,αd1;λ1,ρ1),α≥0(αa1,αc1,αb1,αd1;λ1,ρ1),α<0
In this section, the existing ranking approach [8, 19] are briefly discussed.
3.1Chen and Sanguansat ranking approachLet A = (a1, b1,c1, d1;wA)and B = (a2, b2, c2, d2;wB)be two generalized fuzzy numbers, then use the following steps to compare A and B.
Step 1.Standardize each generalized fuzzy number A and B into A*and B* as follows:
where,k=maxa1,b1,c1,d1, |a1|,|b1|,|c1|,|d1|denoted the absolute value of a1,b1, c1, d1 respectively, and a1,b1,c1,d1 denoted the upper bound of |a1|,|b1|,|c1|,|d1| respectively.
Where k=maxa2,b2,c2,d2, |a2|,|b2|,|c2|,|d2| denoted the absolute value of a2,b2,c2,d2 respectively, and a2,b2,c2,d2 denoted the upper bound of |a2|,|b2|,|c2|,|d2| respectively.
Step 2.Calculate the areas AreaAL− and AreaAR−, respectively, which denote the areas from the membership function curves of μAL and μAR respectively, to the membership function curve of the generalized fuzzy number (−1, −1, −1, −1; wA) respectively, where
and
Then, calculate the areas AreaAL+ and AreaAR+, respectively, which denote the areas from the membership function curves of μAL and μAR defined in Eqs. (3) and, (4), respectively, to the membership function curve of the generalized fuzzy number (−1, −1, −1, −1;wA), where
Step 3.Calculate the values
and
Step 4.Calculate the ranking score Score(A*) and Score(B*) of each generalized trapezoidal fuzzy number A* and B*as follows:
and
The following three cases may arise
- (i)
If Score(A*) > Score(B*), then A≻B.
- (ii)
If Score(A*) < Score(B*), then A≺B.
- (iii)
If Score(A*) = Score(B*), then A~B
Let A = (a1,b1,c1;w1,u1) and B = (a2,b2,c2;w2,u2)be two triangular intuitionistic fuzzy numbers then use the following steps to compare A and B:
Step 1.Calculate
V(A,α) = Vμ(A) + α(Vv(A) − Vμ(A)),
A(A,α) = Av(A) − α(Av(A) − Aμ(A)), where
and
V(B,α) = Vμ(B) + α(Vv(B) − Vμ(B))
A(B,α) = Av(B) − α(Av(B) − Aμ(B)), where
Step 2.Calculate
The following three cases may arise
- (i)
If ℜ(A,α) < ℜ(B,α), thenA≺B.
- (ii)
If ℜ(A,α) > ℜ(B,α), then A≻B.
- (iii)
If ℜ(A,α) = ℜ(B,α), then A~B
In this section, the shortcomings of the existing ranking approaches [8, 19] are Pointed out.
4.1Shortcomings of Chen and Sanguansat ranking approachHere we pointed out the shortcomings of Chen and Sanguansat ranking approach [8], on the basis of reasonable properties of fuzzy quantities [34] and on the basis of height of fuzzy numbers.
4.1.1On the basis of reasonable properties for fuzzy quantities.With the help of some examples it shown that the ranking function, proposed by Chen and Sanguansat [8] does not satisfy the reasonable property, A≻B⇒AΘB≻BΘB, for the ordering of fuzzy quantities i.e., according to Chen and Sanguansat approach [8] A≻BAΘB≻BΘB, which is a contradiction according to Wang and Lee [34].
Example 1.Let A = (0.1,0.3,0.3,0.5;0.8), and B = (0.1,0.3,0.3,0.5;1) be two generalized trapezoidal fuzzy numbers then according to Chen and Sanguansat approach [8] B≻A but BΘA≺AΘA i.e., B≻A⇏BΘA≻AΘA.
Example 2.Let A = (0.1,0.3,0.3,0.5;1), and B = (0.3,0.5,0.5,0.7;1) be two generalized trapezoidal fuzzy numbers then according to Chen and Sanguansat approach [8] B≻A but BΘA≺AΘA i.e., B≻A⇏BΘA≻AΘA.
Example3.Let A = (−0.5, −0.3, −0.3, −0.1;1), and B = (0.1,0.3,0.3,0.5;1) be two generalized trapezoidal fuzzy numbers then according to Chen and Sanguansat approach [8] B≻A but BΘA≺AΘA i.e., B≻A⇏BΘA≻AΘA.
4.1.2On the basis of height of fuzzy numbersIn some cases Chen and Sanguansat approach [8] indicates that the ranking of fuzzy numbers depends upon height of fuzzy numbers while in several cases it indicates that the ranking of fuzzy number does not depend upon the height of fuzzy numbers, which is not reasonable.
Let A = (a1,a2,a3,a4;w1)and B = (a1,a2,a3,a4;w2) be two generalized trapezoidal fuzzy numbers then according to Chen and Sanguansat approach [8]
Case (i) If (a1+a2+a3+a4) ≠ 0 then
Case (ii) If (a1+a2+a3+a4) = 0 then A~B for all values of w1 and w2.
Example 4.Let A = (1,1,1,1;w1) and B = (1,1,1,1;w2) be two generalized trapezoidal fuzzy numbers then according to Chen and Sanguansat approach [8]
Example5.Let A = (−0.4, −0.2, −0.1,0.7;w1) and B = (−0.4, −0.2, −0.1,0.7;w2), be two generalized trapezoidal fuzzy numbers then A~B for all values of w1 and w2.
According to Chen and Sanguansat approach [8], in first case ranking of fuzzy numbers depends upon height and in second case ranking does not depend upon the height which is not reasonable.
4.2Shortcomings of Li ranking approachLi [19] pointed out the shortcomings of all the existing approaches for the ranking of intuitionistic fuzzy numbers and proposed a new approach for the ranking of intuitionistic fuzzy numbers. In this section, the shortcomings of existing approach [19] are pointed out.
(i) The existing results, presented in Theorem 1 to Theorem 6 [19], are correct only if both ~ A and ~B are intuitionistic fuzzy numbers with same degree of membership and the same degree of non-membership but in the real life problems, we need to compare the intuitionistic fuzzy numbers with different degree of membership and degree of non-membership.
If we have two intuitionistic fuzzy numbers with unequal degree of membership and degree of non-membership than the existing approach [19] can not be used, also in that case the ranking function does not satisfy the reasonable property,A≻B⇒AΘB≻BΘB for the fuzzy quantities [34] i.e., ℜ(A,α)>ℜ(B,α)ℜ(AΘB,α)>ℜ(BΘB,α).
Example 6.Let A = (1,3,5;0.3,0.2) and A = (4,8,9;0.4,0.1) be two triangular intuitionistic fuzzy numbers. According to existing ranking approach [19] the values of ℜ(A,12) and ℜ(B,12) are 0.6347 and 0.822 respectively so A≺B but the values of ℜ(AΘB) and ℜ(BΘB) are −10.2 and 0 respectively which is a contradiction i.e., ℜ(AΘB,12)≯ℜ(BΘB,12)
Hence, the results, obtained by using the existing ranking approach [19], are valid for intuitionistic fuzzy numbers with equal degree of membership and degree of non-membership.
(ii) In some cases, the existing approach [19] indicates that the ranking of intuitionistic fuzzy numbers depends upon degree of membership and degree of nonmembership of intuitionistic fuzzy numbers while in several cases the ranking does not upon degree of membership and degree of non-membership of intuitionistic fuzzy numbers.
Let A = (a1,a2,a3;w1,u1) and B = (a1,a2,a3;w2, u2) be two intuitionistic fuzzy numbers then according to existing approach [19].
Case (i) If (a1 +4a2+ a3) ≠ 0 then
Case (ii) If (a1+4a2+a3) = 0 then A~B for all values of w1,u1,w2 and u2.
Example 7.Let A = (−0.2,0,0.2; w1, u1) and B = (−0.2,0,0.2;w2,u2) be two intuitionitsic fuzzy numbers then, according to existing approach [19] A~B for all values of w1, u1, w2and u2.
Example8.Let A = (−8,1,4; w1,u1) and B = (−8,1,4;w2, u2) be two intuitionitsic fuzzy numbers then, according to existing approach [19] A~B for all values of w1, u1,w2 and u2.
Example 9.Let A = (1,1,1;w1,u1) and B = (1,1,1;w2,u2) be two intuitionitsic fuzzy numbers then, according to existing approach [19]
- •
A≺B if α(1−u1) + (1−α)w1 < α(1−u2) + (1−α)w2
- •
A≻B if α(1−u1) + (1−α) w1 > α(1−u2) + (1−α)w2,
- •
A~B if α(1−u1) + (1−α) w1 = α(1−u2) + (1−α)w2,
According to existing approach [19], case (i) shows that ranking of fuzzy numbers depends upon degree of membership and degree of non-membership of intuitionistic fuzzy numbers while case (ii) shows ranking does not depend upon degree of membership and degree of non-membership of intuitionistic fuzzy numbers, which is again not reasonable.
5Proposed approachLet A = (a1,b1,c1,d1;λ1,ρ1) and B = (a2,b2,c2,d2;λ2,ρ2) be two exponential vague sets, where a1 ≤ b1 ≤ c1 ≤ d1 ≤ λ1 ≤ ρ1 and a2 ≤ b2 ≤ c2 ≤ d2 ≤ λ2 ≤ ρ2 then use the following steps to compare A and B :
Step 1.Find (λ,ρ) = (min(λ1,λ2),min(ρ1,ρ2)).
Step 2.Find
Now, ℜ(A) = ℜ(Aλ) + ℜ(Aρ−λ)
Similarly ℜ(B) = ℜ(Bλ) + ℜ(Bρ−λ)
Step 3.Check ℜ(A) > ℜ(B) or ℜ(A) < ℜ(B) or ℜ(A) = ℜ(B)
Case (i) if ℜ(A) > ℜ(B) then A≻B∀α.
Case (ii) if ℜ(A)< ℜ(B)then A≺B∀α.
Case (i) if ℜ(A) = ℜ(B)then A~B∀α
It can be easily shown that the proposed ranking formula for the ordering of vague sets is generalization of existing ranking approaches [1, 7, 20].
Corollary 1.If 0 ≤ λ = ρ ≤ 1, then (17) reduces to ℜ(A)=λ(a1+d1)2, which is the ranking formula for generalized exponential fuzzy numbers [7].
Corollary 2.If 0 ≤ λ = ρ ≤ 1 and left and right membership functions of A as linear functions, then (17) reduces to ℜ(A)=12(λ(a1+d1)+λ(b1−a1+c1−d1)3)=λ(a1+b1+c1+d1)4, which is the ranking formula for generalized trapezoidal fuzzy numbers [20].
Corollary 3.If 0 ≤ λ = ρ ≤ 1, b1 = c1 and left and right membership functions of A as linear functions, then (17) reduces to ℜ(A)12(λ(a1+d1)+λ(b1−a1+b1−d1)3)=λ(a1+2b1+d1)4, which is the ranking formula for generalized triangular fuzzy numbers [20].
Corollary 4.If 0 ≤ λ = ρ ≤ 1 and left and right membership functions of A as linear functions, then (17) reduces ℜ(A)12((a1+d1)+(b1−a1+c1−d1)3)=(a1+b1+c1+d1)4 which is the ranking formula for normal trapezoidal fuzzy numbers [1, 20].
Corollary 5.If 0 ≤ λ = ρ ≤ 1, b1 = c1 and left and right membership functions of A as linear functions, then (17) reduces to ℜ(A)12((a1+d1)+(b1−a1+b1−d1)3)=(a1+2b1+d1)4, which 2 is the ranking formula for generalized triangular fuzzy numbers [1,20].
Corollary 6.If left and right membership functions of A as linear functions, then (17) reduces toℜ(A)=α{λ(a1+b1)2+(ρ−λ)2(b1+a1+λρ(b1−a1))}+(1−α){λ(d1+c1)2+(ρ−λ)2(d1+c1+λρ(d1−c1))}, which is the ranking formula for trapezoidal vague sets.
Corollary 7.If left and right membership functions of A as linear functions and b = c, then (17) reduces to ℜ(A)=αλ(a1+b1)2+(ρ−λ)2(b1+a1+λρ(b1−a1))+(1−α)λ(d1+c1)2+(ρ−λ)2(d1+b1+λρ(d1−b1)), which is the ranking formula for triangular vague sets.
6Results and discussionIn this section, it is proved that the proposed ranking function satisfies the reasonable properties for the ordering of fuzzy quantities. Also some examples are taken to show, shortcoming that exits in existing methods are not occurred in proposed approach.
Results of the proposed approach are compared with the existing ranking approaches.
6.1Reasonable properties: Validation of proposed ranking approachWang and Kerre [33] proposed some axioms as a reasonable properties of ordering fuzzy quantities for the ranking approach ℜ. These properties are:
P1. For an arbitrary subset S of F and A ∈ S, A≻˜A by ℜ on S where, F is a set of exponential vague sets.
P2. For an arbitrary subset S of F and a,b ∈ s, A≻˜B and B≻˜A by ℜ on S, then A~B by ℜ on S.
P3. For an arbitrary subset S of F and a,b,c ∈ s, A≻˜B and B≻˜C and by ℜ on S, then A≻˜C by ℜ on.
P4. If A∩B=0 and A is on the right of B then A≻˜B.
P5. Let S and S′ be two arbitrary finite sets of exponential vague sets in which proposed ranking function can be applied, and A,B∈S∩S, we obtain the ranking order A≻˜B by ℜ in S iff A≻˜B by ℜin S′.
P6. If A≻˜Bby ℜ, then A+C≻˜B+C by ℜwhen C ≠ 0.
P7. Let A,B,AC,BC be the elements of Sand C ≥ 0. A≻˜B by ℜ⇒AC≻˜BC by ℜ.
Now, we prove that proposed ranking function satisfies the some of the reasonable properties.
Proposition 1.For an arbitrary subset S of F and A ∈ S, A≻˜A by ℜ on S where, F is a set of exponential vague sets.
Proof.Since A ∈ S ⇒ A,A ∈ S and ℜ(A)≥ℜ(A)⇒A≻˜A by proposed ranking function.
Proposition 2.For an arbitrary subset S of F and A,B ∈ S,A≻˜B and B≻˜A by ℜ on S, then A~B by ℜon S.
Proof.By proposed ranking function, A≻˜B means ℜ(A) ≥ℜ(B) and B≻˜A means ℜ(A)≤ ℜ(B) and hence ℜ(A)=ℜ(B) ⇒ A~B.
Proposition 3.For an arbitrary subset S of F and A,B,C ∈ S, A≻˜B and B≻˜C by ℜ on S, then A≻˜C by ℜon.
Proof.A≻˜B⇒ℜ(A)≥ℜ(B) and B≻˜C⇒ℜ(B)≥ℜ(C). Since Ranking of exponential vague sets is a crisp number i.e., the ranking function map each exponential vague set into a real line, Therefore ℜ(A) ≥ ℜ(C) hence A≻˜C.
Proposition 4.If A∩B=0 and A is on the right of B then A≻˜B.
Proof.If A∩B=0 and A is on the right of B, then ℜ(A) ≥ℜ(B) ie., A≻˜B.
Proposition 5.Let S and S′ be two arbitrary finite sets of exponential vague sets in which proposed ranking function can be applied, and A,B∈S∩S, we obtain the ranking order A≻˜B by ℜ in S iff A≻˜B by ℜin S′.
Proof.Given that A≻˜B in S′⇔ℜ(A) ≥ℜ(B) in S′
Proposition 6.If A≻˜B by ℜ, then A+C≻˜B+C by ℜ when ℜ(C) ≠ 0 with degree of membership and non membership of C is less than or equal to the degree of membership of both, A and B.
Proof.If A≻˜B⇒ℜ(A)≥ℜ(B)⇒ℜ(A)+ℜ(C)≥ℜ(B)+ℜ(C)⇒ℜ(A+C)+ℜ(B+C) (∵ degree of membership and non membership of C is less than or equal to the degree of membership of both, A and B) ⇒A+C≻˜B+C.
We take the examples from Section 4, and solved them with proposed ranking approach, to show that shortcomings are now removed.
Example 10.Let A = (0.1,0.3,0.3,0.5;0.8), and B = (0.1,0.3,0.3,0.5;1) be two generalized trapezoidal fuzzy numbers then AΘB = (−0.4,0,0,0.4;0.8) and BΘB = (−0.4,0,0,0.4;1)
Step 1.min(0.8,1) = 0.8
Step 2.ℜ(AΘB) = 0.4(0.4−0.8α) and (ℜ(BΘB) = 0.4(0.4 −0.8α). Since, ℜ(AΘB) = ℜ(BΘB) ∀α, so AΘB~BΘB.
Example 11.Let A = (0.1,0.3,0.3,0.5;1), and B = (0.3,0.5,0.5,0.7;1) be two generalized trapezo idal fuzzy numbers then AΘB = (−0.6,-0.2,-0.2,0.2;1) and BΘB = (−0.4,0,0,0.4;1)
Step 1.min(1,1) = 1
Step 2.ℜ(AΘB)=12(−0.8α) and ℜ(BΘB)=12(0.4−0.8α).
For a pessimistic decision maker, with α = 0, ℜ(AΘB) = 0 and ℜ(BΘB) = 0.2. Since ℜ(AΘB) < ℜ(BΘB), so (AΘB)≺(BΘB).
For optimistic decision maker, with α = 1, ℜ(AΘB) = −0.4 and ℜ(BΘB) = −0.2. Since ℜ(AΘB) < ℜ(BΘB), so (AΘB)≺(BΘB).
For moderate decision maker with α = 0.5, ℜ(AΘB) = −0.2 and ℜ(BΘB) = 0. Since ℜ(AΘB) < ℜ(BΘB), so (AΘB)≺(BΘB).
Example 12.Let A = (−0.5, −0.3, −0.3, −0.1;1), and B = (0.1,0.3,0.3,0.5;1) be two generalized trapezoidal fuzzy numbers then AΘB = (−0.6, −0.2, −0.2,0.2;1) and BΘB = (−0.4,0,0,0.4;1)
Step 1.min(1,1) = 1
Step 2.ℜ(AΘB)=12(−0.8+2.4α) and ℜ(BΘB)=12(0.4+0.8α)
For a pessimistic decision maker, with α = 0, ℜ(AΘB) = −0.4 and ℜ(BΘB) = 0.2. Since ℜ(AΘB) < ℜ(BΘB), so (AΘB)≺(BΘB).
For optimistic decision maker, with α = 1, ℜ(AΘB) = −0.266 and ℜ(BΘB) = −0.2. Since ℜ(AΘB) > ℜ(BΘB), so (AΘB)≻(BΘB).
For moderate decision maker with α = 0.5, ℜ(AΘB) = 0.2 and ℜ(BΘB) = 0. Since ℜ(AΘB) > ℜ(BΘB), so (AΘB)≻(BΘB).
Example 13.Let A = (1,1,1,1;w1) and B = (1,1,1,1;w2) be two generalized trapezoidal fuzzy numbers then
Step 1.min(w1,w2) = w (say)
Step 2.ℜ(AΘB)=w22α+(1−α)2=w and
Since, ℜ(A) = ℜ(B) ∀α, so A~B.
Example 14.Let A = (−0.4, −0.2, −0.1,0.7;w1) and B = (−0.4, −0.2, −0.1,0.7;w2), be two generalized trapezoidal fuzzy numbers
Step 1.min(w1,w2) = w(say)
Step 2.ℜ(AΘB)=w2−0.6α+(1−α)0.6=0.3w and ℜ(BΘB)=w2−0.6α+(1−α)0.6=0.3w. Since, ℜ(A) = ℜ(B) ∀α, so A~B.
Example 15.Let A = (1,3,5;0.3,0.8), and B = (4,8,9;0.4,0.9) be two generalized triangular vague sets then AΘB = (−8, −5,1;0.3,0.8) and BΘB = (−5,0,5;0.4,0.9).
Step 1.min(0.3,0.4) = 0.3 and min(0.8,0.9) = 0.8.
Step 2.ℜAΘB=12(−1.037−3.881α) and ℜBΘB=12(2.47−0.94α).
For a pessimistic decision maker, with α = 0, ℜ(AΘB) = −1.0375 and ℜ(BΘB) = 2.47. Since ℜ(AΘB) < ℜ(BΘB), so (AΘB)≺(BΘB).
For optimistic decision maker, with α = 1, ℜ(AΘB) = −4.919 and ℜ(BΘB) = 1.53. Since ℜ(AΘB) < ℜ(BΘB), so (AΘB)≺(BΘB).
For moderate decision maker with α = 0.5, ℜ(AΘB) = −2.978 and ℜ(BΘB) = 2 Since ℜ(AΘB) < ℜ(BΘB), so (AΘB)≺(BΘB).
Example 16.Let A = (−2,0,2;λ1,ρ1), and B = (−2,0,2; λ2,ρ2) be two triangular vague numbers then AΘB = (−0.4,0,0.4;λ3,ρ3) where λ3 =min(λ1,λ2) and BΘB = (−0.4,0,0.4 λ2,ρ2)
Step 1.min(λ3,λ2) = λ and min(ρ3,ρ2) = ρ
Step 2.Since, ℜ(AΘB) = ℜ(BΘB),∀α so AΘB~BΘB.
Example17.Let A = (−8,1,4; λ1,ρ1), and B = (−8,1,4; λ2,ρ2) be be two triangular vague numbers then AΘB = (−12,0,12; λ3,ρ3) where λ3 = min(λ1,λ2) and BΘB = (−12,0,12;λ2,ρ2)
Step 1.min(λ3,λ2) = λ and min(ρ3,ρ2) = ρ
Step 2.Since ℜ (AΘB) = ℜ (BΘB) ∀α so AΘB~BΘB.
Example 18.Let A = (1,1,1;λ1,ρ1), and B = (1,1,1;λ2,ρ2) be be two triangular vague numbers then AΘB = (0,0,0;λ3,ρ3) where λ3 = min(λ1, λ2) and BΘB = (0,0,0,;λ2,ρ2)
Step 1.min(λ3,λ2) = λ and min(ρ3,ρ2) = ρ
Step 2.Since, ℜ (AΘB) = ℜ (BΘB) ∀α so AΘB~BΘB.
6.2Comparative studyDifferent sets of fuzzy sets and vague sets are taken to compare the results of proposed and existing ranking approaches.
Set 1.Let A = (0.1,0.3,0.3,0.5;0.8) and B = (0.1,0.3,0.3,0.5;1) be two trapezoidal fuzzy sets, take α=12
Step 1.min(0.8,1) = 0.8
Step 2.ℜ(A) = 0.24 and ℜ(B) = 0.24. Since ℜ(A) = ℜ(B), so A~B.
Set 2.Let A = (0.1,0.3,0.3,0.5;1) and B = (0.3,0.5,0.5,0.7;1) be two trapezoidal fuzzy sets, take α=12
Step 1.min(1,1) = 1
Step 2.ℜ(A) = 0.3 and ℜ(B) = 0.5. Since ℜ(A) < ℜ(B), so A≺B.
Set 3.Let A = (0.1,0.3,0.3,0.5;0.8) and B = (−0.5, −0.3, −0.3,0.1;1) be two trapezoidal fuzzy sets, take α=12
Step 1.min(1,1) = 1
Step 2.ℜ(A) = 0.3 and ℜ(B) = −0.3. Since ℜ(A)> ℜ(B), so A≻B.
Set 4.Let A = (5,7,9,11;0.4) and B = (2,4,8,9;0.2) be two generalized exponential trapezoidal fuzzy sets, take α=12
Step 1.min(0.4,0.2) = 0.2
Step 2.ℜ(A) = 1.6 and ℜ(B) = 1.1. Since ℜ(A)> ℜ(B), so A≻B.
Set 5.Let A = (3,6,7,14;0.2,0.7) and A = (1,4,6,9;0.3,0.4) be two exponential vague fuzzy sets, take α=12
Step 1.min(0.2,0.3) = 0.2and min(0.7,0.4) = 0.4
Step 2.ℜ(A) = 1.52 and ℜ(B) = 1.13. Since ℜ(A)> ℜ(B), so A≻B.
Comparison of proposed ranking approach with existing ranking approach where N.A denotes the not applicable.
| Methods | Set 1 | Set 2 | Set 3 | Set 4 | Set5 |
|---|---|---|---|---|---|
| Yager [36] | A~ B | A~ B | A~ B | N.A | N.A |
| Liou and Wang [20] | A~ B | A≻B | A≻B | N.A | N.A |
| Cheng [9] | A≺B | A≺B | A~B | N.A | N.A |
| Murakami et al. [26] | A≺B | A≺B | A≻B | N.A | N.A |
| Chen and Li [7] | A~B | A≺B | A≻B | A≻B | N.A |
| Chen and Chen [6] | A≺B | A≺B | A≻B | N.A | N.A |
| Chen and Sanguansat [8] | A≺B | A≺B | A≻B | N.A | N.A |
| Li [19] | A≺B | A≺B | A≻B | N.A | N.A |
| Nehi [28] | N.A | A≺B | A≻B | N.A | N.A |
| Kumar et al. [15, 16, 17] | A~B | A≺B | A≻B | N.A | N.A |
| Proposed approach | A~B | A≺B | A≻B | A≻B | A≻B |
Let A = {A1,A2,…,An} be a set of alternatives and let C = {C1,C2,…,Cn}be set of criteria. The values of an alternative on criteria Cj (j =1,2,…,n) are exponential vague sets Sij, which indicates the degree that the alternative Ai satisfies or does not satisfies the criterion Cj given by decision makers or experts according to linguistic values of exponential sets for linguistic terms.
The weights of criterion Cj (j = 1,2,…,n) are represented by exponential sets. The ranking weight value wj for exponential vague set is obtained by Eq. (17). The normalized weights are obtained using the following equation:
Therefore, the weighted ranking value for an alternative Ai(i = 1,2,…,m) is given by:
Thus, the calculated weighted ranking value for an alternative is used to rank alternatives and then to select the best one in all the alternatives.
The above method can be summarized as follows:
- (i)
Calculate the ranking weight value wj for criterion Cj(j = 1,2,…,n) by using Eq. (17) and (18).
- (ii)
Calculate the weighted ranking value for alternative Ai(i = 1,2,…,m) by using Eq. (17) and (19).
- (iii)
Rank the alternative and select the best one in accordance with weighted ranking vales ℜwj(Ai).
A numerical example has been taken to show the applicability of ranking function in multicriteria decision making problem.
Suppose there is a panel with three alternative to invest the money: (i) A1 is car company, (ii) A2 is food company, (iii) A3 is computer company.
The investment must take a decision according to the following three criteria: (i) C1 is the riskanalysis, (ii) C2 is the growth analysis, (iii) C3 is the environmental impact analysis.
The three possible alternative are to be evaluated under the above three criteria by corresponding to linguistic values of exponential sets for linguistic terms, as shown in Table 2.
Linguistic vales of exponential vague sets for linguistic terms.
| Linguistic terms | Linguistic values of exponential vague sets |
|---|---|
| Absolute value | (0.0,0.0,0.0,0.0;0.0,0.0) |
| Low | (0.0,0.1,0.2,0.3;0.1,0.2) |
| Fairly low | (0.0,0.2,0.3,0.4;0.2,0.5) |
| Medium | (0.3,0.4,0.5,0.6;0.4,0.5) |
| Fairly high | (0.5,0.6,0.7,0.8;0.5,0.7) |
| High | (0.7,0.8,0.9,1.0;0.8,0.9) |
| Absolutely high | (1.0,1.0,1.0,1.0;1.0,1.0) |
Suppose we called three experts (k = 3) to make the decision. They give the linguistic values of exponential vague sets.
The values of alternatives and criteria weights based on the decision makers or expert’s knowledge are shown in Table 3.
Linguistic vales of exponentia l vague sets for linguistic terms.
| k | C1 | C2 | C3 | |
|---|---|---|---|---|
| A1 | 1 | (0.1,0.2,0.3,0.4;0.2,0.3) | (0.2,0.3,0.5,0.7;0.3,0.6) | (0.3,0.4,0.6,0.7;0.8,0.9) |
| 2 | (0.3,0.5,0.6,0.8;0.5,0.7) | (0.2,0.3,0.5,0.7;0.3,0.6) | (0.3,0.4,0.6,0.7;0.8,0.9) | |
| 3 | (0.3,0.5,0.6,0.8;0.5,0.7) | (0.2,0.3,0.5,0.7;0.3,0.6) | (0.3,0.5,0.6,0.8;0.5,0.7) | |
| A2 | (0.3,0.4,0.6,0.7;0.8,0.9) | (0.1,0.2,0.3,0.4;0.2,0.3) | (0.1,0.4,0.6,0.7;0.5,0.6) | |
| 2 | (0.3,0.4,0.6,0.7;0.8,0.9) | (0.2,0.3,0.5,0.70.3,0.6) | (0.1,0.4,0.6,0.7;0.5,0.6) | |
| 3 | (0.1,0.2,0.3,0.4;0.2,0.3) | (0.1,0.4,0.6,0.7;0.5,0.6) | (0.1,0.4,0.6,0.7;0.5,0.6) | |
| A3 | 1 | (0.2,0.3,0.5,0.70.3,0.6) | (0.1,0.4,0.6,0.7;0.5,0.6) | (0.2,0.3,0.5,0.7;0.3,0.6) |
| 2 | (0.1,0.4,0.6,0.7;0.5,0.6) | (0.3,0.5,0.6,0.8;0.5,0.7) | (0.1,0.4,0.6,0.7;0.5,0.6) | |
| 3 | (0.3,0.5,0.6,0.8;0.5,0.7) | (0.1,0.4,0.6,0.7;0.5,0.6) | (0.1,0.4,0.6,0.7;0.5,0.6) | |
| weight | 1 | (0.1,0.4,0.6,0.7;0.5,0.6) | (0.1,0.4,0.6,0.7;0.5,0.6) | (0.2,0.3,0.5,0.7;0.3,0.6) |
| 2 | (0.3,0.4,0.6,0.7;0.8,0.9) | (0.1,0.4,0.6,0.7;0.5,0.6) | (0.1,0.4,0.6,0.7;0.5,0.6) | |
| 3 | (0.3,0.5,0.6,0.8;0.5,0.7) | (0.3,0.4,0.6,0.7;0.8,0.9) | (0.3,0.4,0.6,0.7;0.8,0.9) |
Use the following steps to find the best alternative.
- (i)
Using Eqs. (17) and (18), we get the ranking weight value wj for criterion Cj(j = 1,2,3), w1 =0.383, w2= 0.271, w3= 0.345.
- (ii)
Using Eqs. (17) and (19), we get the weighted ranking value for alternative Ai(i=1,2,3), ℜw1(A1)=0.901,ℜw2(A2)=0.778,ℜw3(A3)=0.937.
- (iii)
Rank the alternative as follows: A1≺A2≺A3
Thus according to above results the most desirable alternative is A3.
8ConclusionsIn this paper, we present a new approach for the ranking of exponential vague sets. New representation and arithmetic operations between two exponential vague sets has been introduced. Some shortcomings of existing ranking approaches [8, 19] are pointed out. The proposed method consider not only the rank but also the decision maker optimistic attitude also with the help of some comparative examples it is shown that proposed ranking approach is more intuitive than the existing ranking approaches. Also the proposed ranking function satisfies the reasonable properties for the ordering of fuzzy quantity. Further the proposed ranking approach can effectively rank of various types of fuzzy sets and vague sets (normal, generalized, triangular, trapezoidal and exponential), which is another advantage of proposed ranking approach over the other exiting ranking approaches. For practical use, proposed ranking approach is applied to decision making problem.
The author is very grateful to the Editor-in-Chief, and the anonymous referees, for their constructive comments and suggestions that led to an improved version of this paper. The author was supported by the Education for Competitiveness Operational Programme project “Encourage the creation of excellent research teams and intersectoral mobility at Palacky University in Olomouc” reg. no. CZ.1.07/2.3.00/30.0004, which is co-financed by the European Social Fund and the state budget of the Czech Republic.