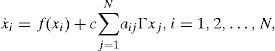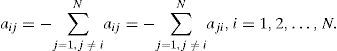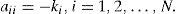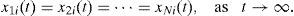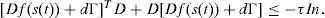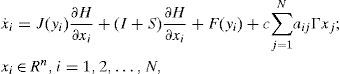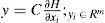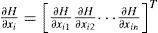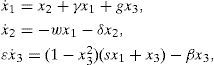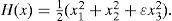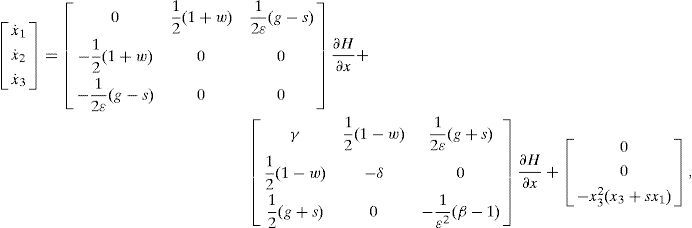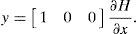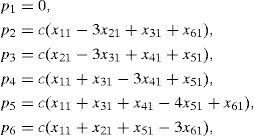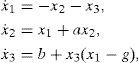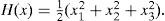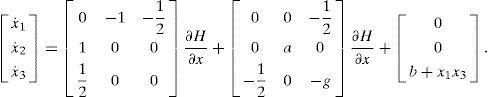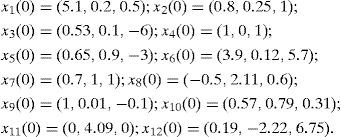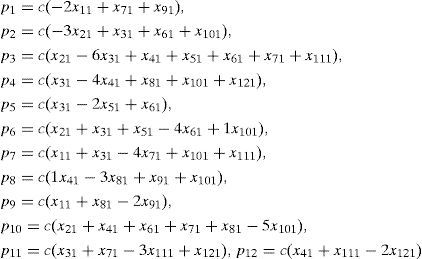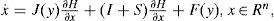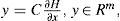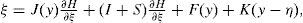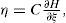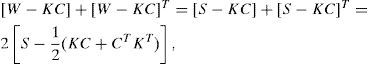Synchronization of multiple chaotic oscillators in Hamiltonian form is numerically studied and is achieved by appealing to complex systems theory [1–5]. The topology that we consider is the irregular coupled network. Two cases are considered: i) chaotic synchronization without master oscillator (where the final collective behaviour is a new chaotic state) and ii) chaotic synchronization with master oscillator (where the final collective behaviour is imposed by the dynamics of the master oscillator to multiple slave oscillators). The Hysteretic and Rössler chaotic oscillators in Hamiltonian form will be used as examples.
La sincronización de múltiples osciladores caóticos en forma Hamiltoniana es numéricamente estudiada y se logra apelando a la teoría de sistemas complejos [1–5]. La topología que consideramos es la red compleja irregular. Dos casos se consideran: i) sincronización caótica sin oscilador maestro (donde el comportamiento colectivo final de la red compleja es un estado caótico nuevo y ii) sincronización caótica con oscilador maestro (donde el comportamiento colectivo final de la red caótica es impuesto por la dinámica del oscilador maestro a los osciladores esclavos). Los osciladores caóticos de Rössler e Histéresis en forma Hamiltoniana se utilizan como ejemplos.
Since synchronization discovery, the scientific community has paid special attention to this phenomenon due to its importance in science and technology. In the late years, especially since the appearance of the article by Pecora and Carroll [6], the scientific community has turned their eyes into complex network synchronization. Ever since, lots of ideas have emerged, posing interesting new ways to synchronize diverse dynamical systems [7–8], as well as exciting new findings in science.
Some of the first accounts of synchronization behavior might be referenced to the well-known story of the Bible, when the Jericho walls were destroyed by highly coupled sounds of trumpets and an army marching around the city. Nevertheless, the first research report on synchronization in general is due to Christiaan Huygens [9–10] in the mid 1600's. He suspended two pendulum clocks through a common wooden beam. The tiny vibrations from the clocks synchronize the pendulums' movements giving place to rhythmic swings. Ever since this property has been reported in systems of different nature such as chemical, biological, social, physical and so on, e.g. fire-flies bioluminescence communication [11–12], bamboo mast flowering [13], sound pipes quenching [14] and heavenly bodies movements [15]. In general, we can understand synchronization as the “adjustment of rhythms of oscillating objects due to their weak interaction” [16]. It can be said that synchronization is one of the most widespread phenomena among oscillating dynamical systems.
A prevailing occurrence in nature is the gathering of systems or individuals in common tasks, such large numbers of highly interconnected dynamical systems render a collective behavior completely different to the individually shown by its units. Classic examples run from the nervous system (a network by itself) to human societies, from a grass hopper in the garden to swarms of locust on the fields, and from a tiny personal system such as a smart phone to entire computer networks that drive the lives of modern world.
All of these cases can be characterized as structures made of individual entities, called nodes (with an individual behavior known or not), weak connections among them and, depending on the nature of the system, the existence of a driving force which imposes its dynamics to the network, we call this entity a master node. The nodes' dynamical nature plus the structure of the connections dictate the network's behavior, which can be simple or capriciously complicated. These phenomena can be translated to benefices to the human race (e.g. the heart pace maker), which stresses the importance of the study of this topic nowadays.
The nodes used in this work are chaotic oscillators, the richness of its dynamics due to its random behavior challenges many paradigms of synchronization techniques. This chaotic nature became popular among the scientific community in the mid 1960's thanks to Edward Lorenz [17] who, while trying to forecast weather, discovered a defining feature of chaos, any difference in the initial conditions of certain dynamical systems, no matter how small it might be, has huge effects on its outcome. Its understanding unraveled lots of nature's “code”, as Prof. Marcus du Sautoy [18–19] would say. Examples of this can be found in the population growth of some insects [20], weather forecasting [17], economics [21–22], social behavior, movement of artificial satellites [23], chemical reactions, electronic circuits [27], etc.
Complex dynamical networks can be defined as an interconnection of individual dynamical systems interacting in several ways [28]. Such interconnections might have different forms or topologies, every arrangement of units affect the final behavior of the system. In networking, irregular arrays have no formal or regular construction, and pose an evolving research topic, showing that even when nature has its own mathematical order, disorder is most likely to be found.
In this work we study the synchronization of complex networks made by chaotic dynamical nodes (we call these oscillators from now) in irregular arrays and two main arrangements, with and without a master node. Such systems exhibit emergence and synchronization to the master node behavior.
The paper is organized as follows: in Section 2 a brief summary on synchronization in complex dynamical networks is given. For Section 3, an approach to solve networks given in Hamiltonian Generalized form, followed by Section 4 where two examples are given. Finally conclusions are given in Section 5. In Appendix A, the essentials of Hamiltonian Generalized form systems, and its synchronization is included.
2Synchronization of Complex NetworksA complex dynamical network is defined as a set of interconnected oscillators. An oscillator is the basic element of a network, whose behavior depends on its nature [4]. Consider a dynamical network that is made of N identical linearly and diffusively coupled oscillators, and each oscillator is an n-dimensional system with chaotic behavior. The state equations of the complex network are given by:
Where x¿i=(xi1,xi2,…,xin)T∈Rn, is the state vector of the oscillator i. The constant c > 0 is the coupling strength of the complex network. ¿ ∈ Rn×n is a constant matrix and it is assumed that ¿=diag(r1, r2, …, rn) is a diagonal matrix with ri=1 for a particular i and rj=0 for j ≠ i. This means that two coupled oscillators are linked through their i th state variables. Coupling matrix A=(aij) ∈ RN×N represents the coupling configuration of the complex network. If there is a connection between oscillator i and oscillator j, then aij=1; otherwise, aij=0 (i ≠ j).
The diagonal elements of matrix are defined as
Clearly, if the degree of oscillator i is ki, then
The complex dynamical network (1), is said to achieve (asymptotically) synchronization, if
Theorem 2.1[2, 24] Consider a dynamical network (1). Let 0=¿1 > ¿2 ≥ ¿3≥ … ≥ ¿n be the eigenvalues of its coupling matrix A. Suppose that there exists a n × n diagonal matrix D > 0 and two constants d < 0 and ¿ > 0, such that
For all d≤d¯, where In ∈ Rn×n is the identity matrix. If, moreover, c¿2≤d¯, then the synchronization state (4) of the dynamical network (1) is exponentially stable.
3Hamiltonian NetworksHamiltonian systems theory is an energy approach to dynamical systems, a brief description of the results of this theory can be found in Appendix A. Due to the defined output signal property of Hamiltonian systems, the Hamiltonian method can use an observer to synchronize two oscillators in master-slave configuration; this paper extends the previous result to multiple oscillators.
Consider two cases where the synchronization must be applied to a complex network of more than two oscillators: i) regular topology where the oscillators are connected following a connection rule irregular and i) irregular topology where the oscillators are connected without a connection rule (in this paper, irregular topology of complex network is studied). In this case, the Hamiltonian observer method seen above may not suffice.
Therefore, in order to solve this problem, a complex network approach must be used. The network synchronization methodology defined by Wang [2, 24], as well as the Hamiltonian approach [3] are applied to the studied systems to achieve the chaotic synchronization of the network. The dynamics of complex network where the oscillators are given in Hamiltonian form can be determined as follows:
where ẋi=(xi1, xi2, …, xin)T ∈ Rn, is the state vector of the oscillator; i=1, 2, …, N refers to the oscillator; J(yi)∂H / ∂xi exhibits the conservative part of the system; S is a constant symmetric matrix, not necessarily of definite sign; I is a constant skew symmetric matrix; yi is referred to as the system output; C is a constant matrix; F represents a locally destabilizing vector field; c > 0 is the coupling strength of the complex network; ¿ ∈ Rn×n is a constant matrix, and it is assumed that ¿=diag(r1, r2, …, rn) is a diagonal matrix with ri=1 for a particular i and rj=0 for j ≠ i; A=(aij) ∈ RN×N, is called coupling matrix, represents the coupling configuration of the complex network; H(xi) denotes a smooth Hamiltonian energy function which is globally positive Rn; ∂H/∂xi is the columns gradient vector and is assumed to exist everywhere. For an oscillator in a network configuration, the following notation will be used:4ExamplesExample 1:Hysteretic chaotic circuit in an irregular network with a master oscillator. Consider the Hysteretic chaotic oscillator [3] as the oscillator (or fundamental node) of an irregular array network. The nonlinear equations:
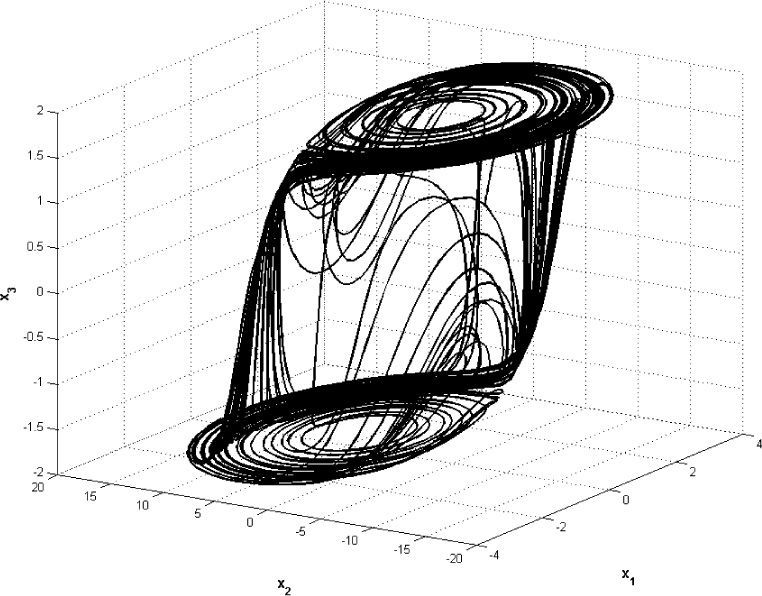
Phase space of the chaotic attractor generated by oscillator (9), projected onto (x1, x2, x3).
The energy function for system (9) can be expressed as follows:
From equations (A.1) and (A.2) and theorem (A.1), system (9) can be expressed in the generalized Hamiltonian form, as below:
And the output of the system, is denoted by
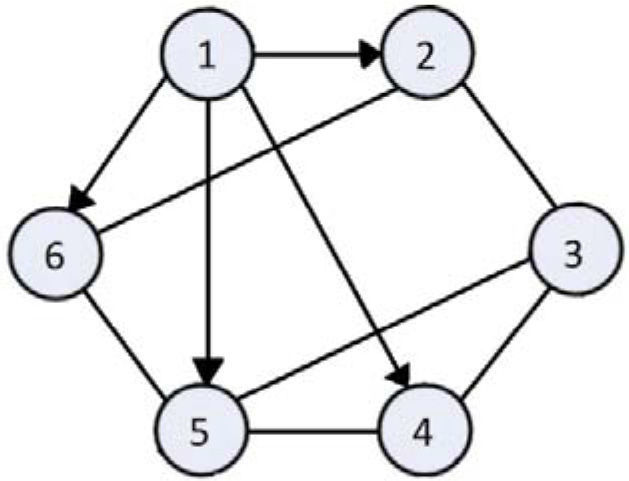
Assume the network is generated by six oscillators coupled in an irregular array, as shown on figure 2.
Six irregularly coupled oscillators with master oscillator (1).
The coupling matrix A for the system is:
The initial conditions for the respective oscillators are: x1(0)=(1.9, – 2, 0.5); x2(0)=(4.8, 4, -1);
x3(0)=(6, 1, 0); x4(0)=(−3, 0, 7);
x5(0)=(−2.8, 2.9, 3.7); x6 (0)=(0, 2, 5.7).
According to theorem (A.1), the chaotic synchronization of the system is achieved using a coupling strength of c=2.
Using the following gradient vectors:
System (11) can be expressed as:
The coupling signals for this network, are given in an explicit way as
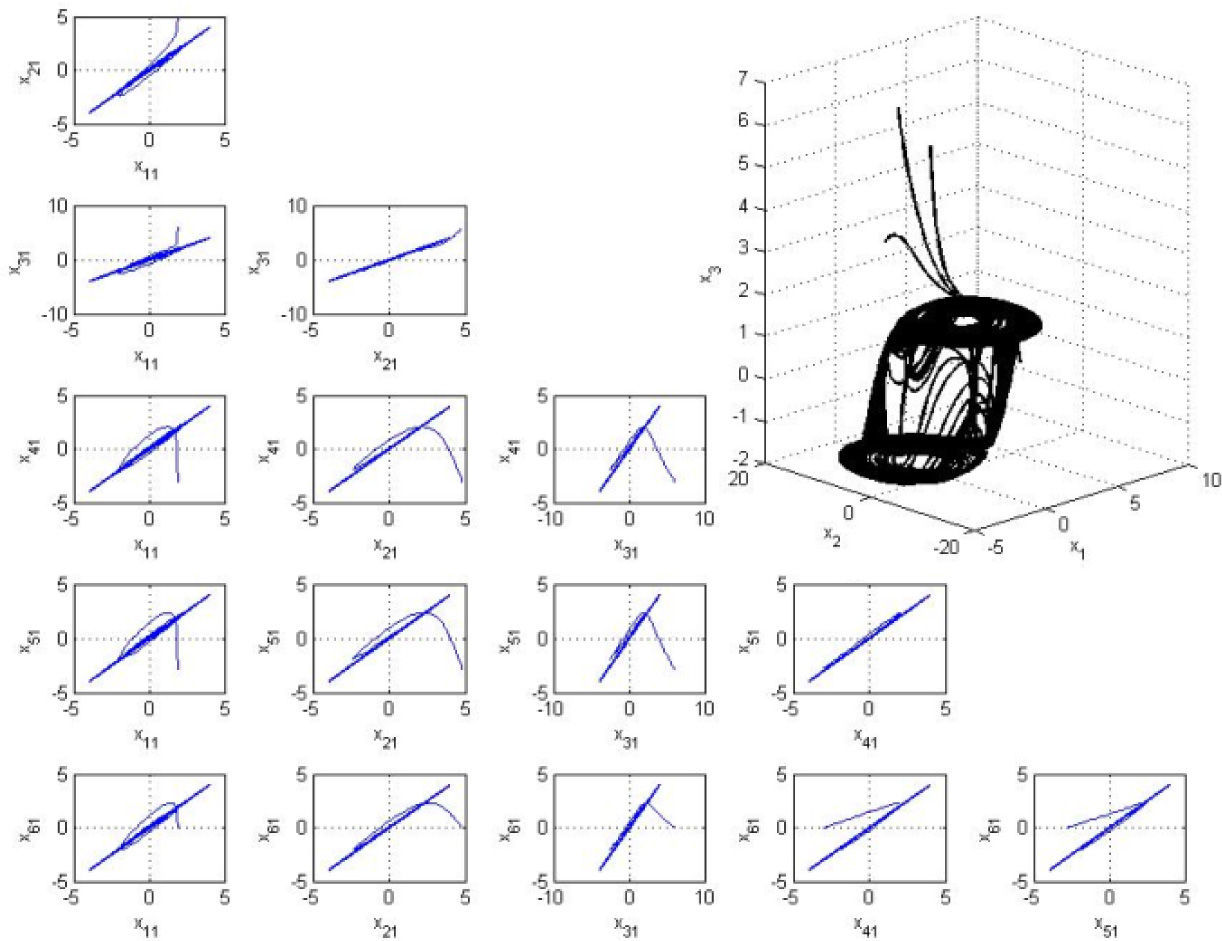
Figure 3 shows chaotic synchronization in the first state of the six hysteretic oscillators, xi1, i=1, 2, …, 6 and the chaotic attractor of the collective behavior imposed by master oscillator 1 to the dynamical network, projected onto space (x1, x2, x3).
A diagonal line in the phase graph, as shown in the figure 3, means that synchronization is achieved after a finite period of time. This shows that synchronization in every xi1i=1, 2, …, 6 is obtained, hence theorem (A.1) holds. States xi2 and xi3 also synchronize to the respective states of the master oscillator, i.e. in this case, all the states synchronize to the master oscillator 1. The phase diagrams for the rest of the states are not shown due to space restrictions.
Example 2:Rössler chaotic oscillator in a 12 node irregular network without a master node. Consider a Rössler chaotic oscillator [3] as the basic oscillator in an irregular array network. The nonlinear equations (9), with parameters a=0.4, b=2, g=−4 exhibit a chaotic behavior in the Rössler oscillators shown in figure 4:
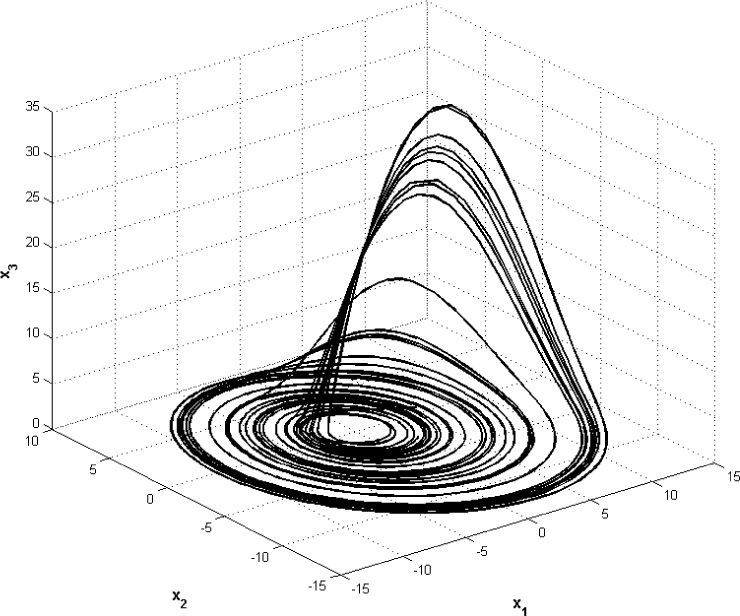
Phase space of the chaotic attractor generated by Rössler oscillator (13), projected onto (x1, x2, x3).
The energy function for system (9) can be expressed as:
Applying equations (A.1) and (A.2) and theorem (A.1), the system (13) can be expressed in the generalized Hamiltonian form as:
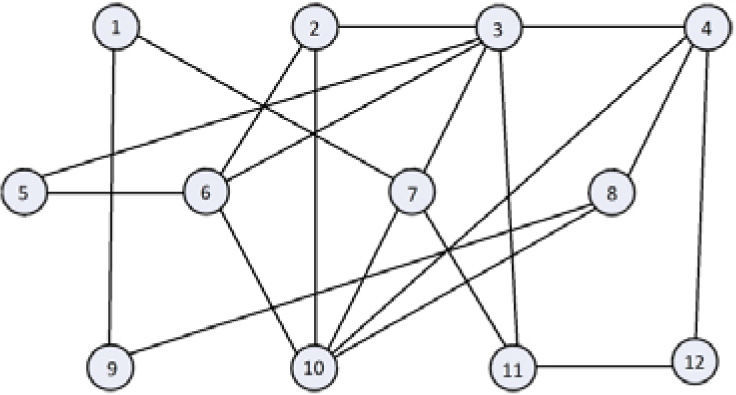
Assume the network is generated by twelve oscillators coupled in an irregular array, as shown on figure 5.
The coupling matrix A is:
The initial conditions for the respective nodes are:
According to theorem (A.1), the chaotic synchronization of the system is achieved using a coupling strength of c=0.35.
If the following gradient vectors are used:
system (15), can be expressed as:And the explicit expression of the coupling signals for this network, are given as:
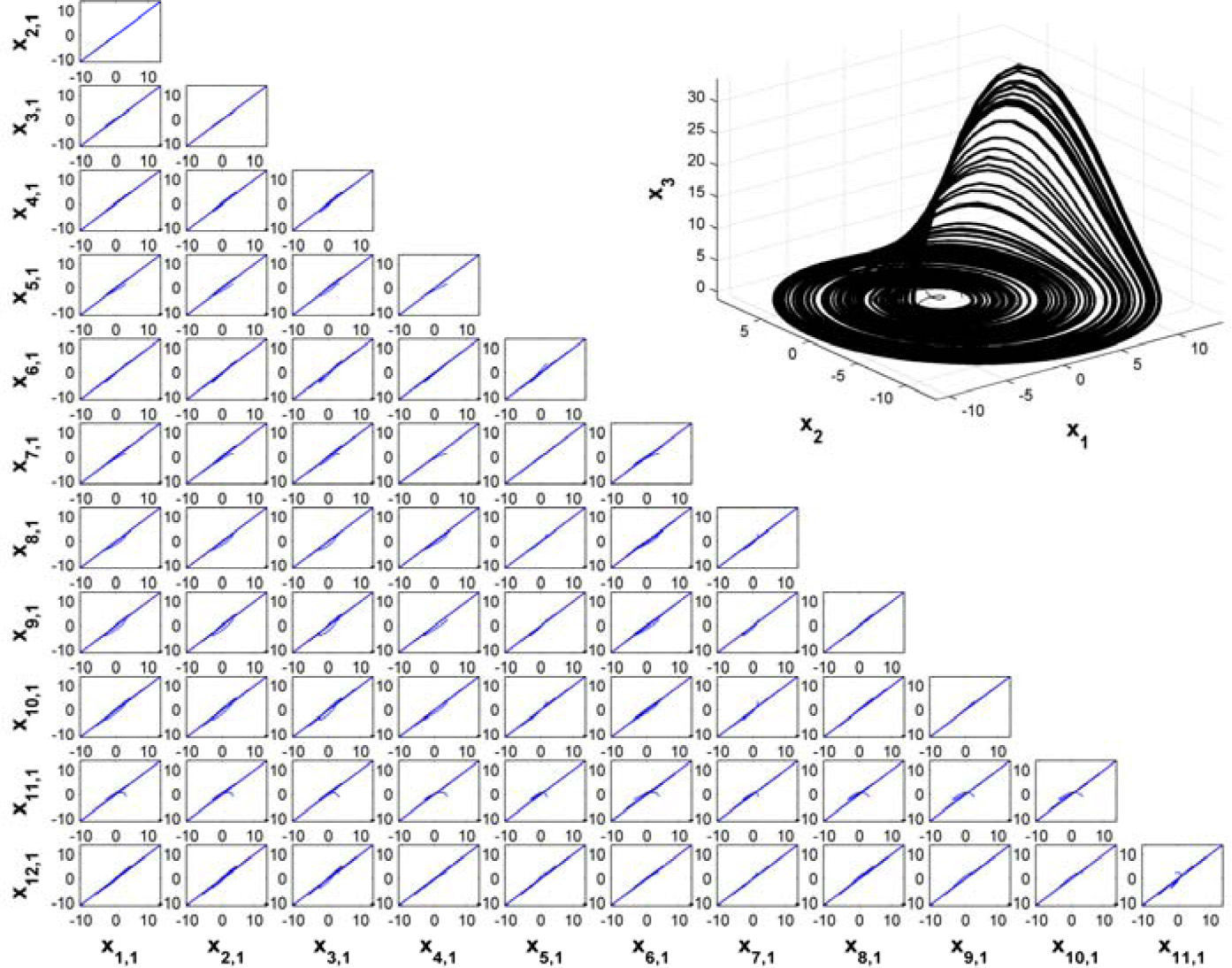
A diagonal line in the phase graph, as shown in the figure 6, means that synchronization is achieved after a finite period of time. This shows that synchronization in the first state of every one of the twelve systems xi1i=1, 2,…, 12 is attained, hence theorem (A.1) holds. States xi2 and xi3 also synchronize, i.e. in this case, all the states synchronize. The phase diagrams for the rest of the states are not shown due to space restrictions.
5ConclusionsIn this paper, we have presented synchronization of N-coupled chaotic oscillators in a Hamiltonian generalized form, using the coupled network theory. The irregular networks featured and the initial conditions were totally random. We have achieved synchronization in the designed irregular complex dynamical network, with and without chaotic master oscillator. It was shown that, independently of the connection topology used in the network, there exist properties that characterize such network, and that synchronization purposes, are determined by the highest nonzero eigenvalue A2 and the coupled strength c.
Synchronization is achieved with chaotic Hysteretic oscillators and chaotic Rössler oscillators in Hamiltonian generalized form; synchronization in all states of every one of the systems is achieved.
As for the method itself, many other chaotic oscillators in Hamiltonian generalized form have been used; but more trials must be done in the future. For this paper only chaotic oscillators were considered, this does not means that other kind of oscillators cannot be used. Recent studies on synchronization of complex dynamical networks may shed new light on behavior and understanding of synchronization itself or complexity in network dynamics.
This work was supported by CONACYT, México under Research Grant No. 166654 and by FIME-UANL.
Some of the chaotic oscillators can be placed in a generalized Hamiltonian canonical form [25, 26]. The advantages for that are, that if synchronization is the goal, it can be achieved systematically; the method bypasses the need to calculate the Lyapunov exponents; it is not required that the initial conditions lay in the same attraction point; the reconstructibility of the state vector, from a defined output signal, may be defined from the observability or the lack of it, analyzing the detectability of a pair of constant matrices [3].
We consider a special class of Generalized Hamiltonian systems with destabilizing vector fields and linear output map, given by:
where J(y)∂H/∂x exhibits the conservative part of the system and it is also referred to as the workless part of the system. S is a constant symmetric matrix, not necessarily of definite sign. The matrix I is a constant skew symmetric matrix. F(y) represents a locally destabilizing vector field. The vector variable y is referred to as the system output. The matrix C is a constant matrix. H(x) denotes a smooth energy function which is globally positive Rn. The columns gradient vector of H, denoted by ∂H/∂X, is assumed to exist everywhere. We denote the estimate of the state vector x by ¿, and the Hamiltonian energy function H(¿) to be the particularization of H in terms of ¿. We denote by ¿ the estimated output, computed in terms of the estimated state ¿. A dynamic nonlinear state observer for the system (A.1) is readily obtained aswhere K is a constant vector, known as the observer gain, and we set, I + S=W, as needed.Theorem A.1[3] The state x of the nonlinear system (A.1) can be globally, exponentially, asymptotically estimated by the state ¿ of an observer of the form (A.3), if the pair of matrices (C,W), or the pair (C,S), is either observable or, at least, detectable. Observability condition on either of the pairs (C,W), or (C, S), is clearly a sufficient but not necessary condition for asymptotic state reconstruction.
Theorem A.2[3] The state x of the nonlinear system (A.1) can be globally, exponentially, asymptotically estimated, by the state ¿ of the observer (A.3) if and only if there exists a constant matrix K such that the symmetric matrix
is negative definite.Synchronization state x of the nonlinear oscillator (A.1) is synchronized with the state ¿ of the observer (A.3) if theorem A.1 or theorem A.2 is achieved.