The optimization of sustainable smart cities is an essential endeavor in modern urban development, aiming to enhance the quality of life for citizens while minimizing environmental impacts. Big data plays a critical role in achieving these goals by enabling the collection, analysis, and utilization of vast amounts of information to make informed decisions. However, implementing big data in smart cities faces significant barriers, including data-sharing challenges, technical limitations, and organizational non-cooperation. Addressing these barriers is crucial for the successful deployment of smart city initiatives. We propose a novel approach to tackle these challenges using the Improved Zero-Sum Grey Game (IZSGG) theory and the Grey Best-Worst Method (G-BWM). This method comprehensively analyzes the risks and uncertainties associated with big data implementation in smart cities. By modeling the interactions between different stakeholders and their competing interests, IZSGG theory provides a framework to identify optimal strategies for data management. The G-BWM further refines these strategies by evaluating and prioritizing the various factors influencing big data utilization. Our findings reveal that the worst-case scenario for a smart city involves the simultaneous occurrence of several risks, all of which have positive values, indicating their potential to significantly disrupt smart city operations. The specific risks identified include: the sharing of data and information, the collection and recording of data, technical limitations and challenges associated with technology, the non-cooperation of organizations, and issues related to the interpretation of complex information. The technical barrier is the most significant with a weight of w(T)=0.6152, indicating its critical role compared to other barriers. Within this category, the sub-barrier of technical and technological constraints is particularly critical, with a weight of 0.39267375.
An urban area that collects data using various electronic technologies and sensors is called a smart city. The use of this data enables the efficient management of urban resources, assets, and services. Information systems, waste management, crime detection, power plants, municipal facilities, water supply networks, transportation systems, schools, libraries, hospitals, and other social services are just a few of the places where data from citizens, devices, and urban resources are gathered, processed, and analyzed (Ajaj, Buniya, Wuni & Yousif, 2024; Lin et al., 2021). To improve service delivery, streamline urban processes, and engage effectively with residents, a smart city aims to integrate information and communication technology (ICT) with a variety of physical devices that are linked to the Internet of Things (IoT) (Del-Real, Ward & Sartipi, 2023; Khan, Siddiqui, Rahmani & Husain, 2022). City officials can respond quickly to the needs of the city and its residents by interacting directly with the community and urban infrastructure thanks to smart city technology (Janurova et al., 2020).
A sustainable smart city is composed of various components that together create a coordinated and effective combination to improve the quality of life for citizens. One of the essential components of sustainable smart cities is the use of big data. Big data refers to large volumes of data collected from various sources (Ajaj et al., 2024; Khazaei, Zareian, Veleda & Litoiu, 2016). This data can come from sources such as sensors, social networks, public transportation systems, and more. The importance of big data in smart cities lies in its ability to extract usable information and valuable patterns for urban management through the analysis of large datasets. This data helps city officials make better decisions regarding traffic management, energy consumption optimization, forecasting citizen needs, and improving urban services. In other words, big data aids smart cities in enhancing decision-making and providing urban services (Barham & Daim, 2018; Hashem et al., 2016; Lin et al., 2021).
Big data is a powerful tool in a smart city that can significantly improve urban management and service delivery. Applications of big data in a smart city include traffic prediction, energy management improvement, better urban service delivery, and improved crisis management. Although big data plays a crucial role in transforming cities into smart cities, its implementation faces several challenges (Janurova et al., 2020; Lin et al., 2021). One of the primary obstacles to implementing big data in smart cities is the issue of data privacy and security. The collection and use of sensitive data can lead to fears and security concerns among citizens. Additionally, technical issues related to processing and storing large volumes of data can pose barriers to the successful implementation of big data in smart cities. To address these challenges, common policies and standards regarding privacy, data security, and large-scale data management are needed (Ajaj et al., 2024; Hashem et al., 2016; Khan et al., 2022; Khazaei et al., 2016; Mutambik, 2024).
Numerous studies have investigated the use of big data in smart cities and the challenges and risks associated with it. For example, Villegas-Ch et al. (2019) highlighted that the need for substantial investments in socio-economic and technical resources creates barriers to big data implementation in smart cities. Rathore et al. (2018) pointed out the difficulties in integrating IoT devices and smart systems to efficiently gather and process vast amounts of urban data in real time. Khan (2021) identified data complexity, the framework for big data adoption, and the lack of necessary technologies as major obstacles to incorporating big data analytics in smart city development. Rjab et al. (2023) investigated the barriers to AI adoption in smart cities, while Khan, Khan, Khan and Haleem (2023) analyzed big data challenges in smart cities using an integrated fuzzy approach based on Interpretive Structural Modelling (ISM) and Decision-Making Trial and Evaluation Laboratory (DEMATEL). Paes et al. (2023) reviewed the challenges facing future smart and sustainable cities. These studies collectively suggest that the implementation of big data in smart cities faces significant hurdles, including high investment costs, technical issues like integrating IoT devices, data complexity, and the lack of appropriate technologies and frameworks.
In previous research, there was no comprehensive model that simultaneously examined the barriers and challenges while also considering the optimal solution. Preliminary reviews and research show a gap in comprehensive studies that rank these obstacles and analyze big data solutions specifically for smart cities in developing countries. As an initial innovation, this research intends to identify the obstacles and challenges of implementing big data in smart cities in developing countries in the first phase, and then rank these obstacles using Multi-Criteria Decision-Making (MCDM) methods. In the second phase, solutions to these obstacles will be analyzed using game theory under conditions of uncertainty.
The advantage and innovation of this research lie in the use of an integrated approach combining MCDM and game theory to identify obstacles and determine the optimal solutions to address these obstacles. For this purpose, an integrated MCDM and game theory model in a grey environment will be used. In evaluating the solutions to the obstacles and challenges of implementing big data in smart cities in developing countries, game theory can be employed as an effective analytical tool. In this method, the obstacles are considered as one player and the counter-strategies as another player. Therefore, the advantage of this proposed research method is that the solutions are not merely ranked; instead, the model identifies the optimal solution among all possible solutions. This is crucial as, in the real world, ranking solutions might not be sufficient, and a combination of solutions may better address the problem.
The grey environment comprises quantitative methods that use interval data instead of precise numbers, unlike traditional methods (Li, Kisacikoglu, Liu, Singh & Erol-Kantarci, 2017). The grey theory, which was introduced by Deng (1982), is a mathematical concept widely used in MCDM. This theory is particularly effective in tackling problems involving uncertainty, especially when information is unknown or incomplete (Cui, Chan, Zhou, Dai & Lim, 2019). Generally, the information about decision-maker's (DMs) preferences regarding criteria is expressed based on their qualitative judgment for various reasons. Additionally, in practice, the judgments of DMs are often uncertain and cannot be expressed with precise numerical values (KamaliSaraji & Streimikiene, 2024; Li et al., 2017).
Grey theory is a method used to study uncertainty and incomplete information, and its application in the mathematical analysis of systems with incomplete data is expanding. Unlike precise numerical values, grey numbers explicitly represent uncertainty and inaccuracy. This flexibility allows DMs to incorporate subjective judgments, incomplete information, and varying degrees of importance assigned to different criteria. Grey numbers are similar to fuzzy numbers; however, the key difference is that with grey numbers, the exact value is unknown, but the range within which the value lies is known. In other words, the precise bounds of the left and right intervals of the number are determined and known (Bouzon, Govindan & Rodriguez, 2018; Cui et al., 2019; Li, Zhao, Wu & Qiu, 2022). On the other hand, a fuzzy number depends on a membership function and is defined as an interval whose left and right bounds have unknown values. The computation of the membership function for the upper and lower bounds of a fuzzy number requires intricate computations, which makes calculations involving grey numbers more straightforward than those involving fuzzy numbers. Thus, the contributions of the present research are as follows:
- i.
Improving the performance of the zero-sum grey game theory by defining the grey payoff matrix,
- ii.
Integration of the Grey Best-Worst Method (G-BWM) with the Improved Zero-Sum Grey Game (IZSGG) for evaluating and ranking the barriers to big data implementation in smart cities, and
- iii.
Developing the game theory with a grey decision matrix to build up an optimal model to address the challenges of implementing big data in sustainable smart cities.
The research questions of this study are as follows:
- i.
What are the most significant barriers to the implementation of big data in sustainable smart cities?
- ii.
What is the worst-case risk scenario for the implementation of big data in sustainable smart cities?
- iii.
Which optimal strategies can effectively address the barriers to the implementation of big data in sustainable smart cities?
In Section 2, the study discusses the barriers to implementing big data in sustainable smart cities. Section 3 reviews and explains the integrated research methodology. Section 4 addresses the case study, including data collection and questionnaires and problem-solving and evaluating the findings. Section 5 discusses the research findings and offers practical recommendations based on the results. Finally, Section 6 presents the overall conclusions, summarizing the research and suggesting directions for future studies.
Literature reviewSmart citiesSmart cities utilize advanced technologies, including big data analytics, to address urban challenges and promote sustainable development. While big data holds immense potential for optimizing resource allocation, reducing environmental impact, and enhancing citizen services, its implementation in smart city initiatives faces various challenges and obstacles (Aloqaily, Otoum, Ridhawi & Jararweh, 2019; Kudva & Ye, 2017; Vilajosana et al., 2013). This literature review aims to identify and analyze the key challenges hindering the effective utilization of big data in achieving sustainability goals within smart cities. One of the primary challenges associated with big data in smart cities is ensuring the privacy and security of sensitive information (Ajaj et al., 2024; Khan et al., 2022; Mutambik, 2024; Vilajosana et al., 2013). The collection, storage, and analysis of vast amounts of data raise concerns regarding individual privacy rights and the potential for data breaches (Aloqaily et al., 2019; Korczak & Kijewska, 2019). Safeguarding personal data while enabling data-driven decision-making poses a significant challenge for smart city planners and policymakers. Another obstacle to the successful implementation of big data in smart cities is the lack of interoperability among different data sources and systems (Ali et al., 2020; Korczak & Kijewska, 2019; Razmjoo, Østergaard, Denaï, Nezhad & Mirjalili, 2021). Data silos and incompatible formats hinder the seamless exchange and integration of information from various sources, limiting the effectiveness of data analytics initiatives. The infrastructure required to support big data analytics in smart cities is often inadequate or outdated (Khan, 2021; Paes et al., 2023). Limited bandwidth, storage capacity, and computing resources constrain the scalability and performance of data analytics platforms, hindering their ability to process and analyze large datasets in real time (Khan, 2021; Korczak & Kijewska, 2019). The digital divide, characterized by unequal access to technology and digital services, poses a significant challenge to the equitable deployment of smart city solutions. Socioeconomic disparities in access to high-speed internet, digital devices, and technical skills exacerbate existing inequalities and impede the participation of marginalized communities in smart city initiatives (Ahmed, Basha, Ramachandran, Daneshmand & Gandomi, 2023, 2023; Ajaj et al., 2024).
The primary research topics in smart city studies can be categorized into three main areas: concepts and elements, smart cities and the IoT, and the future vision of smart cities (Zhao, Tang & Zou, 2019). Big data challenges in sustainable smart cities include managing the vast amounts of data produced by devices, vehicles, and power grids, and integrating this data with smart city policies to enhance transportation and energy efficiency (Li et al., 2017). Khan et al. (2022) identified major barriers to sustainable smart city development, including the lack of necessary technologies, a robust big data analytics framework, the inherent nature of big data, and the limited availability of analytics platforms. Visualizing big data in smart cities is complex due to the diversity of data sources and user groups, making it difficult for DMs to interpret intricate dashboards (Lavalle, Teruel, Maté & Trujillo, 2020). Moreover, the integration of IoT and big data introduces new challenges in realizing the principles and requirements of smart city applications, particularly in business and technology contexts (Hashem et al., 2016). Secure Data Analytics (SDA) in smart grid systems faces issues such as secure data collection, preprocessing, load data processing, load prediction, load management, data security, and communication (Kumari et al., 2020). Pal, Triyason and Padungweang (2018) highlighted challenges in big data analytics for smart cities, including data heterogeneity, conflicting processing requirements, and the necessity for a four-tier framework comprising sensing, storage, processing, and application hubs. Khan (2021) demonstrated that diverse populations and inadequate infrastructure significantly hinder the integration of big data in smart city development. Apache Sedona's parallel processing system has shown superior performance in read, write, join, and clustering operations for sustainable smart city applications (Mete et al., 2023). Srivastava and Singh (2018) identified challenges such as the growth of data marts and datasets and the need for an IoT framework to improve smart city functionality. Big data technologies can support smart transportation, traffic management, waste management, energy, environment, infrastructure, safety, healthcare, urban planning, and citizen participation, thereby improving urban living standards (Wu, Yan, Huang & Sarker, 2022). Ma, Li, Xie and Zhang (2018) introduced city profiling as a method for constructing digital urban spaces, utilizing big data to enhance urban management and operational capabilities. Chen et al. (2021) examined the challenges of using big data for sustainable smart cities, focusing on privacy, security, confidentiality, and authenticity in data management interfaces. The most widely used MCDM methods for city rankings are Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), Analytical Hierarchy Process (AHP), and Preference Ranking for Organization Method for Enrichment Evaluation (PROMETHEE), though integrating these with other methods remains challenging (Ogrodnik, 2023). The effective implementation of big data in sustainable smart city development faces numerous obstacles. Key issues such as data privacy and security, interoperability limitations, infrastructure constraints, and the digital divide must be addressed to fully realize the potential of big data analytics in promoting sustainability and enhancing urban livability. Future research should aim to develop innovative solutions and policy frameworks to overcome these challenges, fostering the equitable and inclusive deployment of smart city technologies.
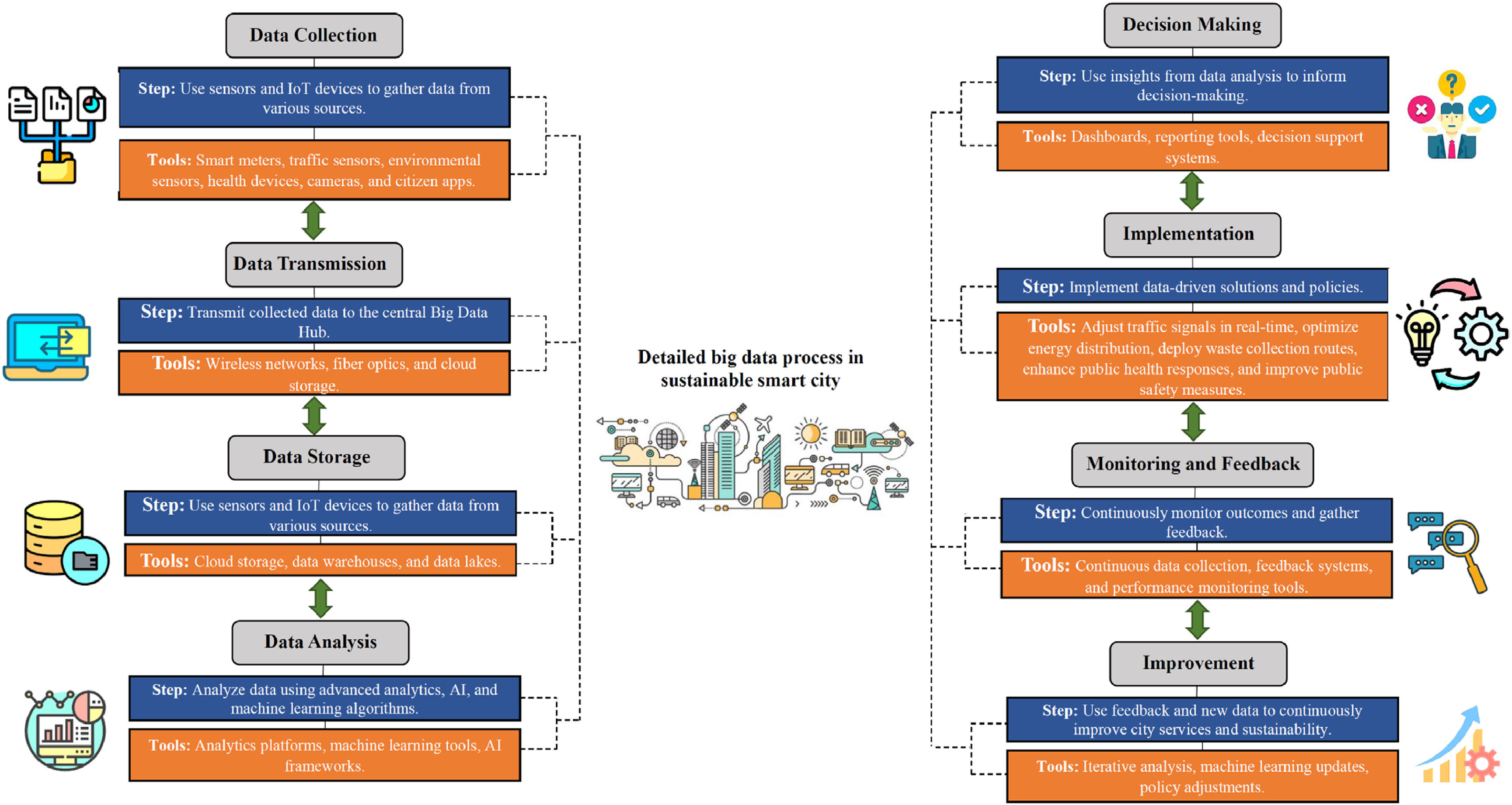
Big data implementation for sustainable smart cityBig data plays a crucial role in the implementation of sustainable smart cities by enabling efficient data management and analysis for various aspects of urban development (Barham & Daim, 2018; Vilajosana et al., 2013; Zhang, Tai, Cao, Wei & Cheng, 2024). Leveraging technologies such as Geographic Information Systems (GIS), cloud computing, and the IoT allows for the creation of predictive data science tools that support green initiatives such as green building and energy conservation. The integration of big data facilitates the development of smart governance frameworks, improving decision-making processes and improving urban services (Khan, 2021; Mutambik, 2024; Vilajosana et al., 2013). By utilizing geospatial intelligence and parallel computing systems, cities can address environmental challenges, optimize resource allocation, and enhance overall sustainability. Implementing big data solutions in smart cities not only boosts operational efficiency but also fosters innovation and resilience in the face of urbanization and environmental issues (Al Dakheel, Del Pero, Aste & Leonforte, 2020; Ali et al., 2020; Khan, 2021; Razmjoo et al., 2021). Fig. 1 depicts a detailed big data scheme in sustainable smart cities.
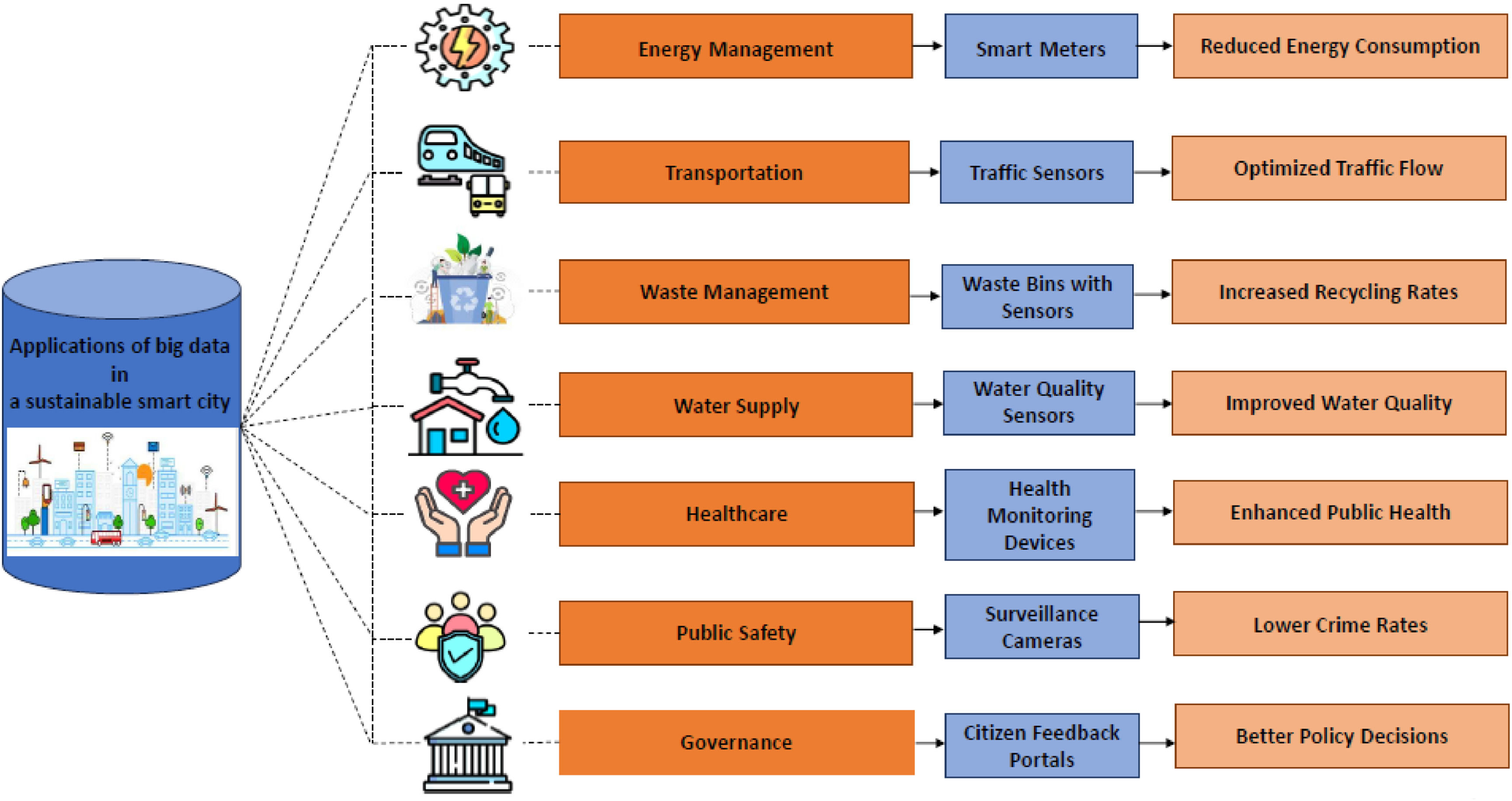
Implementing big data for sustainable smart cities offers numerous advantages. It enables more efficient urban management by providing real-time data for better decision-making, which can optimize resource allocation and reduce waste. Big data analytics can improve public services by improving traffic management, predicting and mitigating environmental impacts, and increasing energy efficiency (Barham & Daim, 2018; Korczak & Kijewska, 2019; Vilajosana et al., 2013). It also supports proactive maintenance of infrastructure by identifying potential issues before they become critical. Moreover, big data facilitates better citizen engagement and service personalization through the analysis of social and behavioral patterns, leading to improved quality of life. The integration of big data in smart cities contributes to their sustainability by fostering innovation, resilience, and adaptability (Khan, 2021; Razmjoo et al., 2021; Vilajosana et al., 2013). Big data applications in sustainable smart cities span various domains, enhancing efficiency and improving quality of life. In traffic management, big data helps optimize traffic flow and reduce congestion through real-time data analysis and predictive modeling. Energy management benefits from big data by enabling smart grids that optimize energy distribution and consumption, leading to reduced waste and lower carbon footprints (Ahmed et al., 2023; Paes et al., 2023). Environmental monitoring uses big data to track pollution levels, predict weather patterns, and manage natural resources sustainably. Public safety is improved through big data analytics that improves crime detection and emergency response times. Additionally, healthcare services are optimized by analyzing large datasets to improve patient care and resource allocation. In waste management, big data supports efficient collection, recycling, and disposal processes (Al Dakheel et al., 2020; Paes et al., 2023). Fig. 2 displays the applications of big data in a sustainable smart city.
The precise process of big data in a sustainable smart city encompasses various applications and solutions that contribute to the optimization of urban management and sustainability. By harnessing the power of data analytics, cities can improve efficiency, reduce waste, and enhance the quality of life for their residents. This optimization of big data involves seven key areas, each addressing specific challenges and opportunities within the urban environment (Ahmed et al., 2023; Khan et al., 2022; Paes et al., 2023). These areas include traffic flow management, energy consumption optimization, air quality monitoring, public transportation optimization, water supply management, smart grid load balancing, and waste management. Each of these applications leverages big data to provide real-time insights, predictive analytics, and data-driven decision-making, ensuring that city operations are more responsive, efficient, and sustainable (Khan, 2021; Razmjoo et al., 2021; Vilajosana et al., 2013). In the following, we delve deeper into each of these seven areas, explaining how big data solutions contribute to the creation of smarter, more sustainable urban landscapes:
Traffic flow managementIn order to manage traffic flow in sustainable smart cities, big data is essential. Urban planners can forecast and alleviate traffic congestion by gathering and evaluating real-time data from multiple sources, including GPS units, social media platforms, and traffic cameras. Utilizing sophisticated algorithms, this data is processed to optimize traffic signals, reroute traffic during peak hours, and give drivers real-time updates via smart navigation systems (Ahmed et al., 2023; Paes et al., 2023). This not only reduces travel time and fuel consumption but also lowers carbon emissions, contributing to a more sustainable urban environment. The fundamental traffic flow is defined as follows:
whereq = traffic flow (vehicles per hour),
k = traffic density (vehicles per kilometer),
v = traffic speed (kilometer per hour).
Energy consumption optimizationBy combining information from smart meters, sensors, and weather forecasts, big data makes it possible to optimize energy use in sustainable smart cities. With the use of this data, energy supply can be modified to meet anticipated demand. By using this data to distribute energy more effectively and guarantee a steady supply, smart grids minimize waste. Big data analytics can help consumers save energy and promote the growth of renewable energy sources by spotting patterns and abnormalities in energy usage. This improves the sustainability of the city as a whole (Ahmed et al., 2023; Paes et al., 2023). For optimizing energy consumption in a smart city, the following dynamic Eq. (2) can be employed for the total energy consumption E(t) over time t:
wherePi(t) = power consumption of the i-th device at time t,
Δt = time interval,
n = number of devices.
Air quality monitoringBig data applications help to improve air quality monitoring in smart city environments. To find pollution sources and trends, data on different pollutants is gathered by sensors positioned throughout the city and analyzed. With this data, authorities can take focused action to improve the quality of the air. For example, they can modify traffic patterns in high-pollution areas to minimize emissions or inform the public about health precautions to take when the air quality is less than ideal. Ensuring a healthy urban environment and developing long-term pollution control strategies are made easier with the aid of ongoing monitoring and data analysis (Khan, 2021; Razmjoo et al., 2021; Vilajosana et al., 2013). For monitoring air quality, we can model the concentration of pollutants over time using a differential Eq. (3):
whereC(t) = concentration of pollutants at time t,
k = decay constant (the rate at which pollutants dissipate),
I(t) = input rate of pollutants at time t.
Public transportation optimizationIn sustainable smart cities, big data greatly increases the effectiveness of public transportation systems. City planners can optimize routes, schedules, and resource allocation by analyzing data from transit systems, passenger counts, and travel patterns. With the use of real-time data, service reliability can be increased and wait times can be decreased by making dynamic adjustments to account for variations in demand. This lessens the impact of urban transportation systems on the environment, promotes the use of public transportation, and reduces traffic congestion (Khan, 2021; Razmjoo et al., 2021; Vilajosana et al., 2013). The optimal scheduling and routing of public transportation can be modeled using the following Linear Programming (LP) model:
subject towherecij = cost of assigning vehicle i to route j,
xij = binary variable (1 if vehicle i is assigned to route j, 0 otherwise),
n = number of vehicles,
m = number of routes.
Water supply managementIn smart cities, big data is pivotal for managing water supply systems. Data from sensors in water distribution networks is analyzed to detect leaks, monitor water quality, and manage usage patterns. This enables proactive maintenance, reduces water wastage, and ensures a consistent and safe water supply. Predictive analytics can forecast demand and optimize water distribution, especially during droughts or peak usage times, contributing to the sustainability of water resources in urban areas. For managing the water supply, the water balance Eq. (5) can be utilized:
whereS(t) = water storage at time t,
I(t) = inflow rate at time t,
O(t) = outflow rate at time t.
Smart grid load balancingBig data aids in balancing the load on smart grids by analyzing data from energy consumption patterns, renewable energy inputs, and grid performance. This analysis helps in predicting peak demand periods and managing the distribution of electricity accordingly. By dynamically adjusting the supply and demand balance, smart grids prevent overloading and blackouts, improve energy efficiency, and support the integration of renewable energy sources. This leads to a more reliable and sustainable energy infrastructure (Khan, 2021; Razmjoo et al., 2021; Vilajosana et al., 2013). For load balancing in a smart grid, the dynamic load balancing is defined based on Eq. (6):
whereL(t) = load at time t,
Ldemand(t) = electricity demand at time t,
Lgeneration(t) = electricity generation at time t.
Waste managementBig data transforms waste management in sustainable smart cities by optimizing the collection, recycling, and disposal processes. Data from sensors on waste bins, collection vehicles, and recycling facilities is analyzed to streamline operations. Predictive analytics can forecast waste generation patterns, allowing for efficient route planning and resource allocation. This reduces operational costs, minimizes environmental impact, and enhances recycling rates. Effective waste management supported by big data contributes to cleaner cities and better resource utilization, aligning with sustainability goals (Khan, 2021; Razmjoo et al., 2021; Vilajosana et al., 2013). For dynamic waste management, the waste generation rate can be modeled by Eq. (7):
whereW(t) = total waste at time t,
W0 = initial amount of waste,
r = rate of waste generation.
Big data adoption barriers for sustainable smart cityImplementing big data is not without its challenges and risks. Despite its potential benefits, there are several obstacles that cities must overcome when deploying big data solutions in the context of sustainable smart cities. Some of these challenges include issues related to data privacy and security, the complexity of data integration from various sources, the high costs associated with infrastructure and technology investments, and the need for skilled personnel to manage and analyze large volumes of data effectively. Numerous studies have been conducted on the obstacles of big data across various domains and applications. Khan (2021) aimed to identify and prioritize the challenges of big data adoption in smart cities using the Best-Worst Method (BWM). This study focused on several key issues such as data complexity and the lack of a standardized mechanism for big data usage, thus providing a structured way to prioritize these challenges with the help of expert judgments. Khan (2021), on the other hand, attempted to explore issues related to working out BIG DATA in smart cities through an integrated approach through fuzzy ISM and fuzzy-DEMATEL techniques. Fourteen challenges were outlined within the research, with special attention drawn to a diverse population and poor infrastructure as major barriers. This integrated fuzzy ISM-DEMATEL approach allowed the researchers to conceptualize the interrelationships among these challenges, thus providing valuable insights for practitioners and policymakers engaged in smart city projects.
Bibri (2020) examined the role of big data in the development of smart cities using a game-theoretical approach. The study explored how strategic interactions between city planners and technology providers could be analyzed to develop cooperative strategies for overcoming the impediments to the adoption of big data. The application of the game-theoretical approach in this study provided deeper insight into how the challenges of big data technology implementation within smart cities could be overcome through collaborative efforts. Hashem et al. (2016) investigated the very early challenges in integrating big data into the framework of a smart city regarding data security, privacy, and scalability. Their work acted as a foundational point for later studies in identifying the key challenges and providing early conceptual frameworks for implementing big data technologies within an urban setting.
Liu et al. (2020) developed a novel MCDM method that is based on Dempster-Shafer (DS) theory and the Fuzzy Best-Worst Method (FBWM) to assess four technologies, with incineration identified as the most sustainable option. The DS-FBWM approach proved to be particularly effective in addressing incomplete information, thereby providing a robust decision-making framework for stakeholders to evaluate various energy conversion technologies. Trivedi, Jakhar and Sinha (2021) applied DEMATEL and ISM methodology to examine the barriers to Inland Waterway Transport (IWT) in India. Their findings revealed that the barriers of governance challenges, policy bias, and high-cost requirements are the most prevalent. The research explained cause-effect relationships among these impediments and set strategic insight for the policymaker to fight against such inhibitors and inspire sustainable transportation in India.
Table 1 presents an in-depth view of research focusing on sustainable development and smart city initiatives. From these research works, the most dominant and general trend observed relates to integrating and optimizing big data technologies for better development and sustainability of smart cities. The objectives mainly focus on the challenges and barriers that surround the effective use of big data analytics for improving urban living standards, ensuring the resources are used efficiently, and improving the quality of life in urban areas. According to Table 1, it is revealed that the previous studies delved into various aspects such as privacy, technical integration, environmental impacts, transportation logistics, and security risks associated with implementing big data solutions across smart city frameworks. They contributed valuable insights into overcoming these challenges and optimizing the benefits of big data in urban sustainability and development. The present study examines the challenges of big data in sustainable smart cities and proposes optimal solutions for big data optimization within smart urban contexts. The research aims to identify and analyze obstacles related to data integration, privacy concerns, technical limitations, and environmental impacts. By leveraging a combined approach of MCDM and game theory under uncertainty, the study offers insights into addressing these challenges effectively. It seeks to provide a framework for implementing big data solutions that enhance the efficiency, sustainability, and resilience of smart city initiatives. Based on a literature review, the challenges of implementing blockchain in sustainable smart cities are summarized in Table 2 (Ajaj et al., 2024; Khan, 2021; Kudva & Ye, 2017; Mutambik, 2024; Paes et al., 2023; Razmjoo et al., 2021). These barriers underscore the complexity involved in integrating blockchain solutions effectively within smart city frameworks, highlighting the need for innovative approaches and robust strategies to mitigate these challenges.
Literature review.
| Reference | Methodology | Objectives | No. of Criteria | Case study | Solution evaluation | Obstacles assessment | Uncertainty | Sustainability |
|---|---|---|---|---|---|---|---|---|
| (B. Li et al., 2017) | Regression methods | Charging, efficiency, capacity assessment | 4 | Beijing | ✓ | |||
| (M. A. Khan et al., 2022) | Delphi andBWM | Analyze barriers to sustainability | 14 | developing country | ✓ | ✓ | ||
| (Lavalle et al., 2020) | Visualization techniques | Improving the evidence-gathering process | 11 | Fire department | ✓ | ✓ | ||
| (Hashem et al., 2016) | Computational intelligence algorithms | Big data analytics to support smart cities | 4 | Stockholm | ✓ | ✓ | ||
| (Kumari & Tanwar, 2020) | SDA | Improving the quality of life with a sustainable environment | 6 | Electrical energy system | ✓ | ✓ | ✓ | |
| (Pal et al., 2018) | Top-level snapshot | Smart city data analytics | 5 | Seoul, Singapore, Masdar, Yokohama, Nakhon Nayok, Barcelona, HafenCity, Copenhagen, Tel-Aviv, New York | ✓ | ✓ | ||
| (M. A. Khan et al., 2022) | fuzzy-ISM,fuzzy-DEMATEL | Big data application challenges | 14 | City developers and city officials | ✓ | ✓ | ✓ | |
| (Mete, 2023) | GIS,key technological drivers and cloud computing | Holistic big data infrastructure | 4 | England and Wales | ✓ | ✓ | ||
| (Srivastava & Singh, 2018) | DEL and JAI | Handling big data challenges | 4 | New Delhi | ✓ | ✓ | ||
| (Wu et al., 2022) | PRISMA | Potential of big data technologies | 10 | Stakeholders in policy, planning, designing | ✓ | ✓ | ||
| (Ma et al., 2018) | CPSS | Urban big data utilization | 6 | Nanjing | ✓ | ✓ | ||
| (Chen, Ramanathan & Alazab, 2021) | HBDIAIM | Improve the privacy and security aspects of data management | 4 | Health care service | ✓ | |||
| (Dahmani et al., 2020) | UML diagram | Effect of big data on urban living | 6 | City dwellers | ✓ | ✓ | ||
| (Ogrodnik, 2023) | PROMETHEE and TOPSIS | City rankings | 43 | Polish | ✓ | ✓ | ||
| Present study | G-BWM and IZSGG | Optimizing a sustainable smart city with big data implementation | 12 | Sustainable Smart city | ✓ | ✓ | ✓ | ✓ |
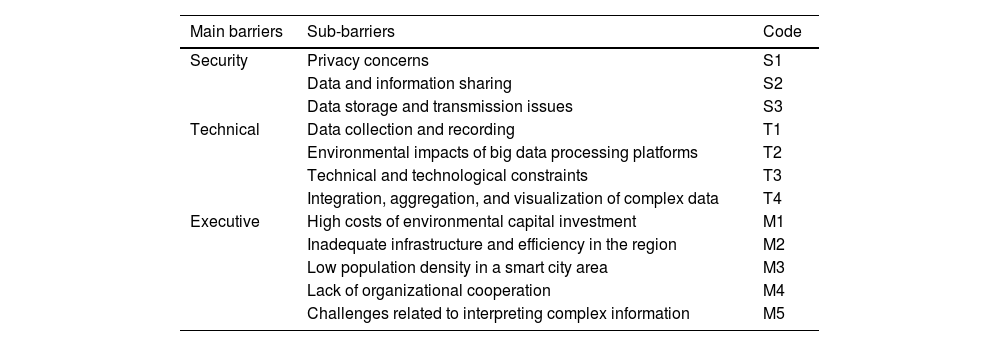
Main barriers and sub-barriers facing the implementation of big data in a sustainable smart city.
Grey numbers, introduced by Deng (1982), are a form of quantitative representation that differs from traditional crisp numbers and fuzzy numbers. Grey numbers are particularly useful in decision-making contexts where uncertainty and incomplete information exist. Unlike crisp numbers, which denote precise values, and fuzzy numbers, which represent uncertainty through membership functions, grey numbers provide a range within which the precise value is unknown but bounded (Mubarik, Kazmi & Zaman, 2021). This characteristic makes grey numbers suitable for situations where DMs need to consider qualitative judgments, incomplete information, and varying degrees of importance assigned to different criteria. In practical applications, grey numbers are employed in areas such as optimization, decision analysis, and risk assessment, offering a middle ground between crisp certainty and fuzzy uncertainty. They facilitate a more flexible approach to decision-making by accommodating imprecise data and mitigating the impact of uncertainty on outcomes (Bouzon et al., 2018; Cui et al., 2019; Li et al., 2022; Radovanović et al., 2023). A grey number is denoted as X~ and can be represented as an interval X~=[X‾,X¯], where X‾ is the lower bound of the interval and X¯ is the upper bound of the interval So that X‾≤X¯(Azar & Ardakani, 2014).
Operators for grey numbersSome fundamental operations defined for grey numbers along with their formulas:
Definition 1 (Li et al., 2022; Mubarik et al., 2021). For two grey numbers X~=[X‾,X¯] and Y~=[Y‾,Y¯], the sum of numbers is defined as the X~+Y~=[X‾+Y‾,X¯+Y¯].
Definition 2 (Mubarik et al., 2021). For two grey numbers X~=[X‾,X¯] and Y~=[Y‾,Y¯], the Subtraction of numbers is defined as the X~−Y~=[X‾−Y‾,X¯−Y¯].
Definition 3 (Li et al., 2022). For two grey numbers X~=[X‾,X¯] and Y~=[Y‾,Y¯], the Multiplication of numbers is defined as the X~×Y~=[min(XY‾,X‾Y¯,X¯Y‾,XY‾),max(XY‾,X‾Y¯,X¯Y‾,XY‾)]
Definition 4 (Mubarik et al., 2021). For two grey numbers X~=[X‾,X¯] and Y~=[Y‾,Y¯]where0∉[Y‾,Y¯], the Division of numbers is defined as the X~÷Y~=[min(XY‾,Y¯‾Y¯,X¯Y‾,X¯‾Y¯),max(X‾Y‾,XY¯,X¯Y‾,X¯Y¯)]
Definition 5 (Liu et al., 2020). Scalar Multiplication of a grey number by a grey number X~=[X‾,X¯]:
If a≥0,
If a<0,
Definition 6 (Bouzon et al., 2018). Negation of a Grey Number X~=[X‾,X¯] is as −X~=[−X¯,−X‾]
Definition 7 (Cui et al., 2019). The length of ⊗X is calculated by Eq. (10):
Eq. (11) is employed to calculate the greyness degree of ⊗ X in order to compare the grey numbers.
In this case, Ω stands for the grey number background and μ for the grey number background length.
For two grey numbers ⊗X=[X‾,X¯] and ⊗B=[Y,Y¯], if ⊗X^<⊗Y^, then ⊗X
The grey possibility degree for numbers ⊗X=[X‾,X¯] and ⊗Y=[Y‾,Y¯] is calculated by Eq. (12) (Han & An, 2007; Zare Mehrjerdi, 2018):
BWM extended by grey numbersBWM is a popular technique in MCDM for determining the weights of criteria by comparing the best and worst criteria to all other criteria. Here, we extend BWM to handle grey numbers, which represent uncertain or imprecise information using intervals (Bitarafan, Hosseini & Zolfani, 2023; Ulutaş et al., 2022).
Step-by-Step Algorithm with grey numbers is as follows (Bitarafan et al., 2023; Mahmoudi, Mi, Liao, Feylizadeh & Turskis, 2020; Ulutaş et al., 2022):
Step 1. Identify Criteria and DMs
Step 2. Define the set of criteria {C1,C2,…,Cn}
Step 3. Identify the DMs who will provide the pairwise comparisons
Step 4. Determine the best and worst criteria
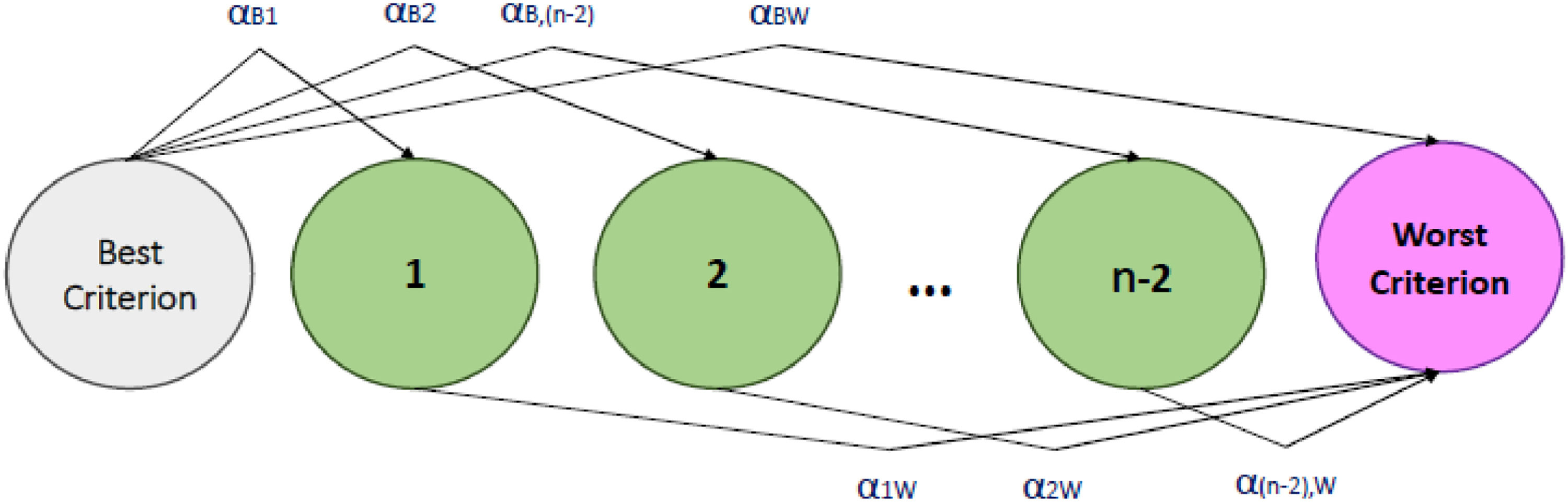
Each DM identifies the best criterion CB and the worst criterion CW based on their judgments (Fig. 3).
Step 5. Construct pairwise comparison vectors
- •
Construct the Best-to-Others (BO) vector: Each DM provides grey number comparisons between the best criterion CB and all other criteria Ci by Eq. (13):
- •
Construct the Others-to-Worst (OW) vector: Each DM provides grey number comparisons between all criteria Ci and the worst criterion CW by Eq. (14):
Step 6. Define the weights of criteria as grey numbers (w~i=[w‾i,w¯i])
- •
Objective: Minimize the maximum absolute difference between the calculated weight ratios and the provided grey number comparisons.
The optimization problem is now formulated as follows:
subject toStep 7. Solve the optimization problem
Appropriate optimization techniques (e.g., LP, interval programming) are utilized to solve the formulated problem and find the grey weights w~i=[w‾i,w¯i].
Step 8. Consistency check
In the context of grey numbers, consistency check involves verifying that the derived weights satisfy the interval comparisons with acceptable tolerance levels. If multiple DMs are involved, aggregate the weights of criteria from different DMs. This can be done using methods such as interval arithmetic or fuzzy aggregation techniques (Bitarafan et al., 2023; Ulutaş et al., 2022).
Grey number comparisons are calculated using Eq. (17):
Now, the weight ratios are obtained as follows:
The objective function is displayed as Eq. (19):
subject to (consistency constraints)By following these steps and using these formulas, you can extend the BWM to handle DMs with grey numbers, allowing for more robust handling of uncertainty and imprecision in the evaluation process.
The objective is to minimize the maximum deviation from the provided comparisons, incorporating the consistency constraints to create the model, and also the conditions to accept the weights are defined below:
whereConsistency constraints in G-BWMIn the BWM, consistency constraints ensure that the preferences provided by DMs are logically coherent and aligned. When extending BWM to handle grey numbers, these constraints ensure that the grey number comparisons between criteria maintain a reasonable degree of consistency despite the inherent uncertainty. Consistency in the context of G-BWM involves ensuring that the grey number comparisons (represented as intervals) are logically consistent (Cui et al., 2019; Li et al., 2017). This means that the derived weights of criteria should respect the relative comparisons given by the DMs, even when those comparisons are imprecise (Bitarafan et al., 2023; Bouzon et al., 2018; Cui et al., 2019; Li et al., 2017; Mahmoudi et al., 2020; Ulutaş et al., 2022):
The consistency constraints ensure that the derived grey weights respect the grey number comparisons. These constraints can be formulated as follows.
BO comparisons are calculated using Eq. (22):
whereOW comparisons are computed using Eq. (24):
To ensure that the weights are normalized by Eq. (25):
For each pair of comparisons (BO and OW), the CR values are computed as
Now, we need to combine the CRs from both BOand OW to form an overall CR using Eq. (28):
If the overall CR is below a certain threshold (usually 0.1 or 0.2), the comparisons are considered consistent. Otherwise, if the CR exceeds the threshold, the DM's preferences are inconsistent, indicating the need to re-evaluate and adjust the comparisons.
In the G-BWM, similar to classical BWM, the DM identifies the best and worst criteria and compares other criteria relative to these extremes. However, in contrast to the classical BWM, G-BWM employs grey numbers for these comparisons. Grey numbers are intervals rather than fixed values, and thus they allow the modeling of uncertainty in the DM's judgments. G-BWM solves a series of LP problems that aim to minimize the maximum deviation of the grey comparison ratios from their ideal values (Bitarafan et al., 2023; Bouzon et al., 2018; Cui et al., 2019; Li et al., 2017; Mahmoudi et al., 2020; Ulutaş et al., 2022). The GBWM involves the formulation of an LP model where the objective function aims to minimize the maximum deviation of actual comparison ratios, represented by grey numbers, from the optimal one derived from the best and worst criteria. The constraints included in this LP model are derived from grey comparison matrices that ensure consistency in the relative importance of each criterion within the defined grey intervals (Bouzon et al., 2018; Cui et al., 2019; Li et al., 2017; Ulutaş et al., 2022). This approach contrasts with traditional methods in MCDM, such as the classical BWM, since, in the BWM, fixed point comparisons lead to a simpler LP model but without the capacity for incorporating uncertainty. In comparing the G-BWM with other MCDM methods from the perspective of LP, its superiority in handling uncertainty by way of grey numbers and robustness in maintaining consistency within the decision model is high. With this, however, comes the price to be paid in additional computational complexity, since solving LP problems with interval coefficients is generally harder than solving those with fixed coefficients (Bitarafan et al., 2023; Li et al., 2017; Mahmoudi et al., 2020; Ulutaş et al., 2022).
However, the key differences in GBWM concerning the popular weighting methods (e.g., AHP, Simple Additive Weighting (SAW), and Entropy) are the treatment of uncertainty and imprecision, and number of the required comparisons. For example, similar to BWM, AHP is a pairwise comparison that does not inherently address issues of uncertainty. AHP mandates exact numerical comparisons and is prone to inconsistency whenever the judgment of the DM is not perfectly transitive. On the other hand, SAW directly gives the criteria weights according to their order of importance but is found to be lacking in any systematic approach to the occurrence of uncertainty or inconsistency in the process of weighting. The Entropy method used for objective weighting determines weights based on data variation, which does not involve subjective judgment and hence does not handle uncertainty in the subjective sense either. In turn, G-BWM represents such a weighting process with grey numbers, one which is more flexible and robust, especially when the DM is uncertain about the precise importance of the criteria (Bitarafan et al., 2023; Li et al., 2017; Mahmoudi et al., 2020; Ulutaş et al., 2022). The LP model of this method ensures that derived weights will be consistent with the grey comparisons provided by the DM; hence, more reliable in cases under uncertainty. While this makes it computationally more complicated compared to simpler methods such as SAW or Entropy, its main advantage lies in the fact that G-BWM works in a more articulated way, closer to real situations in which information is often incomplete or imprecise. Hence, mathematically speaking, the ability of G-BWM to integrate uncertainty directly into the weighting process cements its position, as an improved method for decision-making in a complex environment (Cui et al., 2019; Li et al., 2017; Mahmoudi et al., 2020; Ulutaş et al., 2022).
The CRiteria Importance Through Inter-criteria Correlation (CRITIC) method is an objective weighting technique for which weights are calculated and assigned to different criteria according to the contrast intensity of each criterion, considering variation and the conflict (correlation) that may exist between the criteria. It does not require any subjective input from the DM; rather, it uses data from the alternatives to calculate the weights themselves. This reveals that the CRITIC method essentially needs the presence of alternatives to function properly (since it calculates the weights based on the criteria differentiation capability related to different options). Similarly, the Stepwise Weight Assessment Ratio Analysis (SWARA) methodology stands for a subjective weighting method that involves the DMs in ranking criteria and further adjusting the weights by a successive ratio approach (Bitarafan et al., 2023; Bouzon et al., 2018; Cui et al., 2019). In addition, SWARA usually relies on the presence of alternatives, since DMs assess the importance of criteria based on their impact level on the designated alternatives. The iterative process inherent in the SWARA method, which adjusts the weight of each criterion based on the ranking of the previously assessed criterion, necessitates the existence of alternatives to effectively evaluate the significance of every criterion. Conversely, the G-BWM approach does not depend on the availability of alternatives for the establishment of weights. Rather, it emphasizes the identification of the optimal and least favorable criteria, facilitating comparisons in relation to these two extremes, irrespective of alternatives. This makes G-BWM particularly useful when decision makers must assess the weights of the criteria in advance, or when the alternatives are not defined. Compared to other methods, such as AHP, in the G-BWM and BWM, fewer pairwise comparisons are required, which brings less cognitive load for the DMs and, at the same time minimizes the possible inconsistencies. While the AHP requires a full pairwise comparison matrix against all the criteria, GBWM requires just the comparisons with respect to the best and worst criteria, hence less cumbersome or more effective when the number of criteria becomes large (Cui et al., 2019; Li et al., 2017; Mahmoudi et al., 2020; Ulutaş et al., 2022).
Improved zero-sum grey game theoryThe zero-sum game theory defines scenarios in game theory where one player's gain is exactly equal to the other player's loss. Extending this concept to grey numbers allows for handling uncertainty and imprecision in the payoffs. The method involves finding optimal strategies for both players when payoffs are represented as intervals (grey numbers).
First, we need to define the grey payoff matrix. Grey theory, also known as grey systems theory, is used to handle systems with uncertain, incomplete, or partially known information. A decision matrix in the context of grey theory uses grey numbers to represent the elements, capturing the uncertainty in the decision-making process. An improved grey payoff decision matrix is an extension of a traditional decision matrix where the performance ratings of alternatives against criteria are represented by grey numbers. This matrix helps in evaluating and comparing different alternatives under uncertainty.
The elements of a grey decision matrix is defined as follows (Dahmani, Cheref & Larabi, 2020; Khanzadi, Turskis, Ghodrati Amiri & Chalekaee, 2017):
- ✓
Alternatives (A): The set of options or solutions to be evaluated (A1,A2,…,Am).
- ✓
Criteria (C): The set of factors or attributes based on which the alternatives are evaluated (C1,C2,…,Cn).
- ✓
Grey numbers (x~ij): The performance ratings of each alternative Ai under each criterion Cj are represented by grey numbers x~ij=[x‾ij,x¯ij].
Now, the proposed algorithm is described as follows:
Step 1. Collect the performance ratings of each alternative against each criterion as intervals, forming grey numbers
Step 2. Structure of a grey decision matrix
The grey decision matrix X~ is defined as Eq. (29):
where x~ij=[x‾ij,x¯ij] is the grey number representing the performance of alternative Ai under criterion Cj.Step 3. Normalize the grey decision matrix
- •
Normalize the elements of the matrix to ensure comparability, especially when criteria are measured in different units. This can be done using Eq. (30):
Let the payoff matrix be represented with grey numbers P~ij=[P‾ij,P¯ij], where P~ij is the payoff when player 1 chooses strategy i and player 2 chooses strategy j.
Step 4. Formulate the LP problems
- •
Primary LP Problem for Player 1: Define the grey number strategies for player 1 as x~=(x~1,x~2,…,x~m), where x~i=[x‾i,x¯i] and ∑i=1mx~i=1.
Player 1 wishes to maximize their minimum expected payoff is calculated with Eq. (31):
- •
Convert to an LP problem:
maximizez subject to
- •
Primary LP Problem for Player 2: Define the grey number strategies for player 2 as y~=(y~1,y~2,…,y~n), where y~j=[y‾j,y¯j] and ∑j=1ny~j=1.
Player 2 wishes to minimize their maximum expected loss by Eq. (33):
- •
Convert to LP problem by Formulas (34) and (35):
Step 6. Solve the primary LP problems
- •
Use LP techniques to solve the primary LP problems for both players, obtaining the optimal strategies x~ for player 1 and y~ for player 2.
- •
Secondary LP Problem for Player 1: Refine the optimal strategy to ensure robustness against imprecision by Formulas (36) and (37):
- •
Secondary LP Problem for Player 2: Refine the optimal strategy to ensure robustness against imprecision by Formulas (38) and (39):
Step 7. Solve the secondary LP problems
- •
Use LP techniques to solve the secondary LP problems for both players, refining the optimal strategies x~ for player 1 and y~ for player 2.
By following these steps and using these LP formulations, you can extend the two zero-sum game methods to handle Decision-Making with grey numbers, allowing for a robust approach to managing uncertainty and imprecision in the payoffs.
The IZSGG theory is a modification of the classical zero-sum game theory by incorporating the grey systems theory, which deals with problems involving both partially known and partially unknown information. According to the zero-sum game theory, two players compete in such a way that the benefits gained by one player are exactly offset by the losses of the other players. The model assumes complete information at hand about the system-a situation rarely encountered in reality. IZSGG theory relaxes this assumption by allowing for "grey" factors (uncertain, incomplete, and partially known information) to be taken into consideration, and as such, offers a more realistic modeling of complex competitive environments when complete information is not attainable or even assured. Besides, grey LP can determine the bounds of the optimal values to provide a range of possible solutions rather than just a single answer. This feature is very valuable in solving strategic decision-making problems in which the exact return is not well known. The feasible region is bounded by the lower and upper limits of the grey parameters that mark out the area within which practical solutions should lie. Grey LP would not provide an exact solution with a single point but rather with an interval. An interval solution does imply the uncertainty which is dealt with by the parameters and gives the DMs an interval solution that may turn out to be optimal in different scenarios.
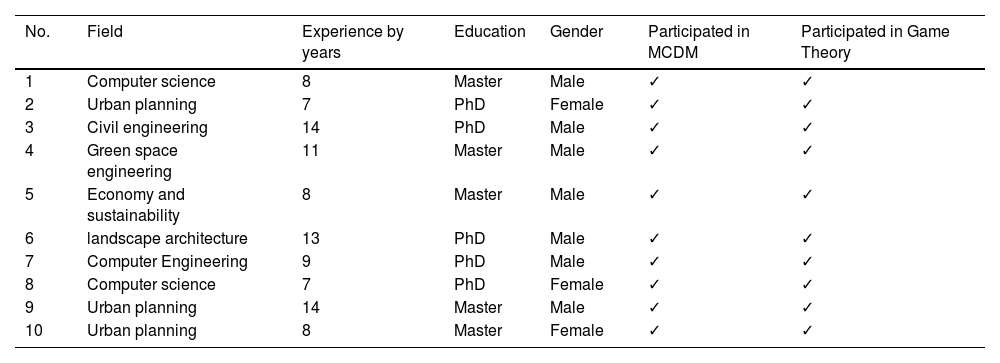
ResultCase studyAn academic two-phase research methodology is proposed to prioritize the significant barriers to big data adoption for sustainable smart city development. The first phase involves identifying major barriers related to big data through a comprehensive literature review, as shown in Table 2. These initial barriers are then refined with feedback from experts in smart city development and business analytics. The expert panel consists of ten members whose details are provided in Table 3. The industry experts are currently based in Iran but have international work experience, the consultant provides global services, and the academic experts possess deep knowledge of smart cities and big data. This diverse group was selected for their extensive experience and managerial positions, with over seven years of individual experience, making their feedback valuable and credible. A structured questionnaire is developed and distributed to the expert group for completion. Before filling out the questionnaire, the primary author presents the G-BWM to the experts, providing an overview of the methodology and the related questionnaire. After collecting the responses, the steps of the G-BWM are applied to obtain the results. Additionally, a second questionnaire regarding IZSGG is distributed, querying the experts on the impact of these barriers on solutions and necessary actions for sustainable smart city development.
Expert's information.
The Grey theory-developed BWM was applied in this step. As previously indicated, weighting can be accomplished just by having criteria present; this method, like the AHP method, is one of the few that doesn't require alternatives. However, compared to the BWM, the AHP approach requires more pairwise comparisons. Owing to the large number of criteria (12 barriers), they must be separated into more manageable clusters in order to be ranked and weighted. "Technical and Technological" has four sub-barriers, "Executive" has five, and "Privacy and Security" has three. These three clusters represent the three main barriers and their respective weights. Based on the expert survey and their consensus, the best and worst criteria (i.e., the most and least significant barriers) were chosen for the primary barriers in the first stage (Table 4). The grey spectrum of the pairwise comparison of elements is outlined in Table 5. The comparison of the best criterion (BO) with other criteria in the main barriers and sub-barriers is described in Tables 6-9, while the comparison of other criteria with the worst criteria (OW) in the main barriers and sub-barriers is given in Tables 10-13.
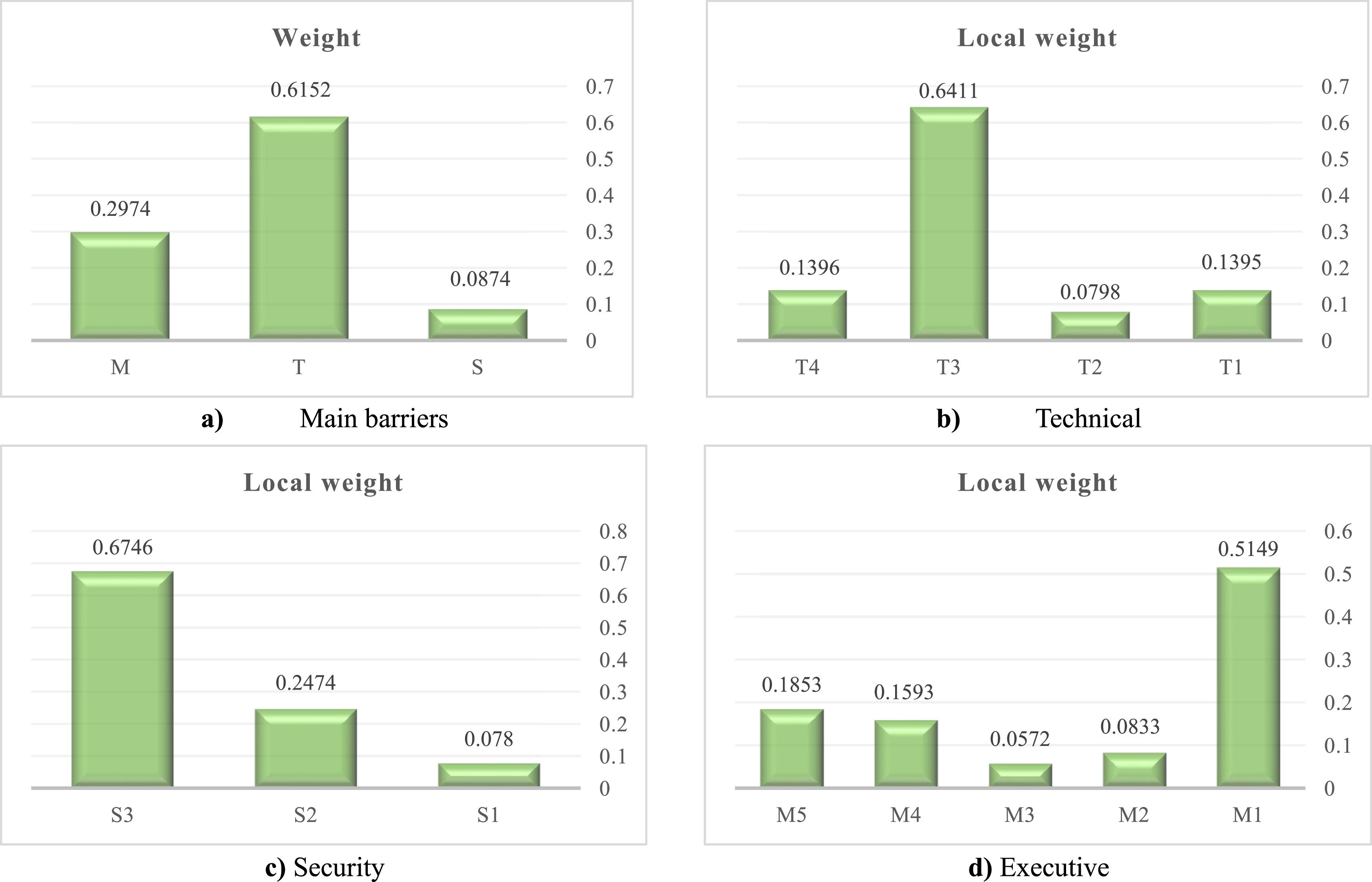
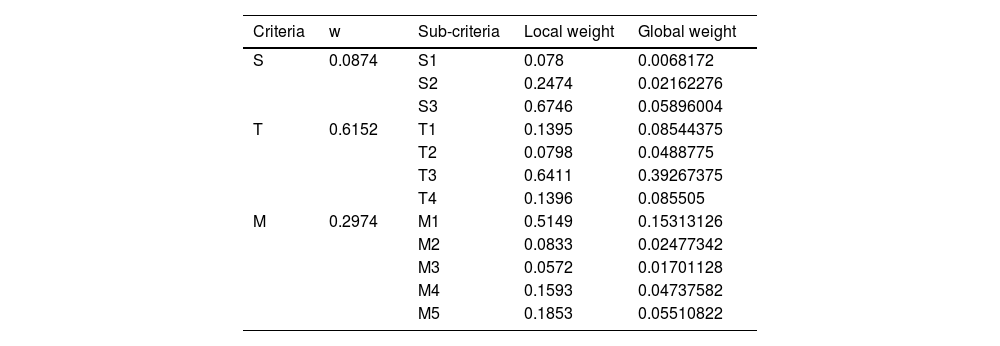
After solving the problem using the G-BWM method in grey numbers, in response to the question of the most important barriers to the implementation of big data in sustainable smart cities, the results are as follows, with the weights of criteria and sub-criteria specified. The optimal weights for the main criteria are: (w(T)=0.6152),(w(M)=0.2974),and(w(S)=0.0874). For the sub-criteria, the optimal weights are: (w(S1)=0.0780),(w(S2)=0.2474),and(w(S3)=0.6746). The optimal weights for the technical sub-criteria are:(w(T1)=0.1395),(w(T2)=0.0798),(w(T3)=0.6411),and(w(T4)=0.1396). Lastly, the optimal weights for the managerial sub-criteria are: (w(M1)=0.5149),(w(M2)=0.0833),(w(M3)=0.0572),(w(M4)=0.1593),and(w(M5)=0.1853). These results highlight the relative importance of each criterion and sub-criterion in the context of the problem, providing a structured approach to address the challenges effectively (See table 14).
Relative Weights of the barriers and sub-barriers.
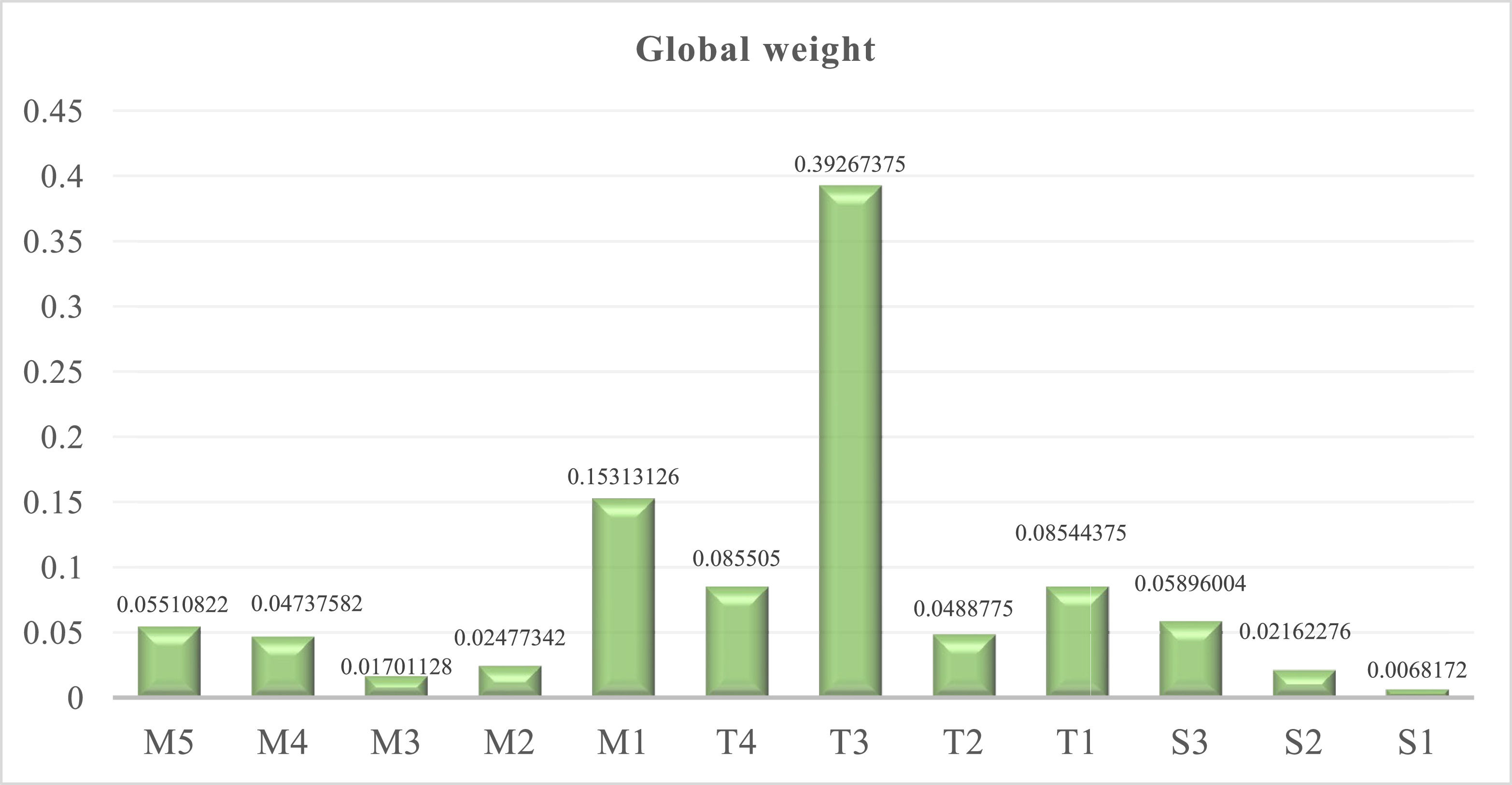
The weight of the sub-criteria is shown separately for each main criterion in Table 16 and Fig. 4 and the global weight for sub-barriers is in Fig. 5 and Table 15.
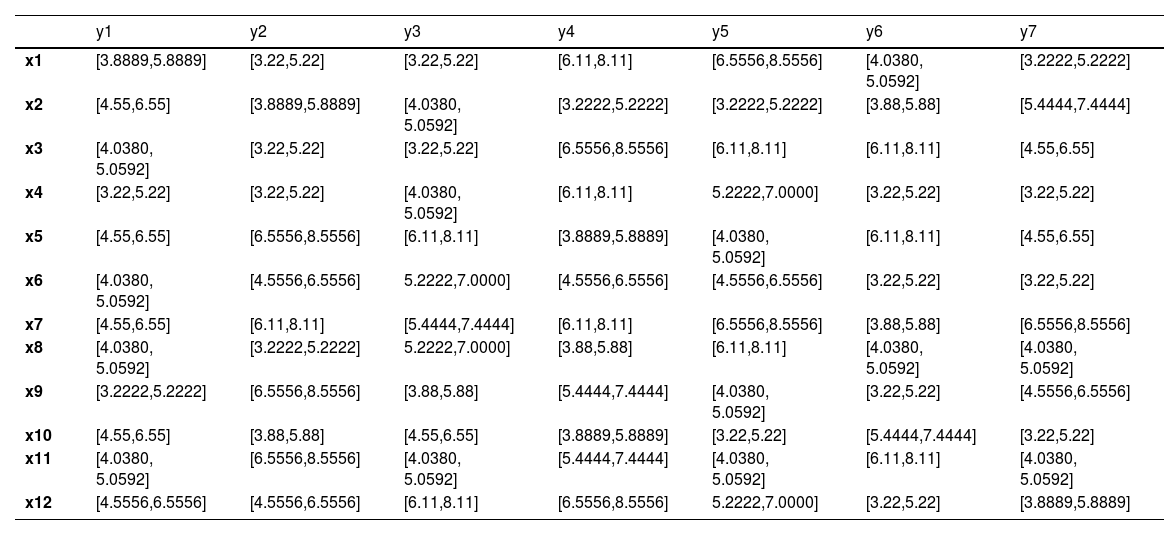
Game theory result matrix under the grey logic.
At this stage, the game theory matrix is first formed (Table 15), which consists of the impact of the obstacles examined in the paper as first player x on the solutions for implementing big data in a sustainable smart city as second player y. Obviously, we are looking for a model whose optimal solution is to maximize y and minimize x. We consider strategies as: Traffic Flow Management (y1); Public Transportation Optimization(y2); Water supply Management (y3); Smart Grid Load Balancing(y4); Waste Management(y5); Energy Consumption Optimization(y6); Air Quality Monitoring(y7).
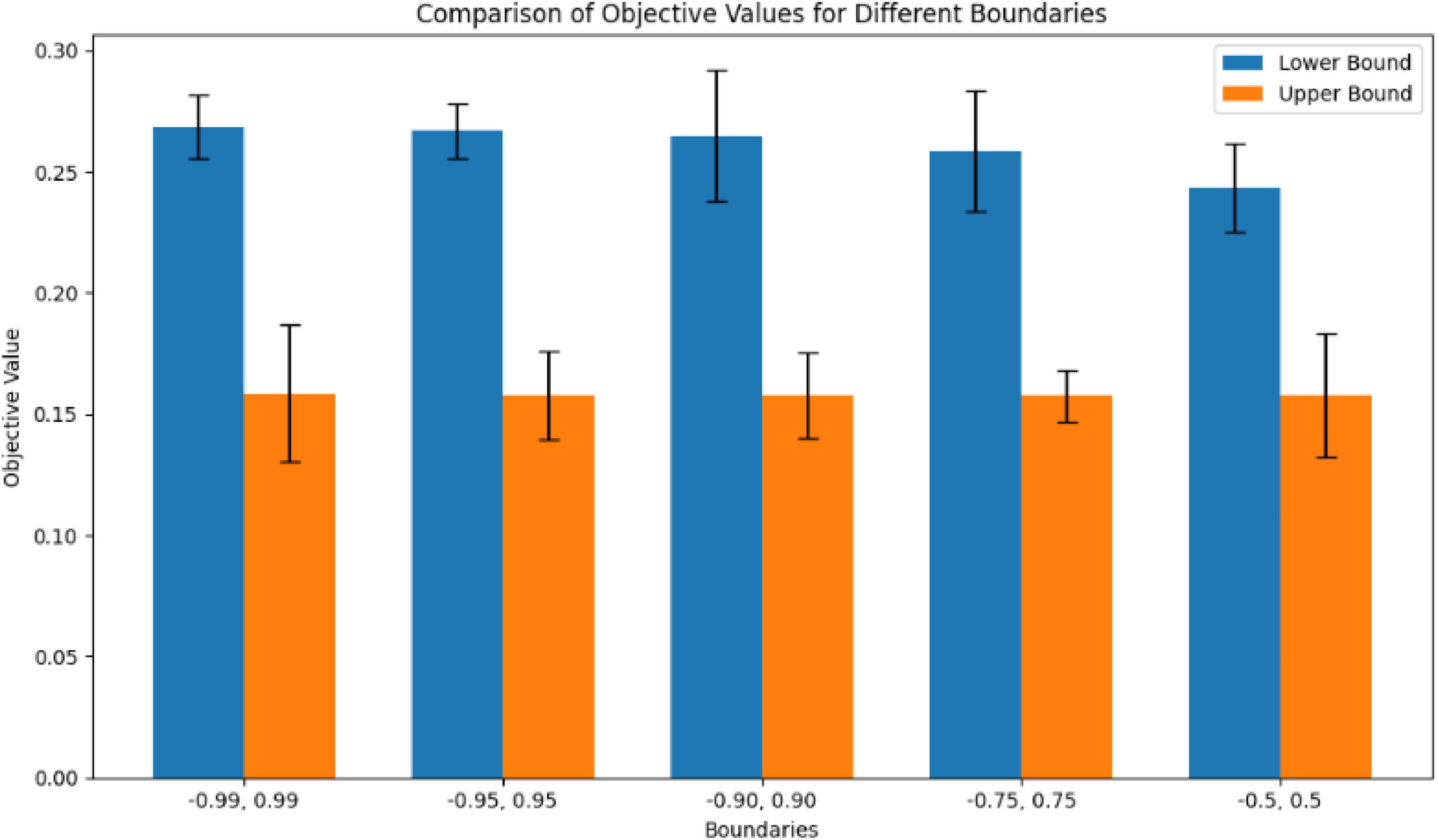
Now, it is evident from the data that the maximin value for the lower limits is 3.8889, while the maxmin value for the upper limits is 5.88. Conversely, the maxmin value for the lower limits is 6.5556, and the maxmin value for the upper limits is 3.22. These values indicate the optimal minimum and maximum thresholds for the lower and upper limits, respectively, providing a clear understanding of the decision boundaries within the given context.
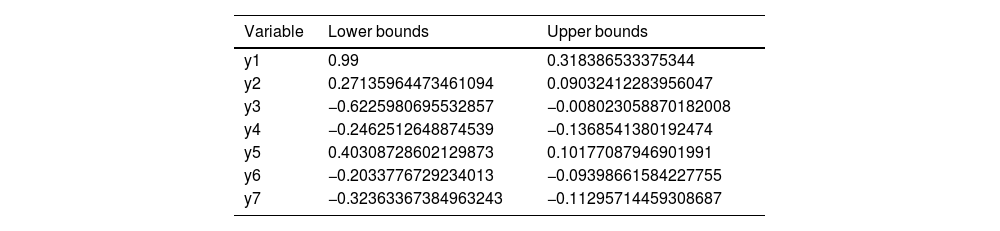
In this section, we seek to understand which optimal strategy can effectively overcome the barriers to implementing big data in sustainable smart cities. According to Tables 16 and 17, the optimal solution is equal to 0.2685862495421363. Based on the game theory results, the following actions are identified as the most important for a smart city due to their positive values:
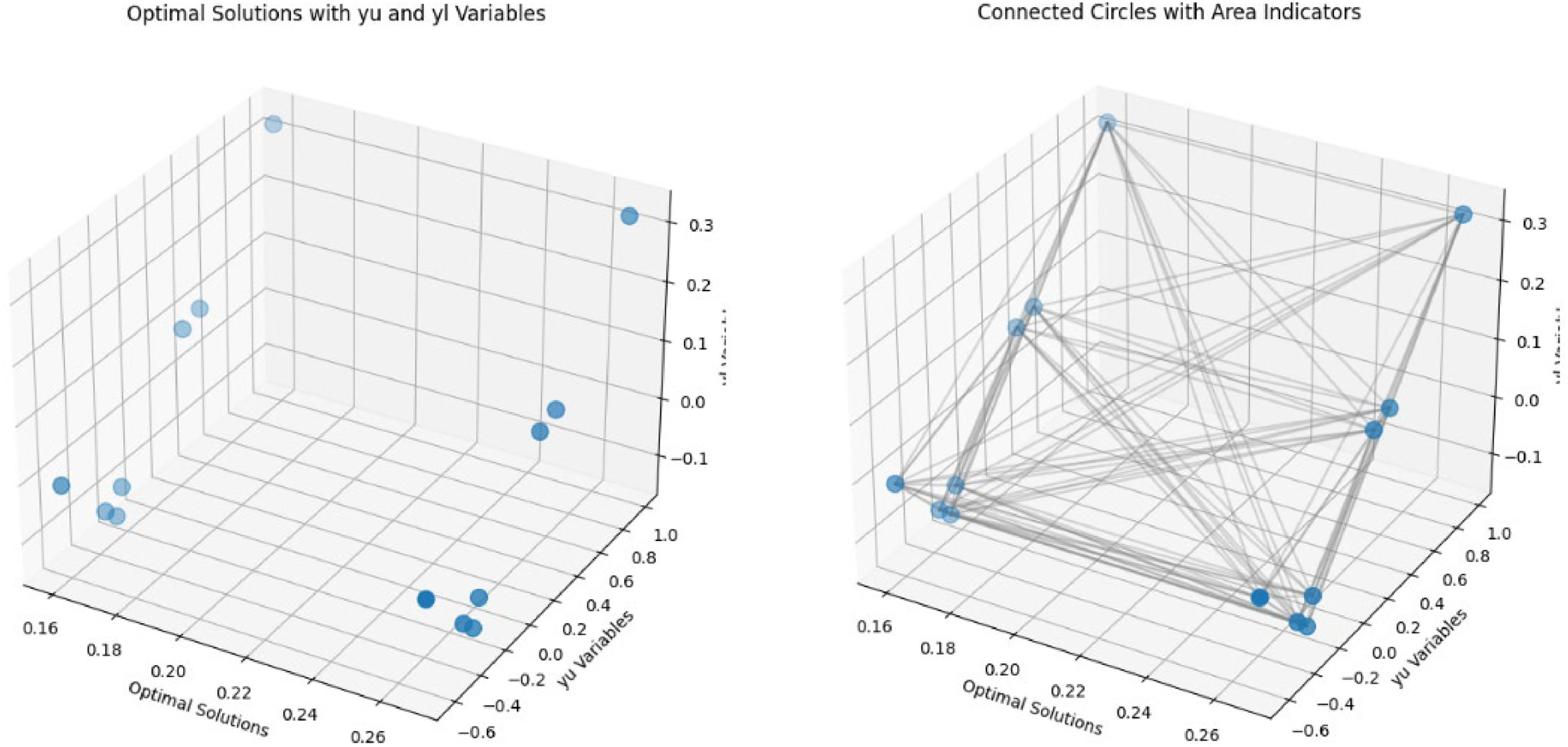
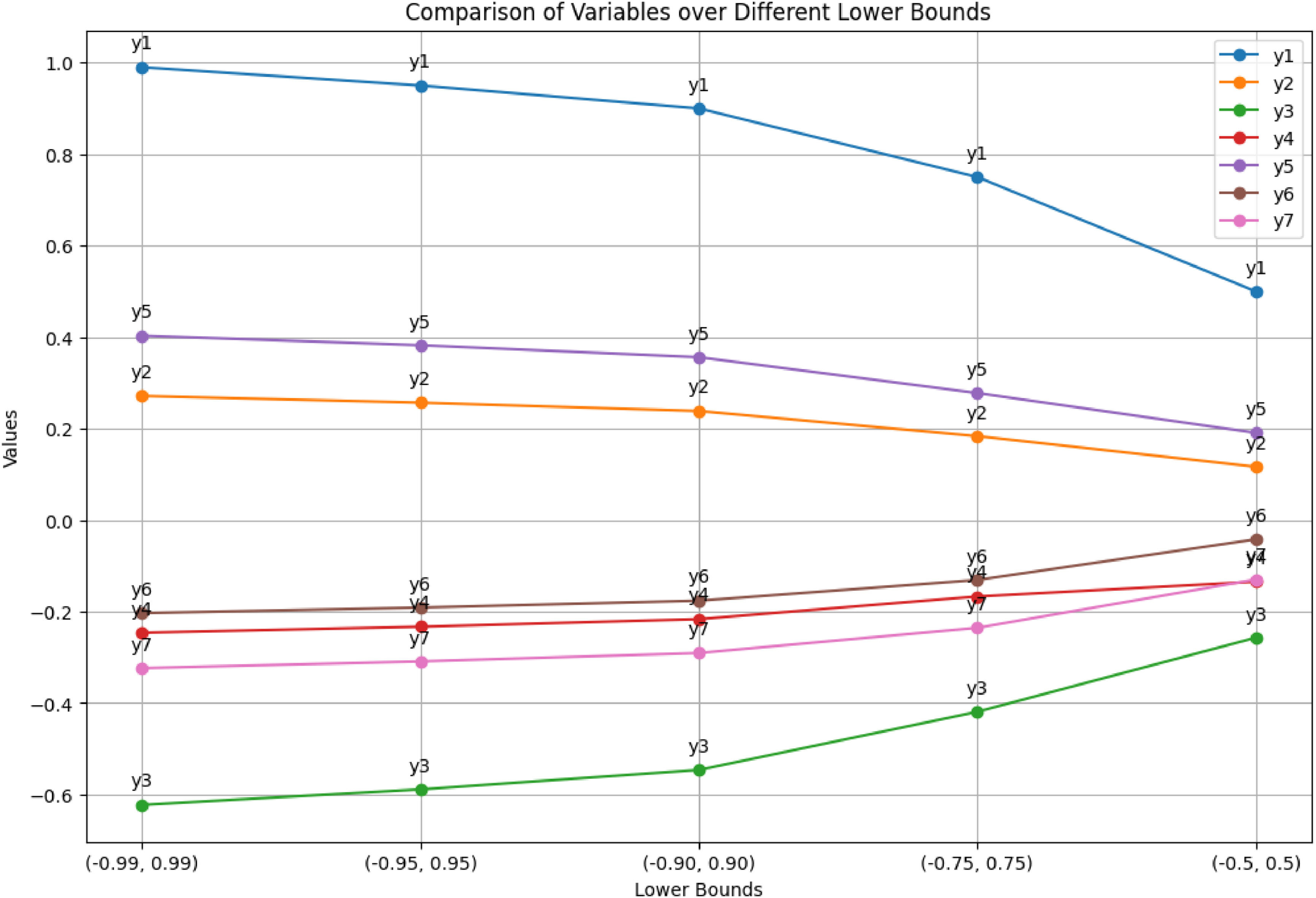
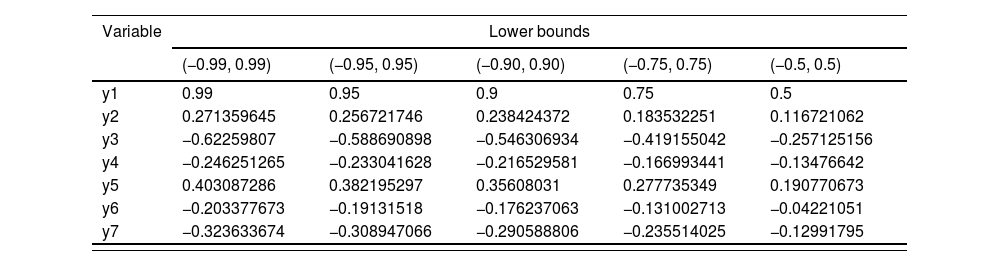
Value of the y variables in lower and upper bounds.
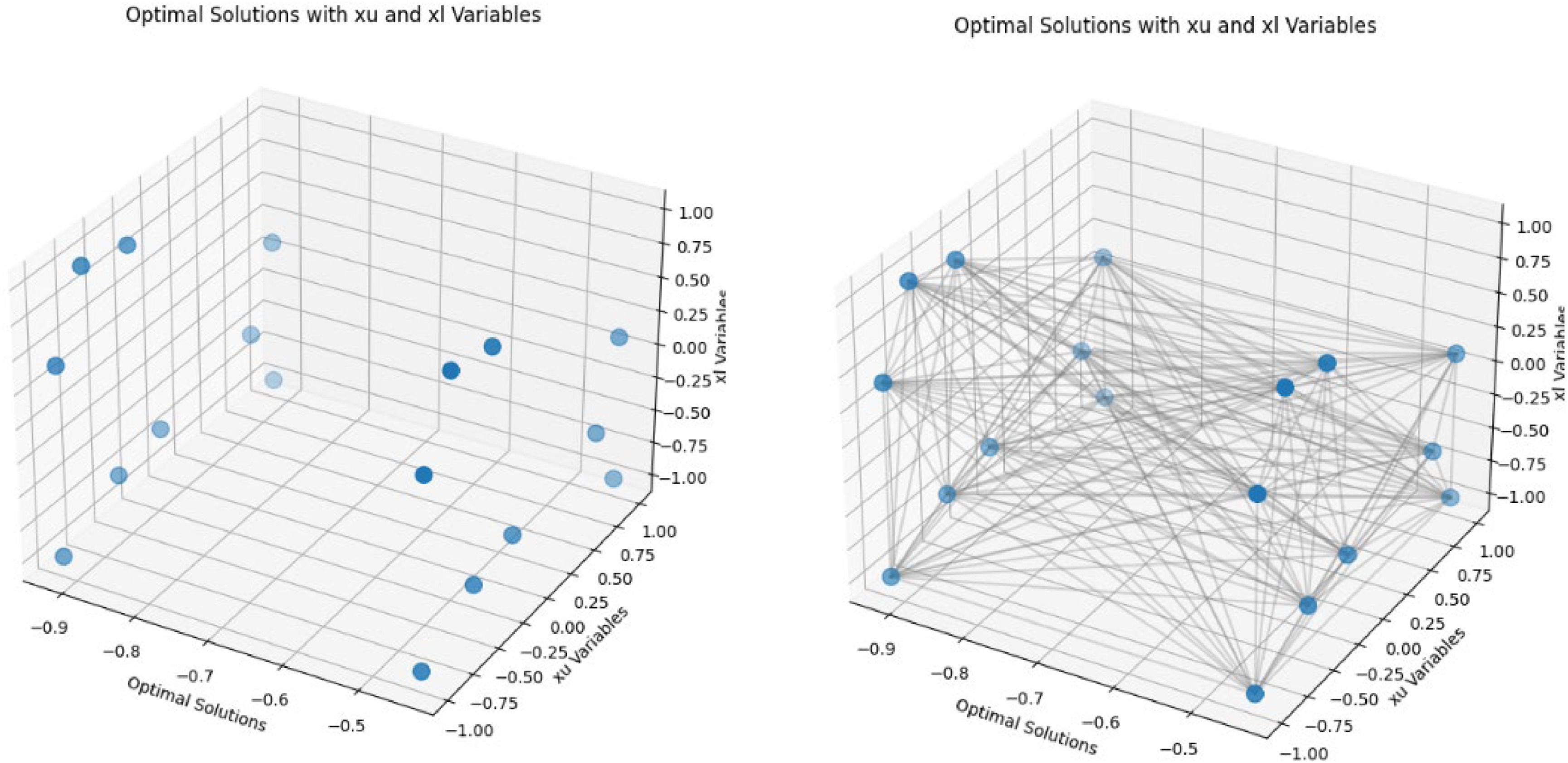
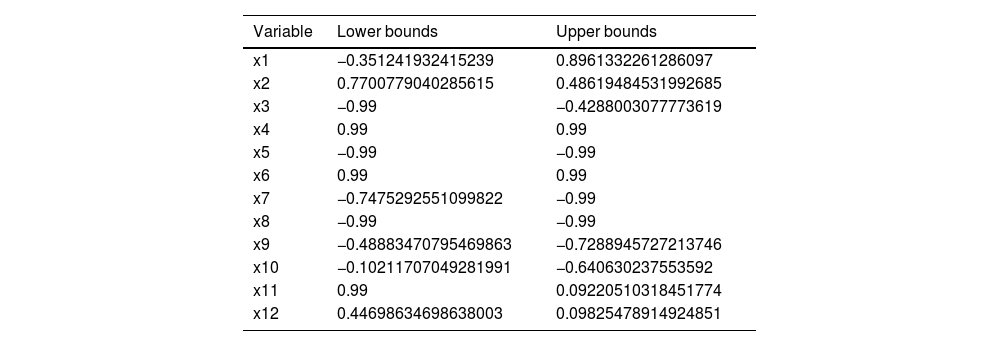
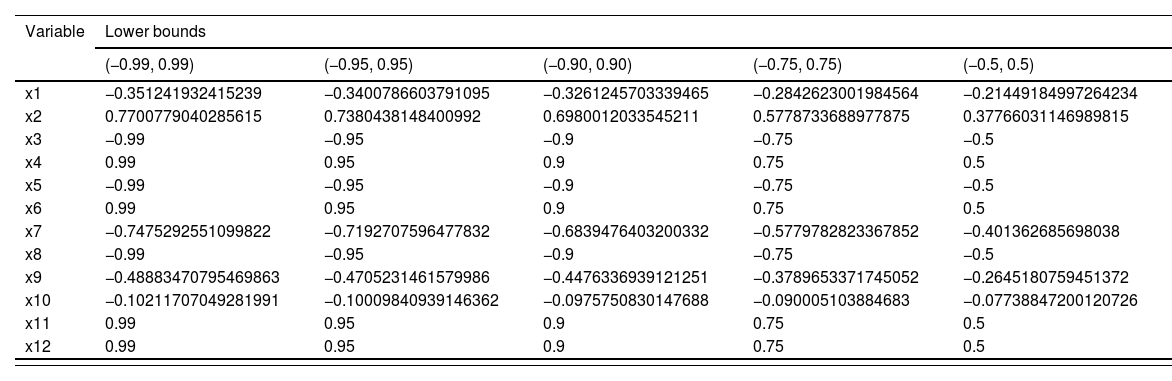
Value of the x variables in lower and upper bounds.
Traffic Flow Management with Lower Bound = 0.99 and Upper Bound = 0.318386533375344, Public Transportation Optimization with Lower Bound = 0.27135964473461094 and Upper Bound = 0.09032412283956047 and Waste Management with Lower Bound = 0.40308728602129873 and Upper Bound = 0.10177087946901991.
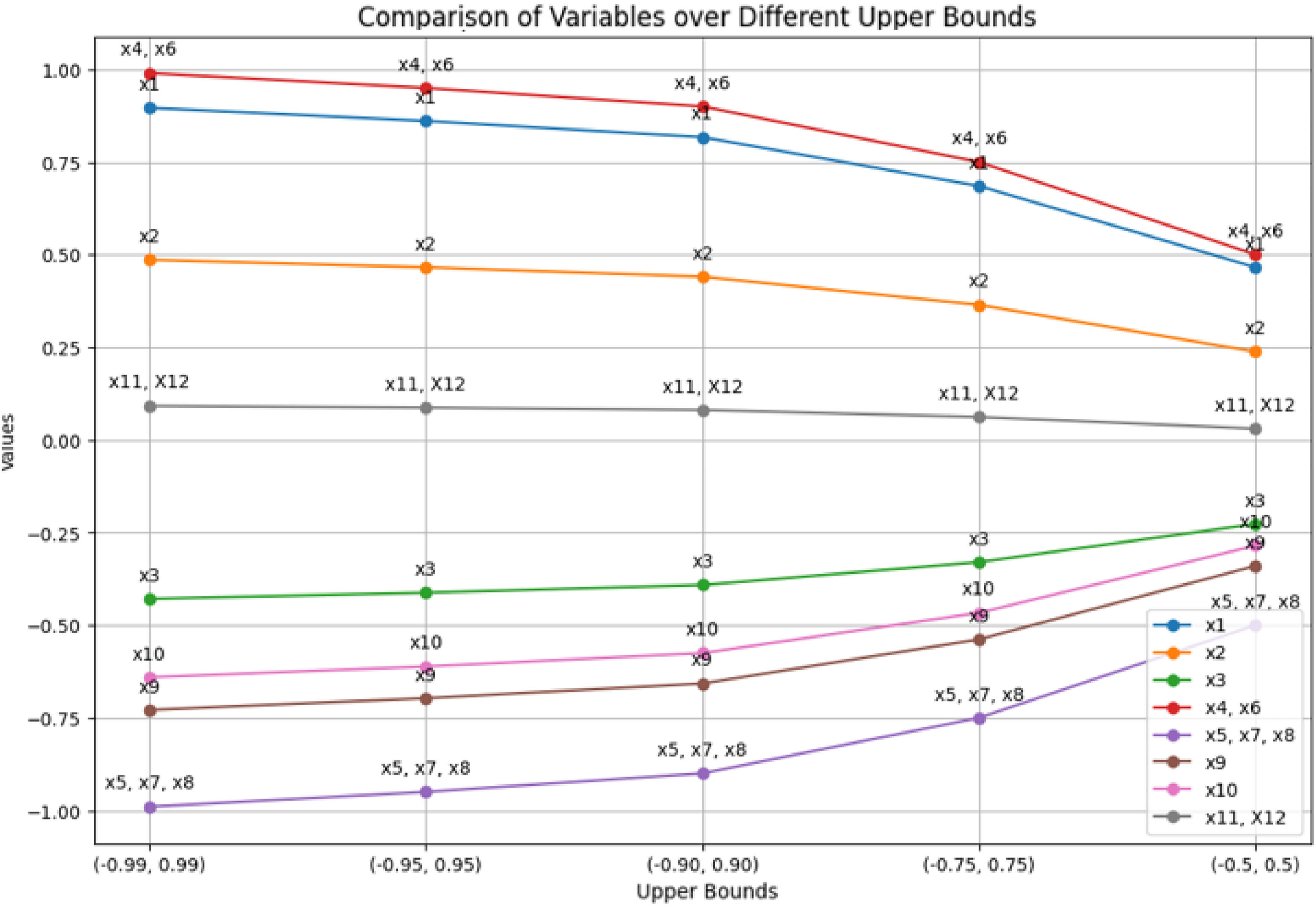
Now, we seek to understand what is the worst-case risk scenario for implementing big data in sustainable smart cities. The optimal solution (Figs. 6 and 7) is equal to 0.15866057835913056. The worst-case scenario for a smart city involves the simultaneous occurrence of several risks, all of which have positive values, indicating their potential to significantly disrupt smart city operations (x2, x4, x6, x11, x12):
- i.
Sharing Data and Information,
- ii.
Collecting and Recording Data,
- iii.
Technical Limitations and Technology,
- iv.
Non-cooperation of Organizations,
- v.
Issues Related to the Interpretation of Complex Information.
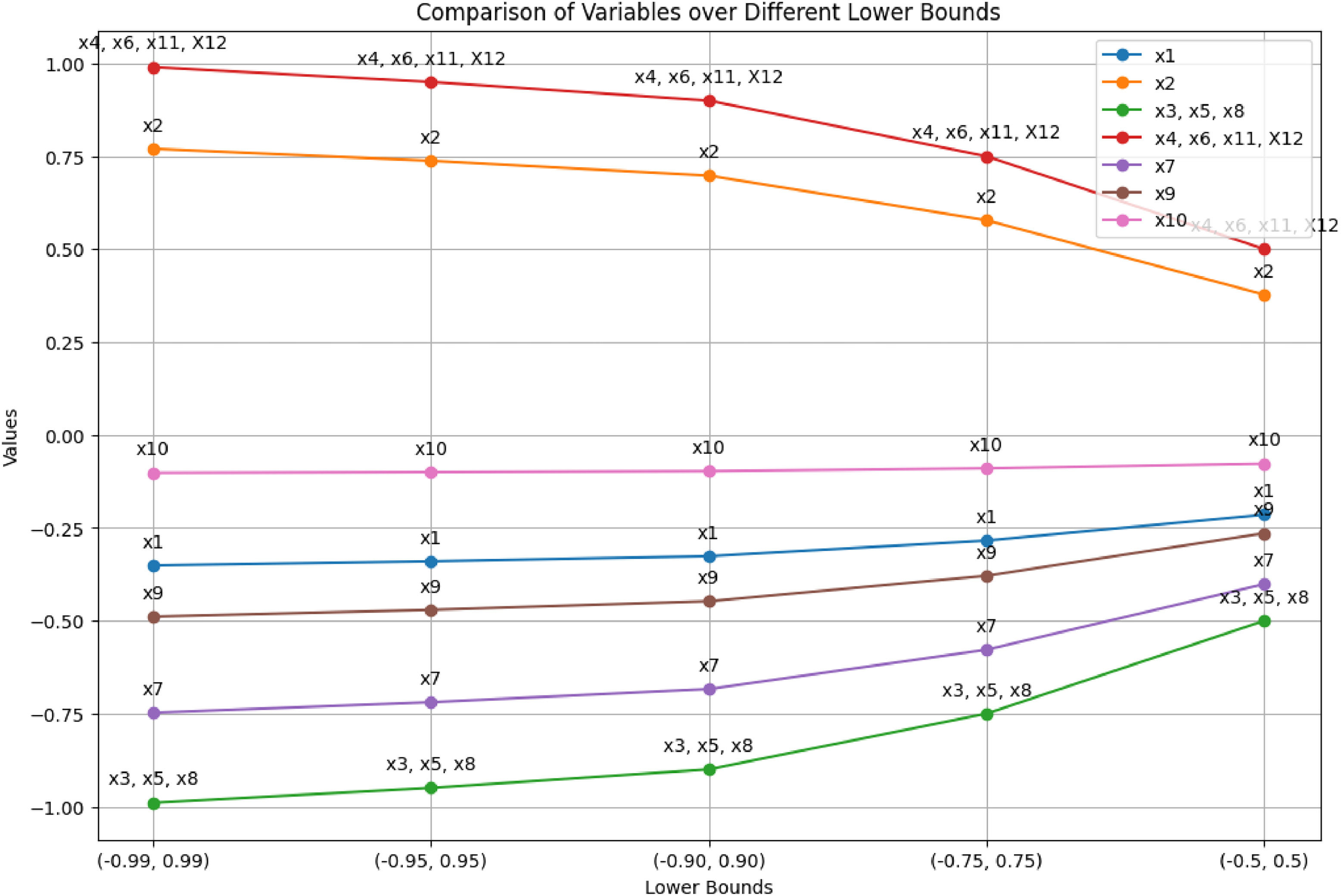
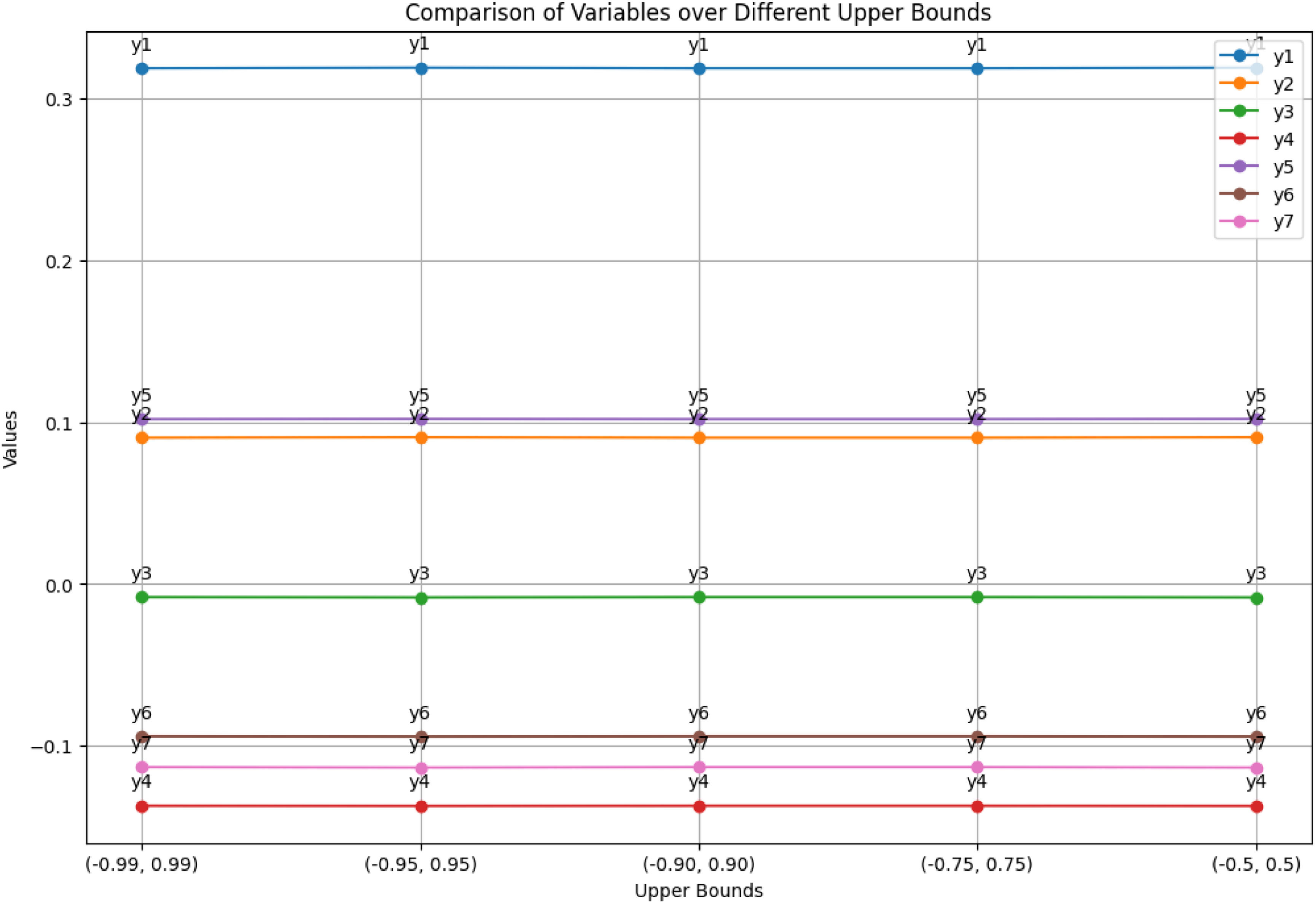
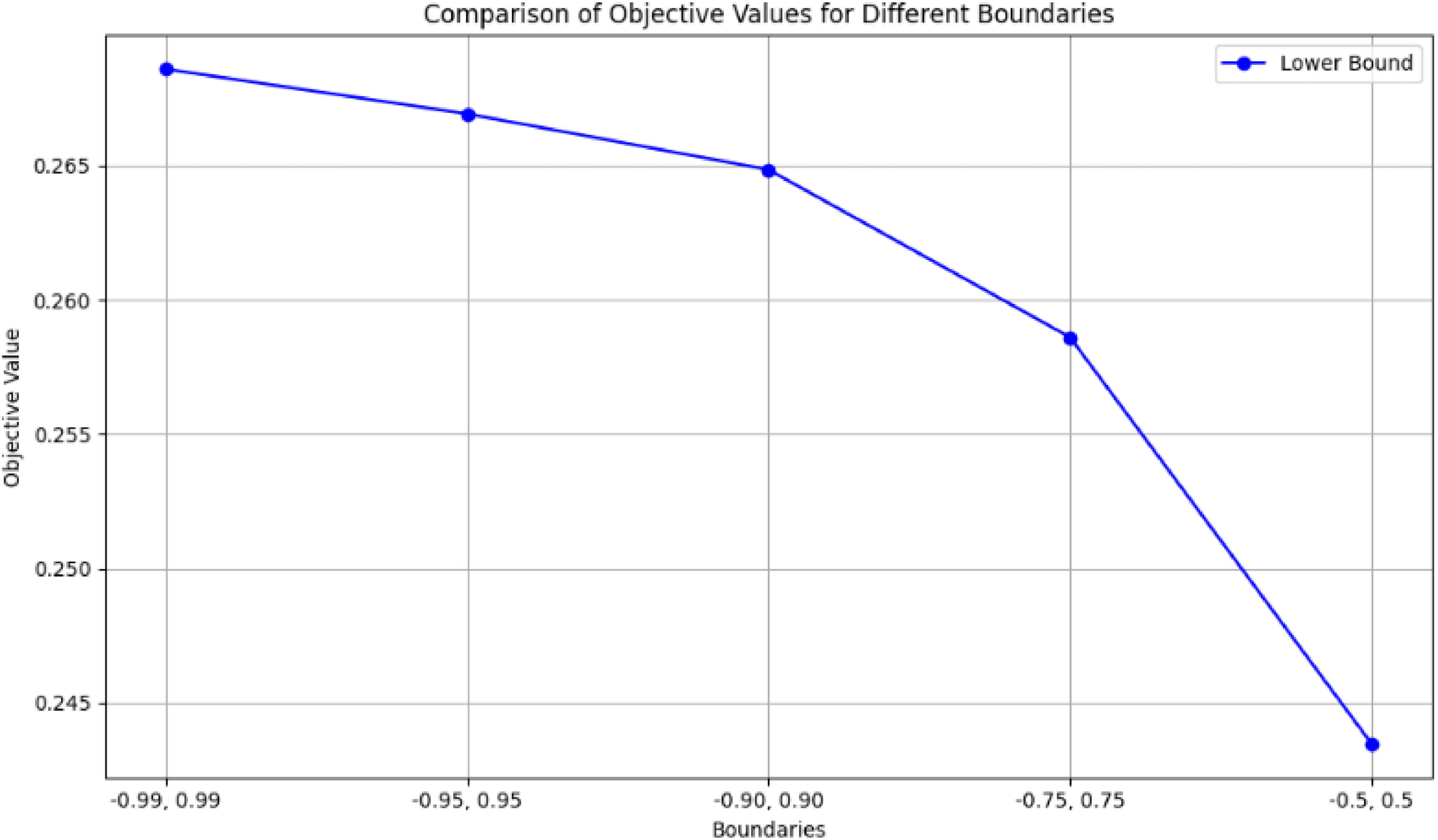
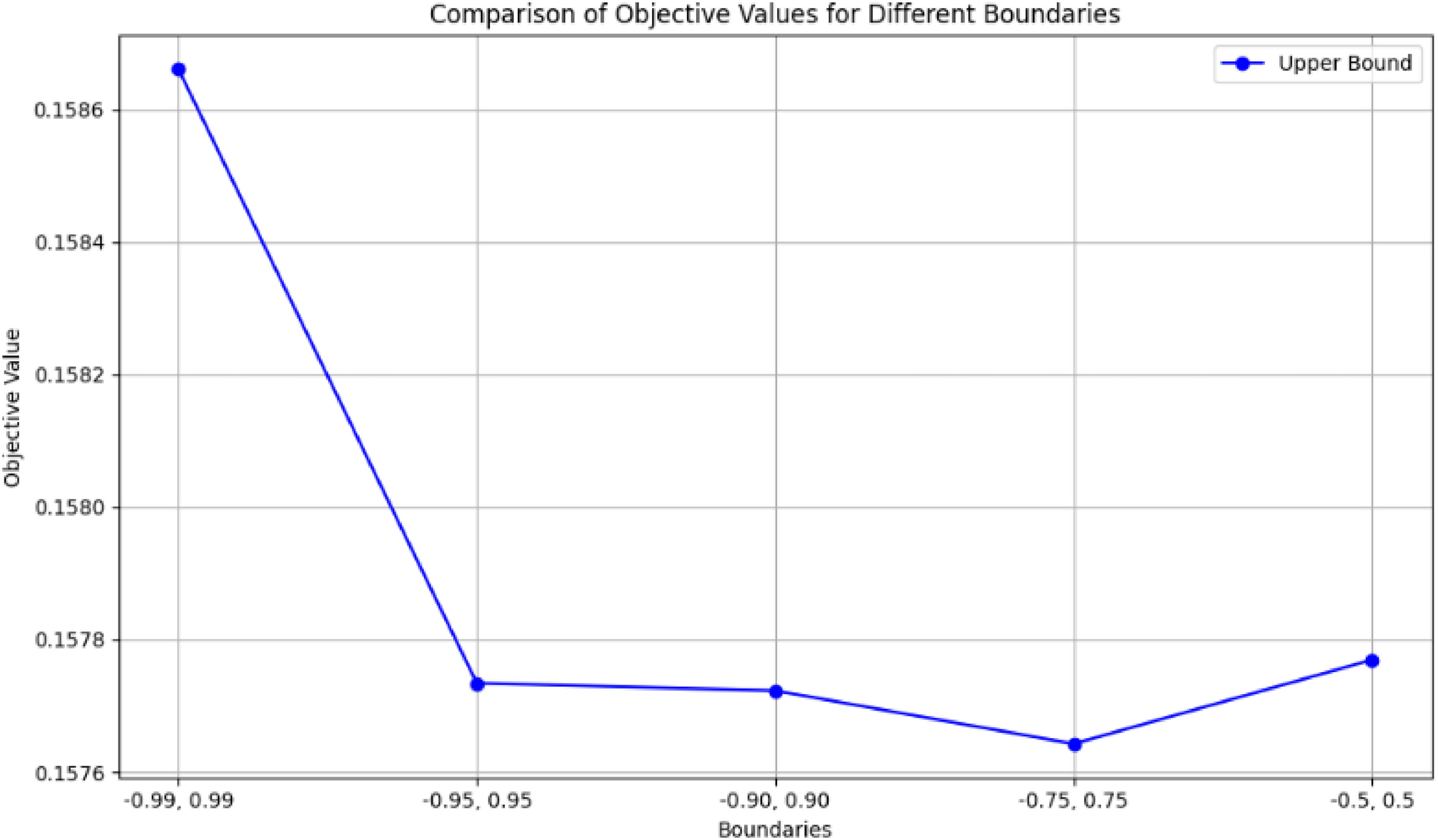
Sensitivity analysis is a technique used to assess how variations in an independent variable influence a specific dependent variable within a defined set of assumptions. This method operates within certain boundaries that depend on one or more input variables. It is primarily employed to identify which variables have the most significant impact on the outcome of a model. In this study, we conducted an analysis testing variable ranges across five different intervals, examining optimal solutions and variable values. Our findings indicate that varying the intervals did not lead to significant changes in the optimal solution. This suggests that the model's performance and outcomes remain relatively stable across the tested ranges of intervals, highlighting the robustness of the results with respect to changes in variable bounds. This stability in optimal solution across different intervals enhances confidence in the reliability and consistency of the model under varying conditions of input constraints.
The comparison of variables over different upper bounds for the variable x is displayed in Table 18 and Figs. 8-9, and also for the variable y is shown in Table 19 and Figs. 10-11.
Sensitivity analysis of the xi.
Sensitivity analysis of the yi.
In this research, varying the intervals of variables did not result in significant changes in the optimal solution or the objective function values. This consistency across different interval ranges demonstrates the robustness and validity of the study's results. The negligible variations in optimal solutions indicate that the model's performance is reliable and not heavily dependent on the specific bounds of the variables tested findings that are depicted in Figs. 12-14. This consistency strengthens the confidence in the accuracy and effectiveness of the conducted analysis, ensuring that the conclusions drawn are likely to hold under different scenarios and input constraints, thereby validating the reliability of the research.
DiscussionThe analysis of the barriers to implementing big data systems in smart cities has highlighted significant challenges, particularly in the realm of technical constraints. With a weight of 0.6152, technical barriers are identified as the most critical among the primary obstacles. Within this category, the sub-barrier T3, which pertains to technical and technological limitations, emerges as the most significant with a weight of 0.6746. This indicates a pressing need to address the limitations in current technologies and infrastructure that impede the effective deployment of big data systems. In the context of security, the sub-barrier S3, concerning issues related to data storage and transfer, holds the highest importance with a weight of 0.6411. This underscores the necessity of robust data security measures to protect sensitive information and ensure seamless data flow across systems. Additionally, the sub-barrier M1, related to high environmental investment costs, is notable with a weight of 0.5149, highlighting the financial challenges in adopting environmentally sustainable practices.
Given these findings, it is clear that overcoming technical and technological limitations (T3), which carry the highest overall importance with a weight of 0.39267375, should be a priority. To address these barriers effectively, several practical recommendations can be proposed. Firstly, investing in research and development to advance technological capabilities is crucial. This includes the development of more efficient data processing and storage technologies that can handle the vast amounts of data generated in smart cities. Secondly, augmenting collaboration between public and private sectors can facilitate the sharing of resources and expertise, thereby mitigating the financial burden of environmental investments. Thirdly, implementing comprehensive training programs for personnel can ensure that the workforce is adept at managing new technologies and adhering to stringent security protocols. Lastly, policymakers should focus on creating supportive regulatory frameworks that encourage innovation while ensuring data security and environmental sustainability. By addressing these critical barriers, the deployment of big data systems in smart cities can be significantly improved, paving the way for smarter, more efficient urban environments.
The game theory analysis of necessary measures for a smart city reveals critical insights into key areas that require attention. Among these, (Traffic Flow Management), (Public Transportation Optimization), and (Waste Management) stand out as vital components. Specifically, for Traffic Flow Management, the lower bounds are set at 0.99 and the upper bounds at 0.318, indicating a significant range that necessitates robust strategies to optimize vehicle movement and reduce congestion. For Public Transportation Optimization, the lower bounds are 0.271 and the upper bounds 0.090, suggesting that there is room for substantial improvement in enhancing the efficiency and effectiveness of public transit systems. Lastly, Waste Management, with lower bounds at 0.403 and upper bounds at 0.101, highlights the importance of effective waste collection, disposal, and recycling processes to maintain urban hygiene and sustainability.
To address these measures effectively, targeted strategies should be implemented. For Traffic Flow Management, investing in smart traffic lights, real-time traffic monitoring systems, and adaptive traffic control technologies can significantly reduce congestion and improve flow. In the realm of Public Transportation Optimization, integrating smart ticketing systems, real-time tracking of public transport vehicles, and improving connectivity between different modes of transport can make public transit more attractive and efficient for residents. For Waste Management, deploying smart bins that signal when they need emptying, enhancing recycling programs, and utilizing waste-to-energy technologies can improve waste processing efficiency and environmental sustainability.
The worst-case scenario for a smart city involves the simultaneous occurrence of several risks, including issues related to “Sharing Data and Information”, “Collecting and Recording Data”, “Technical Limitations and Technology”, “Non-cooperation of Organizations”, and “Issues Related to the Interpretation of Complex Information”. These risks are significant because their values are positive, indicating their potential to adversely impact smart city operations.
To mitigate these risks, a multi-faceted approach is necessary. Improving data-sharing and information security protocols can build trust among stakeholders and ensure the integrity of shared data. Implementing standardized data collection and recording practices can improve data accuracy and reliability. Addressing technical limitations through continuous investment in research and development, as well as adopting cutting-edge technologies, can overcome existing technical barriers. Promoting collaboration between organizations through formal agreements and incentives can enhance cooperation and streamline operations. Lastly, developing advanced analytical tools and training programs can aid in the accurate interpretation of complex information, ensuring that DMs have reliable insights to guide their actions. By focusing on these measures and mitigating the identified risks, smart cities can improve their resilience and effectiveness, leading to improved urban living conditions and sustainable development.
Conclusions and outlookThe study on optimizing a sustainable smart city by addressing barriers to big data implementation through the IZSGG theory and G-BWM has provided valuable insights. The analysis of barriers to implementing big data systems in smart cities reveals significant challenges, particularly in the realm of technical constraints.
Overcoming the challenges of adopting big data within sustainable smart cities requires a well-framed strategy from both technical and managerial perspectives, especially using optimized methodologies such as Lower-Bounded Traffic Flow Management, Public Transportation Optimization, and Waste Management. In such regard, traffic flow management with lower bounds refers to the area of using big data analytics for real-time prediction and regulation of traffic, with a guarantee that congestion is minimized and the flow within the transportation network is well managed. This methodology utilizes historical traffic information, meteorological factors, and real-time sensor data in simulating and optimizing the flow of traffic, therefore reducing both travel time and emission. Managerially, this strategic solution involves integrating multifarious sources of data by urban planners, transportation agencies, and information technologists to ensure that the traffic management systems work efficiently. The infrastructure investments would be primarily in smart traffic lights, sensors, and computing. These investments would include setting up a central data platform, real-time analytical information dissemination to build stakeholder collaboration, and informing the public about the use of various public transport systems as much as possible.
Public transport improvements are thereby enabled through large data sets that constantly update and optimize routes, schedules, and various transit capacities to maximize such an experience of reduced waiting time, increased reliability of service, and overall efficiency. If public transport systems could handle passenger flows, demand patterns, and operational performance indicators, it would better serve the needs of the population. Only proper governance can oversee planning, implementation, and continuous improvement if optimization is to be truly effective. Key measures therein would be data analytics focused on route optimization, capacity management through dynamic pricing or demand-responsive services, real-time passenger feedback mechanisms, and alignment with sustainability objectives through low-emission vehicles and multi-modal options. Big data allows for massive improvements in smart city waste management through optimizations of routes for waste collection, predicting waste generation patterns, and improving recycling rates. Waste bin fill-level can be tracked by sensors, while data analytics can plan collection schedules and routes for minimal fuel consumption and operational costs. Again, effective waste management does call for strong managerial coordination across departments, public awareness drives, and adherence to sustainability-focused policies. Implementation of predictive analytics of the waste generated, deployment of smart sensor bins, analysis of the effectiveness of recycling programs, and public education campaigns are pragmatic approaches toward waste management. All these need to be integrated into one single urban planning framework for a sustainable data-driven smart city. The focus shall be on technological solutions such as real-time analytics, predictive modeling, and sensor-based monitoring, combined with strong managerial oversight. It will be enabled through a focus on data integration, collaboration among stakeholders, public engagement, and continuous improvement. Eventually, it will improve urban sustainability and the quality of life of its citizens by making cities more efficient, resilient, and adaptive to future challenges.
Technical barriers, identified as the most critical barriers with a weight of 0.6152, highlight the pressing need to address limitations in current technologies and infrastructure. Specifically, technical and technological limitations (sub-barrier T3) are the most significant within this category, with a weight of 0.6746, emphasizing the need for advancements in technology and infrastructure to support effective big data deployment. In the context of security, issues related to data storage and transfer (sub-barrier S3) are crucial, with a weight of 0.6411, underscoring the necessity for robust data security measures. Additionally, high environmental investment costs (sub-barrier M1) pose financial challenges, with a weight of 0.5149. Addressing these critical barriers requires a multifaceted approach. Among all, technical and technological constraints are the most critical, with a weight of 0.39267375, indicating their paramount importance in the overall risk landscape.
According to the findings, the worst-case scenario for a smart city involves multiple risks, including issues with data-sharing, data collection and recording, technical limitations, non-cooperation of organizations, and interpreting complex information. Mitigating these risks requires improving data security protocols, standardizing data collection practices, continuous investment in technology, promoting organizational collaboration, and developing advanced analytical tools. In such a scenario, even minor disruptions in technology can cascade into broader operational failures, exacerbating the other risks and creating a complex web of issues that are difficult to resolve. Therefore, smart cities must prioritize overcoming these technical and technological barriers to safeguard their operations against such worst-case scenarios. By addressing these measures and mitigating identified risks, smart cities can improve their resilience and effectiveness, leading to improved urban living conditions and sustainable development. The findings underscore the necessity of advancing technological capabilities, enhancing collaboration between public and private sectors, implementing comprehensive training programs, and creating supportive regulatory frameworks. Additionally, the game theory analysis identified critical areas such as traffic flow management, public transportation optimization, and waste management as vital components for smart city development. By investing in smart technologies, improving data security, promoting organizational cooperation, and addressing financial and technical challenges, cities can overcome these barriers and enhance the deployment of big data systems.
IZSGG utilizes the theories of grey numbers and grey matrices in the representation of uncertainties involved with the payoff matrices of the game. That will, in turn, enable the derivation of strategies incorporating the fuzzy nature of some elements in the system. This, in turn, enables the IZSGG theory to capture a wider range of scenarios, including cases of partial or incomplete knowledge about specific facts. Thus, the IZSGG theory is more applicable to realistic situations that require decisions based on incomplete information. The theory further utilizes advanced optimization techniques in determining the points of equilibrium, which are informed not only by established values but also take into consideration the grey components of those values, hence providing a more refined solution to the game. One key advantage of the IZSGG with respect to the traditional Zero-Sum Game theory is the ability to deal with uncertainty and incomplete information, something that often characterizes realistic applications. Unlike the usual method, which might give too optimistic or pessimistic strategies due to the assumption of full information, IZSGG offers more robust and realistic strategic solutions that take into account and integrate all ambiguities imbued in the data.
Ultimately, this approach will lead to more efficient, resilient, and sustainable urban environments, paving the way for the future of smart cities. Future research could focus on developing advanced data processing and storage technologies that are more efficient and scalable. Another important area is the creation of robust regulatory frameworks that balance innovation with data security and environmental sustainability. Moreover, future research must examine the integration of emerging technologies, such as artificial intelligence and the IoT, to enhance smart city infrastructure and services.
CRediT authorship contribution statementBehnam Razavian: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. S.Masoud Hamed: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Maryam Fayyaz: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Peiman Ghasemi: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Seckin Ozkul: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization. Erfan Babaee Tirkolaee: Writing – review & editing, Writing – original draft, Visualization, Validation, Supervision, Software, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Data curation, Conceptualization.