Technological capabilities in the era of the digital economy for integration into cyber-physical systems and the IoT using decision-making approach

Abstract

In the digital economy, innovators have to deal with the value-capture problem, which necessitates different capabilities. They need to be fully aware of the dynamics of platforms and ecosystems. Such capabilities are needed to enable technologies mainly focused on in the present study. The current digital economy (where businesses are experiencing a big shift from a traditional setting to a widely-digitalized setting) requires companies and enterprises to incorporate innovation into their performance. The present paper aims to offer a novel realm of modern technologies by recognizing the roles the technological capabilities could play in the digital economy regarding for integration of cyber-physical systems (CPS) and the Internet of Things (IoT) into the digital economy. This paper develops an integrated decision-making framework called the Pythagorean fuzzy (PF)- method based on the removal effects of criteria (MEREC)-rank sum (RS)-double normalization-based multiple aggregation (DNMA) model by combining the PF-MEREC-RS and PF-DNMA methods. In this framework, the PF-MEREC-RS method computes the subjective and objective weights of the technological capabilities of the digital economy for the integration of IoT and the CPS. The PF-DNMA method uses to obtain the firms’ preference order over various technological capabilities in the digital economy for integration of the IoT and the CPS. In addition, this paper involves an empirical case study evaluating the key technological capabilities in the digital economy for integration of the IoT and the CPS. Furthermore, comparison and sensitivity investigation are made to show the superiority of the developed framework.

Introduction

Digital technologies have transformed national economies worldwide (Ballestar et al., 2021; Skare & Riberio Soriano, 2021). These technologies are unceasingly evolving and expanding, and this way, they open the doors to a novel, smart, data-driven, and learning economy (Hanna, 2016). It has been empirically shown that the digital sector is less than 10% of most economies if measured by value-added, income, or employment (Szeles & Simionescu, 2020); however, in a broad sense, the modern economy is a “digital economy” because digitalization is now playing a key role in almost all economic activities (Ma et al., 2022; Pan et al., 2022). The motivation and capability of policymakers to control the digital revolution for economic development are not the same in different countries; for that reason, technology and digitalization have different impacts on different regions and national economies (Hanna, 2016). In this sense, digital transformation plays a critical role, and its most significant challenge is how to ensure developmental payoffs largely and equitably (Bullini Orlandi et al., 2019). Remember that such transformation is something more than the mere development of advanced digital technologies (Troise et al., 2022; Zhang et al., 2022). To be accomplished well, there is a need for investment in institutions and the provision of efficient economic policies since if this does not happen, in spite of the extensive utilization of the internet, only some limited benefits could be expected from digitalization. In recent years, several strategic frameworks have been developed to facilitate the construction of digital transformation ecosystems (Hanna & Knight, 2012).

The remarkable progress that has occurred in both Internet of Things (IoT) and Cyber-Physical Systems (CPS) has created a robust foundation upon which new concepts such as Industry 4.0 (Kumar et al., 2022; Srivastava et al., 2022), the Industrial Internet of Things (Hussain et al., 2022; Liu et al., 2022), and the digital economy (Pivoto et al., 2021; Radanliev et al., 2019c; Viriyasitavat et al., 2019) could be well developed. In 1999, the term ‘Internet of Things’ originated, and at the same time, it was discussed by relevant scholars how an IoT-based setting might look in the future (Yerpude & Singhal, 2022). However, the term ‘cyber-physical system’ incorporates the complicated and multi-disciplinary aspects of ‘smart’ systems that depend on the interactions between the computational and physical components (Alwan et al., 2022). The CPS theory was originally extracted from the control theory and control systems engineering, which is mainly concentrated on interconnecting the physical components and employing complicated software entities in a way to create novel network and systems capacities. Therefore, it can be said that CPS connects the physical and engineered systems and makes the cyber world well linked to the physical world. On the other hand, the theory of IoT was taken out of the computer science and internet technologies, with a focus upon interoperability, interconnectivity, and also the physical components integration on the Internet setting (Cranmer et al., 2022; Novak & Hoffman, 2019). A full integration leading to several progresses, e.g., real-time enabled CPS platforms, IoT automation of CPS, and automated CPS guiding skilled workers within production environments, could be expected if IoT would be completely adopted during the following decade.

By integrating new concepts such as machine learning, IoT, artificial intelligence (AI), and cloud, we could create systems of machines that can easily interact with human beings (Radanliev et al., 2019a, 2019e). At the present time, the digital economy can speculate people's behaviors in the market (Radanliev et al., 2019a), and it is capable of determining their purchasing behaviors (Radanliev et al., 2019d). In the digital economy, autonomous machines are expected to adopt these methods when predetermining human beings’ behaviors. In such a setting of the new economy, people, data, processes, and things are brought together, which enhances the importance of networked connections and transactions to people, things, and organizations. As a result, for key management technologies, there is a need to 1) integrate physical, financial, and information flows, 2) provide innovative approaches to the management of operational processes, 3) exploit the IoT and industrial digitization in a way to achieve good degrees of competitiveness, and 4) apply Big Data to the enhancement of the efficiency of production processes and products/services quality. The emergent categories in fact signify that digital economy is decomposed into domain communities, digital societies, digital processes, and social platforms. When the digital economy is connected to human and physical networks, it would be capable of operating as the system of systems; it can directly distribute real-time feedback from users and markets.

The literature lacks adequate research on the economic influences of IoT and CPS infrastructure (Radanliev et al., 2018a). IoT and CPS can presently be operated largely in the digital economy; therefore, a novel model is needed to provide an overall understanding of the development, design, and evolution of such technologies. This model should be able to combine the theories of IoT, physical systems control, and their interactions with human beings. It briefly explains the connection we expect to be made between social machines and the digital economy. The digital economy is connected and is capable of processing data in real-time, which are gathered from humans and machines and could be considered digital assets with economic value (Nicolescu et al., 2018; Radanliev et al., 2018a). On the other hand, a big challenge in this regard is that such connection is exposed to cyber risks that are not clear yet (Nurse et al., 2017, 2018), and also there are no data required for performing risk assessments (Radanliev et al., 2019f). The integration of the physical world with the cyber world could be associated with an inherent risk. As explained earlier, the digital economy operates as a social machine; for that reason, the risk impact assessment needs to be also changed into a cyber-financial assessment (Radanliev et al., 2018c). To do this, it is necessary to understand the digital economy network well and to quantify the novel cyber-financial risk elements, e.g., the intellectual properties of digital information (Radanliev et al., 2018c). Cyber risks encompass more than the financial costs of information security (Radanliev et al., 2019b); they also cover digital assets' intellectual properties (Ruan, 2017). No study or database has yet investigated cyber risks from the perspective of cyber-financial risk assessment of new technologies. As a result, the current study is aimed at defining the data collection parameters. The results could aid governmental agencies in gathering the correct data and determining what data is required and what data is not.

The intuitionistic fuzzy sets (IFSs) developed by Atanassov (1996) are characterized by two concepts, i.e., belongingness degree (BD) and non-belongingness degree (ND), and IFSs fulfill the constraint that the sum of the BD and ND is less than or equal to 1. However, in the decision-making problem, a condition may happen in which decision experts (DEs) allocate the value of 0.8 once an alternative satisfies the attribute and the value of 0.5 if it dissatisfies that. Then, 0.8+0.5>1, and IFS cannot properly address the situation (Yager, 2014; Zhang & Xu, 2014). To cope with that, Yager (2013) and Yager (2014) suggested the Pythagorean fuzzy sets (PFSs) that meet the constraint that the square sum of BD and ND is less than or equal to 1. As a result, in describing the nature of ambiguity, PFSs perform more powerfully compared to IFSs. Because of the exclusive benefits of PFSs, Zhang and Xu (2014) introduced the basic operations of Pythagorean fuzzy numbers (PFNs) that was capable of solving the concerns of group decision-making issues. Peng and Yang (2016) extended the multi-attributive border approximation area comparison (MABAC) model with the Choquet integral for PFSs. In more recent years, Rani et al. (2019) developed integrated multi-criteria decision-making (MCDM) model with information measures to evaluate the renewable energy source selection in India. In addition, an extended technique for order of preference by similarity to ideal solution (TOPSIS) method was developed by Rani et al. (2020c) to choose the best sustainable recycling partner in the context of PFSs. Rani et al. (2020a) extended the complex proportional assessment (COPRAS) method under PFSs to assess the problem of pharmacological therapy assessment for type-2 diabetes. (Rani et al., 2020b) suggested a novel PF-weighted aggregated sum product assessment (WASPAS) method for a multi-criteria physician selection problem with uncertain information.

With the ever-increasing intricacy and wide-ranging challenges of today's environment, numerous MCDM approaches have been introduced by copious authors. The MCDM methods can be categorized into (i) Outranking approaches and (ii) utility degree-based approaches. The utility-based approaches only employed a single normalization technique to non-dimensionalize assessment values under diverse criteria. In this sense, a predefined normalization technique may bias the outcomes when the normalization tool is inappropriate. To conquer this issue, Liao and Wu (2020) intended a new utility value-based approach, namely, the double normalization-based multiple aggregation (DNMA) model, which takes the benefits of different normalization methods and aggregation functions and appropriately combines them. The final integration function of the DNMA approach widely considers the subordinate utility values and the ranks of alternatives, and thus, the final ranking result has high reliability. Nie et al. (2019) proposed a multi-expert MCDM technique by combining the DNMA method with a cardinal consensus-reaching process under hesitant fuzzy linguistic term sets the context. Wang and Rani (2021) extended the double normalization-based multiple aggregations (DNMA) approach IFSs environment to identify, rank, and evaluate the sustainability risk factors in supply chain management. Also, Keshavarz-Ghorabaee et al. (2021) pioneered an innovative objective weighting model for assessing the criteria weights and named it as a method based on the removal effects of criteria (MEREC). This approach utilizes each attribute's removal effect on the assessment of alternatives to obtain the weights of the attributes. Considering the deviations, the assessment of an option based on removing attributes is a new concept for determining the attribute weights. Rani et al. (2022) discussed the MEREC-based additive ratio assessment (ARAS) method to treat the food waste treatment method assessment on “Fermatean fuzzy sets (FFSs)”. In this study, the MEREC model is first combined with the multiattribute multi-objective optimization based on the ratio analysis (MULTIMOORA) method under the SVNS context. For the subjective weighting model, a procedure of rank-sum (RS) method was given by Stillwell et al. (1981) to help the decision-maker to give their ranking values for selected criteria. Until now, no one has developed an integrated MEREC-RS weighting and DNMA-based method under the PFSs setting for evaluating the technological capabilities in the digital economy to integrate IoT and cyber-physical.

There are also studies in the literature on the economic effects of digitization. Speaking of technological capabilities for the transition to a digital economy, it has to be noted that the question is, first and foremost, about forming a new model of economic practices. At the same time, the objectives of economics as the science studying the use of resources remain unchanged: to maintain or improve the quality of life under the condition of scarce resources. Consequently, the digital economy as a new economic model ought to provide digital space for all spheres of a country's life in order to improve the quality of life of its population. The capabilities for this can be both internal (in-country) and external (Kunzman, 2016). This paper contributed to the current knowledge attempts to fill the gap identified in the literature and offers a complex theoretical framework to properly define and understand the technological capacities of the digital economy for being well integrated with IoT and cyber-physical systems. One of the contributions of this study is the provision of a novel general theory concerning the impacts of digitalization on the digital economy. In addition, the present article attempts to answer the following question: Considering the technological capabilities, can digitization be viewed as the motor of transformation for the digital economy to the integration of IoT and cyber-physical?

To take the flexibility and efficacy of PFSs, the paper aims to introduce an innovative discrimination measure and discuss its elegant properties. A DNMA framework for evaluating the MCDM problem on PFSs has been developed based on it. Owing to its flexibility and efficiency, this research focuses on the context of PFSs. On the other hand, the new methodology of the PF-MEREC-RS weight-finding technique to compute the criteria weights or significance degrees of criteria. Then, the DNMA method is a new elegant approach to handling MCDM problems. Thus, in this study, we have developed a new approach to the MCDM method using the PF-MEREC-RS and PF-DNMA methods and, further implemented for the evaluation of the technological capabilities in the digital economy to the integration of the internet of things (IoT) and the cyber-physical systems (CPS). The primary outcomes of the developed work are given by

• •

  To conduct a survey approach using the current literature review and expert interviews to identify the main technological capabilities in the digital economy to the integration of the IoT and the CPS.

• •

  To develop a comprehensive framework using a survey approach to investigate the main technological capabilities in the digital economy to the integration of the IoT and the CPS.

• •

  To introduce an integrated decision-making approach using PFSs analysis, the developed framework to evaluate the technological capabilities in the digital economy for integration of the IoT and the CPS.

• •

  To propose an integrated decision-making approach using the PF-MEREC-RS and PF-DNMA models under PFSs with the aim of ranking the organizations and also analyzing and assessing the main technological capabilities in the digital economy to the integration of the IoT and the CPS.

• •

  The PF-MEREC-RS approach is utilized to evaluate and rank the main technological capabilities in the digital economy for the integration of the IoT and the CPS.

• •

  The sensitivity and comparison analyses are presented to validate the integrated PF-MEREC-RS-DNMA approach.

The remainder of this paper is provided based on the following sections. Section 2 presents the related works to the digital economy and digital technologies with applications. Section 3 provides the proposed PF-MEREC-RS-DNMA approach and the basic concept of PFSs. Section 4 presents the results of the study, the case study, the sensitivity investigation, and the comparative study. Finally, section 5 discusses the conclusion of the study.

Literature review

Digital economy

The literature consists of several studies concentrating on the concepts of digitalization and digital economy, as these concepts have old roots dating back to 1997. However, only limited research has been conducted on the related regional aspects of these concepts. In addition, the literature still lacks widely-accepted definitions for terms such as digital products, the digital sector, and digital transactions (Mesenbourg, 2001). For that reason, the digital economy has been conceptualized, ranging from the activities carried out based on online platforms to the activities that employ digitized data. Such uncertainty in the definition has caused scholars working in this domain to fail to consistently estimate the size of the digital economy (Oostrom et al., 2016). The literature comprises a variety of indicators for conceptualizing and operationalizing technological progress beyond digitalization and the digital economy. At first, the digital economy was described as an economic system characterized by the extensive utilization of Information and Communications Technology (ICT) with the use of base infrastructures, e-commerce, and e-business. Gradually, the scope of this concept has widened in line with the progress of digital technologies. The digital density index proposed in 2015 contains a total of 50 indicators classified into 4 activity areas and 18 groups of metrics (Macchi et al., 2015). Many researchers have discussed the digital economy in terms of its main drivers, indicators, and dimensions by concentrating on definite dimensions of this concept and conducting numerous cross-country analyses. Some of the variables generally considered when operationalizing the digital economy are Internet usage, e-commerce, and human resources in ICT. These variables are also included in the most commonly-used indexes of digital economy, for instance, the Digital Economy and Society Index (DESI).

The concept of technological transformation, which has perturbed billions of people, has now gone beyond the concept of the differentiation of machinery and equipment and has started to be discussed as the digitization of everything (Dufva & Dufva, 2019). Digitalization has now manifested itself in all areas of industries. A very wide range of matters, from the use of social media by individuals to digital literacy, from companies carrying all their assets and brands to digital media and public services being transferred into electronic environments, has been associated with the concept of information technologies or the concept of digital transformation. In other words, transformation is no longer due to technology or computers but to a more integral perspective of digitalization itself. Digitalization manifests itself in all areas of life and continues to expand in all areas, from the proliferation of mobile devices to the delivery of the internet to wider audiences, from e-commerce applications to e-government services. In this context, digitalization is regarded as a dynamic that has a significant and widespread effect on transforming the individual, society, state, and economy (Dufva & Dufva, 2019).

Humanity is entering a new stage of scientific and technological development (Stremousova & Buchinskaia, 2019a). It consists of the transition to new technologies based on the widespread use of information technologies in all spheres of human activity. The ongoing and upcoming changes cause many organizational, economic, and technical issues. There is still no consensus on how to characterize and name the upcoming changes: new industrialization, industry 4.0, network economy, or digital economy (Rainnie & Dean, 2020). There is no unity since it is still difficult to find an integrating definition characterizing the essence of the upcoming changes in the socioeconomic sphere under the influence of new achievements in science and technology. The internationally adopted methodologies for assessing the transition to digital technologies are based on determining such integral indicators as the DEI, IDI, or DECA (Stremousova & Buchinskaia, 2019b). These methods are an important tool for comparative analysis of the development of the information and communication services market and digital technologies growth. They may help to characterize the technical and technological capabilities of each country to transition to digital technologies (Ardolino et al., 2018; Prencipe, 2000). All the above-mentioned indices do not characterize the opportunities of the transition to the digital economy, and they do not integrate the influence of digitalization processes economic opportunities with the results of economic activity.

The digital economy could be successfully developed by strengthening the firms’ positions, enhancing their corporate governance, and improving the clarity and interaction of the relevant structures of financial institutions (Chernyakov & Chernyakova, 2018; Yuan et al., 2020). Such changes are more important than the initial changes to the ICT field, which greatly contribute to the digital economy growth (Domazet et al., 2018; Martin-Shields & Bodanac, 2018). These changes may occur in every sector of the market, such as the customers’ preferences, competitive structures, consumers’ purchasing habits, marketing, and advertising strategies, production operations, internal management systems, supply chain mechanisms, and the opening up of the global economy. Managers assume that the uncertainty and risks associated with the management of their businesses increase as a result of such changes. The key to survival in the digital economy lies in the ability of managers to effectively use ICT to manage these uncertainties and risks (Bob & Clare, 2005). The influence of digital technologies on the change of socioeconomic systems is readily evident; however, most of the consequential issues remain poorly studied (Chernyakova, 2018). Very little attention is paid to the impact of risk on the development of digital potential, which can contribute to the innovative growth of corporations. As a result, business development problems in the context of the digital economy are poorly described. Also, the emergence of new risks specific to the digital economy are not reflected in the overall system of modern economic relations.

The current setting has a great dependency upon technological capacities, and being in line with contemporary developments is of high significance at both macro and micro levels. The industrial revolutions that have taken place during the past three centuries have highly affected societal characteristics. Throughout history, revolutions have occurred when innovative technologies and new methods of perceiving the world have profoundly altered social structures and economic systems (Philbeck & Davis, 2018). The first industrial revolution and steam machine occurred in the 1760s; technology experienced great and exponential development after that. The technology, from that time, has regularly upgraded itself and behaved as a sort of recursion where the old technologies have created novel technologies. During the late 19th and early 20th centuries, the second revolution took place owing to the growth of electricity, which caused a surge in mass production. Then, in the 20th century, computers started to shape the digital revolution with the introduction of personal computers and the Internet. As a final point, founded upon the preceding digital revolution, the 4th industrial revolution is driven nowadays by machine learning, artificial intelligence, and IoT (Krafft et al., 2020; Syam & Sharma, 2018). Schumpeter explained this phenomenon through his waves of innovation, where he claimed each wave of innovation does not last equally; the lengths of the innovation waves are shortened because of the quick progress of novel technologies (Jakšić et al., 2018). Now, the 5th wave of innovation is running, through which digital solutions push the changes. In addition, the human being is living now in the 3rd era of digital transformation, which has brought about several new challenges to governments, organizations, firms, entrepreneurs, and consumers (Schwab, 2017). According to Tang (2021), in the current era, digital capabilities are applied to processes, products, and assets to enhance efficiency, improve customer value, manage risks, and discover novel monetization opportunities. Likewise, Bertini (2016) asserted that not only individuals’ lives but also their experiences are seriously affected by digital transformation.

Digital technologies and applications

In general, digital platforms are multi-sided, which causes interfaces with and among two or more groups of economic actors upon the different platform sides, including the providers of complementary assets (Eferin et al., 2019; Trabucchi & Buganza, 2020). As Teece (2018) and others have argued, the world is undergoing a digital revolution at a new frontier of knowledge. Technology that underpins physical devices is changing from analog electronic, and mechanical to digital, and content is transferred by digital rather than physical means. Teece (2018) focuses on digital platform-based ecosystems at the forefront of this change, specifically on platform leaders, as we do here. To set the stage for our analysis, we next define terms and briefly summarize the key characteristics of these ecosystems. Digital transformation refers to integrating digital technology into the economy; this can fundamentally change how the world does business is, communicates, and is developed on national and international levels (Arrigoni et al., 2020; Li et al., 2021). The breakthroughs occurred to the technology have considerably changed the consumers’ habits (Abbasian Fereidouni & Kawa, 2019; Hojeghan & Esfangareh, 2011).

Digitization has brought about numerous novel opportunities in the economy industry, which could be exploited by providers in this domain Pantielieieva et al., (2018). On the other hand, the market is experiencing intense competition, and firms must keep pace with digitization and not stay behind. During the past decades, ICT has dramatically impacted the economy. Such conditions necessitate understanding the nature of the economy and call on incessant research on the ways digitization impacts enterprises in terms of their economic progress. The existing literature is mostly concentrated on the use of IT in various sectors and also the technology advantages and uses (Abbasian Fereidouni & Kawa, 2019; Del Chiappa & Baggio, 2015; Huang et al., 2017). However, limited research has been carried out focusing on the drawbacks of these new technologies (Gretzel, 2011). Industry 4.0 makes use of the capacities of IoT and CPS in the industry and production processes. This has accelerated the growth of digital technology and has caused the gradual depletion of the development potential and efficiency of conventional economic, industrial, and social systems (Berman, 2012; Thoben et al., 2017).

The advent of digital technologies and applications, for example, CPSs, artificial intelligence (AI), augmented reality, IoT, robotics, cloud, and big data, has significantly changed industries and society. As a result, new opportunities are being offered in industries, with a huge power for reforming and renovating business ways (Kiel et al., 2019; Müller et al., 2018). This condition has led to the emergence of Industry 4.0 (I4.0). The technological potential of this new form of the industry can go beyond merely influencing firms and business sectors; rather, it can also benefit the environment and society at large (Bai et al., 2020; Ghobakhloo, 2020). Nowadays, the world is experiencing several challenges at the global level, e.g., aging populations, natural disasters, economic disparity, resource depletion, and the current COVID-19 pandemic. To address such challenges properly, there is a need for the entire exploitation of digital technologies to resolve them in effective and efficient ways so that society could benefit at large.

The objective of I4.0 is to digitalize all physical assets and integrate them into a digital ecosystem with the partners engaged in the value-added chain. To establish smart manufacturing, a key prerequisite is cyber-physical integration. Digital technology helps to establish network interactions among machines, buildings, equipment, and information systems (Zhukovskiy & Malov, 2018). In such systems, ‘things’ are responsible for monitoring and analyzing the environment, production processes, and products’ state in real-time. Moreover, if the control and decision-making functions are entirely transferred to intelligent systems and algorithms, enterprises would encounter a great change in the paradigm of technological development. Two commonly-favored means of such integration are CPS and digital twins (DTs). The former refers to multi-dimensional and complex systems that aid in uniting the dynamic physical world with the cyber world. DT refers to the software analog of a physical device or process used to model a physical object's behaviors under the impact of disturbances, interference, human factor, and environment. Two factors are required to monitor and control the physical objects reliably, securely, collaboratively, and efficiently, i.e., Cyber-physical integration and real-time interaction. DTs are used to create high-quality virtual models of physical objects in virtual space to simulate their behaviors in the real world and provide feedback. CPS and DT are two tools that help achieve cyber-physical integration and set the stage for intelligent manufacturing. They could cause a fundamental transformation to the currently-used manufacturing systems and business models.

As a result, the integration of technology into society will be a highly important issue in the future. Although there is a growing interest in the I4.0 social impacts (Beier et al., 2020; Stock et al., 2018), the academic literature demonstrates a number of shortages, which may result in the development of a new paradigm termed ‘Society 5.0 (S5.0)’ where human beings will be at the center of innovation and will be able to take advantage of the impacts of technology and the outcomes of I4.0. Note that S5.0 was introduced in January 2016 as a growth strategy for Japan, aiming to create a human-centric society where everyone could have access to economic and technological developments. In fact, S5.0 is a society wherein the technologies offered by I4.0 are actively applied to all aspects of people's everyday lives to achieve progress, technological advancements, and individual well-being (Fukuyama, 2018). Moreover, in recent years, the European Commission has confirmed that it is interested in a more humanized vision of I4.0 technologies, which requires incorporating more humanistic and societal factors into the concept of a desirable digital future.

The I4.0-related literature has been mainly focused on the significance of the interaction between machine and human and manufacturing processes (Brozzi et al., 2020; Frank et al., 2019); however, S5.0 is primarily concentrated on social workers-related issues (Pinzone et al., 2020) and it takes into consideration the influence of technology and the I4.0 outcomes on the enhancement of individuals’ quality of life, social responsibilities, and sustainability (Onday, 2019). In fact, there is a need to apply new human-focused approaches and methods to develop and introduce novel digital technologies together with considering I4.0-enabled works (Kadir et al., 2019). It is necessary to implement innovative holistic approaches to set for a digital transformation that could benefit all people in society. Although, the literature lacks research concentrating on the best ways to create solutions and products capable of exploiting the I4.0 technological potentials in a way that is beneficial to the whole society with the help of the S5.0 program 5. For that reason, the current paper is primarily aimed at filling this gap by proposing a new approach to creating and designing more solutions with a focus on humanistic aspects, i.e., Society 5.0 solutions, to better integrate the I4.0-based technologies with human beings’ requirements. Briefly, this paper attempts to understand how the S5.0-based solutions can be innovated and then used in a way to benefit various communities, e.g., users, governments, citizens, regions, nations, organizations, and industries. However, in this study, to recognize the main technological capabilities in the digital economy to the integration of IoT and cyber-physical, we perform a survey method with the recent literature review, in total, we have identified 17 technological capabilities and presented in Table 1.

Table 1.

Technological capabilities in the digital economy to the integration of IoT and cyber-physical.

Technological capabilities	Sources
Software assurance and application security (t1)	DiMase et al. (2020); Collier et al. (2021)
Big data platform (t2)	Xinhua et al. (2015); Wilcox et al. (2019)
Mobile CPS (t3)	Chaudhary and Rawat (2021); Su et al. (2022)
Condition-based monitoring (t4)	Kampitsis and Panagiotidou (2022); Patra et al. (2021)
Life cycle and anti-counterfeit (t5)	Popović et al. (2021); Hakola et al. (2021)
Task-specific human-machine interfaces (t6)	Wang et al. (2021); Ardanza et al. (2019)
Self-aware machines and components (t7)	Dell'Agnola et al. (2021); Pudukotai Dinakarrao (2021)
Anti-malicious and anti-tamper (t8)	Radanliev and De Roure (2021); Ijemaru et al. (2021)
Loosely time-triggered architectures (t9)	Bae and Ölveczky (2021); Benveniste (2010)
Structure dynamics control (t10)	Sokolov et al. (2016); Ivanov and Sokolov (2012)
Prognostics and health management (t11)	Meraghni et al. (2018); Xia and Xi (2019)
Electronic and physical security (t12)	DiMase et al. (2015); Radanliev et al. (2018b)
Real-time data acquisition and storage solutions (t13)	Radanliev et al. (2020); Uhlemann et al. (2017)
The fleet of machines (t14)	Kao et al. (2015); Waschull et al. (2020)
Adaptive analysis (t15)	Tsoukalas et al. (2017); Zhang et al. (2020)
Cyber-physical systems (t16)	Dey et al. (2018); Ochoa et al. (2017)
Peer-to-peer monitoring (t17)	Antoniou (2021); Feldstein and Coussons (2021)

Proposed research methodology

Preliminaries

In the subsection, we present some fundamental ideas related to the Pythagorean fuzzy set.

Definition 1 (Yager (2013). Let V={x1,x2,...,xn} be a fixed set. A Pythagorean fuzzy set (PFS) F on V is defined as

where μF:V→[0,1] and νF:V→[0,1] denote the degrees of belongingness and non-belongingness of the element xi∈V to F, respectively, with the condition that 0≤(μF(xi))2+(νF(xi))2≤1. For each xi∈V, the degree of indeterminacy or hesitation is given by πF(xi)=1−μF2(xi)−νF2(xi). For simplicity, Zhang and Xu (2014) denoted the Pythagorean fuzzy number (PFN) by ℘=(μ℘,ν℘) which fulfills μ℘,ν℘∈[0,1] and 0≤μ℘2+ν℘2≤1.

Definition 2 (Zhang & Xu, 2014). Let ℘=(μ℘,ν℘) be PFN. The score function and the accuracy function are defined by

For any two PFNs ℘1=(μ℘1,ν℘1) and ℘2=(μ℘2,ν℘2), then the ordering scheme is defined by

• lower Roman (%1)

  (i) If S(℘1)>S(℘2), then ℘1≻℘2,

• lower Roman (%1)

  (ii) If S(℘1)=S(℘2),then

• (a)

  if h(℘1)>h(℘2), then ℘2≻℘2,

• (b)

  if h(℘1)=h(℘2), then ℘1=℘2.

Definition 3 (Yager, 2014). Let ℘=(μ℘2,ν℘2),℘1=(μ℘1,ν℘1) and ℘2=(μ℘2,ν℘2) are three PFNs. Then, the following operations are satisfied for PFSs:

℘c=(ν℘,μ℘),

℘1⊕℘2=(μ℘12+μ℘22−μ℘12μ℘22,ν℘1ν℘2),

℘1⊗℘2=(μ℘1μ℘2,ν℘12+ν℘22−ν℘12ν℘22),

λ℘=(1−(1−μ℘2)λ,(ν℘)λ),λ>0,

℘λ=((μ℘)λ,1−(1−ν℘2)λ),λ>0.

Definition 4 (Zhang and Xu (2014). Let ℘1=(μ℘1,ν℘1) and ℘2=(μ℘2,ν℘2) be the PFNs. Then the distance between ℘2 and ℘2 is defined as

Proposed PF-MEREC-RS-DNMA approach

This section develops a PF-MEREC-RS-DNMA method under the PFSs setting for solving decision-making applications. The calculation procedure of the proposed method is given by

Step 1: Generate a “linguistic decision matrix (LDM)”.

A set of l _“Decision Experts (DEs)”A={A1,A2,...,Aℓ} determine the sets of m optionsO={o1,o2,...,om} and n criteria T={t1,t2,...,tn}, respectively. Owing to the vagueness of the human mind, lack of data, and imprecise knowledge about the options, the DEs allocate “linguistic values (LVs)” to evaluate his/her decision on option o_i concerning a criterion t_j. Assume that Z(k)=(ξij(k))m×n,i=1,2,...,m,j=1,2,...,n is the suggested LDM by DEs, where ξij(k) refer to the evaluation of an option o_i over a criterion t_j in the form of LVs given by k^th expert.

Step 2: Compute the weights of DEs

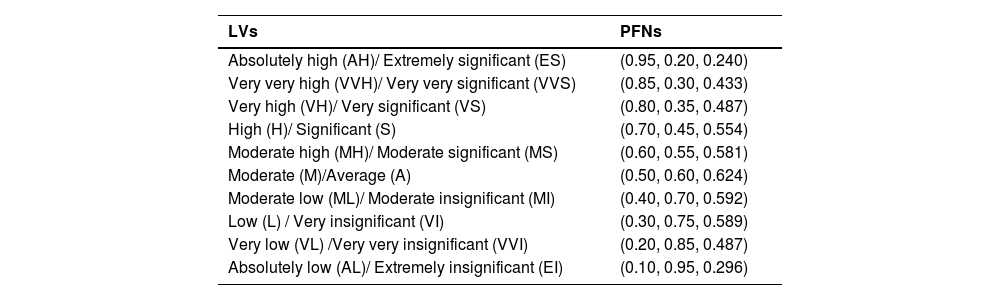
To determine the DEs’ weights, firstly, the importance degrees of the DEs are assumed as Linguistic Terms (LTs) and then expressed by PFNs. To compute the k^th DE, let Ak=(μk,νk,πk) be the PFN. Now, the expert weight is obtained by

Here, ϖk≥0 and ∑k=1lϖk=1.

Step 3: Aggregate all PF-DMs

To create the aggregated PF-decision matrix (A-PF-DM), the PF-weighted averaging (PFWA) operator is used, and then Z=(ξij)m×n, where

Step 4: Proposed PF-subjective and objective weighting approach.

Case I: Determination of objective weights by the method of PF-MEREC

All the criteria are not presumed to be of equal importance. Suppose w=(w1,w2,...,wn)T is the weight of the criterion set with ∑j=1nwj=1 and wj∈[0,1]. Now, to find the criteria weights, the classical MEREC (Keshavarz-Ghorabaee et al., 2021) model is extended under the PFSs environment. In the following, the procedure of the MEREC is presented by

Step 4a: Normalize the A-PF-DM.

In this step, a simple linear normalization is used to scale the elements of the A-PF-DM Z=(ξij)m×n and generate the normalized A-PF-DM N=(ςij)m×n. If t_b shows the benefit-type criteria set and t_n represents the cost-type criteria set, then we utilize the following equation for normalization:

Step 4b: Find the score matrix.

With the use of the following formula (Rani et al., 2020b), the score matrix Ω=(ηij)m×n of each PFN ςij is calculated:

Step 4c: Compute the alternatives’ overall performance.

This step involves the application of a logarithmic measure with equal criteria weights for the obtainment of the alternatives’ overall performances (Keshavarz-Ghorabaee et al., 2021). Based on the normalized values attained at the former step, it can be ensured that the smaller the ηij values, the greater the performance values. To compute the overall performance, Eq. (8) is used as follows:

Step 4d: Calculate the performance of the alternatives by removing each criterion.

This step applies the logarithmic measure in a way comparable to the former step. The difference between this step and Step 4c is that the alternatives’ performances are calculated through the removal of each criterion separately. As a result, there are n sets of performances accompanied by n criteria. In this calculation Si′ stands for the overall performance of the i^th alternative concerning the removal of j^th criterion. The following equation is used for the calculations of this step:

Step 4e: Compute the summation of absolute deviations.

This step computes the removal effect of the j^th criterion concerning the values attained at Steps 4c and 4d Here, Vj stands for the effect of the j^th criterion removal. Eq. (10) can be used for the calculation of the Vj values as follows:

Step 4f: Determine the final criteria weights.

At this step, the objective weight of each criterion is computed with the use of the removal effects (Vj) of Step 4e. In Eq. (11), wjo signifies the j^th criterion's weight. Eq. (11) is employed in order to calculatewjo:

Case II: Determine the subjective weights by the PF-RS method

The subjective weighting system here enables us to reflect on the thoughts and intrinsic values of decision-makers. In the process of decision-making, the decision-makers opinion of each alternative with dependent criteria is very important when selecting the best choice for the given problem. In this critical situation, the decision-maker gives subjective weight (Stillwell et al., 1981; Narayanamoorthy et al., 2020). Here, the procedure of the rank sum weight method is to help the decision-maker to give their ranking values for selected criteria. The formula of this method is given as follows:

where wjs represents the weights for each criteria j and n represents the number of criteria, rj denotes the rank of each criterion, j = 1,2,3,…,n.

Case III: Integrated weights using the objective and subjective weights:

In A-PF-DM, the decision-maker wants to utilize both subjective and objective weights; for that following integrated weighted equation is given.

where γ∈[0,1] is an objective factor of A-PF-DM weights.wjo represents the objective weight and wjs represents the subjective weight, respectively.

Step 5: Assessment of the normalized A-PF-DM

Here, we discuss linear and vector normalization formulae. These formulae manage both the numerical values and PFNs.

The linear normalization removes the dimensions of attributes using the principle with the interval maximum-minimum. A linear normalization procedure is defined as

where S(.) is an improved score function of PFNs.

The vector normalization has been used to normalize the A-PF-DM Z=(ξij)m×n, with zij=(μij,νij) into N(2)=(ηij(2))m×n, where ηij(2)=(μ¯ij(2),ν¯ij(2)) such that

Step 6: Using the subordinate aggregation models

Here, different types of aggregation models are developed using the following normalization procedures.

Step 6.1: The Complete Compensatory Method (CCM)

The CCM can be defined based on the PFWA operator as follows:

where wj represents the attribute weight and η⁽¹⁾_ij  shows the target-based linear normalization value. The alternatives can be ordered by arranging C1(oi):i=1,2,⋯,m in a decreasing manner, and we obtain the ranking outcomes ρ1(oi):i=1,2,⋯,m.

Step 6.2: The Un-Compensatory Method (UCM)

For the avoidance of a situation in which the chosen solution has a very improper performance in the case of a certain criterion, the weighted maximum operator is used for the purpose of composing the second aggregation function, as shown below:

The options can be prioritized by arranging C2(oi):i=1,2,⋯,m in a decreasing way, and we obtain the ranking outcomes ρ2(oi):i=1,2,⋯,m.

Step 6.3: The Incomplete Compensatory Method (ICM)

We utilize the vector normalization of the third aggregation procedure as Eq. (17) by the PFWG operator:

where wj signifies the attribute weight and η⁽²⁾_ij denotes the target-based vector normalized value. The alternatives can be arranged by listing C3(oi):i=1,2,⋯,m in a descending manner, and we get the ranking outcomes ρ3(oi):i=1,2,⋯,m.

Step 7: Combination of subordinate “Utility Degrees (UDs)” and priority orders

The last phase necessitates the achievement of an all-inclusive ranking by combining the outcomes of the three given models. These are considered as three parameters or criteria: CCM(Q1), UCM (Q2) and ICM (Q3). Each alternative Ii has two kinds of degrees: the “utility degree (UD)” Cτ(oi):i=1,2,⋯,m and the preference order ρτ(oi):i=1,2,⋯,m over each attribute Qτ:τ=1,2,3. Evidently, we generate two “Decision Matrices (DMs)”: the utility degree-DM ¿(C)=[Cτ(oi)]m×3 and the ranking-DM ¿(ρ)=[ρτ(oi)]m×3.

To preserve the inventive assessment of the subordinate UDs Cτ(oi):τ=1,2,3, the normalized versions are given by

Step 8: Compute the “overall utility degree (OUD)” of each alternative

A parameter ξ∈[0,1] is taken to show the subordinate UDs and the subordinate preferences of alternatives. Here, we take ξ=0.5. The OUD of each option presented by

where w1,w2 and w3 are the weight of the CCM, UCM, and ICM, respectively, such that w1+w2+w3=1. Here, the weight w1,w2 and w3 are obtained using the developed PF-RS model. The ultimate preference set ρ={ρ(o1),ρ(o2),ρ(o3),...,ρ(om)} is obtained in decreasing order of Ui:i=1,2,⋯,m.

Step 9: End.

Results and discussion

Case study

The implementation of the PF-MEREC-RS-DNMA method is discussed as follows:

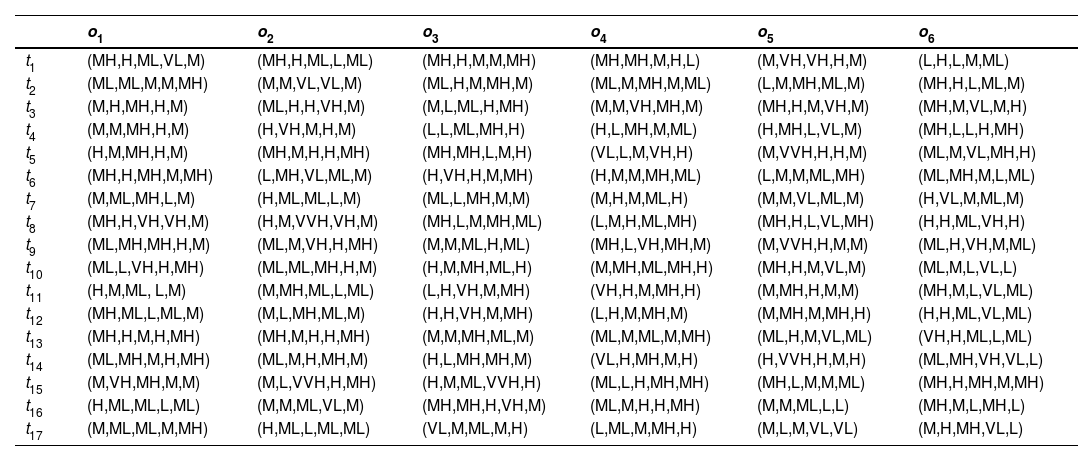
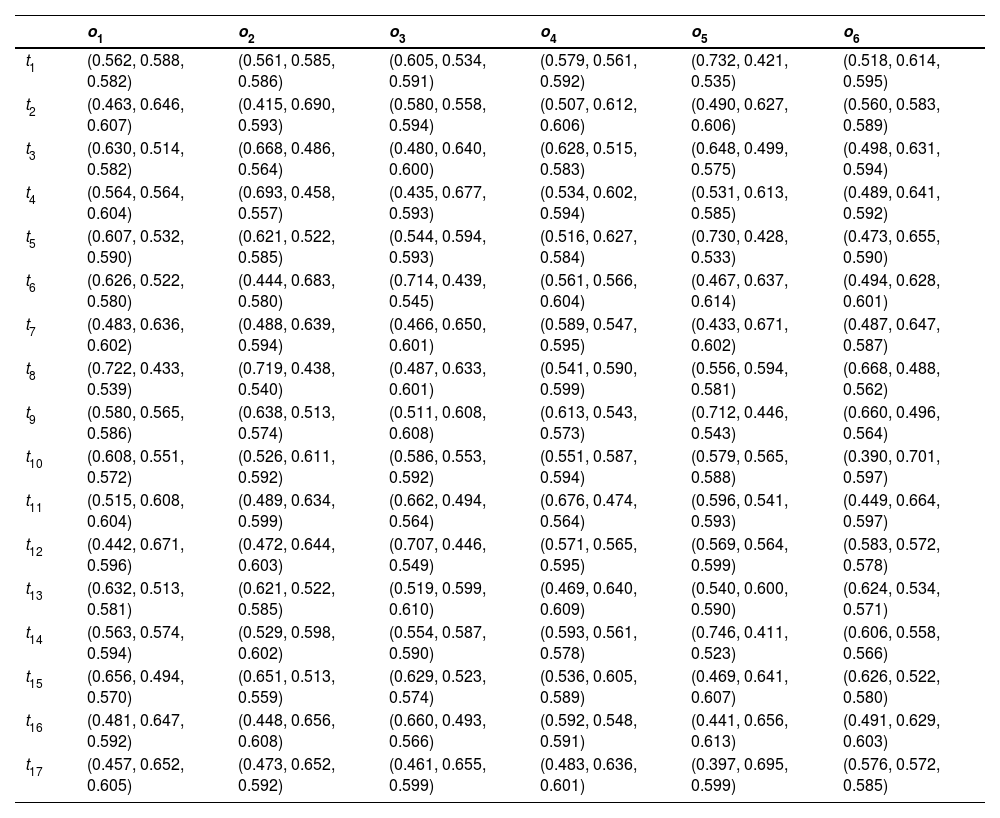
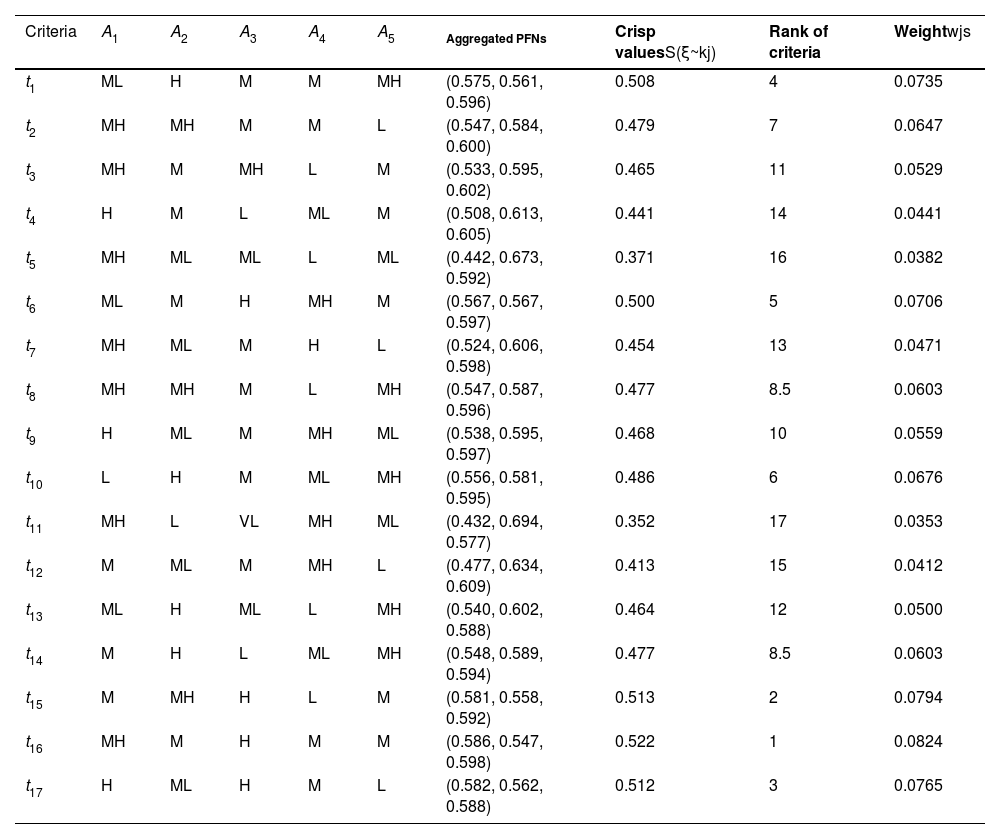
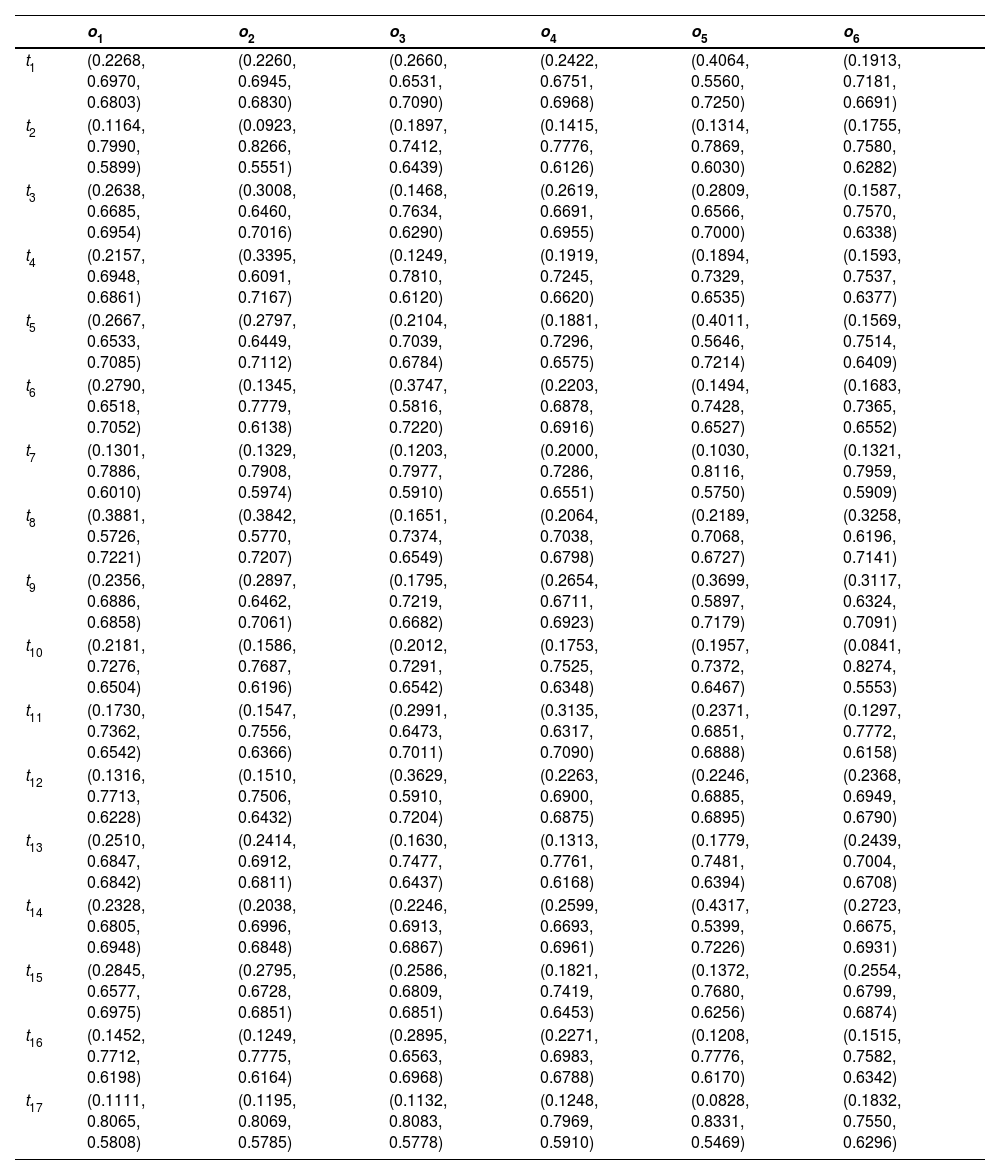
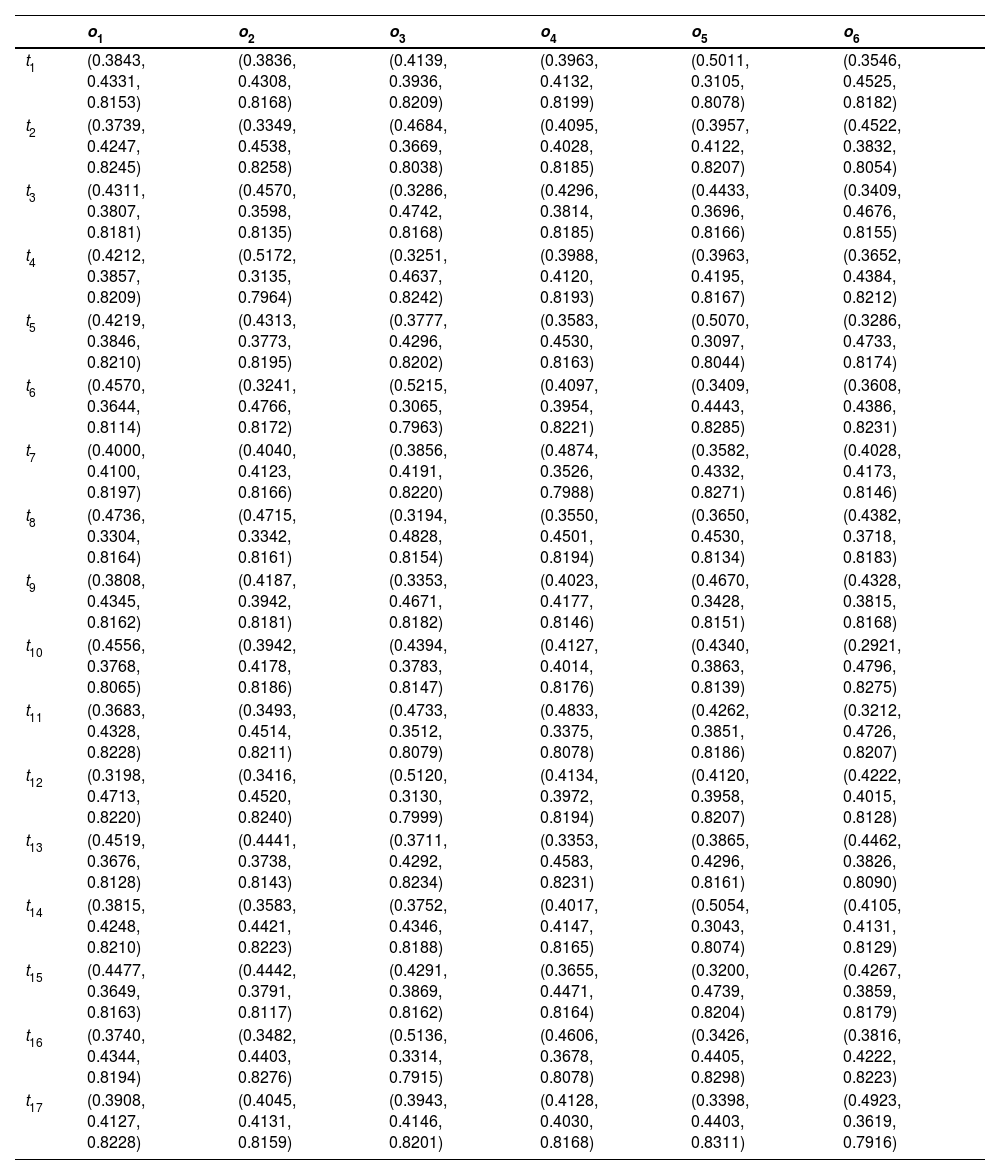
Steps 1–3:Table 2, adopted from Rani et al. (2020a) and Liu et al. (2021), depicts the significance of the DEs and criteria in the form of LVs and then converted into PFNs. Table 3 presents the DEs weight based on Table 2 and Eq. (4). Table 4 describes the LDM of each DE to evaluate the options and the assessments of options concerning each criterion.

Table 2.

Performance ratings of alternatives over criteria and DEs regarding the LVs.

LVs	PFNs
Absolutely high (AH)/ Extremely significant (ES)	(0.95, 0.20, 0.240)
Very very high (VVH)/ Very very significant (VVS)	(0.85, 0.30, 0.433)
Very high (VH)/ Very significant (VS)	(0.80, 0.35, 0.487)
High (H)/ Significant (S)	(0.70, 0.45, 0.554)
Moderate high (MH)/ Moderate significant (MS)	(0.60, 0.55, 0.581)
Moderate (M)/Average (A)	(0.50, 0.60, 0.624)
Moderate low (ML)/ Moderate insignificant (MI)	(0.40, 0.70, 0.592)
Low (L) / Very insignificant (VI)	(0.30, 0.75, 0.589)
Very low (VL) /Very very insignificant (VVI)	(0.20, 0.85, 0.487)
Absolutely low (AL)/ Extremely insignificant (EI)	(0.10, 0.95, 0.296)

Table 3.

Weight of DEs to the technological capabilities in the digital economy.

DEs	LVs	PFNs	Score	Rank	Weights
A1	S	(0.70, 0.45, 0.554)	0.6437	3	0.2003
A2	VVS	(0.85, 0.30, 0.433)	0.8162	1	0.3197
A3	VS	(0.80, 0.35, 0.487)	0.7588	2	0.2616
A4	MS	(0.60, 0.55, 0.581)	0.5287	4	0.1390
A5	M	(0.50, 0.60, 0.624)	0.4450	5	0.0794

Table 4.

LVs by DEs to the technological capabilities in the digital economy.

	o1	o2	o3	o4	o5	o6
t1	(MH,H,ML,VL,M)	(MH,H,ML,L,ML)	(MH,H,M,M,MH)	(MH,MH,M,H,L)	(M,VH,VH,H,M)	(L,H,L,M,ML)
t2	(ML,ML,M,M,MH)	(M,M,VL,VL,M)	(ML,H,M,MH,M)	(ML,M,MH,M,ML)	(L,M,MH,ML,M)	(MH,H,L,ML,M)
t3	(M,H,MH,H,M)	(ML,H,H,VH,M)	(M,L,ML,H,MH)	(M,M,VH,MH,M)	(MH,H,M,VH,M)	(MH,M,VL,M,H)
t4	(M,M,MH,H,M)	(H,VH,M,H,M)	(L,L,ML,MH,H)	(H,L,MH,M,ML)	(H,MH,L,VL,M)	(MH,L,L,H,MH)
t5	(H,M,MH,H,M)	(MH,M,H,H,MH)	(MH,MH,L,M,H)	(VL,L,M,VH,H)	(M,VVH,H,H,M)	(ML,M,VL,MH,H)
t6	(MH,H,MH,M,MH)	(L,MH,VL,ML,M)	(H,VH,H,M,MH)	(H,M,M,MH,ML)	(L,M,M,ML,MH)	(ML,MH,M,L,ML)
t7	(M,ML,MH,L,M)	(H,ML,ML,L,M)	(ML,L,MH,M,M)	(M,H,M,ML,H)	(M,M,VL,ML,M)	(H,VL,M,ML,M)
t8	(MH,H,VH,VH,M)	(H,M,VVH,VH,M)	(MH,L,M,MH,ML)	(L,M,H,ML,MH)	(MH,H,L,VL,MH)	(H,H,ML,VH,H)
t9	(ML,MH,MH,H,M)	(ML,M,VH,H,MH)	(M,M,ML,H,ML)	(MH,L,VH,MH,M)	(M,VVH,H,M,M)	(ML,H,VH,M,ML)
t10	(ML,L,VH,H,MH)	(ML,ML,MH,H,M)	(H,M,MH,ML,H)	(M,MH,ML,MH,H)	(MH,H,M,VL,M)	(ML,M,L,VL,L)
t11	(H,M,ML, L,M)	(M,MH,ML,L,ML)	(L,H,VH,M,MH)	(VH,H,M,MH,H)	(M,MH,H,M,M)	(MH,M,L,VL,ML)
t12	(MH,ML,L,ML,M)	(M,L,MH,ML,M)	(H,H,VH,M,MH)	(L,H,M,MH,M)	(M,MH,M,MH,H)	(H,H,ML,VL,ML)
t13	(MH,H,M,H,MH)	(MH,M,H,H,MH)	(M,M,MH,ML,M)	(ML,M,ML,M,MH)	(ML,H,M,VL,ML)	(VH,H,ML,L,ML)
t14	(ML,MH,M,H,MH)	(ML,M,H,MH,M)	(H,L,MH,MH,M)	(VL,H,MH,M,H)	(H,VVH,H,M,H)	(ML,MH,VH,VL,L)
t15	(M,VH,MH,M,M)	(M,L,VVH,H,MH)	(H,M,ML,VVH,H)	(ML,L,H,MH,MH)	(MH,L,M,M,ML)	(MH,H,MH,M,MH)
t16	(H,ML,ML,L,ML)	(M,M,ML,VL,M)	(MH,MH,H,VH,M)	(ML,M,H,H,MH)	(M,M,ML,L,L)	(MH,M,L,MH,L)
t17	(M,ML,ML,M,MH)	(H,ML,L,ML,ML)	(VL,M,ML,M,H)	(L,ML,M,MH,H)	(M,L,M,VL,VL)	(M,H,MH,VL,L)

The judgment provided by five DEs has been aggregated utilizing Eq. (5) into a cumulative PF-DM Z=(ξij)m×n, taking into effect the importance of individual DEs and are provided in Table 5.

Table 5.

A-PF-DM to evaluate the technological capabilities in the digital economy.

	o1	o2	o3	o4	o5	o6
t1	(0.562, 0.588, 0.582)	(0.561, 0.585, 0.586)	(0.605, 0.534, 0.591)	(0.579, 0.561, 0.592)	(0.732, 0.421, 0.535)	(0.518, 0.614, 0.595)
t2	(0.463, 0.646, 0.607)	(0.415, 0.690, 0.593)	(0.580, 0.558, 0.594)	(0.507, 0.612, 0.606)	(0.490, 0.627, 0.606)	(0.560, 0.583, 0.589)
t3	(0.630, 0.514, 0.582)	(0.668, 0.486, 0.564)	(0.480, 0.640, 0.600)	(0.628, 0.515, 0.583)	(0.648, 0.499, 0.575)	(0.498, 0.631, 0.594)
t4	(0.564, 0.564, 0.604)	(0.693, 0.458, 0.557)	(0.435, 0.677, 0.593)	(0.534, 0.602, 0.594)	(0.531, 0.613, 0.585)	(0.489, 0.641, 0.592)
t5	(0.607, 0.532, 0.590)	(0.621, 0.522, 0.585)	(0.544, 0.594, 0.593)	(0.516, 0.627, 0.584)	(0.730, 0.428, 0.533)	(0.473, 0.655, 0.590)
t6	(0.626, 0.522, 0.580)	(0.444, 0.683, 0.580)	(0.714, 0.439, 0.545)	(0.561, 0.566, 0.604)	(0.467, 0.637, 0.614)	(0.494, 0.628, 0.601)
t7	(0.483, 0.636, 0.602)	(0.488, 0.639, 0.594)	(0.466, 0.650, 0.601)	(0.589, 0.547, 0.595)	(0.433, 0.671, 0.602)	(0.487, 0.647, 0.587)
t8	(0.722, 0.433, 0.539)	(0.719, 0.438, 0.540)	(0.487, 0.633, 0.601)	(0.541, 0.590, 0.599)	(0.556, 0.594, 0.581)	(0.668, 0.488, 0.562)
t9	(0.580, 0.565, 0.586)	(0.638, 0.513, 0.574)	(0.511, 0.608, 0.608)	(0.613, 0.543, 0.573)	(0.712, 0.446, 0.543)	(0.660, 0.496, 0.564)
t10	(0.608, 0.551, 0.572)	(0.526, 0.611, 0.592)	(0.586, 0.553, 0.592)	(0.551, 0.587, 0.594)	(0.579, 0.565, 0.588)	(0.390, 0.701, 0.597)
t11	(0.515, 0.608, 0.604)	(0.489, 0.634, 0.599)	(0.662, 0.494, 0.564)	(0.676, 0.474, 0.564)	(0.596, 0.541, 0.593)	(0.449, 0.664, 0.597)
t12	(0.442, 0.671, 0.596)	(0.472, 0.644, 0.603)	(0.707, 0.446, 0.549)	(0.571, 0.565, 0.595)	(0.569, 0.564, 0.599)	(0.583, 0.572, 0.578)
t13	(0.632, 0.513, 0.581)	(0.621, 0.522, 0.585)	(0.519, 0.599, 0.610)	(0.469, 0.640, 0.609)	(0.540, 0.600, 0.590)	(0.624, 0.534, 0.571)
t14	(0.563, 0.574, 0.594)	(0.529, 0.598, 0.602)	(0.554, 0.587, 0.590)	(0.593, 0.561, 0.578)	(0.746, 0.411, 0.523)	(0.606, 0.558, 0.566)
t15	(0.656, 0.494, 0.570)	(0.651, 0.513, 0.559)	(0.629, 0.523, 0.574)	(0.536, 0.605, 0.589)	(0.469, 0.641, 0.607)	(0.626, 0.522, 0.580)
t16	(0.481, 0.647, 0.592)	(0.448, 0.656, 0.608)	(0.660, 0.493, 0.566)	(0.592, 0.548, 0.591)	(0.441, 0.656, 0.613)	(0.491, 0.629, 0.603)
t17	(0.457, 0.652, 0.605)	(0.473, 0.652, 0.592)	(0.461, 0.655, 0.599)	(0.483, 0.636, 0.601)	(0.397, 0.695, 0.599)	(0.576, 0.572, 0.585)

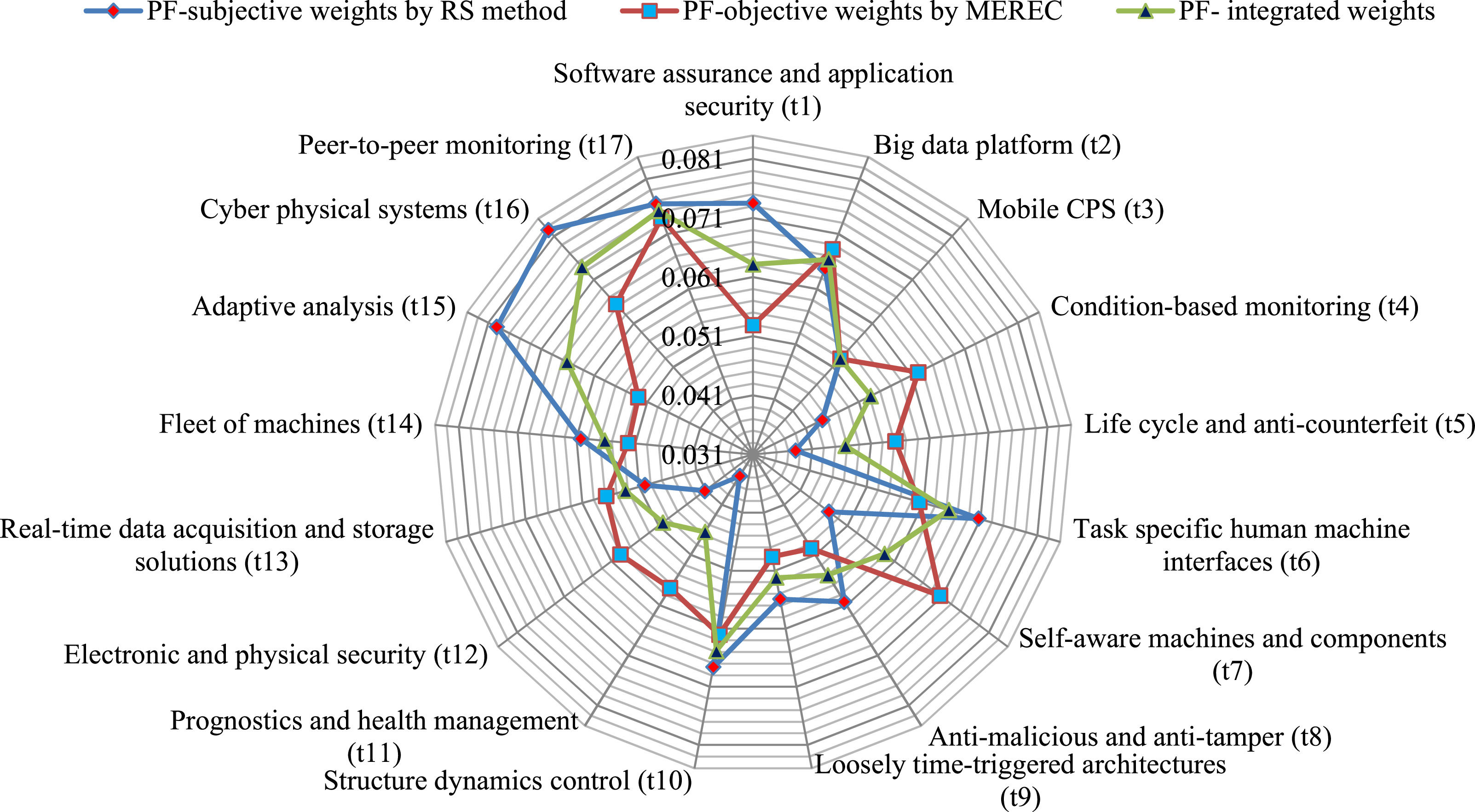
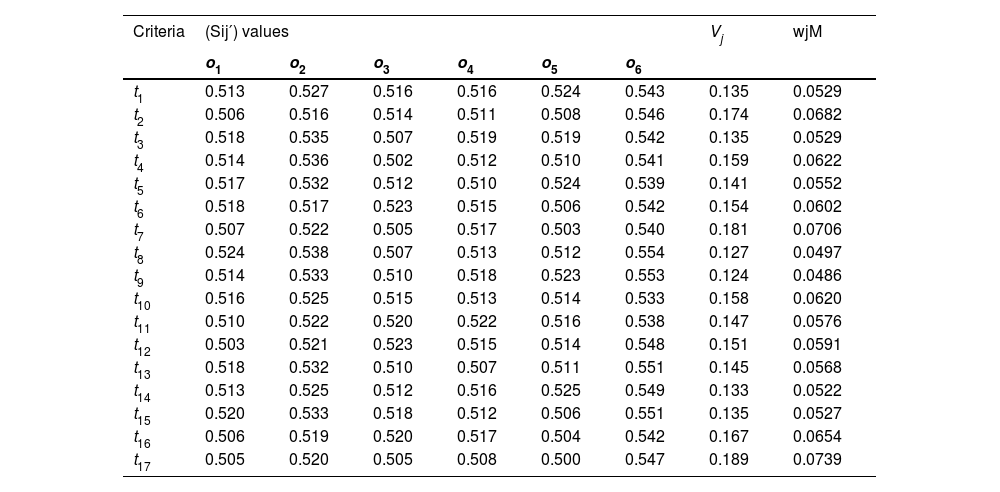
Step 4. To determine the criteria weights with the use of the PF-MEREC method, we computed the overall performance of the alternatives values on the basis of Eq. (7) and presented them as S₁ = 0.538, S₂ = 0.552, S₃ = 0.538, S₄ = 0.539, S₅ = 0.538, and S₆ = 0.571. Based on Eq. (8), the alternatives’ overall performances(Sij′) are determined through the removal of each criterion (displayed in Table 6). After that, the removal effect of each criterion on the overall performance of the alternatives is calculated using the deviation-based formula of Eq. (9). The weight of each criterion is computed concerning the impact of their removal upon the performance V_j of the alternatives with Eq. (10). With the help of Eq. (11) and the V_j values, we compute the technological capabilities’ weights in the digital economy for the integration of IoT and cyber-physical and are given in the last column of Table 6. The resultant values are in Fig. 1.

Table 6.

The implementation of the PF-MEREC weighting approach for computing the criteria weights.

Criteria	(Sij′) values						Vj	wjM
	o1	o2	o3	o4	o5	o6
t1	0.513	0.527	0.516	0.516	0.524	0.543	0.135	0.0529
t2	0.506	0.516	0.514	0.511	0.508	0.546	0.174	0.0682
t3	0.518	0.535	0.507	0.519	0.519	0.542	0.135	0.0529
t4	0.514	0.536	0.502	0.512	0.510	0.541	0.159	0.0622
t5	0.517	0.532	0.512	0.510	0.524	0.539	0.141	0.0552
t6	0.518	0.517	0.523	0.515	0.506	0.542	0.154	0.0602
t7	0.507	0.522	0.505	0.517	0.503	0.540	0.181	0.0706
t8	0.524	0.538	0.507	0.513	0.512	0.554	0.127	0.0497
t9	0.514	0.533	0.510	0.518	0.523	0.553	0.124	0.0486
t10	0.516	0.525	0.515	0.513	0.514	0.533	0.158	0.0620
t11	0.510	0.522	0.520	0.522	0.516	0.538	0.147	0.0576
t12	0.503	0.521	0.523	0.515	0.514	0.548	0.151	0.0591
t13	0.518	0.532	0.510	0.507	0.511	0.551	0.145	0.0568
t14	0.513	0.525	0.512	0.516	0.525	0.549	0.133	0.0522
t15	0.520	0.533	0.518	0.512	0.506	0.551	0.135	0.0527
t16	0.506	0.519	0.520	0.517	0.504	0.542	0.167	0.0654
t17	0.505	0.520	0.505	0.508	0.500	0.547	0.189	0.0739

Fig. 1.

Weight of the technological capabilities in the digital economy to the integration of IoT and cyber-physical.

From Eq. (12), we have calculated the subjective weights using the PF-rank sum (RS) weight procedure of each criterion to the technological capabilities in the digital economy to the integration of IoT and cyber-physical. The resultant values are given in Table 7 and shown in Fig. 1.

Table 7.

Weights of the technological capabilities in the digital economy using the RS method.

Criteria	A1	A2	A3	A4	A5	Aggregated PFNs	Crisp valuesS(ξ~kj)	Rank of criteria	Weightwjs
t1	ML	H	M	M	MH	(0.575, 0.561, 0.596)	0.508	4	0.0735
t2	MH	MH	M	M	L	(0.547, 0.584, 0.600)	0.479	7	0.0647
t3	MH	M	MH	L	M	(0.533, 0.595, 0.602)	0.465	11	0.0529
t4	H	M	L	ML	M	(0.508, 0.613, 0.605)	0.441	14	0.0441
t5	MH	ML	ML	L	ML	(0.442, 0.673, 0.592)	0.371	16	0.0382
t6	ML	M	H	MH	M	(0.567, 0.567, 0.597)	0.500	5	0.0706
t7	MH	ML	M	H	L	(0.524, 0.606, 0.598)	0.454	13	0.0471
t8	MH	MH	M	L	MH	(0.547, 0.587, 0.596)	0.477	8.5	0.0603
t9	H	ML	M	MH	ML	(0.538, 0.595, 0.597)	0.468	10	0.0559
t10	L	H	M	ML	MH	(0.556, 0.581, 0.595)	0.486	6	0.0676
t11	MH	L	VL	MH	ML	(0.432, 0.694, 0.577)	0.352	17	0.0353
t12	M	ML	M	MH	L	(0.477, 0.634, 0.609)	0.413	15	0.0412
t13	ML	H	ML	L	MH	(0.540, 0.602, 0.588)	0.464	12	0.0500
t14	M	H	L	ML	MH	(0.548, 0.589, 0.594)	0.477	8.5	0.0603
t15	M	MH	H	L	M	(0.581, 0.558, 0.592)	0.513	2	0.0794
t16	MH	M	H	M	M	(0.586, 0.547, 0.598)	0.522	1	0.0824
t17	H	ML	H	M	L	(0.582, 0.562, 0.588)	0.512	3	0.0765

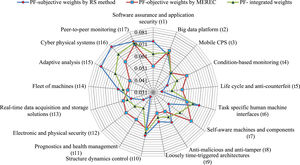
From the algorithm of the proposed PF-MEREC-RS method, we have to combine the PF-MEREC for objective weighting and PF-RS weight for subjective weighting by using Eq. (13). The integrated weight for τ=0.5 is shown in Fig. 1 and given as follows:

w_j = (0.0632, 0.0664, 0.0529, 0.0532, 0.0467, 0.0654, 0.0589, 0.0550, 0.0522, 0.0648, 0.0464, 0.0501, 0.0534, 0.0562, 0.0661, 0.0739, 0.0752).

Fig. 1 demonstrates the weights of various technological capabilities in the digital economy for the integration of IoT and cyber-physical with respect to the goal of this paper. Peer-to-peer monitoring (t17), with a weight value of 0.0752, has become the most important technological capability in the digital economy to integrate IoT and cyber-physical. Cyber-physical systems (t16) with a weight value of 0.0739 are the second most important technological capabilities in the digital economy to the integration of IoT and cyber-physical. Big data platform (t2) has third with a significance value of 0.0664, Adaptive analysis (t15) has fourth with a weight value of 0.0661, Structure dynamics control (t10) with a significance value of 0.0648 has fifth most important technological capability in the digital economy to the integration of IoT and cyber-physical, and others are considered crucial technological capabilities in the digital economy to the integration of IoT and cyber-physical.

Step 5: According to the Eq. (14)-Eq. (16) and Table 5, the linear and vector normalization values are estimated and given in Tables 8 and 9.

Table 8.

Linear normalization matrix for each option.

	o1	o2	o3	o4	o5	o6
t1	(0.2268, 0.6970, 0.6803)	(0.2260, 0.6945, 0.6830)	(0.2660, 0.6531, 0.7090)	(0.2422, 0.6751, 0.6968)	(0.4064, 0.5560, 0.7250)	(0.1913, 0.7181, 0.6691)
t2	(0.1164, 0.7990, 0.5899)	(0.0923, 0.8266, 0.5551)	(0.1897, 0.7412, 0.6439)	(0.1415, 0.7776, 0.6126)	(0.1314, 0.7869, 0.6030)	(0.1755, 0.7580, 0.6282)
t3	(0.2638, 0.6685, 0.6954)	(0.3008, 0.6460, 0.7016)	(0.1468, 0.7634, 0.6290)	(0.2619, 0.6691, 0.6955)	(0.2809, 0.6566, 0.7000)	(0.1587, 0.7570, 0.6338)
t4	(0.2157, 0.6948, 0.6861)	(0.3395, 0.6091, 0.7167)	(0.1249, 0.7810, 0.6120)	(0.1919, 0.7245, 0.6620)	(0.1894, 0.7329, 0.6535)	(0.1593, 0.7537, 0.6377)
t5	(0.2667, 0.6533, 0.7085)	(0.2797, 0.6449, 0.7112)	(0.2104, 0.7039, 0.6784)	(0.1881, 0.7296, 0.6575)	(0.4011, 0.5646, 0.7214)	(0.1569, 0.7514, 0.6409)
t6	(0.2790, 0.6518, 0.7052)	(0.1345, 0.7779, 0.6138)	(0.3747, 0.5816, 0.7220)	(0.2203, 0.6878, 0.6916)	(0.1494, 0.7428, 0.6527)	(0.1683, 0.7365, 0.6552)
t7	(0.1301, 0.7886, 0.6010)	(0.1329, 0.7908, 0.5974)	(0.1203, 0.7977, 0.5910)	(0.2000, 0.7286, 0.6551)	(0.1030, 0.8116, 0.5750)	(0.1321, 0.7959, 0.5909)
t8	(0.3881, 0.5726, 0.7221)	(0.3842, 0.5770, 0.7207)	(0.1651, 0.7374, 0.6549)	(0.2064, 0.7038, 0.6798)	(0.2189, 0.7068, 0.6727)	(0.3258, 0.6196, 0.7141)
t9	(0.2356, 0.6886, 0.6858)	(0.2897, 0.6462, 0.7061)	(0.1795, 0.7219, 0.6682)	(0.2654, 0.6711, 0.6923)	(0.3699, 0.5897, 0.7179)	(0.3117, 0.6324, 0.7091)
t10	(0.2181, 0.7276, 0.6504)	(0.1586, 0.7687, 0.6196)	(0.2012, 0.7291, 0.6542)	(0.1753, 0.7525, 0.6348)	(0.1957, 0.7372, 0.6467)	(0.0841, 0.8274, 0.5553)
t11	(0.1730, 0.7362, 0.6542)	(0.1547, 0.7556, 0.6366)	(0.2991, 0.6473, 0.7011)	(0.3135, 0.6317, 0.7090)	(0.2371, 0.6851, 0.6888)	(0.1297, 0.7772, 0.6158)
t12	(0.1316, 0.7713, 0.6228)	(0.1510, 0.7506, 0.6432)	(0.3629, 0.5910, 0.7204)	(0.2263, 0.6900, 0.6875)	(0.2246, 0.6885, 0.6895)	(0.2368, 0.6949, 0.6790)
t13	(0.2510, 0.6847, 0.6842)	(0.2414, 0.6912, 0.6811)	(0.1630, 0.7477, 0.6437)	(0.1313, 0.7761, 0.6168)	(0.1779, 0.7481, 0.6394)	(0.2439, 0.7004, 0.6708)
t14	(0.2328, 0.6805, 0.6948)	(0.2038, 0.6996, 0.6848)	(0.2246, 0.6913, 0.6867)	(0.2599, 0.6693, 0.6961)	(0.4317, 0.5399, 0.7226)	(0.2723, 0.6675, 0.6931)
t15	(0.2845, 0.6577, 0.6975)	(0.2795, 0.6728, 0.6851)	(0.2586, 0.6809, 0.6851)	(0.1821, 0.7419, 0.6453)	(0.1372, 0.7680, 0.6256)	(0.2554, 0.6799, 0.6874)
t16	(0.1452, 0.7712, 0.6198)	(0.1249, 0.7775, 0.6164)	(0.2895, 0.6563, 0.6968)	(0.2271, 0.6983, 0.6788)	(0.1208, 0.7776, 0.6170)	(0.1515, 0.7582, 0.6342)
t17	(0.1111, 0.8065, 0.5808)	(0.1195, 0.8069, 0.5785)	(0.1132, 0.8083, 0.5778)	(0.1248, 0.7969, 0.5910)	(0.0828, 0.8331, 0.5469)	(0.1832, 0.7550, 0.6296)

Table 9.

Vector normalization matrix for each option.

	o1	o2	o3	o4	o5	o6
t1	(0.3843, 0.4331, 0.8153)	(0.3836, 0.4308, 0.8168)	(0.4139, 0.3936, 0.8209)	(0.3963, 0.4132, 0.8199)	(0.5011, 0.3105, 0.8078)	(0.3546, 0.4525, 0.8182)
t2	(0.3739, 0.4247, 0.8245)	(0.3349, 0.4538, 0.8258)	(0.4684, 0.3669, 0.8038)	(0.4095, 0.4028, 0.8185)	(0.3957, 0.4122, 0.8207)	(0.4522, 0.3832, 0.8054)
t3	(0.4311, 0.3807, 0.8181)	(0.4570, 0.3598, 0.8135)	(0.3286, 0.4742, 0.8168)	(0.4296, 0.3814, 0.8185)	(0.4433, 0.3696, 0.8166)	(0.3409, 0.4676, 0.8155)
t4	(0.4212, 0.3857, 0.8209)	(0.5172, 0.3135, 0.7964)	(0.3251, 0.4637, 0.8242)	(0.3988, 0.4120, 0.8193)	(0.3963, 0.4195, 0.8167)	(0.3652, 0.4384, 0.8212)
t5	(0.4219, 0.3846, 0.8210)	(0.4313, 0.3773, 0.8195)	(0.3777, 0.4296, 0.8202)	(0.3583, 0.4530, 0.8163)	(0.5070, 0.3097, 0.8044)	(0.3286, 0.4733, 0.8174)
t6	(0.4570, 0.3644, 0.8114)	(0.3241, 0.4766, 0.8172)	(0.5215, 0.3065, 0.7963)	(0.4097, 0.3954, 0.8221)	(0.3409, 0.4443, 0.8285)	(0.3608, 0.4386, 0.8231)
t7	(0.4000, 0.4100, 0.8197)	(0.4040, 0.4123, 0.8166)	(0.3856, 0.4191, 0.8220)	(0.4874, 0.3526, 0.7988)	(0.3582, 0.4332, 0.8271)	(0.4028, 0.4173, 0.8146)
t8	(0.4736, 0.3304, 0.8164)	(0.4715, 0.3342, 0.8161)	(0.3194, 0.4828, 0.8154)	(0.3550, 0.4501, 0.8194)	(0.3650, 0.4530, 0.8134)	(0.4382, 0.3718, 0.8183)
t9	(0.3808, 0.4345, 0.8162)	(0.4187, 0.3942, 0.8181)	(0.3353, 0.4671, 0.8182)	(0.4023, 0.4177, 0.8146)	(0.4670, 0.3428, 0.8151)	(0.4328, 0.3815, 0.8168)
t10	(0.4556, 0.3768, 0.8065)	(0.3942, 0.4178, 0.8186)	(0.4394, 0.3783, 0.8147)	(0.4127, 0.4014, 0.8176)	(0.4340, 0.3863, 0.8139)	(0.2921, 0.4796, 0.8275)
t11	(0.3683, 0.4328, 0.8228)	(0.3493, 0.4514, 0.8211)	(0.4733, 0.3512, 0.8079)	(0.4833, 0.3375, 0.8078)	(0.4262, 0.3851, 0.8186)	(0.3212, 0.4726, 0.8207)
t12	(0.3198, 0.4713, 0.8220)	(0.3416, 0.4520, 0.8240)	(0.5120, 0.3130, 0.7999)	(0.4134, 0.3972, 0.8194)	(0.4120, 0.3958, 0.8207)	(0.4222, 0.4015, 0.8128)
t13	(0.4519, 0.3676, 0.8128)	(0.4441, 0.3738, 0.8143)	(0.3711, 0.4292, 0.8234)	(0.3353, 0.4583, 0.8231)	(0.3865, 0.4296, 0.8161)	(0.4462, 0.3826, 0.8090)
t14	(0.3815, 0.4248, 0.8210)	(0.3583, 0.4421, 0.8223)	(0.3752, 0.4346, 0.8188)	(0.4017, 0.4147, 0.8165)	(0.5054, 0.3043, 0.8074)	(0.4105, 0.4131, 0.8129)
t15	(0.4477, 0.3649, 0.8163)	(0.4442, 0.3791, 0.8117)	(0.4291, 0.3869, 0.8162)	(0.3655, 0.4471, 0.8164)	(0.3200, 0.4739, 0.8204)	(0.4267, 0.3859, 0.8179)
t16	(0.3740, 0.4344, 0.8194)	(0.3482, 0.4403, 0.8276)	(0.5136, 0.3314, 0.7915)	(0.4606, 0.3678, 0.8078)	(0.3426, 0.4405, 0.8298)	(0.3816, 0.4222, 0.8223)
t17	(0.3908, 0.4127, 0.8228)	(0.4045, 0.4131, 0.8159)	(0.3943, 0.4146, 0.8201)	(0.4128, 0.4030, 0.8168)	(0.3398, 0.4403, 0.8311)	(0.4923, 0.3619, 0.7916)

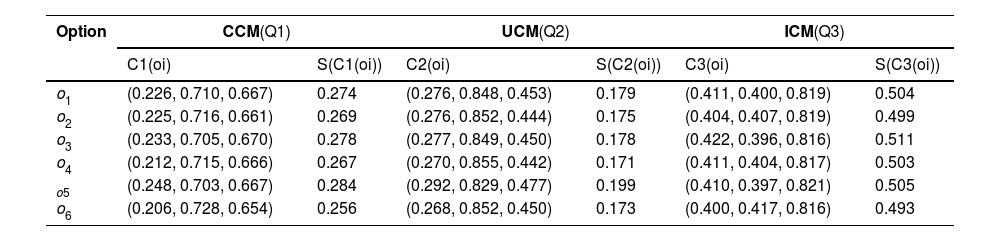
Step 6: The subordinate utility degrees of the CCM, UCM, and ICM are estimated by Eq. (17)-Eq. (19) and portrayed in Table 10.

Table 10.

The CCM, UCM, and ICM values for each option.

Option	CCM(Q1)		UCM(Q2)		ICM(Q3)
	C1(oi)	S(C1(oi))	C2(oi)	S(C2(oi))	C3(oi)	S(C3(oi))
o1	(0.226, 0.710, 0.667)	0.274	(0.276, 0.848, 0.453)	0.179	(0.411, 0.400, 0.819)	0.504
o2	(0.225, 0.716, 0.661)	0.269	(0.276, 0.852, 0.444)	0.175	(0.404, 0.407, 0.819)	0.499
o3	(0.233, 0.705, 0.670)	0.278	(0.277, 0.849, 0.450)	0.178	(0.422, 0.396, 0.816)	0.511
o4	(0.212, 0.715, 0.666)	0.267	(0.270, 0.855, 0.442)	0.171	(0.411, 0.404, 0.817)	0.503
o5	(0.248, 0.703, 0.667)	0.284	(0.292, 0.829, 0.477)	0.199	(0.410, 0.397, 0.821)	0.505
o6	(0.206, 0.728, 0.654)	0.256	(0.268, 0.852, 0.450)	0.173	(0.400, 0.417, 0.816)	0.493

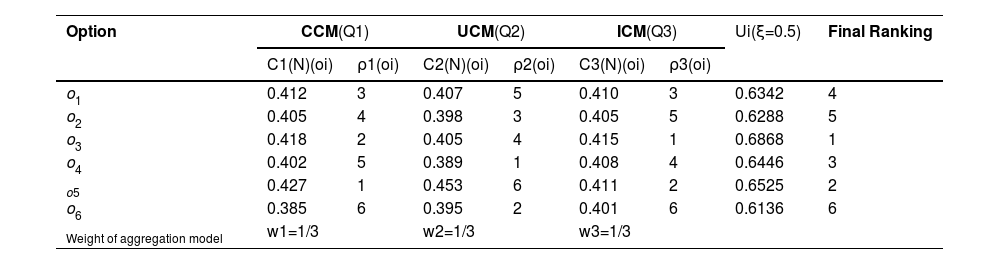
Step 7: Corresponding to Eq. (20), the normalized degrees of the subordinate UDs of CCM, UCM, and ICM are estimated, and their preferences are also obtained and are shown in Table 11. Next, the normalized subordinate UDs and the weights of subordinate UDs are calculated and mentioned in Table 11.

Table 11.

Normalized CCM, UCM, and ICM degrees and OUDs of the options.

Option	CCM(Q1)		UCM(Q2)		ICM(Q3)		Ui(ξ=0.5)	Final Ranking
	C1(N)(oi)	ρ1(oi)	C2(N)(oi)	ρ2(oi)	C3(N)(oi)	ρ3(oi)
o1	0.412	3	0.407	5	0.410	3	0.6342	4
o2	0.405	4	0.398	3	0.405	5	0.6288	5
o3	0.418	2	0.405	4	0.415	1	0.6868	1
o4	0.402	5	0.389	1	0.408	4	0.6446	3
o5	0.427	1	0.453	6	0.411	2	0.6525	2
o6	0.385	6	0.395	2	0.401	6	0.6136	6
Weight of aggregation model	w1=1/3		w2=1/3		w3=1/3

Step 8: From Eq. (21), the subordinate normalized UDs and ranks, the OUDs, and the final preference orders of option are obtained and depicted in Table 11. Regardless of assuming w1=w2=w3=1/3, the weights can be chosen as per the preferences of DEs on the basis of the comprehensive accomplishment by the alternatives or of their poor performances. CCM is preferred if the attention of the alternatives‟ comprehensive abilities can be drawn from DEs. If the DEs is not interested in taking risks, then a large weight can be attached to the UCM. It is pertinent to mention that ICM can be endowed by a large weight when the DEs focus solely on the comprehensive performance and the decision risks. Furthermore, when we preserve the property that linear normalization is much more efficient than vector normalization, then it can genuinely be possible to attribute a large weight to both the CCM and UCM models and fail, which inculcates to comply with a big weight to ICM. Hence, the preference order of options is o3≻o5≻o4≻o1≻o2≻o6, and option o₃ is with the highest UD of the appropriateness of options.

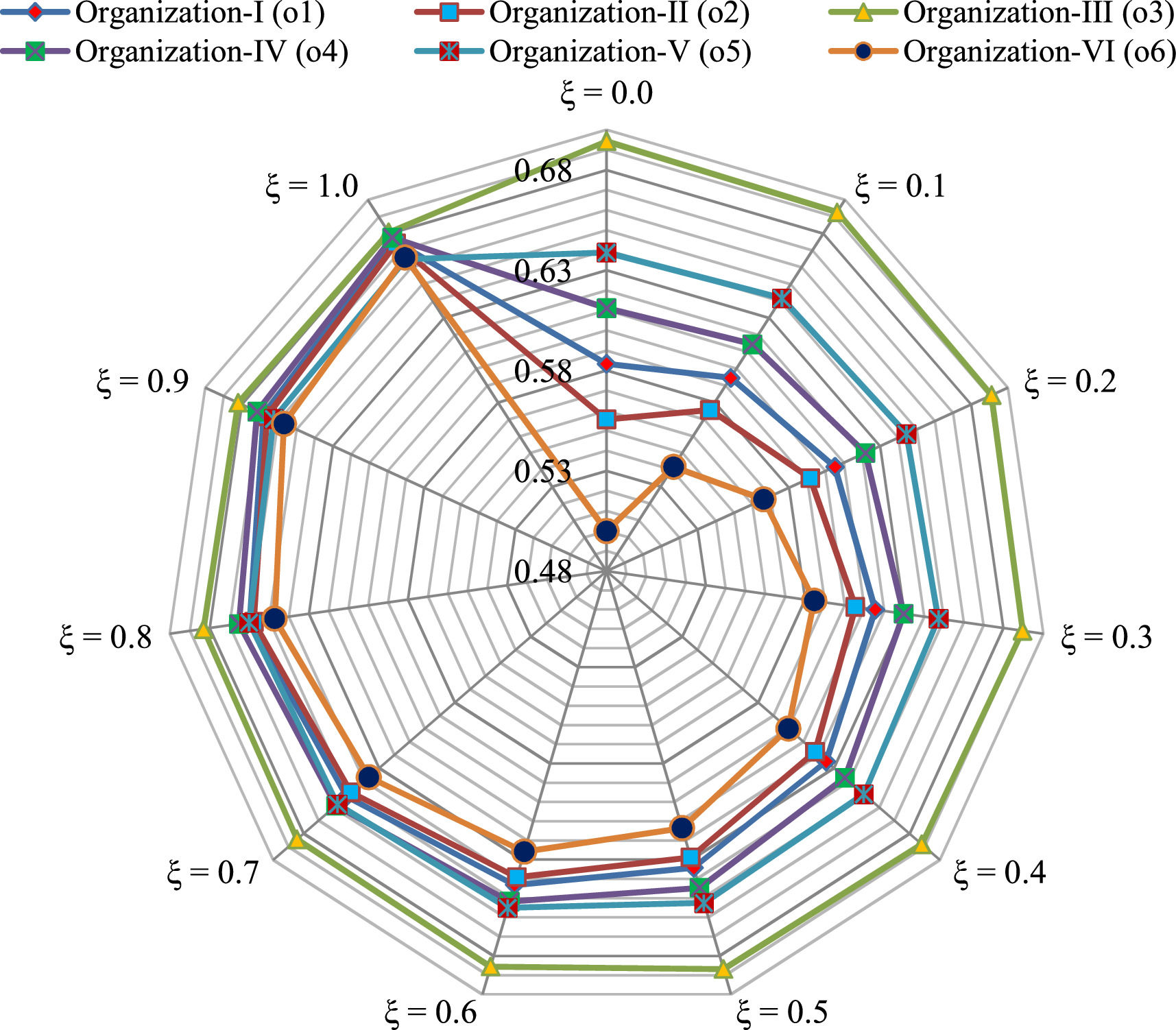
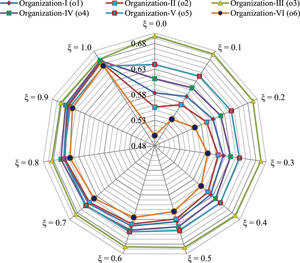
Sensitivity investigation

This subsection shows a sensitivity investigation associated with the parameter ξ. The variation of ξ is a useful issue in helping to evaluate the sensitivity level of the approach, changing from subordinate UDs to subordinate preferences. In addition, changing the values of ξ is applied to the investigation of the sensitivity of the proposed method to the eminence of attribute weights.

Fig. 2 represents the sensitivity analysis of the alternatives for diverse values of the utility parameter ξ. Based on the assessments, we obtain similar preferences o3≻o5≻o4≻o1≻o2≻o6 for ξ=0.0 to ξ=0.6,o3≻o4≻o5≻o1≻o2≻o6 for ξ=0.7 to ξ=0.8,o3≻o4≻o1≻o2≻o5≻o6 for ξ=0.9 and o3≻o4≻o1≻o2≻o6≻o5 for ξ=1.0, which implies o₃ is at the top of the ranking for each value of ξ, while the o₆ has the last rank for ξ=0.0 to ξ=0.9 and the o₅ has the last rank forξ=1.0. Therefore, it is observable that the developed method possesses adequate stability with numerous parameter values. As shown clearly in Fig. 2, the developed PF-MEREC-RS-DNMA methodology is capable of generating stable and, at the same time, flexible preference results in a variety of utility parameters. This property is of high importance for MCDM procedures and decision-making reality.

Fig. 2.

Sensitivity outcomes of the Ui values over the utility parameter ξ.

Comparison with existing methods

In the current part of the study, we present a comparative study between the proposed and existing PF-TOPSIS model (Zhang & Xu, 2014) and PF-WASPAS (Rani et al., 2020c) for solving MCDM problems under the PFSs context as follows:

PF-TOPSIS model

Steps 1–4: Follow the steps of the PF-TOPSIS method

Step 5: Calculate the discriminations of each alternative from “PF-positive ideal solution (PIS)” and “PF-negative-ideal solution (NIS)”.

In this method, calculating the PF-PIS and PF-NIS values of each criterion is a key concern for DMs. Let ϕ+ and ϕ− be the PF-PIS and PF-NIS, respectively, which are computed with the use of Eq. (20) and Eq. (21) as follows:

Step 6: Derive the degrees of distances of options from PF-PIS and PF-NIS.

In accordance with Eq. (1), estimate the degree of distance D(oi,ϕ+) among the option oi and the PF-PIS ϕ+.

and the degree of distance D(oi,ϕ−) among the options oi and the PF-NIS ϕ− is given as follows:

Step 7: Compute the relative closeness index (CI)

Based on the values of CI, the most suitable candidate and the prioritization order of all alternatives are determined. The maximum value of C(ok) determines the most appropriate choice.

Next, we implement the PF-TOPSIS on the abovementioned case study. For this, firstly, we have computed the PF-PIS and PF-NIS by means of Eq. (22)-Eq. (23), and then we have

ϕ+={(0.732, 0.421, 0.535), (0.580, 0.558, 0.594), (0.668, 0.486, 0.564), (0.693, 0.458, 0.557), (0.730, 0.428, 0.533), (0.714, 0.439, 0.545), (0.589, 0.547, 0.595), (0.722, 0.433, 0.539), (0.712, 0.446, 0.543), (0.608, 0.551, 0.572), (0.676, 0.474, 0.564), (0.707, 0.446, 0.549), (0.632, 0.513, 0.581), (0.746, 0.411, 0.523), (0.656, 0.494, 0.570), (0.660, 0.493, 0.566), (0.576, 0.572, 0.585)}.

ϕ−={(0.518, 0.614, 0.595), (0.415, 0.690, 0.593), (0.480, 0.640, 0.600), (0.435, 0.677, 0.593), (0.473, 0.655, 0.590), (0.444, 0.683, 0.580), (0.433, 0.671, 0.602), (0.487, 0.633, 0.601), (0.511, 0.608, 0.608), (0.390, 0.701, 0.597), (0.449, 0.664, 0.597), (0.442, 0.671, 0.596), (0.469, 0.640, 0.609), (0.529, 0.598, 0.602), (0.469, 0.641, 0.607), (0.441, 0.656, 0.613), (0.397, 0.695, 0.599)}.

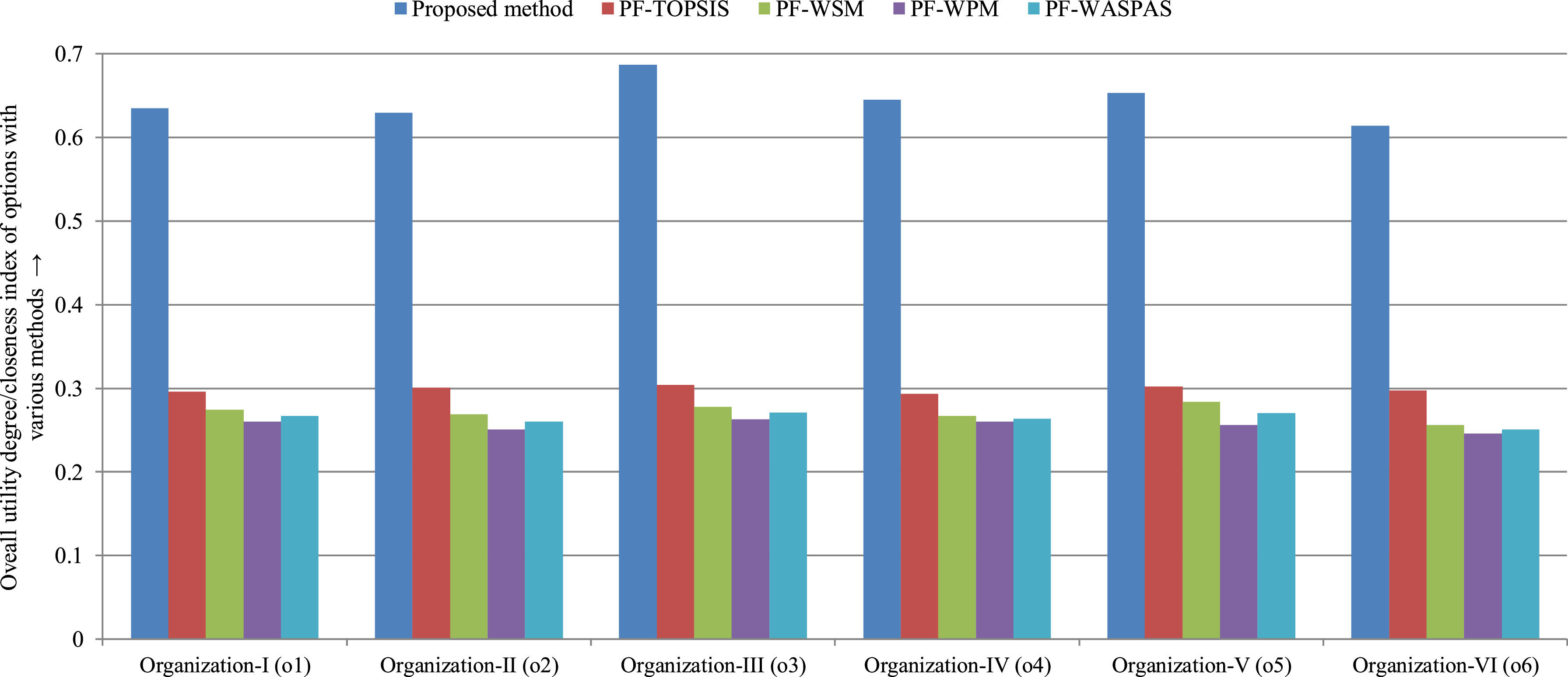
Using Eq. (24)-Eq. (26), the relative closeness index (CI) of the options to the technological capabilities in the digital economy to the integration of IoT and cyber-physical are presented as o₁ = 0.296, o₂ = 0.301, o₃ = 0.304, o₄ = 0.293, o₅ = 0.302 and o₆ = 0.297. Hence, the desirable organization option is o₅ to the technological capabilities in the digital economy to the integration of IoT and cyber-physical. The priority order of options is o3≻o5≻o1≻o4≻o2≻o6 to the evaluation of the technological capabilities in the digital economy to integrate IoT and cyber-physical.

PF-WASPAS model

The PF-WASPAS method is implemented to handle the decision-making problem. The description of the PF-WASPAS method is given as follows:

Steps 1–4: As the aforementioned model

Step 5: Utilize the weighted sum model (WSM) Ci(1) in the following expression

Step 6: Apply the weighted product model (WPM) Ci(2) in the following expression

Step 7: Obtain the UD of the WASPAS model in the following expression

where ‘λ’ means the decision strategy parameter, where λ∈[0,1] (when λ=0 and λ=1, WASPAS is transformed into the WPM and the WSM, respectively).

Step 8: Based on UDCi, prioritize the options.

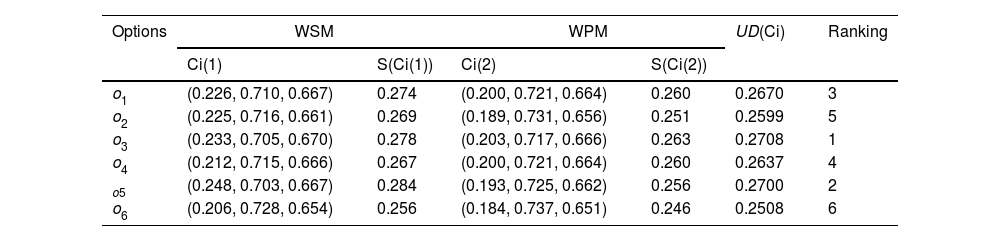
Using Eq. (27)-Eq. (28), the WSM and WPM values are estimated. Then, the UD of WASPAS for each organization to the evaluation of the technological capabilities in the digital economy to the integration of IoT and cyber-physical is obtained with the use of Eq. (29) and mentioned in Table 12.

Table 12.

The UD of option to the evaluation of the technological capabilities in the digital economy.

Options	WSM		WPM		UD(Ci)	Ranking
	Ci(1)	S(Ci(1))	Ci(2)	S(Ci(2))
o1	(0.226, 0.710, 0.667)	0.274	(0.200, 0.721, 0.664)	0.260	0.2670	3
o2	(0.225, 0.716, 0.661)	0.269	(0.189, 0.731, 0.656)	0.251	0.2599	5
o3	(0.233, 0.705, 0.670)	0.278	(0.203, 0.717, 0.666)	0.263	0.2708	1
o4	(0.212, 0.715, 0.666)	0.267	(0.200, 0.721, 0.664)	0.260	0.2637	4
o5	(0.248, 0.703, 0.667)	0.284	(0.193, 0.725, 0.662)	0.256	0.2700	2
o6	(0.206, 0.728, 0.654)	0.256	(0.184, 0.737, 0.651)	0.246	0.2508	6

The priority order of options is o3≻o5≻o1≻o4≻o2≻o6. Thus, the organization-III (o₃) option is the best one for the evaluation of the technological capabilities in the digital economy to the integration of IoT and cyber-physical.

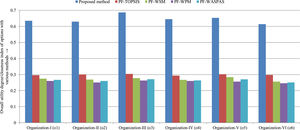
As a whole, the benefits of the PF-MEREC-RS-DNMA method over the extant method are given as follows (see Fig. 3):

• ■

  In the developed method, the subjective weights of attributes are obtained by the PF-RS method, and the objective weights of criteria are computed by MEREC, whereas in PF-WASPAS, only objective weights of criteria are obtained by entropy and divergence measure-based weighting procedure, and in PF-TOPSIS, the criteria weights are chosen arbitrarily.

• ■

  In Zhang and Xu (2014), the distance is calculated between the overall attribute value of an alternative R_i and the PF-IS and the PF-AIS to describe the CI of each option on the given attributes. The PF-PIS and PF-NIS could be considered two benchmarks against which the performance of the alternatives on each attribute could be assessed. Remember that the two above-mentioned benchmarks it is too unrealistic to be achieved practically. On the other hand, it should be noted that the proposed PF-MEREC-RS-DNMA uses strength points of various normalization methods and aggregation functions, and it can integrate all of them appropriately. The final integration function of the DNMA approach takes into consideration widely the subordinate UDs and the ranks of options; this way, the final ranking results could be highly reliable and more realistic than the DEs could not only know about the best and worst performance of alternatives on the defined attributes but also compare their performance.

Fig. 3.

Comparison of utility degree of each industry with various methods.

Conclusions

The digital revolution has converted analog information to digital information, which makes it ready for automated processing. Digitized information can move more easily among different media, and across vast distances, with more reliable reproduction. Remember that this has significant engineering and organizational consequences. For example, the extensive use of digital sensors has caused the lines between manufacturing and services to get blurred. To analyze, rank, and evaluate the main technological capabilities in the digital economy to the integration of the IoT and the CPS, this study introduced an integrated decision-making method using PFSs. In this regard, a novel decision-making approach using PF-MEREC-RS and PF-DNMA methods called the PF-MEREC-RS-DNMA method is introduced to evaluate the main technological capabilities in the digital economy to the integration of the IoT and the CPS and the industries to implement Industry 4.0 smart manufacturing systems. To rank the main technological capabilities in the digital economy to the integration of the IoT and the CPS, the PF-MEREC-RS method is utilized, and to compute the preference order of different organizations to the evaluation of the technological capabilities in the digital economy to the integration of IoT and cyber-physical, the PF-DNMA method is used. To validation of the results of this study, a comparison using the PF-TOPSIS, PF-WSM, PF-WPM, and PF-WASPAS methods is conducted.

Enabling technologies play important roles in industry and the market. However, no market mechanism is able to ensure adequate investment in enabling technologies to offer the level of innovation desired by society. It is difficult for innovators to effectively solve the bargaining problem because of the intrinsic difficulty of identifying the recombinant possibilities ex-ante and establishing a contract so that the necessary coordination can be well achieved. The digital economy consists of numerous standards; it often integrates the elements of interoperability and technology development. To make suitable policies in this regard, there is a need to distinguish between standards-setting and standards development. The goal of standards-setting is interoperability; however, it does not need to involve the creation of new technology. On the other hand, the goal of standards development is to develop technology, and also it has implications for value capture. Managers need to understand that value capture is required to be a part of every exercise in the strategies, business model design, and innovation. To be merely a pioneer is not everything; rather, policymakers need to be aware of the challenges encountered by innovators when they seek to capture enough value to keep on their innovation in the future. In the case of inventors of enabling and general-purpose technologies, the challenges are even greater. To keep innovation in societies, governments require to give thoughtful support not only to value creation but also to value capture. If it cannot be properly accomplished, the innovation incentives would be compromised and/or the government itself would have to fund enabling technologies at levels not contemplated yet.

Here, we discuss the presented PF-MEREC-RS-DNMA method and illustrate how to apply it for realistic applications. Since the PF-MEREC-RS and PF-DNMA are powerful and straightforward, therefore, various further research concerns are well worth exploring on the setting the PF-MEREC-RS-DNMA method as

• •

  The main issue is exploring group decision-making with the PF-MEREC-RS-DNMA method to consider the combination of subjective and objective weights for the expert's weight determination.

• •

  To develop a consensus-reaching process if the number of experts is large, which ensures the final decision result is more reasonable.

• •

  The other interesting aspect of the PF-MEREC-RS-DNMA method is combining the PF-MEREC-RS DNMA method with other models, such as the prospect theory, the analytic hierarchy process (AHP) method, and the information-measure-based method. Combining the PF-MEREC-RS-DNMA method with other models can make the method more applicable.

• •

  Also, authors can expand the study by using diverse MCDM models such as the combined compromise solution (CoCoSo), COPRAS, measurement alternatives and ranking based on compromise solution (MARCOS), or WASPAS to evaluate the main technological capabilities in the digital economy for integration of the IoT and the CPS. Furthermore, the developed PF-MEREC-RS-DNMA approach can also be utilized to solve the MCDM problems encountered in various disciplines: low carbon supplier selection, green supply chain management, barriers to the intelligent transportation system, and different branches of engineering.

Acknowledgement

This paper was supported by this project Social Science Planning Project of Shandong Province, "invisible government" in the field of administrative examination and approval in the context of interest game (Project No: JG17S07).