Know your data: Evaluation of normality for continuous variables and tools to deal with non-normal distributions

Rodriguez, Adrian
doi:10.1016/j.medcle.2019.05.011
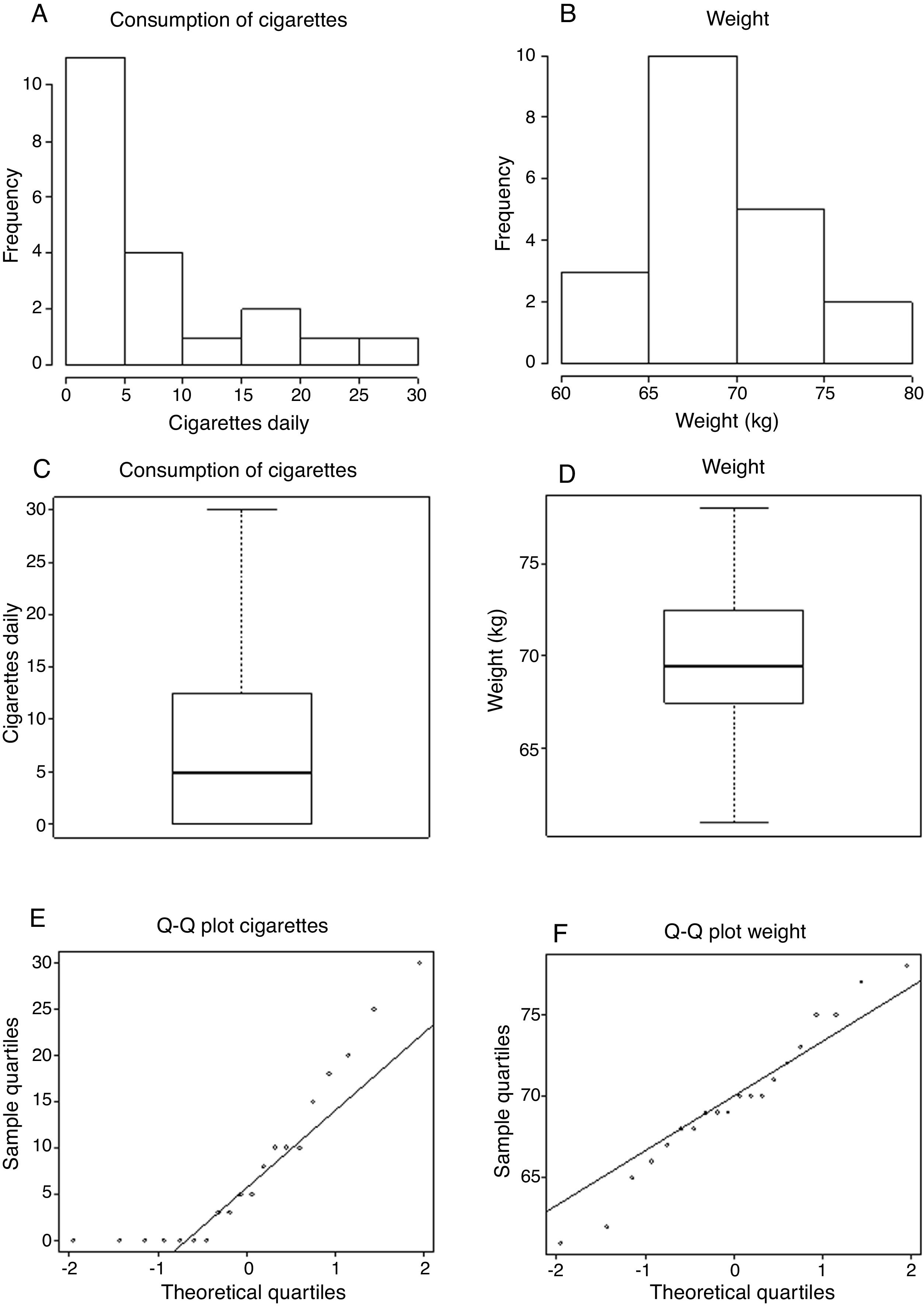
 array:24 [
  "pii" => "S2387020619305650"
  "issn" => "23870206"
  "doi" => "10.1016/j.medcle.2019.05.011"
  "estado" => "S300"
  "fechaPublicacion" => "2020-02-28"
  "aid" => "4908"
  "copyright" => "Elsevier Espa&#241;a&#44; S&#46;L&#46;U&#46;. All rights reserved"
  "copyrightAnyo" => "2019"
  "documento" => "article"
  "crossmark" => 1
  "subdocumento" => "sco"
  "cita" => "Med Clin. 2020;154:142-5"
  "abierto" => array:3 [
    "ES" => false
    "ES2" => false
    "LATM" => false
  ]
  "gratuito" => false
  "lecturas" => array:1 [
    "total" => 0
  ]
  "Traduccion" => array:1 [
    "es" => array:19 [
      "pii" => "S0025775319304269"
      "issn" => "00257753"
      "doi" => "10.1016/j.medcli.2019.05.017"
      "estado" => "S300"
      "fechaPublicacion" => "2020-02-28"
      "aid" => "4908"
      "copyright" => "Elsevier Espa&#241;a&#44; S&#46;L&#46;U&#46;"
      "documento" => "article"
      "crossmark" => 1
      "subdocumento" => "sco"
      "cita" => "Med Clin. 2020;154:142-5"
      "abierto" => array:3 [
        "ES" => false
        "ES2" => false
        "LATM" => false
      ]
      "gratuito" => false
      "lecturas" => array:1 [
        "total" => 0
      ]
      "es" => array:11 [
        "idiomaDefecto" => true
        "cabecera" => "<span class="elsevierStyleTextfn">Art&#237;culo especial</span>"
        "titulo" => "Conoce tus datos&#58; evaluaci&#243;n de la normalidad de variables continuas y estrategias para tratar con distribuciones no normales"
        "tienePdf" => "es"
        "tieneTextoCompleto" => "es"
        "paginas" => array:1 [
          0 => array:2 [
            "paginaInicial" => "142"
            "paginaFinal" => "145"
          ]
        ]
        "titulosAlternativos" => array:1 [
          "en" => array:1 [
            "titulo" => "Know your data&#58; Evaluation of normality for continuous variables and tools to deal with non-normal distributions"
          ]
        ]
        "contieneTextoCompleto" => array:1 [
          "es" => true
        ]
        "contienePdf" => array:1 [
          "es" => true
        ]
        "resumenGrafico" => array:2 [
          "original" => 0
          "multimedia" => array:7 [
            "identificador" => "fig0005"
            "etiqueta" => "Figura 1"
            "tipo" => "MULTIMEDIAFIGURA"
            "mostrarFloat" => true
            "mostrarDisplay" => false
            "figura" => array:1 [
              0 => array:4 [
                "imagen" => "gr1.jpeg"
                "Alto" => 3076
                "Ancho" => 2173
                "Tamanyo" => 206864
              ]
            ]
            "descripcion" => array:1 [
              "es" => "<p id="spar0005" class="elsevierStyleSimplePara elsevierViewall">Gr&#225;ficos para comprobar la normalidad de los datos&#58; histogramas &#40;A y B&#41;&#44; diagrama de cajas &#40;C y D&#41; y gr&#225;ficos Q-Q &#40;E y F&#41; para las variables n&#250;mero de cigarrillos y peso&#46;</p>"
            ]
          ]
        ]
        "autores" => array:1 [
          0 => array:2 [
            "autoresLista" => "Adrian Rodriguez"
            "autores" => array:1 [
              0 => array:2 [
                "nombre" => "Adrian"
                "apellidos" => "Rodriguez"
              ]
            ]
          ]
        ]
      ]
      "idiomaDefecto" => "es"
      "Traduccion" => array:1 [
        "en" => array:9 [
          "pii" => "S2387020619305650"
          "doi" => "10.1016/j.medcle.2019.05.011"
          "estado" => "S300"
          "subdocumento" => ""
          "abierto" => array:3 [
            "ES" => false
            "ES2" => false
            "LATM" => false
          ]
          "gratuito" => false
          "lecturas" => array:1 [
            "total" => 0
          ]
          "idiomaDefecto" => "en"
          "EPUB" => "https://multimedia.elsevier.es/PublicationsMultimediaV1/item/epub/S2387020619305650?idApp=UINPBA00004N"
        ]
      ]
      "EPUB" => "https://multimedia.elsevier.es/PublicationsMultimediaV1/item/epub/S0025775319304269?idApp=UINPBA00004N"
      "url" => "/00257753/0000015400000004/v1_202002120627/S0025775319304269/v1_202002120627/es/main.assets"
    ]
  ]
  "itemSiguiente" => array:19 [
    "pii" => "S2387020619305583"
    "issn" => "23870206"
    "doi" => "10.1016/j.medcle.2018.10.039"
    "estado" => "S300"
    "fechaPublicacion" => "2020-02-28"
    "aid" => "4662"
    "copyright" => "Elsevier Espa&#241;a&#44; S&#46;L&#46;U&#46;"
    "documento" => "simple-article"
    "crossmark" => 1
    "subdocumento" => "crp"
    "cita" => "Med Clin. 2020;154:146"
    "abierto" => array:3 [
      "ES" => false
      "ES2" => false
      "LATM" => false
    ]
    "gratuito" => false
    "lecturas" => array:1 [
      "total" => 0
    ]
    "en" => array:10 [
      "idiomaDefecto" => true
      "cabecera" => "<span class="elsevierStyleTextfn">Scientific letter</span>"
      "titulo" => "Silicosis&#44; sarcoidosis and systemic sclerosis in the same patient"
      "tienePdf" => "en"
      "tieneTextoCompleto" => "en"
      "paginas" => array:1 [
        0 => array:1 [
          "paginaInicial" => "146"
        ]
      ]
      "titulosAlternativos" => array:1 [
        "es" => array:1 [
          "titulo" => "Silicosis&#44; sarcoidosis y esclerosis sist&#233;mica en un mismo paciente"
        ]
      ]
      "contieneTextoCompleto" => array:1 [
        "en" => true
      ]
      "contienePdf" => array:1 [
        "en" => true
      ]
      "autores" => array:1 [
        0 => array:2 [
          "autoresLista" => "Noel&#237; Reguart Oto, Anna Soler Sendra, Vera Ortiz Santamaria"
          "autores" => array:3 [
            0 => array:2 [
              "nombre" => "Noel&#237;"
              "apellidos" => "Reguart Oto"
            ]
            1 => array:2 [
              "nombre" => "Anna"
              "apellidos" => "Soler Sendra"
            ]
            2 => array:2 [
              "nombre" => "Vera"
              "apellidos" => "Ortiz Santamaria"
            ]
          ]
        ]
      ]
    ]
    "idiomaDefecto" => "en"
    "Traduccion" => array:1 [
      "es" => array:9 [
        "pii" => "S0025775318306328"
        "doi" => "10.1016/j.medcli.2018.10.007"
        "estado" => "S300"
        "subdocumento" => ""
        "abierto" => array:3 [
          "ES" => false
          "ES2" => false
          "LATM" => false
        ]
        "gratuito" => false
        "lecturas" => array:1 [
          "total" => 0
        ]
        "idiomaDefecto" => "es"
        "EPUB" => "https://multimedia.elsevier.es/PublicationsMultimediaV1/item/epub/S0025775318306328?idApp=UINPBA00004N"
      ]
    ]
    "EPUB" => "https://multimedia.elsevier.es/PublicationsMultimediaV1/item/epub/S2387020619305583?idApp=UINPBA00004N"
    "url" => "/23870206/0000015400000004/v1_202002201732/S2387020619305583/v1_202002201732/en/main.assets"
  ]
  "itemAnterior" => array:19 [
    "pii" => "S2387020619305662"
    "issn" => "23870206"
    "doi" => "10.1016/j.medcle.2019.08.004"
    "estado" => "S300"
    "fechaPublicacion" => "2020-02-28"
    "aid" => "5037"
    "copyright" => "Elsevier Espa&#241;a&#44; S&#46;L&#46;U&#46;"
    "documento" => "article"
    "crossmark" => 1
    "subdocumento" => "rev"
    "cita" => "Med Clin. 2020;154:134-41"
    "abierto" => array:3 [
      "ES" => false
      "ES2" => false
      "LATM" => false
    ]
    "gratuito" => false
    "lecturas" => array:1 [
      "total" => 0
    ]
    "en" => array:13 [
      "idiomaDefecto" => true
      "cabecera" => "<span class="elsevierStyleTextfn">Review</span>"
      "titulo" => "Beyond CAR-T cells&#58; Natural killer cells immunotherapy"
      "tienePdf" => "en"
      "tieneTextoCompleto" => "en"
      "tieneResumen" => array:2 [
        0 => "en"
        1 => "es"
      ]
      "paginas" => array:1 [
        0 => array:2 [
          "paginaInicial" => "134"
          "paginaFinal" => "141"
        ]
      ]
      "titulosAlternativos" => array:1 [
        "es" => array:1 [
          "titulo" => "M&#225;s all&#225; de las c&#233;lulas CAR-T&#44; inmunoterapia con linfocitos <span class="elsevierStyleItalic">natural killer</span>"
        ]
      ]
      "contieneResumen" => array:2 [
        "en" => true
        "es" => true
      ]
      "contieneTextoCompleto" => array:1 [
        "en" => true
      ]
      "contienePdf" => array:1 [
        "en" => true
      ]
      "resumenGrafico" => array:2 [
        "original" => 0
        "multimedia" => array:8 [
          "identificador" => "fig0015"
          "etiqueta" => "Figure 3"
          "tipo" => "MULTIMEDIAFIGURA"
          "mostrarFloat" => true
          "mostrarDisplay" => false
          "figura" => array:1 [
            0 => array:4 [
              "imagen" => "gr3.jpeg"
              "Alto" => 2075
              "Ancho" => 2319
              "Tamanyo" => 263746
            ]
          ]
          "detalles" => array:1 [
            0 => array:3 [
              "identificador" => "at0015"
              "detalle" => "Figure "
              "rol" => "short"
            ]
          ]
          "descripcion" => array:1 [
            "en" => "<p id="spar0015" class="elsevierStyleSimplePara elsevierViewall">Progressive increase in the percentage of cells with NK phenotype &#40;CD56&#43; CD3&#8722;&#41; during coculture&#46; The phenotype of the different cell populations was determined by flow cytometry&#46; A progressive increase is observed in the proportion of CD56&#43; CD3&#8722; with purging of the rest of the cell lines&#44; mainly from day 14 of culture&#46;</p>"
          ]
        ]
      ]
      "autores" => array:1 [
        0 => array:2 [
          "autoresLista" => "Mar&#237;a Dolores Corral S&#225;nchez, Luc&#237;a Fern&#225;ndez Casanova, Antonio P&#233;rez-Mart&#237;nez"
          "autores" => array:3 [
            0 => array:2 [
              "nombre" => "Mar&#237;a Dolores"
              "apellidos" => "Corral S&#225;nchez"
            ]
            1 => array:2 [
              "nombre" => "Luc&#237;a"
              "apellidos" => "Fern&#225;ndez Casanova"
            ]
            2 => array:2 [
              "nombre" => "Antonio"
              "apellidos" => "P&#233;rez-Mart&#237;nez"
            ]
          ]
        ]
      ]
    ]
    "idiomaDefecto" => "en"
    "Traduccion" => array:1 [
      "es" => array:9 [
        "pii" => "S0025775319306438"
        "doi" => "10.1016/j.medcli.2019.08.008"
        "estado" => "S300"
        "subdocumento" => ""
        "abierto" => array:3 [
          "ES" => false
          "ES2" => false
          "LATM" => false
        ]
        "gratuito" => false
        "lecturas" => array:1 [
          "total" => 0
        ]
        "idiomaDefecto" => "es"
        "EPUB" => "https://multimedia.elsevier.es/PublicationsMultimediaV1/item/epub/S0025775319306438?idApp=UINPBA00004N"
      ]
    ]
    "EPUB" => "https://multimedia.elsevier.es/PublicationsMultimediaV1/item/epub/S2387020619305662?idApp=UINPBA00004N"
    "url" => "/23870206/0000015400000004/v1_202002201732/S2387020619305662/v1_202002201732/en/main.assets"
  ]
  "en" => array:17 [
    "idiomaDefecto" => true
    "cabecera" => "<span class="elsevierStyleTextfn">Special article</span>"
    "titulo" => "Know your data&#58; Evaluation of normality for continuous variables and tools to deal with non-normal distributions"
    "tieneTextoCompleto" => true
    "paginas" => array:1 [
      0 => array:2 [
        "paginaInicial" => "142"
        "paginaFinal" => "145"
      ]
    ]
    "autores" => array:1 [
      0 => array:3 [
        "autoresLista" => "Adrian Rodriguez"
        "autores" => array:1 [
          0 => array:3 [
            "nombre" => "Adrian"
            "apellidos" => "Rodriguez"
            "email" => array:1 [
              0 => "adri.statistics@gmail.com"
            ]
          ]
        ]
        "afiliaciones" => array:1 [
          0 => array:2 [
            "entidad" => "Universit&#224; Cattolica del Sacro Cuore&#44; Rome&#44; Italy"
            "identificador" => "aff0005"
          ]
        ]
      ]
    ]
    "titulosAlternativos" => array:1 [
      "es" => array:1 [
        "titulo" => "Conoce tus datos&#58; evaluaci&#243;n de la normalidad de variables continuas y estrategias para tratar con distribuciones no normales"
      ]
    ]
    "resumenGrafico" => array:2 [
      "original" => 0
      "multimedia" => array:8 [
        "identificador" => "fig0005"
        "etiqueta" => "Fig&#46; 1"
        "tipo" => "MULTIMEDIAFIGURA"
        "mostrarFloat" => true
        "mostrarDisplay" => false
        "figura" => array:1 [
          0 => array:4 [
            "imagen" => "gr1.jpeg"
            "Alto" => 3552
            "Ancho" => 2507
            "Tamanyo" => 284067
          ]
        ]
        "detalles" => array:1 [
          0 => array:3 [
            "identificador" => "at0005"
            "detalle" => "Fig&#46; "
            "rol" => "short"
          ]
        ]
        "descripcion" => array:1 [
          "en" => "<p id="spar0005" class="elsevierStyleSimplePara elsevierViewall">Graphs to demonstrate the normality of the data&#58; histograms &#40;A and B&#41;&#44; box plots &#40;C and D&#41; and Q-Q plots &#40;E and F&#41; for the variables &#8216;number of cigarettes&#8217; and &#8216;weight&#8217;&#46;</p>"
        ]
      ]
    ]
    "textoCompleto" => "<span class="elsevierStyleSections"><p id="par0005" class="elsevierStylePara elsevierViewall">The analysis of continuous quantitative variables is widespread in medical literature&#58; blood or urinary levels&#44; pain scales or anthropometric measurements are some examples of widely used continuous variables&#46; To synthesize the data&#44; researchers can use a measure of central tendency&#44; such as the mean or median&#44; accompanied by measures of dispersion&#44; such as the standard deviation&#44; the interquartile range or the range&#46; However&#44; although many researchers are tempted to use the mean arbitrarily&#44; it is not always the best way to summaries a series of data&#46; If the variable in question does not have a normal &#40;or Gaussian&#41; distribution&#44; the median is usually a better estimate as a measure of central tendency&#46;</p><p id="par0010" class="elsevierStylePara elsevierViewall">Something similar happens when we have to decide which statistical analysis or test to use to compare a continuous quantitative variable in 2 or more groups&#46; Many researchers tend to use the Student&#39;s t-test or the one-way ANOVA to compare the means between different groups&#46; However&#44; these statistical tests have several assumptions that must be met and&#44; probably&#44; the most important is that the variable is distributed normally&#46; Alternatives to these are the Mann Whitney U test or the Kruskal&#8211;Wallis test&#44; which do not assume any particular distribution of the data&#46; This means that they can always be used&#44; regardless of whether the variable of interest is distributed normally or not&#46;</p><p id="par0015" class="elsevierStylePara elsevierViewall">This article reviews the different ways of establishing whether a variable follows a normal distribution or not&#44; and the alternatives that we can use in the case of dealing with non-normal distributions&#46;</p><span id="sec0005" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0005">Normality analysis</span><p id="par0020" class="elsevierStylePara elsevierViewall">When studying the normality of the data&#44; it is convenient to follow a multiple approach in which we evaluate the data using the different tools available&#46; There are specific statistical tests to check if the data follow a normal distribution&#46; The best-known tests are the Shapiro&#8211;Wilk test and the Kolmogorov&#8211;Smirnov test&#46; However&#44; these tests are very sensitive to the sample size&#44; and it is not convenient to rely solely on them to make a decision&#46; However&#44; there are a series of simple graphs that we can represent and that can help us decide if the data follows a normal distribution&#46; These graphs are the histograms&#44; the <span class="elsevierStyleItalic">box plot</span>&#44; and the Q-Q plots&#46;</p></span><span id="sec0010" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0010">Graphs</span><p id="par0025" class="elsevierStylePara elsevierViewall">To illustrate how to interpret these graphs&#44; we will take a series of hypothetical data summarized in <a class="elsevierStyleCrossRef" href="#tbl0005">Table 1</a>&#46; This table shows the weight and daily consumption of cigarettes of a hypothetical series of 20 subjects&#46; If we look at the table&#44; we can see that&#44; in the row of cigarette consumption&#44; there are a large number of people &#40;specifically 7 of 20&#41; who are not smokers&#46; This is usually common in surveys on alcohol and tobacco consumption&#44; where there is a high percentage of the population that are not smokers or consume alcohol&#46;</p><elsevierMultimedia ident="tbl0005"></elsevierMultimedia><p id="par0030" class="elsevierStylePara elsevierViewall">The first graphs represented in <a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a> are the histograms for both variables &#40;<a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>A and B for cigarette consumption and weight&#44; respectively&#41;&#46; A histogram represents the frequency with which a certain value of the variable appears versus the values of that variable&#46; Thus&#44; for the first case&#44; the X axis shows the number of cigarettes per day and the Y axis shows the frequency with which that value of cigarettes per day appears in our sample&#46; In the second case&#44; the X axis shows the weight of the participants and the Y axis shows the frequency with which these weights appear&#46; These histograms are very useful to clarify if the data of our variable of interest follows a normal distribution&#46; In the first case &#40;<a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>A&#41; a histogram appears with what is called &#8220;scewed right&#8221;&#46; This occurs when there is a high percentage of the data that have small values of the variable&#46; We could easily deduce that the data is not distributed according to a normal distribution&#46; However&#44; in the case of weight &#40;<a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>B&#41;&#44; the histogram is shaped like &#8220;bell-curve&#8221;&#44; so it seems that the data does follow a normal distribution&#46;</p><elsevierMultimedia ident="fig0005"></elsevierMultimedia><p id="par0035" class="elsevierStylePara elsevierViewall">Then&#44; in <a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>C and D&#44; the <span class="elsevierStyleItalic">box-plot</span> &#40;box and whisker plot&#41; is represented&#46; This is a particularly useful graph&#44; not only to evaluate the distribution of the data but also as a summary of them&#46; This diagram consists of the following parts&#58; a horizontal line with the rectangle &#40;or box&#41;&#44; which represents the median of the 50th percentile&#46; It should be remembered that the median is the value of the data that leaves the bottom 50&#37; of the values below it and the top 50&#37; above it&#46; The 25th percentile is the below the box&#46; That is&#44; the value that leaves 25&#37; of the smallest data below and the remaining 75&#37; above&#46; Therefore&#44; the top of the box is the 75th percentile&#46; Finally&#44; 2 segments &#40;or &#8220;whiskers&#8221;&#41; join&#46; In one case&#44; the 75th percentile with the highest value and&#44; in the other case&#44; the 25th percentile with the lowest value&#46; These graphs are very useful because&#44; with a quick look&#44; we can know the maximum and minimum values of the sample&#44; the value of the median and what are the 25th and 75th percentiles&#46; In addition&#44; in the case at hand&#44; they can also help to clarify whether the data follows an approximate normal distribution&#46; When the <span class="elsevierStyleItalic">box-plot</span> has quite a lot of symmetry&#44; it indicates that the data is distributed normally&#46; In the case of cigarette smoking &#40;<a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>C&#41;&#44; the <span class="elsevierStyleItalic">box-plot</span> is clearly not symmetrical&#44; since the lowest point and the 25th percentile coincide&#46; However&#44; for the weight variable &#40;<a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>D&#41; the <span class="elsevierStyleItalic">box-plot</span> is quite symmetrical&#44; which is further proof that the data can be considered normally distributed&#46;</p><p id="par0040" class="elsevierStylePara elsevierViewall">The last type of graph that we can analyse when evaluating the normality of the data is the quantile-quantile graphs&#44; better known as Q-Q plots&#46; These graphs can be generated with most statistical packages &#40;SPSS&#44; R or Stata&#44; etc&#46;&#41;&#46; If the points on the graph are located on the theoretical line&#44; the distribution can be considered as normal&#46; Obviously&#44; it cannot be expected that all the points are exactly on the line&#44; but it is easy to see whether the deviation from normality is great or not&#46; For example&#44; in the case of the consumption of cigarettes &#40;<a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>E&#41; it can be deduced that the points are very far from being uniformly on the line&#44; while in the case of weight &#40;<a class="elsevierStyleCrossRef" href="#fig0005">Fig&#46; 1</a>F&#41; the points are quite close to the line&#46;</p><p id="par0045" class="elsevierStylePara elsevierViewall">Thus&#44; these 3 graphs allow us to easily conclude that&#44; in our hypothetical data set&#44; cigarette consumption does not meet the requirements to be considered a normally distributed variable&#44; but weight does&#46;</p></span><span id="sec0015" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0015">Specific statistical tests</span><p id="par0050" class="elsevierStylePara elsevierViewall">Although in the vast majority of cases&#44; these 3 graphs can be considered as conclusive&#44; many authors prefer to use specific statistical tests to analyse the normality of the data&#46; These tests are called Shapiro&#8211;Wilk and Kolmogorov&#8211;Smirnov tests&#46; In both cases&#44; the null hypothesis is that the results follow a normal distribution&#46; Thus&#44; assuming the classic 95&#37; confidence level&#44; if p&#8239;&#60;&#8239;0&#46;05&#44; the null hypothesis is rejected&#44; and it is concluded that the distribution is not normal&#46; However&#44; these tests should be complementary to the graphs described above&#44; especially since they are very sensitive to the sample size&#46; If the sample size is small&#44; we can obtain a p&#8239;&#62;&#8239;0&#46;05 and we would conclude that the distribution is normal&#44; when the reality is that the distribution is far from normal&#46; On the other hand&#44; very large sample sizes favour the statistical test being significant &#40;p&#8239;&#60;&#8239;0&#46;05&#41; even for small deviations from normal&#44; and we could erroneously conclude that the distribution is not normal&#44; when in fact it could be considered as such&#46; Therefore&#44; these tests must be used with great discretion&#44; and the aim should be to use them as complementary tests to the normality graphs&#44; which offer more and better information&#46; By applying the Shapiro&#8211;Wilk test to our set of hypothetical data we see that&#44; for weight&#44; p&#8239;&#61;&#8239;0&#46;84 and for the consumption of cigarettes p&#8239;&#61;&#8239;0&#46;004&#46; Thus&#44; again&#44; in this first case we would retain the null hypothesis normality data&#44; while in the case of the cigarette consumption variable we would discard the null hypothesis and conclude that the data is not distributed normally&#46;</p></span><span id="sec0020" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0020">Description of the data</span><p id="par0055" class="elsevierStylePara elsevierViewall">Once we have seen how to evaluate the normality of the data&#44; we must consider how to report that data in an article or communication&#44; and what types of statistical tests to apply in each case&#46; When the data follow a normal distribution&#44; the most common occurrence is to report the mean as a measure of central tendency of said data&#44; and the standard deviation &#40;or standard error in some cases&#41; as a measure of dispersion&#46; On the other hand&#44; the confidence intervals of the mean can be reported&#44; generally at 95&#37;&#46; For example&#44; in the case of our hypothetical weight variable&#44; the mean &#40;standard deviation&#41; is 70 &#40;4&#41; kg&#44; and the 95&#37; confidence interval for the average is &#40;68&#8211;72&#41;&#46;</p><p id="par0060" class="elsevierStylePara elsevierViewall">On the other hand&#44; in the case of cigarette consumption&#44; the mean would not be a good measure of central tendency&#44; since the distribution is far from normal&#46; Thus&#44; the alternative is to use measures of central tendency that do not assume any distribution of the data&#46; Without a doubt&#44; the most used is the median&#46; As a measure of dispersion&#44; the interquartile path is generally used &#40;which is the difference between the 25th and 75th percentiles&#41;&#44; although the percentiles or the range &#40;minimum and maximum values&#41; can also be reported&#46; In our hypothetical data set&#44; the median cigarette consumption is 5&#46; The 25th and 75th percentiles are&#44; respectively&#44; 0 and 11 cigarettes&#44; so the interquartile range is 11&#46; The range is 0&#8211;30&#46;</p></span><span id="sec0025" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0025">Data analysis</span><p id="par0065" class="elsevierStylePara elsevierViewall">When analysing data&#44; it is important to keep in mind that there is nothing inherently wrong in the fact that the data does not follow a normal distribution&#46; There are simply variables that are not distributed according to this model&#46; Luckily&#44; we have tools so that the data ends up well expressed and summarised in both cases&#46; In addition&#44; it should be borne in mind that&#44; whenever possible&#44; the mean is usually used&#46; But this does not mean that using the median in the case of normal distributions is incorrect&#59; the median can always be used&#44; since it does not presuppose a specific distribution of the data&#46; However&#44; there is a clear consensus among statisticians that&#44; whenever possible&#44; it is better to use the mean as a measure of central tendency and the so-called parametric tests for hypothesis contrasts&#46;</p><p id="par0070" class="elsevierStylePara elsevierViewall">Once again&#44; the statistical tests will depend on the distribution of the data&#46;<a class="elsevierStyleCrossRef" href="#bib0005"><span class="elsevierStyleSup">1</span></a> This article aims to be an introduction to the study of the normality of the data&#44; so not all statistical tests will be explained in detail&#46; However&#44; it is important to have an overview&#44; to know when a certain statistical test can be applied and to take into account the assumptions to be analysed&#46; To illustrate&#44; I will focus on the tests to compare a quantitative variable between 2 or more groups&#46;</p><p id="par0075" class="elsevierStylePara elsevierViewall">The so-called &#8220;parametric&#8221; alternatives estimate a parameter of a given distribution&#44; so it is assumed that the dependent variable of interest follows that distribution &#40;in our case&#44; the normal distribution&#41;&#46; Thus&#44; before proceeding to apply this type of statistical test&#44; we must check the normality of the data&#46; This check is only critical when we have small sample sizes&#44; as explained below&#46; For example&#44; when we want to compare the means between 2 or more independent groups&#44; we would use the Student&#8217;s t-test or the one-way analysis of variance &#40;one-way ANOVA&#41;&#44; respectively&#46; However&#44; when we have small sample sizes and the data does not follow a normal distribution&#44; non-parametric methods can be used&#46; Specifically&#44; in this case&#44; we would be talking about the Mann&#8211;Whitney U test &#40;sometimes known as &#8220;Wilcoxon Rank-Sum test&#8221;&#41; or the Kruskal&#8211;Wallis test&#44; which would be the non-parametric alternatives to the Student&#39;s t test and the one-way ANOVA&#44; respectively&#46; The primary difference is that the non-parametric tests do not assume any type of data distribution to estimate a specific parameter and&#44; therefore&#44; they can be used for any data set&#46;</p><p id="par0080" class="elsevierStylePara elsevierViewall">Although it is true that non-parametric tests are relatively known and used in medical literature&#44; some authors advise against their use&#44; while others use them for any type of analysis&#46; In the opinion of the author&#44; non-parametric tests are useful in some cases&#44; but parametric tests are normally preferable&#44; provided that due assumptions are met&#44; since they provide confidence intervals in addition to a p-value&#44; and they can be generalised to be used in more complex statistical analyses&#46;</p></span><span id="sec0030" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0030">Alternatives to non-parametric tests</span><p id="par0085" class="elsevierStylePara elsevierViewall">One of the alternatives that we can use when the distribution of the data is not normal&#44; and when we do not want to resort to non-parametric tests&#44; is to perform a data transformation&#46;<a class="elsevierStyleCrossRef" href="#bib0010"><span class="elsevierStyleSup">2</span></a> In many cases&#44; if we perform a mathematical operation on the data &#40;for example&#44; a decimal logarithm or a square root&#41;&#44; the transformed data does follow a normal distribution and&#44; therefore&#44; we could use parametric tests&#46; Although some authors have defended its use&#44; the truth is that its use is not widespread in medical literature&#46; The reason is that the statistics must be carried out on the transformed data&#46; Therefore&#44; the reported confidence intervals will also be based on the transformed data and their interpretation may result in errors or be somewhat complex&#46;</p><p id="par0090" class="elsevierStylePara elsevierViewall">Throughout this article I have repeated several times that the assumption of normality in parametric tests is only essential when the sample size is small&#46; Although there is no established cut-off point&#44; there is a fairly broad consensus that&#44; when sample sizes are greater than 80&#8211;100&#44; the premise of normal distribution loses importance&#44; in a way&#44; when choosing between a parametric test or a non-parametric one&#46;<a class="elsevierStyleCrossRef" href="#bib0015"><span class="elsevierStyleSup">3</span></a> This is because of the so-called central limit theorem&#46;<a class="elsevierStyleCrossRef" href="#bib0020"><span class="elsevierStyleSup">4</span></a> Without going into detail&#44; this theorem establishes that&#44; although the distribution of the data is not normal&#44; the distribution of the means is normal&#46; This theorem allows parametric tests to be applied when the sample size is high&#44; even when the variable of interest is not distributed normally&#46;</p></span><span id="sec0035" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0035">Conclusion</span><p id="par0095" class="elsevierStylePara elsevierViewall">When reporting a measure of central tendency for a certain quantitative variable or when choosing a certain statistical test&#44; in many cases it is important to examine the normality of the data&#46; For this&#44; we have different tools&#44; such as graphs and statistical tests&#44; which can be very useful for this purpose&#46; The contrasting statistical hypothesis testing for normal distribution should be interpreted with caution&#44; and always as a complementary test to the graphic description of the data&#46;</p></span><span id="sec0040" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0040">Financing</span><p id="par0100" class="elsevierStylePara elsevierViewall">The author confirms that there has been no financial support for the preparation of this article&#46;</p></span><span id="sec0045" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0045">Conflict of interests</span><p id="par0105" class="elsevierStylePara elsevierViewall">The author confirms that there is no conflict of interests&#46;</p></span><span id="sec0050" class="elsevierStyleSection elsevierViewall"><span class="elsevierStyleSectionTitle" id="sect0050">Thanks</span><p id="par0110" class="elsevierStylePara elsevierViewall">The author thanks the Alfonso Mart&#237;n Escudero Foundation for the financing of the postdoctoral fellowship he currently enjoys&#46;</p></span></span>"
    "textoCompletoSecciones" => array:1 [
      "secciones" => array:11 [
        0 => array:2 [
          "identificador" => "sec0005"
          "titulo" => "Normality analysis"
        ]
        1 => array:2 [
          "identificador" => "sec0010"
          "titulo" => "Graphs"
        ]
        2 => array:2 [
          "identificador" => "sec0015"
          "titulo" => "Specific statistical tests"
        ]
        3 => array:2 [
          "identificador" => "sec0020"
          "titulo" => "Description of the data"
        ]
        4 => array:2 [
          "identificador" => "sec0025"
          "titulo" => "Data analysis"
        ]
        5 => array:2 [
          "identificador" => "sec0030"
          "titulo" => "Alternatives to non-parametric tests"
        ]
        6 => array:2 [
          "identificador" => "sec0035"
          "titulo" => "Conclusion"
        ]
        7 => array:2 [
          "identificador" => "sec0040"
          "titulo" => "Financing"
        ]
        8 => array:2 [
          "identificador" => "sec0045"
          "titulo" => "Conflict of interests"
        ]
        9 => array:2 [
          "identificador" => "sec0050"
          "titulo" => "Thanks"
        ]
        10 => array:1 [
          "titulo" => "References"
        ]
      ]
    ]
    "pdfFichero" => "main.pdf"
    "tienePdf" => true
    "fechaRecibido" => "2019-04-29"
    "fechaAceptado" => "2019-05-09"
    "NotaPie" => array:1 [
      0 => array:2 [
        "etiqueta" => "&#9734;"
        "nota" => "<p class="elsevierStyleNotepara" id="npar0005">Please cite this article as&#58; Rodriguez A&#46; Conoce tus datos&#58; evaluaci&#243;n de la normalidad de variables continuas y estrategias para tratar con distribuciones no normales&#46; Med Clin &#40;Barc&#41;&#46; 2020&#59;154&#58;142&#8211;145&#46;</p>"
      ]
    ]
    "multimedia" => array:2 [
      0 => array:8 [
        "identificador" => "fig0005"
        "etiqueta" => "Fig&#46; 1"
        "tipo" => "MULTIMEDIAFIGURA"
        "mostrarFloat" => true
        "mostrarDisplay" => false
        "figura" => array:1 [
          0 => array:4 [
            "imagen" => "gr1.jpeg"
            "Alto" => 3552
            "Ancho" => 2507
            "Tamanyo" => 284067
          ]
        ]
        "detalles" => array:1 [
          0 => array:3 [
            "identificador" => "at0005"
            "detalle" => "Fig&#46; "
            "rol" => "short"
          ]
        ]
        "descripcion" => array:1 [
          "en" => "<p id="spar0005" class="elsevierStyleSimplePara elsevierViewall">Graphs to demonstrate the normality of the data&#58; histograms &#40;A and B&#41;&#44; box plots &#40;C and D&#41; and Q-Q plots &#40;E and F&#41; for the variables &#8216;number of cigarettes&#8217; and &#8216;weight&#8217;&#46;</p>"
        ]
      ]
      1 => array:8 [
        "identificador" => "tbl0005"
        "etiqueta" => "Table 1"
        "tipo" => "MULTIMEDIATABLA"
        "mostrarFloat" => true
        "mostrarDisplay" => false
        "detalles" => array:1 [
          0 => array:3 [
            "identificador" => "at0010"
            "detalle" => "Table "
            "rol" => "short"
          ]
        ]
        "tabla" => array:1 [
          "tablatextoimagen" => array:1 [
            0 => array:2 [
              "tabla" => array:1 [
                0 => """
                  <table border="0" frame="\n
                  \t\t\t\t\tvoid\n
                  \t\t\t\t" class=""><thead title="thead"><tr title="table-row"><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">Subject&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">1&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">2&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">3&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">4&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">5&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">6&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">7&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">8&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">9&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">10&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">11&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">12&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">13&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">14&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">15&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">16&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">17&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">18&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">19&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th><th class="td" title="\n
                  \t\t\t\t\ttable-head\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t" scope="col">20&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t\t\t</th></tr></thead><tbody title="tbody"><tr title="table-row"><td class="td-with-role" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t ; entry_with_role_rowhead " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">Cigarettes&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">0&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">0&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">10&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">15&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">0&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">5&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">0&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">30&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">0&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">3&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">10&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">0&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">8&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">0&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">5&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">10&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">20&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">3&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">18&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">25&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td></tr><tr title="table-row"><td class="td-with-role" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t ; entry_with_role_rowhead " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">Weight &#40;kg&#41;&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">61&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">72&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">65&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">73&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">69&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">69&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">70&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">70&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">78&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">71&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">77&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">70&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">75&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">75&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">69&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">66&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">67&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">68&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">62&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td><td class="td" title="\n
                  \t\t\t\t\ttable-entry\n
                  \t\t\t\t  " align="left" valign="\n
                  \t\t\t\t\ttop\n
                  \t\t\t\t">68&nbsp;\t\t\t\t\t\t\n
                  \t\t\t\t</td></tr></tbody></table>
                  """
              ]
              "imagenFichero" => array:1 [
                0 => "xTab2245935.png"
              ]
            ]
          ]
        ]
        "descripcion" => array:1 [
          "en" => "<p id="spar0010" class="elsevierStyleSimplePara elsevierViewall">Daily cigarette consumption and weight &#40;kg&#41; in a hypothetical series of 20 subjects&#46;</p>"
        ]
      ]
    ]
    "bibliografia" => array:2 [
      "titulo" => "References"
      "seccion" => array:1 [
        0 => array:2 [
          "identificador" => "bibs0005"
          "bibliografiaReferencia" => array:4 [
            0 => array:3 [
              "identificador" => "bib0005"
              "etiqueta" => "1"
              "referencia" => array:1 [
                0 => array:2 [
                  "contribucion" => array:1 [
                    0 => array:2 [
                      "titulo" => "Parametric vs non-parametric methods for data analysis"
                      "autores" => array:1 [
                        0 => array:2 [
                          "etal" => false
                          "autores" => array:2 [
                            0 => "D&#46;G&#46; Altman"
                            1 => "J&#46;M&#46; Bland"
                          ]
                        ]
                      ]
                    ]
                  ]
                  "host" => array:1 [
                    0 => array:2 [
                      "doi" => "10.1136/bmj.a3167"
                      "Revista" => array:5 [
                        "tituloSerie" => "BMJ"
                        "fecha" => "2009"
                        "volumen" => "338"
                        "paginaInicial" => "a3167"
                        "link" => array:1 [
                          0 => array:2 [
                            "url" => "https://www.ncbi.nlm.nih.gov/pubmed/19342403"
                            "web" => "Medline"
                          ]
                        ]
                      ]
                    ]
                  ]
                ]
              ]
            ]
            1 => array:3 [
              "identificador" => "bib0010"
              "etiqueta" => "2"
              "referencia" => array:1 [
                0 => array:2 [
                  "contribucion" => array:1 [
                    0 => array:2 [
                      "titulo" => "Log transformation&#58; application and interpretation in biomedical research"
                      "autores" => array:1 [
                        0 => array:2 [
                          "etal" => false
                          "autores" => array:4 [
                            0 => "C&#46; Feng"
                            1 => "H&#46; Wang"
                            2 => "N&#46; Lu"
                            3 => "X&#46;M&#46; Tu"
                          ]
                        ]
                      ]
                    ]
                  ]
                  "host" => array:1 [
                    0 => array:2 [
                      "doi" => "10.1002/sim.5486"
                      "Revista" => array:6 [
                        "tituloSerie" => "Stat Med"
                        "fecha" => "2013"
                        "volumen" => "32"
                        "paginaInicial" => "230"
                        "paginaFinal" => "239"
                        "link" => array:1 [
                          0 => array:2 [
                            "url" => "https://www.ncbi.nlm.nih.gov/pubmed/22806695"
                            "web" => "Medline"
                          ]
                        ]
                      ]
                    ]
                  ]
                ]
              ]
            ]
            2 => array:3 [
              "identificador" => "bib0015"
              "etiqueta" => "3"
              "referencia" => array:1 [
                0 => array:2 [
                  "contribucion" => array:1 [
                    0 => array:2 [
                      "titulo" => "Dealing with non-normal data"
                      "autores" => array:1 [
                        0 => array:2 [
                          "etal" => false
                          "autores" => array:1 [
                            0 => "K&#46;L&#46; Sainani"
                          ]
                        ]
                      ]
                    ]
                  ]
                  "host" => array:1 [
                    0 => array:2 [
                      "doi" => "10.1016/j.pmrj.2012.10.013"
                      "Revista" => array:6 [
                        "tituloSerie" => "PM R"
                        "fecha" => "2012"
                        "volumen" => "4"
                        "paginaInicial" => "1001"
                        "paginaFinal" => "1005"
                        "link" => array:1 [
                          0 => array:2 [
                            "url" => "https://www.ncbi.nlm.nih.gov/pubmed/23245662"
                            "web" => "Medline"
                          ]
                        ]
                      ]
                    ]
                  ]
                ]
              ]
            ]
            3 => array:3 [
              "identificador" => "bib0020"
              "etiqueta" => "4"
              "referencia" => array:1 [
                0 => array:2 [
                  "contribucion" => array:1 [
                    0 => array:2 [
                      "titulo" => "Central limit theorem&#58; the cornerstone of modern statistics"
                      "autores" => array:1 [
                        0 => array:2 [
                          "etal" => false
                          "autores" => array:2 [
                            0 => "S&#46;G&#46; Kwak"
                            1 => "J&#46;H&#46; Kim"
                          ]
                        ]
                      ]
                    ]
                  ]
                  "host" => array:1 [
                    0 => array:2 [
                      "doi" => "10.4097/kjae.2017.70.2.144"
                      "Revista" => array:6 [
                        "tituloSerie" => "Korean J Anesthesiol"
                        "fecha" => "2017"
                        "volumen" => "70"
                        "paginaInicial" => "144"
                        "paginaFinal" => "156"
                        "link" => array:1 [
                          0 => array:2 [
                            "url" => "https://www.ncbi.nlm.nih.gov/pubmed/28367284"
                            "web" => "Medline"
                          ]
                        ]
                      ]
                    ]
                  ]
                ]
              ]
            ]
          ]
        ]
      ]
    ]
  ]
  "idiomaDefecto" => "en"
  "url" => "/23870206/0000015400000004/v1_202002201732/S2387020619305650/v1_202002201732/en/main.assets"
  "Apartado" => array:4 [
    "identificador" => "44145"
    "tipo" => "SECCION"
    "en" => array:2 [
      "titulo" => "Special article"
      "idiomaDefecto" => true
    ]
    "idiomaDefecto" => "en"
  ]
  "PDF" => "https://static.elsevier.es/multimedia/23870206/0000015400000004/v1_202002201732/S2387020619305650/v1_202002201732/en/main.pdf?idApp=UINPBA00004N&text.app=https://www.elsevier.es/"
  "EPUB" => "https://multimedia.elsevier.es/PublicationsMultimediaV1/item/epub/S2387020619305650?idApp=UINPBA00004N"
]
Indexed in:

Follow us:

Subscribe:

Article

Indexed in:

Follow us:

Subscribe:

Article

Subscribe to our newsletter
