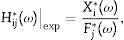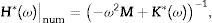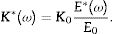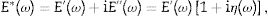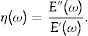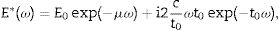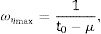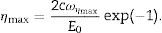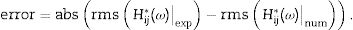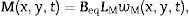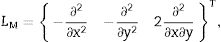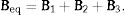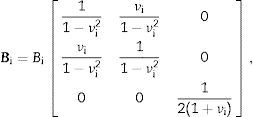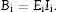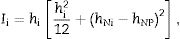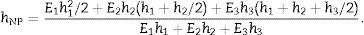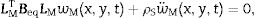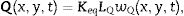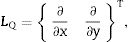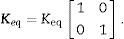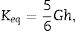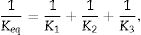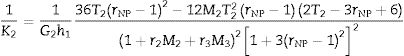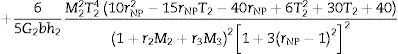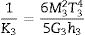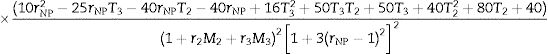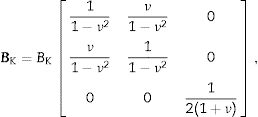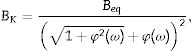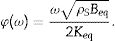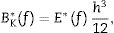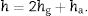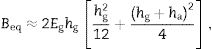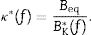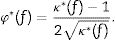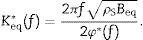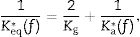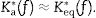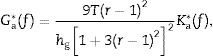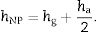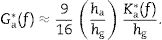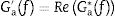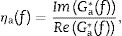Characterization of the dynamic properties of an automotive laminated glass ceiling

Abstract

This article presents a methodology for the characterization of the dynamic properties of a laminated glass automotive ceiling, motivated by the inherent difficulty in obtaining laboratory samples from this kind of components. This methodology is based on the identification of the effective complex modulus of the laminated glass ceiling through Experimental Modal Analysis in conjunction with a finite element model. Besides, a material behaviour model is proposed for the effective complex module. Then, the dynamic properties of the laminated glass core are extracted from the latter using a reverse homogenized formulation of sandwich plates specifically developed in this work. As a result, a methodology to accurately predict the dynamic behaviour of these key automotive components has been achieved. An additional advantage of this methodology is that the identification of properties is carried out from a manufactured component and not from samples of reduced geometries, considering the impact of the manufacturing process.

Resumen

Este artículo presenta una metodología para la caracterización de las propiedades dinámicas de un techo de vidrio laminado de automoción, metodología motivada por la dificultad inherente de obtener muestras de laboratorio de este tipo de componentes. Esta metodología se basa en la identificación del módulo complejo efectivo del techo de vidrio laminado mediante análisis modal experimental y mediante un modelo de elementos finitos. Además, se propone un modelo de comportamiento del material para el módulo complejo efectivo. A continuación, las propiedades dinámicas del núcleo de vidrio laminado se extraen de este último utilizando una formulación homogeneizada inversa de placas sándwich específicamente desarrollada en este trabajo. Como resultado, se ha conseguido una metodología para predecir con precisión el comportamiento dinámico de estos componentes clave de la automoción. Una ventaja adicional de esta metodología es que la identificación de propiedades se realiza a partir de un componente fabricado y no a partir de muestras de geometrías reducidas, considerando el impacto del proceso de fabricación.

Introduction

Ride comfort is a critical factor to evaluate the vehicle performance and has been an interesting topic for researchers working on comfort, performance, and health. Human comfort can be understood as a measurement of the vibrational and sound pressure level experienced by the final user of the car as a result of the excitations in the system, especially those coming from the engine, aerodynamics and the road. These excitations are vibrations transmitted through the chassis of the vehicle resulting in the passengers and drivers experiencing discomfort. In consequence, automobile designers give great attention to the isolation of vibrations in the car in order to provide a comfortable ride for the passengers. Once the internal combustion engine, the major source of vibration in the vehicle, is eliminated, other sources of discomfort arises and the dynamic behaviour of different vehicle components affects vibroacoustic comfort perception, being therefore, particularly relevant for electric and autonomous vehicles where on the one hand light weighting is key and on the other hand, comfort has become the main indicator of the quality of the vehicle becoming top priority in purchasing decisions.

Concerning sound and vibration transmission in vehicles, three stakeholders are implied. These are: (i) primary sources, being the engine, the road, the aerodynamics and ancillary systems, those that impose motion and therefore those that generate sound and vibration; (ii) secondary sources, chassis structure and car body panels, those that get excited by primary sources becoming a new source of excitation; (iii) and finally, transmission paths, those that connect sources to receptor, i.e. the joints.

As wide glass solar roofs are a significant secondary source, this investigation is focused on the characterization of their dynamic material properties for further ride and comfort modelling. Besides, properties identification techniques on manufactured components rather than reduced geometries samples is preferred to account for complex manufacturing process impact and enabling simulations testing to take place much earlier in the development process at lower cost, meaning the vehicle is closer to production when the physical prototypes are produced. Hence, simulation techniques are an integral part of the vehicle development cycle as they provide a natural link between the phases of car design, from computer modelling to laboratory testing and, finally, to the test track. Therefore, it is essential to develop reliable vehicle components models that allow the validation of new developments and functionalities of components before the prototyping phase.

The mechanical behaviour of laminated glass is strongly affected by the polymeric interlayer placed between glass layers, and the property that defines its mechanical behaviour is the complex modulus E*(ω). A method to obtain the complex modulus E*(ω) of each material, the storage modulus E′(ω) and the loss modulus E″(ω), which can be obtained from the relaxation modulus E(t) is by using analytical interconversions from static tests [1]. Tensile or bending tests carried out in a dynamic mechanical thermal analyser DMTA equipment can be used to define the dynamic response of the interlayer material. Other methodology to determine the mechanical behaviour of laminated glass subjected to dynamic loads is using a monolithic model and a stress effective complex modulus [2]. The technique to predict the dynamic response of laminated glass elements using a linear elastic monolithic model is based on the relationship of constant thickness and effective complex modulus [3]. Once the linear elastic monolithic model with constant stiffness and mass per unit length is obtained, the natural frequencies and mass normalized mode shapes can be calculated.

In order to empirically characterize the dynamic properties of polymeric materials [4], and particularly their complex modulus, several methods considering free and forced vibrations with and without resonance can be used [5] depending on the desired frequency range [6]. The techniques used in these tests vary: rheological methods [7], Dynamic Mechanical Thermal Analysis DMTA [8] or the standard test method ASTM E 756-05 [9]. The ASTM E 756-05 is extensively applied to estimate the dynamic properties of a wide range of materials. It characterizes the material by means of constrained layer damping (CLD) specimens [10] where the core of the CLD [11] sandwich is subjected to shear stress, and its properties can be obtained by means of the well-known RKU model [12–14]. This is a well-known homogenization method where a model is built to identify the properties of the sandwich by means of an equivalent complex flexural stiffness as if it were a homogeneous beam. However, it was proved that the RKU method tends to rigidize the sandwich [15], that is, it models the structure stiffer than the actual one, specially at high frequencies or for thick beams. As a consequence, the value for storage modulus obtained with the ASTM E 756-05 standard is lower than the real one, and errors can be made specially if the identified properties are used in thick beams or plates. Cortés and Sarría [15] considered a quadratic shear model in a CLD beam to overcome this limitation. Therefore, this paper extends this model to sandwich plates to allow the identification of damping properties of viscoelastic sandwich cores complementing the standard ASTM E 756-05. Both the model proposed in this paper and that of Ref. [15] are built on the same basis of the mechanics of structural members in bending and shearing, but the latter can be applied only for thin beams according to the Euler–Bernoulli theory, while the presented in this extends to plates according to the Love–Kirchhoff theory.

In short, this research proposes a methodology for the identification and modelling of the dynamic properties of viscoelastic cores of automotive laminated glass ceilings based on the identification of the homogenized properties of the component which are further used to extract the viscoelastic core properties through a numerical formulation for multilayer plates.

The article is structured as follows:

• 1.

  First, the modal behaviour of the laminated glass roof is characterized via Experimental Modal Analysis (EMA).

• 2.

  Then, the homogenized dynamic properties are identified by a numerical procedure and a material model is proposed.

• 3.

  Third, a method to identify the dynamic mechanical properties of soft not self-supporting viscoelastic materials for multilayer plates is presented.

As a result, the proposed methodology allows to properly characterize the dynamic mechanical properties of automotive laminated glass components considering the impact of the manufacturing processes and over the real component so they can be considered in the comfort analysis during the design of the vehicle.

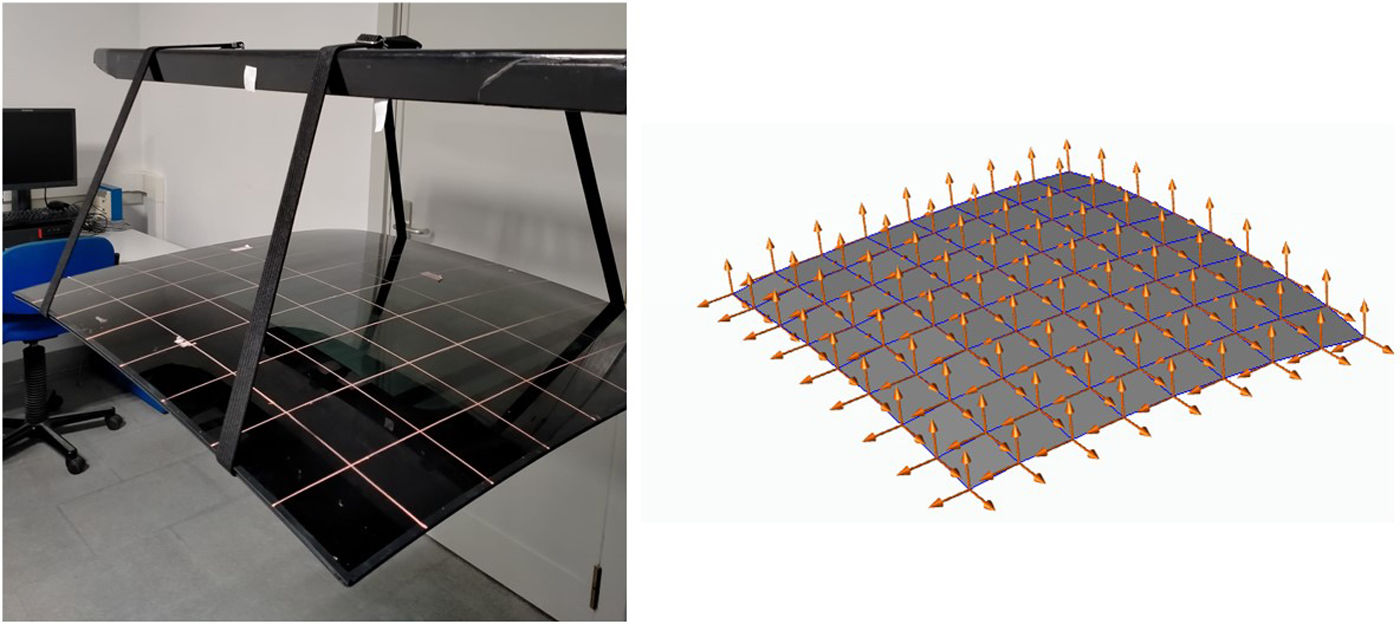
Experimental procedure

This section presents the experimental procedure to characterize the dynamic behaviour of the laminated glass ceiling by means of the frequency response functions (FRF) and modal properties where free-free conditions are considered as shown in Fig. 1. Concretely 81 measurements points uniformly distributed in a square grid are measured where excitation is imposed perpendicularly to the glass on a single point.

Fig. 1.

Experimental set-up: (a) laminated glass ceiling; (b) experimental model.

The laminated glass ceil shows an irregular curvature, and the top projection can be assumed to be a rectangle. The general geometrical properties are summarized in Table 1. The measured mass was 8.54 kg, thus the corresponding density is ρ=2702   kg m−3, and the surface density ρS=10.40   kg m−2. The laminated glass is manufactured by two sheets of tempered glass stuck with a sheet of PVB (polyvinyl butyral).

Table 1.

Laminated glass dimensions.

Length x (m)	Length y (m)	Thickness h (m)	Glass thickness hg (m)	Adhesive thickness ha (m)	Surface area (m^2)
0.923	0.8632	0.00385	0.001715	0.00042	0.8212

The experimental testing was performed at room temperature being the frequency range 0–80 Hz with a resolution of 0.25 Hz. The impact hammer used for exciting the system was an 8206-003 of Brüel and Kjaer (B&K) and the signals were acquired using a triaxial accelerometer 4535-B of the same manufacturer on a 4-ch input Module LAN XI also from B&K, where the exciting location was fixed while measuring location was mobile. The locations of the elastic supports were placed close to vibration nodes of the low order modal shapes that were previously estimated by numerical modelling in order to minimize the impact on non-rigid low order modes.

The excitation impact is on 1Z- (see Fig. 1) and five consecutive hits are measured to obtain each experimental FRF where exponential windows were used both on excitation and response time signals. Besides, as the glass is a curved surface, a Computer Aided Design (CAD) model has been used to extract each rotation matrix between the local coordinate system defined by each accelerometer and a global one (see Fig. 1) in which the 429 experimental FRF's are expressed before performing the modal extraction. This modal analysis has been performed using the Rational Fraction Polynomial – Z [16] where Complex Mode Indicator Function (CMIF) is used for pole selection. The transfer functions were computed as

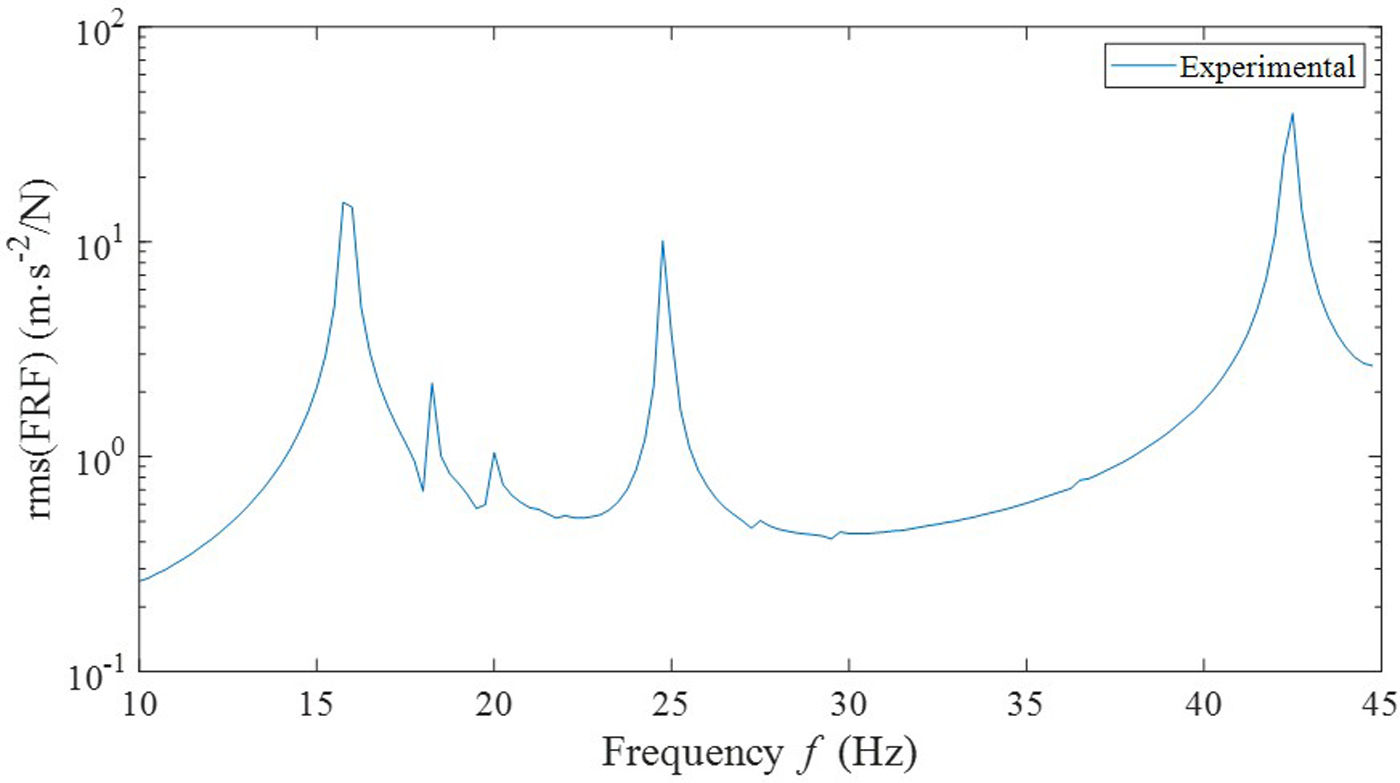
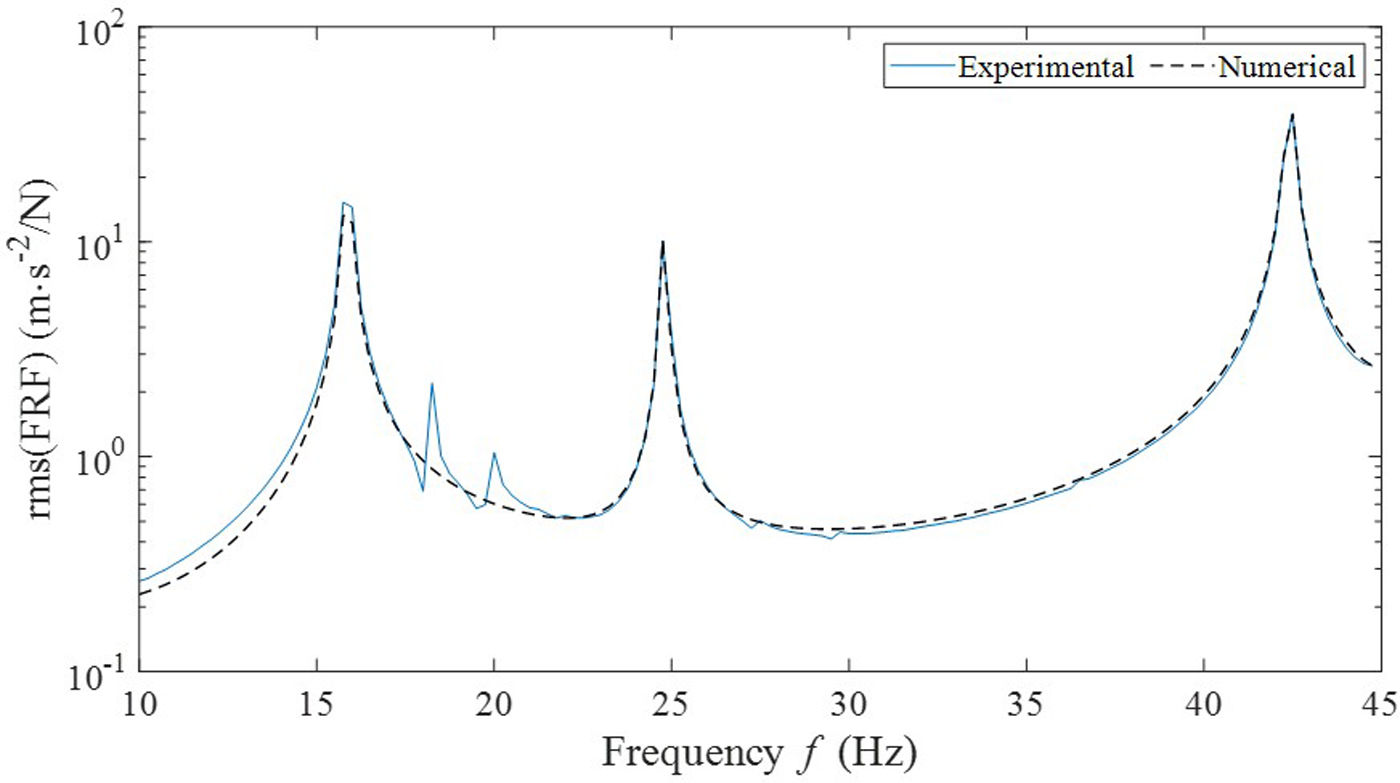
using the H1(ω) definition where Xi*(ω) represents the cross-spectrum between input fj(t) and output xj(t) and Fj(ω) the input auto-spectrum. Modal properties were computed from these transfer functions where 3 modes where found. Fig. 2 shows the Root Mean Square (RMS) of the transfer functions computed as

where N is the number of measured points and j=1 represents the excitation location. This RMS function is the employed in the next section to obtain the effective complex modulus of the laminated glass.

Fig. 2.

RMS of the experimental transfer functions.

For Fig. 2, it can be verified that three vibration modes are found on the analyzed range. Regarding the extra peaks at 18 and 20 Hz, they are two resonances from the support system exerting no influence on the glass vibration modes, as their amplitudes are negligible respect the magnitude of the three glass vibration modes.

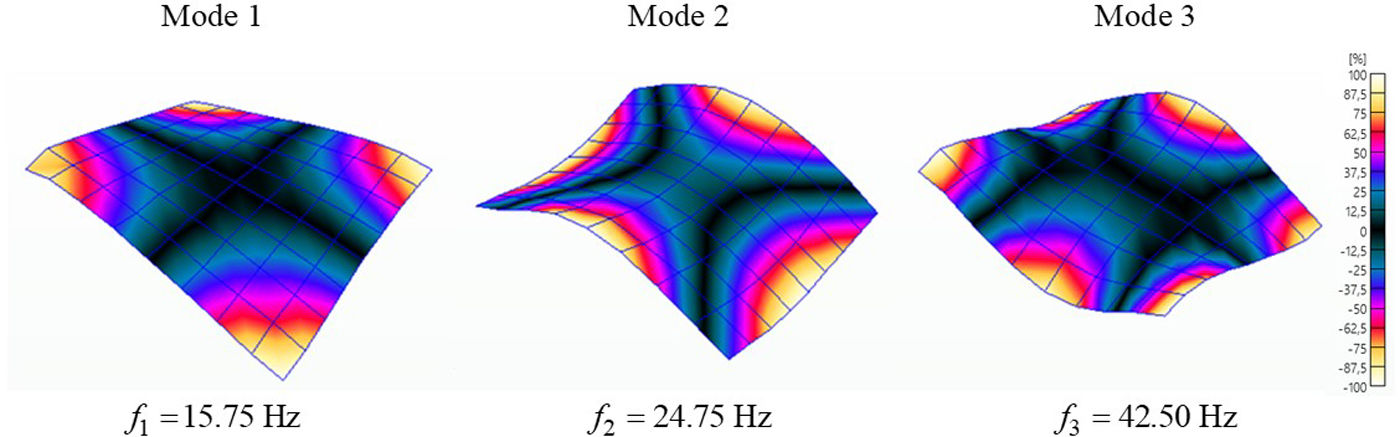
Accordingly, Fig. 3 shows the associated mode shapes and natural frequencies obtained by means of BK Connect commercial software.

Fig. 3.

Laminated glass mode shapes.

From Fig. 3, it can be verified that associated mode shapes for the laminated glass component are similar to those of a regular plate [17]. The obtained natural frequencies are an important reference for the methodology employed to obtain the effective complex modulus of the laminated glass, as described in the next section.

Laminated glass complex modulus identification

The homogenized or effective complex modulus of the laminated glass has been identified through an error minimization procedure between the experimentally obtained RMS transfer functions given by Eq. (2) and that numerically obtained by means of a finite element model with 2D 4 node iso-parametric shell elements, whose meshing is equivalent to the one of the experimental model represented in Fig. 1. The matrix of the transfer functions is given by

where M and K* represents the mass and complex stiffness matrices respectively, where

In this equation, K0 is the real stiffness matrix for ω=0, in which a constant modulus E₀ is considered, and the complex modulus E* is

where E′ represents the storage modulus, E″ the loss modulus and η the loss factor, defined as

For the complex modulus, a model adapted from [18] is proposed,

where E₀, μ, c and t₀ are parameters of the model. E₀ is the relaxed modulus, i.e., the value of the modulus for ω=0; t₀ and μ are the time-decay constants of the storage and loss moduli, respectively, which are related with the angular frequency at which the loss factor is maximum by

where t0>μ; and c is the viscous constant, which gives the maximum loss factor

These four parameters have to be obtained from the minimization of the error function given by

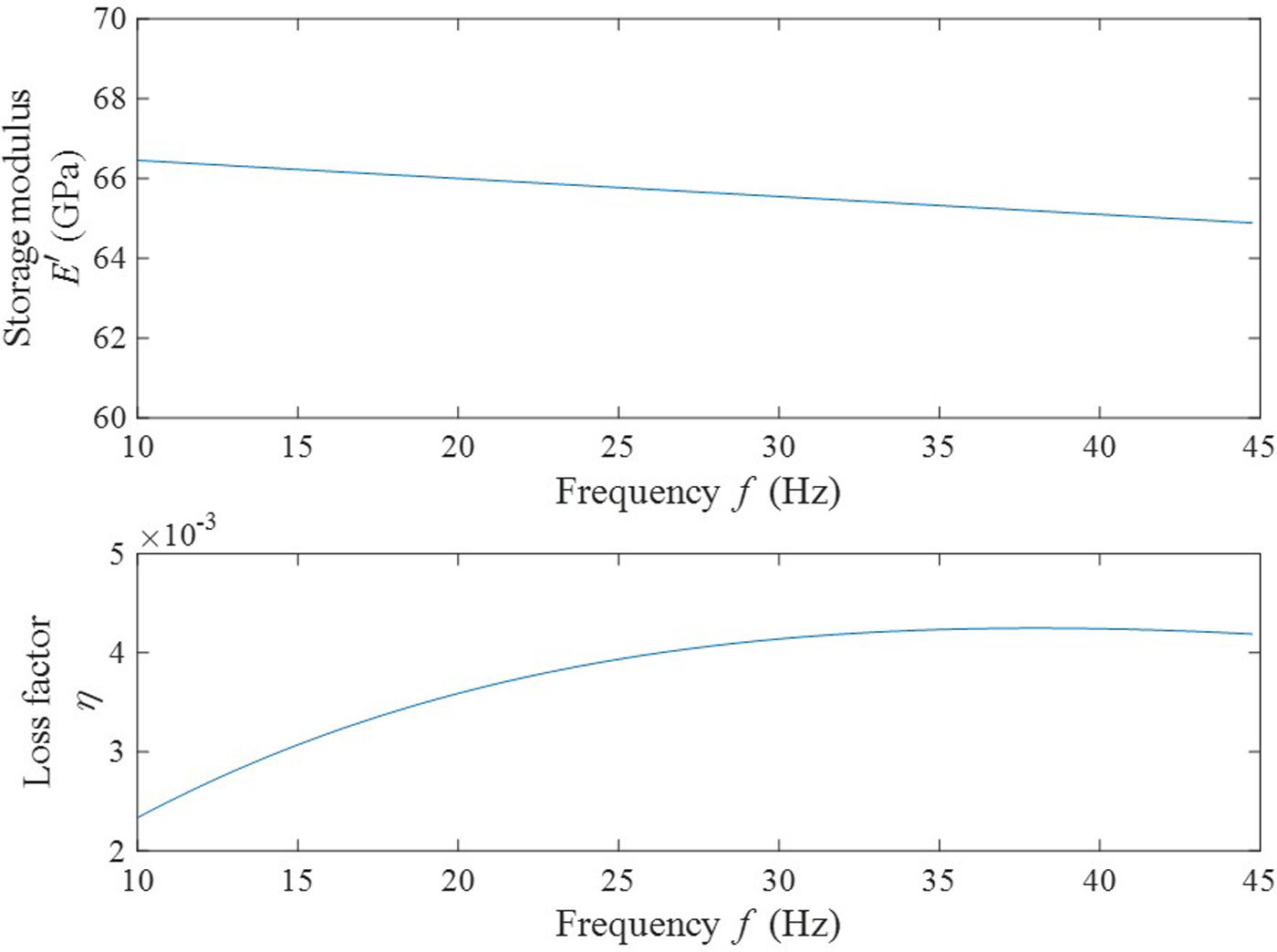
For the numerical RMS transfer function, only the first column of the matrix of the transfer functions is taken into account, i.e., j = 1, the same way as for the experimental case defined in Eq. (2). Table 2 shows the results of the model parameters obtained and Fig. 4 shows the storage modulus and the loss factor obtained from Eq. (7).

Table 2.

Model parameters.

E0(GPa)	μ10−3s	t010−3s	c106Pa s
67.45	0.686	4.295	1.617

Fig. 4.

Laminated glass complex modulus: (a) storage modulus, (b) loss factor.

From Fig. 4, it can be concluded that both storage modulus and loss factor of the laminated glass depends indeed on frequency where the former decreases as frequency increases. It can be noted that, on the one hand, the storage modulus of this laminated glass is between 65 and 67 GPa, while the Young modulus of the glass is 70 GPa [1,19–21]. On the other hand, the loss factor of the laminated glass is comprised between 2.5×10−3 and 4×10−3, while the one of the glass is between 1×10−5 and 2×10−4[21]. Therefore, the effect of the adhesive on the laminated glass is evident, significantly increasing the damping capacity of this vehicle component without hardly reducing the stiffness.

Fig. 5 compares the experimental and numerical RMS functions, wherefrom it can be verified the accuracy of the proposed procedure.

Fig. 5.

Experimental numerical correlation of the RMS of the transfer functions.

The resonance frequencies, peak amplitudes and modal damping obtained from these two curves are shown in Table 3.

Table 3.

Comparison between the experimental and numerical modal parameters.

	Frequency f (Hz)			Amplitude A (m)			Damping ratio ξ
	fexp	fnum	ε%	Aexp	Anum	ε%	ξexp	ξnum	ε%
Mode 1	15.75	15.75	0	15.26	13.32	12.7	0.0195	0.0196	0.61
Mode 2	24.75	24.75	0	10.11	10.22	1.01	0.0071	0.0068	4.32
Mode 3	42.50	42.50	0	39.63	39.42	0.60	0.0063	0.0064	2.11

As it can be verified from Table 3, the proposed methodology reaches an accuracy over 95% for frequency, amplitude and damping for every one of the three analyzed modes, but for the amplitude of the first one where the frequency resolution (Δf=0.25 Hz) is affecting the rms(Hij*(ω)num).

Adhesive core dynamic properties identification

The dynamic mechanical properties of non-self-supporting materials as the adhesive of the core of the laminated glass studied in this work can be obtained according to the ASTM E756-05 standard [9]. According to this standard, beam-like specimens have to be tested and the RKU method [13] is applied using the experimental frequency responses to obtain the shear complex modulus of the core material. Due to the inherent difficulty of producing beam like specimens from this laminated glass ceiling, in this work, a methodology to obtain the properties of the core material directly from the homogenized complex modulus is presented (see section “Laminated glass complex modulus identification”). Thus, the method proposed in [22] for sandwich beams, based on the homogenization method of Ref. [15] previously mentioned, is adapted to be applicable to sandwich plates. The basis of both models, that of [22] and the one presented in this section, are equivalent. Both models are formulated with the idea of including the shear effects in an equivalent flexural stiffness by means of the homogenization of beams and plates. The former was developed for thin beams with small width according to the Euler–Bernoulli theory, whereas the presented in this paper consist in an adaptation of the former without restrictions for the surface dimensions to apply the theory of Love–Kirchhoff.

Hence, next the bases of the homogenization method are presented and then, the method to extract the properties of the core material from those of the homogenized one.

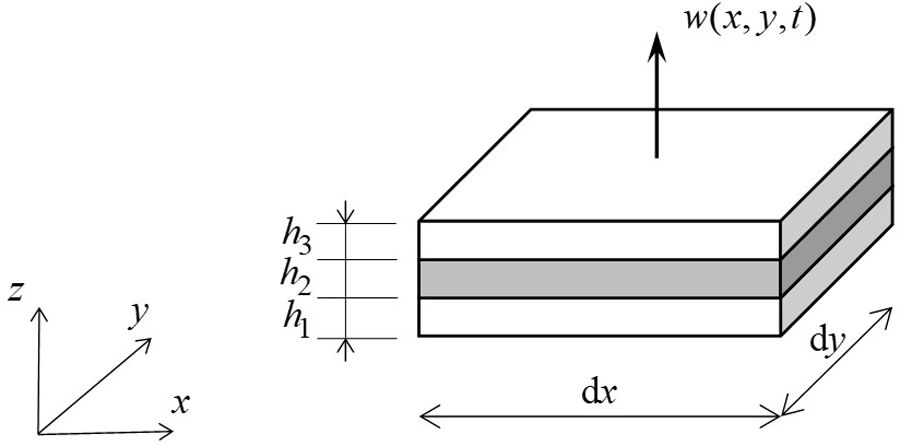
Homogenization of a three-layer sandwich plate

This section presents the adaptation for sandwich plates of the method proposed in Ref. [22]. The main idea is to obtain a homogenized or equivalent bending stiffness of a sandwich plate that considers the deformations due to bending moments and to shear forces also. In this way, this homogenized stiffness can replace the stiffness of the corresponding to the Love–Kirchhoff theory but considering deformations due to shear forces, instead of using a more complex formulation as the one of Reissner–Mindlin. For this aim, let us consider an infinitesimal cell of a three-layer sandwich plate in the x−y plane with dimensions dx×dy, as Fig. 6 shows.

Fig. 6.

Representation of an infinitesimal cell of a sandwich plate.

The transverse displacement w(x,y,t) of the neutral plane of the cell can be obtained by adding the term wM(x,y,t) due to the bending moments and the term wQ(x,y,t) derived by the shear forces,

On the one hand, regarding small deformation, the term wM(x,y,t) is related with the bending moment density vector M(x,y,t) by

where LM is the curvature operator given by

and the flexural stiffness matrix Beq of a three-layer plate is obtained from

In this last equation, Bi represents the flexural stiffness matrix of the ith layer of the sandwich, and it is given by

where νi is the Poisson ratio and

For the ith layer, E_i is the Young modulus and I_i is given by

where h_i is the thickness and h_Ni is the position of its middle plane with respect the lower surface of the plate. The position of the neutral plane of the plate becomes

Then, the transverse displacement due to bending could be solved from the Love–Kirchhoff equation,

where ρS is the mass per unit of surface area of the plate.

On the other hand, if shear deformations were considered, a more complex theory such as Reissner–Mindlin theory have to be considered. In this, the relationship between the shear force density vector Q(x,y,t) and the corresponding transverse displacement wQ(x,y,t) is given by an equivalent shear stiffness matrix Keq as

where LQ denotes the operator

and the shear stiffness matrix is given by

For the case of a plate made of a unique layer with shear modulus G and thickness h, Keq can be considered as

where the coefficient 5/6 is usually employed considering that the shear stress is not constant along thickness but parabolic [23]. In the case of a three-layer sandwich, the equivalent shear stiffness Keq depends on the thickness and on the properties of the materials, and may be decomposed as a function of the stiffness Ki of the ith layer as [15]

where

and

respectively, where M2=E2/E1, M3=E3/E1,T2=h2/h1, T3=h3/h1, rNP=2hNP/h1, r2=I2/I1, and r3=I3/I1. In that way, shear stress is considered parabolic in each layer, and it can be remarked that if the three materials had the same properties, Eq. (23) would be retrieved.

Finally, similarly as the static problems of symmetric laminated glass with thin polymeric core, the Poisson ratio of the laminated glass can be considered as the one of the glass, and the stiffness of the plate can be homogenized similarly as beams [24,25]. Then, the shear coefficient Keq form plates can be assimilated as the one of the given by Timoshenko's formula for beams, and the homogenized flexural stiffness matrix Beq of Eq. (19) can be transformed in the homogenized matrix BK given by

where the homogenized stiffness BK is given by

where

and the function φ(ω) considers the shear effects and being given by

Then, in the frequency domain, Eq. (19) becomes

where W(x,y,ω) is the frequency displacement amplitude due to bending and shear, because the homogenized matrix BK(ω) is built considering bending and shear. The advantage of this method is that using the equations of the Love–Kirchhoff theory, by means of this homogenized stiffness, shear deformations are taken into consideration without using complex theories such as the one of Reissner–Mindlin. Certainly, unlike the Love–Kirchhoff theory, the Reissner–Mindlin theory takes shear effects into account, it allows for large angular deformations of the plate and does not assume that the middle surface remains flat after deformation. As a consequence, it is more computationally complex, especially in numerical analysis, because a set of three equations in partial derivatives with three unknowns (the transverse displacement and the two rotations) must be solved. On the contrary, the Love–Kirchhoff theory ignores shear effects, meaning that the middle surface remains flat after deformation, and the motion of the plate is characterized by only the transverse displacement due to bending that is solved from by Eq. (19). But thanks to the method presented in this work, this equation is transformed into (32), and shear deformations can be taken into account in a simpler way than with the Reissner–Mindlin theory with good accuracy.

Identification of the complex modulus of the adhesive

In this section the dynamic properties of the laminated glass core are identified from the homogenized complex modulus measurements of section “Laminated glass complex modulus identification”, by means of the homogenization method of sandwich plates presented in the previous section. To identify the complex modulus of the adhesive core, this homogenization method must to be applied in the inverse sense, i.e. from the homogenized data to the individual properties of the layers. For that, first, the experimental complex stiffness BK*(f) is obtained as

from the results of homogenized complex modulus E*f of Fig. 4 (where ω=2πf), where h is the total thickness of the sandwich plate,

The values of the thickness of each layer are in Table 1. To compute the equivalent flexural bending Beq of Eq. (30), the one of the adhesive layer can be neglected regarding the one of the glass layers, then

where the modulus of the glass is assumed to be Eg=70   GPa[1,19–21].

The relationship between the bending and the experimental homogenized stiffness results

The modulus of this complex stiffness ratio |κ∗(f)|>1 for all f because shear makes the beam less rigid. From this relationship, it can be defined the function φ∗(f) that considers the frequency dependence of shear effects,

Next, the equivalent shear stiffness of Keq∗(f) can be calculated as

Once the equivalent shear stiffness Keq∗(f) is obtained, it can be related to the shear stiffness of each layer of the beam as

where K_g is the shear stiffness of one of the glass layers, according to K₁ or K₃ of Eqs. (25) and (27), and the unknown term Ka*(f) must be solved. If the shear stiffness of the glass layers is much larger than that of the adhesive one, then Ka*(f) could be directly solved from Eq. (39) as

Finally, the complex shear modulus of the adhesive material yields

where T=ha/hg, and r=2hNP/hg, in which hNP is the position of the neutral plane for a symmetric sandwich defined as

For the particular case of a very thin adhesive layer, Eq. (41) could be simplified as follows,

Finally, the shear storage modulus and the loss factor of the adhesive core of the laminated glass yield

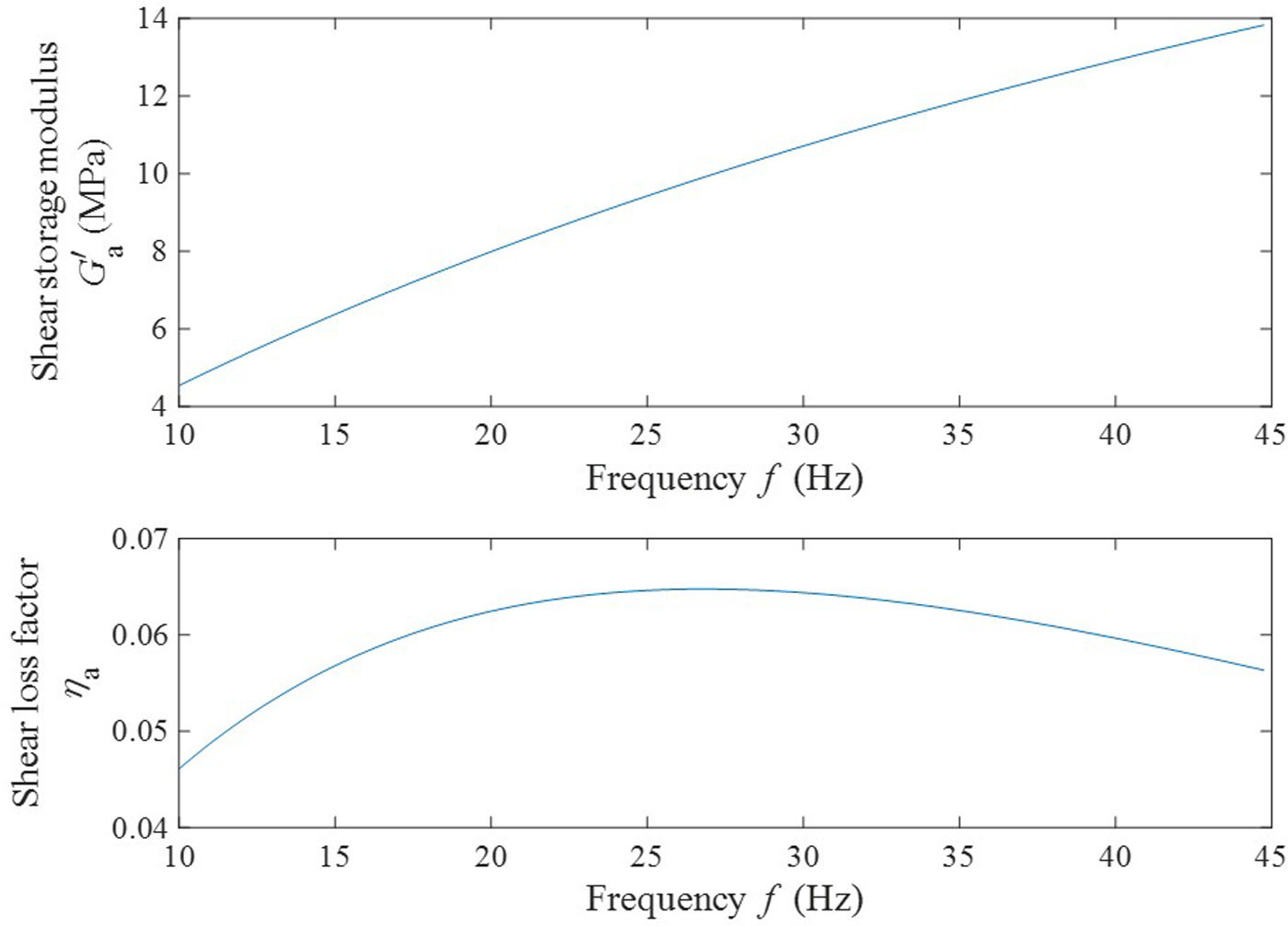
and

respectively. The obtained results are represented in Fig. 7. In this figure, it can be remarked that the shear storage modulus of the adhesive G′a increases from 4.5 MPa to 13.8 MPa in the studied frequency range. Regarding the loss factor ηa, this presents a maximum value of 0.065 at 26.75 Hz, and the values at the lower and higher frequencies are 0.046 and 0.056, respectively.

Fig. 7.

Shear complex modulus of the adhesive of the laminated plate: (a) shear storage modulus and (b) shear loss factor.

From the obtained results it can be drawn two observations. On the one hand, according to [26], the discomfort in vehicles due to rigid body oscillations on the suspensions, resonances of engine and unsprung masses are given below 25 Hz. This signifies that this adhesive is adequate for automotive applications to reduce vibration due to those effect. On the other hand, the resonance frequencies of the three first modes of the own glass ceiling shown in Table 3 are between 16 Hz and 43 Hz, frequency range at which the loss factor presents the highest values. As a consequence, it can be also concluded that this adhesive gives the maximum values at the frequency range adequate to mitigate the resonances of the glass ceiling.

Conclusions

In this paper, a methodology for the identification of the homogenized dynamic properties of automotive laminated glass ceilings has been presented and a dynamic material model has been proposed. These homogenized properties have been further used to extract the viscoelastic core properties through a numerical formulation for multilayer plates opening the door to the design of wide laminated glass roof ceiling from ride and comfort perspective.

• 1.

  The proposed methodology is capable to extract the homogenized dynamic properties of the laminated glass ceiling avoiding the need of simplified samples preparation and allowing to consider the actual effect of manufacturing processes into the dynamic behaviour of the real automotive component.

• 2.

  Once the homogenized dynamic properties are obtained and modelled, a method to identify the dynamic mechanical properties of soft not self-supporting viscoelastic materials for multilayer plates has been presented overcoming the limitations of the sample preparation derived from ASTM E 756-05.

As a result, the proposed methodology is able to precisely predict the dynamic behaviour of laminated glass ceilings in terms of amplitude, frequency and damping making it suitable for and ride and comfort analysis for the automotive sector.

Funding

This study received financial support from the Basque Government through the Research Group programIT1507-22 and from the PREVICOM project (KK-2022/00029).

Acknowledgments

The work presented in this paper has been carried out with the great support and the technological capabilities of CIE Automotive.