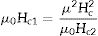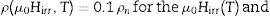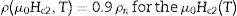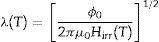Contribution of vanadium particles to thermal movement of correlated two-dimensional pancake Abrikosov vortices in Bi-2223 superconducting system

Abstract

This article breaks new ground in understanding of variation in the magnetic strength performance, flux pinning and energy dissipation mechanism of polycrystalline bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0O_y (Bi-2223) superconducting materials added with the different vanadium concentration level (0.0 ≤ x ≤ 0.30) under the magnetic field strengths applied up to 5 T for the first time. We provide the sophisticated and phenomenological discussions on the magnetoresistivity measurement results in three main sections along the paper. All the findings show that the increase of both the vanadium concentration in the crystal structure and external magnetic field strength damages significantly the magnetic strength performance, vortex dynamics, flux pinning ability and vortex lattice elasticity of bulk Bi-2223 superconducting ceramics. The vanadium addition promotes thermally the movement of correlated two-dimensional (2D) pancake Abrikosov vortices between the in-plane Cu–O₂ layers in the valance band, vortex lattice elasticity, vortex dynamics, distance for interlayer Josephson couplings and flux pinning centers and the theoretical computations confirm the remarkable degradation in the formation of super-electrons in the Bi-2223 crystal system. Thus, the vanadium addition is anticipated to be one of the best selectable materials to examine the differentiation in the thermal movement of correlated 2D Pancake Abrikosov vortices in the bulk Bi-2223 superconducting system.

Resumen

Este artículo abre nuevos caminos en la comprensión de la variación en el rendimiento de la fuerza magnética, fijación de flujo y mecanismo de disipación de energía de los materiales superconductores Bi1.8Sr2.0Ca2.2Cu3.0Oy (Bi-2223) a granel policristalino agregados con los diferentes niveles de concentración de vanadio (0.0≤ x ≤ 0,30) bajo las intensidades de campo magnético aplicadas hasta 5 T por primera vez. Proporcionamos discusiones sofisticadas y fenomenológicas sobre los resultados de la medición de magnetorresistividad en tres secciones principales a lo largo del documento. Todos los hallazgos muestran que el aumento tanto de la concentración de vanadio en la estructura cristalina como de la fuerza del campo magnético externo daña significativamente el rendimiento de la fuerza magnética, la dinámica del vórtice, la capacidad de fijación del flujo y la elasticidad del retículo del vórtice de las cerámicas superconductoras Bi-2223 a granel. La adición de vanadio promueve térmicamente el movimiento de los vórtices de Abrikosov tipo panqueque bidimensionales (2D) correlacionados entre las capas de Cu₂O en el plano en la banda de cenefa, la elasticidad del retículo de vórtice, la dinámica de vórtice, la distancia para los acoplamientos de Josephson entre capas y los centros de fijación de flujo. Los cálculos teóricos confirman la notable degradación en la formación de superelectrones en el sistema cristalino Bi-2223. Por lo tanto, se prevé que la adición de vanadio sea uno de los mejores materiales seleccionables para examinar la diferenciación en el movimiento térmico de los vórtices 2D pancake Abrikosov correlacionados en el sistema superconductor Bi-2223 a granel.

Introduction

With the increment in the usage of superconducting materials in today's technology, the humanity breathes a sigh of relief. This is because, some problematic phenomena such as the global population growth rate, inexplicable advance in technology and new generation usage habits increasing harshly the energy consumption requirements. Thus, the scientists should consider the following concepts: energy production, energy consumption and related disciplines including the climate protection, resource conservation and cost savings in their scientific research. As for the duty of humanity, new policies on the efficient energy use and energy efficiency should be developed to restrict the amount of energy used. Especially the energy losses grounded on the dissipation (ohmic resistance) mechanism in the power tools are the problems in themselves. In this context, the usage of superconducting materials seems to solve these kinds of problems due to their intrinsic zero resistance, economic life, power quality, cheap production, and superior efficiency.

Among the superconducting materials, the Bi-containing parents discovered in the late 1980s possess three various superconducting phases with regard to the conducting in-plane Cu–O₂ layers in the crystal system [1–3]. These phases are arranged as: superconducting high phase (Bi-2223) with the T_c ≈ 110 K, low phase (Bi-2212) with the T_c ≈ 85 K and very low phase (Bi-2201) with the T_c of near 20 K [4]. Namely, the material family can be defined by a homologous series as Bi₂Sr₂Ca_n−1Cu_nO_4+2n+x according to the n number. As understood from the critical transition temperature values, of the family members the Bi-2223 superconductor possesses two Ca atoms and three Cu–O₂ layers in the unit cell and exhibits the largest magnetic field and current carrying capacity and application temperature regions. Similarly, there are a number of superior characteristic features, namely rather larger critical temperature (about 110 K as mentioned above) and thermodynamic stability, extremely higher magnetic field (bigger than 100 T nearly at the irreversibility line temperature of 35 K) carrying and current density (greater than 10⁷ A/cm²) capability and naturally lesser power consumption and dissipations [5–10]. Similarly, the Bi-2223 superconducting ceramic material can simply be prepared in the desired phase and presents the stability against the compositional contents and is resistant towards to the water/humid atmosphere [9,10]. Moreover, the micaceous structure due to the presence of Bi-O layers in the crystal structure allow the Bi-2223 compound to be deformed, rolled and shaped easily for the long cable construction over 1 km in length [11] and production of tape-casting and feature texturing materials [12]. In this regard, the usage in much more areas of Bi-2223 superconducting material with its alluring features under the relatively higher external magnetic field in daily life is important for the decrease of energy consumption requirements.

In the present work, we try to analyze the change of magnetic strength performance, flux pinning and energy dissipation mechanism of polycrystalline bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting materials with the vanadium addition in case of the external dc magnetic field strengths applied up to 5 T so that we can discuss the fundamental energy dissipation mechanisms grounded on the thermal fluxon motions of 2D discrete pancakelike vortices within the discrete pancakelike nature, jumping to neighboring states, interplane connection energy and flux pinning energy parameters. Similarly, we investigate the variation of temperature-dependent thermodynamics and quantum mechanical quantities with vanadium concentration to discuss the energy barriers, vortex lattice elasticity, vortex dynamics, distance for interlayer Josephson couplings and flux pinning centers. We also provide a strong link between inter-grain boundary coupling problems (due to the vanadium addition) and energy dissipation mechanisms to determine the change in susceptibility to the applied magnetic field strength. It is found that the vanadium addition is noted to damage the general magnetic strength performance. Accordingly, it can be concluded that the vanadium addition in the Bi-2223 crystal lattice is not the preferred method to meet the energy consumption requirements.

Experimental details

In the previous scientific papers published [13–15], we deal with the role of vanadium addition in the polycrystalline bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting materials prepared within the mole-to-mole ratio of 0.0 ≤ x ≤ 0.30 on the fundamental electrical, superconducting, crystallographic, microstructural, morphological, magneto-resistivity performance features with the aid of dc electrical curves depending on the temperature, powder X-ray diffraction, scanning electron microscopy, electron dispersive X-ray and magneto-transport measurement setups. We also make some theoretical discussions computations grounded on the electrical findings, formation of effective flux pinning centers, gap coefficients, two-stage transition temperatures and structural disorders-defects. One can see all the experimental procedures (material preparation by the standard solid-state reaction route, chemicals with their purities, experimental setup, measurement temperature ranges) in detail in Refs. [13–15]. The key findings deduced from the papers depend on the fact that the presence of vanadium damages dramatically the fundamental characteristic features of Bi-2223 ceramic superconducting materials. In fact, the properties get more and more degraded with the increase of addition level and some of them are unobservable. Thus, the vanadium addition idea in the crystal structure is not turned to be a useful solution for the usage of Bi-2223 superconducting ceramics in the advanced engineering and large-scale application fields.

This study provides some critical detail about how the pair-breaking mechanism (based on the orbital limit effect) proposed by Abrikosov-Gorkov, Arrhenius activation law, Ginzburg Landau relation, power law and intercept of extrapolation approaches use to determine the thermodynamics and quantum mechanical quantities. Accordingly, the crucial roles of vanadium and external magnetic field strength on the sophisticated and phenomenological discussions such as the thermal fluxon motions (small whiskers) of two-dimension (2D) discrete pancakelike vortices (related to the vortex dynamics), vortex lattice elasticity, flux pinning energy, jumping to neighboring states, interplane connection energy, variation in the distance for the flux pinning centers, energy barriers between in-plane Cu–O₂ layers and distance between interlayer Josephson couplings are thoroughly discussed in detail.

In the paper, the pure and vanadium added bulk Bi-2223 superconducting compounds prepared at the different molar concentration level of x = 0, 0.01, 0.03, 0.05, 0.07, 0.10 and 0.30 will thenceforward be named as pure V1, V2, V3, V4, V5, and V6, respectively. As for the experimental parts, the magneto-transport measurements belonging to the materials were conducted in the cryostat system in case of 5 mA current applied on specimen surfaces at different applied magnetic field strengths (up to 5 T). The measurement signals were gathered in a temperature range of 8 K ≤ T ≤ 120 K and one can see all the experimental evidence in Ref. [15] in detail. However, it is obvious that much more sophisticated interpretation is needed for the full magnetic performance characterization. Thus, in the current work the measurement results are converted to Arrhenius (ln ρ/ρ_120K versus 1/T) curves grounded on the logarithmic resistivity variation with reciprocal of temperature to calculate the flux pinning energy values (in K unit) using the slopes of linear parts in low magnetoresistivity regions at different external magnetic fields applied for all the bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting ceramic compounds. Right after, we have a chance to discuss the effect of vanadium addition and applied magnetic field strength on the flux pinning (activation) energies for the motion of 2D pancake vortices in the Bi-2223 superconducting matrix. We also define the dependence (sensitivity) of flux pinning energy on the external magnetic field strengths by means of power-law approach to establish a strong link between the activation energy and inter-grain boundary coupling problems (weak-interactions) due to the vanadium addition in the Bi-2223 superconducting crystal structure. At the same time, the magnetoresistivity curves enable us to find the temperature-dependent thermodynamics and quantum mechanical quantities as regards thermodynamic critical (μ₀H_c), lower critical (μ₀H_c1), irreversibility (μ₀H_irr), upper critical fields (μ₀H_c2), coherence length (ξ), penetration depth (λ), and Ginzburg Landau parameter (κ) so that we can easily scientifically interpret the differentiation in the magnetic strength performance, vortex dynamics, flux pinning ability, vortex lattice elasticity, formation of super-electrons (cooper-pair probabilities) in the crystal system, energy barrier size and discrete pancakelike nature of vortices (characterized by the normal cores) depending on the vanadium addition level and applied magnetic field strength.

Results and discussion

Prior to this part, we declare that the current work is a continuation of a book chapter published in Ref. [15] and prepared to bring the unfinished study on the magnetic strength performance in the literature. In more detail, the present work delves deeply into the effect of vanadium addition on the energy dissipation mechanisms related to the thermal fluxon motions of 2D discrete pancakelike vortices (vortex dynamics), jumping to neighboring states, interplane connection energy and flux pinning energy. Similarly, the numerical data (related to the thermodynamics and quantum mechanical calculations, viz. the thermodynamic critical, lower critical, irreversibility, upper critical fields, corresponding activation (flux pinning) energy, coherence length, penetration depth and Ginzburg Landau parameter) enable us to discuss the differentiation in the length between flux pinning centers, vortex lattice elasticity, energy barriers between in-plane Cu–O₂ layers in the valance band and distance for the interlayer Josephson couplings depending on the vanadium addition. Besides, we describe a strong relationship between the vanadium addition level and discrete pancakelike vortices in the bulk Bi-2223 crystal system for the first time.

Shortly, this paper focuses mainly on three basic sections. The first of them consists of change in the flux pinning energy with vanadium addition level and applied magnetic field strength. The second one is directly interested in the finding the parameters of μ₀H_irr, μ₀H_c1, μ₀H_c, μ₀H_c2 and μ₀H_c3, and understanding of fundamental features mentioned above. The last section paves way to calculate the parameters of ξ, λ, and κ and describe the influence of vanadium concentration and external magnetic field strength on the vortex dynamics, flux pinning ability and vortex lattice elasticity in the bulk Bi-2223 crystal structure.

Change in flux pinning energy

It is without any doubt that the intrinsic characteristics affect seriously the application fields of materials. For our samples studied in this work, the typical anisotropy grounded on the crystalline directions leads to limit seriously the usage of Bi-2223 superconducting materials in the advanced engineering and large-scale application fields due to the weak flux pinning ability under relatively small external magnetic field strength and current applications. This is because, the applied magnetic field moves and accelerates the 2D discrete pancakelike vortices as a consequence of the decrease in the vortex dynamics, flux pinning ability and vortex lattice elasticity in the bulk Bi-2223 crystal structure. That is to say, the applied magnetic field automatically improves the decoupling (discrete pancakelike or recoupling linelike nature of localized magnetic fluxoids) of in-plane Cu–O₂ (adjacent multilayers) layers in the valance bands of bulk Bi-2223 superconducting ceramics. Therefore, the interplane interaction energy immediately increases and the related distance for interlayer Josephson couplings decreases remarkably. Consequently, the 2D discrete pancakelike vortices begin to thermally move and accelerate to be able to jump towards near neighboring states with much higher energy barriers at the external magnetic field strength higher than certain value for the materials [16,17]. This fact triggers to generate the heat energy with the beginning of resistivity (energy losses) in the system [18]. As of now, the fluxoids (Abrikosov vortices within the 2D discrete pancakelike nature) are thermally activated to overcome the pinning energy barrier. In the present work, we give some detail for the change of vortex dynamics, elasticity of vortex lattice, effective flux pinning ability, potential energy barriers belonging to the pinning centers and flux pinning energy values in the polycrystalline bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting materials depending on the vanadium concentrations (0.0 ≤ x ≤ 0.30) and external magnetic field strengths (up to 5 T) using the Arrhenius activation law grounded on thermally activated flux flow (abbreviated as TAFF) approach [19,20]. According to Arrhenius activation law, one can see below how to calculate the flux pinning energy values for the movement (hop to neighborhoods over potential energy barriers) of Abrikosov vortices within the 2D discrete pancakelike nature:

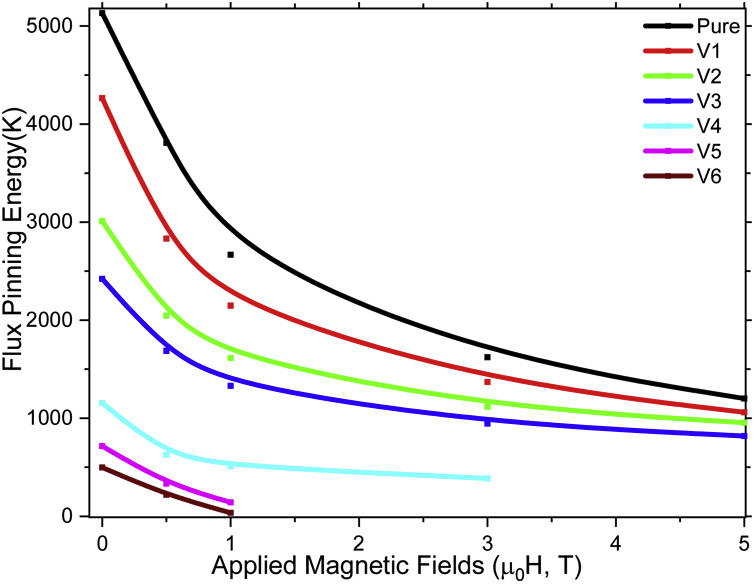
in the relation, k_B presents Boltzmann's constant, ρ shows the certain value for dissipation mechanism at any temperature region when ρ₀ displays the field-independent pre-exponential factor (for our samples the factor is chosen to be the resistivity value at 120 K) [21]. The abbreviation of U₀ shows the flux pinning energy value. In the Arrhenius graphics provided at various applied magnetic fields (up to the value of 5T), we can determine the U₀ values from linear slope points in broadening tail regions. One can see all the Arrhenius activation curves founded on the logarithmic resistivity variation with reciprocal of temperature (ln ρ/ρ_120K versus 1/T) of polycrystalline bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting materials in Fig. 1a–e. It is apparent from the figure that the increment in the vanadium concentration value and external magnetic field strength affect seriously the magnetic strength performance, vortex dynamics, flux pinning ability and vortex lattice elasticity in the Bi-2223 crystal structure. The main reason in the change of magnetic characteristics can be explained by the energy dissipation mechanism stemmed from the sudden movement (hop to neighborhoods over potential energy barriers) of Abrikosov vortices within the 2D discrete pancakelike nature. In fact, from the vanadium concentration level of x = 0.05 onwards we cannot determine the flux pinning energy values for the movement of 2D discrete pancakelike Abrikosov vortices at the applied field of 5 T for the V4 sample, and 1 T and higher field level for the bulk V5 and V6 sample because of the complete loss of superconductivity at the applied fields. Shortly, Fig. 1a–e displays that the vanadium addition as well as the external magnetic field strength is not good for the flux pinning capability of bulk Bi-2223 superconducting ceramics compound due to the presence of pair-breaking mechanism proposed by Abrikosov-Gorkov. We also provide numerically the flux pinning energy parameters (extracted from the Arrhenius activation curves) for every superconducting material studied at various external magnetic field strengths in Table 1. One can easily understand that the U₀ values (the potential energy barriers for the movement of Abrikosov vortices) are found to decrease dramatically with the enhancement in the vanadium concentration level and external magnetic field strength. In this respect, the maximum pinning energy value of 5132 K is obtained for the pure sample whereas the V6 compound exhibits the U₀ value of 498 K at zero applied magnetic field strength. The other (V1, V2, V3, V4 and V5) materials possess the moderate U₀ values between 4265 K (for the V1 sample) and 716 K (for the V5 sample). As the external magnetic field strength increases towards to the maximum value of 5 T, the pure sample presents the flux pinning energy value of 1201 K for the movement of Abrikosov vortices as against the value of about 819 K for the V3 material. For the V4 compound, we can determine the U₀ value as 387 K for the maximum 3 T external field strength whereas the flux pinning energy values such as 142 K and 36 K can be found at the maximum 1 T applied field for the V5 and V6 compound, respectively. In other words, it is not possible to stop the movement of Abrikosov vortices at such an applied magnetic field strength slightly greater than 1 T, and accordingly the energy losses (dissipations) begin immediately in the crystal structure. The descriptors show that the presence of vanadium particles in the Bi-2223 superconducting matrix leads to increase harshly the interplane interaction energy and inter-grain boundary coupling problems (weak-interactions) due to the reduction of nucleation centers with the capacity of flux pinning. Even, the degradation in both the crystallinity quality and appearance of surface morphology has already been discussed in Refs. [13,14] where it has been found that the crystal structural was found to diminish depending on the vanadium addition level due to the increment in the grain misorientations, problems of grain alignment and size distributions, porosity, microvoids, intra/inter-grain boundary interactions between the grains and formation of new internal, structural and microscopic problems in the crystal system” depending on the vanadium addition level. Besides, the SEM images showed that the increase in the vanadium addition considerably harms on the well linked flaky layers of platelet-like shape, uniform surface view, porous and granular structure for superconducting grains [13]. All in all, the related distance for interlayer Josephson couplings and the flux pinning centers as well as the energy barriers between in-plane Cu–O₂ layers decrease considerably depending on the vanadium concentration level. In the light of observed results, the rule of thumb is that the variation in the fundamental characteristics mentioned above damages significantly the magnetic strength performance.

Fig. 1.

Change in ln ρ/ρ_120K over 1/T (K⁻¹) curves of polycrystalline bulk Vanadium added Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting materials. Activation energy values for materials are inferred from slopes of linear parts in low magnetoresistivity regions at different external magnetic fields.

Table 1.

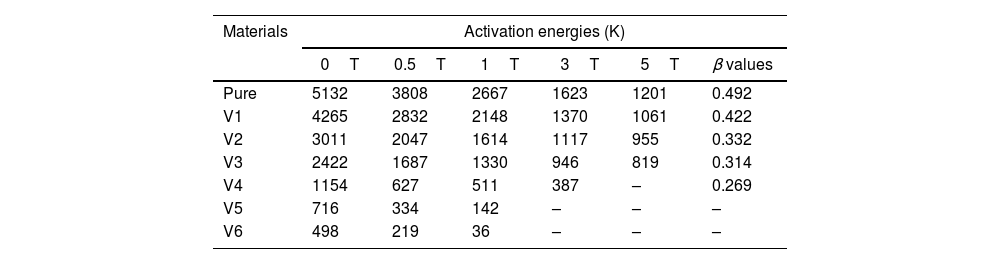
Flux pinning energy parameters for movement of correlated 2D Pancake Abrikosov vortices and applied magnetic field-dependent activation energy values for Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting materials.

Materials	Activation energies (K)
	0 T	0.5 T	1 T	3 T	5 T	β values
Pure	5132	3808	2667	1623	1201	0.492
V1	4265	2832	2148	1370	1061	0.422
V2	3011	2047	1614	1117	955	0.332
V3	2422	1687	1330	946	819	0.314
V4	1154	627	511	387	–	0.269
V5	716	334	142	–	–	–
V6	498	219	36	–	–	–

Furthermore, we scrutinize the differentiation of flux pinning energy values against the external magnetic field strengths (see Fig. 2) to reveal the role of vanadium on the magnetic strength performance of bulk Bi-2223 superconductor. It is visible from the figure that the activation energy curves for every material (including V4, V5 and V6) exhibit the sharp/exponential decrease up to 1 T applied magnetic field strength after which the curves follow the slight softer decrease for the pure, V1, V2 and V3 compounds followed by the linear reduction trend in the curve for the V4 sample. Besides, the magnetic performance will have already been invisible for the other compounds (V5 and V6) at even higher applied magnetic field strengths. The scenario is based on the fact that the external magnetic field firstly penetrates into inter-granular regions; thus, 2D discrete pancakelike Abrikosov vortices begin to move immediately (beginning of thermal small whisker motions) due to the presence of inter-grain boundary coupling problems in the Bi-2223 crystal system [22]. From the applied magnetic field strength of 1 T onwards the applied magnetic field lines can easily penetrate totally into the material. It should be declared here that the resistivity mechanism (beginning of Abrikosov vortices and entangled with each other) starts below 1 T external magnetic field strength applied.

Fig. 2.

Differentiation of flux pinning energy values for movement of correlated 2D Pancake Abrikosov vortices in crystal system with magnetic field strengths applied up to 5 T. (Continuous lines guide to the eye, and slopes are grounded on linear regression).

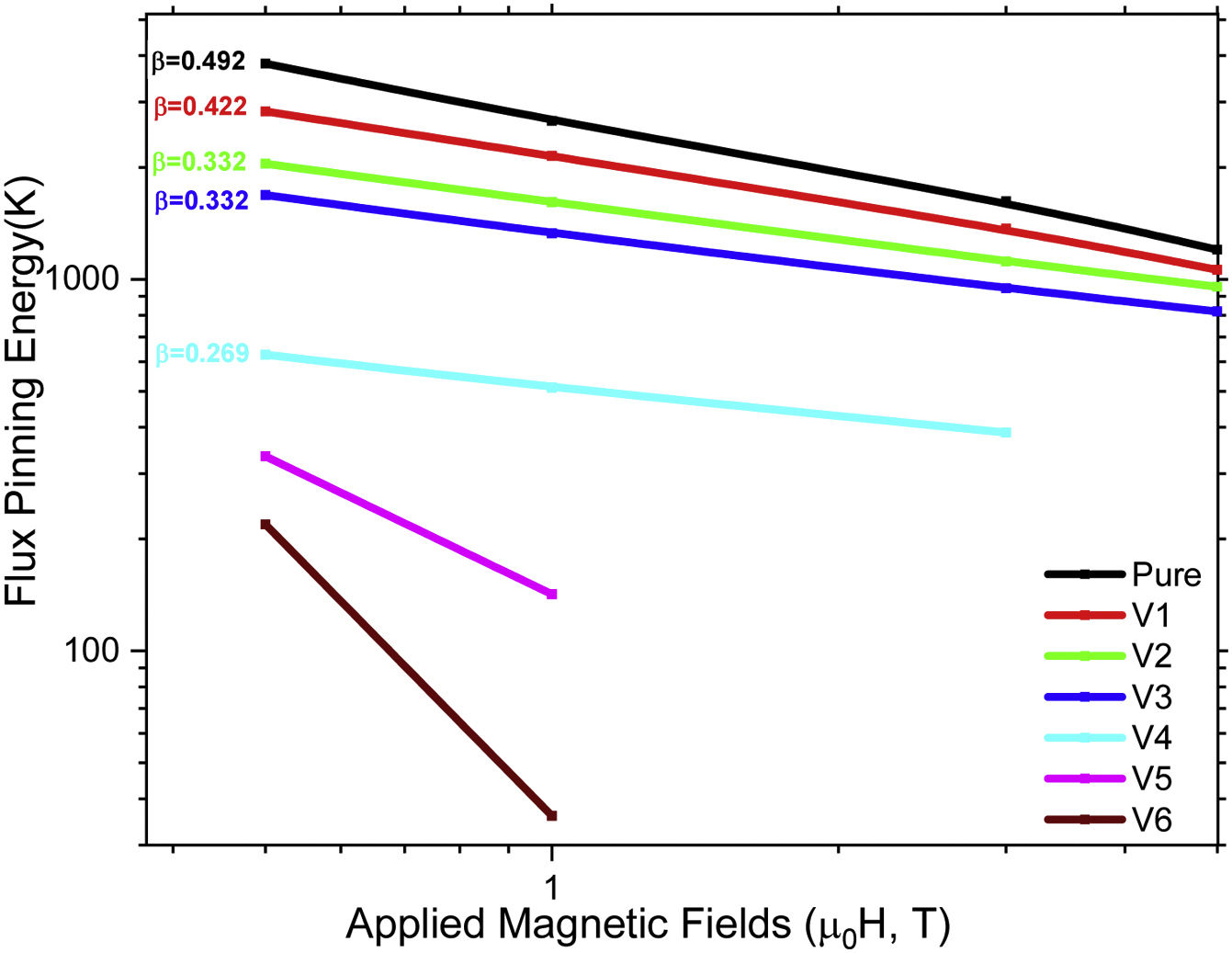
At the same time, the flux pinning curves interested in the variation in the activation energy values for the movement of Abrikosov vortices over the external magnetic field strengths enable us to examine the sensitivity of flux pinning energy on the external magnetic field strengths using power-law approaches so that we can easily develop a strong relationship between the activation energy and inter-grain boundary coupling problems with the vanadium addition in the polycrystalline Bi-2223 superconducting system, even already confirmed clearly by the XRD and SEM measurement results displayed in Refs. [13,14]. In this context, the log-log curves are graphed in Fig. 3 where all the curves behave as if it were linear. Hence, it is obvious that we can use the power law to define the dependence of flux pinning energy for the correlated 2D pancake Abrikosov vortices on the applied magnetic field strength. Namely,

Fig. 3.

Variation in flux pinning energy values as a function of magnetic field strengths applied up to 5 T for every material studied. (Continuous lines guide to the eye, and slopes are grounded on linear regression).

in the power law equation, the variable of β displays the orientation of external magnetic field strength depending on the basal plane. When fitting the results, the β values are found to decrease from 0.492 until 0.269 with the increment in the vanadium concentration level and in fact we could not compute the β constant for the V5 and V6 samples because of the insufficient data. On this basis, the pure sample shows the maximum β value of 0.492 whereas the minimum value of 0.269 ascribes to the bulk V4 sample. The gradual reduction of β values with the addition level results from the augmentation of inter-grain boundary coupling problems (weak interactions between the adjacent multilayers) in the crystal structure, even already expressed in Refs. [13,14]. To sum up, the pure sample with finest crystal structure presents the least sensitivity to applied magnetic field whereas the sensitivity to external magnetic field tends to increase gradually with the vanadium addition. This comprehensive result is known to exhibit in parallel with the resistivity and barrier height of junction [23–26].

Variation of temperature-dependent thermodynamics and quantum mechanical quantities of Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconductors with vanadium concentration

The effect of vanadium concentration in the Bi-2223 superconducting materials on the vortex lattice elasticity and vortex dynamics in the crystal system is analyzed by the critical field parameters. The main approach is based on the entanglement (broadening nature) of correlated 2D pancake Abrikosov vortices (quantized fluxoids carrying the flux quantum of Φ=h/2e) in the high temperature superconducting cuprates at even lower external field strength as a consequence of characteristic negative surface energy of materials. The state is previously studied in the scientific paper published in Ref. [27]. As a result, any applied magnetic field strength can damage seriously the formation of super-electrons (cooper-pair probabilities) in the crystal system. The first thing that comes to mind is the presence of temperature-dependent thermodynamics and quantum mechanical quantities such as μ₀H_irr, μ₀H_c1, μ₀H_c, μ₀H_c2 and μ₀H_c3 parameters. To introduce the parameters briefly, the smallest critical field (called as lower critical field, μ₀H_c1) at the vicinity of which the external magnetic field is wholly expelled by the solid material, being the perfect Meissner effect behavior [28]. Namely, in case of smaller applied magnetic field than μ₀H_c1 value the magnetic flux could not penetrate into the material. If only higher external magnetic field than μ₀H_c1 value is applied, the magnetic fluxes penetrate. It is to be emphasized here that the value cannot be determined easily for the high temperature superconducting materials. As in other studies, we define the H_c1 values for our prepared samples from the μ₀H_irr parameters with the aid of following relation:

As for the irreversibility field (μ₀H_irr) parameter, the value locates between μ₀H_c1 and μ₀H_c2 values, where any external magnetic field strength can partially penetrate into the solid compound in the form of quantized fluxons within the discrete nature (correlated 2D pancake Abrikosov vortices). This case is called as Schubnikov phase of mixed state in which the applied magnetic field mostly damages the formation of super-electrons in the crystal system [29].

Moreover, the other term is upper critical field (μ₀H_c2) where the average penetrated field equals the external magnetic field. At higher applied magnetic field than μ₀H_c2, the superconductivity phenomenon in the system breaks and slowly disappears due to 2nd order phase transition.

Additionally, the other term is thermodynamic critical field (μ₀H_c) and in case of without any applied magnetic field the parameter provides a measurement of the degree to which the superconductivity state is promoted over the normal state. The μ₀H_c value can be calculated from the following relation:

The last term of μ₀H_c3 before which the material exhibits the superconductivity phenomenon within a thin surface layer can theoretically be calculated from the formula of μ₀H_c3 ≈ 1.69 μ₀H_c2 (last tangent point of superconductivity). However, it should be known that the superconductivity vanishes totally from the material.

There are a number of literature works serving as finding the temperature-dependent thermodynamics and quantum mechanical quantities mentioned above so that the scientists can easily discuss the vortex lattice elasticity and vortex dynamics for the high temperature superconducting ceramic materials. Among the techniques, the dc magnetization, ac susceptibility and magnetoresistivity measurements can be arranged as the most popular methods [30,31]. All the methods possess some advantages over the other approaches. For example, the magnetoresistivity measurement method provides the superior information about the vortex lattice elasticity, resistive transitions, vortex dynamics and pinning or movement of correlated 2D pancake Abrikosov vortices as compared to other ones [32,33]. In our investigation for this paper, we exert the magnetoresistivity measurements at the magnetic field strengths applied up to 5 T to describe the influence of vanadium addition concentration on the fundamental thermodynamics and quantum mechanical quantities. Initially, we determine the μ₀H_irr and μ₀H_c2 values from the temperature-dependent magnetoresistivity measurements as provided below [34,35], and then we calculate the other parameters of μ₀H_c1, μ₀H_c, and μ₀H_c3 with the aid of μ₀H_irr and μ₀H_c2 values (having already given above). Namely,

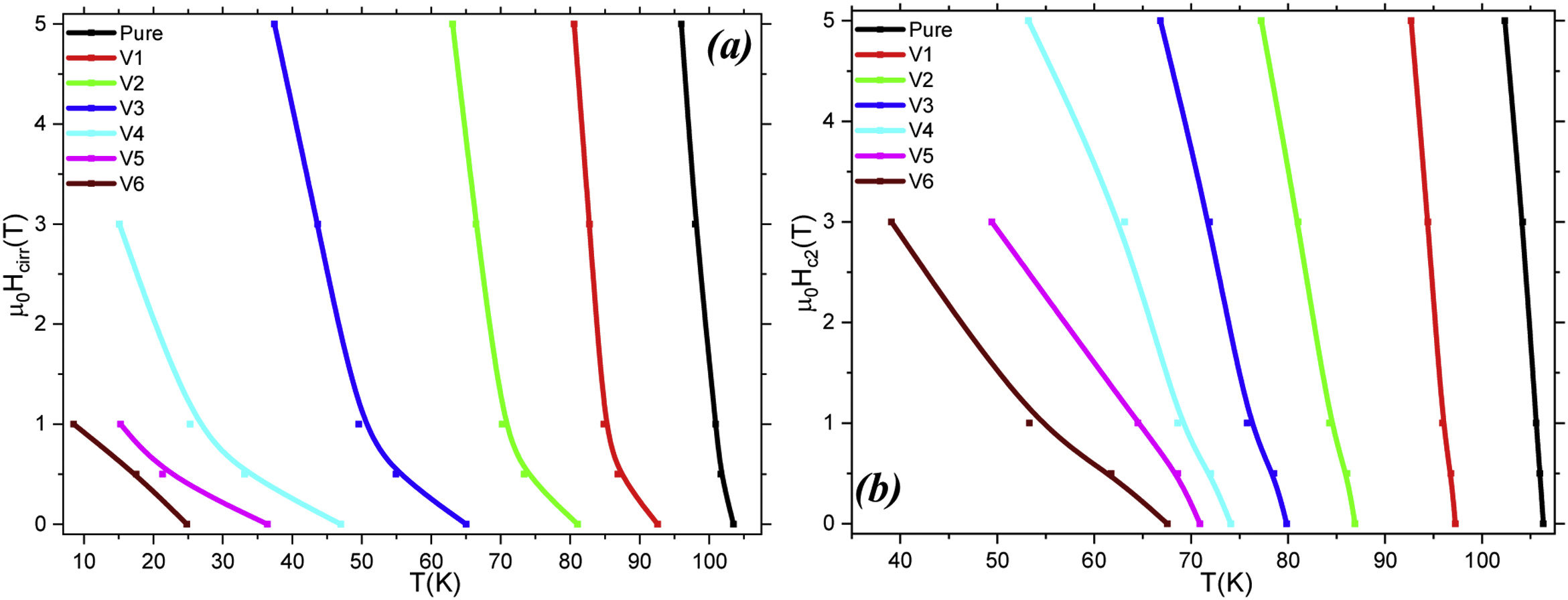
in the relations ρ_n presents the normal state resistivity values of bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting ceramic compounds at such a temperature of 120 K. At Schubnikov phase we separately find the μ₀H_irr(T) and μ₀H_c2(T) values for all the materials, and we need to determine μ₀H_irr(0) and μ₀H_c2(0) at zero point value to calculate the coherence length (ξ), penetration depth (λ), and Ginzburg Landau parameter (κ) for every material. It is well-known that there are numerous methods such as Almeida-Thouless (AT), Abrikosov-flux dynamics, Ginzburg Landau (GL), Werthamer–Helfand–Hohenberg, intercept of extrapolation of parameters to zero in the temperature axis, etc. in the literature to determine the change in the fundamental aspects of thermodynamics and quantum mechanical (and related) quantities; namely, the thermodynamic critical, lower critical, irreversibility, upper critical fields, corresponding flux pinning energy, coherence length, penetration depth and Ginzburg Landau parameter [36–40]. The method used in the paper for the determination of μ₀H_irr(0) and μ₀H_c2(0) we prefer is the relatively easy to define the effect of vanadium addition mechanism on the fundamental characteristic features mentioned above. Similarly, it is to be emphasized here that the model used in our work is also preferred in several papers including different types of superconductors [38,39,41–43]. Besides, it is important to declare that some scientific papers directly claim that the calculation for the μ₀H_c2 parameter at 0 K by WHH model is rather less than that of GL model [35,36]. Thus, it is clear that the model preferred in this paper is useful and reliable to discuss the magnetic performance features mentioned above. Hence, for absolute zero temperature we use the interpolation to approximate values on y-axis to find the values of μ₀H_irr(0) and μ₀H_c2(0), respectively [43], the μ₀H_c, μ₀H_c1, and μ₀H_c3 parameters at absolute zero temperature as they do. One can observe graphically the temperature-dependent μ₀H_irr(T) and μ₀H_c2(T) values for all the bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting ceramic compounds in Fig. 4. The obtained numerical results are listed in Table 2. It is visible from the table that the μ₀H_irr(0) and μ₀H_c2(0) values are found to decrease regularly with the systematic increase in the vanadium concentration level in the bulk Bi-2223 crystal structure. The decrease trend stems directly from the reduction of flux pinning capability and pair-breaking mechanism. Numerically, the maximum μ₀H_irr(0) and μ₀H_c2(0) values are found to be about 70.01 T and 134.68 T for the pure sample whereas the V6 sample possesses the global minimum values of 1.54 T and 6.93 T for the μ₀H_irr(0) and μ₀H_c2(0) parameters, respectively. Depending on these values, μ₀H_c1(0), μ₀H_c(0) and μ₀H_c3(0) parameters are calculated to be about 0.3501 T (0.0077 T), 6.87 T (0.23 T) and 227.61 T (146.30 T) for the pure (V6) compound. The other materials prepared have the moderate values for the thermodynamics and quantum mechanical quantities. The last findings reveal why we cannot record the temperature-dependent magnetoresisitivity experimental measurement results at relatively higher external field strength applied. Besides, it is fair to summarize that the dramatic reduction of thermodynamics and quantum mechanical quantities is due to the diminish of vortex lattice elasticity, vortex dynamics, flux pinning mechanism (force) and Josephson coupling length [44].

Fig. 4.

Temperature-dependent (a) Irreversibility critical fields and (b) Upper critical fields. (Continuous lines guide to the eye, and slopes are determined with regard to linear regression).

Table 2.

Temperature-dependent thermodynamics and quantum mechanical quantities including μ₀H_irr, μ₀H_c1, μ₀H_c, μ₀H_c2, μ₀H_c3, λ, ξ and κ for every compound studied in this work.

Compounds	Hc1(0) (T)	Hirr(0) (T)	Hc2(0) (T)	Hc(0) (T)	Hc3(0) (T)	λ(0) (Å)	ξ(0) (Å)	κ(0)
Pure	0.3501	70.01	134.68	6.87	227.61	21.70	15.65	1.39
V1	0.1776	35.51	107.60	4.37	181.85	30.47	17.50	1.74
V2	0.1048	20.95	45.14	2.18	76.29	39.67	27.02	1.47
V3	0.0548	10.95	30.91	1.30	52.24	54.86	32.66	1.68
V4	0.0191	3.82	18.21	0.59	30.78	92.89	42.55	2.18
V5	0.0080	1.59	9.74	0.28	16.46	143.98	58.17	2.48
V6	0.0077	1.54	6.93	0.23	11.71	146.30	68.97	2.12

Coherence length, penetration depth and Ginzburg Landau parameter

In the last part of paper dealing with the magnetic strength performance, we search the differentiation in the coherence length (ξ), penetration depth (λ) and related Ginzburg Landau parameter (κ) depending on the vanadium addition level. To remind, with the penetration of magnetic field lines into the superconducting material the correlated 2D pancake fluxons begin to move thermally. Thus, the findings allow us to display why the movement of correlated 2D pancake Abrikosov vortices (discrete pancakelike nature) in the in-plane Cu–O₂ layers increases with the vanadium addition level in detail. It is another advantage of determination of the parameters that we can easily decide the type (type-I or type-II) of superconducting compounds prepared. Similarly, the variation of ξ and λ parameters enables us to determine the role of vanadium concentration on the strength of type-II nature. Based on the quantum mechanical approach, the ξ parameter is related to a cylindrical core of a radius while the λ parameter is in accordance with a distance for the current circulating around the core [45]. Nevertheless, it is well-known that it is very difficult to obtain the experimental parameters from the measurements and in fact it is impossible to determine at the absolute zero temperature. On this basis, the μ₀H_irr(0) and μ₀H_c2(0) parameters are appropriate to define the effect of vanadium addition level on the ξ and λ parameters. In the current study, the parameters of ξ and λ at the absolute zero temperature are calculated from the following equations:

where ϕ0 equals 2.07×10−15 Tm2. One can see all the computations for the ξ(0) and λ(0) values in Table 2. According to the table, there seems to increase trend in the parameters depending on the vanadium concentration level. In this regard, the pure sample possesses the minimum ξ(0) and λ(0) parameters of 15.65 Å and 21.70 Å, respectively. On the other hand, the maximum values of 68.97 Å and 146.30 Å ascribe to the bulk V6 superconducting compound for the ξ(0) and λ(0) parameters, respectively. The other samples have the moderate values. It is to be mentioned here that the presence of vanadium accelerates the 2D pancake Abrikosov vortices within the discrete pancakelike nature as a result of the decrease in the energy barrier level. Likewise, it can be interpreted that the vanadium addition idea in the Bi-2223 crystal structure hinders the formation of super-electrons (cooper-pair probabilities) in the crystal system. We also compute the κ(0) parameters for all the bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting ceramic compounds from the ratio of ξ/λ and insert numerically the obtained data in Table 2 to discuss the magnetic strength of materials to the applied magnetic field strength. It is apparent from the table that the smallest κ(0) value is calculated to be about 1.39 for the pure sample due to its own highest magnetic strength to the external magnetic field (strength of type-II nature). Besides, it can be explained that all the materials prepared in this work exhibit the London type superconductors in the electrodynamics locality due to the κ value higher than the value of 1/2.

Conclusion

To conclude that, in the current work we provide some crucial detail for the effect of vanadium addition (within the different mole-to-mole ratios of 0.0 ≤ x ≤ 0.30 for the stoichiometric bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting system) on the magnetic strength performance, flux pinning and energy dissipation mechanism under the magnetic field strengths applied up to 5 T. For this aim, we divide the paper in three main sections: (I) role of vanadium addition and different external magnetic field strengths on the flux pinning energy values for 2D pancake Abrikosov vortices within the discrete pancakelike nature; (II) differentiation in the temperature-dependent thermodynamics and quantum mechanical quantities with vanadium concentration and research of vortex dynamics; (III) establishment a link between the vanadium addition and quantum mechanical quantities (Coherence length, penetration depth and Ginzburg Landau parameter). According to the results obtained from the first part, it is found that the magnetic strength performance, vortex dynamics, flux pinning ability and vortex lattice elasticity are seriously degraded with the increment in the vanadium concentration value and external magnetic field strength. Thus, the excess vanadium ions cause the dissipation at relatively smaller magnetic field due to the beginning of movement of correlated 2D pancake Abrikosov vortices between the in-plane Cu–O₂ layers in the valance band. Similarly, the enhancement in the interplane interaction energy and inter-grain boundary coupling problems (weak-interactions) due to the reduction of nucleation centers with the capacity of flux pinning with the vanadium addition causes the dramatic decrease in the flux pinning energy. It is another strong claim for the decrease in the flux pinning capability and magnetic strength performance that the presence of vanadium particles in the polycrystalline Bi-2223 structure harshly truncates the energy barriers, distance for interlayer Josephson couplings and flux pinning centers. The second part also shows that the μ₀H_irr, μ₀H_c1, μ₀H_c, μ₀H_c2 and μ₀H_c3 parameters are found to considerably decrease with the increase in the vanadium addition level. This is correlated to the reduction of flux pinning capability, vortex lattice elasticity, vortex dynamics, flux pinning mechanism (force) and Josephson coupling length. In the third part, we find that all the bulk Bi_1.8Sr_2.0Ca_2.2Cu_3.0V_xO_y superconducting ceramic compounds falls into the London type superconductors in the electrodynamics locality as a result of their κ values. Besides, it is pointed out that the vanadium addition in the Bi-2223 matrix hinders the formation of super-electrons (cooper-pair probabilities) in the crystal system. To sum up, the vanadium addition idea is not good for the flux pinning capability of bulk Bi-2223 superconducting ceramics compound due to the presence of pair-breaking mechanism proposed by Abrikosov-Gorkov.