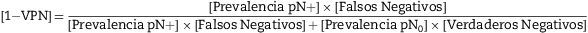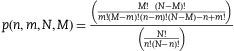Un método para individualizar el riesgo de una errónea clasificación ganglionar negativa en el cáncer de colon

Resumen

Introducción y objetivos

En el cáncer de colon, el número de ganglios linfáticos que se deberían analizar antes de clasificar a un paciente como libre de afectación ganglionar ha sido ampliamente discutido. Se propone un modelo matemático basado en el teorema de Bayes para calcular la probabilidad de error (PE) similar al utilizado habitualmente para la evaluación de una prueba diagnóstica pero adaptado a una variable cuantitativa como es un recuento ganglionar.

Métodos

Se revisaron las historias clínicas de 480 pacientes intervenidos de forma programada de cáncer de colon con intención curativa, excluyendo los casos que presentaban metástasis de cualquier tipo. Con el fin de calcular las PE, para la serie completa y para diversos subgrupos de pacientes (tumores T2, T3, y T4) se aplicó la fórmula que proponemos basada en dicho teorema de Bayes.

Resultados

Para las probabilidades de error al clasificar un paciente como N negativo que oscilaran entre un 5% hasta un 1‰ (próximo o prácticamente 0), la mínima cifra de ganglios negativos necesarios para analizar fluctuó entre 7 y 17 respectivamente para la serie completa. Esta cifra mínima también fue cambiante para los diversos subgrupos (tumores T2, T3, y T4) considerados. Fundamentalmente, tales cifras dependen de las características de la casuística de un grupo de trabajo concreto en cuanto a prevalencia de casos N+ que manejen, y de su capacidad históricamente demostrada para recolectar e identificar ganglios positivos en los pacientes que los presentaran.

Conclusión

Desde el punto de vista matemático, el número mínimo de ganglios que se deberían analizar en el cáncer de colon para clasificar a un paciente como N negativo no es una constante. Este depende del error que se esté dispuesto a asumir para tal diagnóstico, puede estar en función de ciertos rasgos del tumor, y además, se debería adaptar a la casuística de cada grupo de trabajo.

Abstract

Introduction

In cancer of the colon, the number of lymph nodes that should be analysed before a patient is classified as free of lymph node involvement has been widely discussed. A mathematical model is proposed which is based on the Bayes Theorem for calculating the probality of error (PE) similar to that normally used to evaluate a diagnostic test, but adapted to a quantitative variable, the lymph node count.

Methods

The clinical histories of 480 patients routinely operated on in attempt to cure cancer of the colon were reviewed. Cases with any kind of mesttasis were excluded. The proposed formula based on the Bayes Theorem was applied with the aim of calculating the PEs for the complete series and for different patient sub-groups (T2, T3, and T4 tumours).

Results

For the probabilities of error of classifying a patient as N negative, which varied between 5% and 1% (near or practically 0), the minimum number of negative lymph nodes required for analysis fluctuated between 7 and 17, respectively, for the complete series. This minimum figure was also variable for the different sub-groups (T2, T3, and T4 tumours) studied. These numbers mainly depended on the case characteristics of a specific study group as regards the prevalence of the N+ cases that they dealt with, and of its historically demonstrated ability to collect and identify positive lymph nodes in those patients that had them.

Conclusion

From a mathematical point of view, the minimum number of lymph nodes that have to be analysed in cancer of the colon in order to classify a patient as N negative is not a constant. This depends on the error that is prepared to be assumed for that diagnosis, possibly depending on certain tumour traits, and also may be adapted to the cases of each study group.

Introducción

La clasificación como N negativo (pN₀) de todo paciente intervenido por cáncer de colon tiene importantes implicaciones. En primer lugar, sobre el propio pronóstico de supervivencia. En segundo lugar, sobre la indicación de tratamientos adyuvantes postoperatorios. Por lo tanto, cualquier error en esta clasificación puede tener repercusiones notables.

Hasta la fecha, la mayoría de grupos de trabajo siguen algunas recomendaciones de índole general para valorar la seguridad de una estadificación ganglionar negativa, como es la de analizar un mínimo de 12 ganglios negativos. Esta recomendación proviene de la clasificación TNM y de diversos grupos de expertos^1–5, pero tiene el inconveniente de no medir la probabilidad de error en un enfermo individualmente considerado, especialmente, si en dicho enfermo no se ha conseguido analizar ese número mínimo de ganglios. En cualquier serie de casos y por diversos motivos, siempre existe la posibilidad de que en algún paciente no se alcance esa cifra.

En 1992, Kiricuta y Tausch⁶ publicaron un modelo matemático basado en el teorema de Bayes, que permite aproximarse al cálculo del valor predictivo negativo (VPN) de cada paciente ante un número concreto de ganglios axilares analizados en el cáncer de mama. En el presente estudio se utiliza un modelo similar, con el fin de aproximarse al riesgo de error en la clasificación de un paciente como pN_0, basado en la misma ley universal de probabilidades condicionales que constituye el teorema de Bayes, tomando como ejemplo el cáncer de colon y utilizando como patrón de referencia las características históricas de una serie de casos, tal como es lícito hacer en la evaluación de cualquier prueba diagnóstica (bayesianismo empírico).

Material y método

Estudio retrospectivo de una serie de 480 pacientes consecutivos intervenidos de forma programada y con resección tumoral por neoplasia maligna de colon no metastásica en el Hospital General Universitario de Castellón durante el periodo de tiempo de 8 años, desde el 1 de enero de 1994 hasta 31 de diciembre de 2001 y que completaron un periodo de seguimiento posterior de, al menos, 5 años según el protocolo de nuestro hospital. Tras la intervención quirúrgica los pacientes fueron clasificados según la 6.^a edición de la clasificación TNM. Un total de 328 pacientes se clasificaron como pN₀. Se anotó el número de ganglios linfáticos que habían sido analizados y el número de ganglios positivos en cada paciente si es que los había. Finalmente se anotó el estado del enfermo en la fecha del último control disponible. El estudio histológico ganglionar, en todos los casos, se realizó según la técnica consistente en la identificación manual de las adenopatías, sección por la línea media y tinción con hematoxilina y eosina. No se utilizaron otras técnicas de detección como el aclaramiento de la grasa, la sección por sectores ni técnicas inmunohistoquímicas o moleculares. No intervino ningún facultativo, patólogo o cirujano, especialmente dedicado o especializado en patología colorrectal puesto que en tales fechas no estaba en funcionamiento en nuestro hospital una unidad especializada en dicha materia. Participaron un total de 16 cirujanos generales y 12 patólogos. Los criterios de radicalidad oncológica en las resecciones no fueron totalmente uniformes dentro de los estándares generales aceptados en la actualidad. En este sentido, solo 6 cirujanos practicaron por lo general ligaduras de los pedículos en su misma raíz, representando el 58% del total de las intervenciones realizadas. Sin embargo, el total de ganglios recolectados por ellos no difirió estadísticamente con respecto al grupo restante.

La aplicación del modelo matemático se deriva de la fórmula del teorema de Bayes para el cálculo de [1-Valor Predictivo Negativo] que representa la probabilidad final de error ante una clasificación ganglionar negativa:

La prevalencia de ganglios positivos [Prevalencia pN+] es un simple cociente entre el número de pacientes con algún ganglio positivo y el total de casos de la serie. La prevalencia de ganglios negativos [Prevalencia pN₀] será la cifra complementaria de la anterior [1-Prevalencia pN+]. La probabilidad de Verdaderos Negativos, o Especificidad diagnóstica, es siempre igual a 1, puesto que si el patólogo encuentra ganglios positivos no es posible la existencia de falsos positivos.

De acuerdo con Kiricuta y Tausch⁶, la probabilidad de Falsos Negativos [1-Sensibilidad diagnóstica] para una variable cuantitativa, como es un recuento ganglionar, se puede calcular aplicando una distribución hipergeométrica con 4 parámetros, que en la materia que nos ocupa serían los siguientes: (A) la suma total de ganglios aislados en todos los pacientes pN₁ y pN₂ (pN+) de la serie, o bien, de un subgrupo determinado; (B) la suma total de ganglios positivos encontrados en estos pacientes; (C) el número total de ganglios aislados en un paciente inicialmente etiquetado como pN₀; y (D) el parámetro 0, es decir, 0 ganglios positivos, que define a estos pacientes pN₀. En términos matemáticos, la distribución hipergeométrica se expresa de la siguiente manera:

De este modo, el cálculo de p(n−/N+) mediante la distribución hipergeométrica se compondrá de 4 parámetros, a saber: 1) la suma de ganglios obtenidos en la serie completa (o en un subgrupo determinado de pacientes) que hayan sido finalmente diagnosticados como N+(M, en la fórmula anterior); 2) la suma de los ganglios positivos dentro de este total de ganglios analizados (N, en la fórmula); 3) cada supuesto de un paciente concreto que se analice, es decir, el número de ganglios analizados en este paciente (n, en la fórmula), y 4) un parámetro final igual a cero que indica que en él no se hallaron ganglios positivos (m, en la fórmula)⁷.

En realidad, esta probabilidad, y la misma fórmula del teorema de Bayes, se computan fácilmente utilizando las funciones estadísticas habituales de cualquier hoja de cálculo comercial (Anexo 1). De esta manera, el valor final de [1-VPN] se refiere a un paciente concreto en el que se ha analizado un número también concreto de ganglios negativos. De ello se deriva que el número mínimo de ganglios negativos a analizar, en dicho paciente, para considerarlo como verdadero pN₀ sería aquel que produjera un valor suficientemente bajo de [1-VPN], valor que se debe de establecer de forma arbitraria según el límite de seguridad que nos impongamos.

En este estudio se ha utilizado el programa estadístico SPSS versión 15 para los cálculos descriptivos, y una hoja de cálculo Excel^® para los cálculos probabilísticos.

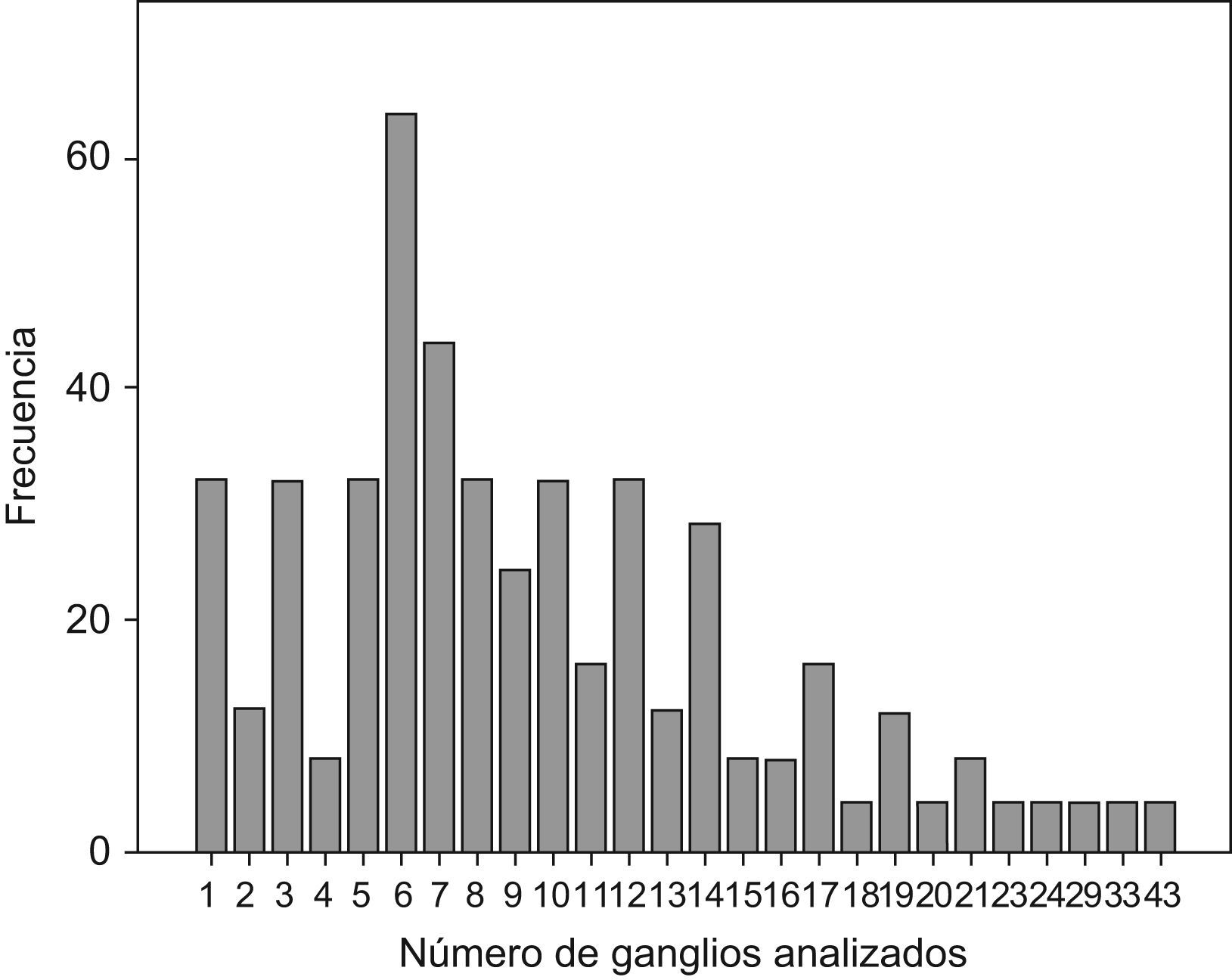
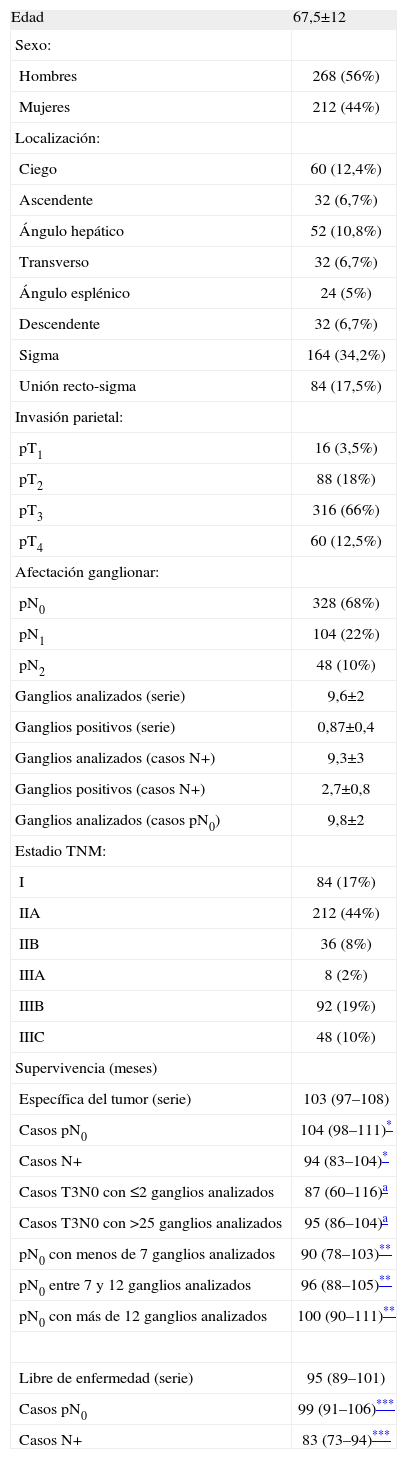
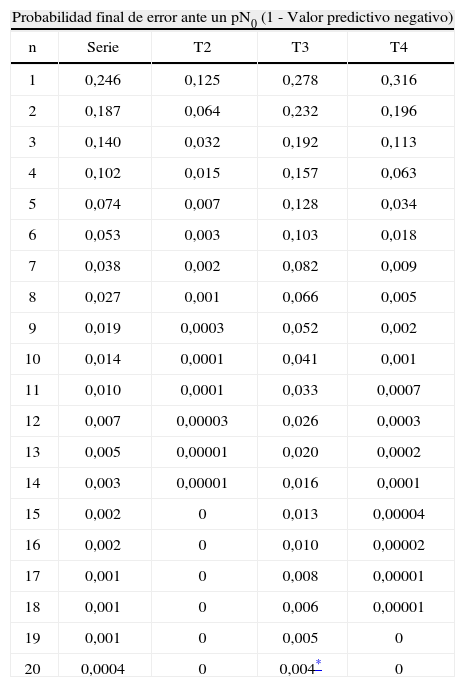
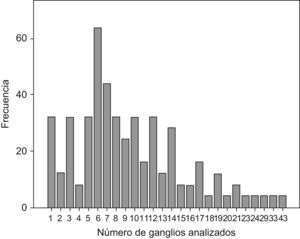
Resultados

Las características demográficas y relativas al tumor de los 480 casos analizados se resumen en la Tabla 1. En la fig. 1 se puede observar la frecuencia de cada cifra de ganglios analizados. En la Tabla 2 se muestran los rasgos de la serie necesarios para el desarrollo de los cálculos. En la Tabla 3 se muestran los resultados tras la aplicación del modelo. Se puede observar que si nos exigimos una probabilidad de error en la catalogación de un paciente como N negativo menor del 5% para la serie completa de casos, se precisaría analizar al menos 7 ganglios negativos. Sin embargo, el mínimo necesario de ganglios analizados sería 12 si el límite de error lo situamos en cifras menores del 1%, incluso debería ser de 20 o más si queremos tener una probabilidad de error menor del 1‰, límite que en la práctica podría considerarse cercano o similar a 0. Estos cálculos se repiten para ciertos subgrupos que hemos elegido simplemente como ejemplo. Así, para un paciente con un tumor T2 este límite del 1‰ se obtendría en nuestra serie de pacientes recolectando 8 ganglios negativos, mientras que para un T3 se precisarían al menos 26 ganglios negativos. Naturalmente, si para otro grupo de trabajo las cifras de la Tabla 2 que definen la capacidad de encontrar ganglios positivos fueran diferentes, estos resultados no coincidirían con los nuestros. Pero en cualquier supuesto, cifras elevadas de ganglios negativos analizados van a dar siempre probabilidades muy bajas de error diagnóstico, como es lógico imaginar. De este modo, lo que se logra con el modelo propuesto es cuantificar esta probabilidad de error diagnóstico de un modo adaptado a los rasgos de cada serie de casos o de cualquier subgrupo de pacientes dentro de una serie. Los límites de error que se quieran asumir, y por ende, el mínimo número de ganglios a analizar de acuerdo con tales límites dependerá de la autoexigencia de cada cual. Insistimos en que el objetivo de este trabajo no es fijar ninguno de estos límites sino ofrecer una manera de aproximarse a su cálculo sean cuales fueren.

Tabla 1.

Características generales de la serie analizada (480 Pacientes)

Edad	67,5±12
Sexo:
Hombres	268 (56%)
Mujeres	212 (44%)
Localización:
Ciego	60 (12,4%)
Ascendente	32 (6,7%)
Ángulo hepático	52 (10,8%)
Transverso	32 (6,7%)
Ángulo esplénico	24 (5%)
Descendente	32 (6,7%)
Sigma	164 (34,2%)
Unión recto-sigma	84 (17,5%)
Invasión parietal:
pT1	16 (3,5%)
pT2	88 (18%)
pT3	316 (66%)
pT4	60 (12,5%)
Afectación ganglionar:
pN0	328 (68%)
pN1	104 (22%)
pN2	48 (10%)
Ganglios analizados (serie)	9,6±2
Ganglios positivos (serie)	0,87±0,4
Ganglios analizados (casos N+)	9,3±3
Ganglios positivos (casos N+)	2,7±0,8
Ganglios analizados (casos pN0)	9,8±2
Estadio TNM:
I	84 (17%)
IIA	212 (44%)
IIB	36 (8%)
IIIA	8 (2%)
IIIB	92 (19%)
IIIC	48 (10%)
Supervivencia (meses)
Específica del tumor (serie)	103 (97–108)
Casos pN0	104 (98–111)^*
Casos N+	94 (83–104)^*
Casos T3N0 con ≤2 ganglios analizados	87 (60–116)^a
Casos T3N0 con >25 ganglios analizados	95 (86–104)^a
pN0 con menos de 7 ganglios analizados	90 (78–103)^**
pN0 entre 7 y 12 ganglios analizados	96 (88–105)^**
pN0 con más de 12 ganglios analizados	100 (90–111)^**
Libre de enfermedad (serie)	95 (89–101)
Casos pN0	99 (91–106)^***
Casos N+	83 (73–94)^***

media±desviación estándar; frecuencias (%); supervivencia: medias según método actuarial (intervalo de confianza al 95% de seguridad). No es posible calcular medianas porque no se alcanza en ningún grupo una probabilidad ≤50%.

¿

Valor p (Long-Rank)=0,802.

¿¿

Valor p (Long-Rank)=0,02.

¿¿¿

Valor p (Long-Rank)=0,177.

a

Valor p (Long-Rank)=0,236.

Figura 1.

Frecuencia en el número de ganglios analizados por paciente para la serie completa.

Tabla 2.

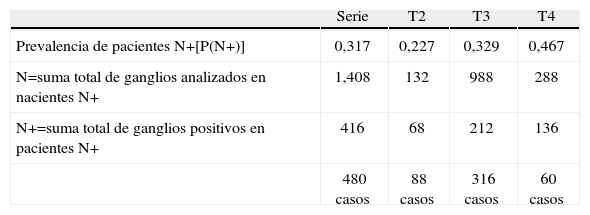
Datos necesarios para construir el modelo propuesto

	Serie	T2	T3	T4
Prevalencia de pacientes N+[P(N+)]	0,317	0,227	0,329	0,467
N=suma total de ganglios analizados en nacientes N+	1,408	132	988	288
N+=suma total de ganglios positivos en pacientes N+	416	68	212	136
	480 casos	88 casos	316 casos	60 casos

Tabla 3.

Resultados de las probabilidades de error según el número de ganglios analizados

Probabilidad final de error ante un pN0 (1 - Valor predictivo negativo)
n	Serie	T2	T3	T4
1	0,246	0,125	0,278	0,316
2	0,187	0,064	0,232	0,196
3	0,140	0,032	0,192	0,113
4	0,102	0,015	0,157	0,063
5	0,074	0,007	0,128	0,034
6	0,053	0,003	0,103	0,018
7	0,038	0,002	0,082	0,009
8	0,027	0,001	0,066	0,005
9	0,019	0,0003	0,052	0,002
10	0,014	0,0001	0,041	0,001
11	0,010	0,0001	0,033	0,0007
12	0,007	0,00003	0,026	0,0003
13	0,005	0,00001	0,020	0,0002
14	0,003	0,00001	0,016	0,0001
15	0,002	0	0,013	0,00004
16	0,002	0	0,010	0,00002
17	0,001	0	0,008	0,00001
18	0,001	0	0,006	0,00001
19	0,001	0	0,005	0
20	0,0004	0	0,004^*	0

n=total de ganglios negativos recolectados en un paciente pN₀.

¿

en losT3, para <0,001 se precisan 26 o mas ganglios negativos analizados.

Discusión

Ante todo, el modelo bayesiano ofrece una información adicional nada despreciable en los pacientes que no cumplen la recomendación de tener 12 ganglios analizados. Los factores que modifican el número de ganglios linfáticos analizados pueden agruparse, de forma sencilla, en tres categorías: 1) los dependientes de la anatomía del enfermo; 2) los dependientes de acto quirúrgico, y 3) los dependientes del estudio anatomopatológico^8,9. La principal ventaja de este modelo matemático es que adapta los resultados de cada grupo a estas tres variables.

No obstante, un valor predictivo negativo, o su valor complementario que aquí denominamos PE, no es extrapolable a otras series porque, por definición, carece de validez externa. De este modo, cada grupo de trabajo debería calcular el punto de corte del número mínimo de ganglios analizados según el modelo propuesto y un determinado límite de error. Como ha sido publicado en diferentes trabajos^10–13, las modificaciones tanto en la técnica quirúrgica como en el estudio anatomopatológico del espécimen pueden ser importantes de una institución a otra. Por esta razón, las diferencias entre los distintos centros en cuanto al número de ganglios analizados pueden llegar a ser considerables, lo que provoca, asimismo, diferencias en las probabilidades de error ante estadificaciones ganglionares negativas. De este modo, por ejemplo, no tendrá la misma probabilidad de error un equipo que realice resecciones intestinales más amplias o cuyo estudio anatomopatológico incluya técnicas de detección más sensibles como el aclaramiento de la grasa, técnicas inmunohistoquímicas o moleculares. Pensamos, pues, que las recomendaciones sobre el número de ganglios que se deben analizar para obtener una baja probabilidad de error no podrán ser universales, es decir, deberán estar adaptadas al medio en el que se realicen, a sus técnicas quirúrgicas y a sus estudios anatomopatológicos. De este modo, no existe un número mínimo y negativo de ganglios para analizar, sino que este número dependerá de la capacidad de recolección ganglionar de cirujanos y patólogos y del error diagnóstico que estemos dispuestos a asumir.

Hay que destacar que el modelo propuesto permite calcular unas probabilidades individualizadas para cada paciente del posible riesgo de mala clasificación como pN₀, a diferencia de las recomendaciones de índole general, y muy especialmente cuando estas recomendaciones no se han podido cumplir. Ahí radica su principal utilidad práctica. De hecho, la principal novedad de este modelo matemático con respecto a otros modelos basados en el teorema de probabilidad de Bayes radica en que, al utilizar para los cálculos únicamente los datos de los pacientes con algún ganglio linfático afectado [lo referido a la prevalencia de pacientes con ganglios positivos P(N+) y a la insensibilidad o tasa de posibles falsos negativos P(n−/N+)], permite la individualización de los resultados y su adaptación en el tiempo, si es que cambiaran las circunstancias operativas del grupo de trabajo. El modelo se actualiza automáticamente conforme añadimos los datos de nuevos pacientes. De este modo, un grupo de trabajo que, de forma habitual, detecte más ganglios linfáticos tendrá unos resultados, en cuanto a seguridad diagnóstica, distintos de aquellos grupos en los que la capacidad de detección sea inferior. Esta característica se deriva de la naturaleza de los cálculos de probabilidades que permite el teorema de Bayes. Las recomendaciones generales que conocemos derivan de los métodos estadísticos clásicos, como la estadística multivariante, los cuales no permiten una interpretación individualizada de las probabilidades obtenidas, sino solo dentro de un conjunto de casos considerados globalmente. El hecho de clasificar a un paciente como pN₀ es el resultado de efectuar un diagnóstico como otro cualquiera, por lo tanto, está sujeto a las mismas leyes probabilísticas que rigen cualquier proceso diagnóstico, definidas por el teorema de Bayes o teorema de las probabilidades condicionales, en lo referente a la probabilidad final de ser cierto o falso. En este sentido, nuestro modelo tiene una validez indiscutible puesto que se aplica la misma fórmula y se siguen los mismos pasos que en cualquier proceso de evaluación de una prueba diagnóstica. Sin embargo, al manejar variables cuantitativas, como lo son los recuentos ganglionares, los cálculos son algo más complejos aunque perfectamente accesibles desde una hoja de cálculo de un ordenador personal (Anexo 1).

Diversos autores han investigado la cifra mínima de ganglios negativos a analizar para validar un estadio pN₀ o una correcta clasificación ganglionar en el cáncer de colon^14–24, utilizando métodos de estadística no bayesiana, generalmente pruebas multivariantes como la regresión de Cox. Curiosamente, son métodos mucho más complejos porque precisan de potentes programas de estadística y no de simples hojas de cálculo. Los resultados son dispares entre ellos, como lo serían con el modelo aquí propuesto. Esto se debe a las diferentes características de los casos que componen las diversas series analizadas, porque ni la prevalencia de casos N positivos, o negativos, ni la sensibilidad diagnóstica puede ser idéntica para todos los grupos de trabajo.

La recomendación de 12 ganglios que muchos han propuesto y aceptado^3–5 es una recomendación con intención de ser universal, por lo tanto, tiene que ser necesariamente una recomendación muy segura, como lo son las señales de tráfico que limitan la velocidad. De hecho y para el global de nuestros casos, analizar 12 ganglios negativos en un paciente supondría una probabilidad de error diagnóstico menor del 1%, que ya puede considerarse ciertamente baja. A no ser que tal recomendación se interprete como una ley absoluta, nuestro modelo bayesiano puede añadir los matices necesarios, y la información precisa, sobre en qué pacientes en los que no se han conseguido 12 ganglios es posible asumir, sin demasiado riesgo de error, que son verdaderos pN₀ y que por ello tengan quizás un mejor pronóstico que aquellos que pudieran ser realmente pN₁ o pN₂. Es bien conocido por todos que no siempre se consigue analizar 12 ganglios en el cáncer de colon^25–28 y no resulta despreciable en estos casos tener una información adicional sobre qué riesgo se corre de mala clasificación.

Como conclusión, afirmamos que es posible individualizar el riesgo de una clasificación ganglionar negativa errónea en el cáncer de colon resecado calculando su probabilidad de acuerdo con el teorema de Bayes. Además, puede ser un buen complemento para la recomendación de obtener un mínimo de 12 ganglios para clasificar correctamente el estado ganglionar de estos pacientes, muy especialmente, el estado ganglionar negativo cuando no se ha cumplido tal recomendación. En el momento actual, las implicaciones son importantes en cuanto a ofrecer una buena información adicional, y posiblemente, podría tener incluso implicaciones terapéuticas en las discusiones individuales, por ejemplo, sobre un paciente dado en un Comité de tumores al aportar tal información complementaria.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.