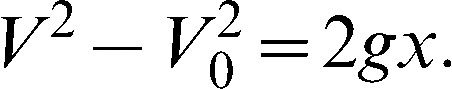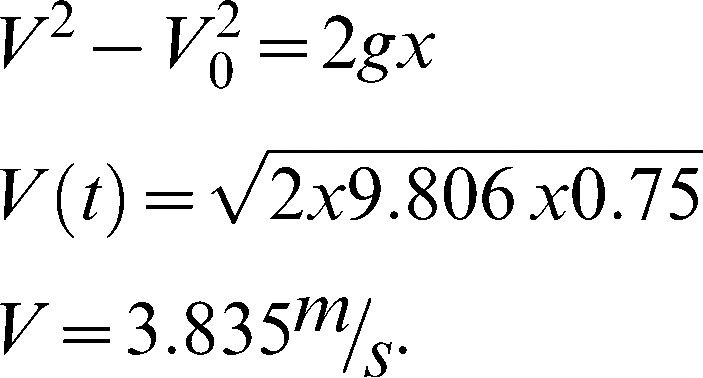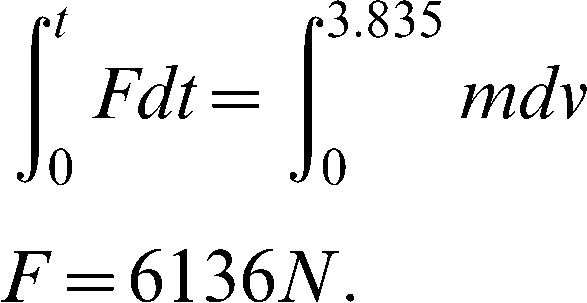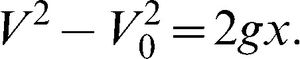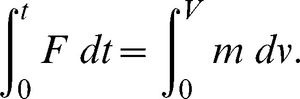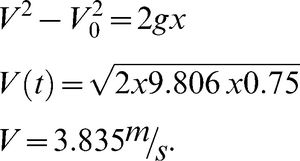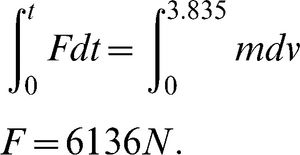Preliminary analysis of knee stress in Full Extension Landing

OBJECTIVE

This study provides an experimental and finite element analysis of knee-joint structure during extended-knee landing based on the extracted impact force, and it numerically identifies the contact pressure, stress distribution and possibility of bone-to-bone contact when a subject lands from a safe height.

METHODS

The impact time and loads were measured via inverse dynamic analysis of free landing without knee flexion from three different heights (25, 50 and 75 cm), using five subjects with an average body mass index of 18.8. Three-dimensional data were developed from computed tomography scans and were reprocessed with modeling software before being imported and analyzed by finite element analysis software. The whole leg was considered to be a fixed middle-hinged structure, while impact loads were applied to the femur in an upward direction.

RESULTS

Straight landing exerted an enormous amount of pressure on the knee joint as a result of the body's inability to utilize the lower extremity muscles, thereby maximizing the threat of injury when the load exceeds the height-safety threshold.

CONCLUSIONS

The researchers conclude that extended-knee landing results in serious deformation of the meniscus and cartilage and increases the risk of bone-to-bone contact and serious knee injury when the load exceeds the threshold safety height. This risk is considerably greater than the risk of injury associated with walking downhill or flexion landing activities.

INTRODUCTION

Extended-knee landing applies a significant impact load on the limited contact area of the knee components, thereby causing great stress and increasing the risk of injury. Approximately five million people visit orthopedic surgeons annually because of knee problems, and approximately 1.1 million people are admitted to hospital emergency rooms as a result of knee injuries caused by unusual activities (1). The human knee is capable of bearing loads of up to 2.5 times body weight (BW) while walking and more than 12 times BW while running and jumping (2). During knee flexion while landing, the muscular system acts as the primary active absorption mechanism; however, the tibia-fibula plays the most important role in dampening the impact (3–5). In contrast, during extended-knee landing, the insufficiency of energy dissipation produced by the body's lower extremity muscles is coupled with the excessive ground reaction force (GRF). The GRF increases the impact stress and aggravates the risk of injury when landing from a particular height (2,6–10). The knee acts as the primary shock absorber in bilateral foot landing, whereas the ankle and hip extensors are the second largest contributors to the absorption of energy (11). The greater magnitudes of GRF, peak posterior shear stress and knee co-contraction index occur between the 0° and 25° knee flexion landing positions (12–14). At the same time, the risk of knee damage increases during extended-knee landing because of the lack of energy dissipation in the lower extremities, which in turn causes significant compressive fracture loads during this type of landing (15-17).

Voigt et al. (16) studied the muscular and mechanical parameters in maximal vertical jumping performance. Selbie and Caldwell (17) investigated the effects of different postures on the amount of force applied to the knee joint. The majority of earlier studies investigated the final stress and the effects of other parameters on the entire moving mechanism as an integrated dynamic system, which included the muscles and ligaments in contact forces (18–21). The effects of all of these parameters on the knee contact pressure complicate the calculation. Kuster et al. (22) reported that three effective parameters (i.e., bone-to-bone contact, muscle force and GRF) exhibited pressures equal to eight, six and two times BW, respectively, during downhill walking. However, only a limited number of investigations have studied the risks of knee-joint injuries as the result of performing activities that involve a flexed knee (1,15,23). The current study analyzed possible deformations that can lead to bone-to-bone contact and, subsequently, to the risk of serious injuries to the knee joints as a result of extended-knee landing.

This study used experimental and numerical methods to identify the critical impact force on the knee joints during extended-knee landing from threshold heights. Finite element analysis (FEA) ABAQUS software (ABAQUS Inc., 108 Providence, RI, USA) was used to identify the contact areas and the effects of stress on the meniscus, tibial and femoral cartilage after, landing based on the extracted force from the experimental data. Moreover, FEA was used to analyze the contact pressure variations and stress distributions of the main deformable knee components. The results revealed a significant deformation in the components of the knee joints during landing, which increased the risk of bone-to-bone contact during extended-knee landing. The values of stress and impact force could be applicable to the unpredictable conditions of several sporting activities, such as skydiving and skiing on water and snow. Moreover, threshold stress could be considered when designing methods to enhance the performance of artificial knee materials.

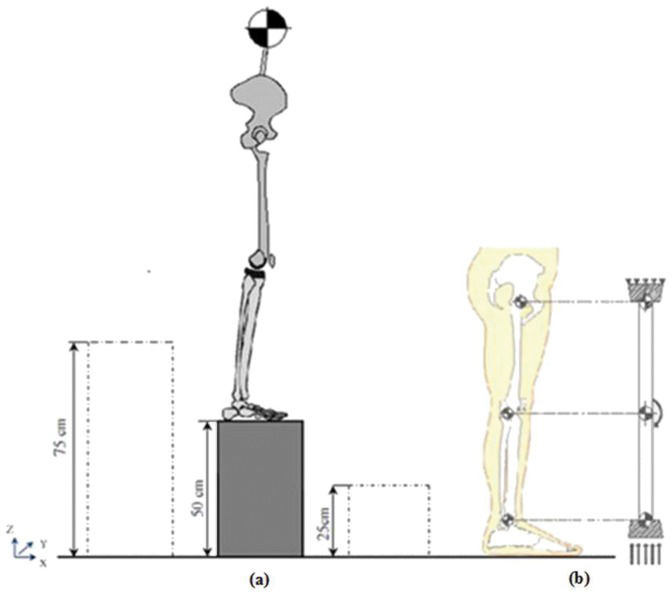
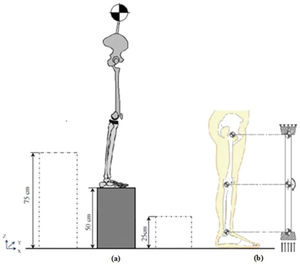
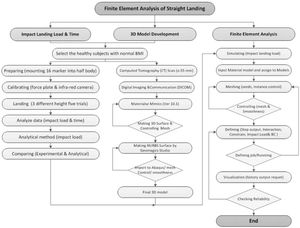
MATERIALS AND METHODS

Experimental analysis

Experimental data were collected at the Motion Analysis Laboratory of the Faculty of Engineering of the University of Malaya. The university's ethics committee approved the study, and all of the subjects provided written informed consent. A physical therapist from the university sports department verified that the selected five subjects were physically healthy and had no history of lower limb joint injury or instability. The subjects had an average weight of 64 kg, average BMI of 18.8 and average age of 24 years and 8 months old. Each subject landed on a force plate from three different heights (25, 50 and 75 cm), and five individual trials were performed for each height. Vertical impact loads and time were measured and compared via analytical examination. One-way repeated measures ANOVA was used to evaluate the effects of landing from the three heights. Prior to the test, the subjects warmed up by cycling for 10 minutes with a low workload. Following the warm-up, the subjects performed double-flexion landings on the force plate from the predetermined heights. Both knee joints of each subject were braced using a Contender Knee Brace (Corflex, UK) to ensure that the knee hinge was fixed in full extension, to prevent any unintentional flexion and to maintain the knee in a straight position during landing. The landing force, impact period (the interval between the time the subjects touched the “Kistler” force plate and the maximum load) and velocity were recorded for every trial. Markers were attached to the subjects at various locations on their body according to the Helen Hayes (Davis) marker placement system. The cameras (Vicon), force plate (Kistler) and markers were calibrated prior to the testing. Body motion was captured upon landing using seven infrared calibrated cameras that recorded data at a frequency of 200 Hz. The results were analyzed using Vicon Nexus 512 software (Figure 1).

Figure 1.

Force simulation of free extended-knee landing.

Theoretical analysis

The peak vertical ground reaction force (N) and the impact time (ms) were recorded for every landing. Moreover, the impact time and force were theoretically calculated and were compared with the corresponding experimental results. Given that the maximum distance (75 cm) caused the highest landing velocity and greater risk of more serious injury, this velocity was determined using Equation 2.1:

V₀ and V refer to the initial and final speed of the subject (m/s), respectively, when standing on the platform and having finally touched the force plate, g is equal to 9.8 m/s ², and x is the height in meters. The force was determined from Equation 2.2, while the timing was extracted from the maximum heights of the jump:

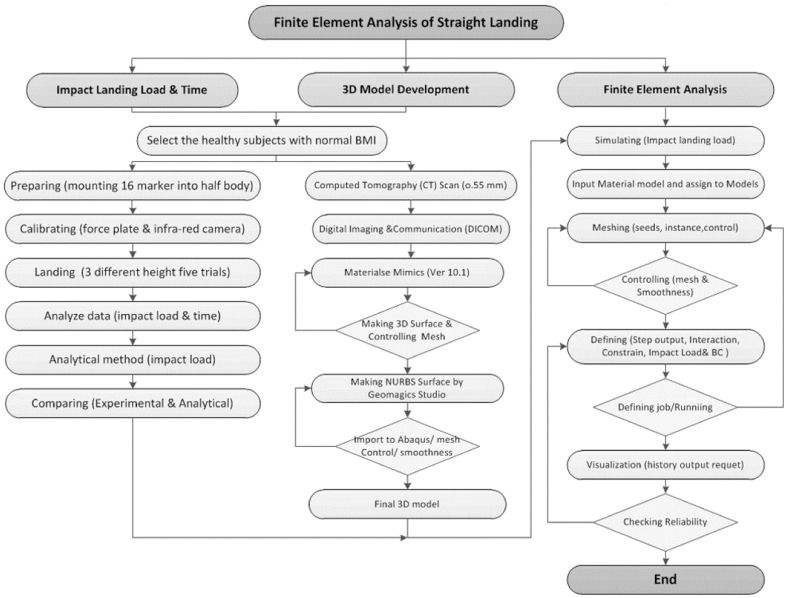
As part of the preliminary FEM analysis, the desired experimental data (impact load and timing) were applied to the developed three-dimensional (3D) model using the FEA software. Dynamic explicit analysis was used to calculate the contact pressure and stresses during extended-knee landing. The data analysis process that was applied in this study is presented in Figure 2.

Figure 2.

General part development and finite element analysis flowchart.

Geometry development

A geometric 3D data model was developed by obtaining 2D images of the whole leg using a computed tomography (CT) scan (Siemens Somatom Sensation 16). The resulting data were developed at 0° flexion, based on the scanned images of the entire leg of a 24-year-old subject. The volumetric 3D images of both legs consisted of parallel digital images with a 0.539 mm slice thicknesses on the sagittal, coronal and axial planes, each of which was measured by an in-plane pixel resolution of 512 pixels ×512 pixels. The 2D images were converted to 3D surface models using MIMICS software. GEOMAGIC STUDIO (version 11.7) was used to convert the resultant triangular meshes from MIMICS into a smooth, non-uniform, rational B-spline (NURBS) surface. Thereafter, the knee components were imported into ABAQUS FEA software.

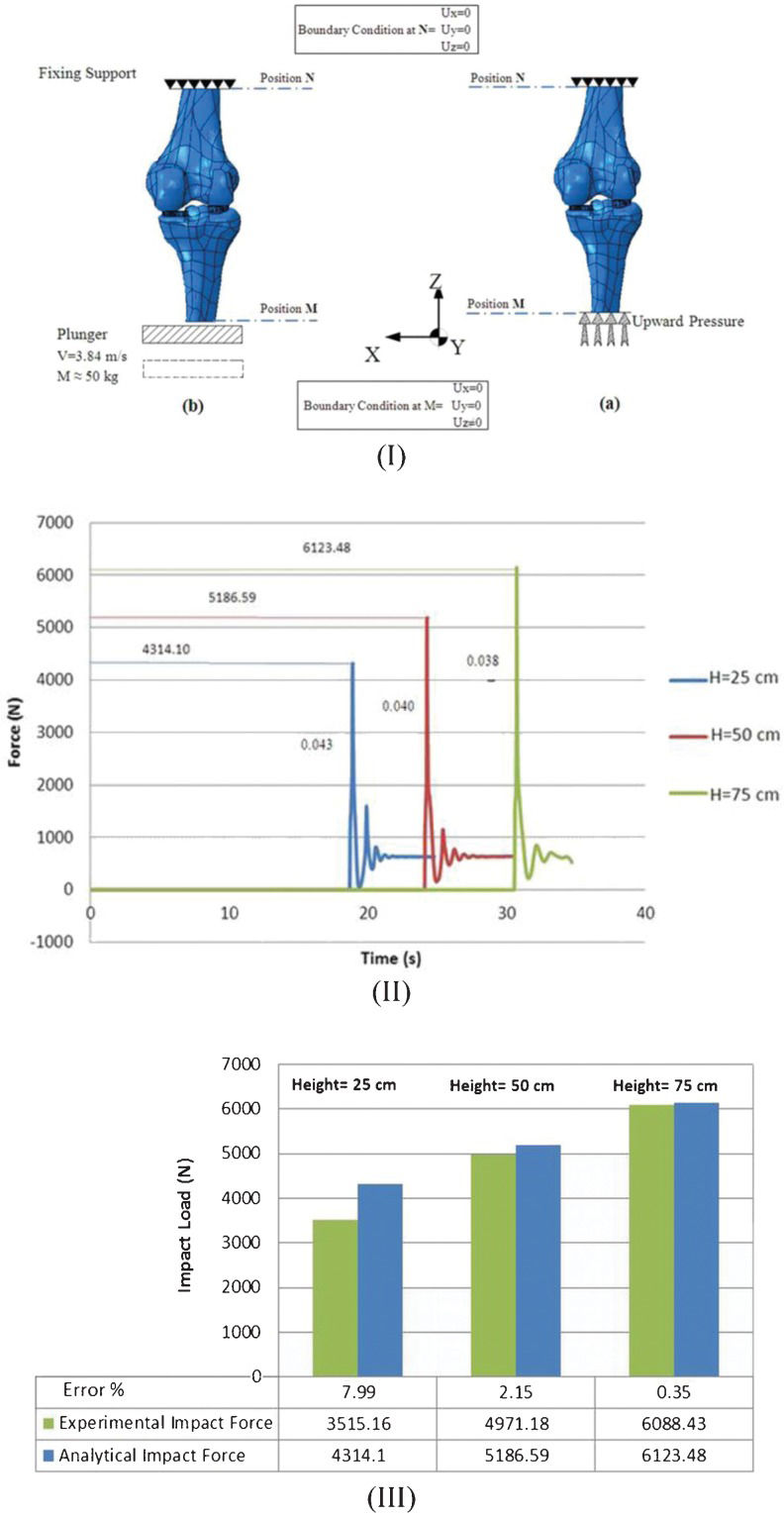
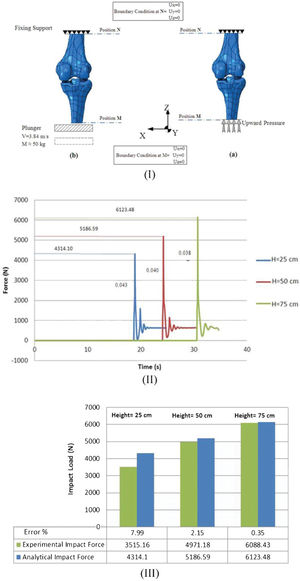
Knee structure simulation

The human knee has complex geometries, and adequately modeling this joint can be significantly challenging (24,25). The knee was placed in a closed-packed position (lock position) during extended landing, which minimized the possibility of rotation and increased the rigidity, to transfer the energy to the knee (26,27). This position is usually at the extreme end of the range of motion (ROM), in which the joint surfaces are maximally congruent, whereas the ligaments and capsules provide the greatest stability against tensile forces and are completely taut (28,29). Landing with the bilateral braced knee confines the knee's side movements and causes the landing force to pass through the knee-joint components and compress the distance between the tibia and the femur. A developed safety mechanism was added to the brace. It unclasped if the load extended beyond the threshold and did not allow the subjects to be injured. The ACL only reacts under tension loading and cannot withstand axial compression force; consequently, it could be omitted in the compression FE analysis. In flexion landing, the contribution of the muscles to the dissipation of kinetic energy decreases through the reduction of the flexion angle; the minimum contribution corresponds to a 0° flexion angle (23,30). The inability of the lower extremity muscles to dampen the impact load adequately during full-extension landing causes major impact load transfer to the knee-joint components. In the current study, the poor contribution of muscles toward dampening the landing force was deduced from the total applied load in the FEA simulation. A simplified fixed-hinge mechanism was chosen to simulate the behavior of the whole leg in extended-knee landing (Figure 1-b). The instant load was applied in an upward direction, while the rotation of the knee (middle-hinged) was fixed (Figure 3-I-a).

Figure 3.

I-a Moving plate with specified velocity (b) applying instant load to (II) vertical impact force across different heights (III) Analytical and experimental comparison of impact force across different heights.

Material and boundary conditions

The behavior of the knee-joint components (meniscus and cartilage) changes according to the analysis condition (i.e., the type [static or dynamic], load direction [tension or compression] and loading time) (31). This behavior complicates the identification of the exact material behavior from the predefined material FEA model. The biphasic (solid and fluid) and time-dependent behaviors of the meniscus and cartilage depend on both the magnitude and rate of loading (32). In the present study, instant loading (Figure 3-II) did not allow the meniscus or cartilage to reach the fluid phase and present their viscoelastic behaviors, wherein the impact load is less than 1 s (33). Thus, the mechanical properties of the solid phase were considered to be biphasic (34,35). Given that extreme strain occurs in the Z-direction (other directions were confined), the mechanical analyses were determined in the vertical direction (36). The material behaviors of the tibia, femur, meniscus and cartilage were assumed to be isotropic linear elastics (37,38). Their properties were derived from the existing literature (Table 1-I).

Table 1.

(I) The mechanical property of knee components. (II) Knee component's finite element data.

Name	Young's modulus (MPa)	Poisson's ratio	Density (kg/m^3)	Reference
Tibia/Femur	11000	0.3	180 1800-2100	(45), (46)
Cartilage	5	0.46	1000	(31), (47)
Meniscus	59	0.49	1500	(47), (48)

	Tibia	Femur	Femoral Cartilage	Tibia Cartilage	Meniscus	Total
Volume (m^3)	7.26E-05	1.08E-04	1.02E-05	7.55E-06	2.60E-06	2.01E-04
Mass (kg)	0.152	0.226	1.15E-02	7.55E-03	3.90E-03	0.402
Nodes	49411	10620	45579	1045	44534	151189
Elements	27975	5770	26681	4.15E+02	26266	87107

Two methods were adopted in this study for the purpose of a free-falling dynamic impulse load simulation. In the first case (Figure 3-I-a), an equivalent instant load was applied in an upward direction from the excised tibia during full extension. The femur was considered to be constrained fully (six degrees of freedom), whereas the tibia moved in a vertical direction to transfer the impact load to the entire structure. The surface-to-surface contact among the tibia plateau cartilage, articular cartilage and meniscus was defined as a tie; their movements were simultaneously confined, with the exception of the vertical direction. Both the proximal femur and the distal tibia were fully fixed. In the second case (Figure 3-I-b), a plunger with a weight equal to the subject's mass and landing velocity (velocity when the subject touched the force plate, Equation 1) occurred in the Z direction to the M position of the tibia, to duplicate the same landing force that was produced during landing.

The applied pressure on the tibia was 14 MPa, and the cross-sectional area of the cut tibia was 381.83 mm², which corresponded to an applied force that was almost 11 times BW. The finite element data of the knee components are summarized in Table 1-II.

RESULTS

Experimental and theoretical impact force

The applied load on the feet during free landing varies according to the height, ground softness, footwear softness, joint flexion, landing positions and direction. Three different vertical landings are illustrated in Figure 3-II. The magnitude of the load was increased via height increments, whereas the impact time decreased. Considering that no significant differences were found among the falling periods from various heights, the impact time (impact duration) was quite short. Therefore, an average time of 0.04 s was applied in the analysis. The landing lag time was 20 s (subject's delay time in every landing), but to obtain appreciable graph clarification, a 5-s lag time was added to each landing time until the point at which the fluctuation of the subsequent landing was stabilized in terms of BW. The velocity of the subject during free-fall from a height of 75 cm could be estimated using Equation 3.1:

The average impact time derived during the experimental test was equal to 0.04 s. This time allows that the impact load to be identified using the following equation:

The values of the average theoretical, experimental impact forces and error percentages across the five trials are similar to those shown in Figure 3-III.

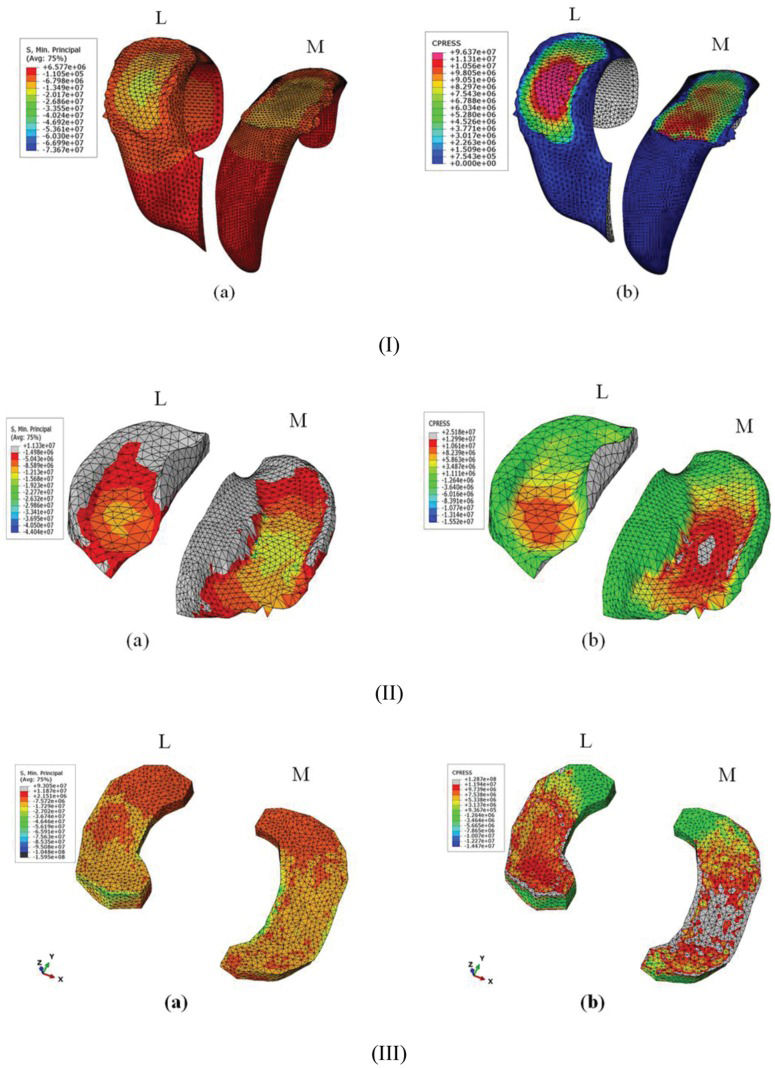
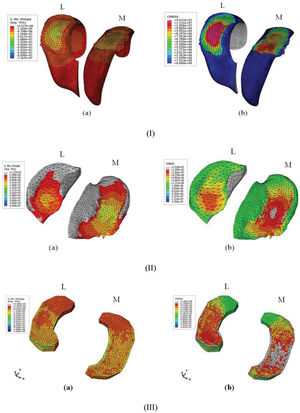
Stress and contact pressure distribution

The stress distribution and contact pressure of the femoral cartilage during extended-knee landing, with an impact load from a height of 75 cm, are shown in Figures 4-I-a and b, respectively. At a pressure of -13.5 MPa, the compressive stress on the lateral femoral cartilage was greater than that on the medial cartilage, which was recorded at -6.8 MPa. Moreover, the peak nodal stress of -60.3 MPa on the penetrated wall in the lateral area was greater than that in the medial area (-46.9 MPa). Both tail sides carried a stress value of +6.6 MPa. As illustrated in Figure 4-I-b, the sections in which a pressure of 96.4 MPa was applied at the center of the convex area in the lateral femoral cartilage were considerably larger than the medial sections, with the stressed area at 11.3 MPa. In addition, the pressure around the penetrated wall on both sides was observed at 2.3 MPa. The instant load was applied in 0.04 s, which caused significant deformation. The convex shape of the femoral cartilage allowed for fewer contact points and caused high-compression stress deformation. In addition, the defined material model might not have fully supported the real viscoelastic behavior of the cartilage to show smooth energy absorption during the impact load.

Figure 4.

I) Maximum stress on the femoral cartilage and b) the contact pressure on the femoral cartilage; II) a) the maximum stress on the tibial cartilage and b) the contact pressure on the tibial cartilage; III) a) the maximum stress on the meniscus and b) the contact pressure on the meniscus.

The compressive stress on the tibial cartilage is depicted in Figure 4-II-a. The femoral cartilage was notably the first knee-joint component exposed to the impact force (upward load). Therefore, this component absorbed the greatest impact. As such, the penetration and stress concentration must have been higher in the femoral cartilage. The medial tibial cartilage (12.1 MPa) was similarly found to have withstood more stress than the lateral cartilage (8.6 MPa). Furthermore, the pick nodal stress value of the medial cartilage in the penetrated wall was 33.4 MPa. Given that the Young's modulus of the meniscus is approximately 10 times that of the cartilage, cartilage deformation should be greater than that of the meniscus when transmitting the impulse load. As demonstrated in Figure 4-II-b, the contact pressure in the medial cartilage was greater than that in the lateral cartilage, thus producing greater pressure on the medial cartilage (25.2 MPa) than on the lateral cartilage (13.0 MPa).

The contact area of the medial meniscus was much greater than that of the lateral meniscus, and the peak value of the contact area was observed at 56.19 and 7.57 MPa on the peripheral and central areas, respectively (Figure 4-III-a). The peak contact pressure value was recorded at 128.7 MPa, with an average of 11.94 MPa, whereas the peak contact area on the anterior of the lateral meniscus was recorded at an average pressure of 9.739 MPa (Figure 4-III-b).

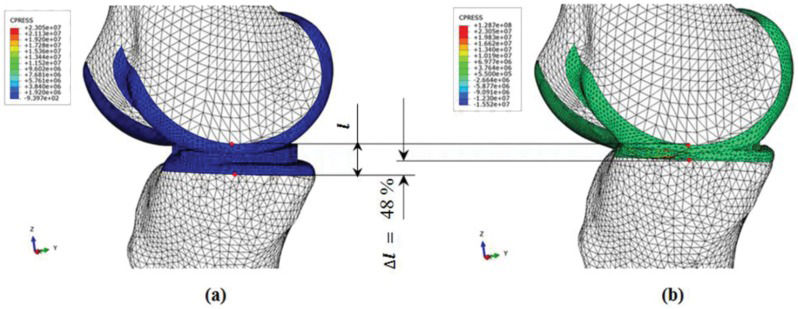
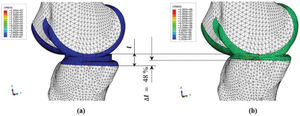
This contact pressure caused depressions among the tibial cartilage, femoral cartilage and meniscus. This depression was measured between two nodes before and after the maximum height landing. The contact pressure during the first landing height was 23.1 MPa, which increased to 128.7 MPa for the last landing height. The depression percentage (Δl, contraction of knee-joint components) was approximately 48%. Previous studies have revealed that significant injuries can occur if the distance between the tibia plateau and the femoral condyle decreases by up to 50% of its normal distance (29,39). The knee during this test approached the lower limit for the incidence of significant injuries (Figure 5).

Figure 5.

Maximum penetration of the knee joints: a) the distance before landing and b) the distance after landing.

DISCUSSION

This study focused on FEA and a simulation model of human legs during free-fall extension landing with the aim of identifying the critical stress distributions and contact pressure on the knee components. The results indicate that the applied impact loads during extended-knee landing were relatively greater than they were during knee flexion during landing (28,40). Several studies have indicated that the greatest fracture stress can occur as a result of repetitive impact stress, which is induced during running activities (15,26,41). However, the stress measured during extended-knee landing was far greater than that produced during running activities and that the stress was applied instantly might have resulted in serious damage. As such, safety factors should be considered for all predicted critical conditions (42) to offer more reliable structures for artificial knee components.

The maximal stability and greatest risk of injury occur when the knee joint locks in full extension during an upright standing position (13,39,43). However, the femoral condyles roll and glide in their contact positions and act as a hinge that serves to decrease direct knee-impact force. If the impact loads had been applied directly to the tibia without considering knee flexion and bone buckling, the results would have been high stress, deformation and pain. People bend their knees unintentionally during landing to transform the direct load to moment, which allows the impact to be dampened by the muscles, instead of the knee structure. The impact force during landing is extremely high, causing the corresponding high deflection in the vertical direction to exceed the threshold stress (maximum tolerable stress), which causes contact between the tibia and the femur.

Furthermore, the central mass of the human body produces a moment, which causes the knee to react by bending. Nigg et al. (6) discussed the observed maximum flexion during jumping activities. Piazza et al. and Kuster et al. (22,44) illustrated that the impact load during flexion while walking downhill was shared by three types of reaction force: bone-to-bone compressive force, muscle force and GRF, with pressures equal to eight, six and two times BW, respectively. During extended-knee landing, the majority of the force is dampened by bone-on-bone contact and GRF. This force is significantly greater than that demonstrated during flexion landing. The off-centricity of the center of mass of the human body can cause the tibia to rotate after landing to stabilize the body.

In the present study, the severity of extended-knee landing was investigated. Significant deformation occurs within the knee components, meniscus and cartilage during full-extension landing as the result of a lack of energy dissipated in the lower extremity. This state increases the risk of bone-on-bone contact and knee injury. This risk is considerably greater than the risk of injury associated with walking downhill or flexion landing activities. The computed stress value could be of use in artificial knee components or in the geometrical design of these components, which could be used in related industries and in future studies.

AUTHOR CONTRIBUTIONS

Makinejad MD conducted the experimental and FE analysis and data analysis and assisted in writing the manuscript. Abu Osman NA was the main investigator of the project, prepared the experimental facilities and edited the manuscript. Wan Abas WAB was the co-investigator of the project and prepared the testing facilities. Bayat M assisted the author with the FE analysis and in writing the manuscript.

ACKNOWLEDGMENTS

This research was supported by a Malaysia UM/MOHE/HIR grant (project no. D000010-16001).