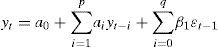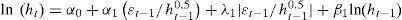El objetivo de este trabajo es analizar el riesgo de mercado de dos tipos de fondos de inversión: SIEFORE básica 1 (SB1) y SIEFORE básica 2 (SB2).Para hacer esto, se propone un índice de rendimientos que se utilizará en modelos ARIMA-GARCH, y varias de sus extensiones, con el fin de examinar el comportamiento dinámico de los rendimientos y la volatilidad de las mencionadas sociedades de inversión. Asimismo, se analiza el premio al riesgo de ambos tipos de fondos. Uno de los resultados relevantes de la investigación es que los rendimientos obtenidos por estas sociedades, durante el periodo estudiado, no son suficientes para compensar el riesgo adicional asumido por los fondos de pensiones que incluyen componentes de renta variable. Por último, se hacen algunos comentarios, en materia de política de inversión, sobre la forma en que se está midiendo y administrando el riesgo de mercado en dichos fondos.
The aim of this paper is to analyze the market risk of two types of investment funds, Basic SIEFORE 1 (SB1) and Basic SIEFORE 2 (SB2). To do this, we propose a performance index that will be used in ARIMA-GARCH models and some of its extensions, with the purpose of examining the dynamic behavior of the returns and their volatility on such investment funds. Moreover, the risk premium of both types of funds is analyzed. One of the relevant research results is that yields obtained by these funds in the period studied, are not sufficient to offset the additional risk assumed by the pension funds including equity components. Finally, some remarks are made, on investment policy, about the market risk and how it is being measured and managed in these funds.
Uno de los propósitos del actual sistema de pensiones, clasificado como sistema de contribuciones definidas y bajo el cual se encuentra la mayoría de los trabajadores formales en el país, es que los recursos depositados en las cuentas individuales de los trabajadores, que se concentran en los fondos de inversión llamados Sociedades de Inversión Especializadas en Fondos para el Retiro (SIEFORE) sean suficientes para que los trabajadores tengan un retiro digno con su ahorro acumulado. Por esta razón, estos fondos deben obtener la rentabilidad más alta posible y evitar que incurran en riesgos innecesarios que pongan en peligro el ahorro de los trabajadores para su retiro.
El sistema de pensiones que prevalece actualmente en el país es conocido como AFORES, aunque en realidad estas siglas corresponden a las administradoras de los fondos que canalizan los recursos de los trabajadores. La principal característica de este sistema —que reemplazó al esquema tradicional de reparto o de beneficios definidos— es que es administrado por el sector privado a través de cuentas individuales que concentran las aportaciones tripartitas provenientes de trabajadores, empleadores y gobierno. En este esquema el tiempo mínimo de cotización es de 25 años y la pensión dependerá de la situación de cada trabajador. Lo anterior significa que el monto que tendrá el trabajador para su jubilación dependerá del tiempo durante el cual haya cotizado, de las cantidades depositadas y de los rendimientos que se hayan generado y acumulado en su cuenta individual a lo largo de su vida activa. Esta última característica está ligada a los movimientos de los mercados financieros, ya que los recursos de los trabajadores en fondos de inversión conocidos como Sociedades de Inversión Especializadas de Fondos para el Retiro (SIEFORE) se destinan a la compra de instrumentos financieros cuyos rendimientos dependerán de los movimientos de los precios de los activos que conforman los portafolios de inversión.
Con el propósito de que las sociedades de inversión destinadas a las pensiones puedan ofrecer a los trabajadores, una vez que se jubilen, un nivel de subsistencia por encima del mínimo garantizado por el gobierno, las autoridades han anunciado múltiples modificaciones al régimen de inversión para procurar que los fondos obtengan la rentabilidad más alta posible evitando riesgos innecesarios; esto permitirá la creación de distintos tipos de fondos de inversión con diferentes niveles de riesgo.
El objetivo de este trabajo es realizar un análisis comparativo del riesgo de mercado en que han incurrido las SIEFORE básicas 1 y las SIEFORE básicas 2. Para lograr lo anterior se construyó un índice con los precios de cierre diarios1 de las sociedades de inversión que cotizaron entre el 1 de julio 1997 y el 31 diciembre de 2010 para las SB1, y del 1° de septiembre de 2004 al 31 de diciembre de 2010 para las SB2. Posteriormente, el comportamiento de los índices acumulados diarios de las SB1 y de las SB2 se modelan con procesos ARIMA-GARCH, y varias de sus extensiones con el fin de examinar el comportamiento dinámico de sus rendimientos y su volatilidad. Asimismo, se hacen algunos comentarios en materia de política de inversión sobre la forma en que se está midiendo y administrando el riesgo de mercado en dichos fondos.
Este trabajo se organiza en seis secciones. En la siguiente sección se presentan las principales características del sistema pensionario del país y se proporciona una visión general del riesgo que asumen los trabajadores en este tipo de sistemas pensionarios; después se muestran los periodos que se eligieron para el análisis de la volatilidad y la metodología utilizada en el análisis comparativo, incluyendo la usada en la construcción del índice acumulado diario, los modelos autorregresivos y la prima de riesgo; más adelante se muestra el comportamiento general de los tipos de fondos de pensión estudiados; posteriormente, se presentan los resultados y el análisis del desempeño de las SIEFORE básicas 1 y 2; por último, se ofrecen las conclusiones.
Panorama general del sistema pensionario del paísEl sistema pensionario de contribuciones definidas empezó a funcionar en julio de 1997. Actualmente, incluye a la mayoría de trabajadores formales del país porque beneficia a los trabajadores del Instituto Mexicano del Seguro Social (IMSS) y a aquellos que cotizan en el Instituto de Seguridad y Servicios Sociales para los Trabajadores del Estado (ISSSTE), quienes se incorporaron a este sistema pensionario en diciembre de 20082. A pesar de incluir a gran parte de los trabajadores en activo del país, este nuevo sistema pensionario aún coexiste con el esquema tradicional de reparto con beneficios definidos, el cualincluye a los trabajadores que cotizan en empresas paraestatales como la Comisión Federal de Electricidad (CFE), Petróleos Mexicanos (PEMEX) y Nacional Financiera (NAFIN), aunque la tendencia es que estos fondos de pensión también se transformen en esquemas de contribuciones definidas y se manejen mediante cuentas individuales de manera privada.
Este sistema reemplazó a los esquemas tradicionales de pensiones que administraba el IMSS desde 1943. El primero que se utilizó suponía la creación de reservas con las aportaciones que los trabajadores activos hacían durante su vida laboral para que, años más tarde, con este fondo se financiara su retiro, pero una vez que las reservas del fondo se agotaron, este esquema se modificó a uno de reparto. El sistema anterior funcionó bien mientras se mantuvo una cantidad pequeña de pensionados con respecto al número de trabajadores activos. Sin embargo, factores demográficos como el envejecimiento de la población gracias a los avances de la medicina; la reducción de las tasas de natalidad y de mortalidad infantil; el crecimiento de la proporción de los trabajadores pensionados con relación a los trabajadores activos y factores de naturaleza diversa como las condiciones de jubilación establecidas, especialmente aquellas referentes a la edad de retiro; aunadas a una administración deficiente que canalizó gran parte de los recursos de las pensiones hacia otros servicios para el trabajador, en especial hacia los servicios de salud, fueron las razones principales que provocaron que el esquema pensionario de reparto (beneficios definidos) pasara a uno de cuentas individuales (contribuciones definidas). Alrededor de 1995, el IMSS proyectó que si se continuaba con el sistema tradicional de pensiones sin ninguna modificación sólo hasta 2005 se podría mantener un superávit y a partir de esa fecha se generaría un déficit de rápido crecimiento, el cual sería muy costoso de financiar para el año 2020. Sin embargo, aunque hubo diversas opiniones sobre la magnitud del déficit que el gobierno federal tendría que asumir, tanto estudios efectuados dentro del IMSS (1995) como el Proyecto de Reforma (1998), que se presentó ante el Banco Mundial, así como investigaciones de analistas externos (Espinosa-Vega y Tapen, 2000; Ham, 2000), que analizaron la incidencia de factores demográficos en los sistemas de pensiones y más tarde el caso del ISSSTE (Villagómez y García, 2005), coincidieron en señalar que el sistema de beneficios definidos, tal y como estaba estructurado, resultaría imposible de mantener por más de 20 años sin tener que asumir graves consecuencias tanto económicas como sociales.
Desde el nuevo mecanismo, los trabajadores, empleadores y gobierno realizarán aportaciones a cuentas individuales en donde se acumularán los ahorros de cada trabajador durante un mínimo de 25 años.
Como se mencionó anteriormente, las cuentas individuales—elemento central del nuevo sistema pensionario—son manejadas por instituciones financieras llamadas administradoras de fondos para el retiro (AFORE), de ahí que coloquialmente el nuevo esquema pensionario sea conocido por este nombre. Estas administradoras canalizan los ahorros de la cuenta individual al mercado bursátil mediante las sociedades de inversión especializadas en fondos para el retiro (SIEFORE).
Como consecuencia de la reforma a las políticas de inversión en abril de 2004se crean dos tipos diferentes de SIEFORE, aunque las nuevas SIEFORE básicas 2 empezaron a funcionar hasta septiembre de ese mismo año. Las SIEFORE básicas 1 (SB1)3 quedaron como obligatorias para todas la AFORE. Este tipo de fondo está destinado a aquellos trabajadores de 56 años o más, o a trabajadores menores de 56 años que no deseen asumir riesgos mayores. Las SB1no aceptan valores de renta variable o notas estructuradas, pero sí aceptan valores de deuda internacionales siempre y cuando no excedan los límites y grados de inversión establecidos (ver cuadro 2). Por su parte, las SIEFORE básicas 2 (SB2) se destinaron a trabajadores que estuvieran dispuestos a asumir un mayor riesgo a cambio de mayores rendimientos y que tuvieran menos de 56 años. Esta cartera, además de los instrumentos contemplados en la SB1, podrá también incluir notas de deuda con capital protegido al vencimiento (NDCP).
En 2007 nuevamente se modificó la política de inversión en la Ley de los Sistemas de Ahorro para el Retiro. Esta modificación dio pie a la creación de cinco tipos diferentes de SIEFORE que le ofrecen al trabajador acceso a sociedades de inversión con distintos niveles de riesgos4, “[…]con la finalidad de ofrecer nuevas y mejores opciones al ahorro de los trabajadores, atendiendo a las características de cada uno de ellos” referente a su edad, perfil de inversión y ciclo de vida5.El trabajador sólo podrá optar por aquellos fondos que correspondan a trabajadores de igual o mayor edad. Así se autorizó la creación de cinco tipos de fondos que permitieron la introducción de instrumentos financieros como componentes de renta variable, notas estructuradas, FIBRAS e instrumentos bursatilizados nacionales y extranjeros con distintos límites de inversión según el tipo de SIEFORE (ver cuadros 1 y 2).
Límites de inversión en las SIEFORE
| Tipo de riesgo | Origen | Concepto | Límite*por tipo de SIEFORE Básica | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| RIESGO DE MERCADO | Valor en riesgo (VAR histórico) | 0.60% | 1.00% | 1.30% | 1.60% | 2.00% | |
| Renta variable** | 0% | 15% | 20% | 25% | 30% | ||
| Instrumentos en Divisas (dólares, euros, yenes u otras para índices accionarios) | 30% | 30% | 30% | 30% | 30% | ||
| Derivados | SI | SI | SI | SI | SI | ||
| RIESGO DE CONCENTRACIÓN POR EMISOR O DE CONTRAPARTE | Nacional | Instrumentos mx AAA*** o en divisas BBB+ | 5% | 5% | 5% | 5% | 5% |
| Instrumentos mx AA o en divisas BBB− | 3% | 3% | 3% | 3% | 3% | ||
| Instrumentos mx A | 2% | 2% | 2% | 2% | 2% | ||
| Instrumentos mx BBB o en divisas BB | 0% | 1% | 1% | 1% | 1% | ||
| Extran jero | Instrumentos en Divisas A– un sólo emisor o contraparte | 5% | 5% | 5% | 5% | 5% | |
| Sobre una sola emisión | 35% | 35% | 35% | 35% | 35% | ||
| OTROS LÍMITES | Valores extranjeros (en caso de deuda, mínimo A−) | 20% | 20% | 20% | 20% | 20% | |
| Instrumentos bursatilizados | 10% | 10% | 10% | 10% | 10% | ||
| Instrumentos Estructurados (incluyen CKDs y FIBRAS) | 0% | 10% | 15% | 15% | 16% | ||
| Protección inflacionaria | Si (51% mín) NO | NO | NO | NO | |||
| CONFLICTOS DE INTERÉS | Instrumentos de entidades relacionadas entre sí | 15% | 15% | 15% | 15% | 15% | |
| Instrumentos de entidades con nexo patrimonial con la AFGRE | 5% | 5% | 5% | 5% | 5% | ||
Todos los límites son porcentajes máximos respecto a los activos netos manejados por cada SIEFORE, excepto el de protección inflacionaria que es un mínimo.
La crisis financiera de 2008 que afectó a los mercados financieros internacionales—incluyendo el mercado accionario mexicano—llevó a la Consar a que autorizara6, en febrero de 2010, que las SIEFGRE básicas, que antes sólo incluían componentes de renta variable, añadieran en sus carteras de inversión acciones individuales de empresas siempre y cuando se trataran de acciones de empresas mexicanas de tamaño pequeño o mediano, que no estuviesen incluidas en ningún índice aprobado en el régimen de inversión de las SIEFORE, así como acciones de empresas con capitalización y bursatilización mediana o grande que estuvieran incluidas en algún índice aprobado por el régimen de inversión de las SIEFORE siempre y cuando el porcentaje para la acción no excediera al aprobado en el índice compuesto del mercado accionario (IPC CompMx)7, o al límite máximo autorizado en el tipo de SIEFGRE que se trate para instrumentos de renta variable.
El propósito de las modificaciones de 2007 y 2010 fue permitir que los trabajadores tuvieran acceso a instrumentos con mayores rendimientos y que se redujera el riesgo de los fondos. Sin embargo, al observar la composición de los fondos de inversión, la alta concentración de deuda gubernamental, fue quizá, otra razón que tuvieron las autoridades para permitir la diversificación de las SIEFORE. Al cierre de 2004 la deuda gubernamental ocupaba el 83% del valor total de la cartera de los fondos y en 2007 el 70%, porcentaje que es aún alto. A finales de 2010 este porcentaje bajó ligeramente a aproximadamente 63% en promedio a pesar de las modificaciones al régimen de inversión. Esta pequeña baja se debe muy probablemente a la incertidumbre provocada por la crisis financiera. Los valores privados pasaron de representar el 15% del valor total de la cartera de los fondos de pensión al cierre de 2004, a 36% al cierre de 2010. Por otra parte, los valores bancarios han mantenido una participación muy marginal, alcanzando menos del 1.6% del valor total de la cartera de las SIEFGRE al cierre de 20108.
Riesgo y el sistema de contribuciones definidasTanto el Banco Mundial (Banco Mundial, 1994), el Fondo Monetario Internacional (Holzmann, 1997), la Organización para la Cooperación y el Desarrollo Económico (OCDE, 1998), así como una gran parte de los gobiernos que cambiaron su sistema pensionario de beneficios definidos a contribuciones definidas han argumentado algunas de las ventajas de pasar de un sistema a otro. Entre los atributos de los esquemas de cuentas individuales comparados con los tradicionales se encuentran los argumentos que destacan que con estos nuevos sistemas e apoyaría el incremento del ahorro nacional y, por ende, el crecimiento económico, además que los trabajadores, al final de su vida laboral, podrían gozar de mayores recursos. Sin embargo, las implicaciones de transferir un sistema de pensiones de beneficios definidos a uno de contribuciones definidas está rodeado de una serie de mitos (Orszag y Stiglitz, 1999) que hacen difícil que se hagan realidad las ventajas universales con que se anunció su aplicación en países con circunstancias nacionales tan distintas como Argentina, Bolivia, Colombia, Hungría, Kazakhtan, Latvia, Perú, o México, por mencionar algunos de los países que han adoptado este sistema desde su adopción por Chile. Las aplicaciones de este nuevo sistema tienen una gran variedad de implicaciones. Hay que tener en cuenta que ni el ahorro ni el crecimiento económico son los fines últimos de los programas de pensión (Diamond y Stiglitz,1974). Se puede incrementar el ahorro total al exponer a los trabajadores a riesgos mayores, aunque se debe analizar cuidadosamente si después de un tiempo también reporta un mayor bienestar para la población. Se deben evaluar cuidadosamente las características específicas de cada nacional elegir y aplicar un esquema pensionario. Según la opinión de expertos en pensiones, el Banco Mundial y algunos gobiernos nacionales han cometido errores analíticos tanto al aplicar ciertos esquemas jubilatorios como al analizar su desempeño (Barr y Diamond, 2009).
Otro punto importante es que al cambiar de un sistema de reparto a uno de contribuciones definidas se transfiere el riesgo a distintos agentes económicos. El riesgo, en los esquemas de beneficios definidos, queda entre los contribuyentes y entre generaciones; sin embargo, en un sistema de contribuciones definidas con cuentas privadas y administradas por el sector privado o público el riesgo recae en los trabajadores de manera individual. Los riesgos que asume el trabajador bajo un plan de contribuciones definidas durante la fase de acumulación9 incluyen que el trabajador pague cargos y costos altos que imponen los administradores de las cuentas individuales y de los fondos de pensión; que el total de contribuciones sea insuficiente (por desempleo, enfermedad o falta de trabajo estable); y que el riesgo de mercado, derivado de las variaciones en los precios de los activos financieros que conforman los fondos de pensión recaiga sobre el trabajador al final de su vida laboral (Blake et al., 2001). Una vez que los trabajadores se retiran, durante la fase de distribución, asumen el riesgo de tasa de interés, de inflación y, por tanto, de ingresos fluctuantes. Según Blake, los esquemas de contribuciones definidas tienen riesgos más grandes que aquellos que aceptan los administradores de los fondos de pensión y las autoridades; además, estos riesgos son mayores que aquellos que enfrentan los planes de beneficios definidos.
MetodologíaSe observaron los movimientos de las SIEFGRE básicas 1 (SB1) en dos periodos: desde su creación en junio de 1997 a agosto de 2004 (primer periodo), y de septiembre de 2004 a diciembre de 2010 (segundo periodo). Se tomó como horizonte de tiempo para el estudio de las SIEFGRE básicas 2 (SB2) de septiembre de 2004, fecha en que inician operaciones, a diciembre de 2010, de tal manera que el segundo periodo coincidan las SB1 con las SB2 para hacerlas comparables. Esta comparación, durante el segundo periodo, es la parte fundamental de este trabajo. Para el análisis que aquí se presenta no se consideraron las SIEFORE básicas 3, 4 y 5 ya que estos fondos funcionan tan sólo desde marzo de 2008, lo cual representa un periodo de análisis muy corto y, además, de alta volatilidad. Tampoco se analizan los efectos de los costos de transacción ni efectos inflacionarios.
A diferencia de otras sociedades de inversión que cotizan en la Bolsa Mexicana de Valores10, Consar no presenta un índice general acumulado de este tipo, únicamente pone a disposición del público un indicador de rendimiento neto11 y los precios diarios de cierre. Para estar en posibilidades de analizar el comportamiento de las SB1 y SB2, el primer paso fue construir un índice. El índice de las SB1 se construyó con los precios de cierre diarios12 de las sociedades de inversión que cotizaron durante cada periodo, del 1° de julio 1997 a diciembre de 2010 (primero y segundo periodos). El índice de las SB2 también se creó con los precios de cierre diarios para este tipo de sociedades, de septiembre de 2004 a diciembre de 2010 (segundo periodo). A partir de los datos diarios del índice se calcularon los rendimientos13 y la volatilidad promedio anual tanto para el primero como para el segundo periodo de las SB1 y para el segundo periodo de las SB2, los cuales serán usados en los modelos aquí presentados. Los índices acumulados diarios se construyeron como se presenta a continuación:
donde:It = Índice el día t.
It − 1 = Índice el día t−1.
Pit = Precio de cotización (proporcionado por CGNSAR) de la SIEFGRE i el día t.
Pit − 1 = Precio de la SIEFGRE i el día anterior.
n = número de SIEFGRE que cotizaron
Se modeló el comportamiento de las SB1 y SB2 utilizando las primeras diferencias de los logaritmos de los valores del índice acumulado diario.
Para modelar los rendimientos se tomó un modelo ARIMA, el cual es un modelo que combina procesos autorregresivos integrados con medias móviles. Este modelo por un lado capta los procesos autorregresivos, la parte AR del modelo, donde el valor de los rendimientos (yt) depende de la suma ponderada de los valores pasados de yt y de un término de error εt; y, por otro, los procesos de medias móviles, la parte MA del modelo, donde yt depende de la suma ponderada de los errores rezagados más un término que incluye la perturbación actual. La I, en ARIMA, se refiere a que es un modelo integrado, una serie de tiempo es integrada de orden 1, si sus primeras diferencias son I(0) y, por tanto, estacionarias. Así el modelo utilizado tiene la forma ARIMA14 (p, 1, q):
Dado que el objetivo de este trabajo es analizar el riesgo de las SIEFORE, se consideraron modelos autorregresivos con heteroscedasticidad condicional, ARCH15, Engle (1982), bajo la variante de modelos autorregresivos con heteroscedasticidad condicional generalizados, GARCH16, Bollerslev (1986), para modelar la volatilidad de estos fondos de pensión, de la forma:
así, todas las perturbaciones de t a εt − q tienen un efecto directo sobre εt, de tal forma que la varianza condicional actúa como un proceso autorregresivo de orden q17:donde:ht = la varianza del error, εt, es condicional a la información disponible en el tiempo t, y los parámetros deben satisfacer α0>0 y αi≥0 para i=1,2,…, q.
εt=el proceso del error que se modelará.
De esta manera el modelo GARCH permite modelar la varianza condicional (ht), tanto como resultado de las varianzas condicionales pasadas; es decir, por los valores pasados de sí misma como por pertubaciones pasadas.
En realidad, cuando se estima un modelo GARCH, y variaciones de éste como el modelo EGARCH, que se explica más adelante, se están estimando dos ecuaciones interrelacionadas, la ecuación de la media que puede ser un modelo ARMA (p,q), o como en el caso que se estudia, un modelo ARIMA (p, q) y la ecuación de la varianza condicional ht.
Una variante de este modelo es el modelo GARCH en la media o GARCH-M, Engle, Lilien y Robins (1987). Éste es un modelo utilizado en aplicaciones financieras donde el rendimiento esperado de un activo se relaciona con el riesgo esperado del mismo. El rendimiento esperado excedente de mantener un activo a largo plazo debe ser igual al premio al riesgo:
y suponiendo que el premio al riesgo sea una función de la varianza condicional, esto puede expresarse como:Por otra parte, es común encontrar en las series financieras que las perturbaciones negativas tengan un efecto más pronunciado en la volatilidad que las positivas. En estas series es frecuente encontrar la existencia de una correlación negativa entre el rendimiento actual y la volatilidad futura. El comportamiento asimétrico de las perturbaciones se puede modelar como lo propuso Nelson en su modelo GARCH exponencial, o EGARCH, Nelson (1991)18:
Este modelo permite medir los efectos de apalancamiento. Si εt − 1/(ht − 1)0.5 es positivo, el efecto de la perturbación en el logaritmo de la varianza condicional es α1+λ1. Si εt − 1/(ht − 1)0.5 es negativo, el efecto de la perturbación en el logaritmo de la varianza condicional es −α1+λ1 de tal forma que α1+λ1 y −α1+λ1 reflejan la asimetría en respuesta a las innovaciones positivas y negativas. El modelo tendrá una asimetría si λ≠0. Si εt − 1/(ht − 1)0.5<0 una perturbación externa positiva en los rendimientos hará que la volatilidad se incremente menos que ante una perturbación negativa de la misma magnitud.
Al modelo EGARCH se le puede incluir una variante al igual que en el modelo GARCH-M para calcular el premio al riesgo, incluyendo el siguiente término en la ecuación de la media:
aquí δ es el parámetro que representa el premio al riesgo en la ecuación de la media, igual que en el modelo GARCH-M.Por otra parte, además del premio al riesgo, y de los modelos autorregresivos, también se calculó la prima de riesgo tanto para las SB1 como para las SB2 durante el segundo periodo, como la razón Sharpe. Esta razón se considera como una medida simplificada de la relación entre el rendimiento y el riesgo; se centra en la proporción que existe entre el rendimiento excedente de la cartera estudiada con respecto a la tasa de interés libre de riesgo y la volatilidad del portafolio (Sharpe, 1964). La prima de riesgo19 se calculó como:
donde:Comportamiento de las SIEFORES a través del índice diario acumuladoCONSAR presenta mensualmente, en su página electrónica, un índice de rendimientos netos22 el cual tiene propósitos diferentes al índice aquí propuesto. El propósito23 de CONSAR para crear este indicador es que sirva como referencia en traspasos de cuentas individuales de una AFORE a otra, para la asignación de cuentas individuales de los trabajadores que no eligen una AFORE, y para la fusión de AFORE. Por otra parte, el índice diario acumulado que aquí se propone tiene el propósito de estudiar el desempeño de las SIEFORES. Además del objetivo general, la frecuencia con que se presentan los datos es diferente entre ambos índices. El índice de rendimientos netos de CONSAR es un indicador que desea presentar mensualmente la estabilidad de los rendimientos como el promedio anualizado de éstos en los últimos 36 meses, mientras que el índice aquí presentado tiene el propósito de captar las variaciones que presentan los rendimientos acumulados diarios para poder estimar la volatilidad, como medida del riesgo, en los tipos de SIEFORE básicas estudiadas. Otra diferencia es que el índice de Consar no cubre todo el periodo desde la creación de los instrumentos, mientras que el índice aquí presentado lo hace desde que iniciaron operaciones tanto de las SB1 como las SB2.
Otro punto que distingue ambos indicadores es que los rendimientos promedio anualizados que toma como base el índice de Consar para después restar las comisiones pueden estar sobreestimados por dos razones. La primera se refiere a que los rendimientos que representa Consar consideran un año de 360 días, mientras que el índice acumulado construido aquí considera el número de días que cotizan las SIEFORE en un año, el cual corresponde al número de días de operación de la Bolsa Mexicana de Valores24; la segunda es que el índice de Consar al suavizar las fluctuaciones de periodos de alta volatilidad, no refleja totalmente la volatilidad de los rendimientos promedio.
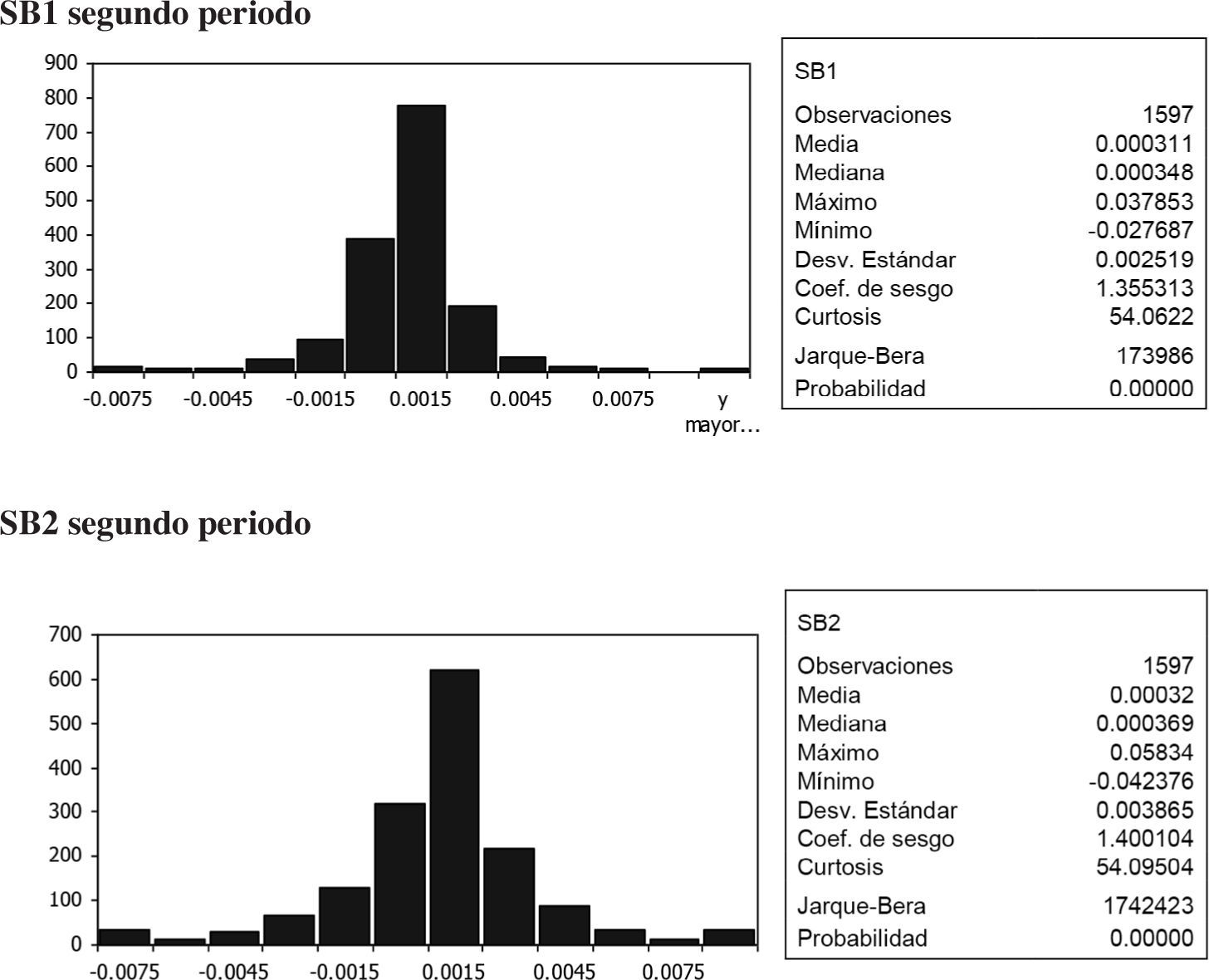
En la gráfica 1 se presentan las estadísticas básicas de los rendimientos de las SB1 y SB2. La media, mediana, valor máximo, valor mínimo y desviación estándar que se presentan en el cuadro que acompaña a la gráfica 1 se refieren a datos diarios. Se consideraron que los de mayor importancia son la media (o rendimiento promedio) y la desviación estándar, los cuales se anualizaron y se presentan en el cuadro 3. La serie estudiada presenta un exceso de curtosis y un coeficiente de sesgo, lo cual hace que no tenga una distribución normal. Las pruebas de normalidad Jarque-Bera constata lo anterior26. Tomando en cuenta que los datos no se distribuyen normalmente, se usaron métodos de cuasimáxima verosimilitud para ajustar el modelo, según se explica más adelante. La presencia de curtosis y sesgo son características muy comunes en las series financieras. Considerando irregularidades de este tipo, con respecto a una distribución normal, aunadas a otras como el hecho que la mayoría de perturbaciones externas tienen una gran persistencia y que su volatilidad es heteroscedástica con tendencia a agruparse se desarrollaron los modelos autorregresivos de heteroscedasticidad condicional, algunos de los cuales se presentaron anteriormente.
Estadísticas básicas de los rendimientos2525 La primera diferencia de los logaritmos de los valores del índice.
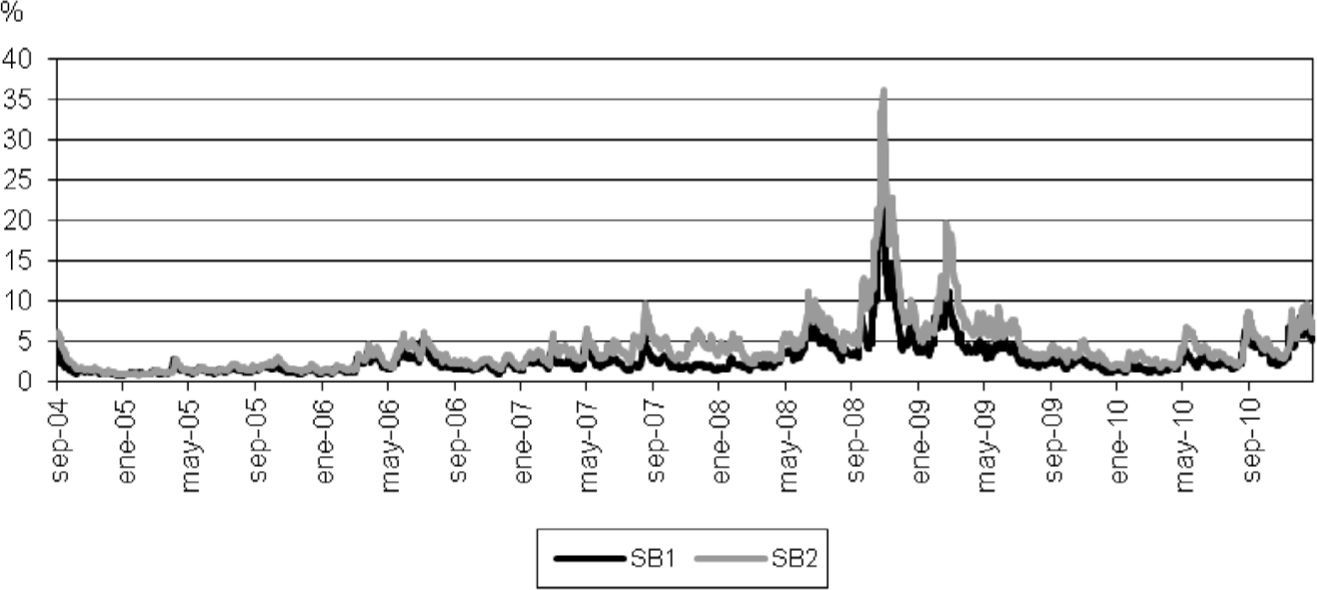
En la gráfica 2 se presenta el comportamiento de los índices y el de los rendimientos para los diferentes periodos estudiados. El comportamiento del índice de las SB1 en el primer periodo fue relativamente estable; en el segundo periodo las fluctuaciones en el índice y los rendimientos de las SB1 y SB2 son similares; sin embargo tienen una magnitud mayor en las SB2, lo cual también se observa en la gráfica 1 de las SB2.
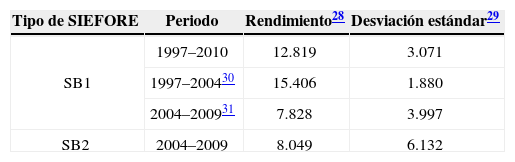
En el cuadro 3, durante el segundo periodo, se observa un comportamiento atípico entre los rendimientos y volatilidad desde las SB1 y las SB2. En éste se muestra cómo la desviación estándar es más grande en las SB2 que en las SB1 durante el mismo periodo. Sin embargo, a pesar de un incremento en el riesgo representado por un aumento de la volatilidad anual promedio del 53.4% de las SB2 con respecto a las SB1, los rendimientos promedio anualizados de las SB2 permanecen casi iguales a los de las SB1 con tal sólo un incremento de2.82%. La teoría financiera coincide en que las carteras formadas por acciones tienen rendimientos a largo plazo, mismos que debieran exceder a los rendimientos de portafolios más conservadores integrados por activos más seguros como los bonos. Esto es debido al hecho que ante un riesgo mayor es necesario que se ofrezca un rendimiento mayor que lo compense27; sin embargo, esto no sucede con las SB1 y las SB2. Estas últimas, que son fondos con mayor riesgo, no compensan éste con un rendimiento significativamente mayor. Este resultado poco convencional también se observa en la prima y el premio al riesgo, como se presenta más adelante.
En la gráfica 3 se muestra un comparativo del índice de las SB132 y de las SB2 para el segundo periodo. En esta gráfica se pueden observar como los rendimientos de las SB2 superan a los de las SB1, antes del inicio de la crisis del 2008, lapso que fue de relativa estabilidad. Este comportamiento sólo se vuelve a apreciar en los últimos meses del 2010.
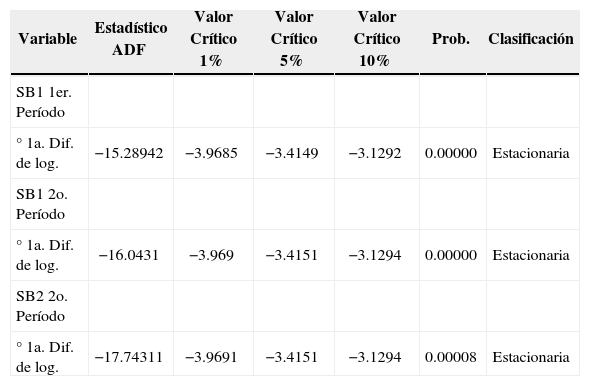
Análisis y resultados de los modelos autorregresivos y la prima de riesgoComo ya se mencionó, se modeló el comportamiento de las SB1 y SB2 con modelos GARCH y varias de sus extensiones utilizando las primeras diferencias de los logaritmos de los valores del índice, comprobando antes que estas series fueran estacionarias por medio de la prueba Dickey-Fuller Aumentada (ADF), que se presenta en el cuadro 4. En esta prueba la hipótesis nula se rechaza (H0: la serie tiene una raíz unitaria), ya que los estadísticos de la prueba ADF son mayores que los valores críticos al 1%, 5% y 10%y, por lo tanto, las series son estacionarias.
Resultado de la prueba Dickey-Fuller Aumentada para las SB1 Y SB2
| Variable | Estadístico ADF | Valor Crítico 1% | Valor Crítico 5% | Valor Crítico 10% | Prob. | Clasificación |
|---|---|---|---|---|---|---|
| SB1 1er. Período | ||||||
| ° 1a. Dif. de log. | −15.28942 | −3.9685 | −3.4149 | −3.1292 | 0.00000 | Estacionaria |
| SB1 2o. Período | ||||||
| ° 1a. Dif. de log. | −16.0431 | −3.969 | −3.4151 | −3.1294 | 0.00000 | Estacionaria |
| SB2 2o. Período | ||||||
| ° 1a. Dif. de log. | −17.74311 | −3.9691 | −3.4151 | −3.1294 | 0.00008 | Estacionaria |
Nota: Prueba ADF con tendencia e intercepto
Los modelos GARCH y EGARCH se calcularon con cuasimáxima verosimilitud, Bollerslev y Wooldridge (1992) debido a que los errores no se distribuyeron normalmente, sino que presentan leptocurtosis (ver cuadro 5). Este ajuste produce estimadores consistentes de los parámetros de una varianza condicional correctamente especificada33. Se realizaron pruebas de normalidad a los residuos estandarizados resultantes de los modelos EGARCH para determinar si éstos exhibían leptocurtosis, lo cual resultó cierto para ambos fondos SB1 y SB2.
Un primer paso para modelar el riesgo de las SIEFORE fue modelar la volatilidad de ambas series con modelos GARCH-M34. Para el caso de las SB1, segundo periodo, los resultados muestran que a1+β1<1; por lo tanto, se puede suponer que el efecto de la crisis ha empezado a desaparecer; sin embargo, de manera muy lenta ya que la suma de ambos coeficientes fue de 92728. La alta persistencia de la volatilidad en las SB2 también se aprecia en a1+β1=.966126, lo cual indica que los efectos de la crisis aún estaban presentes a finales del periodo estudiado y que la persistencia en la SB2 era mayor que en las SB1.
Aunque el efecto ARCH desapareció en ambos modelos GARCH, una prueba de correlaciones cruzadas35 sugirió un efecto de asimetría; por tanto, se decidió ajustar la volatilidad de las series utilizando un modelo EGARCH-M para poder capturar este efecto. Este modelo además de mostrar la asimetría que, como ya se mencionó, se presenta cuando perturbaciones negativas tienen un efecto mayor que aquellas noticias positivas también permite calcular el premio al riesgo en la ecuación de la media.
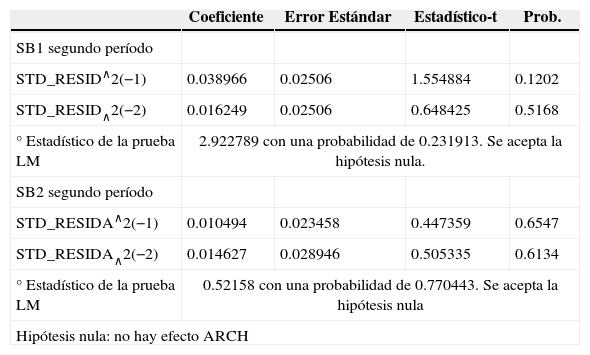
Una vez efectuada la regresión del modelo ARIMA(2, 1)-EGARCH-M(1, 1) se comprobó que no existe un efecto ARCH36 en los modelos propuestos para las SB1 y SB2 (ver cuadro 6). Como se mencionó anteriormente el modelo EGARCH-M consiste en dos ecuaciones interrelacionadas, la ecuación de la media, representada aquí como un modelo ARIMA (p, q) que aparece en la primera parte de los cuadros 7 y 837, y la ecuación de la varianza condicional38 (ht) que aparece en la segunda parte del cuadro de resultados. En estos cuadros se presentan los resultados de los modelos EGARCH para las SB1 y SB2 en el segundo periodo, respectivamente39. El efecto de asimetría se puede apreciar en el coeficiente negativo en la ecuación de la varianza que corresponde al coeficiente λ en la ecuación (3) con lo cual se constató la existencia de un efecto de asimetría sugerido por la prueba de correlaciones cruzadas.
Prueba LM para los modelos EGARCH-M
| Coeficiente | Error Estándar | Estadístico-t | Prob. | |
|---|---|---|---|---|
| SB1 segundo período | ||||
| STD_RESID∧2(−1) | 0.038966 | 0.02506 | 1.554884 | 0.1202 |
| STD_RESID∧2(−2) | 0.016249 | 0.02506 | 0.648425 | 0.5168 |
| ° Estadístico de la prueba LM | 2.922789 con una probabilidad de 0.231913. Se acepta la hipótesis nula. | |||
| SB2 segundo período | ||||
| STD_RESIDA∧2(−1) | 0.010494 | 0.023458 | 0.447359 | 0.6547 |
| STD_RESIDA∧2(−2) | 0.014627 | 0.028946 | 0.505335 | 0.6134 |
| ° Estadístico de la prueba LM | 0.52158 con una probabilidad de 0.770443. Se acepta la hipótesis nula | |||
| Hipótesis nula: no hay efecto ARCH | ||||
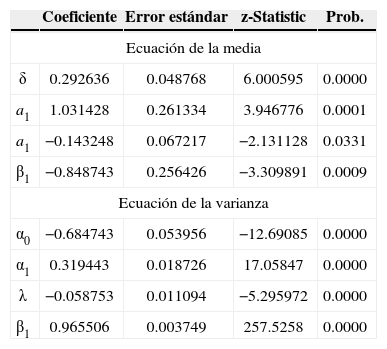
Resultados del modelo ARIMA (2, 1)-EGARCH-M (1, 1) aplicado a las SB (segundo periodo)
| Coeficiente | Error estándar | z-Statistic | Prob. | |
|---|---|---|---|---|
| Ecuación de la media | ||||
| δ | 0.292636 | 0.048768 | 6.000595 | 0.0000 |
| a1 | 1.031428 | 0.261334 | 3.946776 | 0.0001 |
| a1 | −0.143248 | 0.067217 | −2.131128 | 0.0331 |
| β1 | −0.848743 | 0.256426 | −3.309891 | 0.0009 |
| Ecuación de la varianza | ||||
| α0 | −0.684743 | 0.053956 | −12.69085 | 0.0000 |
| α1 | 0.319443 | 0.018726 | 17.05847 | 0.0000 |
| λ | −0.058753 | 0.011094 | −5.295972 | 0.0000 |
| β1 | 0.965506 | 0.003749 | 257.5258 | 0.0000 |
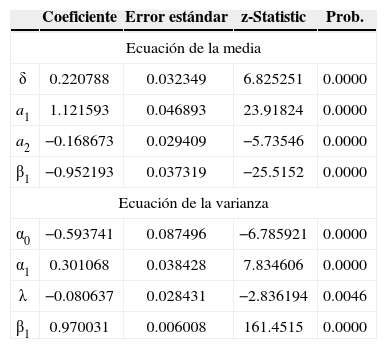
Resultados del modelo ARIMA (2, 1)-EGARCH-M (1, 1)aplicado a las SB2 (segundo periodo)
| Coeficiente | Error estándar | z-Statistic | Prob. | |
|---|---|---|---|---|
| Ecuación de la media | ||||
| δ | 0.220788 | 0.032349 | 6.825251 | 0.0000 |
| a1 | 1.121593 | 0.046893 | 23.91824 | 0.0000 |
| a2 | −0.168673 | 0.029409 | −5.73546 | 0.0000 |
| β1 | −0.952193 | 0.037319 | −25.5152 | 0.0000 |
| Ecuación de la varianza | ||||
| α0 | −0.593741 | 0.087496 | −6.785921 | 0.0000 |
| α1 | 0.301068 | 0.038428 | 7.834606 | 0.0000 |
| λ | −0.080637 | 0.028431 | −2.836194 | 0.0046 |
| β1 | 0.970031 | 0.006008 | 161.4515 | 0.0000 |
Con el coeficiente λ se calculó que el efecto del impacto de una perturbación negativa40 para dos desviaciones estándar, el cual fue 38.06% mayor para las SB2 que el de un evento positivo de la misma magnitud, mientras que el impacto de una perturbación negativa para las SB1 se estimó 26.49% con respecto a un evento positivo de igual tamaño.
En la gráfica 4 aparece el proceso de volatilidad estimada con los modelos ARIMA (2, 1)-EGARCH-M (1, 1) para ambos fondos de retiro. Como en el caso de la desviación estándar promedio presentadas en el cuadro 3las SB2 muestran una volatilidad condicional mayor que las SB1 durante el segundo periodo.
Como se mencionó anteriormente, también se calculó la prima de riesgo con el objetivo de tener como referencia otra medida que considerara los dos parámetros que determinan el riesgo de mercado de los fondos, el rendimiento y la volatilidad. La cantidad acumulada total en las cuentas individuales de los trabajadores es esencial para determinar el nivel de subsistencia de los mismos al final de su vida laboral. Esta cantidad total acumulada no depende únicamente del tiempo durante el cual cotice el trabajador y de los montos de sus aportaciones, sino también del comportamiento del mercado y de la relación rendimiento-riesgode los fondos en los cuales se invierten los recursos de las cuentas individuales de los trabajadores; por lo tanto, conocer las primas de riesgo es importante para determinar si los rendimientos están compensando el riesgo asumido.
La prima de riesgo promedio en términos porcentuales fue de 0.24 para las SB1 y de 0.19 para las SB2; las primas de riesgo acumuladas41 estimadas a partir de las primas diarias, para las SB1 y las SB2, aparecen en la gráfica 5. En esta gráfica se observa cómo la prima de riesgo de las SB2 presenta, durante todo el periodo estudiado, niveles menores a la prima de riesgo de las SB1; no obstante el comportamiento de las SB2 presentó una volatilidad más alta que las SB1.
La prima de riesgo promedio es una evidencia más que las SB2, desde su creación hasta finales de 2010, han ofrecido rendimientos excedentes menores que las SB1 con respecto a su volatilidad. Este resultado es consistente con los datos encontrados en los modelos ARIMA (2, 1)-EGARCH-M (1, 1). El coeficiente que aparece en la ecuación de la media en los cuadros 7 y 8 como el coeficiente δ, para las SB1 y SB2, se refiere al premio al riesgo que, como ya se mencionó, es una función creciente de la varianza condicional ht, lo cual significa que entre mayor sea la varianza condicional de los rendimientos, mayor debe ser la compensación necesaria para que los tenedores de los activos con riesgo decidan mantener este tipo de activos a largo plazo. En ambos casos es positivo, pero al igual que la prima de riesgo calculada el premio pagado por la SB1 es mayor que el de las SB2, 0.292636 y 0.220788, respectivamente.
ConclusionesEntre los argumentos que se ofrecieron a los trabajadores cuando se realizó el cambio de esquema pensionario de reparto con beneficios definidos al de contribuciones definidas no se mencionó que gran parte del riesgo recaerá en los trabajadores. Al introducirse el actual sistema de contribuciones definidas en nuestro país, se destacaron principalmente aspectos como el hecho de que el trabajador podrá elegir la AFORE y el tipo de SIEFORE a la cual canalizar las aportaciones de su cuenta individual, siempre y cuando no rebase su límite de edad, así como el hecho que el monto total en su cuenta individual, al final de su vida activa, dependerá de las cantidades y del tiempo durante el cual se realicen las aportaciones. Asimismo, se mencionó que el trabajador tendría la ventaja de poder decidir sobre su propio fondo, en lugar de depender de las decisiones de administradores de un fondo común o de las reglas generales de un sistema de reparto; sin embargo, en general, los trabajadores difícilmente están capacitados para tomar decisiones sobre la administración de sus fondos, más allá de elegir a la administradora y a la sociedad de inversión—que en realidad éstas son las únicas decisiones que pueden tomar con respecto a sus fondos de pensión, además de hacer aportaciones voluntarias—teniendo sólo como criterio de decisión la tasa de rendimientos netos que publica Consar. El riesgo de mercado, aspecto de suma importancia para determinar la suma final con la que los trabajadores subsistirán durante su vida inactiva, es un elemento que no se da a conocer a los trabajadores. El valor en riesgo(VaR), la medida de riesgo que ofrece Consar, es publicada en su página electrónica en un apartado para las administradoras; sin embargo, su significado escapa a los conocimientos que tiene el público en general.
Dado el carácter de ahorro obligatorio de los fondos de pensión para los trabajadores se hace imperativo analizar el riesgo financiero y en especial el riesgo del mercado, pues precisamente este último es el que afecta el valor total del fondo acumulado, del cual dependerán los trabajadores una vez jubilados. Una crisis de la magnitud como la vivida en 2008, que hizo que disminuyera considerablemente el valor de los fondos acumulados de los trabajadores, quizá tenga poca importancia al principio de la etapa de acumulación cuando los trabajadores inician su vida laboral y tienen muchos años por delante para salvar esta contingencia; sin embargo, las consecuencias de una caída como ésta —cuando los trabajadores están a punto de jubilarse— tiene resultados muy diferentes en los niveles de bienestar de los mismos. Por estas razones, se considera esencial el análisis del riesgo en la evaluación de los sistemas de pensiones.
El desempeño de las SIEFORE no continuó con los niveles de rendimiento y riesgo relativamente estables—que se presentaron durante los primeros siete años de operación— y las modificaciones al régimen de inversión tendientes a diversificar el riesgo de acuerdo con los resultados obtenidos no ofrecieron mayores rendimientos, que era lo esperado al introducir mayor riesgo en las SB2. Hay que considerar que el periodo analizado de 2004 a 2010, y en especial durante 2008, fue de alta volatilidad; sin embargo, se trata de un periodo relativamente corto y, en ese sentido, los resultados de este estudio no son concluyentes, pero los fondos de los trabajadores, en la forma en que actualmente están construidos, difícilmente podrán estar exentos de sufrir las repercusiones de futuras crisis financieras, las cuales podrán impactarlos de manera similar a la analizada en este trabajo.
Por otro lado, se observa que el riesgo adicional asumido por las SB2a través de los componentes de renta variable, acciones y un mayor porcentaje de deuda extranjera privada se tradujo en una mayor volatilidad que la presente en las SB1. De igual manera, el efecto de asimetría—visto como un mayor impacto de perturbaciones negativas que el que hubiera tenido un evento positivo de igual magnitud—fue más grande que en las SB1. Ambos resultados, una mayor volatilidad y una mayor asimetría de las SB2 con respecto a las SB1, eran efectos esperados; sin embargo, dado el mayor riesgo presente en las SB2lo lógico es que éstos fondos ofrecieran un mayor rendimiento para compensar los riesgos adicionales asumidos; sin embargo, el resultado general fue una menor prima de riesgo y un premio al riesgo más bajo que el de las SB1; con esto se concluye que durante el periodo estudiado las SB2 no fueron capaces de compensar el riesgo adicional en el que incurrieron, contradiciendo lo señalado por la teoría financiera al respecto. Esta situación hace necesario evaluar la forma en que se está midiendo y controlando el riesgo, así como evaluar las políticas de inversión. La volatilidad ha provocado que se pierda parte de los ahorros de los trabajadores, teniendo mayor probabilidad de recuperarse de las pérdidas, aquellos fondos destinados a trabajadores más jóvenes, siempre y cuando estas crisis no continúen repitiéndose. De continuar presentándose situaciones de alta volatilidad y de mantenerse la actual estructura de inversión de las SIEFORE difícilmente sus rendimientos reales efectivos podrán compensar el riesgo adicional que se asume al incluir instrumentos de alto riesgo en los fondos de pensión. Esto abre nuevas líneas de investigación, ya que se requiere de instrumentos de medición, optimización y control que logren que los rendimientos y el valor de los fondos no sean impactados con la misma magnitud con que lo fueron en el 2008 por futuras crisis financieras.
La primera diferencia de los logaritmos de los valores del índice.
Estos precios de cierre diarios corresponden a los precios de las SIEFORES básicas registrados en la Bolsa de Valores que publica Consar en su página electrónica.
El 8 de diciembre de 2008 empieza a cotizar en el ISSSTE el fondo de pensiones administrado por PensionISSSTE.
Circular Consar 15–12. Décima Tercera Regla, párrafo II. Adición publicada el 20 de septiembre de 2006.
Ley de los Sistemas de Ahorro para el Retiro. Artículo 47. Publicada en el Diario Oficial de la Federación el 9 de julio de 2007.
Blake et al. (2001) señalan que Samuelson justificaba este tipo de manejo de fondos de pensión, fases conforme a la edad (agephasing), debido a que los rendimientos a largo plazo de activos como acciones, bonos y propiedades presentan reversión a la media; por lo tanto, es racional para los inversionistas, con un horizonte a largo plazo, invertir más en activos de alto riesgo durante los primeros años de acumulación en sus fondos de pensión y cambiar a bonos, dado que son instrumentos de bajo riesgo, en los últimos años de acumulación, antes de su retiro. Esto permitiría que los trabajadores se beneficiaran de la prima de riesgo que ofrecen las acciones.
Circular Consar 15–19 y 15–26, aprobada el 24 de febrero de 2010.
También conocido como IPC composite. Éste es un indicador que incluye en su muestra a las 60 empresas más grandes y con más liquidez que cotizan en la BMV con el propósito de reflejar, en forma amplia, el comportamiento del mercado accionario al agrupar en su muestra acciones de todos los sectores económicos participantes en el mercado accionario del país.
Estos datos fueron calculados con la información disponible en las estadísticas del Banco de México sobre Sociedades inversión especializadas fondos para retiro recursos y obligaciones (Banco de México, 2011).
La fase de acumulación es el tiempo durante el cual el trabajador realiza aportaciones a su cuenta individual durante su vida activa.
BMV publica los índices de las Sociedades de Inversión Comunes, de las Sociedades de Inversión de Deuda para personas físicas y para personas morales, y el de las Sociedades de Inversión de Capital de Riesgos (SINCAS).
El índice de Consar se construye de la siguiente forma: IRN(t−n,t)i=r(t−n,t)i−Cti donde: IRN(t−n,t)i = Índice de Rendimiento Neto desde la fecha t−n hasta la fecha t de la sociedad de inversión i, el periodo de t−n a t corresponde a 36 meses; r(t−n,t)i = rendimiento de gestión compuesto entre la fecha t−n y la fecha t para la sociedad de inversión i, para calcular este rendimiento de gestión se utilizará la serie de precios de gestión; Cti = comisión sobre saldo vigente en la fecha t para la sociedad de inversión i; n= periodo de 36 meses por el que se está calculando el Índice de Rendimiento Neto, expresado en días naturales; t= la fecha para la que se calculará el Índice de Rendimiento Neto para traspasos y para la asignación a 36 meses. Consar calcula el rendimiento de gestión de los últimos 36 meses de una sociedad de inversión como:
Estos precios de cierre diarios corresponden a los precios que publica Consar en su página electrónica bajo el nombre de “Precios de las SIEFGRES BASICAS Registrados en la Bolsa Mexicana de Valores”. Representan los precios que ofrece Consar para la cotización de las SIEFGRES diariamente y son los mismos que Consar toma como base para construir su índice de rendimientos netos. Se hizo un ajuste eliminando aquellos días en que Consar repitió el precio del día anterior. En todo el periodo estudiado se eliminaron 13 precios de los siguientes días: 10 de agosto, 1° de septiembre, 16 de septiembre, 2 de noviembre y 31 de diciembre de 1999, y 21 de marzo, 20 y 21 de abril, 5 de mayo, 5 junio, 5 de julio y 12 de diciembre de 2000 y 18 de noviembre de 2008, estos días la BMV tampoco cotizó con excepción de 10 de agosto de 1999, 5 de junio, 5 de julio y 18 de noviembre de 2008, para la construcción del índice de las SB1. En el caso de las SB2 se eliminó sólo el precio del día 18 de noviembre de 2008.
Los rendimientos se calcularon como las primeras diferencias de los logaritmos de los valores de los índices calculados.
Estos modelos se presentan como en Enders (2010) y Tsay (2005).
ARCH, por sus siglas en inglés Autoregressive Conditional Heteroscedasticity.
GARCH, por sus siglas en inglés, Generalized Autoregressive Conditional Heteroscedasticity.
La varianza condicional de εt está dada por Et−1ϵt2=ht. La varianza condicional de εt es el proceso ARMA dado por la expresión ht en el caso del modelo que nos ocupa, se trata de un modelo ARIMA, ya que incluye las primeras diferencia de los logaritmos de los valores del índice.
El paquete computacional e-views, el cual será utilizado en los modelos autorregresivos aquí efectuados, hace un ajuste en el tercer término al restar 2/π de él, esto hará que el intercepto difiera del modelo presentado por Nelson en λ2/π. Asimismo, en este modelo los errores se han estandarizado ϵt−1/ht−10.5 dividiendo entre ht−10.5.
La prima de riesgo se calculó como la prima de riesgo diaria anualizada.
Los rendimientos diarios se anualizaron multiplicando por el número de días que las SB cotizaron en el año para obtener la tasa anualizada nominal, los rendimientos diarios se estimaron del índice diario acumulado que se construyó.
La volatilidad diaria, calculada a partir de los rendimientos del índice diario acumulado construido aquí, se anualizó multiplicando por la raíz cuadrada del número de días que las SB cotizaron en el año.
Circular Consar 71–1, 21 de diciembre de 2007. Publicada en el Diario Oficial de la Federación el 30 de diciembre de 2007. Entró en vigor el 15 de marzo de 2008.
Consar Circular 71–1, Capítulo 1, Disposiciones generales, p. 5.
El número de días que cotiza la Bolsa Mexicana de Valores al año es de aproximadamente 251.6 días promedio al año.
En la prueba de normalidad Jarque-Bera la hipótesis nula es H0: Existe una distribución normal. El valor que presenta la prueba es muy alto, lo cual lleva al rechazo de la hipótesis nula.
Sin embargo, también existe evidencia empírica que contradice esto; un ejemplo de lo anterior, es un estudio en donde se analizan los mercados accionarios del mundo desde 1900 (Brown et al., 1995).Aquí se muestra que los rendimientos en acciones que se negocian globalmente son mayores por un margen insignificante que los rendimientos de los bonos.
Los rendimientos anuales por periodo se estimaron como:
La desviación estándar anual se calculó como: σa=σd*tp, donde σa es la volatilidad promedio anualizada, σd es la desviación estándar promedio diaria en el periodo estudiado, tp es el número de días promedio en el año durante el periodo estudiado.
Primer periodo corresponde del 1° de julio de 1997 al 31 de agosto de 2004. El 1° de septiembre de 2004 empezaron a cotizar las SB2.
Segundo periodo incluye del 1° de septiembre de 2004 al 31 de diciembre de 2010.
En esta gráfica, el índice de la SB1 se recalculó para que ambos índices iniciaran el 1° de septiembre de 2004 en un nivel de 100, de tal forma que sus fluctuaciones pudieran ser comparables.
Muchos de los paquetes computacionales, incluyendo e-views usan una distribución-t con un grado de libertad en lugar de una normal, realizando así los cómputo con cuasimáxima verosimilitud, permitiendo con ésta una mayor verosimilitud que la que se alcanza con una distribución normal, para series que presentan leptocurtosis.
Se logró el mejor ajuste con un modelo ARMA (2, 1)-GARCH (1, 1) aplicado a las SB1, segundo periodo, y con un modelo AR (1)-GARCH (1, 1) para las SB2, segundo periodo. En la parte de la ecuación GARCH se incluyó una variable ficticia en el periodo de más alta volatilidad que coincide con la caída de los mercados durante la crisis de 2008.
Se refiere a las correlaciones cruzadas entre los residuos estandarizados al cuadrado zt2, y los residuos estandarizados rezagados zt−12, si las correlaciones son cero se trata de un modelo simétrico, si son negativas se trata de un modelo asimétrico. Al correr la prueba la gran mayoría de las correlaciones cruzadas resultaron negativas.
Prueba de multiplicador de Lagrange (LM), o de Efecto (ARCH) propuesta por Engle (1982) para probar la existencia de efectos de heteroscedasticidad condicionada autorregresiva (ARCH).
La ecuación de la media corresponde a la ecuación (1) de la sección 3.
La ecuación de la varianza condicional corresponde a la ecuación (3) de la sección 3.
Los coeficientes presentados en las tablas 7 y 8 son estadísticamente significativos, para un nivel de significancia del 10% y 5% en todos los casos, al rechazarse la hipótesis nula, H0δ=a0=a1=β1=λ1=α1=α1=0.
El efecto de una perturbación negativa se calculó como: Índice de asimetría= e(α1+λ)(−2)/e(−α1+λ)(2) tomadas a dos desviaciones estándar.
La prima de riesgo acumulada se estimo como: Pra=Prt−1ePrt, donde Pra es la prima de riesgo acumulada, Prt−1 prima de riesgo del día anterior y Prt es la prima de riesgo actual.