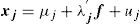We present an improved methodology to estimate the underlying structure of systematic risk in the Mexican Stock Exchange with the use of Principal Component Analysis and Factor Analysis. We consider the estimation of risk factors in an Arbitrage Pricing Theory (APT) framework under a statistical approach, where the systematic risk factors are extracted directly from the observed returns on equities, and there are two differentiated stages, namely, the risk extraction and the risk attribution processes. Our empirical study focuses only on the former; it includes the testing of our models in two versions: returns and returns in excess of the riskless interest rate for weekly and daily databases, and a two-stage methodology for the econometric contrast. First, we extract the underlying systematic risk factors by way of both, the standard linear version of the Principal Component Analysis and the Maximum Likelihood Factor Analysis estimation. Then, we estimate simultaneously, for all the system of equations, the sensitivities to the systematic risk factors (betas) by weighted least squares. Finally, we test the pricing model with the use of an average cross-section methodology via ordinary least squares, corrected by heteroskedasticity and autocorrelation consistent covariances estimation. Our results show that although APT is very sensitive to the extraction technique utilized and to the number of components or factors retained, the evidence found partially supports the APT according to the methodology presented and the sample studied.
Presentamos una metodología mejorada para estimar la estructura subyacente del riesgo sistemático en el mercado accionario mexicano, usando Análisis de Componentes Principales y Análisis Factorial. Consideramos la estimación de factores de riesgo en el marco de la Teoría de Valoración por Arbitraje (APT) bajo un enfoque estadístico, donde los factores de riesgo sistemático son extraídos directamente de los rendimientos accionarios observados y existen dos etapas diferenciadas conocidas como proceso de extracción de riesgo y proceso de atribución de riesgo. Nuestro estudio se enfoca solamente en el primero de estos dos procesos; incluye la contrastación de nuestros modelos en dos versiones: rendimientos y rendimientos en exceso sobre la tasa de interés libre de riesgo para bases de datos semanales y diarias, así como una metodología de dos etapas para el contraste econométrico. Primero, extraemos los factores de riesgo sistemático mediante la versión lineal estándar del Análisis de Componentes Principales y la estimación por Máxima Verosimilitud del Análisis Factorial. Después, estimamos simultáneamente, para todo el sistema de ecuaciones, las sensibilidades a los factores de riesgo sistemático (betas) mediante mínimos cuadrados ponderados. Finalmente, contrastamos el modelo de valoración usando una metodología transversal promedio a través de mínimos cuadrados, corregida por una estimación de heteroscedasticidad y autocorrelación consistente de covarianza. Nuestros resultados muestran que aunque el APT es muy sensible a la técnica de extracción utilizada y al número de componentes o factores retenidos, la evidencia encontrada apoya parcialmente al APT de acuerdo con la metodología presentada y la muestra estudiada.
Following a generative multifactor model of returns and an arbitrage argument, the Arbitrage Pricing Theory (APT) prices an equity by considering a set of common systematic risk factors assumed to influence the return produced. Empirical studies, mainly of developed markets such as the New York (NYSE), American (AMEX), London (LSE) and Tokyo (TSE) Stock Exchanges, have proposed different approaches to identify the types of systematic risk factors considered by multifactor models. Zangari (2003) presents a classification of risk factors based on whether their value is observable or not, dividing them into market, macroeconomic, fundamental, sector, technical and statistical factors. In general, the empirical evidence provided is contradictory, both supporting and rejecting the APT, especially when statistical factors are used. The market factor approach is practically an interpretation of the Capital Asset Pricing Model (CAPM), where there is only one common factor and it is observable. Both macroeconomic and fundamental models have been widely discussed in the literature; in many empirical papers sets of predefined variables, procedures and methodologies, for different countries, are examined.1 Overall, findings have been favourable for both approaches, although there is no generalized consensus about the nature of factors. The macroeconomic approach seeks to identify, a priori, a set of observable macroeconomic time series as proxies of the value of the systematic risk factors. According to Yip et al. (2000), the macroeconomic variables can be classified into four categories: inflation, industrial production, investor confidence and interest rates. On the other hand, in the fundamental approach, the systematic risk factors are approximated by means of predefined financial and accounting variables that reflect the exposure to unobservable factors, such as size, leverage, cash flow, price-earning ratio (PER) and book-to-market ratio. As in the macroeconomic models, there is no general agreement among the different studies on the nature of factors. The main difference between the macroeconomic and the fundamental standpoints is the elements they consider as given in a multifactor model. The former consider the risk premiums for each kind of systematic risk as given and estimate the exposures or sensitivity to each kind of systematic risk, and the latter, vice versa. The other two security-specific approaches use technical and sector variables as proxies of the effects of unobserved factors, although very little empirical investigation has been carried out exclusively under these perspectives. The statistical approach focuses mainly on uncovering a suitable number of pervasive factors, regardless of their nature,2 through latent variables analysis techniques such as Principal Component Analysis (PCA) and Factor Analysis (FA). In this case, both the risk premiums and the exposure to them are usually estimated simultaneously. Roll et al. (1980), Brown et al. (1983), Chen (1983), Bower et al. (1984), Cho et al. (1984)Connor et al. (1988), Lehmann et al. (1988) and Hasbrouck et al. (2001) obtained favourable results, revealing between three and five priced factors in the American stock market; Beenstock et al. (1986) identified twenty priced factors in the UK stock exchange and Elton et al. (1988) found four factors in the Japanese market. Nevertheless, Reinganum (1981) rejected statistical APT as a means of explaining stock price variations for the NYSE and AMEX, as did Gómez-Bezares et al. (1994), Nieto (2001), and Carbonell et al. (2003) for the Spanish Stock Exchange (SSE). Moreover, Abeysekera et al. (1987) obtained mixed results for the London Stock Exchange, as did Jordán et al. (2003) for the Spanish Mutual Funds Market.
There is no clear supremacy of one approach over the others. Among the theoretical and empirical comparative studies made, Maringer (2004) presents a good summary of the advantages, disadvantages and recommended uses of macroeconomic, fundamental and statistical models; Connor (1995) shows that statistical and fundamental models outperform macroeconomic models in terms of explanatory power, and that fundamental models slightly outperform statistical ones for the USA market; Chan et al. (1998) found evidence that fundamental factors perform better than macroeconomic, technical, statistical and market factors in the UK and japanese markets; on the other hand, Teker et al. (1998) showed that the statistical model outperforms the macroeconomic one for the US market; and Cauchie et al. (2004) demonstrated that statistical factors yield a better representation of the determinants of the swiss market stock returns than the macroeconomic ones. In addition, Miller (2006a) makes a new comparison, complementing that of Connor's classic study. Consequently, three well-known risk analysis and portfolio management firms, MSCI-BARRA3, FTSE-BIRR4 and SUNGARD-APT5, have opted mostly for the fundamental, macroeconomic and statistical approaches, respectively, for constructing their worldwide multifactor risk models, portfolio analytics and risk reporting commercial products.
More recent studies have attempted to combine the different approaches. Miller (2006b) proposed a hybrid version of a multifactor model, combining fundamental and statistical factors, in which the latter are used to explain the fundamental model's residual part, obtaining modest results on the japanese market. Liu et al. (2007) proposed that fundamental models can be used as an approach to extract the effect of the macroeconomic factors, by dividing the model's common fundamental factors into two sub-parts: one explained by macroeconomic factors and the other by non-macroeconomic factors.
Empirical investigation of multivariate asset-pricing models in emerging stock markets has been relatively scarce. Most studies have been based on a macroeconomic perspective, finding two or three priced factors. Results have been mixed concerning priced factors across the markets.6 With respect to the present study, only two reviews have used the statistical definition of the APT: Ch'ng et al. (2001) on the Malaysia Stock Market and Dhankar et al. (2005) on the Indian Stock Exchange revealing two and five priced factors, respectively.
Little research has been carried out regarding the application of the APT for the Mexican Stock Exchange. To the best of our knowledge, the only references are Calle (1991), Navarro and Santillán (2001), López-Herrera and Vázquez (2002a y b) and Valdivieso (2004), all of whom used the macroeconomic approach. Although these authors found evidence of around four priced factors, there is a problem of low explanation power in some cases. Recently, Saldaña et al. (2007) used a macroeconomic and fundamental combined approach of the APT applied on the telecommunication sector of the Mexican Stock Exchange, finding favorable evidence of this asset pricing model. Conversely, Treviño (2011) presents a more robust econometric methodology for a longer period of time, finding little evidence in favour of a macroeconomic APT applied on the mexican stock market. Additionally, López-Herrera and Ortiz (2011) carry on a multifactor beta model to explain the relationship between macroeconomic factors and asset pricing in Mexico, United States and Canada, in order to analyze the integration of each market with global macroeconomic variables.
Regarding studies focused on Latin America where APT has been used under different approaches we can mention the following. Arango et al. (2013) carry on the APT under the macroeconomic approach on the Colombian Stock Exchange, using principal component analysis to summarise the set of macroeconomic factors and financial variables utilized in the study. They find that risk perception is the most important variable to explain stock's returns. Kristjanpoller and Morales (2011) apply the APT to the chilean stock market under the macroeconomic approach as well; they find some evidence regarding the impact of some macroeconomic variables on the returns on equities. Londoño et al. (2010) test the APT on the colombian market, under two approaches: a) a macroeconomic and b) a macroeconomic plus international stock markets indicators. Furthermore, they use a multilayer neural network to relate the main index from the Colombian Stock Exchange to the factors considered. Their findings show that the neural network approach is more effective than a traditional statistical one.7Da Costa and Soares (2009) utilize a fundamental version of the APT applied to the Brazilian banking sector, finding weak evidence supporting this model. Oliveira (2011) present a comparative study using both the macroeconomic and the statistical approach of the APT, applied on three groups of countries composed by developed and emerging market, where some Latin American countries such as: Argentina, Chile and Mexico, are included. In this case the statistical factors are extracted by means of principal component analysis. Finally, Tabak and Staub (2007) use the APT to infer the probability of financial institution failure for banks in Brazil.
The aim of the present study is to fill a gap in the financial literature by testing a statistical definition of the APT on an important emerging financial market, the Mexican Stock Exchange. We shall extract the pervasive systematic risk factors by means of two different techniques: Principal Component Analysis and Factor Analysis through Maximum Likelihood. The structure of the present paper is as follows: first, we present the fundamentals of APT and of PCA and FA respectively; secondly, we describe the empirical study; in third place some conclusions are drawn; finally, we present the references, figures and tables.
Arbitrage Pricing Theory (APT)The APT has been proposed as an alternative to the CAPM, but it does not provide a complete solution. The APT has some advantages over the CAPM since it represents a more generalized model; it considers risk factors other than the market, it does not need restrictive assumptions such as normality in the distributions of returns and the investors' utility functions, and the market portfolio does not play any role; however, it shares some of the CAPM's weaknesses, like the linearity of its specification and the requirement of using historical data. Whereas the CAPM begins with the market model, the APT starts with a generative multifactor model of returns defined by the following expression:8
The statistical approach to the APT assumes that the return on equity depends on a set of unobservable factors common to all stocks (F's) and on one specific component (ε).9 The problem here is that the values of the factors are unobservable, and so the betas cannot be estimated through a regression model, as is done in the market model. Subsequently, we need to use extraction techniques, such as Principal Component Analysis or Factor Analysis, to estimate the former equation for all the assets simultaneously, and to be able to extract the value of the factors (F's) and calculate their loadings or betas (β's).
The arbitrage argument or principle of arbitrage absence is based on the following reasoning. Taking into account the “single price law”, in the same market two identical assets should have the same price; otherwise it would be possible to carry out an arbitrage transaction and obtain a differential profit. At the heart of APT and its pricing model lies arbitrage opportunities analysis, since only in its absence can we define a linear relation between the expected returns and the systematic risks. In order to avoid arbitrage possibilities, the return on equity must be equal to the expected return on the portfolio that combines the factor portfolios10 and the riskless asset (the mimicking portfolio, or the arbitrage portfolio). An arbitrage portfolio is any portfolio constructed with no capital invested and no risk taken that yields a null return on average.
By applying the arbitrage argument to the multifactor generative model, we arrive at the fundamental APT pricing equation:11
where λ0 represents the riskless interest rate, λk the risk premium for each kind of systematic risk factor, and βk the sensitivities or exposures to each type of systematic risk.Statistical risk factorsOur investigation is based upon the statistical approach of multivariate asset-pricing models; subsequently, we assume that the values of systematic risk factors are unobservable and that they must be extracted by means of statistical techniques. This approach presents certain advantages over others: gathering the required information is less expensive and more accessible than in macroeconomic or fundamental models; it is less subjectively biased because it does not predefine either the number or the nature of factors, so it is less exposed to an econometric specification error; and finally, the factors extracted are directly supported by a strong asset-pricing theory: the Ross (1976) APT. In addition, it involves two differentiated processes namely, risk extraction and risk attribution, which make it more objective. Conversely, statistical factors do not have a direct economic or financial interpretation, although in a second phase they can be correlated or decomposed with the help of explicit variables.12 In other words, from this standpoint, risk measurement and risk attribution are different steps of the process.13
The two most commonly used multivariate analysis techniques for extracting risk factors are Principal Component Analysis and Factor Analysis, but there is still no firm view as to which one is the ideal technique. Classical studies have utilized both; for example: Roll et al. (1980), in their seminal work, carried out Factor Analysis through Maximum Likelihood (MLFA), suggesting that returns on equities are determined by the factor loadings or betas; however, Chamberlain et al. (1983) and Connor et al. (1988) claimed that eigenvectors obtained by PCA could also be used as factor loadings. In opposition to these views, Shukla et al. (1990) asserted that PCA is only equivalent to FA when the idiosyncratic risk for every asset is the same, since PCA does not consider the specific risks. We could say that FA is closer to the underlying spirit of APT than is PCA; nevertheless, the latter presents the advantage of offering a unique mathematical solution and making no assumptions about the normality of the returns.
Principal Component AnalysisStrictly speaking, PCA is not a model, as it merely represents a geometric transformation and projection of data in order to facilitate their interpretation. PCA seeks to obtain a smaller number of artificial variables, the principal components, via a linear combination of the original ones, assuming two basic restrictions: the principal components must be orthogonal to each other, and they must have decreasing variances. Each original variable contributes with a different weight to the principal component formation. In other words, we want to project the original data onto a smaller dimension where the components will be mutually uncorrelated and at the same time retain the maximal possible variance, i.e. the risk. The mathematical expression of the idea behind PCA is as follows:
where: y denotes the principal components; a, the coefficients or loadings for each variable in each component construction, and x, the original variables. Generalizing in abbreviated matrix notation for the generic principal component h we have:and considering all the equations together for all the observations:In order to estimate the vector ah we have to decompose the covariance matrix by way of the linear algebra concept of eigenvalue decomposition (EVD)14, where ah will be the eigenvector associated with the h-esim eigenvalue (λh) of the covariance or correlation matrix, after been ranked from higher to lower. In the classic version for the econometric contrast of the APT, loadings a will represent the exposures to the pervasive systematic risk factors, the betas of the APT model that will be regressed on the asset returns to obtain the factor returns or factor risk premiums (lambdas in the APT pricing equation).15 These betas or factor loadings, which together form the factor matrix, are the correlation between each variable and the principal components. According to Uriel et al. (2005) we can compute them by using the correlation coefficient rhj between the h-esim component and the j-esim variable, as well.
Finally in PCA, we can obtain as many principal components as there are variables, because the covariance matrix (S) to be decomposed will contain in its main diagonal the total amount of variance represented by the value of one.16 In other words, we will try to explain the total amount of variance of the observed variables.
Factor Analysis (FA)Factor Analysis represents an explicit model with its own hypothesis, assuming that the original variables are a linear combination of the underlying factors. Although FA seeks to obtain a smaller number of factors, like PCA, its philosophy is completely different. In FA, we construct the p variables17 through a linear combination of their m pervasive common factors18 (with m<p), their particular weights or exposures (betas), and a specific error term. In order to construct those factors, it is necessary to estimate the commonality or proportion of the variance explained by the common factors. Then, we have to split the variance and covariance matrix into two parts, one explained by common factors and the other by the error term. The fundamental idea of FA can be expressed in formal terms as follows:
where μ1, μ2 …, μj, … μp denote the vector of means of the variable; x1, x2, …, xj, … xp; the observable variables; f1, f2, …, fh, …, fm, the common factors; λjh, the factor loading h in variable j; and u1, u2, …, up, are the specific factors. Generalizing for the generic variable j, we can express the value of a row of the former equations in condensed vector notation as follows:and gathering all the equations for all the observations:In FA the elements of matrix Λ (the λ coefficients) are the factor loadings applied to the common factors. They constitute the elements of the factor matrix and can be computed by the correlation coefficient rhj in expression 6 as well. There are many techniques to estimate the parameters of the factor model. We can divide them into two approaches: a) based on the eigenvalue decomposition and b) based on the estimation of equations to reconstruct the correlation matrix. In FA, the number of factors (m) is smaller than the number of variables (p) because the correlation matrix of returns to be decomposed contains in its main diagonal an estimation of the initial commonality,19 depending on the estimation technique utilized. In other words we will explain only the amount of variance explained by common factors, i.e., the covariance or correlations among the variables.
To summarize, the main difference between these techniques is that in PCA the components are constructed as a linear combination of the observable variables, whereas in FA, the observable variables are explained by the common factors. Thus, although in PCA we can express the variables in terms of the principal components by way of an algebraic transformation, both methods will not be equivalent unless the error term in FA tends to zero, since in FA we assume that the specific factors are uncorrelated with each other and with the common factors.
Empirical StudyAccording to the above-stated we take the Arbitrage Pricing Theory as our theoretical framework which poses on one hand, a generative multifactor model of returns, and on the another hand, an arbitrage absence principle, that together, produce an asset pricing model. Nevertheless, the scope and limitations of our research are given precisely for the statistical approach to the APT. Our study is focused in the risk extraction process whose main objective is to uncover the underlying multi-factor structure of systematic risk driving the returns on equities, independently of the number and nature of the factors. The risk attribution process is basically out of the scope of the present study, however, in this section we will attempt to provide a first approach to the meaning of the extracted systematic risk factors in order to be able to identify them. Likewise, the test of the arbitrage principle is out of the scope of the current study.20
In other words, the main objective of our empirical study is to uncover the underlying generative multifactor structure of returns of our sample, by way of the use of classic dimension reduction or feature extraction techniques such as PCA and FA. The results will show that the generative multifactor model of returns performs very well; however the systematic risk factors extracted and the betas estimated must be tested in order to verify whether or not they are priced according to the APT pricing model. In a second stage of our methodology, we run an econometric contrast in order to determine which of them are statistically significant and consequently determine whether or not the APT is accepted as an asset pricing model in the context of our study.
The dataThe empirical study was carried out on the Mexican Stock Exchange (BMV); for this, two aspects were taken into account: first, that very little research has been done concerning this institution; second, its relevance as an emergent financial market. The stocks selected for this study form part of the IPC and represent leading companies in the industrial sectors to which they belong; thus, we can consider them to be characteristic securities of the BMV and the Mexican economy. Both the period analysed and the shares selected reflected the availability of data among the diverse information sources consulted. Our basic aim was to build a homogeneous and sufficiently broad database, capable of being processed with the multivariate and econometric techniques involved in the APT model. First, we chose the IPC sample used from February 2005 to January 2006; then, we constructed two return databases taking into account, as the main criterion, that the equities chosen had remained in the IPC sample during all the considered periods for which information was available.21 In accordance with these considerations, we prepared a database made up of 20 companies and 291 weekly quotations (DBWR) ranging from July 7, 2000 to January 27, 2006; in addition, one with 22 shares that included 1 410 observations (DBDR) from July 3, 200022 to January 27s, 2006.23 We calculated the logarithmic weekly returns considering the assets' closing prices24 for each Friday, in accordance with the following expression:25
We also built two other databases considering the returns in excess of the riskless interest rate. The interest rates considered as the riskless interest rate were the average weekly and daily funding interest rates using government securities, published by the Bank of Mexico. For the weekly databases, it was necessary to convert them into the weekly equivalent to make them comparable with our returns on equities. After that, we subtracted the daily and weekly riskless interest rates from the weekly and daily returns on equities, respectively, in the two databases described above. Thus, we produced two more new databases, including the same stocks and observations as in the former, but expressed as returns in excess over the riskless interest rate (DBWE and DBDE). Consequently, our study was applied to the four resulting databases, i.e., we tested the two model specifications for the two different databases.The period analyzed in this study (2000–2006) was considered according to the following criteria: This article represents the first part of a major research, where we are testing different techniques for extracting the underlying systematic risk factors in the context of the Mexican Stock Exchange. Principal Component Analysis and Factor Analysis represent the classic techniques to perform that extraction, under a statistical approach of the systematic risk factors. Both, the techniques used in this article, and the other techniques utilized in the next stages of our research, have an explanatory and a predictive character. We first are carrying out the explanatory approach, which make us to divide our dataset in two blocks: one for explanation or training and another for prediction; i.e., the first period is used for the explanation or training of the model, and the second one, will be used for testing the predictive power of the generative model of returns estimated. Consequently, the data from 2000 to 2006 were used to extract the generative underlying structure of returns, which explains the behavior of the returns of the training period. This estimation will help us in the next stage of prediction, where the model will be tested in subsequent periods of time (from 2006 on). The other techniques that we are employing in our research are the Independent Component Analysis and the Neural Networks Principal Component Analysis; our objective is to be able to compare the results of the four techniques, concerning both their explanatory and predictive power. Therefore, we are using the same training and prediction periods for the four of them. Additionally, other reason for using this period of the dataset, is to be able to compare in further studies, the effects of the 2008–2009 financial crisis in the estimation of the underlying structure of systematic risk, by way of the extraction of the generative model of returns during the crisis and the post-crisis periods, using the four techniques26
First of all, the following tests were carried out to establish the adequacy of the sample to be treated with multivariate techniques.27 The number of observations in all the databases was suitable.28 The correlation matrix structure ensured the existence of a sufficient correlation level among the variables, according to the results of the following tests. Visual inspection of the correlation matrix revealed that a large number of correlation coefficients exceeded the generally accepted parameters.29 Bartlett's sphericity test verified that the correlation matrix was significantly different from the identity matrix.30 The Kaiser-Meyer-Olkin index, in all four databases, was also very good.31 Finally, the anti-image correlation matrix32 and the Measures of Sampling Adequacy (MSA)33 also produced excellent results. Thus, on the basis of the evidence produced, we were able to proceed with confidence to extract the risk factors using PCA and FA.
Extraction of underlying systematic risk factors via PCA and MLFAIn this study, we first obtained the generative multifactor model of returns in expression 1, using the classic multivariate techniques to extract the underlying factors Principal Component Analysis (PCA) and Maximum Likelihood Factor Analysis (MLFA). Using a Matlab® code programmed to perform the PCA and MLFA on our four databases, we obtained the scores of the principal components (Y) and the common factors (F) hierarchically ordered, as well as the matrices of weights for PCA and FA (A and Λ, respectively).
Since there is not a definite widespread criterion to define the best number of components to extract in PCA and in FA, we have used nine different criteria usually accepted in PCA and FA literature. These criteria have been: the arithmetic mean of the eigenvalues, the percentage of explained variance, the exclusion of the components or factors explaining a small amount of variance, the scree plot, the unretained eigenvalue contrast (Q statistic), the likelihood ratio contrast, Akaike's information criterion (AIC), the Bayesian information criterion (BIC), and the maximum number of components feasible to estimate in each technique. Considering that each criterion indicated a different number of factors to extract in each database, for the sake of comparison among techniques and pursuing the main objective of extracting a smaller number of risk factors than the number of stocks, we chose a window test for all the databases ranging from two to nine factors according to the results presented in table 1. Subsequently, we estimated eight different multifactor models to extract from 2 to 9 principal components and common factors for each one of our four databases.34 Then, we proceeded to reconstruct the original variables according to the generation process of each technique by computing the following expression in PCA:35
and the following expression in FA:36Number of Components or Factors to retain
| Criteria | Database of | Database of | Database of | Database of | ||||
|---|---|---|---|---|---|---|---|---|
| Weekly returns | Weekly excesses | Daily returns | Daily excesses | |||||
| PCA | MLFA | PCA | MLFA | PCA | MLFA | PCA | MLFA | |
| Arithmetic mean of the eigenvalues. | 4 | 3 | 4 | 5 | 4 | 2 | 4 | 2 |
| Percentage of explained variance (90%). | 14 | 9 | 14 | 9 | 18 | 9 | 18 | 9 |
| Exclusion of the components/factors explaining a small amount of variance (<1%). | 19 | 13–14 | 19 | 14 | 21 | 13 | 21 | 13 |
| Scree plot. | 3–4 | 4 | 3–4 | 5 | 3–4 | 4 | 3–4 | 3–4 |
| Unretained eigenvalues contrast (Q statistic). | 19 | 12 | 19 | 11 | 21 | 14 | 21 | 14 |
| Likelihood ration contrast. | 4 | 4 | 4 | 4 | 9 | 8 | 10 | 8 |
| Akaike's information criterion (AIC). | 4 | 5 | 4 | 5 | 9 | 9 | 10 | 9 |
| Bayesian information criterion (BIC). | 4 | 2 | 4 | 2 | 9 | 3 | 10 | 3 |
| Maximum number of components / factors feasible to estimate. | 20 | 14 | 20 | 14 | 22 | 15 | 22 | 15 |
| Number of components / factors to be tested. | 3, 4, 14, 19, 20 | 2, 3, 4, 5, 9 12, 13, 14 | 3, 4, 14, 19, 20 | 2, 4, 5, 9, 11, 14 | 3, 4, 9, 18, 21, 22 | 2, 3, 4, 8, 9, 13, 14, 15 | 3, 4, 10, 18, 21 | 2, 3, 4, 8, 9, 13, 14, 15 |
| Comparable number of components / factors to be tested in each database. | 2, 3, 4, 5, 9, 12, 13, 14 | 2, 3, 4, 5, 9, 11, 14 | 2, 3, 4, 7, 8, 9, 13, 14, 15 | 2, 3, 4, 7, 8, 9, 10, 13, 14, 15 | ||||
| Comparable range of components / factors to be tested for all databases looking for a reduction in the dimensionality. | 2–9 | 2–9 | 2–9 | 2–9 | ||||
The reconstruction of the observed returns or excesses was outstanding for almost all the stocks in the four databases, which imply that the estimation of the generative multifactor model in the statistical approach of the APT performed by both PCA and FA was successful. Nevertheless, the highest and lowest peaks in some stocks were not very well reconstructed. For reasons of saving space, we only present the lines and stem plots of the observed and reproduced returns and excesses of the first 5 stocks of each database, which belong to the experiment where we extracted nine underlying factors.37Figures 1 and 2 show the results of PCA and FA, respectively. We can easily observe that the reconstruction is very good in almost all cases.
The amount of variance explained by the extracted components or factors, as well as the accumulated one, is presented in table 2. We can observe that in all cases the three first components and factors explain between the 66% and the 84% of variability, which give some evidence about the importance of those components or factors. Factor analysis overcomes principal component analysis in this aspect, since in the four databases produce higher percentage of accumulated explanation. Moreover, in almost all cases the factors extracted by FA explain higher amounts of variance than those estimated by PCA.
Principal Component Analysis and Factor Analysis. Explained Variance
| Principal Component Analysis | Factor Analysis | |||||
|---|---|---|---|---|---|---|
| Principal Component | Explained Variance (%) | Accumulated Explained Variance (%) | Factor | Explained Variance (%) | Accumulated Explained Variance (%) | |
| Database of weekly returns | 1 | 46.63 | 46.63 | 1 | 45.46 | 45.46 |
| 2 | 13.08 | 59.70 | 2 | 15.67 | 61.13 | |
| 3 | 8.08 | 67.78 | 3 | 10.27 | 71.41 | |
| 4 | 6.90 | 74.68 | 4 | 5.82 | 77.23 | |
| 5 | 6.18 | 80.86 | 5 | 6.44 | 83.67 | |
| 6 | 5.33 | 86.19 | 6 | 6.91 | 90.58 | |
| 7 | 4.94 | 91.13 | 7 | 3.20 | 93.78 | |
| 8 | 4.61 | 95.74 | 8 | 3.36 | 97.15 | |
| 9 | 4.26 | 100.00 | 9 | 2.85 | 100.00 | |
| Database of weekly excesses | 1 | 46.82 | 46.82 | 1 | 45.68 | 45.68 |
| 2 | 13.04 | 59.86 | 2 | 15.68 | 61.36 | |
| 3 | 8.04 | 67.90 | 3 | 10.22 | 71.58 | |
| 4 | 6.88 | 74.78 | 4 | 5.80 | 77.38 | |
| 5 | 6.15 | 80.93 | 5 | 6.41 | 83.79 | |
| 6 | 5.32 | 86.25 | 6 | 6.85 | 90.64 | |
| 7 | 4.92 | 91.17 | 7 | 3.17 | 93.81 | |
| 8 | 4.59 | 95.76 | 8 | 3.35 | 97.16 | |
| 9 | 4.24 | 100.00 | 9 | 2.84 | 100.00 | |
| Database of daily returns | 1 | 46.62 | 46.62 | 1 | 70.63 | 70.63 |
| 2 | 12.81 | 59.43 | 2 | 7.73 | 78.36 | |
| 3 | 7.34 | 66.77 | 3 | 6.31 | 84.68 | |
| 4 | 6.62 | 73.39 | 4 | 3.32 | 88.00 | |
| 5 | 6.04 | 79.43 | 5 | 3.00 | 91.00 | |
| 6 | 5.87 | 85.30 | 6 | 2.54 | 93.54 | |
| 7 | 5.34 | 90.64 | 7 | 2.49 | 96.04 | |
| 8 | 4.89 | 95.53 | 8 | 2.49 | 98.53 | |
| 9 | 4.47 | 100.00 | 9 | 1.47 | 100.00 | |
| Database of daily excesses | 1 | 46.64 | 46.64 | 1 | 71.03 | 71.03 |
| 2 | 12.83 | 59.47 | 2 | 6.95 | 77.98 | |
| 3 | 7.35 | 66.82 | 3 | 6.31 | 84.28 | |
| 4 | 6.60 | 73.42 | 4 | 3.32 | 87.60 | |
| 5 | 6.04 | 79.46 | 5 | 2.83 | 90.43 | |
| 6 | 5.86 | 85.33 | 6 | 2.76 | 93.19 | |
| 7 | 5.33 | 90.66 | 7 | 3.19 | 96.38 | |
| 8 | 4.89 | 95.55 | 8 | 1.95 | 98.33 | |
| 9 | 4.45 | 100.00 | 9 | 1.67 | 100.00 | |
Although the second process of the statistical approach to the APT, i.e., the risk attribution stage, is out of the scope of this study, in this section we will make a first attempt to propose an interpretation of the meaning or nature of the systematic risk factors extracted, following a classic approach which has been widely used when PCA and FA are used to reduce dimensionality or to extract features from a multifactor dataset. This approach is based on using the factor loading matrix estimated in the extraction process to identify the loading of each variable in each component or factor; high factor loadings in absolute terms indicate a strong relation between the variables and the factor. In our context, the factors will be saturated with loadings of one stock or a group o stocks that may help us to indentify those factors with some economic sectors, as a first approach of interpretation of each component or factor.
In line with the previously reported results, we only present the factor loading matrix plots of each database, which belong to the experiment where we extracted nine underlying factors; figure 3 present the results of PCA and figure 4 those for FA. We constructed some tables summarizing the results derived from the analysis of the factor loading matrices and plots, where we propose some economic sector that may be related to each factor. We group together the stocks with the highest loading in each factor according the economic sectors official classification used in the Mexican Stock Exchange; table 3 present this summary. In general, as expected by theory, in both techniques for the four datasets, the first component or factor is clearly related to the market factor. In addition, there is no difference, regarding the interpretation of factors, in the models expressed in returns and those specified in excesses, with the exception of the factor seven extracted via factor analysis in the daily databases. Concerning PCA we can observe that the second and third components are identified with the minery and construction sector, respectively, in the four databases; however, from the fourth to the ninth components we can find a distinction between the interpretation of components extracted from the weekly and the daily databases. Respecting FA, there is a marked difference between the interpretation of factors that affect the weekly and daily returns, as we can observe in the Table 3. Relating both techniques, in addition to the first factor, only the third factor might be identified as the same factor for almost all the datasets and expression of the model, which corresponds to the construction sector. We can remark that we can identify two factors related to two important business groups in Mexico, which we may explain as market movers in the Mexican Stock Exchange. These components or factors are the PC5 extracted by PCA from the weekly databases, that it may be understood as the Salinas Group factor; and the F2, extracted by FA, in the weekly datasets, that we may associate with the Slim Group.
Principal Component Analysis and Factor Analysis. Summary of results. Sector interpretation of components
| Principal Component Analysis | |||
|---|---|---|---|
| Database of Weekly Returns | Database of Daily Excesses | Database of Daily Returns | Database of Weekly Excesses |
| PC1 Market factor | PC1 Market factor | PC1 Market factor | PC1 Market factor |
| PC2 Minery sector factor (Peñoles factor) | PC2 Minery sector factor (Peñoles factor) | PC2 Minery sector factor (Peñoles factor) | PC2 Minery sector factor (Peñoles factor) |
| PC3 Construction sector factor | PC3 Construction sector factor | PC3 Construction sector factor | PC3 Construction sector factor |
| PC4 Capital goods consum sector factor | PC4 Capital goods consum sector factor | PC4 Entertaninment consum sector factor. | PC4 Entertaninment consum sector factor. |
| PC5 Salinas Group sector factor | PC5 Salinas Group sector factor | PC5 Holding / Beverage / Salinas group factor. | PC5 Holding / Beverage / Salinas group factor. |
| PC6 Ordinary consum sector factor | PC6 Ordinary consum sector factor | PC6 Holding / Food and beverage sector factor | PC6 Holding / Food and beverage sector factor |
| PC7 Food sector factor (Bimbo factor) | PC7 Food sector factor (Bimbo factor) | PC7 Ordinary consum sector factor | PC7 Ordinary consum sector factor |
| PC8 Miscellaneous sector factor | PC8 Miscellaneous sector factor | PC8 Miscellaneous sector factor | PC8 Miscellaneous sector factor |
| PC9 Beverages and food sector factor | PC9 Beverages and food sector factor | PC9 Infrastructure / Financial sector factor | PC9 Infrastructure / Financial sector factor |
| FACTOR ANALYSIS | |||
| Database of Weekly Returns | Database of Weekly Excesses | Database of Daily Returns | Database of Daily Excesses |
| F1 Market factor | F1 Market factor | F1 Market factor | F1 Market factor |
| F2 Slim Group factor | F2 Slim Group factor | F2 Communication / commercial sector factor | F2 Communication / commercial sector factor |
| F3 Construction sector factor | F3 Construction sector factor | F3 Radio and television sector factor (Azteca factor) | F3 Radio and television sector factor (Azteca factor) |
| F4 Ordinary consum sector factor | F4 Ordinary consum sector factor | F4 Financial sector factor (GF Norte Factor) | F4 Financial sector factor (GF Norte Factor) |
| F5 Communication / commercial factor | F5 Communication / commercial factor | F5 Miscellaneous sector factor | F5 Miscellaneous sector factor |
| F6 Infrastructure / minery sector factor | F6 Infrastructure / minery sector factor | F6 Beverage / construction / financial sector factor | F6 Beverage / construction / financial sector factor |
| F7 Ordinary consum / entertainment sector factor | F7 Ordinary consum / entertainment sector factor | F7 Minery / beverage sector factor | F7 Minery sector factor (Peñoles factor). |
| F8 Miscellaneous sector factor | F8 Miscellaneous sector factor | F8 Holding / minery / construction sector factor | F8 Financial / brewers / cellulose sector factor |
| F9 Capital goods consum / holding sector factor | F9 Capital goods consum / holding sector factor | F9 Construction / communication / comercial sector factor | F9 Construction sector factor |
Finally, attending to the explained variance of each components or factors extracted (see table 2), we could select the first three of them in each dataset as the main factors, which lead us to think that: the market factor (for all datasets and both techniques), minery factor (for PCA), the Slim Group and communication/commercial factors (for the weekly and daily datasets using FA, respectively), the construction sector (for PCA and weekly databases in FA), and the radio and television sector factor (for daily databases en FA), could be the most important factors explaining the returns on equities in the Mexican Stock Exchange.
Econometric contrastAs a complement to our research, we carried out an econometric contrast of the APT using the underlying systematic risk factors extracted via PCA and FA, in order to test its validity as a suitable pricing model for the sample and periods considered. This contrast represents only a first approach to the econometric validation of the APT using PCA and FA, so the result should be viewed in that light. The APT's pricing equation in expression 2 can be tested by way of an average cross-section methodology estimating the ordinary least squares (OLS) coefficients of the following regression model:
Since both factors and sensitivities are computed simultaneously by the multi-variate techniques usually employed (Amenc and Le Sourd, 2003), the straight methodology for contrasting the APT under the statistical approach, use directly the loadings estimated in expression 1 as the betas in the former regression model (Gómez-Bezares et al, 1994). Nevertheless, as Marin and Rubio (2001) and Nieto (2001) remark, this methodology could present some econometric problems such as heteroskedasticity and autocorrelation in the residuals in addition to error in variables, which would yield inefficient OLS estimators with biased variances. One possible solution to the foregoing problems is to employ a two-stage methodology widely used in the fundamental and macroeconomic approach to the APT, where in a first stage we estimate the betas to use in expression 13 from the scores of the extracted factors, then in a second stage we estimate the lambdas.
Following Bruno et al. (2002)38, in the first stage we estimated the betas or sensitive to the underlying risk factors to use in expression 13, by regressing the factor scores obtained by the PCA or MLFA as a cross-section on the returns and excesses. In order to improve the efficiency of the parameter estimates and to eliminate autocorrelation in the error terms of the regressions, we used weighted least squares (WLS)39 to estimate the entire system of equations at the same time.40 The results of the regressions in the four databases were very good, producing, in almost all cases, statistically significant parameters, high values of the R2 coefficients and results in the Durbin-Watson test of autocorrelation, which lead us to the non-rejection of the null hypothesis of no-autocorrelation.41
In accordance with Jordan and García (2003)42, in the second stage we estimated the lambdas or risk premia in expression 13 by regressing the betas obtained in the first stage as a cross-section on the returns and excesses, using ordinary least squares. In order to avoid the econometric problems of heteroskedasticity and autocorrelation in the residuals of the model estimated through OLS, we used ordinary least squared corrected by heteroskedasticity and autocorrelation by means of the Newey-West heteroskedasticity and autocorrelation consistent covariances estimates (HEC). Additionally, we verified the normality in the residuals by carrying out the Jarque-Bera test of normality. In order to accept the APT pricing model, we require the statistical significance of at least one parameter lambda different from λ0,43 and the equality of the independent term to its theoretic value, i.e., the average returns, in the models expressed in returns:
and zero, in the models expressed in excesses of the riskless interest rate:We used Wald's test to confirm these equalities.In table 4, we present a summary of the results of the econometric contrast for PCA and in table 5 for MLFA. In general, the results of the explanation power, the adjusted R-squared (R2*), the statistical significance of the multivariate test (F), and the Jarque-Bera normality test of the residuals are very good in all the contrasted models, except in the cases where only two factors were extracted using PCA; nevertheless, using FA there are more models that do not produce a good level of explanation and they are not statistically significant in multivariate terms. The univariate tests for the individual statistical significance of the parameters44 priced from one to six factors different from λ0 in PCA and from one to eight in MLFA, thus giving evidence in favour of the APT in 30 models using PCA and 27 utilising FA.45 Nevertheless, only four models in PCA and three in MLFA fulfilled both the statistical significance of the parameters and the equality of the independent term to its theoretic value, in addition to the fulfilment of normality in the residuals. Concerning the PCA these models were the one expressed in weekly returns when seven components were extracted, those expressed in daily returns when three, and nine components were retained, and the model expressed in daily excesses with six components. Regarding the MLFA those models were the ones using five factors in the weekly returns database, and eight and nine, in the daily returns dataset.
Principal Component Analysis. Summary of the econometric contrast. Weekly and Daily databases
| λ0 | λ1 | λ2 | λ3 | λ4 | λ5 | λ6 | λ7 | λ8 | λ9 | R2* | λsig/λtot | F | WALD | J-B | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Database of weekly returns. | |||||||||||||||
| Model with 2 betas | • | • | • | 6.62% | 0.00% | • | ○ | ○ | |||||||
| Model with 3 betas | 0.00563 | • | 0.00296 | −0.0077 | 51.99% | 66.67% | ○ | • | ○ | ||||||
| Model with 4 betas | 0.00574 | • | 0.00292 | −0.00777 | • | 49.02% | 50.00% | ○ | • | ○ | |||||
| Model with 5 betas | 0.00551 | • | 0.003 | −0.00762 | • | • | 46.62% | 40.00% | ○ | • | ○ | ||||
| Model with 6 betas | 0.00572 | • | 0.00292 | −0.00775 | • | • | • | 57.27% | 33.33% | ○ | • | ○ | |||
| Model with 7 betas | 0.00574 | • | 0.00292 | −0.00776 | • | • | • | • | 53.72% | 28.57% | ○ | ○ | ○ | ||
| Model with 8 betas | 0.00583 | • | 0.00288 | −0.00783 | • | • | • | • | • | 53.57% | 25.00% | ○ | • | ○ | |
| Model with 9 betas | 0.00579 | • | 0.0029 | −0.0078 | • | • | • | • | • | • | 48.98% | 22.22% | ○ | • | ○ |
| Database of weekly excesses. | |||||||||||||||
| Model with 2 betas | • | • | • | 6.62% | 0.00% | • | ○ | ○ | |||||||
| Model with 3 betas | 0.00392 | • | 0.00298 | −0.00769 | 51.99% | 66.67% | ○ | • | ○ | ||||||
| Model with 4 betas | 0.00403 | • | 0.00294 | −0.00776 | • | 49.03% | 50.00% | ○ | • | ○ | |||||
| Model with 5 betas | • | • | 0.00303 | −0.00761 | • | • | 46.62% | 40.00% | ○ | • | ○ | ||||
| Model with 6 betas | 0.00402 | • | 0.00295 | −0.00775 | • | • | • | 57.35% | 33.33% | ○ | • | ○ | |||
| Model with 7 betas | • | • | 0.00294 | −0.00776 | • | • | 0.00322 | • | 53.80% | 57.14% | ○ | ○ | ○ | ||
| Model with 8 betas | • | • | 0.0029 | −0.00782 | • | • | • | • | • | 80.53% | 25.00% | ○ | • | ○ | |
| Model with 9 betas | • | • | 0.00292 | −0.0078 | • | • | • | • | • | • | 49.05% | 22.22% | ○ | • | ○ |
| Database of daily returns. | |||||||||||||||
| Model with 2 betas | • | • | −0.00049 | 7.96% | 50.00% | • | ○ | ○ | |||||||
| Model with 3 betas | 0.00053 | • | −0.00057 | −0.001374 | 41.29% | 66.67% | ○ | ○ | ○ | ||||||
| Model with 4 betas | • | • | • | −0.00129 | • | 48.22% | 25.00% | ○ | ○ | ○ | |||||
| Model with 5 betas | • | • | • | −0.001297 | • | • | 49.15% | 20.00% | ○ | • | ○ | ||||
| Model with 6 betas | • | • | • | −0.001299 | • | • | • | 46.66% | 16.67% | ○ | ○ | ○ | |||
| Model with 7 betas | • | • | • | −0.0013 | • | • | • | • | 43.35% | 14.29% | ○ | ○ | ○ | ||
| Model with 8 betas | • | • | • | −0.00131 | • | • | • | • | • | 65.02% | 12.50% | ○ | ○ | ○ | |
| Model with 9 betas | 0.00066 | • | −0.0005 | −0.001357 | −0.00051 | 0.00041 | • | • | • | −0.00094 | 70.55% | 55.56% | ○ | ○ | ○ |
| Database of daily excesses. | |||||||||||||||
| Model with 2 betas | • | • | −0.00052 | −1.42% | 50.00% | • | ○ | ○ | |||||||
| Model with 3 betas | • | • | −0.00061 | −0.001412 | 42.28% | 66.67% | ○ | ○ | • | ||||||
| Model with 4 betas | • | • | • | −0.001322 | • | 49.80% | 25.00% | ○ | ○ | ○ | |||||
| Model with 5 betas | • | • | • | −0.001329 | • | • | 50.60% | 20.00% | ○ | ○ | ○ | ||||
| Model with 6 betas | 0.00089 | −0.00274 | −0.00025 | −0.001331 | −0.00092 | 0.00038 | 0.00019 | 48.44% | 100.00% | ○ | ○ | ○ | |||
| Model with 7 betas | • | • | • | −0.001343 | • | • | • | • | 43.35% | 14.29% | ○ | ○ | ○ | ||
| Model with 8 betas | • | • | • | −0.001343 | • | • | • | • | • | 45.03% | 12.50% | ○ | ○ | ○ | |
| Model with 9 betas | • | • | −0.00052 | −0.001391 | −0.00055 | 0.00041 | • | • | • | 0.00097 | 73.51% | 55.56% | ○ | ○ | ○ |
Notes:
* The level of statistical significance used in all the tests was 5%.
λj: Estimated coefficients. H0: λj=0. Numeric value of the coefficient = Rejection of H0. Parameter significant. • = Non-rejection of H0. Parameter not significant
R2*: Explanatory capacity of the model.
λsig/λtot: Ratio number of significant lambdas / total number of lambdas in the model.
F: Global statistical significance of the model. H0=λ2=λ3= …=λk=0. ○=Rejection of H0. Model globally significant. •=Non-rejection of H0. Model globally not significant.
Wald: Wald's test for coefficient restrictions. Databases in returns: H0: λ0=Average riskless interest rate. Databases in excesses: H0: λ0=0. ○= Non-rejection of H0. The independent term is equal to its theoretic value. •= Rejection of H0. The independent term is not equal to its theoretic value.
J−B: Jarque Bera's test for normality of the residuals. H0=Normality. ○=Non-rejection of H0. The residuals are normally distributed. •=Rejection of H0. The residuals are not normally distributed.
Maximum Likelihood Factor Analysis. Summary of the econometric contrast. Weekly and Daily databases
| λ0 | λ1 | λ2 | λ3 | λ4 | λ5 | λ6 | λ7 | λ8 | λ9 | R2* | λsig/λtot | F | WALD | J-B | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Database of weekly returns. | |||||||||||||||
| Model with 2 betas | 0.00457 | • | • | 0.20% | 0.00% | • | • | ○ | |||||||
| Model with 3 betas | 0.00337 | • | • | 0.127215 | 11.05% | 33.33% | • | ○ | ○ | ||||||
| Model with 4 betas | 0.00376 | • | • | • | 0.1378 | 14.79% | 25.00% | • | ○ | ○ | |||||
| Model with 5 betas | 0.00309 | −0.07078 | • | • | • | 0.210773 | 52.58% | 40.00% | ○ | ○ | ○ | ||||
| Model with 6 betas | 0.00424 | −0.09734 | • | • | • | 0.207821 | −0.13978 | 68.40% | 50.00% | ○ | • | ○ | |||
| Model with 7 betas | 0.00473 | • | • | • | −0.15198 | −0.06563 | 0.072453 | • | 69.06% | 42.86% | ○ | • | ○ | ||
| Model with 8 betas | 0.00593 | −0.10643 | −0.05528 | −0.06844 | 0.12686 | −0.08073 | 0.090677 | 0.07573 | 0.17361 | 80.71% | 100.00% | ○ | • | ○ | |
| Model with 9 betas | 0.00579 | −0.14932 | • | • | 0.05005 | • | 0.168997 | 0.09160 | −0.11678 | 0.10175 | 77.77% | 66.67% | ○ | • | ○ |
| Database of weekly excesses. | |||||||||||||||
| Model with 2 betas | 0.00287 | • | • | 0.05% | 0.00% | • | • | ○ | |||||||
| Model with 3 betas | • | • | • | 0.127579 | 11.09% | 33.33% | • | ○ | ○ | ||||||
| Model with 4 betas | 0.00205 | −0.05436 | −0.00193 | 0.02853 | • | 14.81% | 75.00% | • | ○ | ○ | |||||
| Model with 5 betas | • | −0.07021 | • | • | • | 0.209691 | 52.20% | 40.00% | ○ | ○ | • | ||||
| Model with 6 betas | 0.00255 | −0.09697 | • | • | • | 0.207094 | • | 68.38% | 33.33% | ○ | • | ○ | |||
| Model with 7 betas | 0.00304 | • | • | • | −0.15182 | −0.06446 | • | • | 69.00% | 28.57% | ○ | • | ○ | ||
| Model with 8 betas | 0.00424 | −0.10598 | −0.05599 | −0.06776 | 0.12691 | −0.0809 | 0.08932 | 0.07557 | 0.17512 | 80.76% | 100.00% | ○ | • | ○ | |
| Model with 9 betas | 0.00421 | −0.14882 | • | 0.042799 | 0.04998 | • | 0.16767 | 0.09366 | −0.11721 | 0.10273 | 77.84% | 77.78% | ○ | • | ○ |
| Database of daily returns. | |||||||||||||||
| Model with 2 betas | 0.00094 | −0.04908 | • | 2.31% | 50.00% | • | • | ○ | |||||||
| Model with 3 betas | 0.00086 | −0.03853 | 0.02121 | 0.01201 | −2.64% | 100.00% | • | ○ | ○ | ||||||
| Model with 4 betas | 0.00043 | 0.001128 | 0.02701 | 0.05664 | 0.069242 | 5.03% | 100.00% | • | ○ | ○ | |||||
| Model with 5 betas | • | • | • | • | 0101009 | • | 23.10% | 20.00% | • | ○ | ○ | ||||
| Model with 6 betas | • | • | • | • | • | • | 0.052567 | 33.30% | 16.67% | • | ○ | ○ | |||
| Model with 7 betas | 0.00107 | −0.05676 | • | • | −0.12533 | 0.07379 | • | 0.05998 | 65.17% | 57.14% | ○ | • | ○ | ||
| Model with 8 betas | 0.00078 | • | • | • | • | 0.05464 | −0.14354 | • | • | 71.69% | 25.00% | ○ | ○ | ○ | |
| Model with 9 betas | 0.00092 | • | • | • | −0.1086 | • | • | • | 0.1059 | • | 70.26% | 22.22% | ○ | ○ | ○ |
| Database of daily excesses. | |||||||||||||||
| Model with 2 betas | 0.00072 | −0.04878 | • | 1.65% | 50.00% | • | • | ○ | |||||||
| Model with 3 betas | • | • | • | • | 42.28% | 66.67% | • | ○ | ○ | ||||||
| Model with 4 betas | • | • | • | • | • | 3.51% | 0.00% | • | ○ | ○ | |||||
| Model with 5 betas | • | • | • | • | 0.104552 | • | 23.14% | 20.00% | ○ | ○ | ○ | ||||
| Model with 6 betas | • | • | • | • | • | • | • | 32.27% | 0.00% | • | ○ | ○ | |||
| Model with 7 betas | 0.00087 | −0.05971 | • | • | −0.13575 | • | 0.065795 | 0.07526 | 67.22% | 57.14% | ○ | • | ○ | ||
| Model with 8 betas | 0.00084 | −0.05614 | • | • | 0.063658 | • | −0.14532 | 0.03899 | • | 75.19% | 50.00% | ○ | • | ○ | |
| Model with 9 betas | 0.0008 | • | • | • | −0.10328 | • | • | 0.09296 | −0.07264 | • | 77.63% | 33.33% | ○ | • | ○ |
Notes:
* The level of statistical significance used in all the tests was 5%.
λj: Estimated coefficients. H0: λj = 0. Numeric value of the coefficient = Rejection of H0. Parameter significant. • = Non-rejection of H0. Parameter not significant
R2*: Explanatory capacity of the model.
λsig /λtot: Ratio number of significant lambdas / total number of lambdas in the model.
F: Global statistical significance of the model. H0 = λ2 = λ3 = … = λk = 0. ∘ = Rejection of H0. Model globally significant. • = Non-rejection of H0 Model globally not significant.
Wald: Wald's test for coefficient restrictions. Databases in returns: H0: λ0 = Average riskless interest rate. Databases in excesses: H0: λ0 = 0. ∘ = Non-rejection of H0. The independent term is equal to its theoretic value. • = Rejection of H0. The independent term is not equal to its theoretic value.
J-B: Jarque Bera's test for normality of the residuals. H0 = Normality. ∘ = Non-rejection of H0. The residuals are normally distributed. • = Rejection of H0. The residuals are not normally distributed.
Making a cross validation of the accepted models and the interpretation of factors proposed above, we could state de following: The significant components that affect the weekly model accepted in PCA, are the minery and construction sector factor. For the accepted daily models expressed in returns, the previous components are significant as well, in the models that consider two and nine factors; additionally, the model with nine factors is affected by the entertainment consum, the holding-beverage-Salinas group, and infrastructure-financial sector factors. Model with 6 betas, consider almost the same components, in addition to the market sector factor. Concerning the accepted models in FA, in the weekly database of returns, the significant factors would be the market one, and the communication-commercial sector factor. Finally, for the daily databases of returns, those would be represented by the holding-beverage-Salinas Group, and the holding-food and beverage sector factors, in the case of the model using 8 betas; and the entertainment consum sector factor and a miscellaneous sector factor not clearly identified, in the case of the model with 9 betas.
Interestingly, market factor was statistically significant only in two of the accepted models; further research would be needed about this issue, as well as about the meaning of the undersized value and sign of the estimated individual parameters.
To summarize, for the sample and periods considered, we can accept only partially the validity of the APT using PCA and FA as a pricing model explaining the average returns (and returns in excesses) on equities of the Mexican Stock Exchange. On the other hand, the evidence showed that the APT is very sensitive to the number of factors extracted and to the periodicity and expression of the models.
ConclusionsIn general, and in accordance with the scope and limitations of this study, the estimation of the generative multifactor model of returns by means of PCA and FA reproduced the observed returns on equities of our sample very well; thus we can state that both techniques performed an outstanding extraction of the underlying systematic risk factors driving the returns on equities of our sample, under an statistical approach of the APT.
Regarding the interpretation, according the basic approach carried on in this study, we uncover that factors or components driving the returns are sensitive to the technique used, the periodicity and the expression of the returns used in the model.
Conversely, for the sample and periods considered, we can accept only partially the validity of the APT using PCA and FA, as a pricing model explaining the average returns (and returns in excesses) on equities of the Mexican Stock Exchange. On the other hand, the evidence showed that the APT is very sensitive to the number of factors extracted and to the periodicity and expression of the models. The APT model, as applied in this study, did not produce a clear correspondence with the behavior of the returns in the Mexican Stock Market; nevertheless, we have detected some evidence favourable to the APT revealing the presence of priced pervasive statistical risk factors in a large number of models, as well as seven models that fulfilled completely all the requirements for accepting the APT pricing model.
Consequently, we conclude that the performance of the APT statistical approach with respect to the Mexican Stock Exchange presents some inconsistencies that make it unstable and sensitive to the different techniques used for extracting risk factors. Further research will be required to examine alternative approaches for underlying factor extraction, such as Independent Component Analysis (ICA) and Neural Networks Principal Component Analysis (NNPCA), in order to uncover the true generative structure of returns on equities in this emerging market. Finally, our results are consistent with earlier studies in which this statistical approach was applied to other markets and with the number of priced factors found in Mexico through studies in which a macroeconomic approach was used.46
A revision of empirical studies using approaches other than the statistical one is beyond the scope of this paper; however, interested readers can easily find many references in the financial literature.
In a second stage, it is possible to identify the pervasive factors with some financial or macroeconomic variables by means of correlation procedures or other kind of methodologies.
For a more extensive study of the MSCI-BARRA model see Amenc et al. (2003), Sheikh (1996), BARRA (1998).
For more information about BIRR model see Burmeister et al. (2003).
For more details about Advanced Portfolio Technology (APT) model see Amenc et al. (2003) and SUN-GARD-APT (2010).
Some references are van Rensburg (2000) on Johannesburgh; Ch'ng et al. (2001) on Malaysia; Aquino (2005) on the Philippines; Dhankar et al. (2005) on India; Twerefou et al. (2005) on Ghana; Iqbal et al. (2005) on Karachi; Shum et al. (2005) on Hong Kong, Singapur, and Taiwan; and Fuentes et al. (2006) on Chile.
The better results may be explained by the non-linear specification of the APT, which is out of the scope of this paper but represents a future line of research of the authors as a continuation of the present work.
Where, βji represents the sensitivity of equity i to factor j, Fjt the value of the systematic risk factor j in time t common for all the stocks, and εi the idiosyncratic risk affecting only equity i.
It is assumed that the factors are uncorrelated with each other, as are the model's residual terms, both with each other and with the factors.
Portfolios which mimic the systematic risk factors in the economy.
A mathematical demonstration for obtaining the fundamental pricing equation from the generative multifactor model of returns by the application of the arbitrage argument can be found in Amenc et al. (2003).
See Amenc et al. (2003) and SUNGARD-APT (2010).
On the other hand, the rest of the approaches usually mix these two differentiated processes in one step.
The eigenvalue decomposition implies: S=ULU'; where S is the covariance matrix; U, the eigenvector matrix; L, the eigenvalue matrix, and U' the matrix U transposed. When we use normalized data the matrix S is equal to the correlation matrix R.
In this study we carry on a two-stage version for the econometric contrast explained in the empirical study section.
The value of one will be in the case of using the matrix o f correlation (R).
In our case, returns on equities.
In our case, systematic risk factors.
A number always less than one.
Forthcoming researches will center on the risk attribution process of the statistical approach as well as on the test of the arbitrage principle of the APT.
Survival bias: Equities that did not remain in the IPC sample throughout the entire study period, because they were unlisted, substituted, or only present for some periods, were excluded. The purpose of this criterion was to work with a strong database (from a financial point of view), considering only stocks that had survived as part of the IPC sample throughout this period of time, satisfying all the listing and maintenance requirements established by the BMV. See Gómez-Bezares et al. (1994).
In this case, we started in july because, until 2000, the IPC sample validity was half-yearly, with the new half-yearly sample beginning in july. From 2001 to 2010, the sample validity was yearly, changing each february.
The number of assets and the periods considered were defined by the available information in accordance with the above-stated criteria. Unfortunately, since there are many gaps in the observations of several stocks in the mexican market, it is very difficult to build a dataset of quotations which contains both a long number of observations and a large number of stocks. In our case, the 20 and 22 stocks considered represents the maximum number of shares from which we could obtain a good enough number of observations of all of them, that allowed us to build complete and homogeneous datasets for both periodicities (without missing values). This fact constitutes a very important aspect for the correct application of the extraction techniques presented. In addition, we decided to use two differently structured databases in order to test the case of weekly and daily returns as well as a larger and a smaller number of observations, according to the different studies found in literature.
Although other studies have included other elements such as dividends and application rights to calculate the return on equities in addition to price variation, we could not incorporate them, as this sort of data was not available to us.
Where rit is the return on equity i in time t; ln, the Neperian logarithm; Pit, the equity price i in time t; Pit-1, the equity price i in time t minus 1.
As stated in the introduction of this article this study only focuses in the estimation of the explanatory model using PCA and FA. The estimation of the explanatory models using the other referred techniques, the testing of the prediction power of the estimated models and the comparison of the results in the crisis and post-crisis periods are out of the scope of this article, and represent other stages of the research conducted by the authors of the present document.
Strictly speaking, the first preliminary test would consist in verifying the univariate normal distribution of the returns on equities. We used the Jarque-Bera test on the four databases, finding that in most cases the stocks of our sample did not follow a univariate normal distribution. However, the effects of this condition on our results are beyond the scope of this study.
There were 291 observations in two databases and 1 410 in the other two. Luque (2000) recommends having at least 100 cases and no fewer than 50. Hair et al. (1999) considered it necessary to have five times more observations than variables. In our case, those figures would represent 100 and 110, respectively.
While some authors believe that a suitable correlation level must be higher than 0.3, many others think it must be at least 0.5.
In the four databases we obtained high values in this respect, fluctuating around 2 162.23 and 2 176.19 in the weekly databases, and around 9 707.33 and 9 723.98 in the daily databases, with a significance level of zero in all four cases; we reject the null hypothesis that the correlation matrix was an identity matrix, and conclude that the variables were mutually correlated. The higher the value of the statistic and the smaller the significance level, the less probability that the correlation matrix is an identity matrix. For more details about Bartlett's sphericity test, see Luque (2000).
The results for this statistic in all four databases reached levels higher than 0.90. Its feasible values range from 0 to 1, values over 0.80 are considered to be good to excellent. The objective of this test is to compare the magnitudes of the observed correlation and the partial correlation coefficients among variables. For details, see Visauta et al. (2003).
This test requires small values for the coefficients. The anti-image matrix is formed with the negatives of the partial correlation coefficient for each pair of variables, neutralizing the effect of the others.
The levels obtained were over 0.90 in almost all cases. We found the MSA in the main diagonal of the anti-image correlation matrix. They would be the KMO, but for each variable individually, so their parameters and interpretation are the same as for the KMO. See Visauta et al. (2003).
The total number of estimated multifactor models was 32 for PCA and 32 for MLFA.
This expression represents an algebraic transformation of the expression 5 taken from Peña (2002).
This expression is the same expression that expression 9 but without including the matrix of specific factors U, because this matrix represents the error in reproduction of the original variables, which will be known after the reconstruction process and is computed by: U=X-Xr, where Xr is the matrix X reconstructed.
In this paper we only show results for this experiment, nevertheless, the rest of the estimations when 2, 3, 4, 5, 6, 7 and 8 components or factors where extracted present similar behavior.
In their work, the authors use principal component analysis to extract the underlying risk factors from a set of macroeconomic variables in the spanish market.
According to this methodology as stated in the help of Eviews® (2002): “The equation weights are the inverses of the estimated equation variances, and are derived from unweighted estimation of the parameters of the system”.
Our first attempt to estimate all the betas in the system of equation was a seemingly unrelated regression (SUR), however, the estimation was not possible since the SUR methodology requires computing the inverse of the residual matrix, and our data produce a residual matrix near a singular one; subsequently, it was not feasible to compute its inverse.
For reasons of saving space these results are not presented.
In their study the authors use factor analysis to extract the underlying risk factors from a set of returns on mutual funds in the spanish market.
The ideal situation is that more than one parameter different from λ0 be statistically significant, since the APT assumes that there are multiple underlying risk factors in the economy affecting the returns on equities, not only one.