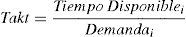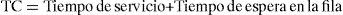Análisis del servicio de Urgencias aplicando teoría de líneas de espera

Resumen

Los responsables de la toma de decisiones de los hospitales son cada vez más conscientes de la necesidad de administrar de manera eficiente los sistemas hospitalarios. Una opción son los modelos de líneas de espera. En el presente trabajo se analiza el servicio del área de Urgencias de un hospital público aplicando los conceptos y relaciones de líneas de espera. A partir de los resultados del modelo se concluye que en el área de Urgencias no se cuenta con la cantidad mínima necesaria de médicos para permitir un flujo constante de pacientes. Con el modelo se calcula el número mínimo de médicos necesarios para satisfacer la demanda actual y futura de servicio, con los mismos tiempos de servicio y la misma disciplina de servicio. Los modelos analíticos permiten entender directamente las relaciones existentes entre demanda de servicio, número de médicos y prioridad de atención del paciente vistos como un sistema de líneas de espera. El trabajo es de utilidad para los administradores y responsables de la gestión de sistemas hospitalarios.

Abstract

Those responsible for making decisions in hospitals are increasingly aware of the need to efficiently manage hospital systems. An option for analysis is done by queuing models. In this paper is analyzed the service area ER, in a public hospital applying the concepts and relationships of waiting lines. From the model results, it is concluded that in the emergency department does not have the required minimum number of doctors to allow a steady flow of patients. With the model, the minimum required number of doctors is calculated to meet current and future demand for service with the same service time and the same discipline of service. Analytical models, allowing direct understand the relationships between service demand, number of doctors and patient care priority viewed as a queuing system. The work is useful for administrators and managers of hospital systems.

Introducción

Los responsables de la toma de decisiones de los hospitales son cada vez más conscientes de la necesidad de administrar de manera más eficiente los recursos hospitalarios a su cargo. Para proporcionar un buen servicio, los responsables deben utilizar herramientas que les permitan analizar, programar, planificar, priorizar y, en general, decidir sobre la mejor forma de administrar los recursos disponibles (Vissers y Beech, 2005; Abraham, Byrnes y Bain, 2009). Un ejemplo del tipo de problemas a analizar es el de estimar el nivel de servicio que se proporciona a los pacientes, el tiempo promedio de espera, la cantidad de pacientes formados, la capacidad utilizada y la probabilidad de que el paciente deba esperar. En los sistemas hospitalarios el tiempo de espera para recibir atención es un elemento clave en la medición de la calidad del servicio, por lo que la disminución de dicho tiempo de espera se ha vuelto un factor de suma importancia en la administración de esta clase de sistemas (Green, 2005, 2010).

Para obtener las propiedades mencionadas arriba se pueden emplear medios analíticos derivados de la teoría de líneas de espera. Las herramientas analíticas permiten entender las relaciones existentes entre cada uno de los elementos de un sistema, a diferencia de otros enfoques de análisis, que con frecuencia asemejan cajas negras (Hopp y Spearman, 2008). El enfoque de simulación, aunque permite obtener las mismas propiedades, es recomendable emplearlo cuando no existe un modelo analítico del sistema a analizar (Law y Kelton, 2000). Por otro lado, no en todos los sistemas hospitalarios se espera tener un programa de simulación especializado; en cambio, el acceso a las fórmulas analíticas es universal y gratuito. Como se menciona en el trabajo de Song, Tucker y Murrel (2013), los estudios empíricos (como el presente) en sistemas hospitalarios son en proporción menos abundantes que su contraparte en los ámbitos de manufactura y producción, lo que genera un área de oportunidad para los profesionistas que administran esta clase de sistemas para aplicar diversas herramientas analíticas bien conocidas en otras áreas.

En este orden de ideas, el presente trabajo muestra el método para analizar el servicio de Urgencias aplicando los conceptos y relaciones de la teoría de líneas de espera. Se toma como caso de estudio el servicio de Urgencias de un hospital público de la ciudad de Celaya, estado de Guanajuato, donde los administradores del área perciben una gran cantidad de pacientes formados esperando a ser atendidos.

El estudio es de interés para administradores, ingenieros, médicos y, en general, para todos aquellos profesionistas que tengan a su cargo la toma de decisiones de sistemas de salud y que desean analizar la demanda de servicio así como la capacidad de atención.

Antecedentes

La administración de un sistema hospitalario requiere la adecuación de los conceptos, como los de investigación de operaciones, a los objetivos y necesidades de esta clase de sistemas. En este sentido, el aspecto monetario no es la única medida de desempeño; también es necesario tomar en cuenta la calidad del servicio prestado y que se traduce, por ejemplo, en medidas como el tiempo de respuesta y el tiempo de atención. En la tabla 1 se presenta una muestra de estudios realizados sobre los sistemas hospitalarios. En dicho cuadro se incluyen tanto la aplicación de modelos de teoría de líneas de espera como de modelos de simulación.

Tabla 1.

Análisis de servicios hospitalarios

Autor	Año	Comentario
Benneyan	1997	Modelo de simulación para analizar el tiempo de atención en el área de pediatría
Whitt	1999	Análisis de la pertinencia de dividir los pacientes y asignar servidores para cada clase
Llorente et al.	2001	Modelo de simulación para analizar la capacidad de atención del área de urgencias generales
Bastani	2007	Aplicación de teoría de líneas de espera para modelar el flujo de pacientes entre el área de Urgencias y el área de Cuidados Intensivos
De Bruin et al.	2007	Análisis de la capacidad de atención en el área de Emergencias Cardíacas. Se analiza el efecto de la variabilidad de la demanda
Fomundam y Herrmann	2007	Estado del arte sobre las aplicaciones de teoría de líneas de espera al análisis y solución de problemas en la administración de sistemas hospitalarios
Oredsson et al.	2011	Estado del arte sobre análisis de los tiempos de espera de los pacientes en el área de Urgencias
Hulshof et al.	2012	Análisis de políticas de atención en el área de consulta externa
Pendharkar et al.	2012	Modelo de simulación para analizar sistemas con capacidad insuficiente. Se aplica al área de trastornos del sueño
Tan et al.	2013	Modelo dinámico de líneas de espera para controlar personal médico en el área de Urgencias
Lin et al.	2013	Análisis del flujo de pacientes en las áreas de Urgencias tomando en cuenta el nivel de urgencia del paciente
Tan et al.	2013	Modelo de líneas de espera para analizar el flujo de pacientes en el área de Urgencias
Yom-Tov y Mandelbaum	2014	Modelo que utiliza en la distribución Erlang para representar los retornos de los clientes en atención hospitalaria

Modelos de líneas de espera

En Whitt (1999) se propone una estrategia de partición del flujo de pacientes que entran al sistema con el objetivo de favorecer el flujo de pacientes asignándoles su propio servidor; sin embargo, el modelo supone que no existe diferencia significativa entre la demanda de cada clase de pacientes.

Bastani (2007) desarrolla un modelo para analizar tres áreas: cuidados intensivos, unidad de coronarias y hospitalización, y supone una disciplina de atención tipo primero-en-entrar-primero-en-salir. En De Bruin, van Rossum, Visser y Koole (2007) se analiza el flujo de pacientes y la capacidad de atención del área de emergencias cardíacas con un modelo donde se permiten readmisiones. Se resalta el hecho de que se distinguen dos clases de pacientes, aunque al momento del análisis se toma la demanda de servicio como una sola.

Hulshof et al. (2012) proponen estrategias para mejorar el flujo de pacientes de consulta externa clasificándolos por los síntomas del paciente y asignándoles sus respectivos médicos (servidores). El modelo analítico se construye tomando como base los cambios en la operación de varios hospitales de Alemania. La misma estrategia de clasificar pacientes y asignarlos a médicos se propone en Tan, Tan y Lau (2013) y Tan, Lau y Lee (2013), donde además se desarrolla un modelo dinámico para analizar el área de urgencias de un hospital en Singapur. El modelo trabaja en tiempo real y se requieren métodos heurísticos para obtener una solución del mismo.

En Lin, Patrick y Labeau (2013) se construye un modelo con etapas en serie para analizar el flujo entre dos áreas de un hospital y estimar los recursos de personal necesarios. Finalmente, en Yom-Tov y Mandelbaum (2014) se propone un modelo donde existen pacientes que regresan (recirculan) y supone un tiempo de servicio tipo Erlang; sin embargo, considera una disciplina primero-en-entrar-primero-en-salir.

Modelos de simulación

En el caso de la simulación aplicada para el análisis se pueden mencionar los trabajos de Benneyan (1997), donde analiza el área de pediatría, requiriendo una inversión de tiempo para análisis considerable por la necesidad de llevar a cabo numerosas corridas. En Llorente, Puente, Alonso, y Arcos (2001) se analiza el área de urgencias de un hospital, pero el modelo supone una disciplina primero-en-entrar-primero-en-salir en lugar de tomar en cuenta las prioridades de urgencia o de atención. En Pendharkar, Bischak y Rogers (2012) el modelo de simulación se aplica para sistemas donde la demanda es mayor a la capacidad de atención.

Finalmente, en la misma tabla 1 se muestran también dos revisiones de la literatura: aplicaciones de las líneas de espera en la administración de sistemas hospitalarios en general (Fomundam y Herrmann, 2007) y aplicaciones específicas al área de consulta externa (Oredsson et al., 2011).

Las contribuciones del presente trabajo son:

• 1.

  Se trata de un análisis empírico realizado en el área de urgencias de un hospital público, de los cuales la literatura no es abundante.

• 2.

  No existen antecedentes sobre estudios similares en enfoque en sistemas hospitalarios en la región Laja-Bajío.

• 3.

  Ejemplifica la aplicación de herramientas estadísticas y matemáticas para apoyar la toma de decisiones en la administración de la capacidad y el control de sistemas hospitalarios.

• 4.

  A diferencia de varios trabajos mencionados en los antecedentes, se emplea un modelo de líneas de espera con prioridades de atención para estimar la capacidad del área y las proyecciones ante incrementos de demanda.

• 5.

  Se emplea simulación como herramienta de validación y no como la principal para el análisis del sistema.

Descripción del área y problemática

Se analizó el área de Urgencias de un hospital público de la ciudad de Celaya, estado de Guanajuato, México. Actualmente la ciudad ha mostrado un incremento en la población debido a la instalación de nuevas fábricas del ramo automotriz; además cuenta con un nudo ferroviario y es paso obligado para el transporte de carga que se dirige hacia el norte de México.

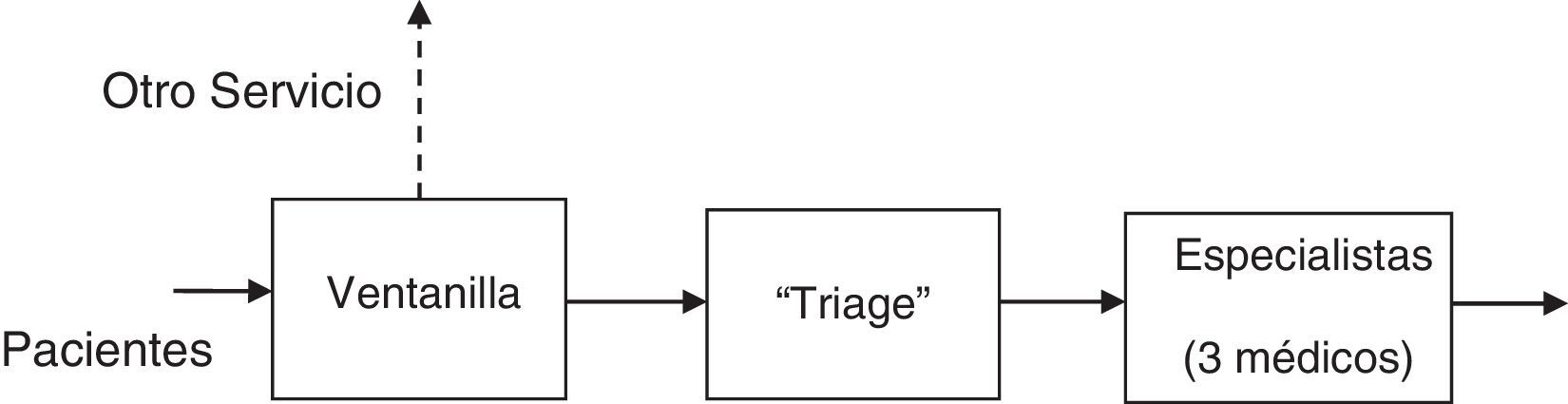
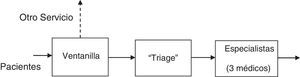
En el área de Urgencias se realiza un proceso que requiere una serie de pasos dispuestos en serie, los cuales son: llegada a ventanilla, atención en la clasificación de acuerdo a padecimiento, para finalizar con el médico de primer contacto que evaluará su estado (fig. 1). El diagnóstico que se le da al paciente en el triage es de gran importancia, ya que determina el tiempo que tardará esa persona en ser atendida por el especialista de la siguiente sección. Existe un pizarrón donde se informa al paciente el tiempo estimado que tardará en ser atendido por el especialista. Los niveles considerados en el estudio son: naranja, 10 min; amarillo, 30-60 min; verde, 60-120 min; azul, 120-240 min.

Figura 1.

Flujo de pacientes en la ventanilla (informes), clasificación (triage) y especialistas.

Fuente: autores.

Las tres etapas comparten un área común de espera. Los administradores han observado un incremento en la demanda del servicio, lo que ha traído como consecuencia que es más frecuente observar una cantidad considerable de personas esperando a ser atendidas. Desde hace varios años operan con tres médicos especialistas que son los que atienden a los pacientes que salen del triage. Las preguntas que desean responder los administradores son:

• •

  ¿Cuál es la demanda en el área de Urgencias? ¿Cuántos pacientes efectivamente son los que se envía al triage?

• •

  ¿Cuál es el tiempo que tarda un paciente en el triage?

• •

  ¿Cuál es el tiempo promedio de espera de los pacientes para ser atendidos por el médico especialista?

• •

  ¿Cuántos pacientes hay formados esperando a ser atendidos en un día normal en el triage y en los médicos?

• •

  ¿Son suficientes los tres médicos especialistas con los que se trabaja actualmente?

• •

  ¿Cuántos médicos son necesarios frente a un incremento de la demanda?

Método de muestreo y análisis

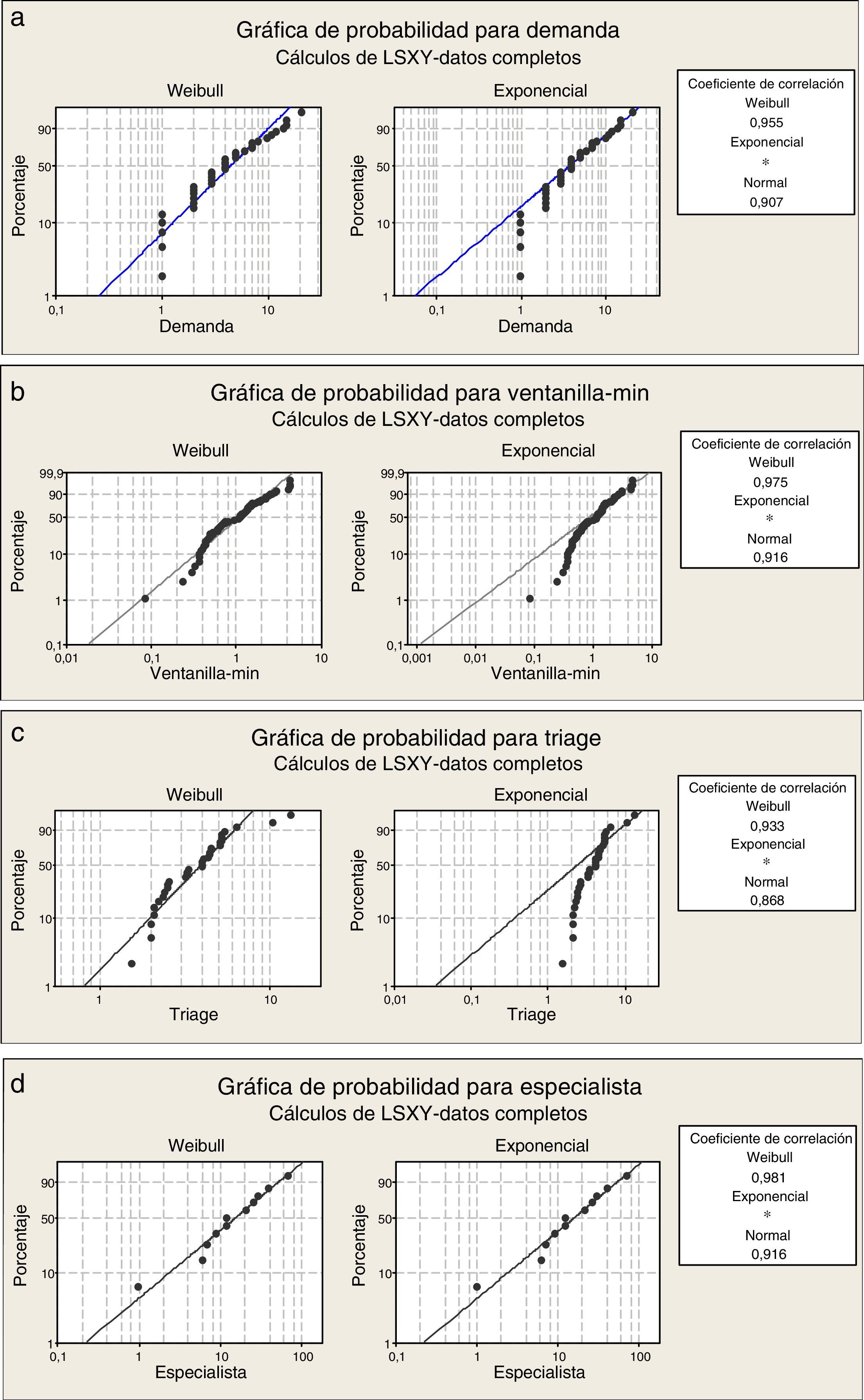
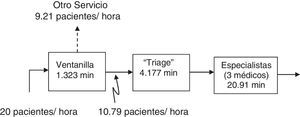
El estudio se llevó a cabo siguiendo los pasos de la figura 2. Para analizar una línea de espera se debe caracterizar la demanda y los tiempos de servicio; una vez obtenida esta información, se continúa con el cálculo de las propiedades. El método de mínimos cuadrados se utilizó para verificar la función que ajusta mejor los datos de los arribos y los servicios. Esto es importante, porque en teoría de líneas de espera varios modelos analíticos suponen que el proceso sigue un tipo de distribución y las funciones relacionadas (Hall, 1991). En caso de omitirla, entonces los resultados analíticos deben tomarse con reserva y se recomienda validarlos de alguna otra manera (simulación, por ejemplo).

Figura 2.

Método para el análisis de una línea de espera.

Fuente: autores.

En el caso de la demanda, esta es recibida en primera instancia en la ventanilla. La observación y el muestreo se llevaron a cabo en días normales de operación durante 4 h (9:00-13:00). Se registró el tiempo de llegada de cada paciente, y posteriormente se obtuvo el tiempo entre arribos tomando la diferencia entre dos pacientes consecutivos.

La observación y el muestreo del tiempo de servicio en ventanilla, el triage y los médicos especialistas se llevaron a cabo en un período de 4 h, considerado como representativo del servicio, durante el cual se registró el tiempo que transcurre desde que el paciente está frente al servidor (los médicos o bien en la ventanilla) hasta que se retira, durante varios días seleccionados al azar (con esto se supone que la demanda es independiente del día, la hora y la época del año), al menos un día diferente para cada estación. La estadística descriptiva y la prueba de mínimos cuadrados aplicada a las muestras de datos se realizaron empleando Minitab 16.

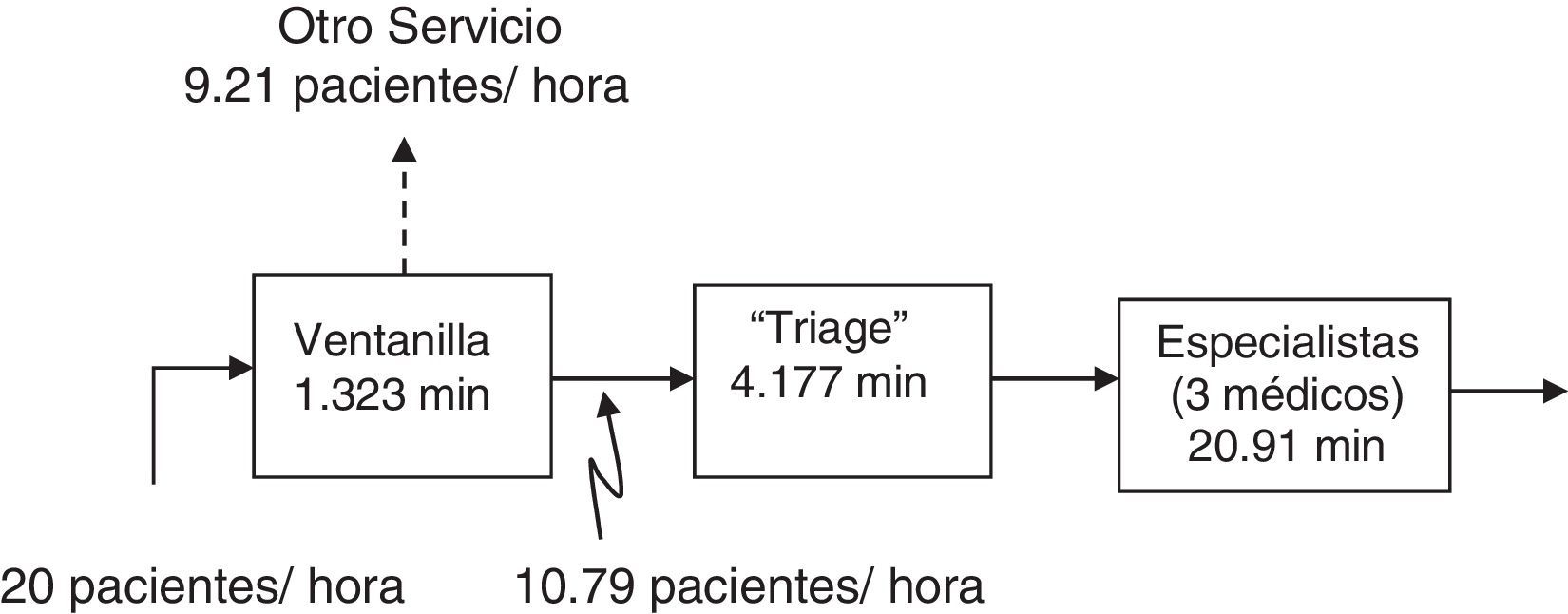
Caracterización de la demanda

Los usuarios llegan en primera instancia a la ventanilla, desde donde son canalizados a las distintas áreas del hospital. Del análisis de los tiempos de arribos se obtuvo que en promedio cada 3 min llega un usuario a la ventanilla para solicitar alguna orientación, siendo la desviación estándar de 2.374 min. La media de 3 min corresponde a 20 usuarios por hora, de los cuales se obtuvo que el 53.95% son los que efectivamente se canalizan a la sección de triage, es decir, alrededor de 10.79 usuarios por hora (tabla 2, fig. 3).

Tabla 2.

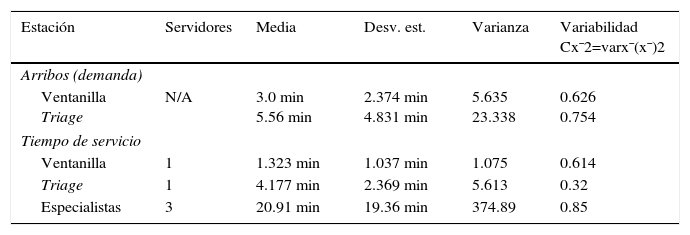
Estadística descriptiva de tiempos

Estación	Servidores	Media	Desv. est.	Varianza	Variabilidad Cx¯2=varx¯(x¯)2
Arribos (demanda)
Ventanilla Triage	N/A	3.0 min 5.56 min	2.374 min 4.831 min	5.635 23.338	0.626 0.754
Tiempo de servicio
Ventanilla	1	1.323 min	1.037 min	1.075	0.614
Triage	1	4.177 min	2.369 min	5.613	0.32
Especialistas	3	20.91 min	19.36 min	374.89	0.85

Figura 3.

Datos operativos del área.

Fuente: autores.

Servicio en ventanilla

Solo hay una ventanilla, por lo que solo hay una persona para atender y brindar la información a los usuarios del servicio. Con los datos recolectados en la fase de ventanilla (tabla 2) se obtuvo el tiempo promedio que tardan los usuarios en recibir información en la ventanilla, el cual fue de 1.32 min, con una desviación estándar de 1.037 min. La variabilidad indica qué tan uniforme es el fenómeno (en este caso el servicio en ventanilla) (Hopp y Spearman, 2008). En el caso de la ventanilla la variabilidad Cx¯2=varx¯(x¯)2, tiene un valor de 0.614, lo cual, al ser menor que 1, indica que el servicio de atención es similar para cada paciente. No todos los pacientes pasan a la siguiente etapa, como se indica en la figura 3: 9.21 pacientes por hora son dirigidos a otras opciones.

Servicio en triage

En esta etapa el paciente es revisado y, de acuerdo a los síntomas, el equipo asigna un nivel de prioridad de atención. Con las muestras observadas en la etapa de triage se obtiene la media del tiempo que están los pacientes dentro del área: 4.17 min. Se tiene una desviación estándar de 2.36 min y una varianza de 5.31 min (tabla 2).

La variabilidad en esta etapa tiene un valor de 0.321, lo cual indica que el servicio presenta variaciones pequeñas, consecuencia del empleo de un protocolo de revisión bien establecido y que es igual para cada paciente.

Servicio en el área de los médicos especialistas

El médico especialista es la última fase en este proceso para atender al paciente y determinar su situación. En el área existen tres especialistas que proporcionan el servicio. En este caso se tomó la muestra de un solo médico para simplificar el análisis posterior. El tiempo promedio resultante es de 20.91 min (tabla 2). En esta sección se observa un valor de variabilidad más alto, consecuencia de que cada paciente requiere un tiempo específico de atención y que no depende del médico sino del padecimiento en particular. Aun así, se considera que en esta sección la variabilidad es moderada.

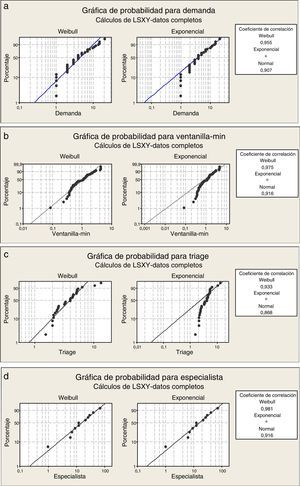
El método de mínimos cuadrados realizado con el paquete Minitab 16 da como resultado que la función Weibull ajusta adecuadamente la demanda y los tiempos de servicio (fig. 4). Se decidió para el análisis aplicar los modelos analíticos correspondientes a cada etapa por separado y al final unir toda la información: el triage es un sistema exponencial con c servidores y disciplina primero-en-entrar-primero-en-salir, y los especialistas corresponden a un sistema exponencial con c servidores y k niveles de prioridad en la atención (tabla 3) (Taylor y Karlin, 1998; Hillier y Lieberman, 2005; Curry y Feldman, 2009). La decisión de utilizar la distribución exponencial basada en una Weibull con parámetro de forma cercano a 1 se vio validada por la bondad de ajuste y por la simulación.

Figura 4.

Método de ajuste de mínimos cuadrados: a) demanda; b) servicio en la ventanilla; c) servicio en el triage; d) servicio en los médicos especialistas.

Fuente: autores.

Tabla 3.

Ecuaciones para el cálculo de propiedades de las estaciones

Fórmulas para sistemas exponenciales (markovianos) con c servidores

Fórmulas para sistemas exponenciales (markovianos) con c servidores y k niveles de prioridad de atención de los clientes

Lq=P0λμcρc!1−ρ2L=Lq+λμTC=TCq+1μP0=∑n=0c−1λμnn!+λμcc!11−λcμ−1 Donde c: número de servidores k: prioridad (Clase) de cliente λ: tasa de llegadas (demanda, 1/tentrearribos) L: número de clientes en el sistema Lk: número de clientes de la clase k en la fila Lq: número de clientes en la fila μ: tasa de servicio (1/tservicio) P0: probabilidad de que el sistema se encuentre vacío TC: tiempo de ciclo en el sistema TCk: tiempo de ciclo en el sistema del cliente de la clase k TCq: tiempo de ciclo en la fila Congestión del sistema(sistema estable): ρ=λc*μ<1

TC=1ABk−1Bk+1μkA=c!cμ−λλμc∑j=0c−1λμcj!+cμB0=1Bk=1−∑i=1kλicμλ=∑i=1NλiLk=λkTCk

Análisis de la capacidad

Existe preocupación debido a que, con la instalación de nuevas fábricas en la zona, la demanda de servicios se incrementará sensiblemente; por lo tanto, es de particular interés para los administradores del hospital determinar la cantidad de médicos que se necesitarían para atender el flujo de pacientes en el área de triage y en el área de médicos especialistas.

Con base en lo expuesto en el párrafo anterior, además de analizar el estado actual es necesario realizar una proyección de los requerimientos de capacidad mínimos para el sistema. Mediante incrementos de la demanda de 10% se estimó el tiempo de ciclo promedio en ambas estaciones. En las tablas 4 y 5 se muestran los resultados del triage y de los especialistas, y se debe señalar que se inicia con el caso base (demanda actual). Para el caso de los médicos especialistas se supone que no existe diferencia entre los médicos, por lo que la media de 20.91 min es la misma para los tres médicos.

Tabla 4.

Tiempo takt de las estaciones

	Tiempo de servicio	Tiempo takt
Ventanilla	1.32 min	240min70pacientes=3.429min
Triage	4.18 min	24070×0.5395=6.355min
Especialistas	20.913=6.97min	24070×0.5395=6.355min

Tabla 5.

Tiempo de ciclo en el triage

		Incremento de la demanda (%)
Actual	Base	10	20	30	40	50
Tiempo de ciclo (min)	16.21 (16.4)	23.3 (22.17)	38 (38.87)	5.4 (5.3)	5.7 (5.6)	6.1 (6.0)
Capacidad utilizada (%)	74.47 (74.0)	82.1 (82.6)	90.14 (89.4)	48.5 (48.8)	52.2 (52.2)	56.0 (55.)
Equipos en el triage (mínimo)	1	1	1	2	2	2

Cada escenario se validó mediante simulación, y el resultado se muestra entre paréntesis. El modelo de simulación discreta se construyó con el programa especializado en simulación ARENA y se efectuaron tres réplicas; cada réplica abarcó 44,000 min de operación, menos 100 min correspondientes al período de calentamiento. Se debe señalar que el modelo de simulación toma en cuenta el nivel de urgencia (prioridad) del paciente.

Un primer acercamiento al análisis de la capacidad y que es útil para efectos de planeación y control es obtener el tiempo necesario para atender el flujo de pacientes o tiempo takt (del alemán Taktzeit, «ritmo») y compararlo contra el tiempo de servicio de la respectiva estación: si el tiempo takt es mayor, entonces existe capacidad para atender la demanda; en caso contrario, la capacidad es insuficiente. El tiempo takt se calcula con la ecuación

Donde i es el índice de la estación. En la tabla 4 se observa que la ventanilla y el triage tienen la capacidad suficiente para atender la demanda; en el caso de los médicos especialistas, de la comparación se aprecia que el tiempo de servicio es 9.67% mayor, lo que se interpreta que en esta estación la demanda es mayor a la capacidad de atención. Cabe señalar que el tiempo takt solamente indica hasta este momento que no existe capacidad. Sin embargo, esto en sí no es suficiente ni puede considerarse como una respuesta para un administrador, ya que ahora es necesario saber cómo incrementar la capacidad. Para soportar esta decisión se aplicarán las relaciones de líneas de espera de la tabla 3.

Los resultados de aplicar los modelos analíticos de la tabla 3 se muestran a continuación. Como se puede apreciar en la tabla 5, la demanda en el triage tiene en esta etapa un 74.47% de su capacidad.

El tiempo de ciclo dentro del sistema está compuesto por los siguientes elementos:

El tiempo de espera formado del paciente en el triage es 16.21 − 4.17 = 12.03 min.

Si la demanda se incrementa un 10% aún es factible emplear un solo equipo y la capacidad utilizada se elevaría a un 82.1%; si la demanda se incrementa un 20% se requiere de un equipo médico adicional; de hecho, esta sección puede mantenerse así hasta para un incremento de la demanda de un 50%, que es el máximo que se analizó.

La conclusión es que en el triage existe capacidad suficiente para atender la demanda con el flujo actual de pacientes provenientes de la ventanilla.

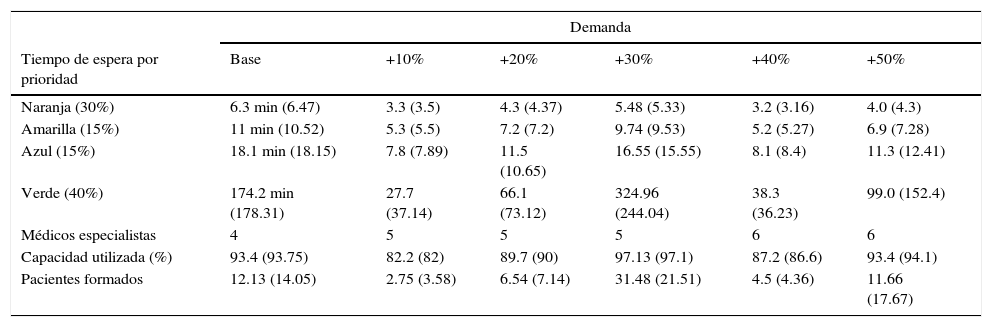
En la tabla 6 se muestra por renglón la distribución estimada de pacientes de acuerdo a la clasificación observada en el triage. También se muestra el tiempo de espera promedio en minutos empezando por el caso base, el número de médicos mínimo necesario, la capacidad utilizada y el número promedio de pacientes formados en el área de los médicos especialistas.

Tabla 6.

Tiempo de espera promedio por tipo de urgencia con el número mínimo de médicos especialistas (entre paréntesis valor obtenido vía simulación)

	Demanda
Tiempo de espera por prioridad	Base	+10%	+20%	+30%	+40%	+50%
Naranja (30%)	6.3 min (6.47)	3.3 (3.5)	4.3 (4.37)	5.48 (5.33)	3.2 (3.16)	4.0 (4.3)
Amarilla (15%)	11 min (10.52)	5.3 (5.5)	7.2 (7.2)	9.74 (9.53)	5.2 (5.27)	6.9 (7.28)
Azul (15%)	18.1 min (18.15)	7.8 (7.89)	11.5 (10.65)	16.55 (15.55)	8.1 (8.4)	11.3 (12.41)
Verde (40%)	174.2 min (178.31)	27.7 (37.14)	66.1 (73.12)	324.96 (244.04)	38.3 (36.23)	99.0 (152.4)
Médicos especialistas	4	5	5	5	6	6
Capacidad utilizada (%)	93.4 (93.75)	82.2 (82)	89.7 (90)	97.13 (97.1)	87.2 (86.6)	93.4 (94.1)
Pacientes formados	12.13 (14.05)	2.75 (3.58)	6.54 (7.14)	31.48 (21.51)	4.5 (4.36)	11.66 (17.67)

En las condiciones actuales, la congestión en los especialistas (ρ) indica que tres médicos no son suficientes para atender la demanda de pacientes; en este caso la demanda es mayor (alrededor del 25.3%) a la capacidad de atención, por lo que la fila de pacientes esperando atención crecerá sin límite. Este valor no se muestra en la tabla 6 porque los resultados de las ecuaciones pierden significado cuando ρ > 1. Como se mencionó anteriormente, la percepción de la situación por parte del administrador era de «una gran cantidad de pacientes esperando servicio».

Del análisis se obtiene la siguiente conjetura: Como ya se mencionó, en el triage se sigue un procedimiento cuyo objetivo es el diagnóstico y para el cual se sigue un protocolo riguroso que favorece el flujo de pacientes en esta sección; por el contrario, en el área de especialistas se debe aplicar el debido tratamiento a cada paciente, que implica una revisión que requiere una mayor inversión de tiempo. En consecuencia, los tiempos de ciclo suelen ser mayores y diferentes para cada paciente. Los médicos no tienen control sobre la clase de paciente que reciben.

Empleando las ecuaciones de la tabla 6 se concluye que se requieren como mínimo 4 médicos para atender la demanda base, y cabe señalar que el área de especialistas se encontrará con una elevada congestión, donde los pacientes de menor prioridad son los que deberán en promedio esperar más tiempo a ser atendidos. El tiempo de respuesta promedio será alrededor de 6 min para los niveles de urgencia más altos (tabla 6).

Si la demanda base se incrementa un 10% es necesario utilizar como mínimo 5 médicos, dando como resultado una capacidad utilizada del 82.2% y un tiempo de respuesta de 3 min; si se incrementa un 20%, la capacidad utilizada será del 89.7%, y cuando se incrementa un 30%, el área de los médicos trabajará a un 97.13% de su capacidad, lo que implica un nivel muy alto de congestión.

Para el escenario de un 40% adicional de la demanda es necesario operar con 6 médicos. Esta capacidad nuevamente soporta un incremento adicional al 50%; sin embargo, nuevamente el nivel de congestión es notablemente alto.

El comportamiento del número de pacientes formados indica que, para el caso base con 4 médicos, el promedio sería de 12.13 pacientes formados, pero el escenario que resalta es el del 30% adicional de demanda, donde se aprecia que trabajar con el mínimo de médicos implica tener en la fila esperando alrededor de 32 pacientes y un tiempo de espera de más de 5 h para los pacientes de prioridad más baja y alrededor de 5.5 min para el nivel más alto de urgencia, lo cual en términos de calidad del servicio no es adecuado.

Los resultados del análisis del área de médicos dan la pauta para analizar la operación de los médicos especialistas en su área de trabajo: tiempo invertido para la búsqueda de información (búsqueda y revisión de los expedientes de los pacientes), empleo de protocolos y de estudios de tiempos y movimientos para mejorar el proceso, así como para buscar estrategias de control y administración que, sin afectar la prioridad de atención que requiere cada paciente, agilicen el flujo de derechohabientes en el hospital.

Las ecuaciones dan al administrador responsable del área una herramienta para analizar el desempeño del sistema, ya que proporcionan una forma de medir la calidad del servicio (por ejemplo a través del tiempo de espera de un paciente), por lo que el administrador está en posibilidades de soportar una decisión como es la de agregar médicos para satisfacer la demanda.

Conclusiones

Los estudios empíricos y la aplicación de modelos de teoría de líneas de espera para la administración de las operaciones en sistemas hospitalarios son un área de investigación que en años recientes ha atraído la atención de la comunidad científica.

La administración de los sistemas hospitalarios implica dar a los pacientes un servicio de calidad. El empleo de herramientas que apoyen la toma de decisiones proporciona a los administradores información sobre el desempeño del sistema que tienen a su cargo. En este punto es importante señalar que estas herramientas, combinadas con el criterio y la experiencia de los administradores, se traducen en un mayor entendimiento del sistema.

La teoría de líneas de espera es una herramienta que permite calcular de manera eficiente y rápida algunas de las medidas de desempeño de mayor interés para la administración y control de los sistemas hospitalarios.

En el área de Urgencias estudiada en Celaya se ha observado un incremento notable en el número de pacientes formados a la espera de atención. De acuerdo a los resultados, las etapas de ventanilla y triage son etapas que prestan servicio y mantienen una holgura en su capacidad; sin embargo, la etapa de los médicos especialistas es el cuello de botella y ha sido sobrepasada por la demanda.

Desde un enfoque de sistemas, el área de Urgencias se encuentra sobrepasada por la demanda de servicio, ya que los pacientes provenientes del triage se acumulan sin límite. Es necesario adicionar un médico en el área de especialistas para favorecer el flujo de pacientes, aunque seguirá siendo el cuello de botella del área de Urgencias.

Del análisis de distintos escenarios de demanda se concluye que mantener el mínimo de médicos implica un nivel de congestión muy alto y tiempos de espera para los pacientes de baja prioridad considerablemente altos, con las respectivas consecuencias de presión y caos que esto acarrea.

Si no es viable mantener un médico adicional fijo, entonces puede optarse por monitorear la demanda a través del número de pacientes en espera. Se puede fijar una política en la que cuando se alcance cierto número de pacientes formados se incorpore un médico para, por ejemplo, atender los pacientes con el menor nivel de urgencia.

Los administradores obtendrán algunos beneficios de los medios analíticos mostrados en este trabajo:

• 1.

  Tienen a su disposición una herramienta para analizar el desempeño del sistema.

• 2.

  Proporcionan una forma de medir la calidad del servicio (por ejemplo, mediante el tiempo de espera de un paciente).

• 3.

  Permiten soportar una decisión como es la de agregar médicos para satisfacer la demanda.

• 4.

  Favorecen el entendimiento del funcionamiento del sistema y su desempeño (por ejemplo, a mayor demanda, mayor tiempo de ciclo y mayor congestión).

Se puede investigar en un trabajo posterior el desempeño de diversas políticas de calidad del servicio (por ejemplo, la probabilidad de que un paciente deba esperar), el análisis de costos o bien tomar en cuenta otras etapas no incluidas en este proyecto, como los estudios realizados a los pacientes (rayos X, tomografías, electrocardiogramas) u hospitalización.

Dado que no existen trabajos similares para los sistemas de salud de la región Laja-Bajío, se espera que esta investigación apoye a los responsables de la administración de sistemas hospitalarios sobre la manera de llevar a cabo un estudio del área.