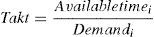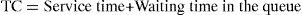Analysis of the emergency service applying the queueing theory

Abstract

Those responsible for the decision-making in hospitals are becoming more aware of the need to efficiently manage hospital systems. One option is the queueing models. In this work, the Emergency service of a public hospital is analyzed by applying the concepts and relations of queues. Based on the results of the model, it is concluded that the Emergency area does not count with the minimum number of doctors necessary for a constant flow of patients. The minimum number of doctors necessary to satisfy the current and future service demand, with the same service times and service disciplines, is calculated using the model. The analytical models allow to directly understand the existing relations between service demand, number of doctors and the attention priority of the patient seen as a system of queues. The work is of use to managers and those responsible for the management of hospital systems.

Resumen

Los responsables de la toma de decisiones de los hospitales son cada vez más conscientes de la necesidad de administrar de manera eficiente los sistemas hospitalarios. Una opción son los modelos de líneas de espera. En el presente trabajo se analiza el servicio del área de Urgencias de un hospital público aplicando los conceptos y relaciones de líneas de espera. A partir de los resultados del modelo se concluye que en el área de Urgencias no se cuenta con la cantidad mínima necesaria de médicos para permitir un flujo constante de pacientes. Con el modelo se calcula el número mínimo de médicos necesarios para satisfacer la demanda actual y futura de servicio, con los mismos tiempos de servicio y la misma disciplina de servicio. Los modelos analíticos permiten entender directamente las relaciones existentes entre demanda de servicio, número de médicos y prioridad de atención del paciente vistos como un sistema de líneas de espera. El trabajo es de utilidad para los administradores y responsables de la gestión de sistemas hospitalarios.

Introduction

Those responsible of the decision-making in hospitals are becoming more aware of the need to more efficiently manage the hospital resources under their control. To provide a good service, those responsible must use tools that allow them to analyze, program, plan, prioritize and, in general, decide on the best way to manage the available resources (Vissers & Beech, 2005; Abraham, Byrnes, & Bain, 2009). An example of the type of problems to be analyzed is that of estimating the level of service provided to the patients, the average waiting time, the number of patients queued, the capacity used, and the probability that the patient needs to wait. In hospital systems, the waiting time to receive attention is a key element in measuring the quality of the service. Therefore, the decrease of said waiting time has become a significant factor in the management of these types of systems (Green, 2005, 2010).

To obtain the abovementioned properties, analytical means derived from the queueing theory can be used. Analytical tools make it possible to understand the existing relations between each of the elements of a system, unlike other analysis approaches which are usually similar to black boxes (Hopp & Spearman, 2008). Although the simulation approach makes it possible to obtain the same properties, it is advisable to use it when there is no analytical model for the system that is going to be analyzed (Law & Kelton, 2000). On the other hand, not all hospital systems are expected to have a specialized simulation program, whereas access to analytical formulas is universal and free. As is mentioned in the work of Song, Tucker, and Murrel (2013), empirical studies (such as this) in hospital systems are proportionately fewer than their counterpart in the areas of manufacture and production, which generates an area of opportunity for the professionals that manage these types of systems to apply different analytical tools that are well known in other areas.

In this vein, this work presents the method to analyze the Emergency service by applying the concepts and relations of the queueing theory. The Emergency service of a public hospital in the city of Celaya in Guanajuato—where the managers of the area receive a great number of patients that wait in line to be taken care of—is taken as case study for this work.

The study is pertinent to administrators, engineers, doctors and, in general, to all those professionals in charge of the decision-making in health systems and those who wish to analyze the service demand as well as the capacity to provide said service.

Background

The administration of a hospital system requires the adaptation of the concepts, such as those of operation research, to the objectives and needs of this type of systems. In this sense, the monetary aspect is not the only performance measure, as it is also necessary to consider the quality of the service provided, which translates into measures such as: response time and service time. Table 1 shows a sample of the studies carried out on hospital systems. This table includes both the application of queueing theory models as well as simulation models.

Table 1.

Hospital services analysis.

Author	Year	Comment
Benneyan	1997	Simulation model to analyze the service time in the pediatrics area.
Whitt	1999	Analysis of the relevance of dividing the patients and assigning servers for each category.
Llorente et al.	2001	Simulation model to analyze the service capacity of the General Emergency area.
Bastani	2007	Application of the queueing theory to model the flow of patients between the Emergency area and the Intensive Care Unit.
de Bruin et al.	2007	Analysis of the service capacity in the Cardiac Emergency area. The effect of the demand variability is analyzed.
Fomundam & Hermann	2007	State of the art on queueing theory application to the analysis and problem solving in the administration of hospital systems.
Oredsson et al.	2011	State of the art on the analysis of the waiting times of the patients in the Emergency area.
Hulshof et al.	2012	Analysis of the service policies in the external consult area.
Pendharkar et al.	2012	Simulation model to analyze systems with insufficient capacity. This is applied to the sleep disorders area.
Tan et al.	2012	Dynamic queueing model to control medical personnel in the Emergency area.
Lin et al.	2013	Analysis of the flow of patients in the Emergency areas taking into consideration the level of emergency of the patient.
Tan et al.	2013	Queueing model to analyze the flow of patients in the Emergency area
Yom-Tov and Maandelbaum	2014	Model used in the Erlang distribution to represent the return of the clients in hospital care

Queueing models

In Whitt (1999), a strategy for the flow division of patients that enter the system is proposed with the objective of favoring the flow of patients, assigning them their own server. However, the model supposes that there is no significant difference between the demands of each type of patients.

Bastani (2007) develops a model to analyze three areas: intensive care, coronary unit and hospitalization. It entails a service discipline of first-come first-served. In de Bruin, van Rossum, Visser, and Koole (2007) the flow of patients and the capacity of service of the cardiac emergency area are analyzed with a model where readmissions are allowed. The fact that two types of patients are distinguished is highlighted, however, at the time of analysis the service demand is considered as a single type.

Hulshof et al. (2012) proposes strategies to improve the flow of external consult patients, classifying them by their symptoms and assigning them their corresponding doctors (servers). The analytical model is built based on the changes in the operation of several hospitals in Germany. The same strategy to classify patients and assign doctors to them is proposed in Tan, Tan, and Lau (2013) and Tan, Lau, and Lee (2013), where a dynamic model to analyze the emergency area of a hospital in Singapore is also developed. The model works in real time, requiring heuristic methods to obtain a solution of the same.

In Lin, Patrick, and Labeau (2013), a model is built with a series of stages to analyze the flow between two areas in a hospital and estimate the necessary personnel resources for it. Finally, in Yom-Tov and Mandelbaum (2014), a model where patients come back (recirculate) is proposed, assuming an Erlang type service; however, it considers a first-come, first-served discipline.

Simulation models

In the case of the simulation applied to the analysis, the works of Benneyan (1997) in which the pediatrics area is analyzed are worth mentioning, requiring an investment of time for considerable analysis due to the need to carry out several runs. In Llorente, Puente, Alonso, and Arcos (2001), the emergency area of a hospital is analyzed, but the model entails a first-come, first-served discipline instead of taking into consideration the emergency or care priorities. In Pendharkar and Bischak (2012), the simulation model is applied to systems where the demand is higher than the service capacity.

Finally, Table 1 also shows two revisions of the literature: the applications of queues in the administration of hospital systems in general (Fomundam & Hermann 2007) and the specific applications in the external consult area (Oredsson et al., 2011).

The contributions of this work are:

• 1.

  It is an empirical analysis of the emergency area of a public hospital, for which the literature is not abundant.

• 2.

  There is no background on similar studies with an approach of hospital systems in the Laja-Bajío region.

• 3.

  It exemplifies the application of statistical and mathematical tools to support the decision-making in the administration of the capacity and control of hospital systems.

• 4.

  Unlike several works mentioned in the background information, a queueing model with service priorities is used to estimate the capacity of the area and the projections when there is an increase in demand.

• 5.

  Simulation is used for validation and not as the main tool for the analysis of the system.

Description of the area and problem

The Emergency area of a public hospital in the city of Celaya, Guanajuato, was analyzed. Presently, the city has shown an increase in population due to the installation of new factories in the automotive industry; furthermore, it has a railway junction and is an obligatory route for cargo transport going to the north of Mexico.

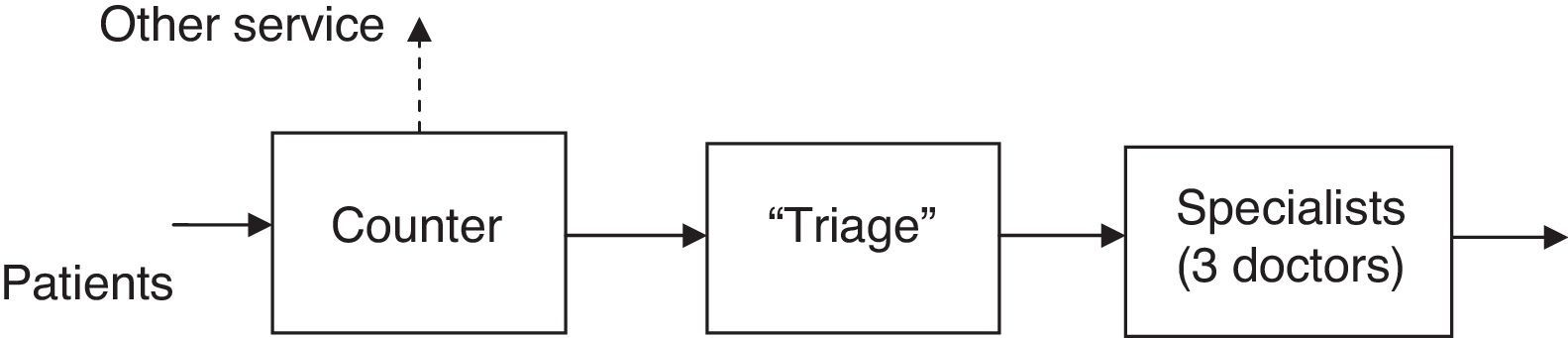
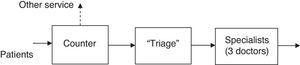
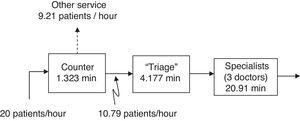
A process that requires a series of steps is carried out in the Emergency area. These steps are: arrival to the counter, attention according to the ailment of the person, finalizing with the first doctor that will evaluate the person's state (Fig. 1).

Fig. 1.

Flow of patients at the counter (information), classification (“triage”) and specialist.

Source: Authors.

The diagnosis given to the patient in the triage is of great significance, as it determines the time that the person will wait to be received by the specialist of the next section. There is a board where the patient is informed of the estimated period of time it will take for them to be taken care of by the specialist. The levels considered in the study are: orange = 10 min, yellow = 30–60 min, green = 60–120 min, blue = 120–240 min.

The three stages share a common waiting area. The administrators have observed an increase in service demand, which has caused it to be more common to see people in line waiting to be assisted. For many years now, they operate with three specialists who see to the patients that leave the triage. The questions that the administrators wish to answer are:

• o

  What is the demand in the Emergency area? How many patients are effectively sent to the triage?

• o

  How long does a patient stay in the triage?

• o

  What is the average waiting time of the patients to be attended by the specialist?

• o

  How many patients are in line waiting to be assisted on any given day in the triage and by the doctors?

• o

  Are the three specialists that currently work there enough?

• o

  How many doctors are necessary when there is an increase in demand?

Sampling method and analysis

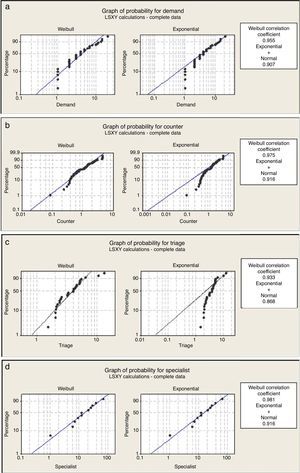
The study was carried out following the steps in Fig. 2. To analyze a queue, the demand and the service times must be characterized. Once this information is obtained, the calculation of the properties is done. The method of least squares was used to verify the function that best suits the data of the arrivals and the services. This is important because in the queueing theory several analytical models assume that the process follows a type of distribution and the related functions (Hall, 1991). In the event that this is omitted, the analytical results must be taken with reservations and it is recommended to validate them in some other way (e.g., through simulation).

Fig. 2.

Method for the analysis of a queue.

Source: Authors.

In the case of the demand, it is first received at the counter. The observation and sampling were carried out in normal business days during a period of 4 h (9:00–13:00). The time of arrival of each patient was recorded and subsequently the time between arrivals was obtained by taking the difference between two consecutive patients.

The observation and sampling of the service time at the counters, triage, and of the specialists was done during a period of 4 h, considered representative of the service, during which the time that passed from the moment the patient stands before the server (the doctors or at the counter) and until they leave. This was done during several randomly selected days (this assumes that the demand is independent of the day, the hour and the time of year), at least a different day for each station. The descriptive statistics and the test of least squares applied to the data samples were done using Minitab16.

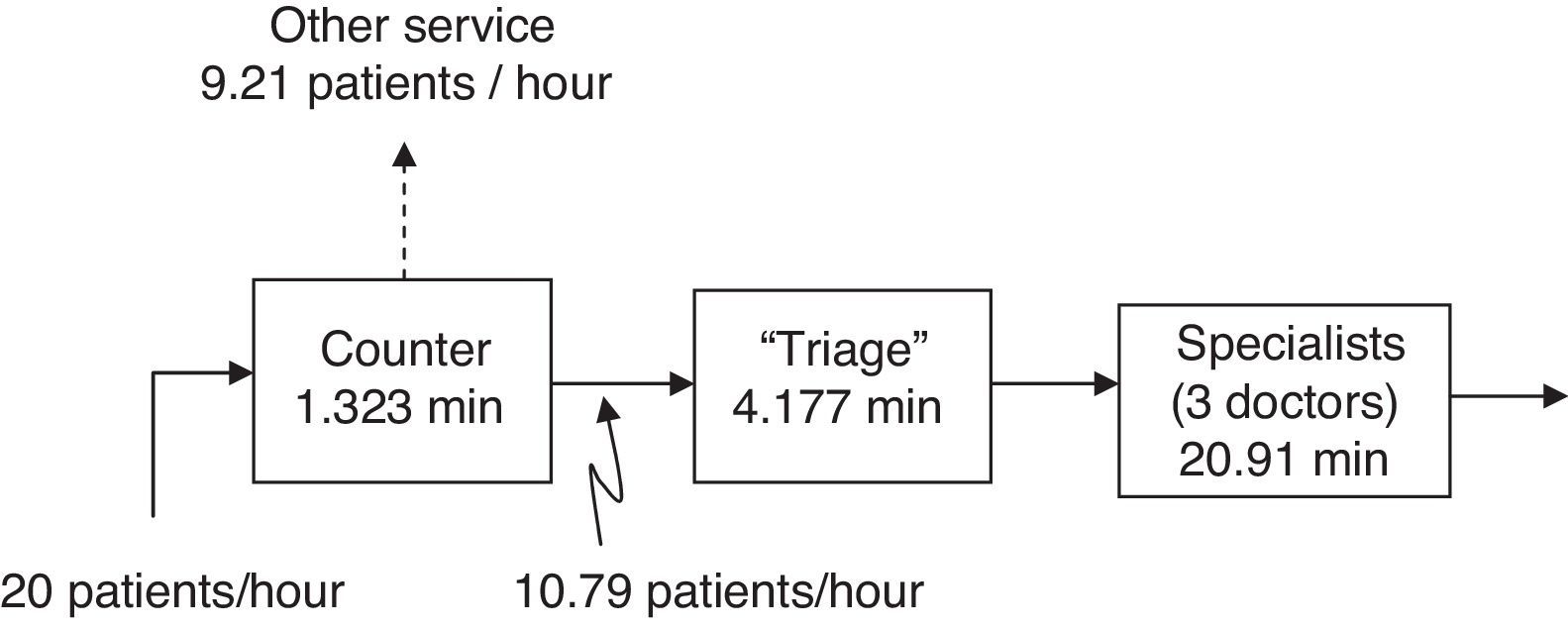
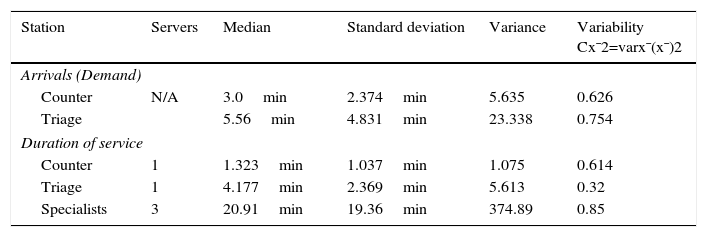
Characterization of the demand

The users arrive first to the counter where they are directed to the different areas of the hospital. From the analysis of the arrival times it was found that approximately every 3 min a user arrives to the counter to request information, with a standard deviation of 2.364 min. The 3 min median corresponds to 20 users per hour, of which 53.95% are effectively channeled to the triage section, that is, approximately 10.79 users per hour (Table 2, Fig. 3).

Table 2.

Descriptive statistics of the times.

Station	Servers	Median	Standard deviation	Variance	Variability Cx¯2=varx¯(x¯)2
Arrivals (Demand)
Counter	N/A	3.0 min	2.374 min	5.635	0.626
Triage		5.56 min	4.831 min	23.338	0.754
Duration of service
Counter	1	1.323 min	1.037 min	1.075	0.614
Triage	1	4.177 min	2.369 min	5.613	0.32
Specialists	3	20.91 min	19.36 min	374.89	0.85

Fig. 3.

Operational data of the area.

Source: Authors.

Over the counter service

There is only one counter, as such there is only one person to assist and provide information to the users of the service. With the collected data in the counter phase (Table 2), the average time that the users take to receive information at the counter was obtained, which was of 1.32 min with a standard deviation of 1.037 min. The variability indicates how uniform the phenomenon is (in this case the over the counter service) (Hopp & Spearman, 2008). In the case of the counter, the variability Cx¯2=varx¯x¯2 has a value of 0.614 which, being below 1, indicates that the service is similar for each patient. Not all patients go to the next stage, as indicated in Fig. 3, 9.21 patients per hour are directed to other options.

Service in “Triage”

The patient is checked in this stage, and according to their symptoms the team assigns a level of attention priority. With the samples observed in the triage stage, the median of the time during which the patients are in the area is obtained: 4.17 min. There is a standard deviation of 2.36 min and a variance of 5.31 min (Table 2).

The variability in this stage has a value of 0.321, which indicates that the service presents small variations as a result of using a well-established review protocol that is the same for each patient.

Service in the area of the specialists

The specialist is the last stage of this process to assist the patient and to determine their situation. There are 3 specialists that provide the service in the area. In this case, the sample was taken from just one doctor to simplify the subsequent analysis. The resulting average time is of 20.91 min (Table 2). A higher variability value is observed in this section, which is the result of each patient requiring a specific assistance time and that does not depend on the doctor, but on the particular ailment of the person. Even so, it is considered that the variability in this section is moderate.

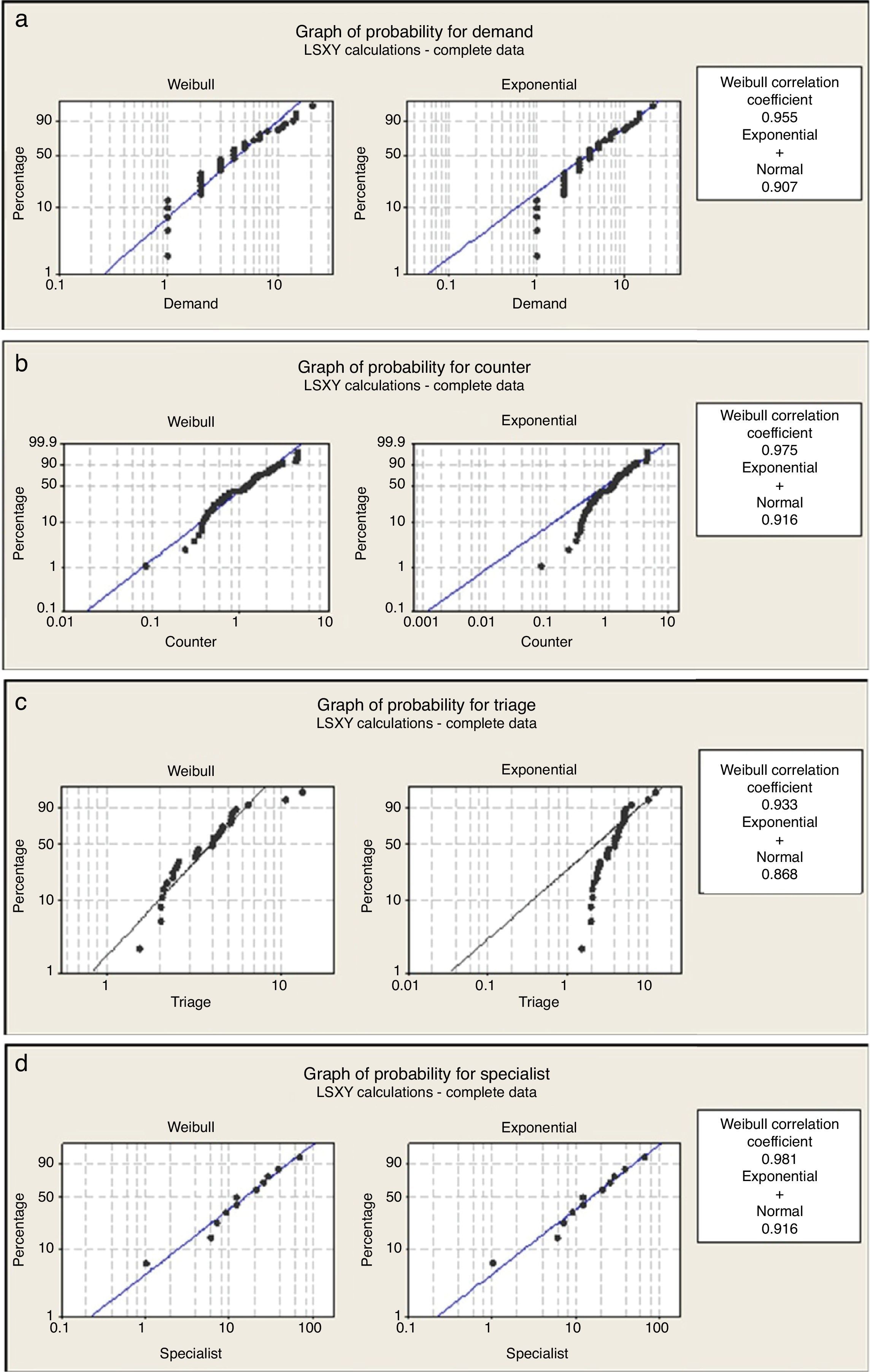
The method of least squares carried out with the Minitab16 results in the Weibull distribution properly meeting the demand and the service times (Fig. 4). It was decided for the analysis to apply the analytical models that correspond to each stage separately and to pull together all of the information at the end: the triage is an exponential system with c servers and a first-come, first-serve discipline, the specialists correspond to an exponential system with c servers and k levels of attention priority (Table 3) (Taylor & Karlin, 1998; Hillier & Lieberman, 2005; Curry & Feldman, 2009). The decision to use exponential distribution, based on a Weibull distribution with a shape parameter close to 1, was validated by the goodness of fit and simulation.

Fig. 4.

Method of least squares adjustment: (a) demand, (b) over the counter service, (c) triage service, and (d) service of the specialists.

Source: Authors.

Table 3.

Equations for the calculation of the properties of the stations.

Formulas for exponential systems (Markovian) with c servers	Formulas for exponential systems (Markovian) with c servers and k levels of client attention priority
Lq=P0λμcρc!1−ρ2L=Lq+λμTC=TCq+1μP0=∑n=0c−1λμnn!+λμcc!11−λcμ−1	TC=1ABk−1Bk+1μkA=c!cμ−λλμc∑j=0c−1λμcj!+cμB0=1Bk=1−∑i=1kλicμλ=∑i=1NλiLk=λkTCk

where TC is the cycle time in the system; TC_q is the cycle time in the queue; L_q is the number of clients in the queue, L is the number of clients in the system, L_k is the number of k type clients in the queue, TC_k is the cycle time in the system of the k type client, P₀ is the probability that the system is empty, c is the number of servers, k is the client (Class) priority, λ is the rate of arrivals (demand, 1/t_{betweenarrivals}), μ is the rate of service (1/t_service), system congestion (stable system) is the ρ = λ/(c * μ) < 1.

Capacity analysis

There are concerns given that with the installation of new factories in the area, the service demand will increase appreciably and is therefore of interest to the hospital administrators to determine the number of doctors needed to assist the flow of patients in the triage area and in the area of the specialists.

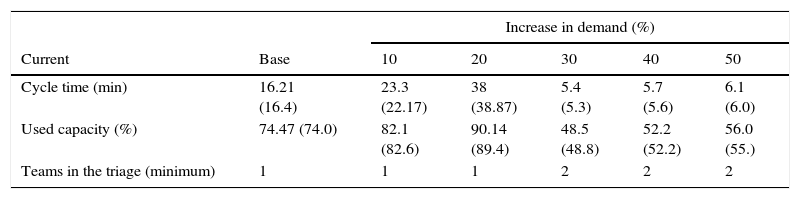
Based on the above, and in addition to analyzing the current state, it is necessary to do a projection of the minimum capacity requirements for the system. Through 10% increases in the demand, the average cycle time was estimated in both stations. Tables 4 and 5 show the results of the triage and of the specialists; it is worth noting that they start with the base case (current demand). For the case of the specialists, the assumption is that there is no difference between the doctors and therefore the median is of 20.91 min for all three doctors.

Table 4.

Takt time of the stations.

	Service time	Takt time
Counter	1.32 min	240 min70 patients=3.429 min
Triage	4.18 min	240(70×0.5395)=6.355 min
Specialists	20.913=6.97 min	240(70×0.5395)=6.355 min

Table 5.

Cycle time in the Triage.

		Increase in demand (%)
Current	Base	10	20	30	40	50
Cycle time (min)	16.21 (16.4)	23.3 (22.17)	38 (38.87)	5.4 (5.3)	5.7 (5.6)	6.1 (6.0)
Used capacity (%)	74.47 (74.0)	82.1 (82.6)	90.14 (89.4)	48.5 (48.8)	52.2 (52.2)	56.0 (55.)
Teams in the triage (minimum)	1	1	1	2	2	2

Each scenario was validated through simulation and the result is shown between parentheses. The discreet simulation model was built with the ARENA simulation specialized program and 3 replicas were done, each replica encompassed 44,000 min of operation, minus 100 min corresponding to the warm-up period. It should be pointed out that the simulation model takes into consideration the level of emergency (priority) of the patient.

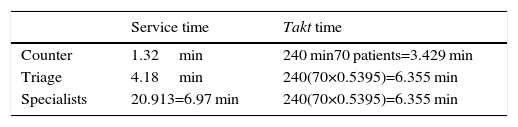
An initial approach at the capacity analysis that is useful for planning purposes and control is to obtain the necessary time to assist the flow of patients or takt time (from the German word Taktzeit, pace) and compare it to the time of service of the corresponding station: if the takt time is higher, then there is capacity to meet the demand, otherwise the capacity is insufficient. The takt time is calculated with the following equation:

where i is the index of the station. Table 4 shows that the counter and the triage have the sufficient capacity to meet the demand; in the case of the specialists in the comparison, it can be seen that the service time is 9.67% greater, which is interpreted as the demand being higher to the attention capacity in this station. It is worth noting that the takt time only indicates that there is no capacity at that moment. However, this alone is not sufficient nor can it be considered an answer for an administrator as it is necessary to know how to increase capacity. To support this decision, the relations of queues of Table 3 will be applied.

The results of applying the analytical models of Table 3 are shown below. As can be observed in Table 5, the demand in the triage at this stage is at 74.47% of its capacity.

The cycle time within the system is comprised by the following elements:

The waiting time of the patient in the queue in the triage is of 16.21–4.17 = 12.03 min.

If the demand increases 10% it is still possible to use just one team and the capacity used would go up to 82.1%, if the demand increases 20% then an additional medical team would be needed; in fact, this section can remain as is for up to an increase in demand of 50%, which is the maximum analyzed.

The conclusion is that the current triage has a sufficient capacity to meet the demand with the current flow of patients being directed from the counter.

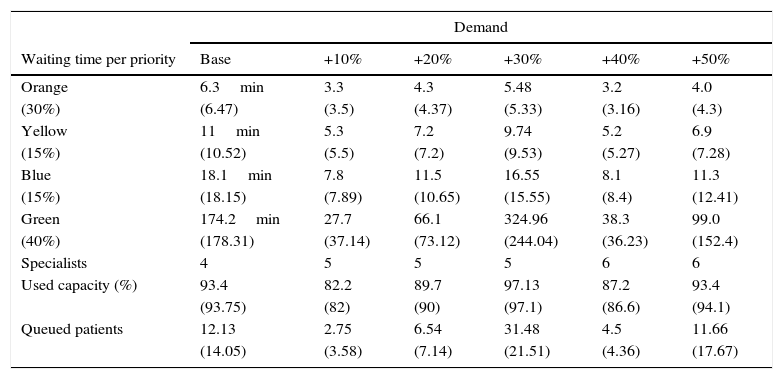
Table 6 shows the estimated distribution of patients according to the classification observed in the triage. It also shows the average waiting time in minutes, starting with the base case, the minimum number of necessary doctors, the used capacity, and the average number of patients in the queue in the specialists’ area.

Table 6.

Average waiting time by type of emergency with the minimum number of specialists (the value obtained through simulation is in parentheses).

	Demand
Waiting time per priority	Base	+10%	+20%	+30%	+40%	+50%
Orange	6.3 min	3.3	4.3	5.48	3.2	4.0
(30%)	(6.47)	(3.5)	(4.37)	(5.33)	(3.16)	(4.3)
Yellow	11 min	5.3	7.2	9.74	5.2	6.9
(15%)	(10.52)	(5.5)	(7.2)	(9.53)	(5.27)	(7.28)
Blue	18.1 min	7.8	11.5	16.55	8.1	11.3
(15%)	(18.15)	(7.89)	(10.65)	(15.55)	(8.4)	(12.41)
Green	174.2 min	27.7	66.1	324.96	38.3	99.0
(40%)	(178.31)	(37.14)	(73.12)	(244.04)	(36.23)	(152.4)
Specialists	4	5	5	5	6	6
Used capacity (%)	93.4	82.2	89.7	97.13	87.2	93.4
	(93.75)	(82)	(90)	(97.1)	(86.6)	(94.1)
Queued patients	12.13	2.75	6.54	31.48	4.5	11.66
	(14.05)	(3.58)	(7.14)	(21.51)	(4.36)	(17.67)

In the current conditions, the congestion in the specialists’ area (ρ) indicates that three doctors are not enough to meet the demand of the patients. In this case, the demand is greater (around 25.3%) to the service capacity and thus the queue of patients waiting to be assisted will grow without limit. This value is not shown in Table 6 because the results of the equations lose significance when (ρ > 1). As previously mentioned, the perception of the situation by the administrator was of “a great number of patients waiting to be assisted”.

The following conjecture is obtained from the analysis: as already mentioned, the triage follows a procedure aimed to diagnose and for which there is a strict protocol that favors the flow of patients in this section. Conversely, in the specialists’ area the proper treatment must be given to each patient, and it entails an inspection that requires a greater investment of time. Therefore, the cycle times tend to be greater and different for each patient. The doctors do not have any control on the type of patient they receive.

Using the equations in Table 3, it is concluded that at least 4 doctors are needed to meet the base demand. It is worth mentioning that the specialists’ area would become greatly congested, a situation in which the patients with a lower priority are the ones that would have to wait more time to be assisted. The average response time would be of about 6 min for the higher levels of emergency (Table 6).

If the base demand increases 10% then it is necessary to have at least 5 doctors, resulting in a used capacity of 82.2% and a response time of 3 min; if it increases 20% then the used capacity would be of 89.7%; and when it increases 30% then the doctors’ area would work at a 97.13% of its capacity, which implies a high level of congestion.

For the scenario of an additional 40% of demand it is necessary to operate with 6 doctors. This capacity once again supports an additional increase of 50%, however, the level of congestion is notably high.

The behavior of the number of patients in line indicates that for the base case with 4 doctors the average would be of 12.13 patients in line. Although the scenario that stands out the most is that of the additional 30% of demand. In this scenario, it is noted that working with the minimum number of doctors implies having around 32 patients waiting in line, and a waiting period of more than 5 h for those patients with the lowest priority, and around 5.5 min for those with the highest levels of emergency. This is not adequate in terms of service quality.

The results of the analysis of the doctors’ area give indication to analyze the performance of the specialist doctors in their area of work: time invested in the search of information (search and review of the patients’ charts), in the use of protocols and time and movement studies to improve the process, as well as to search for control and administration strategies which, without affecting the attention priority that each patient requires, speeds the flow of beneficiaries in the hospital.

The equations give the administrator of the area a tool to analyze the performance of the system, providing a way to measure the quality of the service (e.g., through the waiting time of a patient), and making it possible to support decisions such as adding doctors to satisfy the demand.

Conclusions

The empirical studies and application of queueing theory models for the administration of operations in hospital systems comprise an area of research that has recently caught the attention of the scientific community.

The administration of the systems implies providing the patients with a quality service. The use of tools that help in the decision-making process makes it possible for administrators to obtain information regarding the performance of the system they use. It is important to point out that the tools combined with the criteria and experience of the administrators translate into a better understanding of the system.

The queueing theory is a tool that allows to efficiently and quickly calculate some of the performance measures that are of greater interest for the administration and control of hospital systems.

There has been a significant increase in the number of patients waiting in line for assistance in the emergency area studied in Celaya. According to the results, the counter and triage stages provide a good service and remain well within their capacity. However, the stage of the specialists is the bottleneck of the location and has been overtaken by the demand.

From a systems approach, the Emergency area is overwhelmed by the service demand given that the number of patients that come from the triage area increases without limit. It is necessary to add a doctor in the specialists’ area to improve the flow of patients. Nevertheless, it will remain as the bottleneck of the Emergency area.

From the analysis of different demand scenarios, it is possible to conclude that maintaining the minimum number of doctors implies a very high level of congestion and considerably longer waiting times for those patients with low priority, in addition to the corresponding pressure and chaos that this entails.

If having a permanent additional doctor is not viable, then the other option could be to monitor the demand through the number of waiting patients. It is possible to implement a policy dictating that when the number of patients in line reaches a certain point, one doctor will be assigned to treat those patients with the lowest level of emergency.

The administrators will reap some benefits from the analytical resources shown in this work:

• 1.

  They have at their disposal a tool to analyze the performance of the system.

• 2.

  They provide a way to measure the quality of the service (e.g., through the waiting time of a patient).

• 3.

  They make it possible to support a decision such as bringing in more doctors to satisfy the demand.

• 4.

  They favor the understanding of the system's operation and its performance (e.g., the greater the demand, the greater the cycle time and congestion).

In subsequent works, it would be possible to research the performance of different service quality policies (e.g., the probability that a patient has to wait), carry out a cost analysis, or take into consideration other stages that are not included in this project, such as the studies done on the patients (X-rays, tomography, EKG) or hospitalizations.

Given that there are no similar works for the health systems of the Laja-Bajío region, the aim of this research is to be of help to those people responsible for the administration of hospital systems with regard to the ways of carrying out a study of the area.