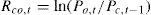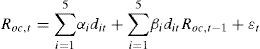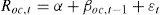Este artículo pretende determinar la existencia de autocorrelación de rendimientos en los principales mercados latinoamericanos y su relación con el efecto día de semana en ellos. Asimismo, se busca dimensionar la importancia de los periodos de no transacción y su incidencia en la rentabilidad de los mercados accionarios. Se puede concluir que existe autocorrelación en la mayoría de los mercados accionarios analizados, tanto en moneda local como en moneda global, junto al fenómeno de día de semana; además, se evidencia correlación entre las rentabilidades del periodo de transacción y la rentabilidad del periodo de no transacción.
This paper aims to determine the evidence of returns autocorrelation for the main Latin American stock markets, and the influence of the day of the week effect on this phenomenon. Also, we analyze the importance of non-trading periods and their incidence on stock markets returns. We determine a high autocorrelation in most of the stock markets analyzed, both in local and global currency and the day-of-the-week effect on only some of the stock markets. Evidence of correlation between trading periods returns and those of non-trading periods is also found.
Las anomalías de mercados es un tema que siempre es interesante investigar, ya que se genera conocimiento que sirve para que los inversionistas y administradores tomen mejores decisiones; al mismo tiempo, su divulgación debiera ayudar a hacer que los mercados accionarios sean más eficientes. Las anomalías de calendario son de las más estudiadas y en especial el efecto día de semana, el cual ha generado la búsqueda de explicaciones racionales que no necesariamente se han encontrado.
Dentro de otras anomalías encontradas está la autocorrelación de primer orden positiva entre los rendimientos, lo cual no concuerda con la teoría que postula que el rendimiento esperado de un día no depende del rendimiento del día anterior. En otras palabras, existe una relación entre el rendimiento de hoy y el rendimiento que se producirá mañana. Desde este contexto, en una fusión de ambos conceptos, autocorrelación y efecto día de semana, se genera la motivación de analizar si la existencia de la autocorrelación es dependiente del día, o sea, si este fenómeno de autocorrelación es más fuerte en algunos días que otros.
Por otro lado, bajo el mismo análisis de autocorrelación, habitualmente se calcula el rendimiento diario de los activos financieros mediante el análisis close-to-close, es decir, el cambio porcentual entre los precios de cierre de dos días seguidos según el calendario de transacción, pero existe la posibilidad de descomponer la rentabilidad tradicional en dos: la rentabilidad close-to-open y la rentabilidad open-to-close. Esto implica que exista una generación de rentabilidad cuando el mercado está cerrado (close-to-open) y otra cuando el mercado está abierto (open-to-close). Entonces se genera la necesidad de poder determinar si existe autocorrelación y efecto día de semana entre estas rentabilidades y su relación con la relación close-to-close.
En la siguiente sección se explica y analiza la evidencia en el nivel mundial y en particular de Latinoamérica de las anomalías dadas en los mercados accionarios. Posteriormente, se explicará la metodología por utilizar, la cual será aplicada a cinco mercados latinoamericanos a través de sus índices bursátiles: Brasil, a través del BOVESPA; México, mediante el Índice de Precios y Cotizaciones (IPC); Chile, con el IPSA; Perú, a través del IGBVL; y Argentina, con el MERVAL. Es importante mencionar la posibilidad de diferentes resultados si se utiliza la rentabilidad derivada de los valores de los índices en moneda local o moneda extranjera, tal cual lo reportan para el efecto enero López y Rodríguez (2010), por lo que en este estudio se realizarán los modelos en ambas para así comparar los efectos según sea la moneda de análisis. El obtener conclusiones divergentes para un mercado según la moneda utilizada evidencia la existencia de un efecto de tipo de cambio, que también sería una anomalía del mercado financiero local.
La metodología que se aplicará consiste en siete modelos de regresión con el objetivo de poder concluir acerca de las anomalías en estos mercados. Primero se simulará un modelo estableciendo un único coeficiente de primer orden de auto-correlación y se evaluará según los rendimientos medidos vía tradicional (close-to-close) y según el método intraday (open-to-close). La idea será establecer si existe autocorrelación significativa, ver alguna presencia de algún efecto día de semana y comparar ambos modelos con el fin de establecer si los periodos de no transacción tienen alguna incidencia. Luego, el mismo modelo se aplica con ambos casos de rentabilidades para coeficientes de autocorrelación, uno para cada día de la semana, con el fin de saber si es que existe autocorrelación para cada día y, en ese caso, cuál es el más frecuente y cuál es el más significativo; asimismo, ver si se mantienen los efectos días de semana y, nuevamente, hacer un paralelo para evaluar la importancia de los periodos de no transacción. Para los casos en que los periodos de no transacción sean significativos, se analizará dicho mercado bajo un nuevo modelo que incluya la rentabilidad (close-to-open) y de esta forma ver qué está condicionando tales diferencias.
En seguida, se concluirán las aseveraciones finales que permitan describir el comportamiento anómalo de cada mercado con sus respectivas características, que nos faciliten su estudio y, sobre todo, que permitan dilucidar futuros comportamientos a lo largo del tiempo, que sirvan como base para que los administradores e inver-sores los consideren.
El determinar evidencia de autocorrelación es un signo de menor eficiencia del mercado accionario, ya que implicaría que la rentabilidad del periodo siguiente está condicionada por rentabilidades de periodos pasados. También el poder deter-minar si la autocorrelación está presente sólo para ciertos días de la semana también es interesante y de existir sería una evidencia de menor eficiencia de mercado. Cualquier evidencia de ineficiencia de mercado debería ser asumida por los agentes al conocerla y aplicarlas en sus estrategias de inversión, lo que traería como consecuencia que desapareciera la anomalía y el mercado sería más eficiente.
García (2008) al analizar los mercados accionarios de Alemania, Francia y España encontró una alta correlación de primer orden en estos mercados, una fuerte correlación entre la rentabilidad del periodo de transacción y el periodo de no transacción, así como retornos anormalmente altos para los días viernes y bajos en los días lunes para el mercado español, o sea, el efecto día lunes y efecto fin de semana. Dada esta evidencia es obvio preguntarse si ésta existe en los principales mercados accionarios latinoamericanos.
Revisión de la literaturaLa estimación de los movimientos de los valores de los mercados accionarios ha sido un tema ampliamente estudiado a través del tiempo, en particular las anomalías que existen y la relación entre la información y los valores. La teoría de los mercados eficientes define que los precios debieran reflejar toda la información que existe en el mercado, tanto privado como público (Grossman y Stiglitz, 1980; Kyle, 1985; Glosten y Milgrom, 1985; Fleming et al., 2006).
Es en este contexto que se genera el análisis del momento en que se conoce la información, pues no toda es entregada en el periodo de transacción, pudiéndose distinguir dos de ellos claramente definidos: el periodo de transacción y el periodo de no transacción. Uno de los primeros estudios que distinguen una diferencia entre las rentabilidades generadas en los periodos de transacción y los periodos de no transacción es Oldfield y Rogalski (1980). French y Roll (1986) evidenciaron que la volatilidad en horario de transacción es mayor que la de los periodos de no transacción.
Tsiakas (2008) analiza la información entregada en periodos de no transacción y modela el impacto de esta información en seis mercados europeos y en Estados Unidos, distinguiendo dentro de los periodos de no transacción entre overnight, feriado, fin de semana y fin de semana largo, concluyendo que se puede predecir de buena manera el desempeño de las acciones que tienen noticias fuera de la jornada de transacción y que existe una asimetría en el impacto dependiendo si el anuncio es positivo o negativo.
Abad et al. (2008) analizan para el mercado español la respuesta que existe en el cambio de precio de las acciones y la velocidad con la cual éstos cambian ante los anuncios de utilidad, haciendo la diferencia si el anuncio fue realizado en periodo de transacción o periodo de no transacción; concluyen que los anuncios que se realizan en el periodo posterior a las transacciones aumentan la liquidez de las acciones involucradas, mientras que los anuncios durante la jornada de transacción tienen un menor efecto de liquidez. Con ello se podría dar explicación a la preferencia de las empresas españolas a entregar sus resultados positivos una vez que la bolsa está cerrada.
Tanto Tsiakas (2008) como Abad, Sanabria y Yagüe (2008) hacen referencia a un estudio no publicado de Del Corral et al. (2003) quienes analizan el horario en el cual se realizan los anuncios de utilidades; encontraron que el 93% de estos anuncios fueron hechos en horarios de no transacción, mientras que el 7% sólo se realizó en jornada bursátil. Con respecto a los anuncios en el periodo de no transacción, el 41% se realizó un poco antes del comienzo de las transacciones, mientras que el 52% se realizó momentos después del cierre del mercado.
Un efecto de anomalía de los mercados accionarios más estudiado es el efecto día de semana, el cual consiste en rentabilidades y volatilidades distintas para cada uno de los días de la semana (Fields, 1931; Cross, 1973; Lakonishok y Levi, 1982; Brooks y Persand, 2001; Berument y Kiymaz, 2003; Ajayi, Mehdian y Perry, 2004; Bodla y Kiran, 2006; García, 2008; Kristjanpoller, 2009; y Charles, 2010). La gran mayoría de ellos —con diferentes metodologías— concluyen que existe el efecto día de semana, en especial del efecto día lunes y del efecto fin de semana. El primero de ellos caracterizado por una rentabilidad menor (e incluso negativa) con respecto a los demás días de la semana y una alta volatilidad; por su parte, el efecto fin de semana se caracteriza por una rentabilidad superior a la de los demás días e incluso en algunos mercados con una volatilidad menor. También existen algunas evidencias que el fenómeno tiende a desaparecer en mercados desarrollados.
Uno de los más emblemáticos estudios sobre el efecto día de semana fue el realizado por French (1980), quien analizó el comportamiento del Índice S&P 500 en el periodo 1953-1977. Para estudiar la presencia del efecto, considera dos hipótesis alternativas de análisis de rendimientos: hipótesis del tiempo calendario, en la cual incorpora el tiempo de no transacción en el día hábil siguiente, e hipótesis del tiempo de transacción, en la cual los días festivos no son tomados en cuenta en la base temporal. Los resultados obtenidos fueron una rentabilidad baja de los lunes en relación con el promedio de todo el periodo analizado, independientemente de la hipótesis adoptada. Más aún, analizando los rendimientos de cada día en subperiodos de cinco años, la rentabilidad promedio de los lunes fue negativa. Este estudio comienza a determinar la importancia de los periodos de no transacción y su cuantificación como tiempo.
García (2008) realiza un estudio para las bolsas de Alemania, Francia y España, analizando los períodos de transacción y de no transacción, el efecto día de semana y la autocorrelación de la rentabilidad siguiendo los enfoques y metodologías propuestas por Admati y Pfleiderer (1989) y Foster y Viswanathan (1990); en ese estudio encontró una alta correlación de primer orden en estos mercados, una fuerte correlación entre la rentabilidad del periodo de transacción y el periodo de no transacción, y rendimientos anormalmente altos para los viernes y bajos en los lunes para el mercado español, en otras palabras, el efecto día lunes y el efecto fin de semana.
Metodología y datosLos mercados accionarios analizados son el brasileño —caracterizado por el BOVESPA—, el mexicano —con el IPC—, el chileno —a través del IPSA—, el peruano —con su índice IGBVL— y el argentino —caracterizado por el MERVAL. El periodo de análisis comprende desde enero de 20011 hasta diciembre de 2010 con valores diarios de los índices, ya que para este periodo se pudo obtener el precio de apertura. Cabe señalar que los precios son obtenidos desde la base de datos Economática.
La metodología que se aplicará está basada en la utilizada por García (2008); ésta mide el efecto día de semana y, por consiguiente, el efecto fin de semana según la autocorrelación en el nivel de rendimiento de valores. Se aplican distintos modelos con el fin de incorporar todas las formas de cálculo y desagregación de rentabilidad. En particular se utilizan las siguientes formas de cálculos:
- •
Rentabilidad del tipoclose-to-close: corresponde a la rentabilidad de la figura al cierre del periodo en relación con el cierre del periodo anterior.
- •
Rentabilidad del tipoopen-to-close: es la rentabilidad de la figura en el periodo de transacción; es decir, desde la apertura de la figura en un periodo hasta el cierre de la misma en el mismo periodo.
- •
Rentabilidad del tipoclose-to-open: rentabilidad que refleja elperiodo de no transacción, o sea, la apertura de una figuraversus el cierre del día anterior.
En el caso de la rentabilidad close-to-close, los rendimientos diarios fueron calculados como:
donde Pc,t representa el precio de cierre del índice en el día t.
Análogamente, en el caso de las rentabilidades open-to-close y close-to-open, las rentabilidades se calculan de la siguiente forma, respectivamente:
donde Po,t corresponde al precio de apertura del índice en el período t.
Al realizar el análisis estadístico descriptivo de las rentabilidades se puede observar que, en promedio para el periodo de estudio, el mercado accionario mexicano ha rentado (close to close) un 0.077% en moneda local, mientras que solamente un 0.067% en dólares. Para ambas monedas la rentabilidad se fundamenta en un gran porcentaje en el cambio de precio cuando el mercado está abierto. Para el caso del mercado accionario brasileño, la rentabilidad en dólares es mayor que la expresada en reales (0.067% versus 0.061%), pero la mayor parte de la rentabilidad se genera en horario de transacción. En el mercado accionario chileno también la rentabilidad en dólares es mayor que la rentabilidad en pesos, mientras que para los mercados accionarios de Perú y Argentina la rentabilidad en moneda doméstica es mayor que la rentabilidad en dólares. En todos los mercados accionarios, independientemente de la moneda en la cual se mida, la rentabilidad se fundamenta en el cambio de precio en horario bursátil. El resumen de la estadística descriptiva de los principales mercados accionarios se puede observar en el cuadro 1.
Estadística descriptiva de las diferentes rentabilidades de los principales mercados accionarios latinoamericanos
| IPC | Moneda doméstica | Moneda global | ||||
|---|---|---|---|---|---|---|
| Rcc | Rco | Roc | Rcc | Rco | Roc | |
| Media | 0.077% | 0.006% | 0.071% | 0.067% | -0.004% | 0.071% |
| Mediana | 0.132% | 0.000% | 0.127% | 0.162% | 0.035% | 0.127% |
| Máximo | 10.441% | 3.423% | 9.953% | 16.038% | 6.461% | 9.953% |
| Mínimo | -7.266% | -3.441% | -7.085% | -11.210% | -7.410% | -7.085% |
| Desv. Est. | 1.407% | 0.218% | 1.381% | 1.717% | 0.701% | 1.381% |
| Skewness | 0.07 | 0.60 | 0.05 | -0.03 | -0.46 | 0.05 |
| Curtosis | 7.90 | 96.49 | 8.01 | 10.51 | 19.99 | 8.01 |
| Obs. | 2.518 | 2.516 | 2.516 | 2.518 | 2.516 | 2.516 |
| BOVESPA | Moneda doméstica | Moneda global | ||||
|---|---|---|---|---|---|---|
| Rcc | Rco | Roc | Rcc | Rco | Roc | |
| Media | 0.061% | 0.011% | 0.049% | 0.067% | 0.018% | 0.049% |
| Mediana | 0.130% | 0.000% | 0.119% | 0.169% | 0.047% | 0.119% |
| Máximo | 13.679% | 1.807% | 13.679% | 19.613% | 9.451% | 13.679% |
| Mínimo | -12.096% | -0.768% | -12.091% | -18.235% | -8.925% | -12.091% |
| Desv. Est. | 1.969% | 0.083% | 1.959% | 2.566% | 1.074% | 1.959% |
| Skewness | -0.12 | 4.64 | -0.12 | -0.26 | -0.02 | -0.12 |
| Curtosis | 7.11 | 106.43 | 7.20 | 8.72 | 13.60 | 7.20 |
| Obs. | 2.475 | 2.475 | 2.475 | 2.475 | 2.475 | 2.475 |
| IGBVL | Moneda doméstica | Moneda global | ||||
|---|---|---|---|---|---|---|
| Rcc | Rco | Roc | Rcc | Rco | Roc | |
| Media | 0.119% | 0.014% | 0.105% | 0.128% | 0.023% | 0.105% |
| Mediana | 0.110% | 0.002% | 0.111% | 0.120% | 0.003% | 0.111% |
| Máximo | 12.816% | 1.022% | 11.915% | 14.764% | 3.864% | 11.915% |
| Mínimo | -11.441% | -0.643% | -12.463% | -11.769% | -3.060% | -12.463% |
| Desv. Est. | 1.498% | 0.099% | 1.507% | 1.597% | 0.357% | 1.507% |
| Skewness | -0.40 | 2.12 | -0.62 | -0.32 | 0.85 | -0.62 |
| Curtosis | 13.44 | 25.54 | 13.31 | 13.85 | 23.42 | 13.31 |
| Obs. | 2.492 | 2.492 | 2.492 | 2.492 | 2.492 | 2.492 |
| IPSA | Moneda doméstica | Moneda global | ||||
|---|---|---|---|---|---|---|
| Rcc | Rco | Roc | Rcc | Rco | Roc | |
| Media | 0.062% | -0.001% | 0.063% | 0.072% | 0.009% | 0.063% |
| Mediana | 0.099% | 0.000% | 0.098% | 0.131% | 0.021% | 0.098% |
| Máximo | 11.785% | 0.258% | 11.785% | 7.722% | 3.799% | 11.785% |
| Mínimo | -6.215% | -0.380% | -6.215% | -9.146% | -4.459% | -6.215% |
| Desv. Est. | 1.045% | 0.013% | 1.045% | 1.243% | 0.656% | 1.045% |
| Skewness | 0.07 | -14.79 | 0.07 | -0.56 | -0.38 | 0.07 |
| Curtosis | 12.86 | 649.93 | 12.87 | 8.01 | 7.58 | 12.87 |
| Obs. | 2.410 | 2.410 | 2.410 | 2.410 | 2.410 | 2.410 |
| MERVAL | Moneda doméstica | Moneda global | ||||
|---|---|---|---|---|---|---|
| Rcc | Rco | Roc | Rcc | Rco | Roc | |
| Media | 0.087% | 0.057% | 0.028% | 0.030% | 0.001% | 0.028% |
| Mediana | 0.147% | 0.013% | 0.103% | 0.156% | 0.009% | 0.103% |
| Máximo | 16.117% | 9.551% | 15.893% | 16.117% | 9.551% | 15.893% |
| Mínimo | -13.204% | -12.244% | -12.944% | -51.837% | -52.190% | -12.944% |
| Desv. Est. | 2.245% | 0.618% | 2.136% | 2.565% | 1.584% | 2.136% |
| Skewness | -0.16 | -3.52 | -0.17 | -3.86 | -21.61 | -0.17 |
| Curtosis | 8.17 | 166.23 | 8.93 | 77.07 | 651.00 | 8.93 |
| Obs. | 2.462 | 2.459 | 2.459 | 2.462 | 2.459 | 2.459 |
En todos los mercados y para ambas monedas se puede observar que la rentabilidad close-to-open es menor que la rentabilidad open-to-close, por lo que se puede concluir que la rentabilidad se genera en mayor proporción cuando el mercado está abierto. El caso del mercado accionario brasileño es donde se evidencia la mayor cuantía de la rentabilidad close-to-open que corresponde a un 18.0% y 26.9% de la rentabilidad close-to-close en moneda doméstica y moneda global, respectivamente. Caso particular es el mercado argentino en moneda local donde la rentabilidad close-to-open explica el 65.5% de la rentabilidad close-to-close, pero en la rentabilidad en moneda global solamente un 3.3%, por lo que claramente se aprecia un efecto tipo de cambio en este mercado producto de su alta volatilidad.
El primer modelo propuesto estima un coeficiente de autocorrelación de primer orden (β) para todos los días de la semana y la rentabilidad medida del modo tradicional (close-to-close):
donde Rcc,t es el rendimiento diario del índice medido desde el precio de cierre del día t-1 hasta el cierre del día t. Las variables d1, d2, d3, d4 y d5 son variables auxiliares asociadas al día de la semana; por ejemplo, d1 es 1 si t corresponde al lunes y 0 para cualquier otro día, d2 es 1 si t corresponde al martes y 0 para cualquier otro día, y así respectivamente.
El segundo modelo busca determinar la autocorrelación sin considerar el periodo de no transacción, es decir, toma como variable de análisis a la rentabilidad open-to-close.
donde Roc,t es el rendimiento diario del índice medido desde el precio de apertura al precio de cierre del día t, el resto de los términos son análogos al modelo anterior.
Para evaluar las diferencias en la autocorrelación en los periodos de no transacción, dependiendo del día de la semana, se generan dos modelos que conceptualmente reflejan lo mismo que los dos modelos anteriores, pero ahora con la existencia de un coeficiente de autocorrelación para cada día de la semana. Los modelos 3 y 4 quedan definidos de la siguiente forma respectivamente:
Las variables son las mismas que en los modelos anteriormente presentados.
Para poder determinar si existe una correlación entre la rentabilidad del día (open-to-close) y la rentabilidad que se genera en el periodo de no transacción (close-to-open) se desarrolla el modelo 5, que mostrará si existe una relación de inercia o de ajuste posterior al cierre de las transacciones; dicho modelo queda definido con la siguiente ecuación:
donde Rco,t es el rendimiento diario del índice medido desde el precio de cierre del día t-1 hasta el precio de apertura del día t, mientras que Roc,t es el rendimiento diario del índice medido desde el precio de apertura del día t hasta el precio de cierre del día t.
El modelo 6 es análogo al anterior, solo que indica la relación que tiene la rentabilidad del periodo de no transacción y la rentabilidad del día. Así el modelo 6 que definido de la siguiente manera:
donde Rco,t es el rendimiento diario del índice medido desde el precio de cierre del día t-1 hasta el precio de apertura del día t.
El modelo 7 no estaba dentro de la metodología seguida por García (2008), pero se incluye porque es interesante saber si la rentabilidad del periodo de no transacción puede ser predictor de la rentabilidad intraday. Así el modelo 6 queda definido de la siguiente manera:
donde Roc,t es el rendimiento diario del índice medido desde el precio de apertura del día t hasta el precio de cierre del día t, mientras que Rco,t es el rendimiento diario del índice medido desde el precio de cierre del día t-1 hasta el precio de apertura del día t.
Por último, se analiza el modelo 8 que analiza los rendimientos asociándolos a los valores anteriores y a la magnitud del rendimiento anterior; se efectúa una discriminación en esta magnitud cuando está en un 10% superior de rentabilidad absoluta, siguiendo el modelo propuesto por García (2008). Así, el modelo queda definido de la siguiente manera:
donde D1 corresponde a una variable auxiliar que tiene valor 1 si Rcc,t-1 está en el 10% de rentabilidad absoluta más alta y 0 para cualquier otro caso.
Análisis de resultadosAl analizar el modelo 1 podemos apreciar que, con la excepción de Brasil, todos los mercados tienen una autocorrelación de la rentabilidad (close-to-close) de su índice con el valor anterior en moneda doméstica o local. Desde el punto de vista del efecto día de semana se puede concluir que en el periodo de análisis Chile es el mercado que más anomalías presenta con efecto de día lunes, miércoles, jueves y viernes. Por su parte, el mercado accionario peruano presenta un fuerte efecto fin de semana. Brasil presenta solamente un tenue efecto de miércoles, mientras que el mercado accionario mexicano y argentino no presentan anomalías de efecto día de semana con este modelo. Los valores obtenidos se pueden apreciar en el cuadro 2.
Modelo con autocorrelación de primer orden y efecto día de semana en los principales mercados accionarios latinoamericanos (modelo 1, moneda doméstica)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| β | 0.0966 | *** | 0.0053 | 0.1540 | *** | 0.1990 | *** | 0.0404 | ** | |
| α1 | 0.0003 | -0.0009 | -0.0008 | * | 0.0007 | -0.0001 | ||||
| α2 | 0.0007 | 0.0006 | 0.0001 | 0.0000 | -0.0002 | |||||
| α3 | 0.0010 | 0.0017 | * | 0.0011 | ** | 0.0011 | * | 0.0015 | ||
| α4 | 0.0008 | 0.0000 | 0.0010 | ** | 0.0007 | 0.0013 | ||||
| α5 | 0.0006 | 0.0014 | 0.0011 | ** | 0.0022 | *** | 0.0016 | |||
| R2 | 0.0097 | 0.0022 | 0.0288 | 0.0417 | 0.0029 | |||||
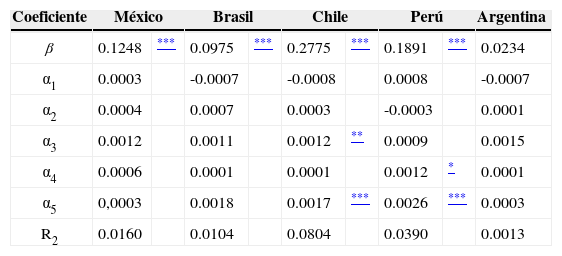
Al analizar el modelo 1, pero con las rentabilidades (close-to-close) de cada mercado expresadas en dólares americanos, se puede apreciar que todos los mercados tienen una autocorrelación de la rentabilidad de su índice con el valor anterior, con la única excepción de Argentina. Brasil, que era la excepción en el análisis anterior, presenta una fuerte autocorrelación en moneda local. Desde el punto de vista del efecto día de semana en moneda global se puede concluir que desaparecen la mayoría de estos fenómenos, solamente existiendo el efecto miércoles y viernes en el mercado chileno y el efecto jueves y viernes para el caso del mercado peruano. Los valores obtenidos se pueden apreciar en el cuadro 3.
Modelo con autocorrelación de primer orden y efecto día de semana en los principales mercados accionarios latinoamericanos (modelo 1, moneda global)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | ||||
|---|---|---|---|---|---|---|---|---|---|
| β | 0.1248 | *** | 0.0975 | *** | 0.2775 | *** | 0.1891 | *** | 0.0234 |
| α1 | 0.0003 | -0.0007 | -0.0008 | 0.0008 | -0.0007 | ||||
| α2 | 0.0004 | 0.0007 | 0.0003 | -0.0003 | 0.0001 | ||||
| α3 | 0.0012 | 0.0011 | 0.0012 | ** | 0.0009 | 0.0015 | |||
| α4 | 0.0006 | 0.0001 | 0.0001 | 0.0012 | * | 0.0001 | |||
| α5 | 0,0003 | 0.0018 | 0.0017 | *** | 0.0026 | *** | 0.0003 | ||
| R2 | 0.0160 | 0.0104 | 0.0804 | 0.0390 | 0.0013 | ||||
El segundo modelo analizado sólo difiere del modelo anterior en que se utilizará la rentabilidad open-to-close en vez de la rentabilidad close-to-close, o sea, sin considerar el periodo de no transacción. Con respecto a la autocorrelación se puede observar el mismo fenómeno que en el modelo anterior en moneda doméstica, donde todos los mercados presentan una fuerte correlación, excepto para el caso del mercado accionario brasileño. Por su parte, para el efecto día de semana se puede apreciar un efecto miércoles, jueves y viernes en el mercado accionario chileno, un fuerte efecto fin de semana en el mercado accionario peruano y un leve efecto miércoles en el caso del mercado brasileño. Los valores obtenidos se pueden apreciar en el cuadro 4.
Modelo con autocorrelación de primer orden y efecto día de semana en los principales mercados accionarios latinoamericanos (modelo 2, moneda doméstica)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| β | 0.1017 | *** | 0.0055 | 0.1521 | *** | 0.2161 | *** | 0.0571 | *** | |
| α1 | 0.0002 | -0.0010 | -0.0008 | 0.0006 | -0.0006 | |||||
| α2 | 0.0007 | 0.0005 | 0.0001 | -0.0002 | -0.0010 | |||||
| α3 | 0.0008 | 0.0016 | * | 0.0011 | ** | 0.0010 | 0.0008 | |||
| α4 | 0.0008 | -0.0001 | 0.0010 | ** | 0.0006 | 0.0007 | ||||
| α5 | 0.0006 | 0.0013 | 0.0012 | ** | 0.0021 | *** | 0.0013 | |||
| R2 | 0.0107 | 0.0023 | 0.0280 | 0.0488 | 0.0050 | |||||
Debido a que las rentabilidades (open-to-close) son calculadas en un mismo día, no aplica el modelo de rentabilidades expresadas en dólares, ya que no difieren al valor en moneda local.
El siguiente modelo analiza el efecto día de semana, pero la autocorrelación se analiza para cada uno de los días por separados. Dicha autocorrelación se presenta en todos los días para los mercados accionarios de Chile y Perú; en el caso del mercado accionario de México también está presente todos los días, excepto para el martes; con respecto al mercado accionario de Argentina sólo se presenta los lunes, martes y miércoles; en tanto que en el mercado accionario de Brasil sólo se puede observar para el martes. El efecto día de semana está presente en el periodo de análisis para el mercado accionario chileno en los lunes, miércoles, jueves y viernes; el mercado accionario peruano presenta un fuerte un fuerte efecto fin de semana y un tenue efecto miércoles; Brasil presenta solamente un tenue efecto de miércoles; por otra parte, los mercados accionarios mexicano y argentino no presentan anomalías de efecto día de semana con este modelo. Los efectos de días de semana son iguales a los obtenidos en el modelo 1 en moneda doméstica. Los valores obtenidos se pueden apreciar en el cuadro 5.
Modelo con autocorrelación de primer orden por día y efecto día de semana en los principales mercados accionarios latinoamericanos (modelo 3, moneda local)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| α1 | 0.0003 | -0.0009 | -0.0008 | * | 0.0007 | -0.0004 | ||||
| α2 | 0.0008 | 0.0005 | 0.0001 | 0.0000 | -0.0002 | |||||
| α3 | 0.0009 | 0.0017 | * | 0.0011 | ** | 0.0011 | * | 0.0015 | ||
| α4 | 0.0008 | 0.0000 | 0.0011 | ** | 0.0006 | 0.0011 | ||||
| α5 | 0.0006 | 0.0014 | 0.0011 | ** | 0.0022 | *** | 0.0016 | |||
| β1 | 0.1817 | *** | 0.0086 | 0.1623 | *** | 0.2382 | *** | 0.2361 | *** | |
| β2 | -0.0393 | -0.0814 | ** | 0.1227 | *** | 0.1463 | *** | -0.0750 | * | |
| β3 | 0.1655 | *** | 0.0094 | 0.2188 | *** | 0.1552 | *** | -0.0351 | ||
| β4 | 0.1408 | *** | 0.0368 | 0.1028 | ** | 0.2778 | *** | 0.1755 | *** | |
| β5 | 0.0906 | ** | 0.0723 | 0.1763 | *** | 0.1940 | *** | 0.0052 | ||
| R2 | 0.0167 | 0.0052 | 0.0305 | 0.0443 | 0.0165 | |||||
Al estimar el modelo 3 con rentabilidades expresadas en dólares, nuevamente se encuentra que la autocorrelación está presente en todos los días para los mercados accionarios de Chile y Perú; en el caso del mercado accionario brasileño también está presente todos los días, excepto para el martes; para el mercado accionario argentino la autocorrelación se presenta en los lunes, jueves y viernes; en tanto que en el mercado accionario mexicano se puede observar para los miércoles, jueves y viernes. El efecto día de semana sólo está presente en el periodo de análisis para el mercado accionario chileno en los miércoles y viernes, y en el mercado accionario peruano los jueves y viernes. Los demás mercados accionarios no presentan anomalías de efecto día de semana con este modelo. Los valores obtenidos se pueden apreciar en el cuadro 6.
Modelo con autocorrelación de primer orden por día y efecto día de semana en los principales mercados accionarios latinoamericanos (modelo 3, moneda global)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| α1 | 0.0003 | -0.0007 | -0.0008 | 0.0006 | -0.0008 | |||||
| α2 | 0.0004 | 0.0006 | 0.0003 | -0.0003 | 0.0001 | |||||
| α3 | 0.0011 | 0.0011 | 0.0012 | ** | 0.0010 | 0.0015 | ||||
| α4 | 0.0005 | 0.0001 | 0.0002 | 0.0012 | * | -0.0001 | ||||
| α5 | 0.0003 | 0.0018 | 0.0017 | *** | 0.0026 | *** | 0.0003 | |||
| β1 | 0.0732 | 0.1031 | ** | 0.2994 | *** | 0.2639 | *** | 0.2551 | *** | |
| β2 | 0.0334 | -0.0100 | 0.2747 | *** | 0.1378 | *** | -0.0213 | |||
| β3 | 0.2679 | *** | 0.1232 | *** | 0.3034 | *** | 0.1380 | *** | -0.0115 | |
| β4 | 0.1550 | *** | 0.1385 | *** | 0.1998 | *** | 0.2591 | *** | 0.1540 | *** |
| β5 | 0.1032 | ** | 0.1614 | *** | 0.3120 | *** | 0.1770 | *** | -0.1018 | ** |
| R2 | 0.0232 | 0.0146 | 0.0821 | 0.0420 | 0.0143 | |||||
El cuarto modelo analizado sólo difiere del modelo anterior en que se utilizará la rentabilidad open-to-close en vez de la rentabilidad close-to-close. Con respecto a la autocorrelación se puede observar que, al igual que en el modelo 3, los mercados accionarios de Chile y Perú presentan una fuerte autocorrelación para todos los días de la semana; los mercados accionarios argentino y mexicano presentan autocorrelación en los lunes, martes, jueves y viernes; Brasil es la excepción con solamente autocorrelación los martes. Por otra parte, el efecto día de semana sólo se encuentra presente en el mercado accionario chileno en los miércoles, jueves y viernes; asimismo, existe un fuerte efecto fin de semana en el mercado accionario peruano y un leve efecto miércoles en el caso del mercado brasileño; Argentina y México no presentan anomalía de efecto día de semana. Los valores obtenidos se pueden apreciar en el cuadro 7.
Modelo con autocorrelación de primer orden por día y efecto día de semana en los principales mercados accionarios latinoamericanos (modelo 4, moneda doméstica)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| α1 | 0.0001 | -0.0010 | -0.0008 | 0.0005 | -0.0008 | |||||
| α2 | 0.0007 | 0.0004 | 0.0001 | -0.0001 | -0.0011 | |||||
| α3 | 0.0008 | 0.0016 | * | 0.0011 | ** | 0.0010 | 0.0007 | |||
| α4 | 0.0008 | -0.0002 | 0.0010 | ** | 0.0005 | 0.0006 | ||||
| α5 | 0.0006 | 0.0013 | 0.0012 | ** | 0.0021 | *** | 0.0013 | |||
| β1 | 0.1792 | *** | 0.0160 | 0.1593 | *** | 0.2479 | *** | 0.2203 | *** | |
| β2 | -0.0221 | -0.0810 | ** | 0.1212 | *** | 0.1648 | *** | -0.0927 | ** | |
| β3 | 0.1657 | *** | 0.0074 | 0.2140 | *** | 0.1674 | *** | -0.0262 | ||
| β4 | 0.1423 | *** | 0.0355 | 0.1012 | ** | 0.3007 | *** | 0.1832 | *** | |
| β5 | 0.0929 | ** | 0.0711 | 0.1777 | *** | 0.2135 | *** | 0.0876 | ** | |
| R2 | 0.0165 | 0.0052 | 0.0297 | 0.0515 | 0.0189 | |||||
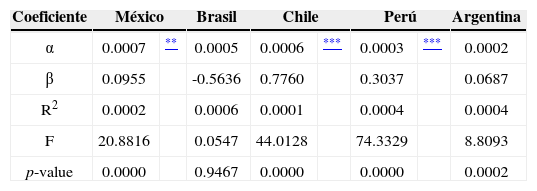
Al determinar si existe una correlación entre la rentabilidad del día (open-to-close) y la rentabilidad que se genera en el periodo siguiente de no transacción (close-to-open), ambas expresadas en moneda doméstica, sólo se puede concluir que en el caso del mercado accionario peruano existe una corrección de signo contrario al terminar la jornada de transacción. Los demás mercados no muestran correlación entre la rentabilidad intraday y la del periodo de no transacción. Los valores obtenidos se pueden apreciar en el cuadro 8.
Modelo de correlación de primer entre la rentabilidad intraday y la rentabilidad del periodo de no transacción en los principales mercados accionarios latinoamericanos (modelo 5, moneda doméstica)
Al analizar el mismo fenómeno, pero con las rentabilidades expresadas en dólares norteamericanos, los resultados son completamente diferentes a los obtenidos en el modelo hecho con rentabilidades expresadas en moneda doméstica. Se puede observar un efecto positivo muy significante en los mercados accionarios de Brasil y Chile, lo que muestra una evidencia de inercia de la rentabilidad intraday que se proyecta al periodo de no transacción; el mercado accionario peruano muestra el mismo efecto que cuando se evaluó en moneda doméstica un efecto de corrección al finalizar la jornada de transacción; por su parte los mercados mexicanos y argentinos no evidencian el efecto. Los valores obtenidos se pueden apreciar en el cuadro 9.
Modelo de correlación de primer entre la rentabilidad intraday y la rentabilidad del periodo de no transacción en los principales mercados accionarios latinoamericanos (modelo 5, moneda global)
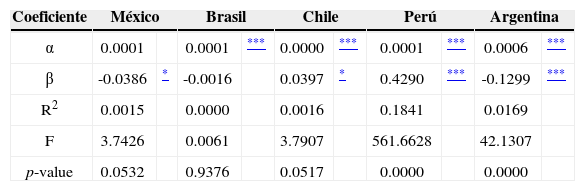
Al analizar la autocorrelación de la rentabilidad, del periodo de no transacción, expresada en moneda local, se puede obtener que existe una alta autocorrelación para los mercados accionarios de Argentina y Perú: en el caso del mercado accionario argentino la autocorrelación es positiva, mientras que para el caso peruano es negativa; también existe un efecto de autocorrelación para los mercados mexicano y chileno pero de menor significancia: positiva en el caso chileno y negativa en el caso mexicano; en el mercado brasileño no existe autocorrelación de la rentabilidad, expresada en moneda local, del periodo de no transacción. Los parámetros del modelo se pueden observar en el cuadro 10.
Modelo de autocorrelación de la rentabilidad de los periodos de no transacción en los principales mercados accionarios latinoamericanos (modelo 6, moneda doméstica)
Al analizar la autocorrelación de la rentabilidad del periodo de no transacción, pero ahora expresada en dólares norteamericanos, se puede apreciar que existe una alta autocorrelación para los mercados accionarios de Brasil, Chile, Argentina y Perú: para los dos primeros mercados es positiva, mientras que para los dos últimos es negativa; en el mercado mexicano no existe autocorrelación de la rentabilidad, expresada en moneda global, del periodo de no transacción. En el cuadro 11 se pueden apreciar las estadísticas del modelo.
Modelo de autocorrelación de la rentabilidad de los periodos de no transacción en los principales mercados accionarios latinoamericanos (modelo 6, moneda global)
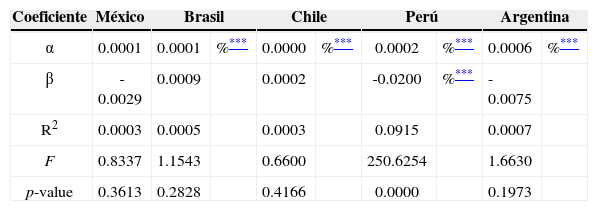
La rentabilidad del periodo de no transacción no es un predictor de la rentabilidad intraday, como se puede observar en el cuadro 12; ambas rentabilidades están expresadas en moneda doméstica.
Modelo de correlación de primer entre la rentabilidad del periodo de no transacción y la rentabilidad intraday en los principales mercados accionarios latinoamericanos
La rentabilidad del periodo de no transacción es un predictor de la rentabilidad intraday cuando se analizan las rentabilidades expresadas en dólares norteamericano para el mercado accionario peruano (fuertemente) y en menor medida para el mercado accionario mexicano; los demás mercados al igual que en el análisis en moneda doméstica no presentan correlación. Los resultados se pueden observar en el cuadro 13.
Modelo de correlación de primer entre la rentabilidad del periodo de no transacción y la rentabilidad intraday en los principales mercados accionarios latinoamericanos (modelo 7, moneda global)
El efecto detectado por Chan (1993), rentabilidades positivas al día siguiente de grandes cambios porcentuales, se pude constatar en los principales mercados accionarios latinoamericanos para el periodo de análisis. De hecho todos los mercados analizados, con la sola excepción de Brasil, evidencian este efecto de manera positiva y con una gran significancia al analizar la rentabilidad expresada en moneda doméstica; asimismo, sigue persistiendo la autocorrelación para los mercados con la excepción de los mercados accionarios de Argentina y Brasil. Los valores del modelo se pueden observar en el cuadro 14.
Modelo con autocorrelación de primer orden y efecto de rentabilidades anormales en los principales mercados accionarios latinoamericanos (modelo 8, moneda doméstica)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | ||||
|---|---|---|---|---|---|---|---|---|---|
| α | 0.0008 | *** | 0.0006 | 0.0006 | *** | 0.0011 | *** | 0.0009 | ** |
| β | 0.0518 | ** | 0.0014 | 0.0860 | *** | 0.0824 | *** | -0.0024 | |
| δ | 0.1993 | *** | 0.0136 | 0.2253 | *** | 0.2640 | *** | 0.1698 | *** |
| R2 | 0.0163 | 0.0000 | 0.0341 | 0.0564 | 0.0071 | ||||
| F | 0.5751 | 1.4178 | 0.2192 | 1.0834 | 0.9736 | ||||
| p-value | 0.4483 | 0.2339 | 0.6397 | 0.2980 | 0.3239 | ||||
Al estimar el modelo de las grandes perturbaciones, pero con la rentabilidad expresada en moneda global, se puede concluir la existencia de este fenómeno de manera positiva y significante para los mercados accionarios de México, Chile y Perú; por otro lado, estos tres mercados junto con el brasileño presentan una fuerte autocorrelación. Los detalles del modelo se encuentran en el cuadro 15.
Modelo con autocorrelación de primer orden y efecto de rentabilidades anormales en los principales mercados accionarios latinoamericanos (modelo 8, moneda global)
| Coeficiente | México | Brasil | Chile | Perú | Argentina | ||||
|---|---|---|---|---|---|---|---|---|---|
| α | 0,0007 | ** | 0,0006 | 0,0007 | *** | 0,0012 | *** | 0,0003 | |
| β | 0,0721 | *** | 0,0805 | *** | 0,1348 | *** | 0,0781 | *** | 0,0204 |
| δ | 0,2050 | *** | 0,0678 | 0,5521 | *** | 0,2611 | *** | 0,0072 | |
| R2 | 0,0237 | 0,0102 | 0,1325 | 0,0522 | 0,0006 | ||||
| F | 3,3848 | 0,0978 | 2,6275 | 16,3713 | 0,5025 | ||||
| p-value | 0,0659 | 0,7545 | 0,1052 | 0,0001 | 0,4785 | ||||
Del análisis completo de la autocorrelación, el efecto día de semana, la descomposición de la rentabilidad tradicional en la rentabilidad del periodo de transacción (open-to-close o intraday) y la rentabilidad del periodo de no transacción (close-to-open) se pudo llegar a la conclusión que los fenómenos sí estuvieron presentes en los principales mercados accionarios de Latinoamérica.
Asimismo, se pudo apreciar que todos los mercados tienen una autocorrelación de la rentabilidad (close-to-close) de su índice con el valor anterior en moneda doméstica, con la excepción de Brasil, y todos, excepto Argentina, en el análisis de rentabilidad en dólar americano. En este modelo se evidencia el efecto día de semana en Chile con efecto en los lunes, miércoles, jueves y viernes; Perú con un fuerte efecto fin de semana; y Brasil con un tenue efecto de miércoles, en el análisis de moneda local. En relación con la moneda global el efecto día de semana desaparece en la mayoría de estos fenómenos, solamente existiendo el efecto miércoles y viernes en el mercado chileno y el efecto jueves y viernes para el caso del mercado peruano.
Con respecto a la autocorrelación de la rentabilidad open-to-close se puede observar que todos los mercados presentan una fuerte correlación, excepto para el caso del mercado brasileño. El efecto día de semana en este modelo se puede apreciar los días miércoles, jueves y viernes en el mercado chileno, un fuerte efecto fin de semana en el peruano y un leve efecto miércoles en el caso del mercado brasileño.
Al analizar la autocorrelación de la rentabilidad close-to-close en moneda local para cada uno de los días por separado se evidencia que este fenómeno está presente en todos los días para los mercados accionarios de Chile y Perú, mientras que para el caso de México también está presente todos los días, excepto el martes. El mercado accionario argentino sólo presenta la autocorrelación los lunes, martes y miércoles, mientras que el mercado brasileño sólo se puede observar en martes. En el análisis de la rentabilidad en moneda global se concluye que la autocorrelación está presente en todos los días para los mercados accionarios de Chile y Perú; para el caso del mercado accionario brasileño también está presente todos los días, excepto el martes; en el mercado accionario argentino los lunes, jueves y viernes; finalmente, en el mercado accionario mexicano se puede observar los miércoles, jueves y viernes.
Con respecto a la autocorrelación de la rentabilidad open-to-close se puede concluir que los mercados accionarios de Chile y Perú presentan una fuerte autocorrelación para todos los días de la semana; los mercados accionarios argentino y mexicano presentan autocorrelación los lunes, martes, jueves y viernes; Brasil solamente evidencia autocorrelación los martes.
Del análisis de la correlación entre la rentabilidad del día (open-to-close) y la rentabilidad que se genera en el periodo siguiente de no transacción (close-to-open), en moneda doméstica, sólo se puede concluir que en el caso del mercado accionario peruano existe una corrección de signo contrario al terminar la jornada de transacción. Con las rentabilidades expresadas en dólares los resultados son completamente diferentes, pues se observa un efecto muy significante positivo en los mercados accionarios de Brasil y Chile, lo que muestra una evidencia de inercia de la rentabilidad intraday que se proyecta al periodo de no transacción; por su parte, el mercado accionario peruano muestra el mismo efecto que en moneda doméstica: un efecto de corrección al finalizar la jornada de transacción.
La autocorrelación de la rentabilidad del periodo de no transacción en el análisis de moneda doméstica existe de manera positiva para los mercados accionarios de Argentina y Chile, mientras que es negativa para Perú y México. Por otro lado, la autocorrelación de la rentabilidad del periodo de no transacción, expresada en dólares norteamericano, se evidenció de manera positiva para los mercados accionarios de Brasil y Chile, mientras que para Argentina y Perú se evidenció de forma negativa.
La rentabilidad del periodo de no transacción no es un predictor de la rentabilidad intraday en moneda doméstica. En el caso del análisis en dólares la rentabilidad del periodo de no transacción es un fuerte predictor de la rentabilidad intraday en el mercado accionario de Perú y en menor medida para el mercado accionario mexicano.
El efecto detectado de rentabilidades positivas al día siguiente de grandes cambios porcentuales se pude constatar en los principales mercados accionarios latinoamericanos para el periodo de análisis con la sola excepción de Brasil. En el análisis de rentabilidad expresada en moneda global, se puede concluir la existencia de este fenómeno de manera positiva y significante para los mercados accionarios de México, Chile y Perú.
Con todas estas evidencias de autocorrelación, efecto día de semana, desagregación de la rentabilidad y grandes perturbaciones, se puede entender mejor las anomalías de los mercados accionarios latinoamericanos y, así, tener más información para tomar decisiones de inversión y administración financiera por parte de los agentes inmersos en estos mercados que siguen creciendo y siendo recomendados para invertir en ellos.