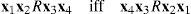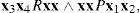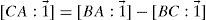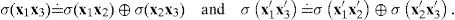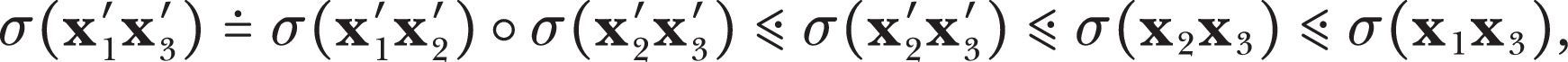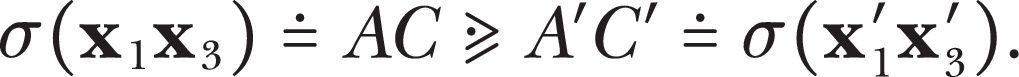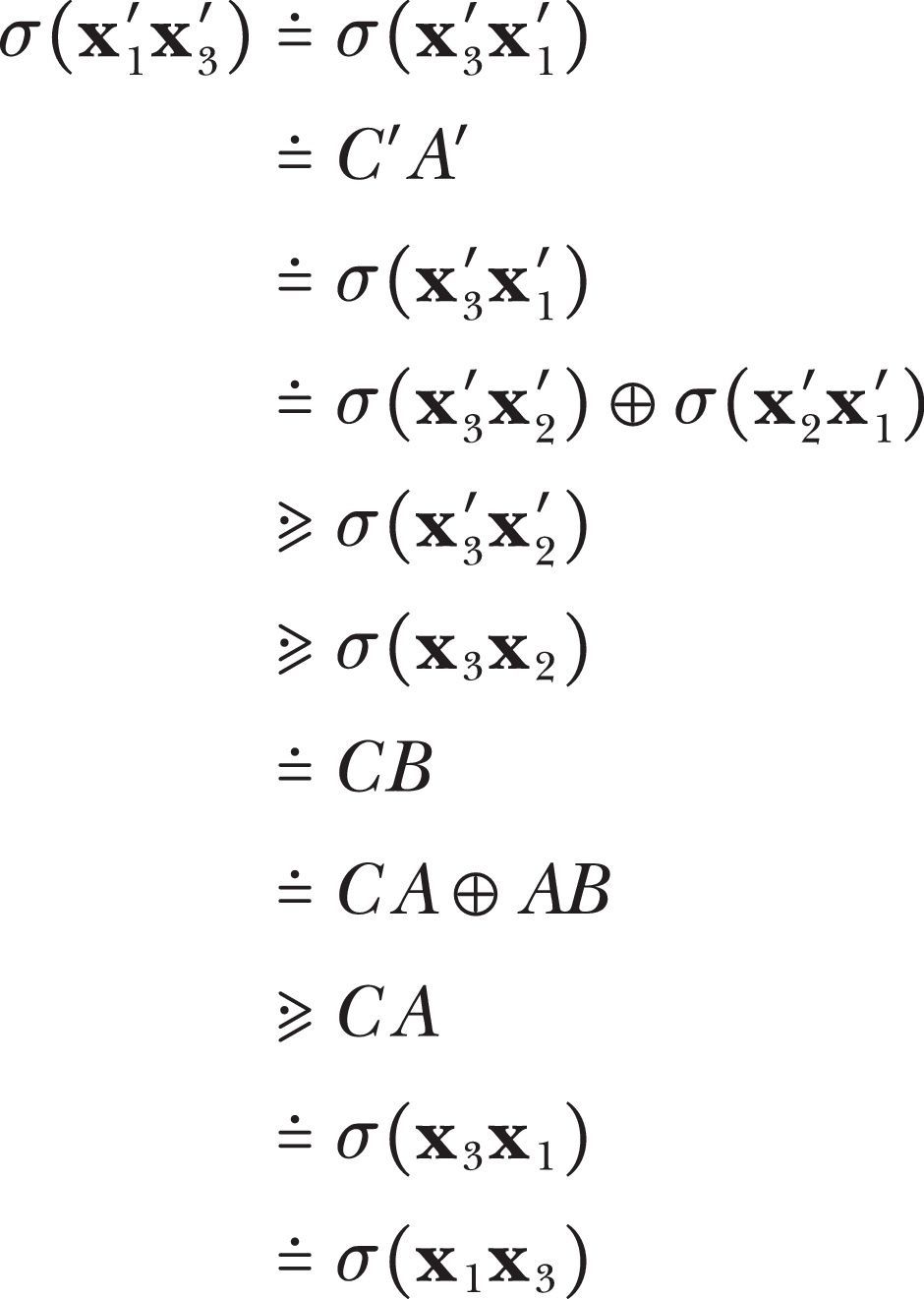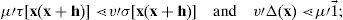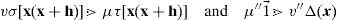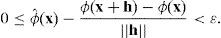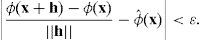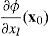Continuously differentiable preferences

Abstract

This is a paper on the foundations of individual rational choice, specifically on the foundations of consumer theory. Neoclassical consumer theory requires that the behavior of the consumer be explained by means of a preference relation, and that all the required properties of the corresponding utility representation be derived from the properties of this relation. Yet, it is not clear what is the meaning of the property of the preference relation required in order to show that it is representable by means of a continuously differentiable C¹ utility function. The aim of the present paper is to propose an explanation of such property and to prove the existence of a C¹ representation.

Resumen

Este es un artículo sobre los fundamentos de la teoría de la elección racional individual, específicamente sobre los fundamentos de la teoría del consumidor. La teoría neoclásica del consumidor requiere que el comportamiento del consumidor sea explicado mediante una relación de preferencia y que todas las propiedades requeridas de la correspondiente función de utilidad que la represente sean derivadas de las propiedades de esta relación. No obstante, no está claro cuál es el significado de la propiedad de la relación de preferencia requerida para mostrar que la misma es representable mediante una función continuamente diferenciable (C¹). El propósito del presente artículo es proponer una explicación de tal propiedad y demostrar la existencia de una representación.

A ratio is a sort of relation in respect of size between two magnitudes of the same kind.

Euclid, Elements

Book V, Definition 3

Introduction

Just as classical dynamics proposed to explain the motion of bodies by means of the concept of force, neoclassical consumer theory proposes to explain the behavior of the consumer by means of the concept of preference. This is done by taking, as a starting point, a regular preference structure defined by axioms that actually attribute empirically meaningful (even though idealized) properties to the preference relation. Among these properties, strict convexity, non-satiation or continuity can be mentioned. Restrictions on preference relations translate into restrictions on the form of the utility functions. For instance, if the preference relation is strictly convex, the corresponding utility representation is strictly quasi-concave; if the relation is non-satiated, the corresponding utility representation is monotonically increasing; if the relation is continuous, the corresponding utility representation is also continuous. Certain specializations of the theory require, additionally, that the utility function representing the preference relation be differentiable, in order to apply methods of nonlinear programming to the derivation of the demand functions.

Even though some of the aforementioned properties are deemed as “non-substantial” and “technical” by economists of a positivist and instrumentalist philosophical persuasion, nonetheless the tendency has been to formulate them by means of natural and intuitive conditions that depict an idealized consumer described by set-theoretical structures into which the empirical data can be imbedded.¹ For the actual meaning of the axioms defining the structures is important: the more idealized they are, the less precise are the empirical consequences of the same, and it is impossible to check intuitively their degree of idealization if their economic meaning is unknown. I think that the reason why it is said (for instance by Barten & Böhm, 1981, pp. 385–386) that even though “Axioms 1–3 [reflexivity, transitivity and completeness] describe order properties of a preference relation that have intuitive meaning in the context of the theory of choice … [this] is much less so with the topological conditions which are usually assumed as well” is that the language of topology obscures such intuitive meaning altogether because it is not suitable to express the economic meaning of such properties.

It is not really difficult to formulate conditions like continuity or convexity in intuitive terms, but the differentiability condition has turned out to be more resilient to such treatment. Certainly, Gerard Debreu (1983a, 1983b) and Andreu Mas-Colell (1985) have provided conditions over a preference relation that imply the existence of continuously differentiable utility functions. The problem is that — in contradistinction to the properties I referred to previously — these conditions are admittedly not intuitive. The first aim of the present paper is to propose a language in which all the usual properties attributed to the preference relation, including differentiability, can be formulated in a natural, intuitive way. Even if differentiability is deemed as a mere technical computational convenience, without any actual empirical meaning, the condition presented here is mathematically simpler (once the language has been assimilated) than the ones presented by Debreu and Mas-Colell (which rely upon the heavy machinery of differential topology), and is formulated within the framework of a unified language and conceptual apparatus that clarifies its relationship with the concept of preference strength.

After discussing, in the second section, the conditions proposed by Gerard Debreu (1983a, 1983b) and Andreu Mas-Colell (1985), in the third I will motivate and state, in intuitive numerical terms, the required differentiability condition. The fourth section will be devoted to introduce the algebraic theory of difference as a preparation to present, in the fifth section, the conceptual and linguistic apparatus required to provide a geometric theory of preference strength within which differentiability (actually all the usual) conditions can be formulated in an intuitive way. The sixth section contains a development of preference theory within the proposed conceptual apparatus, up to the proof of the existence of a C¹ utility function for the preference relation. The seventh section introduces the differentiability condition and the eight and final one discusses the relevance and importance of having a continuously differentiable utility function. The paper ends with a reflection on the convenience of formulating a non-standard version of Hölder's theory in order to formulate the differentiability condition in an even more intuitive way.

The conditions of Debreu and Mas-Colell

According to Mas-Colell et al. (1995, p. 49) “it is possible to give a condition purely in terms of preferences” implying the existence of a C² utility representation of the same:

Intuitively, what is required is that indifference sets be smooth surfaces that fit together nicely so that the rates at which commodities substitute for each other depend differentially of the consumption levels. (Mas-Colell et al., 1995)

The problem is that it is not at all clear which empirically meaningful (even if idealized) property must the preference relation of a consumer have so that its indifference sets “fit together nicely”. What is worse, C² differentiability is restrictive because some demand functions that are derivable do not come from a C² utility function, as the same authors have noticed (Mas-Colell et al., 1995, p. 95, n. 33). Furthermore, as Debreu (1983a, p. 201) has pointed out, it is enough for the utility function to be C¹ in order to guarantee that the corresponding Walrasian demand function be also C¹. Is it possible to find a condition that can be considered sufficiently natural and general for that purpose? My claim is that it is possible, and I intend to substantiate this claim by means of the intuitive discussion motivating Definition 9.

The differentiability condition has been interpreted by Mas-Colell in terms of the concept of a differentiable manifold, giving rise to the following important result.

[Mas-Colell, 1985]. Let X be an open set of ℝL and R a locally nonsatiated preference relation over X, with connected indifference sets. Then, for k≥1, R is representable by a x1,x2,x3,x4,x5x6,x1′x2′x3′εΩ: utility function with no critical point iff the frontier of R is a Ck manifold. (Cf. Mas-Colell, 1985, p. 64)

In terms of the Gaussian curvature of the indifference curve in each point, Debreu obtained the following result.

[Debreu, 1972]. Let X be an open set of ℝL and R a regular preference relation over X which is monotone, continuous, and such that its frontier is a C2 manifold. If the indifference sets of R do not intersect the frontier of X, then there exists a demand function φ of class C1 iff the Gaussian curvature is different from zero in each point of the indifference surfaces. (Cf. Debreu, 1983a, pp. 194–199)

I would like to conclude the present section with a reflection on the meaning of these conditions. In the first place, the definition of Gaussian curvature proposed by Debreu (taken from Hicks, 1965, Section 2.2) presupposes de facto that the indifference surfaces are already differentiable manifolds (actually, Debreu assumes that they are of class C²), and so the condition only translates the problem to a deeper level. For the question is, precisely, What is the property that must be attributed to the consumer in order to guarantee that the indifference surfaces are differentiable manifolds? In Debreu's definition, the question whether the Gaussian curvature of the manifold is different from zero or not arises once the first problem has been solved. It seems clear that Mas-Colell's condition is just a modified generalization of Debreu's and so analogous considerations apply to it.

Motivation

The problem we are concerned with can be formulated thus: Is it possible to find an (idealized) empirically meaningful property over a (cardinal) preference relation that enables a continuously differentiable utility representation of the same?

In order to discuss this question let us recall that, according to consumer theory, the satisfaction of a given agent at a certain consumption menu (i.e., when the menu constitutes his current consumption) reaches a certain level. This level normally changes as he moves from that menu to another one (i.e., when he changes his consumption from the previous menu to a new one). If his preferences are continuous, to small changes in his consumption menu there correspond small changes in his satisfaction level. Hence, it makes sense to ask: How fast is his satisfaction changing as he moves from one consumption menu to another nearby? Let be x an interior point of Ω, the nonnegative orthant of vector space ℝL, and notice that, since is x an interior point of Ω, it is possible to move away from x a little in any direction without abandoning Ω.² As he moves from x to x + ¿u (say), where ¿ is a small number and u is a unit vector in a fixed direction, his satisfaction may change at different speeds. If ¿ is infinitesimal and his preferences are continuous, the change Δϕ in his satisfaction level is indeed infinitesimal, but the order of this infinitesimal can be different from that of ¿. Moreover, even if Δϕ is of the same order as ¿, it might be of a different order for a different choice of ¿. Sheer differentiability requires not only that Δϕ be of the same order for any choice of ¿, but that the quotients Δϕ/¿ be all infinitely close to one and the same real number. This real number measures the speed at which the satisfaction level changes at x as the agent changes his consumption slightly in the direction of u. The given condition does not guarantee, however, the continuity of the directional derivative [∂ϕ/∂u](x).

Continuous differentiability at a vector x ∈ Ω in the direction of u means that the rate of satisfaction change along u is continuous. What this means is that the rates [∂ϕ/∂u](x1) and [∂ϕ/∂u](x2) approximate each other as menus x₁ and x₂ get closer.

It is indeed impossible to formulate this condition within the conceptual apparatus of ordinal preference theory, or even within the usual apparatus of cardinal preference theory. This is due to the fact that the notion of differentiability requires the comparison of intervals of the same kind but different interpretation. It requires the comparison of lengths of satisfaction intervals with lengths of geometric intervals; i.e., the comparison of the distance in satisfaction between menus x₁,x₂ with the geometric distance ||x1−x2|| among them. The problem is that the difference relation R falls short of providing the linguistic and conceptual resources to make this comparison.

But there is an indirect way of making claims about R, of attributing (idealized) empirically meaningful properties to R, using the geometric analogy involved in the notion of a satisfaction “interval”. Actually, the very notion of difference comparison is built upon this analogy: When the agent compares the difference in satisfaction (for her) between the pair of menus x₁,x₂ and the pair x₃,x₄ she is somehow comparing “distances” between them. That the agent actually thinks or feels that the distance between x₁,x₂ is at least as long as that between x₃,x₄ is expressed by the theoretician in economics by means of the formula ‘x₁x₂Rx₃x₄’. Hence, it is not far-fetched, but rather natural, for the theoretician to represent this distance by means of a geometric entity of the obvious sort: An interval within a straight line. It seems to me that a fully general theory of cardinal preference must be grounded upon such a representation. I will try to show below how such a theory would be like, but it will be convenient to start considering the axioms required for the usual numerical representation of relation R.

The algebraic theory of difference

There is no doubt that every consumer has an idea of the satisfaction differences between the consumption menus among which she has to make a choice. Hence, the comparison of these differences is only natural. As we already indicated, it is usual to express this comparison by means of a difference relation R among pairs of consumption menus (represented by points in the nonnegative orthant Ω of ℝL). The simplest such relation is defined as follows.Definition 1

A difference relation R over Ω is a connected and transitive binary relation over Ω; i.e., a weak order. If R is a difference relation over Ω, we say that 〈Ω × Ω,R〉 is a difference structure.

Write x₁x₂Ex₃x₄ if x₁x₂Rx₃x₄ and x₃x₄Rx₁x₂; x₁x₂Sx₃x₄ if x₁x₂Rx₃x₄ but not x₃x₄Rx₁x₂.

In the interpretation we are interested in here, formula ‘x₁x₂Rx₃x₄’ means that the change from menu x₁ to menu x₂ is preferred by the agent to the motion from x₃ to x₄. The change from one to the other can be an improvement or a worsening for the agent. To fix ideas, if we think of the menus as amounts of money, and the agent prefers to have more money to less, a motion from (say) nine thousand (x₁) to twelve thousand (x₂) dollars is better than one from ten thousand (x₃) to eleven thousand (x₄). But, if the agent is to lose money, it is preferable for her to fall from eleven (x₄) to ten (x₃) than from twelve (x₂) to nine (x₁) thousand dollars. Thus, we shall assume (below) that

It will be necessary to introduce, also, the operation of composition of motions. For instance, we can compose the motion from nine thousand (x₁) to twelve thousand (x₂) with the motion from twelve thousand (x₂) to eight thousand (x₃). The result will be a motion from nine thousand (x₂) to eight thousand (x₃) a net loss of one thousand dollars. I will define below, in general terms, the required composition operation among intervals.

In order to formulate axiomatic conditions over R, say that interval x₁x₂ ∈ Ω² is positive (x₁x₂ ∈ X⁺) iff x₁x₂Sxx for any x, which means that moving from x₁ to x₂ is an improvement for the agent. Interval x₁x₂ is negative (x₁x₂ ∈ X⁻) iff x₂x₁ is positive. x₁x₂ is null (x₁x₂ ∈ X⁰) iff x₁x₂ is neither positive nor negative. It is easy to show, out of the axioms that will be introduced below, that all null intervals are equivalent among them selves; i.e., x₁x₂Ex₃x₄ for any null intervals x₁x₂,x₃,x₄; it can be seen also that if x₁x₂ is null, then x₂x₁ is also null.

A standard sequence of elements of Ω is a set {x_k}_k¿K, where K is an initial segment of the set ℤ+ of positive integers (or the whole set), such that x_k+1x_kEx₂x₁ for all x_k, x_k+1 in the sequence, and it is not the case that x₂x₁Ex₁x₁. The sequence is strictly bounded if there exist x′,x″∈Ω such that x′,x″Sxkx1Sx′,x″ for all k ∈ K.

I will assume that relation R satisfies the conditions specified in the following definition.

Definition 2

Difference structure 〈Ω²,R〉 is an algebraic-difference structure³ iff, in addition to being a weak order, it satisfies the following axioms for every x1, x2, x3, x4, x5, x6, x1′, x2′, x3′ εΩ:

• (1)

  If the motion from x₁ to x₂ is at least as good (bad) as the motion from x₃ to x₄, then the motion from x₄ to x₃, is at least as bad (good) as the motion from x₂ to x₁. In symbols, if x₁x₂Rx₃x₄ then x₄x₃Rx₂x₁.

• (2)

  If the motion from x₁ to x₂ is as good (bad) as the motion from x1′ to x2′, and the motion from x₂ to x₃ is as good (bad) as the motion from x2′ to x3′, then the motion from x₁ to x₃ is as good (bad) as that from x1′ to x3′; i.e., if x1x2Rx1′x2′ and x2x3Rx2′x3′ then x1x3Rx1′x3′.

• (3)

  If x₁x₂ and x₃x₄ are segments such that the motion from x₁ to x₂ is at least as good (bad) as the motion from x₃tox₄, it is possible to find a menu x2′ ∈ Ω, slightly less satisfactory than x₂, or just as satisfactory, such that the motion from x₁ to x2′ matches the motion from x₃ to x₄. In the same token, it is possible to find a menu x1′ ∈ Ω slightly more satisfactory than x₁, or just as satisfactory, such that the difference between x1′ and x₂ matches the difference between x₃ and x₄. In symbols, if x₁x₂Rx₃x₄Rxx, then there exist x1′,x2′∈Ω such that x1x2′Ex3x4 and x3x4Ex2′x2.

• (4)

  Every strictly bounded sequence is finite; i.e., for each strictly bounded standard sequence {x_k}_k¿K of elements of Ω, there exists a number N∈ℤ+ such that k < N for each k ∈ K.

It can be proven⁴ that, for any algebraic structure 〈Ω²,R〉, there exists a real-valued function φ on Ω such that, for all x₁,x₂,x₃,x₄ ∈ Ω

ϕ, which is a utility function, is unique up to a positive linear transformation; i.e., if ϕ′ is another such utility function, then there are real constants α,β,α > 0, such that ϕ′ = αu+β This means that ϕ is, indeed, a cardinal utility function.

The geometric theory of difference

It is nearly impossible to formulate differentiability conditions over R within the language and conceptual apparatus of the algebraic theory of difference. What is required is a certain “intermediate” language. In order to introduce this language, let us suppose that a good straight Euclidean line is given in its purity. Following Hölder (1996, 1997), I shall assume that intervals within this straight line are of two kinds, such that any interval is of one and only one kind.

Intervals of the same kind are called “of the same direction”,⁵ and intervals of different kinds are called of opposite direction. The intervals AB and BA are always of opposite direction. Let the intervals of one kind be called “intervals of the first direction” and the fact that AB is an interval of the first direction be expressed as A≻B or B≻A (Hölder 1997, p. 346).

Equality (congruence) of intervals AB and A′B′ will be expressed as AB≐A′B′. Clearly, ≐ is an equivalence relation over the set Λ of all intervals within the straight line.

Furthermore, we assume that points and intervals satisfy Hölder's axioms up to the definition of interval numbers (see 1997, §23, p. 351, equations 53 and 54). Hence, we take for granted that there are arbitrarily designated points N and E, with N≺E such that interval NE is taken as unit. We will denote interval NE eventually as 1→.

On top of ≐, I will use symbols

, ⋖, or their counterparts

and ⋗, to express the congruence comparisons among intervals. The sum of intervals (for its definition, see Hölder, 1997, p. 347) will be denoted by ⊕ (Hölder uses symbol +). Notice that what Hölder (1996) calls ‘magnitudes’ are line intervals in the interpretation intended here. This same interpretation is developed by Hölder (1997).

It is possible, and it will turn out to be convenient, to express the properties that are attributed to R in terms of relations among geometric intervals within the given Euclidean straight line. What this means is that we, as theoreticians, can represent the comparison of the differences felt by the consumer, expressed by symbol ‘R’, by means of comparisons among intervals in Λ. My proposal is to build the theory of relation R by means of these comparisons, trying to express intuitive, empirical (idealized) properties of R in terms of such comparisons.

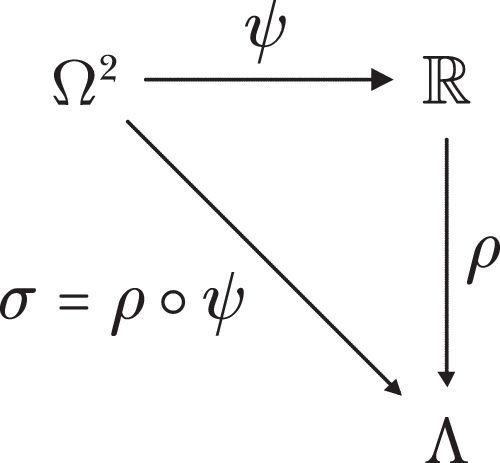
To that end, let me to introduce the function σ:Ω2→Λ, as an application that assigns to each satisfaction interval x₁x₂ a line interval whose length is intended to represent the distance that the agent associates to x₁x₂ (how “far” is x₁ from x₂ in terms of satisfaction), and whose direction is intended to represent whether the motion from x₁ to x₂ would be an improvement, a worsening, or indifferent for the agent. In particular, σ will assign to any interval xx in the diagonal the null line interval, which of course does not exist but we can create by a convenient fiat.

As I just said, it is not merely the distance among menus what has to be considered, but also the direction of the motions and, moreover, also the composition of motions. If x₁x₂ ∈ X⁺, the agent perceives the (actual or potential) change from x₁ to x₂ as an improvement, and that from x₂ to x₁ as a worsening. Yet, interval σ(x₁x₂) is congruent to σ(x₂x₁), which means that they have the same length, the difference being that they are of opposite directions. The composition of motions can be defined as follows.Definition 3

Let 〈Ω²,R〉 be a difference structure. For any menus x₁,x₂,x₃ ∈ Ω, define operation ∘:Λ2→Λ as it is specified in Table 1.

Table 1.

Definition of composition of motions.

Table of motion compositions
Case	σ(x1x2)	σ(x2x3)	Directions	σ(x1x2)∘σ(x1x3)
1	AB	BC	A≺B≺C	AC
2	AB	CB	A≺C≺B	AC
3	BA	BC	B≺A≺C	AC
4	BA	BC	B≺C≺A	CA
5	AB	CB	C≺A≺B	CA
6	BA	CB	C≺B≺A	CA

I introduce formally the concept of a geometric representation by means of the following definition.

Definition 4

Let 〈Ω²,R〉 be a difference structure. A function σ:Ω2→Λ is a geometric representation of R iff it satisfies the following conditions for every x,x₁,x₂,x₂ and x₄ in Ω:

• (1)

  σ(x₁x₂) is an interval of the first direction iff x₁x₂ is positive.

• (2)

  σ(x₁x₂) is an interval of the second direction iff x₁x₂ is negative.

• (3)

  σ(x₁x₂) is the null interval iff x₁x₂ is null.

• (4)

  x₁x₂Px₃x₄ iff either both x₁x₂ and x₃x₄ are positive or null and σ(x1x2)⋗σ(x3x4); or both x₁x₂ and x₃x₄ are negative and σ(x1x2)⋖σ(x3x4); or σ(x₁x₂) is of the first direction, or null σ(x₃x₄), and is negative.

• (5)

  x₁x₂Ex₃x₄ iff both σ(x₁x₂) and σ(x₃x₄) are of the same direction and σ(x1x2)≐σ(x3x4).

• (6)

  σ(x1x3)≐σ(x1x2)∘σ(x2x3).

• (7)

  If AB≐σ(x1x2) for some (x₁x₂), then, for any interval CD

  
  AB (or CD
  
  AB), there exist x1′,x2′∈Ω such that σx1x2′≐CD≐σx1′x2.

It is easy to see that 〈Λ,∘〉 is a group with the null interval as identity element. The following result is immediate, as it is based upon the existence of the numerical representation (Fig. 1).

Fig. 1.

σ is the composition ρ∘ψ:Ω2→Λ.

Theorem 1

If 〈Ω²,R〉 is an algebraic difference structure then there exists a geometric representation σ:Ω2→Λ of R.

Proof

Consider any numerical representation ϕ of R. If is x₁x₂ positive, ψ(x1x2)=ϕ(x2)−ϕ(x1) is a positive real number and so there are points A, B on the line such that A≺B and ψ(x₁x₂) is equal to the interval number (cut) [AB:1→]. Let ρ be the application mapping [a:1→] into a, and define σ as follows (cf. Hölder 1997, pp. 351–352):

Clearly, by construction, σ(x₁x₂) is of the first direction iff x₁x₂ is positive; of the second iff it is negative; and null iff it is neither. Since AB≐BA, notice that σ(x1x2)≐σ(x2x1).

Suppose that x₁x₂ and x₃x₄ are nonnegative and let A, B, C, D, be points such that ψ(x1x2)=[AB:1→] and ψ(x1x2)=[CD:1→]. Then we have

If both x₁x₂ and x₃x₄ are negative, x₂x₁ and x₄x₃ are positive and we have

Given x₁x₂Px₃x₄ when the intervals are of opposite signs, the case when x₁x₂ is negative and x₃x₄ is nonnegative is excluded because in such a case we would have

and so x₁x₂Px₃x₄. Hence, the only case remaining is when x₁x₂ is nonnegative and x₃x₄ is negative.

It has to be shown that σ(x1x3)≐σ(x1x2)∘σ(x2x3). I refer the reader to Table 1, as I shall consider case by case. Keep in mind that it is always true that

(cf. Hölder, 1996, eqn. 19, p. 243). Also, for every x₁,x₂,x₃ ∈ Ω,

In all cases, let ψ(x1,x2)=[AB:1→] and ψ(x2,x3)=[BC:1→]. It will suffice to show that [AC:1→]=ψ(x1,x3)

Case 1: A≺B≺C. We have

and so

Case 2: A≺B≺C. We have

and so

Case 3: B≺A≺C. We have

and so

Case 4: B≺C≺A. We have

or

and so

Case 5: C≺A≺B. We have

or

and so

Case 6: C≺B≺A. We have

and so

Hence, at any rate, σ(x₁x₂) = AC and so axiom (6) of Definition 4 is shown to be satisfied.

Finally, assume that x₁x₂Rx₃x₄ and let [AB:1→]=ψ(x3x4), so that σ(x₃x₄) = AB. By axiom 3 of Definition 2, there exist x1′ and x2′ such that x1x2′Ex3x4Ex1′x2 Setting CD≐σx1x2′≐σx1′x2, condition 7 of Definition 4 is satisfied.

□

We have shown the existence of a geometric representation of an algebraic difference structure. The point of having this representation is that it provides an adequate conceptual and linguistic apparatus to express the differentiability condition we are looking for. Moreover, it can be shown that the existence of a geometric representation for a difference structure D=〈Ω2,R〉 guarantees that D is an algebraic difference structure. For we can express the properties defining the concept of an algebraic difference structure purely in terms of the geometric representation, and show that the structure has these properties out of the axioms regulating σ. The wages of doing this is that we can also express in terms of the geometric representation all the properties of an algebraic difference structure, plus the required differentiability condition, and establish in this way the existence of a C¹ numerical representation of R.

I will prove in what follows that the existence of a geometric representation of difference structure D implies that D is an algebraic difference structure. The following four lemmas, all of which share the assumption that such representation exists, are devoted to this end. I will introduce later the differentiability condition. For the sake of brevity, from now on, that an interval is of the first direction will be expressed by saying that “it is I”; and that “it is II” if it is of the second direction. The null interval will be denoted as 0→Lemma 1

If x₁x₂Rx₃x₄ then x₄x₃Rx₂x₁.

Proof

Suppose that both x₁x₂ and x₃x₄ are in X+∪X0. This means that both σ(x₁x₂) and σ(x₃x₄) are I or null, with σ(x₁x₂)

σ(x₃x₄) Hence, σ(x₂x₁) and σ(x₄x₃) are II or null, with σ(x₂x₁)

σ(x₄x₃). It follows that x₄x₃Rx₂x₁.

If both are II, x₁x₂Rx₃x₄ implies that x₁x₂

x₃x₄ and that x₂x₁ and x₃x₄ are I. Hence, again, x₄x₃Rx₂x₁.

Notice that x₁x₂Rx₃x₄ implies that x₃x₄ cannot be I or null if x₁x₂ is II. Hence, the only remaining case is when x₁x₂ is I or null, and x₃x₄ is II. In this case, x₂x₁ is II or null and x₄x₃ is I. It follows that x₄x₃Px₂x₁ and so, finally, x₄x₃Rx₂x₁.

□Lemma 2

If x1x2Rx1′x2′ and x2x3Rx2′x3′ then x1x3Rx1′x3′.

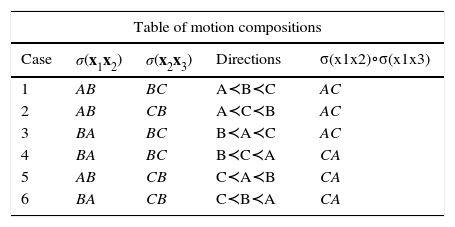
Proof

The proof of this lemma is easy but laborious, since there are several cases to be considered. Excluding the cases precluded by the hypothesis of the proposition, there are still nine cases to consider. They are given in Table 2. The proof is interesting because it yields more insight into the meaning of the geometric representation.

Table 2.

Feasible cases in Lemma 3.

Feasible cases in Lemma 3
Case	σ(x1x2)	σ(x2x3)	σx1′x2′	σx2′x3′	σ(x1x3)	σx1′x3′
1	I or null	I or null	I or null	I or null	I or null	I or null
2	I or null	I or null	I or null	II	I or null	any
3	I or null	I or null	II	I or null	I or null	any
4	I or null	I or null	II	II	I or null	I
5	I or null	I	I or null	II	any	any
6	I or null	I	II	II	any	II
7	II	I or null	II	I or null	any	any
8	II	I or null	II	II	any	II
9	II	II	I	II	II	II

Case 1 is straightforward because all intervals are I or null and so x1x2Rx1′x2′, and x2x3Rx2′x3′ is tantamount to σ(x₁x₂)

σx1′x2′ and σ(x₂x₃)

σx2′x3′. We have

Hence, by Hölder's (1996, p. 238) conclusion 2,

or, equivalently,

In case 4 there is nothing to prove because σ(x₁x₃) is I or null and σx1′x3′ is II.

In cases 2 and 3, σx1′x3′ can be I or null, or II. When it is II, we are done, because σ(x₁x₃) is I or null. When σx1′x3′ is or null, we have

if σx2′x3′0→, or

if σx1′x2′0→

In case 5 we have σ(x₁x₂)

σx1′x2′ and σ(x₂x₂)

σx2′x3′. We have five subcases, setting B = B′ (see Fig. 2).

Fig. 2.

Both AB and A′B′ are I (or null): A≺A′≺B=B′.

Subcase (5.1). A≺A′≺C′≺C≺B=B′. In this case we have that both ψ(x₁x₃) and σx1′x3′ are I or null with

It follows that x1x3Rx1′x3′.

Subcase (5.2). A≺C′≺A′≺C≺B=B′.

Subcase (5.3). A≺C′≺C≺A′≺B=B′.

Subcase (5.4). C′≺A≺C≺A′≺B=B′.

In cases (5.2)–(5.4), AC≐σ(x1x3) is I or null, whereas A′C′≐σx1′x3′ is II. It is immediate that x1x3Rx1′x3′ in these cases.

Subcase (5.5). C′≺C≺A≺A′≺B=B′. In this final case, both AC≐σ(x1x3) and A′C′≐σx1′x3′ are II but σ(x₁x₃)

σx1′x3′, and so x1x3Rx1′x3′.

Case 7 is entirely analogous to case 5.

In cases, 6 and 8 σ(x₁x₃) can be I, null, or II. If it is I or null, we are done. If σ(x₁x₃) is II, in case 6 we have C≺A≺B and C′≺B′≺A′ with

Thus, x1x3Rx1′x3′. An analogous argument leads to the same conclusion in case 8.

Finally, in case 9, all segments are II and we have both σ(x₁x₂)

σx1′x2′ and σ(x₂x₃)

σx2′x3′ Hence, σx1′x3′

σ(x₁x₃) and so x1x3Rx1′x3′.

□Lemma 3

if x₁x₂Rx₃x₄, then there exist x1′,x2′∈Ω such that x1x2′Ex3x4 and x3x4Ex1′x2.

Proof

Assume that x₁x₂Rx₃x₄. If x₁x₂Ex₃x₄, there is nothing to prove, and so we may suppose that x₁x₂Sx₃x₄.

Let CD≐σ(x3x4). By axiom 7 of Definition 4, there exist menus x1′,x2′ such that σx1′x2≐CD≐σx1x2′. It follows that x1′x2Ex3x4Ex1x2′.

□Lemma 4

Every strictly bounded sequence is finite.

Proof

Let (x_k) be a bounded standard sequence and x,x′ ∈ Ω be such that xx′Sx₁x_k for all x_k in the sequence. Let AB = σ(x_kx_k+1) and CD = σ(xx′). Then CDkAB for every k such that x_k is in the sequence. But, (x_k) if were not finite, there would be one such positive integer k with kABCD (cf. Hölder, 1996, p. 239).

□

Using the previous lemmas and Theorem 1, we can establish the following proposition.Theorem 2

There exists a geometric representation of a difference structure D iff D is an algebraic-difference structure.

Hence, the existence of a geometric representation of D is necessary and sufficient for D to be an algebraic-difference structure, and indeed implies the existence of a numerical representation of D. Yet, as the reader shall presently see, the geometric language has more expressive power than the algebraic one.

The theory of preference

A preference relation among consumption menus in Ω can be defined out of the difference relation. As we said, if x₁x₂ is I or null, x₂ is weakly preferred by the agent to x₁. We may express this preference relation by means of symbol ≻˜.Definition 5

For consumption menus x₁,x₂ in Ω, say that x₁ is weakly preferred to x₂, and write x1≻˜x2, iff x₂x₁ is I or null.

The kin notions of strict preference and indifference, denoted by symbols ≻ and ∼, are defined as usual. Clearly, ϕ as characterized by the numerical representation of the difference relation is a utility function representing ≻˜, for we have

Actually, all the properties that have been attributed to the preference relation in microeconomic textbooks can be defined in terms of relations among geometric intervals within the given Euclidean straight line, just as we did with the properties of the difference relation. This shows that the language of intervals, being more powerful than the usual language used in economic theory, is a suitable way of expressing the theories of difference and preference. I hope the reader will find natural this way of expressing the properties of R (some usual ones are given below), particularly the one implying differentiability. We keep assuming that 〈Ω²,R〉 is an algebraic difference structure.

Definition 6

≻˜ is monotonic iff, for all x₁x₂ ∈ Ω, x₁ ≥ x₂ implies that σ(x₂x₁) is an interval of the first direction.

Definition 7

≻˜ is continuous at x₀ ∈ Ω iff, for every interval a∈Λ, as small as you wish, there is a δ > 0 such that x₀ + h ∈ Ω and σ(x0(x0+h))a whenever h<δ.

Definition 8

≻˜ is strictly convex iff, for every α ∈ [0,1] and menus x1,x2∈Ω,x1≠x2,αx1+(1−α)x2∈Ω, and σ(αx₁ + (1 − α)x₂) is of the first direction whenever σ(x₁x₂) is of the first direction.

The great advantage of the language of intervals over the languages typically used to formulate preference theories is that it provides resources by means of which we can also express natural, intuitive differentiability conditions for the preference relation. We turn now to these.

The empirical meaning of differentiability

Derivates are, and cannot be, but ratios between homogeneous magnitudes. That is why it is necessary to represent satisfaction differences by means of intervals within the same geometric space in which distances among consumption vectors are represented. Notice that there is a natural mapping τ from the segments within Ω into Λ, namely τ(x₁x₂) is (the equivalence class of) that interval in Λ whose Euclidean norm is x1−x2. Notice that the cut [τ(x1x2):1→] is precisely x1−x2. Using Hölder's interval numbers (cuts) or measure-numbers (Hölder, 1996, p. 242), as we did in the proof of Theorem 1, it is possible to map the Ω-segments into Λ. In particular all segments of length 1 are mapped by τ into segment 1→≐NE in Λ.

Recall that a real-valued function defined on an open subset D of ℝL is continuously differentiable at x ∈ D iff all its partial derivatives exist throughout a neighborhood of x and are continuous at x. Hence, our aim is to find conditions over the satisfaction differences (or their proxies in Λ) implying the existence of a function ϕ fulfilling these requirements.

The empirical meaning of the differentiability condition is that the agent's tastes have a certain sort of stability. That is to say, the rate of change of the agent's satisfaction is almost constant within a small vicinity of any consumption menu x and, at any rate, it varies continuously in any given direction. This means that, within the infinitesimal neighborhood of x (within the “halo” or “monad” of x) the rate of change of satisfaction of the agent is “almost” constant. This implies, in particular, that in an arbitrarily given direction, determined by the unit vector u, the ratio of the satisfaction difference between any two menus to their physical difference is “almost” constant. How can this condition be expressed in a formal way?

Let x be an arbitrary point in the interior of Ω and u a unit vector in a given fixed direction. Following Newton's conception of the theory of proportions, the ratio of one magnitude to another of the same kind is to be expressed as a real positive number,⁶ and so the required condition is that, for any infinitesimal number ¿, the ratio of the satisfaction segment σ(x(x + ¿u)) to the quantity segment τ(x(x + ¿u)) be infinitely close to a certain positive real number which we can conveniently identify with the cut [Δ(x):1→]. Naturally, we want to identify the cut [Δ(x):1→] with a certain directional derivative. Hence, the condition we are looking for can be formulated, in the language of intervals, in the following way.

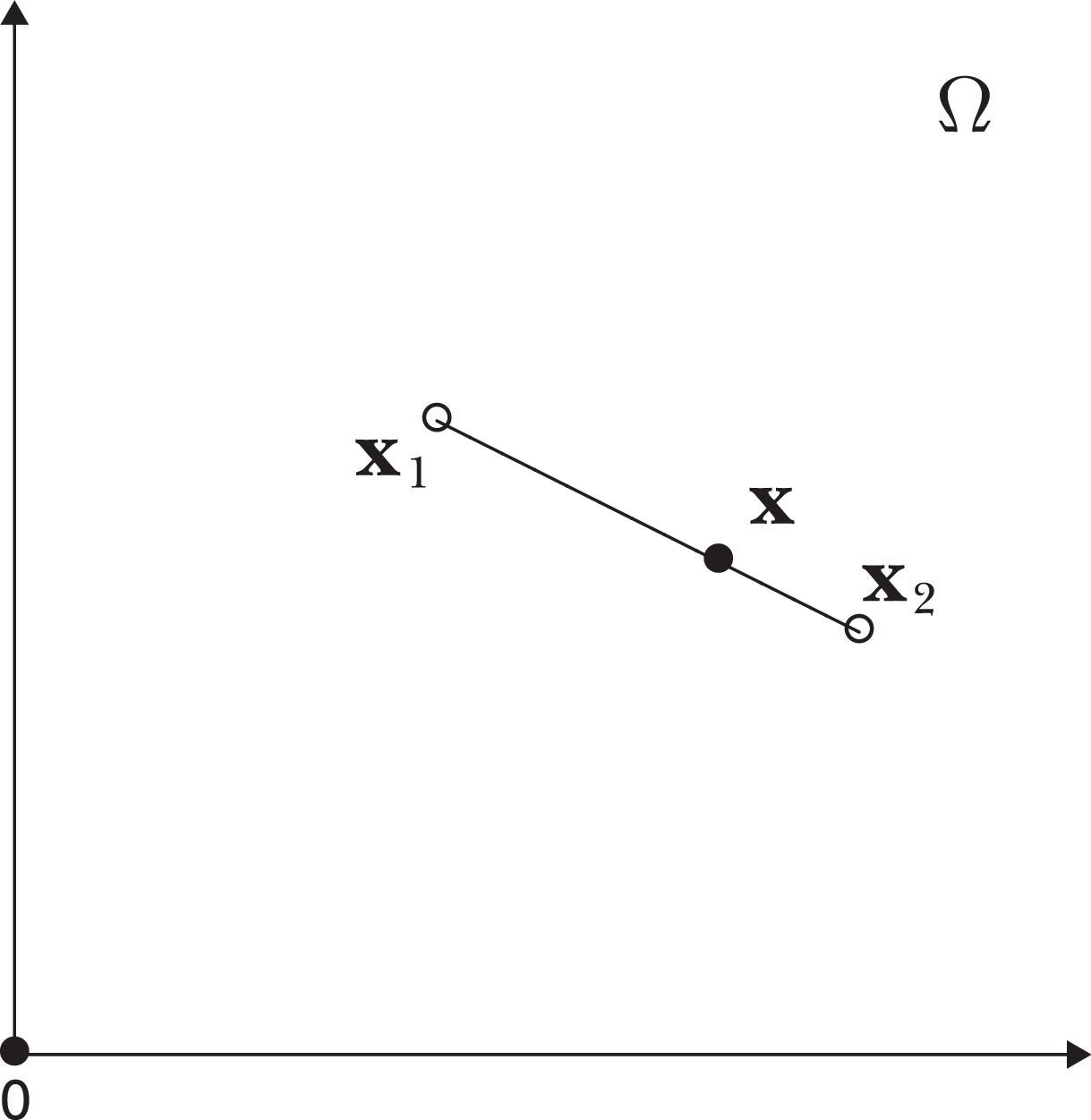
If x₁,x₂ are menus in Ω, let us denote with (x₁,x₂) the set

Notice that the points in (x₁,x₂) are interior points of Ω whenever at least one of the two points x₁,x₂ is an interior point (see Fig. 3).Definition 9

≻˜ is uniformly differentiable or smooth on (x₁, x₂) if there is a function

such that, for any menus x₃,x₄ ∈ (x₁,x₂), any x ∈ (x₃,x₄) and ¿ > 0, there exist positive integers μ,v,μ′,v′,μ″,v″ and δ > 0 such that, whenever h<δ with x+h∈(x1,x2), |μ″/v″−μ/v|<ε and

if

or

if

We say that ≻˜ is uniformly differentiable iff it is uniformly differentiable on every set (x₁,x₂) with at least one of x₁,x₂ being an interior point of Ω.

Theorem 3

If ≻˜ is uniformly differentiable, then there exists a utility function representing ≻˜ which is continuously differentiable in the interior of Ω.

Proof

We will show, first, that there is a uniformly differentiable function ϕˆ on any open interval. Let (x₁,x₂) be any such interval, x₃,x₄ any menus in (x₁,x₂) with x₃ ≠ x₄, x any menu in (x₃,x₄) and ¿ any positive number, as small as you wish.

Fig. 3.

The segment (x₁, x₂) and a point x within it. Notice that the extremes, x₁, x₂, do not belong to the segment.

It follows that there exist positive integers μ,v,μ′,v′,μ″,v″ and δ > 0 such that, whenever h<δ with x|+h∈(x1,x2), |μ″/v″−μ/v|<ε and

if

or

if

Assume that

let ψ(x1x2)=[σ(x1x2):1→], and choose ϕ with ϕ(x₂) − ϕ(x₁) = ψ(x₁x₂). Since

for any segment a∈Λ (cf. Hölder, 1996, p. 244),

If we let ϕˆ be the function defined by condition

it follows that

with

Hence,

The assumption that

leads, by an analogous argument, to

Thus, at any rate,

This establishes that ϕ is uniformly differentiable on the interval (x₁,x₂) (with derivative ϕˆ(x) at point x) and, therefore, the derivative of any point within the interval is continuous.

Consider now, for any interior point x₀ of Ω, in particular, intervals of the form (x0−αel,x0+αel)⊂Ω where e_l is the canonical vector in direction l. The derivative of ϕ at x₀ is then nothing but the partial derivative of ϕ with respect to x_l evaluated at x₀:

Since this derivative is continuous for every l (l = 1, …, L), we may conclude that ϕ is continuously differentiable at x₀. As x₀ was arbitrarily chosen, we may conclude that ϕ is continuously differentiable in the interior of Ω.

□

New foundations of preference theory

The previous argument shows that we can provide a new conceptual apparatus for preference theory by means of which all the usual properties of the preference relation, as well as the differentiability condition, can be expressed. Is it possible to find another conceptual apparatus that allows the expression of some differentiability condition? That is unlikely because differentiability requires the comparison of satisfaction distances with quantity distances within the same space. At any rate, it is incumbent upon those who believe that it is feasible to do so to produce such an apparatus.

By Theorem 2, a difference structure D is an algebraic-difference structure iff D admits a geometric representation. Hence, the new conceptual apparatus for preference theory can be briefly summarized as follows. I use the term ‘geometric-difference’ to avoid confusion.Definition 10

D is a geometric-difference structure iff there exist Ω, R and σ such that

• (1)

  D=〈Ω2,R,σ,Λ〉;

• (2)

  〈Ω²,R〉 is a weak order;

• (3)

  σ:Ω2→Λ is a geometric representation of R.

As pointed out in section ‘The theory of preference’, the preference relation ≻˜ can be defined in terms of σ and all the properties usually attributed to it can be expressed using the language of geometric intervals (see the examples there). The novelty — as I have just shown — is that the smoothness condition can also be so expressed. Thus, using the notion introduced in Definition 9 we can define the concept of a smooth preference structure.

Definition 11

is a smooth preference structure iff there exist Ω and ≻˜ such that

• (1)
  

• (2)

  ≻˜ is a preference relation induced by a geometric-difference structure;

• (3)

  ≻˜ is smooth.

By virtue of Theorem 3, there is a continuously differentiable utility function ϕ:Ω→ℝ representing ≻˜. The relevance and usefulness of having such a function lies in that it allows the application of non-linear programming techniques in order to find the optimal points.

It would be desirable, because the empirical condition would be even more intuitive, to formulate entirely the smoothness condition in non-standard language, by means of the notion of an infinitesimal segment, as intimated in the informal discussion preceding the formal introduction of the condition. That is entirely feasible because Euclid's Archimedian axiom is logically independent of the rest,⁷ but it would require a complete reformulation of Hölder's theory, as well as of the theory of algebraic-difference measurement.