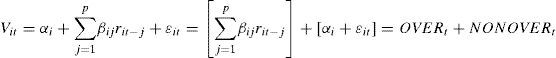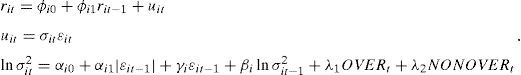Exceso de confianza como determinante de la volatilidad en mercados accionarios latinoamericanos

Resumen

Proponemos un modelo EGARCH con una distribución t de Student estandarizada para las innovaciones. El modelo se usa para describir el comportamiento de la volatilidad de las series de rendimientos de los índices bursátiles para 6 economías latinoamericanas. A la ecuación de la varianza condicional se le agregan factores que representan el exceso de confianza de los inversionistas con lo que se busca determinar si este sesgo cognitivo afecta la volatilidad de los rendimientos. Los resultados sugieren que: 1) Las series de rendimientos analizadas pueden describirse adecuadamente con el modelo propuesto; 2) se cumple la característica de efecto apalancamiento en las series de rendimientos de Chile, Colombia, México y Perú; 3) en general se puede afirmar que el exceso de confianza es un determinante de la volatilidad; y 4) en periodos de crisis se pierde la confianza en los mercados financieros, principalmente el mexicano.

Abstract

We propose an EGARCH model with a standardized Student's t distribution for the innovations. The model is used to describe the behavior of the volatility of 6 Latin American stock indices returns. In the conditional variance equation we incorporated factors that represent investor's overconfidence to determine whether this cognitive bias affects the volatility of returns. The results suggest that: 1) The return series analyzed can be adequately described by the proposed model, 2) the property of leverage effect is observed in the return series, of Chile, Colombia, Mexico and Peru; 3) in general we can say that overconfidence is a determinant of volatility, and 4) in times of crisis the confidence is lost in financial markets, mainly the Mexican.

Introducción

La modelación de las series de tiempo aplicadas a las finanzas es una herramienta que permite describir el comportamiento financiero por lo que se convierte en una herramienta útil para la toma de decisiones ya sea de inversión, valuación de activos o administración de riesgos. Las características propias de este tipo de series las hacen muy volátiles por lo que es importante contar con instrumentos para describir esta volatilidad. Generalmente las series de rendimientos financieros presentan curtosis excesivas (comparados con una distribución normal), clústeres de volatilidad y efecto apalancamiento. Todas estas características pueden describirse con los modelos de la familia ARCH desarrollados por Engle (1982).

Por otro lado, las decisiones financieras pueden afectar o ser afectadas por componentes psicológicos o cognitivos. La disciplina de finanzas cognitivas es un campo del conocimiento que apenas comienza a desarrollarse, en el que se estudia cómo los fenómenos psicológicos afectan el comportamiento financiero y, por lo tanto, uno de sus objetivos es investigar el efecto de los sesgos psicológicos o cognitivos sobre las variables financieras.

El exceso de confianza en los inversionistas es un sesgo cognitivo que puede afectar a la volatilidad de los rendimientos accionarios convirtiéndolo en una posible causa de las crisis financieras como la del 2008 y cuyos efectos seguimos padeciendo.

En este documente se busca describir el comportamiento de los rendimientos de los mercados accionarios y principalmente de su volatilidad en la región de Latinoamérica mediante un modelo completo que contempla una ecuación de la media, con un modelo autorregresivo para los rendimientos y el uso de un modelo Exponential Autoregressive Conditional Heteroskedasticity (EGARCH) para la varianza de los rendimientos pero incorporando en esta ecuación de la varianza condicional el factor de exceso de confianza como determinante de la volatilidad. También se busca determinar si dicho exceso de confianza se mantiene en los periodos de crisis en los que, podría pensarse, los inversionistas tienden a rehuir de los mercados financieros.

El documento está organizado de la siguiente manera. En la segunda sección se hace una breve revisión de la literatura aplicada a la descripción de la volatilidad de las series financieras mediante modelos GARCH en países latinoamericanos así como la incorporación del sesgo de exceso de confianza en dichos modelos. La tercera sección está dedicada a explicar la metodología empleada para este estudio mediante la descripción del modelo EGARCH y cómo se va a trabajar la variable volumen de operaciones para explicar el exceso de confianza. La siguiente sección describe la aplicación de dicha metodología a los 6 índices bursátiles latinoamericanos y los resultados a los que se llega, para terminar con las conclusiones.

Revisión de la literatura

Este trabajo se basa en la estimación econométrica de la volatilidad de los rendimientos de los índices accionarios latinoamericanos empleando modelos de la familia ARCH desarrollados inicialmente por Engle (1982) y generalizados por Bollerslev (1986). Estos modelos permiten describir las características típicas de las series de tiempo financieras como son el exceso de curtosis, la asimetría, los clústeres en volatilidad y el efecto apalancamiento, entre otros. Entre los trabajos que han empleado especificaciones de la familia ARCH a series de tiempo latinoamericanas se encuentra el de Lorenzo-Valdés y Ruiz-Porras (2012a) que desarrollan un ejercicio comparativo de modelación de los rendimientos de los activos bursátiles de México mediante ajustes con modelos Threshold Generalized Autoregressive Conditional Heteroskedasticity (TGARCH) y EGARCH. Los mismos autores (Lorenzo-Valdés y Ruiz-Porras, 2012b) desarrollan un estudio similar para la volatilidad de los rendimientos cambiarios en países de Latinoamérica. De la misma forma Durán-Vázquez et al. (2013) aplican modelos GARCH e inducen un comportamiento asimétrico en la distribución de las innovaciones y lo aplican a índice del mercado accionario mexicano.

También existen algunos autores como Bonilla y Sepulveda (2011) que critican estos modelos para describir el comportamiento de los rendimientos bursátiles de economías emergentes.

A los modelos de tipo ARCH se les puede incorporar aspectos psicológicos que afectan los rendimientos de los activos financieros y propiamente su volatilidad. Shefrin (2009) presenta evidencia de cómo las «trampas psicológicas» o sesgos cognitivos, como el exceso de confianza, tuvieron un papel crucial en la generación de la crisis financiera de 2008. La incertidumbre, propia de los momentos de crisis, amplifica los sesgos cognitivos en la valoración de los activos de mercado y estos, como lo muestra Kumar (2009), son aprovechados por los inversionistas mejor informados. Avgouleas (2008) se apoya en estos factores psicológicos para sugerir un marco regulatorio más efectivo en la supervisión financiera.

Uno de estos sesgos cognitivos es el exceso de confianza, factor que muchos consideran afecta la volatilidad de los activos financieros como lo sugieren los siguientes autores.

Michailova y Schmidt (2011) encuentran evidencia empírica de la relación entre el exceso de confianza del mercado y la aparición de «burbujas» en los precios accionarios.

Gervais y Odean (2001) desarrollan un modelo de mercado de varios periodos que describe el proceso en que los inversionistas muestran exceso de confianza debido a su capacidad de aprendizaje adquirido a través de sus éxitos y fracasos. Se estudia cómo el exceso de confianza determina los patrones en el volumen de operaciones, la volatilidad de los precios y los precios esperados.

Lee (2006) establece que los inversionistas reaccionan de manera exagerada ante la información tangible pero su reacción ante la información intangible es retardada. Sus hallazgos concuerdan con los modelos que incorporan el exceso de confianza de los inversionistas en su información privada.

Odean (1998) muestra que el exceso de confianza provoca que los mercados no reaccionen a la información relevante pero que sí lo hagan ante información no relevante. Para medir el exceso de confianza, este último autor utiliza el volumen de operaciones esperado. De la misma forma Lee y Rui (2001) relacionan el exceso de confianza con el volumen de operaciones y encuentran evidencia empírica, utilizando datos de EE. UU., Japón y Reino Unido, de que el volumen de operaciones y los rendimientos están determinados por componentes no informacionales y componentes informacionales. De la misma manera Chuang y Lee (2006) descomponen el volumen de operaciones en 2 componentes, uno debido al exceso de confianza y el segundo a otros factores. El objetivo de los autores es determinar el impacto que tiene el exceso de confianza sobre el volumen de operaciones independientemente que este último dependa de otras variables que no determinan en su estudio. Los autores encuentran evidencia empírica de que las ganancias del mercado aumentan el exceso de confianza de los inversionistas y por lo tanto se comportan de forma más agresiva en los siguientes periodos y este exceso de confianza contribuye a la excesiva volatilidad observada. Asimismo, al existir exceso de confianza, los inversionistas subestiman el riesgo e invierten en activos más riesgosos.

Abbes (2012) explora la relación del sesgo por exceso de confianza y la volatilidad excesiva presentada durante la crisis financiera en países desarrollados y emergentes. Emplea un modelo EGARCH y encuentra que la volatilidad condicional está relacionada positivamente con el volumen de operaciones causado por el sesgo de exceso de confianza, aunque durante el periodo de crisis no existe tal relación debido a la pérdida de confianza de los inversionistas.

Metodología

El exceso de confianza puede afectar los mercados financieros ya que el volumen de operaciones se incrementa cuando existe un exceso de confianza en los agentes financieros (Odean, 1998).

Chuang y Lee (2006) proporcionan una metodología que consiste en descomponer el volumen de operaciones en 2 componentes, el primero relacionado al exceso de confianza (OVER) y el segundo a otros factores (NONOVER), es decir:

donde V_it es el volumen de operaciones sin tendencia del país i en el periodo t, r_it el rendimiento continuo diario del índice respectivamente calculado a partir del precio de cierre diario del índice accionario del país i en el periodo t, P_it como:

Una de las medidas de riesgo más utilizada en finanzas es la volatilidad. Se puede definir como la desviación estándar condicional y se presenta, generalmente, en forma anualizada. Esta volatilidad es el proceso estocástico utilizado para describir la dispersión de los rendimientos continuos (en logaritmos). Existen muchas aplicaciones de la estimación y predicción de la volatilidad entre las que se encuentran la elección de portafolios con el mínimo riesgo, la estimación del valor en riesgo, la cobertura de portafolios y la valuación de activos como las opciones financieras.

La volatilidad es una medida que no es observable; se tiene que emplear un modelo para su estimación y predicción. No existe una volatilidad «verdadera», siempre depende del modelo utilizado.

La inclusión de la volatilidad en los modelos permite describir ciertas características típicas de las series de tiempo financieras como son: i) la probabilidad de tener rendimientos extremos superiores a los que se tendría si se supone una distribución normal, en este caso la distribución de probabilidades de los rendimientos presenta colas más anchas que una distribución normal, conocido como exceso de curtosis; ii) el efecto apalancamiento, cuando existe una correlación negativa entre el rendimiento y la volatilidad en el sentido de que cuando el rendimiento baja, la volatilidad aumenta y iii) la relación temporal de la volatilidad que forma clústeres, es decir, la volatilidad en un periodo depende de la volatilidad en periodos anteriores.

Algunas de estas características se pueden describir con diferentes modelos de la familia ARCH, desarrollados inicialmente por Engle (1982) y generalizados por Bollerslev (1986).

Pueden ser utilizados modelos de volatilidad condicional de diferentes tipos. Entre otros se encuentran TARCH, PARCH y ACGARC. El objetivo de estos modelos es que describan adecuadamente la volatilidad y las características típicas de las series de tiempo financieras. En particular existen 2 modelos que describen todas las características descritas anteriormente: el modelo TGARCH introducido por Zakoian (1994) y por Glosten, Jagannathan y Runkle (1993) en forma independiente, y el modelo EGARCH que se utilizará en este estudio, propuesto por Nelson (1991). La justificación de la utilización de este modelo es su capacidad de describir las características típicas de los rendimientos accionarios además de proporcionar un excelente ajuste basado en sus residuales y residuales al cuadrado y no presentar restricciones de no negatividad en sus parámetros. Esto último presenta complicaciones en los otros modelos que están restringidos generalmente a parámetros positivos.

En este trabajo se estimará la volatilidad diaria de los rendimientos en logaritmo (tasa de crecimiento continuo de los precios) de los índices accionarios de 6 países latinoamericanos (Argentina, Brasil, Chile, Colombia, México y Perú). Y se tomarán como determinantes los componentes del volumen de operaciones OVER y NONOVER.

El modelo completo utilizado es un AR(1)-EGARCH(1,1) para los rendimientos del índice accionario del país i, incluyendo los componentes del volumen de operaciones como variables independientes en la ecuación de la volatilidad:

Las perturbaciones ¿_it se distribuyen como una t de Student estandarizada y se estiman los grados de libertad (ν). El modelo presenta una ecuación para los rendimientos que, en este caso, se define como un proceso autorregresivo de orden uno al depender los rendimientos del periodo, de los mismos rendimientos en el periodo anterior y una ecuación para la varianza (volatilidad al cuadrado). Esta última ecuación tiene un parámetro γ que mide la posibilidad del efecto apalancamiento que, en el modelo EGARCH, tendría que ser estadísticamente negativo. El parámetro λ₁ representa el efecto del exceso de confianza en la volatilidad y el parámetro λ₂ el efecto de otros factores del volumen de operaciones sobre la volatilidad.

Datos y resultados

Los datos de nuestro estudio empírico consisten en precios de cierre diarios de los índices de los mercados accionarios de Argentina, Brasil, Chile, Colombia, México y Perú así como el volumen de operaciones diario del 3 de enero de 2000 al 8 de enero de 2014. Cabe destacar que se realiza un análisis por separado para el periodo de crisis que va de julio de 2007 a diciembre de 2009. La elección de este periodo se tomó del estudio de Abbes (2012) basado en los resultados de la prueba de Chow de cambio estructural que es coincidente con el trabajo de Avgouleas (2008).

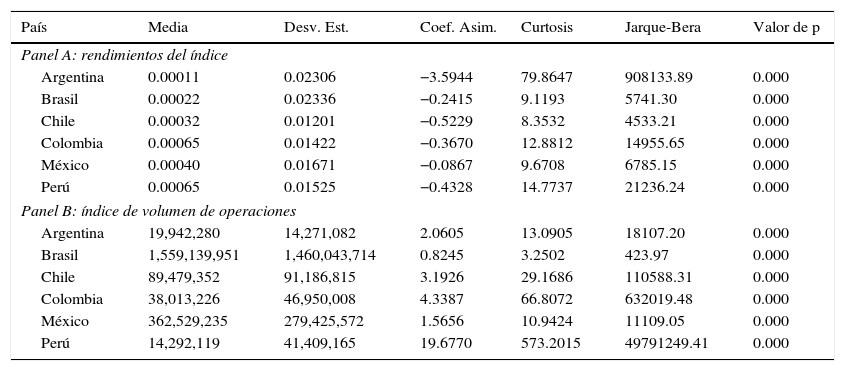
En la tabla 1 se presentan las estadísticas descriptivas de los rendimientos continuos y del volumen de operación.

Tabla 1.

Estadísticas descriptivas de los rendimientos y volumen de operaciones para toda la muestra

País	Media	Desv. Est.	Coef. Asim.	Curtosis	Jarque-Bera	Valor de p
Panel A: rendimientos del índice
Argentina	0.00011	0.02306	−3.5944	79.8647	908133.89	0.000
Brasil	0.00022	0.02336	−0.2415	9.1193	5741.30	0.000
Chile	0.00032	0.01201	−0.5229	8.3532	4533.21	0.000
Colombia	0.00065	0.01422	−0.3670	12.8812	14955.65	0.000
México	0.00040	0.01671	−0.0867	9.6708	6785.15	0.000
Perú	0.00065	0.01525	−0.4328	14.7737	21236.24	0.000
Panel B: índice de volumen de operaciones
Argentina	19,942,280	14,271,082	2.0605	13.0905	18107.20	0.000
Brasil	1,559,139,951	1,460,043,714	0.8245	3.2502	423.97	0.000
Chile	89,479,352	91,186,815	3.1926	29.1686	110588.31	0.000
Colombia	38,013,226	46,950,008	4.3387	66.8072	632019.48	0.000
México	362,529,235	279,425,572	1.5656	10.9424	11109.05	0.000
Perú	14,292,119	41,409,165	19.6770	573.2015	49791249.41	0.000

Fuente: elaboración propia.

En la primera columna del panel A se calcula el rendimiento diario promedio, en la segunda columna se calcula la desviación estándar del rendimiento diario sobre todo el periodo de estudio y este es un estimador estático de la volatilidad. En la tercera columna se calcula el coeficiente de asimetría que mide hacia qué lado está cargada la distribución de los rendimientos diarios, a la izquierda (negativo) a la derecha (positivo). En la siguiente columna aparece la curtosis que mide el ancho de las colas. Por último se presenta la prueba de Jarque-Bera en la que se pretende determinar si los rendimientos se distribuyen como una normal. En todos los casos se rechaza la hipótesis nula de normalidad por lo que podemos concluir que los rendimientos diarios no se distribuyen de esa manera. En el panel B se muestra el equivalente para el volumen de operación.

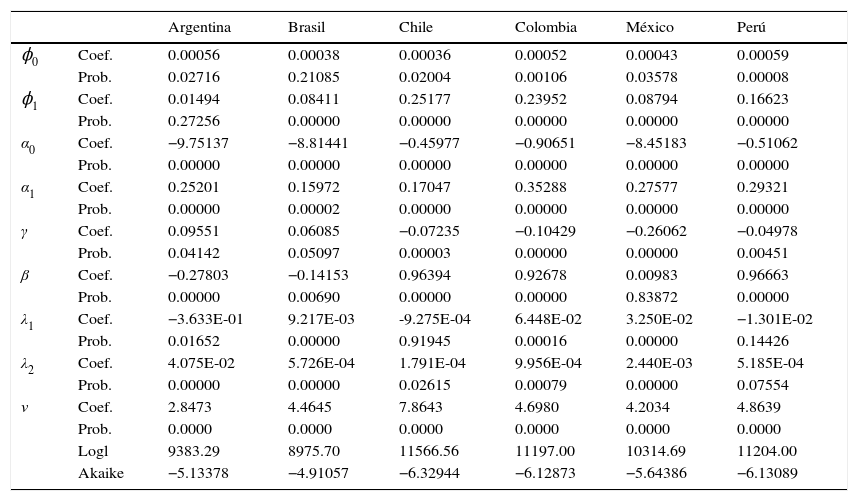
En la tabla 2 se presenta el modelo (3) con los diferentes parámetros estimados así como su valor de p para la muestra completa. También se presenta el estimador de los grados de libertad de la distribución t-estandarizada.

Tabla 2.

Parámetros estimados y errores estándar del modelo AR(1)-EGARCH(1,1) con distribución t asimétrica para toda la muestra

		Argentina	Brasil	Chile	Colombia	México	Perú
ϕ0	Coef.	0.00056	0.00038	0.00036	0.00052	0.00043	0.00059
	Prob.	0.02716	0.21085	0.02004	0.00106	0.03578	0.00008
ϕ1	Coef.	0.01494	0.08411	0.25177	0.23952	0.08794	0.16623
	Prob.	0.27256	0.00000	0.00000	0.00000	0.00000	0.00000
α0	Coef.	−9.75137	−8.81441	−0.45977	−0.90651	−8.45183	−0.51062
	Prob.	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000
α1	Coef.	0.25201	0.15972	0.17047	0.35288	0.27577	0.29321
	Prob.	0.00000	0.00002	0.00000	0.00000	0.00000	0.00000
γ	Coef.	0.09551	0.06085	−0.07235	−0.10429	−0.26062	−0.04978
	Prob.	0.04142	0.05097	0.00003	0.00000	0.00000	0.00451
β	Coef.	−0.27803	−0.14153	0.96394	0.92678	0.00983	0.96663
	Prob.	0.00000	0.00690	0.00000	0.00000	0.83872	0.00000
λ1	Coef.	−3.633E-01	9.217E-03	-9.275E-04	6.448E-02	3.250E-02	−1.301E-02
	Prob.	0.01652	0.00000	0.91945	0.00016	0.00000	0.14426
λ2	Coef.	4.075E-02	5.726E-04	1.791E-04	9.956E-04	2.440E-03	5.185E-04
	Prob.	0.00000	0.00000	0.02615	0.00079	0.00000	0.07554
ν	Coef.	2.8473	4.4645	7.8643	4.6980	4.2034	4.8639
	Prob.	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	Logl	9383.29	8975.70	11566.56	11197.00	10314.69	11204.00
	Akaike	−5.13378	−4.91057	−6.32944	−6.12873	−5.64386	−6.13089

Fuente: elaboración propia.

El ajuste del modelo se realiza revisando los correlogramas de los residuales y de los residuales al cuadrado que tienen que comportarse como ruido blanco lo cual se cumple en todos los casos. Se confirma el efecto apalancamiento medido por el parámetro γ, para Chile, Colombia, México y Perú al ser estadísticamente negativo.

El parámetro de exceso de confianza λ₁ es significativo para la volatilidad del rendimiento de los índices accionarios de Argentina, Brasil, Colombia y México. Para el caso de Argentina este parámetro es negativo, y esto puede ser debido a la pérdida de confianza que se ha generado en el país en su mercado financiero a partir de la crisis de diciembre de 2001. Para el caso de Brasil, Colombia y México, el parámetro es estadísticamente positivo lo que sugiere que el sesgo de exceso de confianza es un determinante en la volatilidad de los rendimientos accionarios.

Para el caso de Chile resulta que el parámetro de exceso de confianza es no significativo y esto podría explicarse a partir del crecimiento financiero que se ha tenido en los últimos años, haciendo que los agentes financieros sean prudentes al tomar sus decisiones. Para el caso de Perú el mercado accionario es muy pequeño por lo que los inversionistas no tienen incentivos para participar en forma importante.

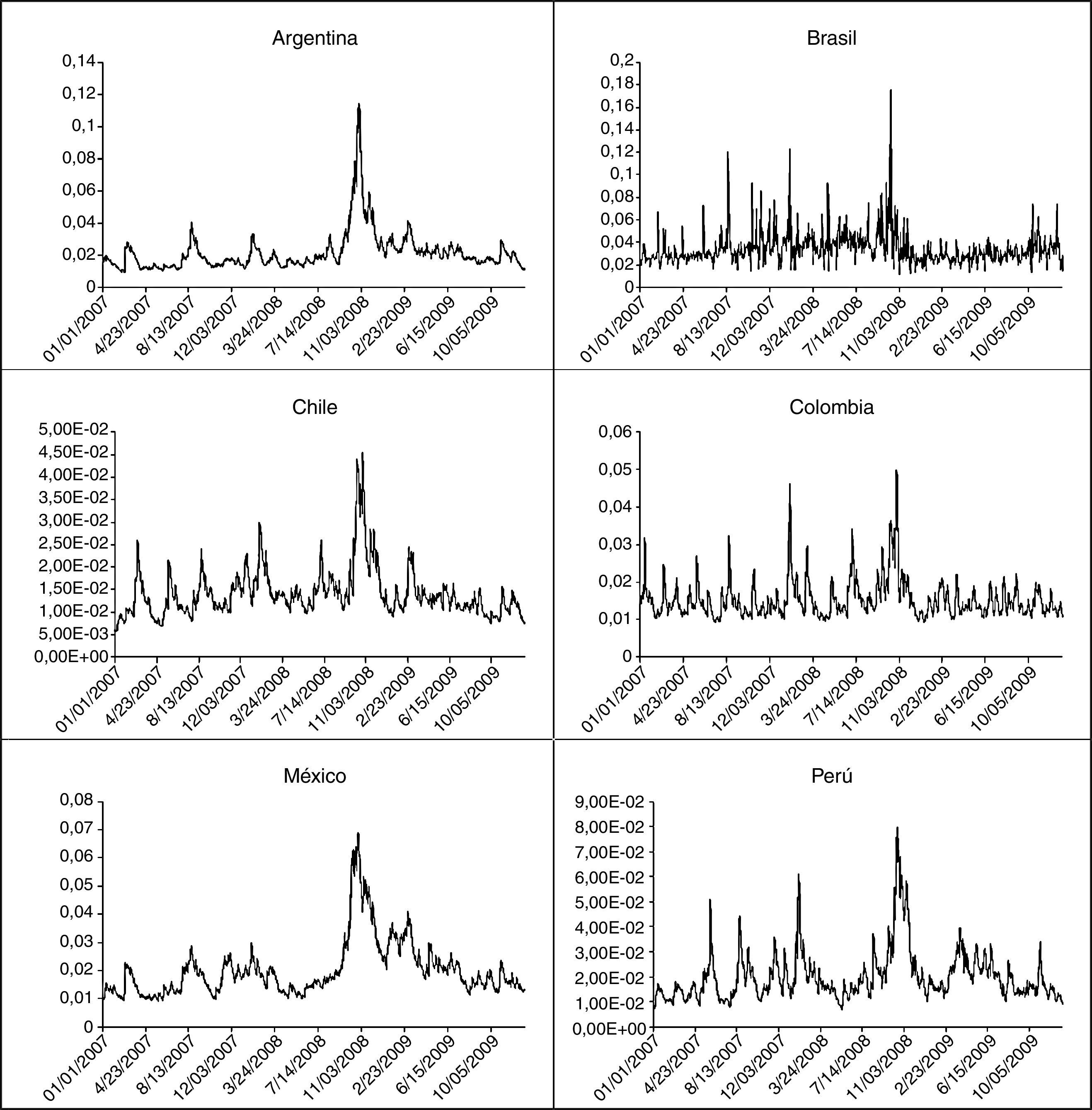
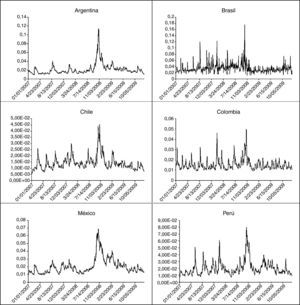
En la figura 1 se presenta la gráfica de la volatilidad estimada para el periodo de la crisis del 2008 donde puede observarse la alta volatilidad a finales del año de 2008 que provoca la pérdida de confianza de los inversionistas que no está presente en el caso brasileño.

Figura 1.

Volatilidades estimadas en el periodo de crisis de 2008.

Fuente: elaboración propia.

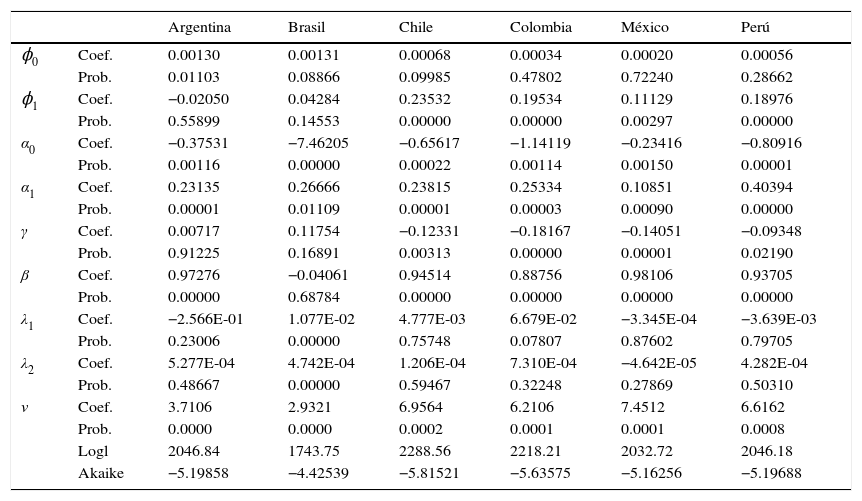
En la tabla 3 se presentan las estimaciones del modelo EGARCH para el periodo de la crisis del 2008 con datos de julio de 2007 a diciembre de 2009,

Tabla 3.

Parámetros estimados y errores estándar del modelo AR(1)-EGARCH(1,1) con distribución t asimétrica para el periodo de julio de 2007 a diciembre de 2009

		Argentina	Brasil	Chile	Colombia	México	Perú
ϕ0	Coef.	0.00130	0.00131	0.00068	0.00034	0.00020	0.00056
	Prob.	0.01103	0.08866	0.09985	0.47802	0.72240	0.28662
ϕ1	Coef.	−0.02050	0.04284	0.23532	0.19534	0.11129	0.18976
	Prob.	0.55899	0.14553	0.00000	0.00000	0.00297	0.00000
α0	Coef.	−0.37531	−7.46205	−0.65617	−1.14119	−0.23416	−0.80916
	Prob.	0.00116	0.00000	0.00022	0.00114	0.00150	0.00001
α1	Coef.	0.23135	0.26666	0.23815	0.25334	0.10851	0.40394
	Prob.	0.00001	0.01109	0.00001	0.00003	0.00090	0.00000
γ	Coef.	0.00717	0.11754	−0.12331	−0.18167	−0.14051	−0.09348
	Prob.	0.91225	0.16891	0.00313	0.00000	0.00001	0.02190
β	Coef.	0.97276	−0.04061	0.94514	0.88756	0.98106	0.93705
	Prob.	0.00000	0.68784	0.00000	0.00000	0.00000	0.00000
λ1	Coef.	−2.566E-01	1.077E-02	4.777E-03	6.679E-02	−3.345E-04	−3.639E-03
	Prob.	0.23006	0.00000	0.75748	0.07807	0.87602	0.79705
λ2	Coef.	5.277E-04	4.742E-04	1.206E-04	7.310E-04	−4.642E-05	4.282E-04
	Prob.	0.48667	0.00000	0.59467	0.32248	0.27869	0.50310
ν	Coef.	3.7106	2.9321	6.9564	6.2106	7.4512	6.6162
	Prob.	0.0000	0.0000	0.0002	0.0001	0.0001	0.0008
	Logl	2046.84	1743.75	2288.56	2218.21	2032.72	2046.18
	Akaike	−5.19858	−4.42539	−5.81521	−5.63575	−5.16256	−5.19688

Fuente: elaboración propia.

Para este caso se puede apreciar que el parámetro de exceso de confianza λ₁ solo es significativo en Brasil y Colombia (con un nivel de significación del 10%). Los países latinoamericanos perdieron la confianza en los mercados financieros en el periodo de crisis. En el caso de Brasil el exceso de confianza puede explicarse al pertenecer al grupo BRIC, lo que genera expectativas positivas para atraer inversión. Una posible explicación en el mercado accionario colombiano podría derivarse de una sensación de aparente estabilidad política al iniciar ciertos acuerdos con las FARC lo que generó en ese momento un exceso de confianza en los mercados financieros. Esto sugiere que en general para Latinoamérica, durante la crisis global, el sesgo de exceso de confianza no tuvo efectos significativos sobre la volatilidad de los activos, lo que indica que se perdió la confianza de los inversionistas en los mercados financieros en este periodo.

Conclusiones

En este trabajo se encuentra evidencia empírica de la dependencia del exceso de confianza en la volatilidad en los mercados accionarios latinoamericanos. El exceso de confianza se ha obtenido como uno de los 2 componentes en que se descompuso el volumen de operaciones desestacionalizado. Ambos componentes fueron incorporados en la ecuación de la varianza condicional empleando un modelo EGARCH con una distribución t de Student estandarizada. Las series analizadas han sido los precios de cierre diarios de los índices accionarios de Argentina, Brasil, Chile, Colombia, México y Perú entre el 3 de enero de 2000 y el 8 de enero de 2014.

Los resultados empíricos del estudio sugieren que: 1) cada una de las series de rendimientos bursátiles analizadas puede describirse adecuadamente con el modelo EGARCH propuesto; 2) se cumple la característica de efecto apalancamiento en las series de rendimientos de Chile, Colombia, México y Perú, 3) el exceso de confianza es un determinante en la volatilidad para Colombia y para las economías grandes de la zona (México y Brasil), no así para las pequeñas como Perú ni las han sufrido financieramente en los últimos años como Argentina o en el caso de Chile, debido a la prudencia de los inversionistas.

Se realiza un análisis para el periodo de crisis considerando datos de julio de 2007 a diciembre del 2009 y se encuentra que de los 3 países que presentaban exceso de confianza, solo se ha perdido en el mercado mexicano. Con lo anterior podríamos concluir que el exceso de confianza no afecta la volatilidad de los mercados latinoamericanos a excepción de las economías grandes como Brasil y México, y que en este último caso se pierde la confianza en tiempos de crisis.

Desde el punto de vista metodológico, los resultados demuestran la conveniencia de usar modelos de varianza condicional para describir el comportamiento de la volatilidad, como son los de la familia ARCH, que asuman las características típicas de las series de tiempo financieras como el efecto apalancamiento. Por esa razón, el modelo EGARCH puede emplearse para describir dichas características y para la toma de decisiones de administración de riesgos, de inversión y de valuación de activos. Al incluir variables exógenas como el exceso de confianza, estos resultados también tienen implicaciones para la teoría de portafolios y el análisis fundamental.

Finalmente, en posibles estudios posteriores se pueden extender estos modelos y considerar otro tipo de distribuciones ya sean simétricas o asimétricas para la distribución de las perturbaciones así como otras variaciones de la familia ARCH como son los modelos TARCH, PARCH y ACGARC y comparar sus resultados.