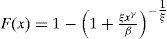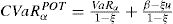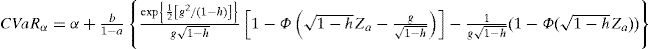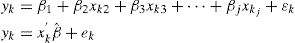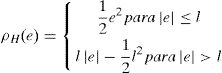Este artículo presenta una revisión del uso de la distribución g-h en riesgo operativo; asimismo, se propone una modificación al método de Hoaglin (1985) para la estimación de los parámetros de la distribución g-h. La diferencia consiste en realizar una regresión robusta cuando se estima el parámetro h; además, se realizan comparaciones de estimados de OpVaR mediante g-h y POT en dos aplicaciones. Los resultados muestran que el empleo del método g-h es de gran utilidad en riesgo operativo, pero debe tenerse cuidado cuando la distribución de las pérdidas exhiben colas extremadamente pesadas.
This paper presents a review of the g-h distribution in operational risk and proposes a modification to the method developed by Hoaglin (1985) to estimating the parameters. The modification consists in the estimation of the parameter h using a robust regression. We estimate OpVaR by g-h and POT methods in two applications. The results show that the g-h method is useful in operational risk, but care must be taken when the distribution of losses presents extremely heavy tails.
En Basilea II se incluye la necesidad de cuantificar capital regulatorio para riesgo operativo por parte de las entidades bancarias. La regulación propone las siguientes tres metodologías para que los bancos cuantifiquen su capital: el enfoque de indicador básico (BIA), el enfoque estándar (SA) y el enfoque de medición avanzada (AMA). Las instituciones financieras que apliquen AMA deberán calcular el valor en riesgo (VaR) al 99.9% en un horizonte de un año. Dentro de los modelos AMA, el más empleado en la práctica es el enfoque de distribución de pérdidas agregadas (LDA), que tiene sus raíces en la teoría de seguros; la finalidad es obtener una distribución de pérdidas agregando el proceso de frecuencia de eventos de pérdida junto con el de las severidades. Debido a que se requiere cuantificar un cuantil alto, es usual ver en la práctica que se combine LDA con la teoría del valor extremo (EVT), que ha sido empleado exitosamente en varios tipos de riesgo financiero y en especial cuando hay presencia de eventos de cola. Una revisión sobre los modelos LDA se puede encontrar en Chaudhury (2010) —donde también se realiza una discusión de los problemas prácticos al cuantificar capital por riesgo operativo y una de las conclusiones es que modelar inadecuadamente la cola de la distribución de severidades conlleva a problemas en la cuantificación del riesgo— y las referencias allí contenidas.
En la revisión de la literatura se ha encontrado que la distribución g-h se ajusta bien a los datos de pérdidas por riesgo operativo. Por lo tanto, este artículo realiza una revisión no exhaustiva de estudios donde involucre la distribución g-h en riesgo operativo y se propone una modificación para la estimación de los parámetros de esta distribución. Así, en primer lugar, se presenta la revisión de estudios previos. Después, se define la distribución g-h y se enuncian sus propiedades básicas; de igual forma, se describe brevemente los métodos existentes para estimar sus parámetros. Más adelante, se presenta dos aplicaciones de estimación de OpVaR y OpCVaR mediante g-h, las cuales se comparan con la metodología POT. Finalmente, se presentan las principales conclusiones de este trabajo.
Estudios de g-h en riesgo operativoDutta y Perry (2006) usan los datos LDCE de 2004 con los que ajustan distribuciones paramétricas, EVT y muestreo empírico (simulación histórica) a las severidades; encuentran que la distribución g-h y el muestreo empírico conllevan a estimados consistentes de cargos de capital. Otras distribuciones paramétricas empleadas para ajustar las severidades son exponencial, gamma, de Pareto generalizada, loglogística, lognormal truncada, Weibull y beta generalizada de segunda clase (GB2). Así como la g-h, la distribución GB2 tiene la característica de poseer cuatro parámetros, por lo que otras distribuciones pueden ser generadas a partir de la GB2 y de la g-h. Degen et al. (2007) encuentran que si los datos de pérdida son bien modelados por una distribución g-h, la estimación de cuantiles altos mediante el método POT (picos sobre un umbral), por lo general, convergerá muy lentamente; por consiguiente, su estimación mediante EVT será imprecisa y —como se vio en el estudio de Dutta y Perry (2006)— la distribución g-h se ajustará bien a las pérdidas por riesgo operativo.
El punto débil del EVT es la selección del umbral porque el parámetro de forma (ξ) de las distribuciones empleadas en EVT puede variar y asimismo el cálculo de cargo de capital. Beirlant et al. (2004) realizan una revisión de métodos para seleccionar el umbral, pero no existe un método óptimo que solucione este problema, puesto que algunos métodos solucionan el problema de varianza en la estimación de los parámetros y otros sólo el de sesgo. Sin embargo, el trabajo de Chávez-Demoulin (1999), basado en estudios de simulación, recomienda escoger un umbral como el percentil al 90% de las datos de pérdidas. Otro trabajo de Chávez-Demoulin y Embrechts (2004) realiza un análisis de sensibilidad con este umbral y muestra que pequeñas variaciones en el umbral escogido no tienen mucho impacto en la estimación de los parámetros requeridos en EVT. Recientemente, Horbenko et al. (2011) emplean técnicas de estadística robusta para estimar los parámetros de la distribución de Pareto generalizada (distribución empleada en el método POT) y lo aplican a datos de pérdida por riesgo operativo de la base de datos Algo OpData (distribuida por la compañía Algorithmics Inc); los autores concluyen que no se puede afirmar que los estimados de OpVaR, usando estadística robusta, siempre serán mayores que los obtenidos mediante máxima verosimilitud (método usualmente empleado para estimar los parámetros de la distribución de Pareto generalizada). Un estudio previo (Dell'Aquila y Embrechts, 2006) señala que la estadística robusta ayuda a mejorar el análisis de datos cuando se emplea EVT.
Pero EVT no podría funcionar bien en ciertas distribuciones; la explicación se puede encontrar analizando la teoría de variación regular de segundo orden. Para detalles de esta teoría y su aplicación a distribuciones de riesgo operativo, puede verse el artículo de Degen y Embrechts (2008) y las referencias allí contenidas. Los autores encuentran que la tasa de convergencia de métodos basados en EVT para estimar ξ y, por ende, cuantiles altos, es muy lenta en distribuciones donde el parámetro de segundo orden ρ es igual a cero. En otras palabras, se pueden obtener estimadores inconsistentes cuando ρ=0. Las distribuciones como loggamma, lognormal, Weibull y g-h son ejemplo de distribuciones con ρ=0.
Jobst (2007) también realiza una comparación de la distribución g-h con las distribuciones paramétricas empleadas en EVT; es decir, la distribución de valor extremo generalizada (GEV, por sus siglas en inglés) y GPD. Los datos que empleó corresponden a los de bancos comerciales en Estados Unidos. Su conclusión es que tanto EVT como g-h arrojan resultados de pérdidas inesperadas confiables y realistas, aunque g-h se desempeña mejor.
Buch-Kromann (2009) compara EVT y g-h en riesgo operativo y adiciona un tercer método basado en la distribución Champernowne que es una distribución de tres parámetros y exhibe colas pesadas; más específicamente, se utiliza el estimador transformado de la densidad kernel de la Champernowne. Otros artículos, cuyas referencias pueden ser encontradas en el citado trabajo de Buch-Kromann, han recomendado el uso de esta distribución para modelar pérdidas por riesgo operativo. Una ventaja que presenta esta distribución es que no toma valores negativos, mientras que g-h y GPD sí. Al utilizar datos de pérdida por riesgo operativo y el método LDA, el autor muestra que la distribución g-h subestima la cola de las pérdidas y, por lo tanto, no arrojaría un estimado prudente de capital requerido. El estimador basado en la distribución Champernowne, por el contario, sobreestima cargo de capital.
En otros estudios relacionados, Peters y Sisson (2006) emplean estadística bayesiana y simulación Monte Carlo de cadenas de Markov (MCMC, por sus siglas en inglés) para encontrar la distribución a posteriori, donde la distribución de pérdidas sigue una distribución g-h. Carrillo-Menéndez y Suárez (2012) utilizan simulaciones de datos, donde la cola sigue una distribución g-h, para estimar medidas de riesgo operativo. A continuación se presenta una definición básica de la distribución g-h y sus propiedades.
Distribución g-hLa distribución g-h fue introducida por Tukey en 1977 y ha sido utilizada en finanzas, en aplicaciones de retornos de acciones e índices, como también para modelar tasas de interés y opciones en tasas de interés (Dutta y Perry, 2006, así como referencias ahí contenidas).
DefiniciónSea Z ~ N(0, 1) una variable aleatoria normal estándar. Una variable aleatoria X se dice que tiene una distribución g-h con parámetros a, b, g, h h ∈ ℝ, si X satisface:
y se denota X ~ g-h.El parámetro g controla la cantidad y dirección de asimetría, mientras que el parámetro h controla la cantidad de elongación (curtosis). La distribución es más sesgada a la derecha a mayores valores de g; y entre mayor es el valor de h mayor es la elongación.
Cuando h=0, la ecuación (1) es X=a+begZ−1g, y la distribución g-h se convierte en la distribución g que corresponde a una distribución lognormal escalada. Cuando g=0, la ecuación (1) se interpreta como X=a+bZehZ2/2, y la distribución es referida como la distribución h. Cuando g=h=0, X se distribuye de manera normal.
Propiedades de la distribución g-hMartínez (1981), Martínez e Iglewicz (1984), Hoaglin (1985), entre otros, han estudiado las propiedades de la distribución g-h. Una propiedad importante es que muchas distribuciones pueden ser generadas a partir de la g-h para valores específicos de los parámetros. Las siguientes propiedades están basadas en Dutta y Babel (2002) y Degen et al. (2007):
- 1.
X es una transformación estrictamente creciente de Z. Esto es, la transformación de una normal estándar a una g-h es uno a uno.
- 2.
Si a=0, entonces X−g,h(Z)=−Xg,h(−Z). Cambiar el signo de g cambia la dirección, pero no el valor de asimetría de la distribución g-h.
- 3.
Para h=0 y g → 0, la distribución g-h converge a una distribución normal.
- 4.
La distribución g es una distribución lognormal escalada.
- 5.
El parámetro de localización a de la distribución g-h es la mediana del conjunto de datos, y el p-ésimo percentil del valor de g está dado por gp=−1ZplnX1−p−X0.5X0.5−Xp. Como Z0.5=0, y al reemplazarlo en (1), se obtiene a=X0.5. Al escoger diversos valores de p se obtienen diferentes estimados del parámetro g. Para solucionar este problema, algunos autores han sugerido usar la mediana de los diferentes valores de gp. Jiménez y Martínez (2006) proponen la estimación del parámetro g de una manera más sencilla cuando h tiende a cero.
- 6.
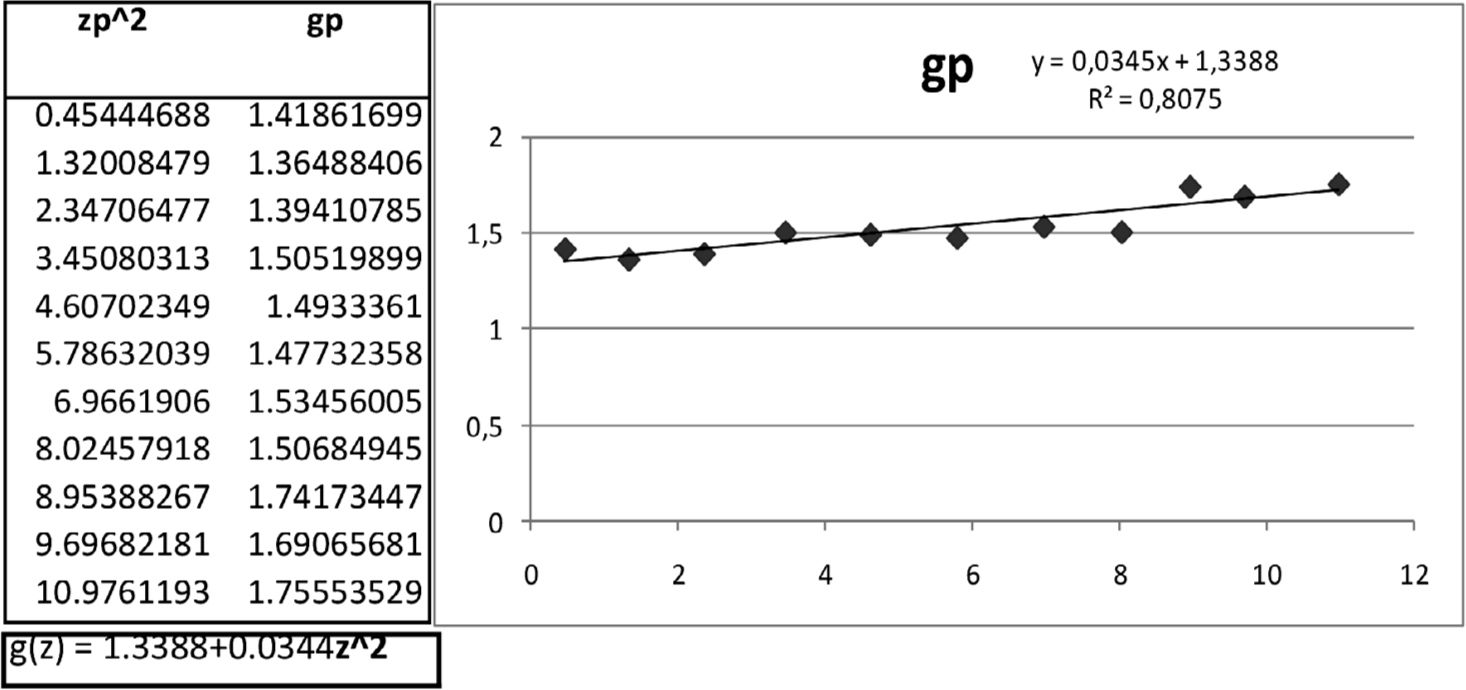
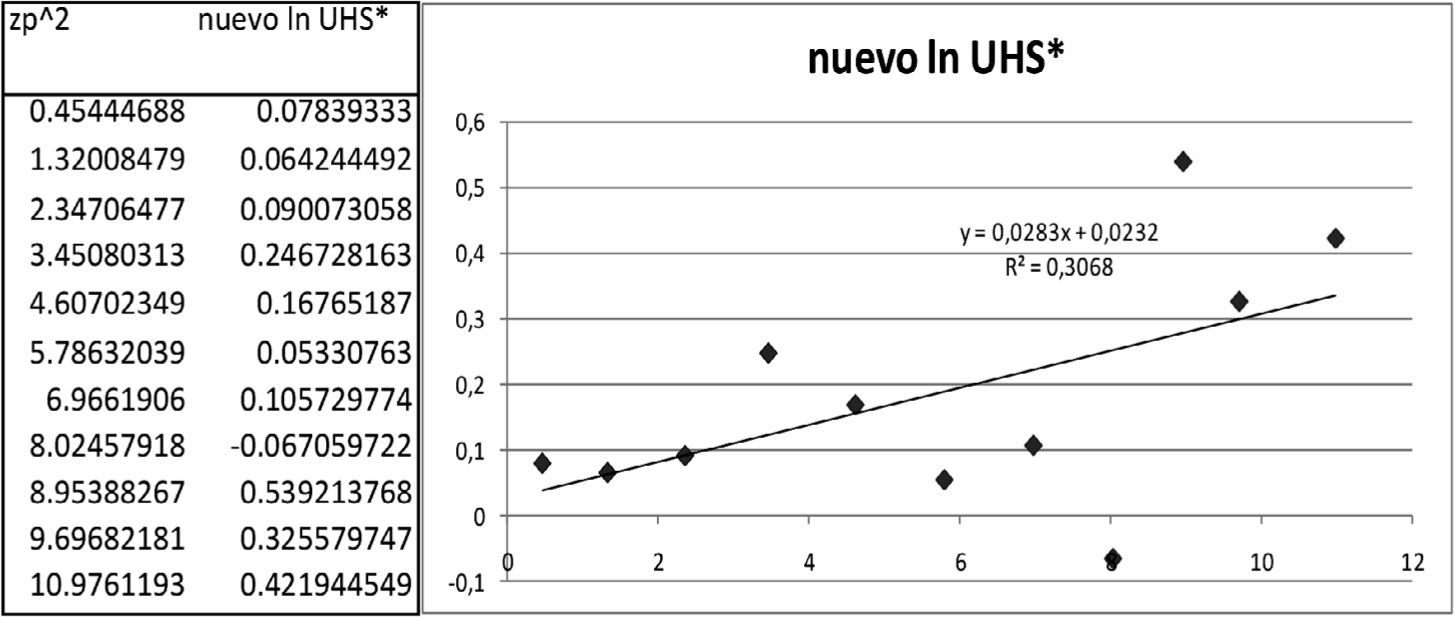
Para un cierto valor de g, el valor de h está dado por lngXp−X1−pegZp−e−gZp=lnb+hZp2/2. De esta manera, se puede obtener el valor de h como el coeficiente de la pendiente de la regresión de lngXp−X1−pegZp−e−gZp=contraZp2/2. El valor de b se obtiene tomando la función exponencial del intercepto de la regresión. La expresión gXp−X1−pegZp−e−gZp es conocida como corrected full spread (FS).
- 7.
La distribución g-h es una función de variación regular con índice −1/h (con h>0). La distribución g es una función subexponencial (estas distribuciones obtienen este nombre debido a que sus colas decaen más lentamente que las de una exponencial); sin embargo, no es de variación regular (ver teorema 2.1 en Degen et al., 2007).
Funciones de variación regular son aquellas que pueden ser representadas por funciones de potencia multiplicadas por funciones de variación lenta. Es decir, si q es una función de variación regular, entonces q(x)=xϱL(x). Mientras que una función de variación lenta L es aquella que comparada con funciones de potencia cambian relativamente lento para valores grandes de x, por ejemplo, ln(x).
Como se mencionó, un resultado importante del artículo de Degen et al. (2007) es que si los datos de pérdida son bien modelados por una distribución g-h (con valores g, h>0), la estimación de cuantiles altos mediante el método POT por lo general convergerá muy lentamente y, por tanto, su estimación mediante EVT será imprecisa. A continuación se presenta como estimar cuantiles de una distribución g-h cuando se han estimado los parámetros de la distribución. Este apartado está basado en la sección 2.1 de Degen et al. (2007).
Estimación del cuantil mediante la aproximación g-hPuesto que k(x)=egx−1gehx2/2 es estrictamente creciente (para h>0), la función de distribución acumulada de una variable aleatoria g-h X se puede escribir como:
donde Φ denota la función de distribución acumulada de una normal estándar. Teniendo en cuenta los parámetros de localización y escala (a y b), el VaR se estima de la siguiente forma:En cuanto a los momentos de la distribución g-h, Martínez (1981) obtiene el n-ésimo momento de esta distribución para ciertos valores de h. Hoaglin (1985) obtiene los cuatro primeros momentos y también se pueden encontrar en el apéndice D de Dutta y Perry (2006).
Métodos de estimación de los parámetros de g-hEn las aplicaciones del método g-h se emplea la metodología propuesta por Hoaglin (1985), en especial la sección 11D para estimar g; está basada en cuantiles y en comparación con otras metodologías —como el método de momentos y máxima verosimilitud— puede ser más preciso en el ajuste de las colas de la distribución, como lo afirman varios autores. Este método no es apropiado para todas las distribuciones; sin embargo, sí es adecuado para g-h, que es una transformación de una normal estándar. Para el método de los momentos se podrían plantear cuatro ecuaciones para resolver cuatro incógnitas, que son la cantidad de parámetros por estimar. Sin embargo, el cuarto momento exige que 0≤h<1/4 y, por ejemplo, Dutta y Perry encuentran un rango para el parámetro h en [0.1, 0.35]. Esto se convierte en una desventaja para el método de los momentos. Aunque no existe una expresión analítica para obtener la función de verosimilitud de una distribución g-h, Rayner y MacGillivray (2002) estudian procedimientos de estimación de los parámetros para una distribución g-h generalizada mediante estimación numérica de la función de máxima verosimilitud. Por su parte, Haynes y Mengersen (2005) exploran computación bayesiana para estimar tales parámetros. En este artículo se presenta una propuesta de estimar el parámetro h como la pendiente de una regresión robusta de lngXp−X1−pegZp−e−gZp=vsZp2/2 (ver propiedad 6). Por lo tanto, el parámetro b será calculado como la función exponencial del intercepto de dicha regresión (véase el apéndice B para una introducción de regresión robusta).
AplicacionesEn esta sección se comparan los estimados de VaR y CVaR mediante las técnicas g-h y POT. La obtención de datos de pérdida por riesgo operativo no es tan fácil. Por tal razón, se recurren a fuentes de datos ya examinadas en estudios anteriores. En el primer caso, los datos, aunque no son de riesgo operativo en un banco, se tratan de pérdidas en las aseguradoras danesas por reclamos causados por incendio; los estimados de VaR y CVaR se realizan en varios niveles de confiabilidad. En el segundo caso, se estima VaR y CVaR al 99.9% en distribuciones de pérdida obtenidas mediante simulación de datos que aparecen en un estudio de riesgo operativo; para este último caso, los autores del estudio presentan las distribuciones y parámetros empleados para el proceso de frecuencia y severidad.
Aplicación 1 (caso Danish Fire Data)Los datos de la aplicación corresponden a 2 167 reclamos en seguro contra incendio en Dinamarca (Danish Fire Data); las pérdidas se expresan en millones de coronas danesas, desde el 1 de marzo de 1980 hasta el 12 de diciembre de 1990. Estos datos han sido previamente estudiados por varios autores bajo el marco de EVT.
A continuación se muestra el resumen del análisis descriptivo y se observa que la distribución de las pérdidas es sesgada a la derecha y presenta alta curtosis, buen ejemplo para estudio de colas pesadas (ver cuadro 1).
En el siguiente cuadro se compara VaR en diferentes niveles de confiabilidad mediante diferentes métodos.
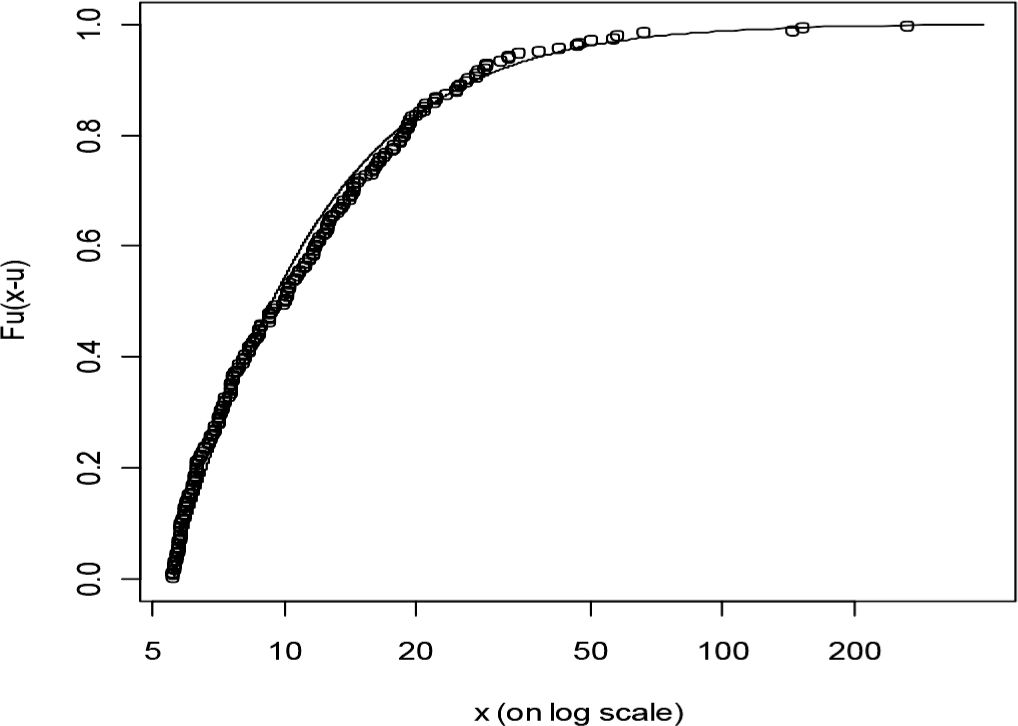
El método POT utiliza un umbral de tal manera que los datos en exceso sean el 10% del total de la muestra (216 datos en exceso), que es equivalente a 5.5617 millones de coronas danesas. Se utiliza este umbral siguiendo los resultados de Chávez-Demoulin (1999). A continuación se muestra el gráfico del ajuste de la distribución de Pareto generalizada a los datos en exceso cuando se emplea el umbral seleccionado. Se puede apreciar que con el umbral escogido, la distribución hace un buen ajuste a los datos de la cola.
POT* es calculado mediante un resultado de computación bayesiana. El primer método g-h es el calculado en Degen et al. (2007); el segundo g-h* es calculado siguiendo la técnica de Hoaglin (1985) y descrito en el apéndice A; el último g-h** corresponde a la aplicación de la regresión robusta.
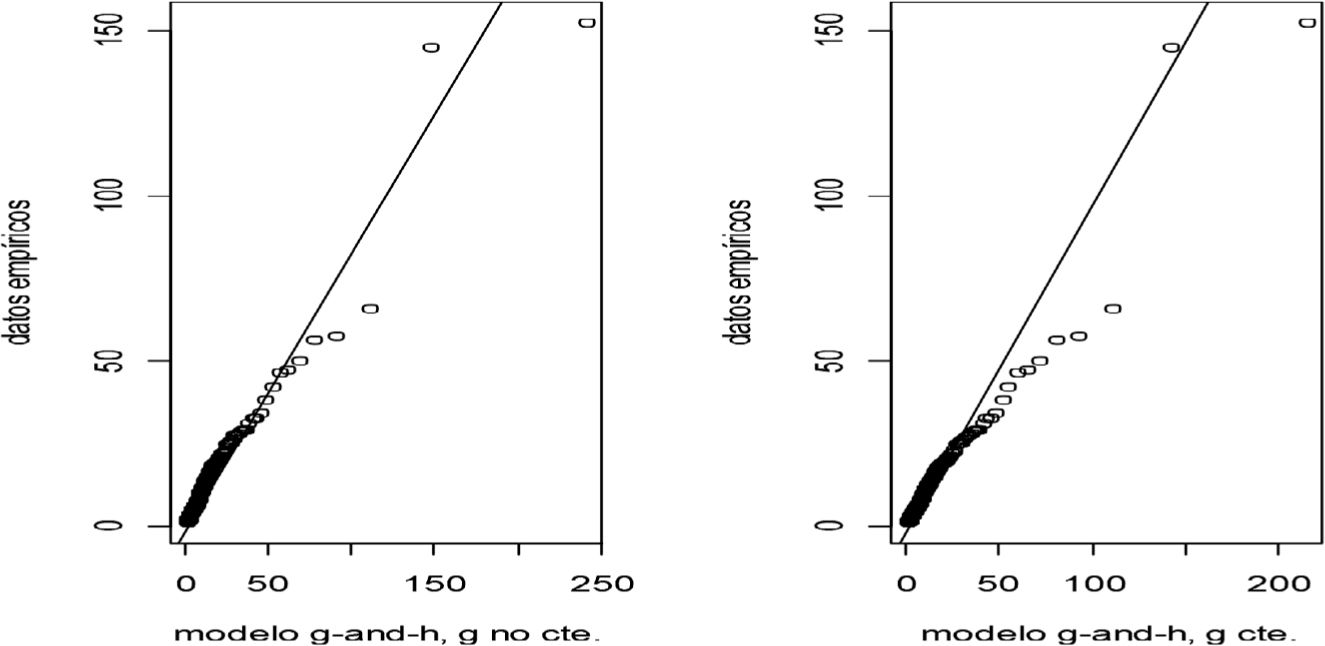
Degen et al. (2007) usan un parámetro g constante, mientras que en este artículo se usa un polinomio de g en z2 (ver apéndice A). Aunque este último método puede brindar una aproximación más cercana a los datos, introducir una variable adicional (z2) reduce robustez en la estimación de los parámetros. Para ello, se propone la estimación g-h**, que consiste en realizar una regresión robusta, como se indicó anteriormente. Los diferentes métodos arrojan estimaciones similares al observar los resultados obtenidos del cuadro 2 para niveles del 90%, 95% y 99%, mientras que para el 99.9% se obtienen resultados diferentes. En la siguiente gráfica se muestra que el modelo de g-h con parámetro g no constante se ajusta mejor a los datos de la aplicación.
En la parte izquierda de la gráfica se emplea parámetro g no constante, mientras que en la parte derecha el parámetro g es constante.
Los resultados de VaR bajo POT han sido calculados mediante la siguiente expresión:
Donde u es el umbral; β, ξ son los parámetros de escala y de forma de la GPD; Nu son los datos en exceso por encima del umbral; y n es el total de los datos. Este estimador de VaR fue inicialmente propuesto por Smith (1987) y ampliamente utilizado bajo EVT. Los parámetros han sido estimados mediante máxima verosimilitud usando el paquete evir de R. Cuando se usa el número de excesos de 216, el umbral es de 5.5617 millones de coronas danesas. Con estos datos de entrada, las estimaciones son 0.5928 y 4.4468 para ξ y β, respectivamente. El método POT-Bayes se basa en los resultados de Vaz de Melo Mendes (2006). En lugar de usar la distribución de Pareto generalizada, se emplea una modificación introduciendo un parámetro γ. Entonces, la función de distribución está dada por:de esta manera, siguiendo los mismos pasos para calcular VaR mediante el estimador de Smith (1987), el VaR para este caso estaría dado por:Vaz de Melo Mendes (2006) obtiene estimados de 0.7346, 3.5943 y 0.1863 para γ, β y ξ, respectivamente. Con estos valores se calcula VaR utilizando la expresión (2).
Conditional value-at-riskEl artículo de Artzner et al. (1999) muestra que una medida coherente de riesgo debe cumplir cuatro axiomas: I) Invarianza traslacional, II) Subaditividad, III) Homogeneidad positiva y IV) Monotonicidad.
El axioma de subaditividad es el axioma más debatido de estas propiedades que caracterizan una medida coherente de riesgo; en ocasiones el VaR viola este axioma (ver por ejemplo la sección 65.8.5 de Venegas, 2006), generando problemas a la regulación, como se verá más adelante. McNeil et al. (2005) argumentan la necesidad de que una medida de riesgo cumpla este axioma, y uno de los más importantes es que una institución financiera puede legalmente dividirse en varias subsidiarias y reportar individualmente su capital regulatorio, reduciendo así sus requerimientos totales de capital (esto se conoce como legal loophole). El ejemplo 6.7 de McNeil et al. (2005) también muestra un caso en que el VaR no cumple con el axioma de subaditividad. Básicamente VaR no es subaditivo por tres razones: a) asimetría, b) colas pesadas y c) dependencia.
Sin embargo, el VaR es subaditivo cuando la función de distribución de pérdidas y ganancias es elíptica; por ejemplo, una función normal o t-Student. Pero en riesgo operativo es común encontrar distribuciones de pérdidas que cumplen las razones a) y b). Debido a los problemas de no subaditividad de una medida de riesgo, Artzner et al. (1999) proponen el uso de expected shortfall (ES) que siempre es una medida coherente de riesgo. ES se puede definir como la pérdida esperada dado que las pérdidas superaron un cierto percentil. Esta medida de riesgo también es conocida como conditional value-at-risk (CVaR) o expected tail loss (ETL), entre otros. A continuación se muestran los resultados de estimar CVaR para los datos de la aplicación 1 (ver cuadro 3).
Se aprecia que el método propuesto arroja valores mayores de CVaR. Para calcular el CVaR en la metodología POT se emplea la ecuación (7.19) de McNeil et al. (2005) que viene dada por:
Los valores de VaRα se toman de los resultados del cuadro 2. Para encontrar el valor de CVaR por el método POT-Bayes, se emplea la definición del CVaR. La medida CVaR se define como el valor esperado de las pérdidas esperadas, dado que las pérdidas superaron el VaR, y se calcula como sigue (ver definición 2.15, McNeil et al., 2005):
Donde VaR viene dada por la expresión (2) para este caso. Analíticamente no es fácil resolver esta integral para la modificación a la distribución de Pareto generalizada; por lo tanto, se utilizan métodos numéricos para aproximar la integral. Específicamente, se utiliza una cuadratura y se emplea la función quad de la librería pracma de R.
Para calcular el CVaR en la distribución g-h se utiliza la aproximación desarrollada en Jiménez y Arunachalam (2011):
Donde Φ denota la función de distribución acumulada de una normal estándar y zα es el percentil de una distribución acumulada de una normal estándar al nivel α; mientras que a, b, g, h son los parámetros de la distribución g-h.
Aplicación 2 (Resultados de Temnov y Warnung, 2008)Temnov y Warnung (2008) comparan tres métodos para obtener la distribución de pérdidas agregadas; los datos provienen de una entidad financiera junto con datos externos de un grupo de bancos. Los autores estiman VaR al 99.9% a las distribuciones obtenidas mediante tres métodos: simulación Monte Carlo (MC), transformada rápida de Fourier (FFT) y la metodología Credit Risk+ (CRP). Entonces, en este artículo, para cada línea de negocio se realiza una simulación de 5 000 réplicas con los datos de la severidad y de frecuencia de la tabla 1 de Temnov y Warnung (2008); luego de obtener la distribución de pérdidas, se calcula VaR y CVaR al 99.9% mediante la técnica POT y g-h propuesta; finalmente, se comparan con el promedio de los tres resultados de Temnov y Warnung.
Shevchenko (2010), con un propósito similar, realiza comparaciones de simulación Monte Carlo, FFT y el algoritmo recursivo de Panjer; el autor concluye que cada método tiene sus fortalezas y debilidades. Por ejemplo, la simulación Monte Carlo es lento, pero es fácil de implementar y permite modelar dependencia, característica que no es fácil de incluir en los métodos de FFT y Panjer. Sin embargo, el método de Panjer es el más fácil de implementar aunque incluye error de discretización. El método de FFT es generalmente más rápido. Lou y Shevchenko (2009) implementan un algoritmo de integración numérica directa adaptativa para calcular VaR y CVAR al 99.9% para distribuciones agregadas. Los resultados muestran que este método funciona mejor que Monte Carlo y que algunas veces es más preciso que FFT. Estos resultados se dan cuando se supone independencia entre el proceso de frecuencia y de severidades.
Compagación del VaR al 99.9% paga difegentes métodos
| M-C | FFT | CRP | Promedio | POT | g-h | |
|---|---|---|---|---|---|---|
| Línea 1 | 662.0 | 656.12 | 656.45 | 658.19 | 489.71 | 627.92 |
| Línea 2 | 67.4 | 68.34 | 68.29 | 68.01 | 47.17 | 48.82 |
| Línea 3,8,9 | 33.5 | 32.33 | 32.60 | 32.81 | 33.51 | 37.50 |
| Línea 4 | 26.0 | 27.30 | 27.26 | 26.85 | 28.49 | 28.31 |
| Línea 6 | 108.5 | 110.17 | 110.31 | 109.66 | 138.97 | 184.51 |
| Línea 7 | 212.0 | 209.47 | 209.76 | 210.41 | 352.20 | 415.78 |
| Total | 1109.4 | 1103.73 | 1104.67 | 1105.93 | 1090.05 | 1342.84 |
Nuevamente la metodología POT ha sido calculada usando un umbral del 90% de los datos, mientras que g-h incluye la regresión robusta. Los resultados de la segunda hasta la cuarta columna son obtenidos de la tabla 1 de Temnov y Warnung (2008).
Sin tener en cuenta la dependencia entre las líneas de negocio (en otras palabras, no se tienen en cuenta los beneficios de diversificación), se observa que el método POT subestima el VaR total con respecto al promedio de los resultados de Temnov y Warnung, mientras que la técnica g-h propuesta lo sobreestima. En valores absolutos, se aprecia una alta sobreestimación por parte de POT y g-h para la línea 7. En este caso, la severidad sigue un “modelo de media infinita”. Estos modelos (o distribuciones) se caracterizan por presentar colas extremadamente pesadas. Nešlehová et al. (2006) presentan una discusión cuando ocurren estos casos y la consecuencia es que el cálculo del VaR puede conllevar a cargos de capital absurdamente altos. Por tal razón, se debe prestar mayor atención al realizar cálculos de VaR mediante cualquier técnica a este tipo de modelos. En estos modelos, medidas como el expected shortfall (o CVaR) no se pueden calcular cuando se estima mediante POT; de ahí el nombre de modelos de media infinita.
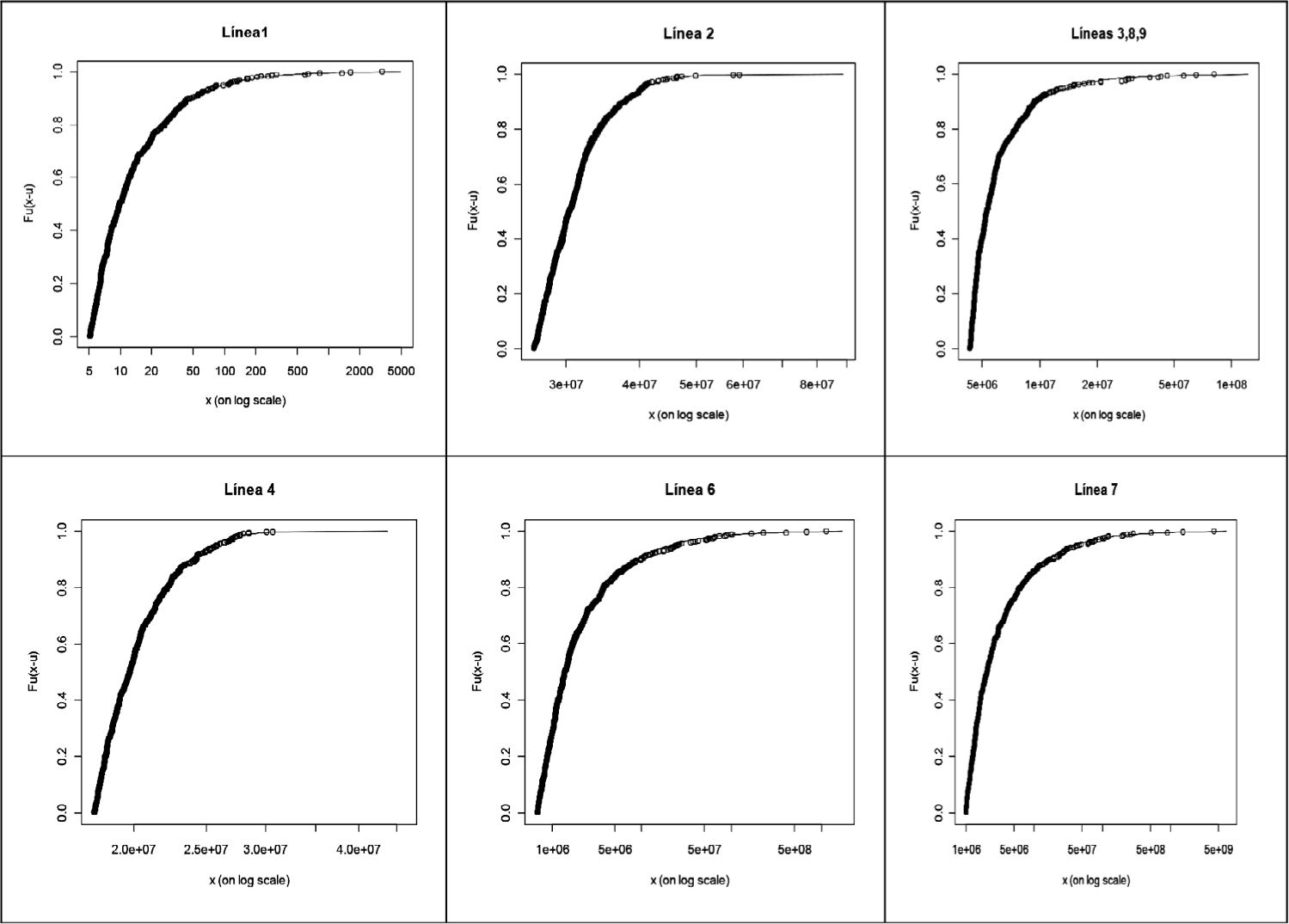
A continuación se muestra el gráfico del ajuste de la distribución de Pareto generalizada a los datos en exceso (simulados) de las diferentes líneas de negocio cuando se emplea el umbral seleccionado.
Otra conclusión del artículo de Nešlehová et al. (2006) es que si EVT se opera correctamente, se puede dar una solución a los problemas de modelos de media infinita. Sin embargo, esto no se tratará en este artículo y será tema de una futura investigación.
ConclusionesEn este artículo se propone una modificación al método de Hoaglin (1985) para la estimación de parámetros de una distribución g-h. El método original emplea la pendiente de una regresión de mínimos cuadrados ordinarios para la estimación del parámetro h. La propuesta es realizar una regresión robusta para mitigar los inconvenientes cuando no se cumplen los supuestos de la regresión por mínimos cuadrados.
En ambos casos de aplicación, se aprecia que el método propuesto de la g-h sobreestima el OpVaR empírico, mientras que el método POT lo subestima. Sin embargo, esto no lleva a una conclusión decisiva de qué método es mejor, pero sí destacar las diferencias en los resultados entre ambas metodologías.
Mediante la revisión de la literatura y las aplicaciones, el uso del método g-h puede ser de gran utilidad en la cuantificación de riesgo operativo, cuyas distribuciones de pérdidas se caracterizan por presentar colas pesadas. Sin embargo, se requiere especial atención al estimar OpVaR bajo modelos de media infinita (distribuciones con cola extremadamente pesadas). Estos modelos pueden conllevar a estimaciones de VaR absurdamente altos, lo que se confirmó en la segunda aplicación. Una futura investigación estará encaminada a estudiar otras metodologías, propuestas en otros trabajos, para resolver este problema. Finalmente, como se puede apreciar en la literatura, las fuentes de datos de pérdidas por riesgo operativo resultan, por lo general, de simulaciones o bases de datos que pueden ser costosas o no son fáciles de conseguir. Por lo tanto, se espera que la industria financiera pueda compartir sus datos a la academia y realizar investigaciones futuras con datos reales y en diversos escenarios, pues diversos autores, como Nešlehová et al. (2006), ya habían reconocido esta necesidad.
| depth | lo | hi | mids | spreads | |
|---|---|---|---|---|---|
| 1 | 1083.5 | 1.778954 | 1.778954 | 1.778954 | 0 |
| 2 | 542 | 1.321119 | 2.970297 | 2.145708 | 1.649178 |
| 3 | 271.5 | 1.151832 | 4.787836 | 2.969834 | 3.636004 |
| 4 | 136 | 1.068482 | 7.792208 | 4.430345 | 6.723726 |
| 5 | 68.5 | 1.028754 | 14.067812 | 7.548283 | 13.039058 |
| 6 | 34.5 | 1.01421 | 20.639631 | 10.826921 | 19.625421 |
| 7 | 17.5 | 1.004819 | 28.8282 | 14.91651 | 27.823381 |
| 8 | 9 | 1 | 46.5 | 23.75 | 45.5 |
| 9 | 5 | 1 | 57.410636 | 29.205318 | 56.410636 |
| 10 | 3 | 1 | 144.657591 | 72.828795 | 143.657591 |
| 11 | 2 | 1 | 152.413209 | 76.706604 | 151.413209 |
| 12 | 1 | 1 | 263.250366 | 132.125183 | 262.250366 |
| P | LHS | UHS | In of ratio | z1-p=-zp | gP |
|---|---|---|---|---|---|
| 0.25012 | 0.457835 | 1.191343 | 0.95632766 | 0.67412675 | 1.41861699 |
| 0.12529 | 0.627122 | 3.008882 | 1.56818276 | 1.14894943 | 1.36488406 |
| 0.06 | 0.710472 | 6.013254 | 2.13579177 | 1.53201331 | 1.39410785 |
| 0.03 | 0.7502 | 12.288858 | 2.79610844 | 1.85763375 | 1.50519899 |
| 0.02 | 0.764744 | 18.860677 | 3.20529331 | 2.14639779 | 1.4933361 |
| 0.01 | 0.774135 | 27.049246 | 3.55366813 | 2.40547716 | 1.47732358 |
| 0.00 | 0.778954 | 44.721046 | 4.0502475 | 2.6393542 | 1.53456005 |
| 0.00 | 0.778954 | 55.631682 | 4.26855614 | 2.83276882 | 1.50684945 |
| 0.00 | 0.778954 | 142.878637 | 5.21179886 | 2.99230391 | 1.74173447 |
| 0.00 | 0.778954 | 150.634255 | 5.26465803 | 3.11397203 | 1.69065681 |
| 0.00 | 0.778954 | 261.471412 | 5.81612824 | 3.31302269 | 1.75553529 |
| UHSp | -zp | g(zp) | g(z)/(exp(-g(z)*zp)-l) | nuevo In UHS* |
|---|---|---|---|---|
| 1.191343 | 0.674126751 | 1.35442499 | 0.907839288 | 0.07839333 |
| 3.008882 | 1.148949428 | 1.3842514 | 0.354401762 | 0.064244492 |
| 6.013254 | 1.532013308 | 1.41963703 | 0.181973724 | 0.090073058 |
| 12.288858 | 1.857633746 | 1.45766744 | 0.104145655 | 0.246728163 |
| 18.860677 | 2.146397794 | 1.49750616 | 0.062697901 | 0.16765187 |
| 27.049246 | 2.405477165 | 1.53814002 | 0.038993844 | 0.05330763 |
| 44.721046 | 2.639354202 | 1.57879362 | 0.02485455 | 0.105729774 |
| 55.631682 | 2.832768819 | 1.61526146 | 0.016809475 | −0.067059722 |
| 142.87864 | 2.992303907 | 1.64728154 | 0.012000802 | 0.539213768 |
| 150.63426 | 3.113972031 | 1.67288025 | 0.009193349 | 0.325579747 |
| 261.47141 | 3.313022686 | 1.71695973 | 0.005832087 | 0.421944549 |
Un modelo de regresión lineal estimado mediante mínimos cuadrados no se puede comportar bien cuando los errores no se distribuyen de manera normal, especialmente cuando su distribución presenta colas pesadas. Esto se debe a la presencia de observaciones influyentes. Una solución es usar el método de la regresión robusta, cuyos estimados no son tan sensibles en la presencia de datos influyentes (Fox, 2002).
El método más común en regresión robusta es la estimación M, desarrollada por Huber en 1964. Sea el modelo de regresión lineal:
Donde x,βˆ es la notación matricial para las variables explicativas y los estimados de los parámetros respectivamente. Entonces el estimador M es el que minimiza la función:Donde ρ brinda la contribución de cada residuo a la función objetivo; ϱ debería tener las siguientes propiedades:- •
ρ(e)≥0
- •
ρ(0)=0
- •
ρ(e)=−e
- •
ρ(ek)≥ρ(ek′) para |ek|>|ek′|
Sea φ la derivada de ρ. Al diferenciar la función objetivo con respecto a los estimados de los coeficientes de la regresión βˆ, y al igualar las derivadas parciales a cero, se obtienen las j ecuaciones para estimar los coeficientes:
Sea la función de pesos w(e)=φ(e)/e y nombre wk=w(ek). Entonces, las ecuaciones por ser estimadas se pueden reescribir como:Y éste se vuelve un problema de mínimos cuadrados ponderados al minimizar ∑k=1nwk2ek2. Sin embargo, los pesos dependen de los residuos, que dependen de los coeficientes estimados y éstos, a su vez, de los pesos. Por lo tanto, se requiere de una solución iterativa, técnica conocida como mínimos cuadrados iterativamente reponderados (IRLS, por sus siglas en inglés). Finalmente, se resuelve iterativamente hasta que los coeficientes convergen.Donde W(t−1)=diagwk(t−1) es la matriz (diagonal) de pesos para la iteración t−1. La función objetivo del estimador M, en específico, el estimador de Huber está dada por:Mientras que la función objetivo para el esitmador de mínimos cuadrados es e2; es una constante de afinamiento. Entre más pequeña es esta constante hay más resistencia a los valores atípicos, pero produce menor eficiencia cuando los errores se distribuyen normal. En particular, para el estimador de Huber, l=1.345σ, donde σ es la desviación estándar de los errores.La estimación mediante mínimos cuadrados ordinarios se puede ver como un caso específico de la estimación mediante mínimos cuadrados ponderados, donde la función de pesos es igual a 1. Esta función en la estimación robusta (Huber) es de la forma:
Al aplicar la regresión robusta para el método g-h en los datos de fuego de Dinamarca se obtienen las siguientes estimaciones:
A=1.778154
B=0.8241551
h=0.1795578
g=1.505642