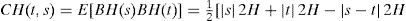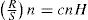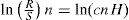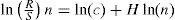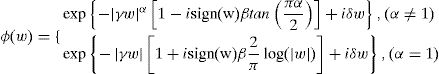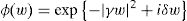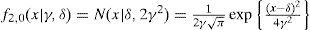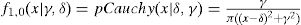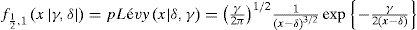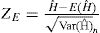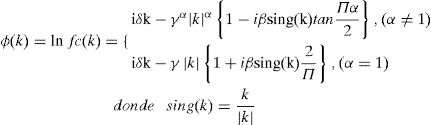Este trabajo aborda la utilidad de estimar, previo a cualquier análisis, el parámetro α de la distribución α-estable y el coeficiente de Hurst para una serie financiera en periodos de alta volatilidad. Mediante la estimación del coeficiente de Hurst y el parámetro α se busca explorar la violación de dos grandes supuestos en la modelación de series financieras: suponer que las series presentan una distribución normal y que los rendimientos sucesivos son independientes; asimismo, se analiza el caso del tipo de cambio Fix peso-dólar en México en el periodo 1992–2011. Uno de los principales resultados es la identificación de características fractales y colas pesadas en la serie para algunos periodos en magnitudes diferenciadas; dichas diferencias se acentúan en periodos de crisis. Caracterizar la serie mediante estos parámetros a través de un índice permitirá mejorar la toma de decisiones sobre el tipo de análisis que es metodológicamente correcto aplicar en una ventana de tiempo específica, ya sea para valuación de activos o para la gestión de riesgos.
This paper addresses the utility of estimating the parameter α of α-stable distribution and the Hurst coefficient for financial series in periods of high volatility. By estimating the Hurst coefficient and the parameter α we seek to explore the violation of two assumptions in modeling financial series, the assumption that the series are normally distributed and that the successive returns are independent. We present the case of the peso dollar Fix Mexico exchange rate in the 1992–2011 period. One of the main results is the identification of fractal characteristics and heavy tails in the series for some periods in different magnitudes, such differences are accentuated during crisis periods. Characterizing the series by these parameters through an index will improve decision-making on the type of analysis that is methodologically correct to apply in a specific time window for asset pricing and risk management.
El análisis de datos financieros es un tema complejo que requiere de rigor analítico para poder realizar estimaciones precisas y lo más apegadas a la realidad. La presencia de colas pesadas y la dependencia de las series respecto al tiempo son dos elementos cruciales al analizar una serie financiera, pues suponer la ausencia de ambos elementos en todos los casos de manera indiscriminada puede generar conclusiones erróneas en los análisis realizados.
Recientemente, en los mercados financieros ha tenido gran auge la aplicación del análisis de la dependencia de los datos a través del tiempo mediante técnicas fractales, dadas las características de las series de datos con que se trabaja. La estimación del coeficiente de Hurst permitirá conocer si es correcto modelar una serie con un movimiento geométrico browniano o considerar la posibilidad de utilizar el movimiento browniano fraccional como una mejor aproximación. Trabajos como el de Díaz Mata (1996) y Sierra (2007) muestran que existen características fractales en el mercado mexicano, así como la aplicación del cálculo fraccional en aquellos casos en que existe dependencia de la serie en el tiempo. Por su parte, Domínguez, Ardila y Moreno (2010) identifican características fractales para el mercado colombiano.
Por otro lado, suponer que la serie se ajusta a una distribución normal es un supuesto demasiado aventurado porque la evidencia empírica demuestra que en los periodos de mayor volatilidad los mercados presentan datos atípicos, la serie es más impulsiva y presenta colas pesadas; por ello, el uso de las distribuciones α-estables es una alternativa para la modelación de datos financieros, sobre todo en periodos de alta volatilidad. McCulloch (1996a), Nolan (2003) y Cartera y Howison (2009) plantean la utilidad y aplicación de las distribuciones α-estables en el análisis de series financieras, mientras que Contreras y Venegas (2011) y Rodríguez y Cruz (2012) analizan la aplicación de las distribuciones α-estables en la valuación de opciones para el mercado mexicano, así como los diferenciales que pueden surgir en la valuación al utilizar una distribución normal y una α-estable ante la presencia de colas pesadas en las series.
Este trabajo analiza la serie del tipo de cambio Fix peso-dólar en el periodo 1992–2011, en el que se consideran cinco subperiodos de alta volatilidad en el mercado mexicano; en ellos se calculó el coeficiente de Hurst y el parámetro α con el objetivo de identificar si existe la violación del supuesto de normalidad y de independencia simultáneamente. Mediante la construcción de un índice se evalúa qué tan alejados se encuentran los datos de los supuestos de independencia y normalidad. Este análisis previo de las series permitirá elegir la metodología correcta por utilizar (ya sea usar cálculo fraccional o distribuciones α-estables en el modelado) para no obtener conclusiones erróneas al suponer normalidad e independencia en cualquier serie y periodo de tiempo de manera indiscriminada.
Además de esta introducción, este texto se organiza de la siguiente forma: en primer lugar se presenta el movimiento browniano fraccional y la obtención del coeficiente de Hurst; después se presentan las distribuciones α-estables; más adelante se estiman ambos parámetros (coeficiente de Hurst y el parámetro α) para la serie de tipo de cambio Fix peso-dólar en los intervalos de tiempo definidos y se construye un índice para conocer qué tan alejados están dichos parámetros de los supuestos de normalidad e independencia; por último se presentan las conclusiones, en las que se destaca la presencia de características fractales y colas pesadas en magnitudes diferenciadas en la serie de tipo de cambio peso-dólar para algunos periodos de alta volatilidad en el mercado cambiario mexicano, las cuales se acentúan en periodos de crisis. Pasar por alto la violación de los supuestos de normalidad e independencia generará resultados alejados de la realidad, sobre todo en periodos de alta volatilidad y de crisis.
El movimiento browniano fraccional y el coeficiente de HurstEl movimiento browniano es uno de los modelos más utilizados para describir la evolución de una serie financiera, considerando a la serie como una realización de este proceso estocástico. El movimiento browniano estándar {B(t);t≥0} es un proceso estocástico con trayectorias continuas que satisface las siguientes propiedades (Venegas, 2008):
- 1.
B(0)=0
- 2.
Los incrementos B(t)−B(s) para t>s son independientes del comportamiento pasado, independientes de B(u) con 0≤u≤s.
- 3.
Los incrementos B(t)−B(s) para t>s se distribuyen normalmente con media 0 y varianza (t−s).
El movimiento geométrico browniano, que trabaja con los logaritmos de los precios, se caracteriza por los siguientes supuestos (Venegas, 2008):
- •
Incrementos estacionarios e independientes.
- •
La varianza en intervalos de duración constante está equidistribuida.
- •
La distribución de sus incrementos es normal.
- •
Siguen trayectorias continuas.
Aun cuando el movimiento browniano es uno de los modelos más utilizados en la descripción del comportamiento de series financieras, éstas no necesariamente se ajustan a los supuestos que implica, ya que los mercados no siempre son normales, completos, eficientes y libres de arbitraje. De acuerdo con la evidencia presentada por diversos autores, los supuestos que generalmente no se cumplen del movimiento browniano son los siguientes (Domínguez, Ardila y Moreno, 2010):
- •
No estacionariedad. Volatilidad de las series no constante en el tiempo.
- •
Dependencia a largo plazo. En general los datos financieros presentan dependencia en el tiempo.
- •
Colas pesadas. Las distribuciones de los rendimientos o variaciones de las series financieras son leptocúrticas.
- •
Discontinuidad en el comportamiento. La sensibilidad de los datos financieros a información externa, permite la presencia de saltos.
Como alternativa para superar las debilidades al modelar asumiendo los supuestos que implica el movimiento geométrico browniano, Mandelbrot (1997) propone un modelo denominado multifractal basado en el movimiento browniano fraccional y los procesos estocásticos multifractales. El movimiento browniano fraccional es un proceso gaussiano obtenido mediante una transformación de la integral estocástica del movimiento browniano unidimensional. Fue considerado por primera vez por el matemático ruso Kolmogórov (1940) y posteriormente por Mandelbrot en 1965.
El movimiento browniano fraccional de índice H, {BH(t); t≥0} donde 0≤H≤1 es un proceso estocástico que satisface (Sierra, 2007):
- 1.
BH(0)=OH
- 2.
E[BH(t)]=0 para todo t ∈ R
- 3.
La covarianza del proceso para dos instantes s,t ∈ R está dada por la expresión:
El índice H es llamado parámetro de Hurst en honor del científico británico Harold Edwin Hurst (1880–1978); se trata de una medida de independencia de las series de tiempo y una forma de caracterizar series fractales. Cabe destacar que el movimiento browniano estándar puede obtenerse del movimiento browniano fraccional si H=12, ya que en este caso particular se tiene la misma función de covarianza.
El movimiento browniano fraccional presenta varianza cíclica no periódica en todas las escalas temporales y tiene en cuenta la dependencia estadística a largo plazo, además de tener dos características típicas de los conjuntos fractales que le confieren una mayor variabilidad de comportamientos (Sierra, 2007):
- 1.
La autoafinidad o autosimilaridad estadística. Al reducir la escala temporal para representar trayectorias del proceso, la apariencia de la serie es semejante a la de la serie en la escala original.
- 2.
Valor no entero de la dimensión. Al caracterizar el proceso la dimensión está relacionada con las variaciones que se experimentan entre puntos próximos, por lo que cuanto mayor es el valor de la dimensión mayor será la variación.
De acuerdo con esto, si una serie temporal tiene la propiedad de una alta dependencia, su modelación debería hacerse mediante movimientos brownianos fraccionales que, a diferencia del movimiento browniano tradicional, incorpora las características de independencia o dependencia propias de las series financieras, partiendo de los mismos supuestos de los modelos desarrollados con el movimiento browniano tradicional.
Para diferenciar las series fractales, una de las técnicas más utilizadas es el análisis de rango reescalado RSn, el cual será utilizado para determinar el coeficiente Hurst (H) asociado a una serie temporal. Hurst desarrolló esta metodología que se puede aplicar a series de tiempo que no necesariamente son movimientos brownianos (Hurst, 1951).
Donde:
RS Es la notación utilizada para el estadístico rango reescalado.
c: es una constante de proporcionalidad.
n: es el número de datos por intervalo.
H: es el coeficiente de Hurst.
RS es un estadístico con media cero, expresado en términos de desviación estándar, cuyo análisis es de tipo no paramétrico. El punto clave en este análisis es la determinación del coeficiente de Hurst. A continuación se describe brevemente la metodología utilizada para su cálculo (Sierra, 2007):
- 1.
Con la serie en el orden original se genera la serie de retornos tomando las diferencias logarítmicas de los datos.
- 2.
Se divide la serie de retornos en intervalos de igual número de datos; el número de intervalos lo llamaremos en adelante particiones de tal forma que el número de particiones por el número de datos en el intervalo sea igual al tamaño de la serie de rendimientos. Al variar el número de particiones se obtiene cada vez la serie dividida en intervalos de igual número de datos; si la serie tiene características autoafines, sin importar el tamaño de los intervalos, debe conservar las mismas características.
- 3.
En cada partición, para cada uno de los intervalos:
- a.
Calcular la media y la desviación estándar.
- b.
Determinar la variación de cada dato con respecto a la media y acumular las diferencias.
- c.
- d.
Se divide el rango por la desviación estándar, obteniendo el rango estandarizado.
- e.
Por propiedades de los logaritmos tenemos que:
- a.
Con la expresión log-lineal determinada por el logaritmo del rango reescalado de todas las particiones que son posibles y por el logaritmo del número de datos para cada partición (ecuación 4), se realiza una regresión para establecer el coeficiente Hurst (H), que corresponde a la pendiente de la recta de regresión. En esta ecuación c representa una constante de proporcionalidad relacionada con el factor de escala.
- 1.
Si 0≤H≤12, se trata de series antipersistentes con reversión a la media. Es decir, si la serie ha estado arriba de un determinado valor que hace las veces de media de largo plazo en el periodo anterior, es más probable que esté abajo en el periodo siguiente y viceversa, por lo que se considera que esta serie presenta ruido rosa.
- 2.
Si H=12, los datos son independientes y se considera que no hay memoria. Se trata de una serie aleatoria que cumple con todas las características del movimiento browniano estándar y presenta ruido blanco.
- 3.
Si 12≤H≤1, la serie es persistente, refuerza la tendencia. Es decir, si la serie estaba arriba (o abajo) de su media de largo plazo en el periodo anterior, lo más probable es que continúe arriba (o abajo) en el periodo siguiente, por lo que se considera que la serie presenta ruido negro y esto aparece generalmente en procesos cíclicos de largo plazo.
- 4.
Si H=1, la serie es determinística.
Para analizar una serie de tiempo se considera recomendable primero establecer el valor del coeficiente Hurst, el cual nos permitirá conocer si se cumple con el supuesto de independencia de los modelos tradicionales. Es decir, si el valor del coeficiente Hurst es aproximadamente 0.5, indica un movimiento browniano estándar y la serie no tiene memoria de largo plazo; en caso contrario, cualquier evento futuro se verá afectado por los datos anteriores.
Distribuciones α-establesAlgunos fenómenos de la naturaleza no pueden ser descritos mediante la suposición normal, pues presentan observaciones con valores extremos, lo cual caracteriza la inestabilidad de la serie y denota la presencia de colas pesadas, efecto conocido como impulsividad; por lo general, los datos financieros presentan un grado de impulsividad mayor que el que la distribución normal es capaz de describir. Estos sucesos descritos mediante una distribución normal serían considerados como muy poco probables.
La teoría de las distribuciones estables fue desarrollada por primera vez en la década de los veinte del siglo pasado por Paul Lévy y Aleksandr Khinchin. Desde entonces, esta distribución ha sido aplicada en diferentes áreas de conocimiento, tales como economía, física, hidrología, biología y procesamiento de señales. Sin embargo, no fue hasta los trabajos de Mandelbrot en economía —en la década de los sesenta— que se popularizó la distribución α-estable; este autor propuso una revolucionaria teoría basada en dicha distribución para resolver el problema de la fluctuación de los precios; más tarde se demostró que muchas otras variables en economía siguen una distribución α-estable.
Cabe resaltar que la distribución α-estable cumple con el teorema central del límite y la propiedad de estabilidad, que denota que las distribuciones estables son isomorfas; además, contiene a la distribución normal como caso particular de ésta. Por otro lado, existe cierta complejidad al trabajar con este tipo de distribuciones porque carecen, en general, de una expresión analítica.
Aunque existen recientes avances computacionales, ahora es posible aplicarlas con mayor factibilidad en diversas áreas. Existen diversas definiciones de una distribución α-estable, pero la de mayor aceptación y uso es la presentada por Nolan, la cual caracteriza a las distribuciones α-estables por cuatro parámetros que son especificados en la siguiente definición:
Una variable aleatoria X tiene distribución α-estable si tiene la siguiente función característica:
,Donde los parámetros de sing(w)=wwyα∈(0,2] se definen de la siguiente forma: α representa el exponente característico, el cual controla el grado de impulsividad de la variable aleatoria W. Por otra parte, el parámetro β ∈ [−1, +1] controla la simetría de la distribución (β=0, para la distribución α-estable simétrica, β=1 y β=−1 para la familia de distribuciones α-estable positiva y negativa, respectivamente). Mientras que γ>0 es un parámetro de escala, también denominado dispersión, y δ es el parámetro de posición.
Cabe destacar que si en la expresión de la función característica el parámetro α=2, el parámetro β pierde significado, ya que βtanπ=0. En ese caso, la función característica queda como:
La expresión anterior es la función característica de una variable aleatoria gaussiana con media δ y varianza σ2=2γ2, por lo que a partir de la definición anterior también se muestra que la distribución normal es un caso particular de distribución α-estable. Dadas las propiedades de la distribución α-estable anteriormente mencionadas se infiere que su uso está justificado en la misma medida que el de la distribución normal y no sólo eso, sino que la distribución normal es un caso particular de la distribución α-estable y por lo tanto el rango de aplicación de las distribuciones α-estables es aún más amplio que el de la distribución normal. Esto es debido, sobre todo, a que la función de densidad de probabilidad α-estable existe y es continua, pero no puede expresarse de manera compacta, salvo unas cuantas excepciones. Dicho de otro modo, la integral respecto a (w) de la función característica (5) sólo tiene solución analítica para los casos que se describen, denotando a la distribución α-estable por cuatro parámetros fα,β(.γ,δ) (Nolan, 2005).
Una distribución α-estable con parámetros:
- •
f2,0(.|γ, δ) es una distribución Normal con media δ y varianza 2γ2 con densidad
- •
f1,0(.|γ, δ) es una distribución de Cauchy con densidad
- •
f12,1(.|γ,δ) es una distribución de Lévy con densidad
Existen en la actualidad sistemas para poder estimar los parámetros de la función de distribución α-estable. De igual forma, el avance en los sistemas de cómputo ha sido un elemento clave para la reciente utilización de este tipo de distribuciones en los mercados financieros.
El coeficiente de Hurst y el parámetro αComo parte de la aplicación de los conceptos introducidos en este trabajo para el análisis de series financieras se estimó el coeficiente de Hurst y el parámetro α para la serie diaria del tipo de cambio Fix peso-dólar en el periodo 1992–2011, publicada por el Banco de México. Se analizan de manera simultánea la impulsividad de una serie representada por el parámetro α y la independencia de los datos en el tiempo mediante el coeficiente de Hurst; esto permitirá caracterizar e identificar cuál es el análisis metodológicamente correcto por aplicar en cada serie y ventana de tiempo en particular. Asimismo, se calculan ambos parámetros para la serie diaria del tipo de cambio peso dólar del periodo 1992–2011 en diferentes ventanas de tiempo. Los cortes transversales de la serie en el tiempo se eligieron por tratarse de periodos de alta volatilidad o crisis financieras.
Estimación del coeficiente de HurstEn primer lugar se presentan los valores correspondientes al coeficiente de Hurst para los diferentes intervalos de tiempo definidos. Las ventanas de tiempo se construyeron con base en la distinción de periodos de alta volatilidad caracterizados por alguna crisis financiera, por lo tanto son periodos de difícil pronóstico en el tiempo.
La metodología utilizada para el cálculo del coeficiente de Hurst es el rango reescalado, considerando los rendimientos logarítmicos del tipo de cambio Fix peso-dólar para el periodo 1992–2011. Se realizaron 180 particiones en promedio para cada periodo tomando en cuenta el número de observaciones de cada periodo; éste es el número máximo de particiones posibles con la menor pérdida de datos. En el cuadro 1 se presentan los intervalos de tiempo definidos para analizar la serie.
Se calculó una prueba de hipótesis para poder evaluar la significancia estadística del coeficiente de Hurst, la prueba planteada es la siguiente:
- H0:
El proceso es aleatorio e independiente (ruido blanco, H=0.5)
- H1:
El proceso está correlacionado (positiva o negativamente, H≠0.5)
También se utiliza la prueba planteada por Esctot (2000), la cual utiliza para el contraste de hipótesis el siguiente estadístico:
El estadístico ZE se contrasta con las tablas de probabilidad de la distribución normal y la hipótesis nula se aceptará con un 95% de confianza. De los cinco periodos analizados, sólo se aceptó la hipótesis nula en el periodo III porque se puede decir que la serie es independiente en el tiempo o se trata de ruido blanco.
Periodo I. Para el primer periodo considerado, que incluye la crisis de finales de 1994, podemos observar los siguientes resultados.
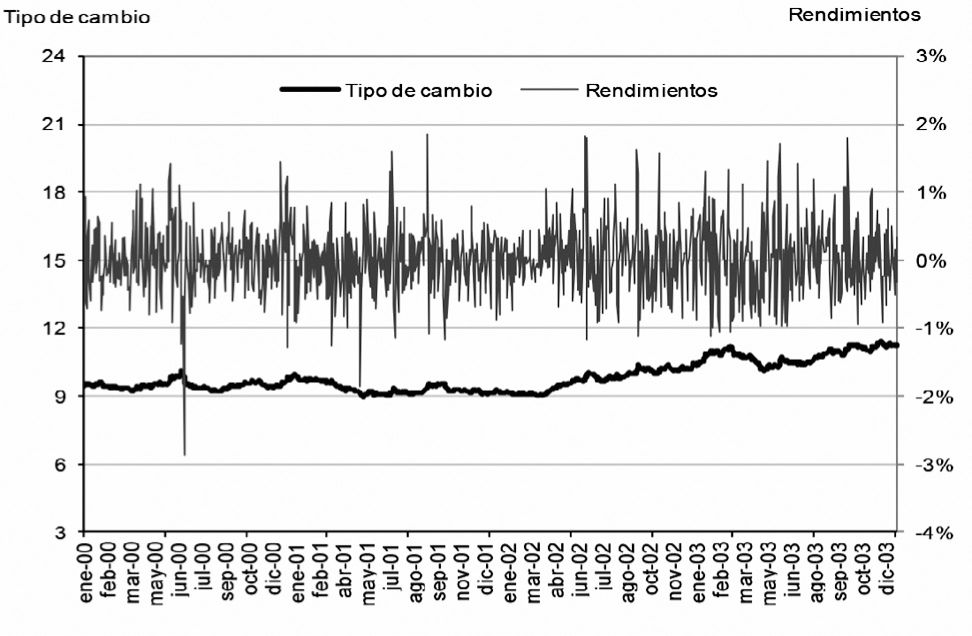
En la figura 1 podemos observar los rendimientos logarítmicos del tipo de cambio (eje del lado derecho) y los valores del tipo de cambio Fix (eje del lado izquierdo) en el periodo 1992–1995. En este periodo de análisis es necesario mencionar que de 1990 a 1994 se mantuvo un tipo de cambio mediante un sistema de bandas cambiarías; por ello, no es sino hasta finales de 1994 que la volatilidad del mercado realmente afecta los mercados cambiarios y es a partir de ese año en que el análisis de series financieras, como se conoce en la actualidad, toma sentido porque a partir del 22 de diciembre el tipo de cambio en México es de libre flotación.
La figura 2 muestra la estimación del coeficiente de Hurst para esta ventana de tiempo. En el eje horizontal se encuentra el logaritmo del número de datos para cada partición y en el eje vertical se encuentra el logaritmo del estadístico de rango reescalado calculado; la pendiente de la regresión estimada con estos dos datos determina el coeficiente de Hurst. El coeficiente estimado para el periodo I, H=0.790, denota que la serie es persistente, por lo que se rechaza H0. Como se mencionó, hasta diciembre de 1994 el tipo de cambio se mantenía controlado mediante una banda de flotación. El objetivo de considerar el periodo completo fue ilustrar el cambio en la política cambiara y considerar intervalos de al menos tres años para las particiones del periodo de estudio para observar los cambios en la serie.
Periodo II. El segundo periodo considerado, que abarca de 1996 a 1999, muestra un comportamiento similar al periodo I, respecto a la dependencia de los datos a través del tiempo.
La figura 3 muestra los rendimientos logarítmicos del tipo de cambio (eje del lado derecho) y los valores del tipo de cambio Fix (eje del lado izquierdo) en el periodo 1996–1999. En este periodo se observa mayor volatilidad del tipo de cambio. De igual forma que en el periodo I, existe persistencia en los datos de acuerdo con el valor del coeficiente de Hurst estimado, H=0.683.
La figura 4 muestra la estimación del coeficiente de Hurst para esta ventana de tiempo. En el eje horizontal se encuentra el logaritmo del número de datos para cada partición y en el eje vertical el logaritmo del estadístico de rango reescalado calculado; la regresión estimada con estos dos datos determina el coeficiente de Hurst como la pendiente de la recta. De acuerdo con el valor estimado de H, se rechaza H0: H=0.5.
Periodo III. El tercer periodo propuesto, que abarca de 2000 a 2003, muestra un comportamiento contrario a los previos, ya que la mayor volatilidad se registra a mitad del año 2000; aun así la dependencia de la serie en el tiempo muestra un comportamiento sin correlación de la serie.
La figura 5 muestra los rendimientos logarítmicos del tipo de cambio y el tipo de cambio Fix en el periodo 2000–2003. El eje del lado izquierdo muestra los valores del tipo de cambio y el del lado derecho los rendimientos logarítmicos.
La figura 6 muestra la estimación del coeficiente de Hurst para esta ventana de tiempo. En el eje horizontal se encuentra el logaritmo del número de datos para cada partición y en el eje vertical el logaritmo del estadístico de rango reescalado calculado; la pendiente de la regresión estimada determina el coeficiente de Hurst. El coeficiente H=0.465 denota que la serie es aleatoria y que existe independencia de la serie en el tiempo, por lo que se acepta H0: H=0.5 (ruido blanco).
Periodo IV. El cuarto periodo propuesto, que abarca de 2004 a 2007, muestra dependencia de la serie en el tiempo, así como un comportamiento antipersistente.
La figura 7 muestra los rendimientos logarítmicos del tipo de cambio (eje del lado derecho) y los valores del tipo de cambio Fix (eje del lado izquierdo) en el periodo 2004–2007. De acuerdo con el valor estimado del coeficiente de Hurst, H=0.74, la serie es antipersistente.
La figura 8 muestra la estimación del coeficiente de Hurst para esta ventana de tiempo. En el eje horizontal se encuentra el logaritmo del número de datos para cada partición y en el eje vertical se encuentra el logaritmo del estadístico de rango reescalado calculado; la pendiente de la regresión estimada determina el coeficiente de Hurst. El ajuste del rango reescalado mediante la regresión estimada nos muestra que el coeficiente de Hurst, H=0.3743, denota que la serie es antipersistente en el tiempo, por lo que se rechaza H0.
Periodo V. El quinto periodo propuesto, que abarca de 2008 a 2011, muestra un comportamiento mucho más volátil; esto se debe por la crisis mundial que se detonó en 2008 y que se ha agravado a la fecha. Podemos ver que nuevamente existe dependencia de la serie respecto al tiempo y que la serie presenta un comportamiento persistente. El tipo de cambio fue una variable que se vio altamente afectada por los desequilibrios económicos internacionales y evidentemente por la alta dependencia de México respecto a la economía de Estados Unidos.
La figura 9 muestra los rendimientos logarítmicos del tipo de cambio (eje del lado derecho) y los valores del tipo de cambio Fix (eje del lado izquierdo) en el periodo 2008–2011. Se puede observar autosimilaridad en la gráfica de los rendimientos.
La figura 10 muestra la estimación del coeficiente de Hurst para esta ventana de tiempo. En el eje horizontal se encuentra el logaritmo del número de datos para cada partición y en el eje vertical se encuentra el logaritmo del estadístico de rango reescalado calculado; la pendiente de la regresión estimada determina el coeficiente de Hurst. El ajuste del rango reescalado mediante la regresión estimada nos muestra que el coeficiente de Hurst, H=0.695, denota que la serie es persistente en el tiempo, por lo que se rechaza H0.
En este último periodo la serie muestra persistencia, dados los periodos de alta volatilidad en todos los años a partir de que se detonó la crisis de 2008 en el mundo; el tipo de cambio es una de las variables que refleja el efecto de la volatilidad del mercado en el mundo y la dependencia de México respecto a la situación económica de Estados Unidos.
Los cinco periodos analizados muestran que la serie del tipo de cambio es una serie que difícilmente presenta ruido blanco en el comportamiento de sus rendimientos; por el contrario, en periodos de alta volatilidad la serie denota ruido negro (antipersistencia) y ruido rosa (persistencia), pero sólo en uno de los cinco periodos analizados se determinó la existencia de ruido blanco en la serie. En el cuadro 2 se presentan los resultados para los cinco periodos determinados para el análisis fractal de la serie de tipo de cambio para México (1992–2011).
Para la serie de tipo de cambio peso-dólar, el coeficiente de Hurst es estadísticamente diferente de H=0.5, lo que denota persistencia y antipersistencia según el valor de H; este comportamiento se identifica en aquellos episodios de alta volatilidad. Sólo en el periodo III se acepta la hipótesis nula H0: H=0.5 (ruido blanco).
Se observa que el último periodo (2008–2011) muestra un coeficiente similar al presentado en los episodios de crisis de 1995 y 1997, de los periodos I y II, donde hubo alta volatilidad o crisis financiera, por lo que presentan un coeficiente de Hurst distinto de 0.5.
Estimación del parámetro αCon el objetivo de evaluar la impulsividad de la serie en los intervalos de tiempo definidos, se estimó el parámetro α correspondiente a la distribución α-estable con base en el software desarrollado por Nolan: estable.exe. Se consideraron los mismos cinco periodos de tiempo analizados previamente y para cada uno de ellos se ajustó la distribución α-estable y se estimó el parámetro α, el cual nos dice que tan impulsiva es una serie y si ésta denota la presencia de valores extremos o colas pesadas. Éste es el caso de muchas variables financieras en periodos de alta volatilidad y que es imposible modelar asumiendo que las series se distribuyen normalmente.
Se consideró la parametrización S1 que es la generalmente utilizada (Samorodnitsky y Taqqu, 1994) para la modelación de datos financieros.
Del ajuste de los datos de los cinco periodos considerados se obtuvieron los parámetros que caracterizan a la distribución por los tres métodos hasta ahora generalmente utilizados: método de máxima verosimilitud, método de cuantiles y método de regresión (Nolan, 2005).
En este caso se utilizó el método de regresión, pues presentó un buen ajuste a los datos de acuerdo con la prueba Kolmogorov Smirnov. Cabe mencionar que en los tres métodos utilizados y para los cinco periodos no se rechaza la prueba de hipótesis H0: la serie se ajusta a una distribución α-estable. Sin embargo, el método de regresión es el mayormente utilizado en el análisis de series financieras porque presenta un mejor ajuste de las colas de la distribución.
El caso normal es aquel que corresponde a un α=2: mientras más se acerca el valor de α a 2 es correcto modelar la serie con el supuesto de normalidad; en otro caso, la presencia de impulsividad en la serie generaría errores y conclusiones equivocadas al usar la distribución normal para modelar estas series.
En los dos periodos en que hay menor volatilidad de la serie (ver cuadro 3) el parámetro a se acerca al caso normal; es decir, la serie no es tan impulsiva, en congruencia con el coeficiente de Hurst estimado en periodos de baja volatilidad, que presenta valores cercanos a 0.5 (ruido blanco). La estimación del parámetro α permite conocer si es correcto o no utilizar la distribución normal al momento de modelar una serie financiera, ya sea para realizar la valuación de activos o para la construcción de modelos de gestión de riesgos.
Es prioritario conocer si la serie presenta impulsividad y dependencia en el tiempo, características que en caso de existir generarían errores en las estimaciones realizadas al trabajar asumiendo normalidad e independencia como una verdad universal en todas las series a lo largo del tiempo de manera indiscriminada.
Grado de ajuste a los supuestos de normalidad e independenciaTomando en consideración el valor de los parámetros que caracterizan el caso en que los datos son normales y cuando no existe dependencia en el tiempo, α=2 y H=0.5, se construyó un índice tomando como valor base (igual a100) el valor de α y H en el caso de normalidad y cuando existe independencia de datos en el tiempo.
Se consideraron los parámetros estimados para cada uno de los subperiodos con el objetivo de tener una magnitud de qué tan alejados se encuentran los datos en cada periodo del caso normal y del nivel de independencia (o grado de autosimilaridad).
En la figura 12 se observa el índice que se construyó para los cinco subperiodos de estudio. En el caso del periodo III y IV la serie se acerca mucho al 100% de cumplimiento de normalidad y no dependencia, mientras que en los otros casos podemos ver que la serie presenta colas pesadas y dependencia en el tiempo. Valores por arriba de 100, para el caso del coeficiente de Hurst, denotan persistencia y por debajo de 100, antipersistencia. De igual forma, valores por debajo de 100 para el caso del parámetro α implican que la serie presenta colas pesadas y valores cercanos a 100 indican que el parámetro α es cercano al caso normal.
Este indicador permitirá al analista evaluar qué modelos son los más óptimos para el análisis de los datos, sin tener que forzar el ajuste al caso normal y suponer de facto independencia de la serie en el tiempo. Asimismo, se puede observar que en los casos donde los índices se acercan al 100 existe mayor grado de cumplimiento de los supuestos analizados en ambos indicadores de manera simultánea. En aquellos periodos en que la serie presenta cierta independencia de los datos en el tiempo, el parámetro α nos indica que la distribución de los rendimientos se ajusta en mayor medida a la distribución normal. Ambos indicadores se complementan denotando la presencia o ausencia de dependencia de la serie en el tiempo y si la distribución de los rendimientos es cercana o muy alejada de la normalidad.
Aun cuando en este análisis sólo se estén considerando dos de los grandes supuestos al analizar series financieras, son dos supuestos de gran trascendencia que permitirán determinar el método de análisis óptimo para cada serie en una ventana de tiempo determinada. En el caso de la presencia de autosimilitud en la serie o dependencia de los datos en el tiempo es posible utilizar el movimiento browniano fraccional como alternativa de modelado. De igual forma, para el caso del la ausencia de normalidad, es posible modelar las series utilizando la distribución α-estable para ajustar correctamente la impulsividad de la serie. Éste es un primer avance hacia la mejora del modelado de series financieras tomando en consideración las características de la serie misma, buscando abandonar en la medida de lo posible los supuestos rígidos que nos pueden llevar a conclusiones erróneas, incompletas y, como lo ha demostrado la evidencia empírica, de poca utilidad en periodos de alta volatilidad.
ConclusionesLa serie de tipo de cambio Fix peso-dólar analizada en el periodo 1992–2011 muestra la presencia de persistencia y antipersistencia en diferentes periodos del horizonte de tiempo considerado; de igual forma, los datos se alejan de la distribución normal porque la serie es impulsiva en esos mismos periodos. Esto nos indica que es necesario realizar análisis previos al estudio y utilización de las series financieras, ya que partir de un dogma absoluto generará conclusiones alejadas de la realidad. Por ello, es preciso identificar las características esenciales de cada serie y con ello definir cuál es la metodología y la herramienta óptima de análisis, sin tratar de encajar la realidad en un paradigma definido para el estudio de las finanzas.
En los cinco periodos analizados, la serie sólo se aproxima al cumplimiento de los supuestos de normalidad e independencia de manera simultánea en aquéllos donde hay menor volatilidad. En un intervalo de 19 años, únicamente en un periodo de seis años se observó este comportamiento; en el resto se detecta dependencia de la serie en el tiempo e impulsividad en los datos. Es necesario tomar en cuenta la estimación de manera simultánea de los parámetros aquí presentados como un paso previo al análisis de las series financieras.
La evaluación de la independencia e impulsividad de las series mediante el análisis aquí propuesto es un primer paso para analizar los datos financieros mediante las propiedades características de los mismos y no ajustando la información a un modelo definido por convención. La teoría fractal incorpora al análisis la dependencia de la serie en el tiempo; por su parte, la utilización de la distribución α-estable permite dar mayor validez al análisis realizado al poder modelar la impulsividad de las series. Ejemplos de las implicaciones de modelar con movimiento browniano fractional y con distribuciones alfa estables en valuación y análisis de riesgos para el mercado mexicano se pueden encontrar en trabajos como los de Díaz Mata (1996), Sierra (2007), Contreras y Venegas (2011), así como Rodríguez y Cruz (2012).
El indicador presentado permite evaluar los supuestos de independencia y normalidad de manera simultánea y práctica para que el analista, una vez identificadas las características de la serie, tome la decisión de cuál es la metodología correcta que debe aplicarse. También se presentan como alternativas de modelaje el uso del movimiento browniano fractional y el uso de las distribuciones α-estables en los casos donde existe dependencia e impulsividad en la serie. Todo lo anterior es un primer avance hacia la mejora del modelado de series financieras tomando en consideración las características propias de la serie, buscando abandonar en la medida de lo posible los supuestos que nos pueden llevar a conclusiones erróneas, incompletas y, como lo ha demostrado la evidencia empírica, de poca utilidad en periodos de alta volatilidad.
En trabajos subsecuentes, con base en el análisis aquí presentado, se buscará construir un índice global con el coeficiente de Hurst y el parámetro α para poder contar con un indicador eficiente y de alta frecuencia que permita determinar en qué momento los mercados se alejan demasiado de los supuestos tradicionales utilizados en la valuación de activos y gestión de riesgos; con ello se puede permitir al analista ajustar los modelos utilizados para obtener un mayor acercamiento a la realidad.