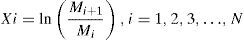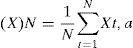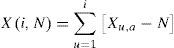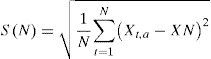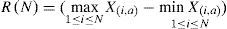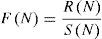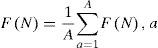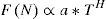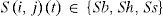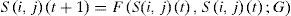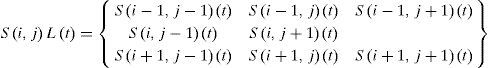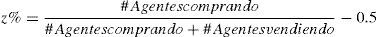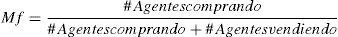El objetivo principal de este artículo es desarrollar un modelo autómata celular en el que interactúen más de un tipo de agentes bursátiles, donde el uso y el intercambio de información entre los inversionistas describen la complejidad medida a través de la estimación del coeficiente de Hurst, que representa un mercado eficiente o aleatorio al tener un valor igual a 0.5. Gracias a las variantes propuestas, en esta investigación se puede determinar que debe existir un componente racional en el simulador con el fin de generar un comportamiento eficiente.
The main objective in this paper is developing a cellular automaton model where interact more than one kind of broker, where the use and exchange of information between the investors explain the complexity through the Hurst coefficient estimation, this, represents an efficient or random market when the value is equal to 0.5. Due to the variants proposed in this research it can be determined that should exist a rational component in the simulator in order to generate an efficient behavior.
La capacidad de hallar patrones y generar predicciones es un comportamiento natural que ha acompañado a la humanidad desde sus orígenes, cuando las primeras personas contemplaban el manto infinito en búsqueda de orientación y respuestas. Desde la Edad Antigua hasta la Contemporánea, el aumento en nivel de certeza ha conferido al hombre un grado de satisfacción y ventaja en su entorno; así mismo, en el campo de las finanzas la facultad de disminuir la incertidumbre y de encontrar patrones no sesgados se traduce en una ventaja al momento de invertir y mejorar la riqueza del inversionista.
Durante la historia del mercado bursátil, diversos estudios se han realizado con el fin de comprender el comportamiento de las acciones, desde planteamientos determinísticos a probabilísticos; sin embargo, a partir de la hipótesis de mercado eficiente (HME), planteada por Fama (1970) —la cual ha perdurado durante décadas como un pilar de las finanzas clásicas o racionales—, se cimentó una base conceptual que daba indicios sobre la incapacidad de tomar ventaja en un mercado que brinda las mismas oportunidades para todos sus agentes; sin embargo, existe evidencia que indica que esta no logra explicar el comportamiento real de la Bolsa.
Debido a ese deseo de entender el comportamiento del mercado bursátil, Mandelbrot (1972) estructura la hipótesis de mercado fractal (HMF), la cual contrapone la HME, puesto que propone un nivel de memoria o tendencia a replicar un comportamiento en las series de precios. Dicha hipótesis fue estudiada por Peters (1994) mediante el análisis de rango re-escalado, para explicar así la volatilidad del mercado real y la eficiencia del mismo. Por otra parte, una nueva teoría de estudio financiero enfocada al comportamiento del inversionista y no a la información del mercado es planteada por Shiller (2003) en la teoría de finanzas conductuales (TFC), que va en contraposición de la HME.
Debido a las diversas hipótesis para explicar el comportamiento de las series de precios y con el fin de poder analizar el comportamiento estadístico del mismo, surgen algoritmos en las denominadas finanzas computacionales (LeBaron, 2006); dichos programas no solo estudian el comportamiento histórico sino, en adición, generan nuevas series que emulan el comportamiento real. Mediante esa metodología, Fan, Ying, Wang y Wei (2009) proponen un modelo autómata celular (MAC) para estudiar el flujo de información y la forma en la cual interactúan los agentes desde la perspectiva de un mercado conductual con comportamiento fractal.
El objetivo de esta investigación es evaluar la influencia del comportamiento del inversionista en un mercado bursátil artificial enfocado al flujo de información y la capacidad de imitar, anti-imitar o ser indiferente al entorno; dicho comportamiento es reflejado en la eficiencia teórica del mercado. Para ello se parte del MAC y se generan escenarios o variantes en las que agentes conductuales interactúan, cambiando la dinámica de oferta y demanda; luego, se modela un MAC con agentes racionales mediante la adaptación de los filtros de Alexander y, finalmente, un MAC mixto en el que los agentes se verán afectados por la información en el mercado y la posición de compra, retención o venta de sus vecinos.
La estructura del presente artículo se dispone de la siguiente manera: en la siguiente sección, revisión general de la complejidad del mercado, seguida de un análisis de publicaciones relacionadas con sistemas complejos y el modelo autómata celular. En la segunda sección, explicación de la técnica aplicada para medir la memoria en la serie de datos y las generalidades para la construcción de las variantes del modelo. A continuación, descripción de las consideraciones para cada simulación. En la sección cuarta, discusión de los resultados obtenidos. Finalmente, conclusiones, apéndices y referencias bibliográficas.
Revisión de la literaturaRevisión de la complejidad del mercadoA finales de los años sesenta, Fama (1965, 1970) estructuró la hipótesis de los mercados eficientes, estudiando el comportamiento aleatorio del precio en diversos activos a través de la tendencia probabilística de sus rentabilidades, definiendo así cinco características que en conjunto se presentaban en los mercados: amplitud, profundidad, transparencia, libertad y flexibilidad. Dicha hipótesis fue contrastada por Mandelbrot (1972), quien diserta, descubriendo que un histórico financiero conserva una memoria a corto plazo, la cual posee características fractales y, por tanto, debe ser estudiada mediante metodologías no lineales. Peters (1994) escribe un libro en el cual analiza el comportamiento de las series de precios aplicando un método de regresión mediante la estimación del coeficiente de Hurst con el fin de evidenciar las características fractales de dichas series y si estas eran aleatorias, persistentes o antipersistentes.
Debido a diversas discrepancias entre la teoría y la realidad en las series financieras, Bulkley y Harris (1997) estudian los retornos a largo plazo en el mercado de Nueva York (1982-1990), encontrando que la volatilidad en los precios en la Bolsa está relacionada con la sobre y subvaloración de las ganancias esperadas; Wermers (1999) analiza el comportamiento del mismo mercado en un periodo diferente (1975-1995), hallando una tendencia a actuar en conjunto, evidenciando así el efecto rebaño de los inversionistas. Chang, Cheng y Khorana (2000), por su parte, recopilan datos financieros en Estados Unidos (1963-1997), Hong Kong (1981-1995), Japón (1976-1995), Corea del Sur (1978-1995) y Taiwán (1976-1995), hallando las mismas características en las Bolsas, y concluyen que estas no dependen de la alta o baja capitalización de activos.
Dichas anomalías en los retornos esperados y el comportamiento de los precios permiten a Grinblatt y Keloharju (2000) realizar un estudio en Finlandia para relacionar el error en la valoración con la manera en la cual los inversionistas toman decisiones. Una categoría resultante de dicha investigación son los agentes de momento, quienes tienen en cuenta el comportamiento histórico de los precios al instante de elegir, y su contraparte, los inversionistas domésticos, que toman sus decisiones con el cambio reciente del precio. Griffin, Harris, y Topaloglu (2003), a partir de los trabajos de Wermers y de Grinblatt, realizan un estudio que relaciona los rendimientos de las acciones con el patrimonio de los inversionistas, encontrando que existen diferencias significativas en la manera en la que empresas y personas comercializan las mismas acciones.
Fromlet (2001) recopila las investigaciones realizadas en la conducta de los inversionistas y en la tipificación de los mismos, exponiendo los fundamentos que verterían en las finanzas conductuales: heurísticas para el tratamiento de información, información disponible variante, filtro o preferencia de noticias, interpretación de la información, psicología de los mensajes transmitidos, expectativas, relevancia, exceso de confianza, ilusión de control, efecto de disposición, sesgo hogareño y efecto manada.
Las finanzas conductuales se consolidan como una variante de las finanzas clásicas al incorporar la conducta de los agentes en el comportamiento de sus inversiones; Shiller (2003) realiza una investigación basada en la volatilidad de los años ochenta tomando el índice Standard & Poor's 500 (S&P500) y concluyendo que los cambios en la serie no corresponden con el comportamiento de un mercado netamente racional; además, contrapuso los supuestos de la HME, sugiriendo que las investigaciones en finanzas deben contemplar la debilidad de esta hipótesis.
Lo (2005), por su parte, recopila estudios sobre el comportamiento de las acciones y la forma en la cual los agentes invierten, relacionando factores como el número de competidores en la Bolsa, la magnitud de las oportunidades (beneficios disponibles) y la capacidad de adaptación de los participantes, y encuentra que dichos factores se relacionan con el grado de eficiencia del mercado, planteando así la hipótesis del mercado adaptativo (HMA), la cual Tseng (2006) integraría con la HME, usando el concepto de racionalidad limitada, finanzas conductuales y neurofinanzas, al analizar la volatilidad de los índices S&P500, Dow Jones Industrial Average (DJIA) y National Association of Securities Dealers Automated Quotation (NASDAQ) (1971-2005), concluyendo que la HMA logra integrar aspectos psicosociales de los inversionistas junto con el concepto de competencia perfecta y equilibrio del mercado.
García (2013) retoma el trabajo de Shiller, resaltando la complejidad del mercado al tener en cuenta dos aspectos en particular para la toma de decisiones financieras: el exceso de confianza y las capacidades cognitivas limitadas.
Revisión de sistemas complejosGardner (1970) genera las bases para los sistemas complejos y modelos autómatas celulares al divulgar el juego de la vida de John Conway; sin embargo, debido a la estructura de dicho modelo, se generaban sesgos en los resultados. Por ende, Ashby (1987) diferencia al modelador de la máquina y el entorno mediante componentes estocásticos que funcionan como insumos, permitiendo el cambio de estados o transformada.
Por su parte, Peters (1994) estudia el mercado bursátil a partir de un sistema complejo, donde la información fluye en la bolsa y los agentes la reciben cambiando de posición; lo anterior, bajo la perspectiva de mercado caótico. Para su análisis revisa las propiedades fractales mediante el rango escalado de los datos. Los sistemas complejos como espacios de relaciones múltiples son abordados de manera multidisciplinar por Tarride (1995), quien incorpora áreas de conocimiento como informática, psicología y matemática, entre otras, con el fin de exponer la trayectoria y la visión del modelamiento de la realidad a través de sistemas complejos.
Posteriormente, LeBaron (2006), tras estudiar el comportamiento de las series financieras simuladas, desarrolla algoritmos para representar el mercado bursátil mediante rastreadores de precio; finalmente, se construye un modelo autómata celular de la mano de Fan et al. (2009), quienes retoman las bases del trabajo de Conway y lo encamina hacia un mercado artificial, con el fin de estudiar la manera en que los agentes (máquinas) reciben la información y cómo esta les induce al cambio de posición (transformada).
MetodologíaCoeficiente de HurstEl análisis de rango re-escalado se enfoca al estudio de la tendencia fractal o memoria de una serie y sus propiedades a través del tiempo, relacionándose así mediante el valor del coeficiente de Hurst con la complejidad o eficiencia de un mercado. Esta se determina calculando su variabilidad a partir del rango de la serie y su grado de desviación.
Considerando que se parte de una serie Mt con un valor de t comprendido entre 1≤t≤T (todos los valores en dicha serie son producidos por el MAC), para ser estudiada bajo la óptica de la complejidad es necesario trabajar con los rendimientos de la misma; después se genera una nueva serie de tiempo X, y esta es relacionada con los datos originales según su suavización logarítmica.
Este periodo de tiempo X se divide en A subperiodos contiguos de longitud n, tal que A*n=N. Se nombra cada uno de los subperiodos o subgrupos I con a=1, 2, 3, ..., A. Cada elemento en I es etiquetado Xk, a, tal que t=1, 2, 3, ..., n. Para cada subperiodo Ia de longitud n, el valor promedio está definido por la siguiente expresión:
El promedio Xt es el valor representante de la serie de datos; sin embargo, no indica cuán variable puede llegar a ser dicha secuencia. Se calcula entonces una relación entre cada valor y la diferencia con su media.
Con el valor promedio y la diferencia entre cada elemento Xi,NyXN se estima la desviación estándar de la muestra, para cada subperiodo Ia
Obteniendo así el primer elemento para el cálculo del rango re-escalado. El segundo elemento es el rango de la serie de tiempo, denominado R(N); dicho valor está dado entre los valores máximos y mínimos de la serie.
La función de rango re-escalado FN se define mediante la relación entre la amplitud de valores de una serie de tiempo y la variabilidad de la misma, para cada subperiodo.
De esta forma se obtiene una unidad de medida, la cual escala el rango al considerar cada desviación estándar; todo esto corresponde a un comportamiento browniano donde dicha función re-escalada es proporcional a la n para una serie de tiempo en la que sus valores no están correlacionados unos con otros. Una vez obtenido todos los FNa se promedian con el fin de tener un estimado de variabilidad escalada para la serie de tiempo
La función del rango re-escaldo es proporcional a la raíz hurstiana de T:
Dicha proporción se puede deducir de forma gráfica mediante el comportamiento de la serie, para un eje LnT confrontado con el LnFT
Cuando el valor estimado del coeficiente de Hurst se acerca a 1 en el intervalo (0.5, 1] se considera una serie persistente; es decir, si los valores se encuentran al alza, lo más probable es que continúe de esa manera. Caso contrario en el intervalo [0,0.5): entre más cercano a cero, su comportamiento será antipersistente, y si en un momento se encontraba al alza, lo más probable es que disminuya a continuación; si H=0.5, se considera una serie aleatoria.
Modelo autómata celularEl desarrollo del código se basó en los resultados de la investigación desarrollada por Fan, Ying, Wang y Wei (2009). Los supuestos básicos son los siguientes:
Un MAC representa un mercado bursátil. Cada ubicación en la grilla del modelo hace referencia a un agente inversionista en el mercado financiero. El estado del espacio en la grilla es consistente con el de la gente; dicho estado es variable y se representa con Si,jt, lo que evita la inversión conductual de la gente en el sitio (i, j) en el tiempo t. Puede ser escogida en tres valores: Sb representa el estado de compra, Sh representa el estado de retención y Ss representa el estado de venta:
Reglas de evolución: generalmente, el estado cambia para dar paso a un nuevo estado, el cual será determinado por su origen en sí, sus vecinos, el momento previo y el control de las variables, las cuales se pueden formular de la siguiente manera:
Donde
Representa el estado de los vecinos en sus respectivas ubicaciones (solo se tiene en cuenta la vecindad para cada agente en la posición [i,j]). G es el vector de variables de control y F es la regla de evolución del modelo autómata celular. Como regla común, se asume que el estado en un espacio de la grilla se verá afectado solamente por el comportamiento de su vecindad, que posee sus propias preferencias de inversión, las cuales son representadas por R en el modelo.
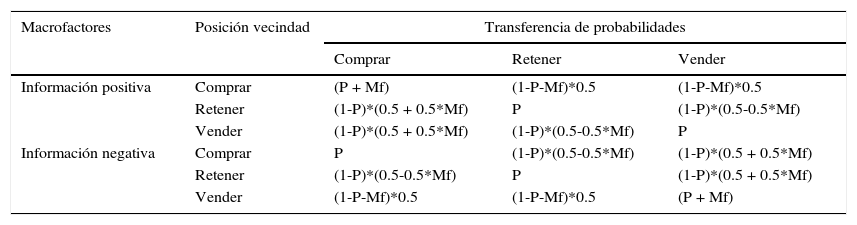
Modelo autómata celular para agentes conductualesEl mercado bursátil artificial se enfoca en la capacidad que tiene un agente para imitar, anti-imitar o ser indiferente a la posición de sus vecinos; para la investigación se trabajó con una probabilidad de transferencia individual Pi,j y, acorde al modelo original de Fan et al. (2009), se estudia la interacción sin tener en cuenta la información del mercado o Mf La matriz general de transferencia de posiciones, basada en el estado de la economía y la tendencia individual a replicar o no, se evidencia en la tabla 1, donde P es la probabilidad de transferencia en el mercado, originalmente definida como una variable probabilística uniforme con dominio entre 0 y 1; Mf es el macrofactor económico o el estado general de la economía definido diariamente; sin embargo, para la validación del modelo y para el estudio del flujo de información se ignora, siendo su valor igual a cero.
Matriz de transferencia de posiciones para un agente conductual
| Macrofactores | Posición vecindad | Transferencia de probabilidades | ||
|---|---|---|---|---|
| Comprar | Retener | Vender | ||
| Información positiva | Comprar | (P + Mf) | (1-P-Mf)*0.5 | (1-P-Mf)*0.5 |
| Retener | (1-P)*(0.5 + 0.5*Mf) | P | (1-P)*(0.5-0.5*Mf) | |
| Vender | (1-P)*(0.5 + 0.5*Mf) | (1-P)*(0.5-0.5*Mf) | P | |
| Información negativa | Comprar | P | (1-P)*(0.5-0.5*Mf) | (1-P)*(0.5 + 0.5*Mf) |
| Retener | (1-P)*(0.5-0.5*Mf) | P | (1-P)*(0.5 + 0.5*Mf) | |
| Vender | (1-P-Mf)*0.5 | (1-P-Mf)*0.5 | (P + Mf) | |
Fuente: elaboración de los autores a partir de Fan et al. (2009).
Para la construcción de un MAC enfocado a agentes racionales se debe definir una regla de evolución; para este caso, se aplicó una variante de los filtros de Alexander, que si bien es una técnica que no aplica rigurosa inferencia estadística, tiene aceptación porque genera una dinámica mediante la gestión activa de series financieras (Duarte y Mascareñas, 2014).
Consiste en invertir y desinvertir durante un determinado tiempo sobre la base de la regla de comprar el activo cuando su precio se incrementa x% y venderlo cuando su precio cae x%; no obstante, como el MAC carece de un generador de precios, el filtro se comparará con un incremento o decremento porcentual z% en la posible compra.
El cambio en posición de un agente racional se relaciona con la información —gratuita y de calidad—, y se define entonces el macrofactor económico o el estado general de la economía como una variable calculada a partir de la dinámica del MAC.
Este Mf funciona como un símil, teniendo en cuenta que no representa el comportamiento económico global de una región —como un macrofactor real—. Sin embargo, sirve para analizar la tendencia probable al cambio. Como el Mf se estima para cada iteración, se puede relacionar con el número de transacciones realizadas durante el día anterior1. Cuando Mf≥0.5, la economía se considera al alza.
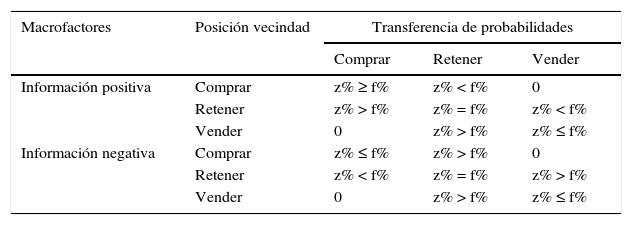
La matriz general de transferencia de posiciones, basada en el estado de la economía y el filtro de decisión, se evidencia en la tabla 2, donde f% simboliza el valor del filtro de Alexander. Según el estado de la economía, el agente puede cambiar o no de posición; sin embargo, de hacerlo, dicho cambio será siempre a la posición más cercana.
Matriz de transferencia de posiciones para un agente racional
| Macrofactores | Posición vecindad | Transferencia de probabilidades | ||
|---|---|---|---|---|
| Comprar | Retener | Vender | ||
| Información positiva | Comprar | z% ≥ f% | z% < f% | 0 |
| Retener | z% > f% | z% = f% | z% < f% | |
| Vender | 0 | z% > f% | z% ≤ f% | |
| Información negativa | Comprar | z% ≤ f% | z% > f% | 0 |
| Retener | z% < f% | z% = f% | z% > f% | |
| Vender | 0 | z% > f% | z% ≤ f% | |
Fuente: Elaboración de los autores.
En el MAC mixto, la información macroeconómica afecta a ambos tipos de agentes. Por tanto, la ecuación (13) es calculada para las dos matrices de transferencia (tablas 1 y 2), y se genera una disposición intercalando agentes conductuales y racionales de manera tal que cada uno siempre tenga cuatro vecinos de cada tipo. La disposición observada en la figura 1 permite que las acciones de los agentes conductuales se vean afectadas por la naturaleza del mercado y el comportamiento de agentes racionales.
Distribución espacial de los agentes.
Fuente: Talero et al. (2015).
Acorde al MAC diseñado por Fan et al. (2009), se construye un mercado de 50*50 celdas, en las cuales la posición inicial de los agentes se distribuye uniformemente entre «comprar», «retener» o «vender» una acción. La simulación se ejecuta durante 100 iteraciones para evidenciar el comportamiento de las posiciones finales de cada versión del modelo. Con respecto al análisis del coeficiente de Hurst y su relación con la complejidad o eficiencia del mercado bursátil, solo se tendrán en cuenta datos equivalentes a la longitud promedio de ciclo original descrita pro Ying Fan, con L=29.
Modelo autómata celular para agentes conductualesSe realiza la simulación con tres tipos de probabilidades para imitar a la vecindad (tabla 3); la primera es la propuesta en el modelo original en la que no existe ninguna predilección; la segunda, la posición de los agentes tiende a evitar ser afectados por los vecinos y, por tanto, la tendencia comportamental es a evitar imitar o llevar la contraria, siguiendo una distribución normal; finalmente, en la tercera se obliga a ir a favor o en contra de la vecindad, pero nunca ser indiferente, y la probabilidad es simétrica.
Distribuciones de P(i,j)
| Distribución | Características |
|---|---|
| Uniforme | Continua en el intervalo [0;1] |
| Normal | Media en 0.5 y desviación estándar de 0.16, dominio [0,1] |
| Anti-indiferencia | Probabilidad de indiferencia (0.5) igual a cero y simétrica, presenta la forma de la figura 2, dominio entre [0,1] |
Fuente: elaboración de los autores.
Distribución anti-indiferencia.
Fuente: Talero et al. (2015).
Se realiza la simulación con tres niveles de filtros para determinar si en un mercado completamente racional los agentes adoptan posiciones y el cambio de estas representa la eficiencia de la Bolsa simulada. El primer filtro es diseñado con el fin de emular un valor de decisión bajo, que facilita la dinámica al permitir rápidos cambios entre comprar, retener o vender; el segundo es un punto de referencia medio para los filtros usados; finalmente, el tercero representa un filtro exigente: el mercado solo cambiará cuando la información bursátil es alentadora. Los tres niveles de filtro, f%, se presentan en la tabla 4.
Modelo autómata celular mixtoSe desarrolla un diseño experimental 32, siendo cada tipo de agente el factor Conductual,Racional y las variantes de los modelos, los niveles a analizar. N1=Uniforme,Normal,Anti−IndiferenciaN2=1%,3%,5%. Se realizan tres réplicas experimentales con el fin de evidenciar la variabilidad de la memoria o eficiencia en el modelo autómata celular.
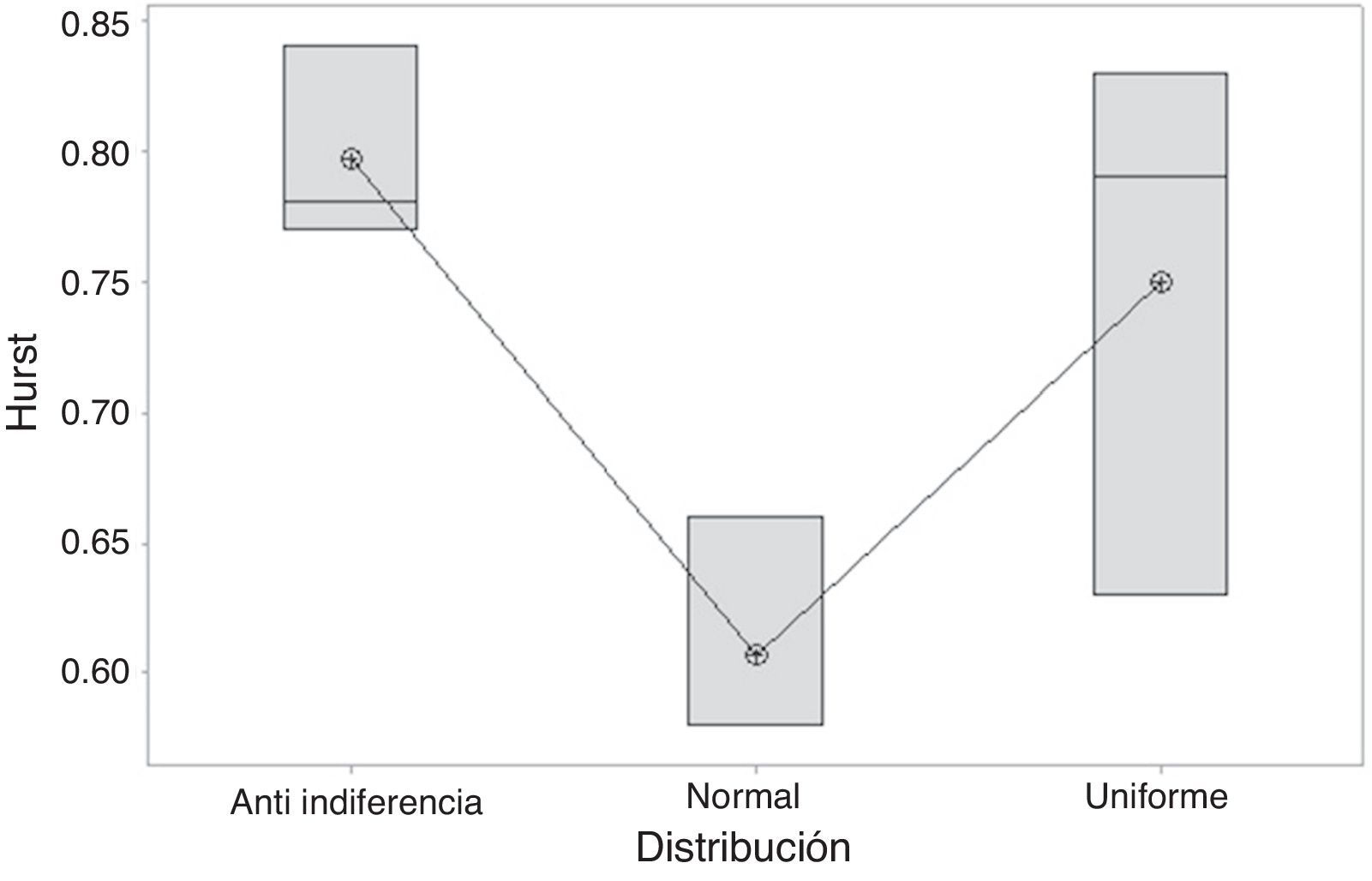
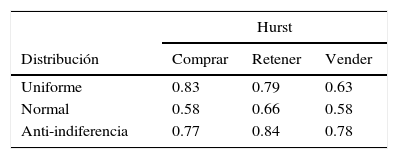
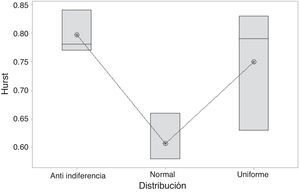
Análisis de resultadosModelo autómata celular para agentes conductualesComo hipótesis inicial H0 tenemos que todas las medias de Hurst son iguales y, como hipótesis alternativa (H1), que al menos una de estas es diferente. Los valores resultantes de la simulación se evidencian en la tabla 5, indicando que existen discrepancias entre la distribución original (uniforme) y las que afectan la tendencia a imitar o no (fig. 3).
Estadísticamente se evidencia mediante ANOVA la diferencia conceptual entre los niveles normal y anti-indiferencia. Sin embargo, la distribución uniforme puede presentar un comportamiento similar a ambas siempre que su probabilidad de cambio de estado sea individual.
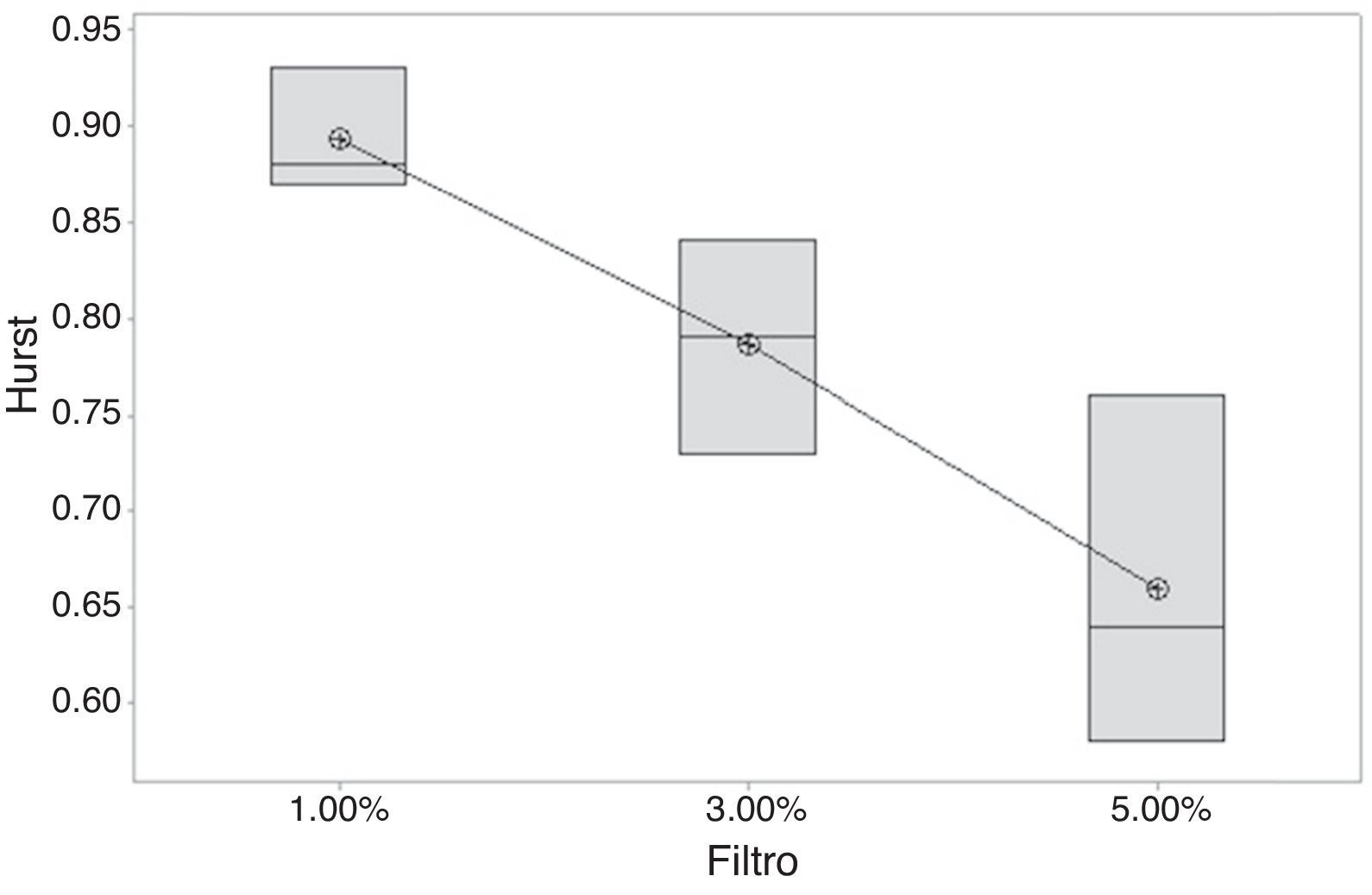
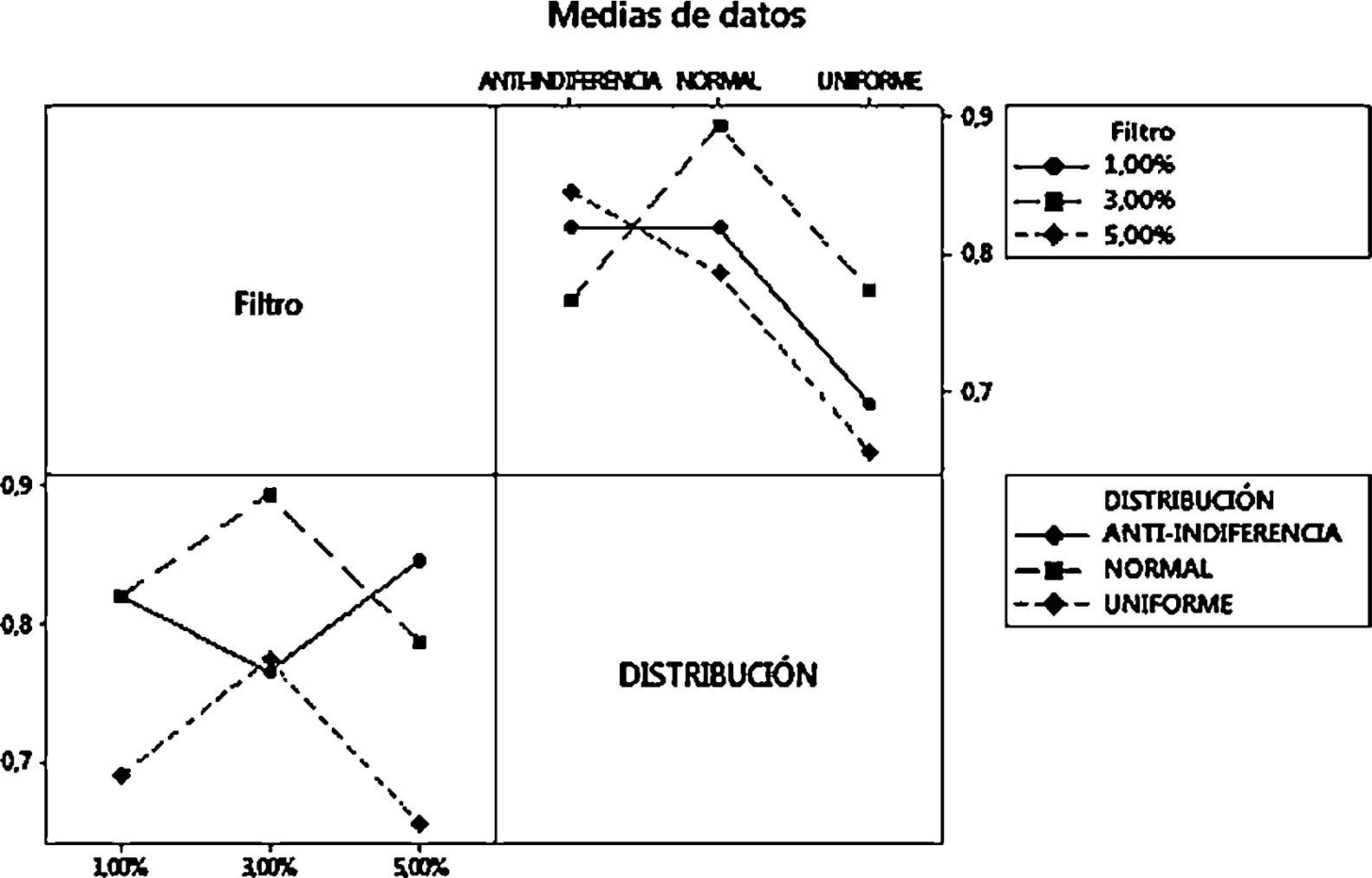
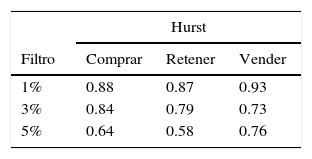
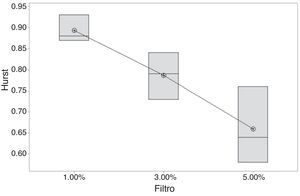
Modelo autómata celular para agentes racionalesComo hipótesis inicial H0 tenemos que todas las medias de Hurst son iguales y, como H1, que al menos una de estas es diferente. Los coeficientes estimados se registran en la tabla 6, indicando que existe una tendencia al caos cuando se aumenta el valor del filtro (fig. 4).
Se evidencia diferencia significativa, tras el ANOVA, entre los niveles extremos del factor filtro; el valor de 3%, al ser un punto intermedio entre estos, estadísticamente puede estimar a ambos.
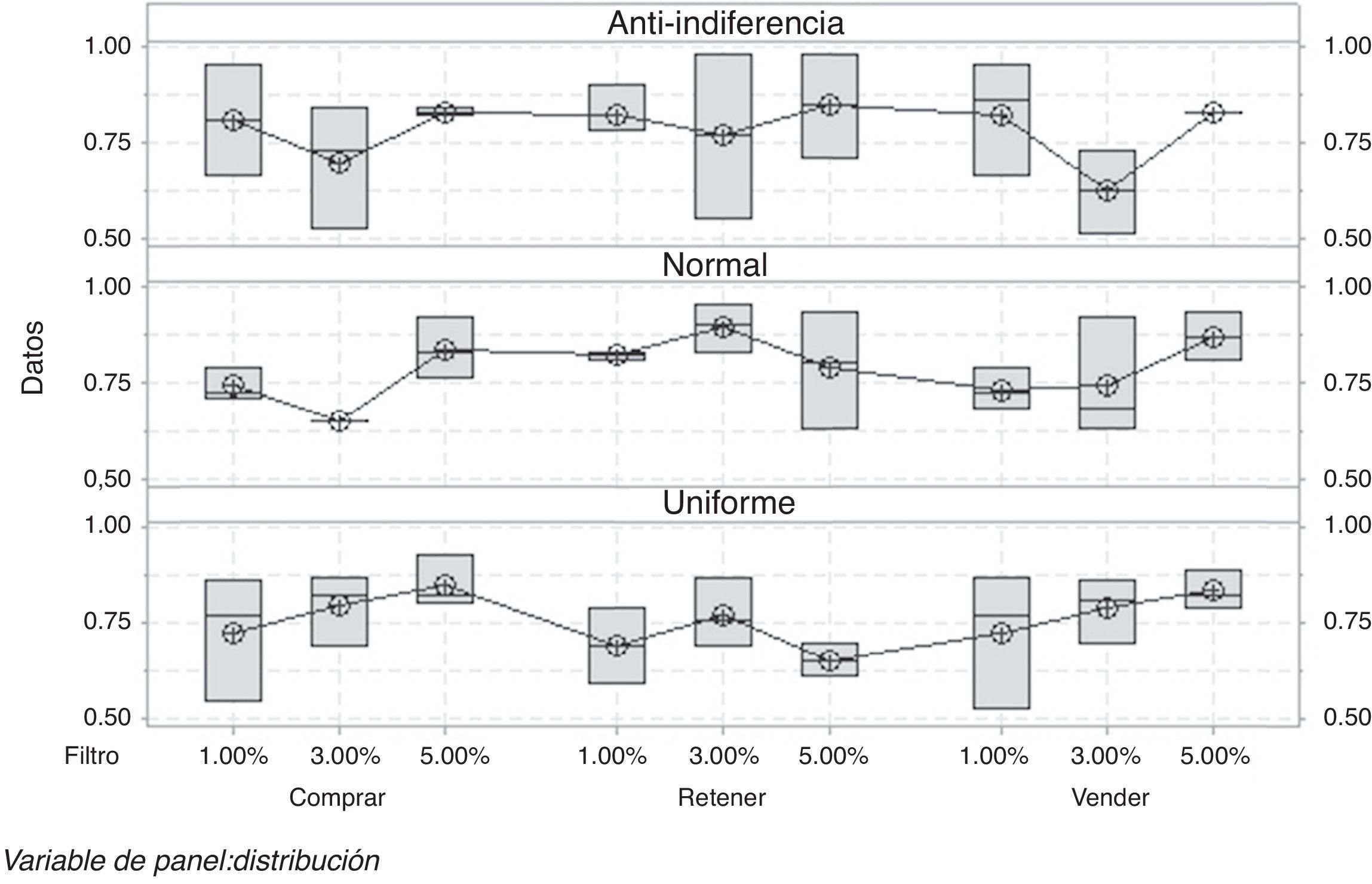
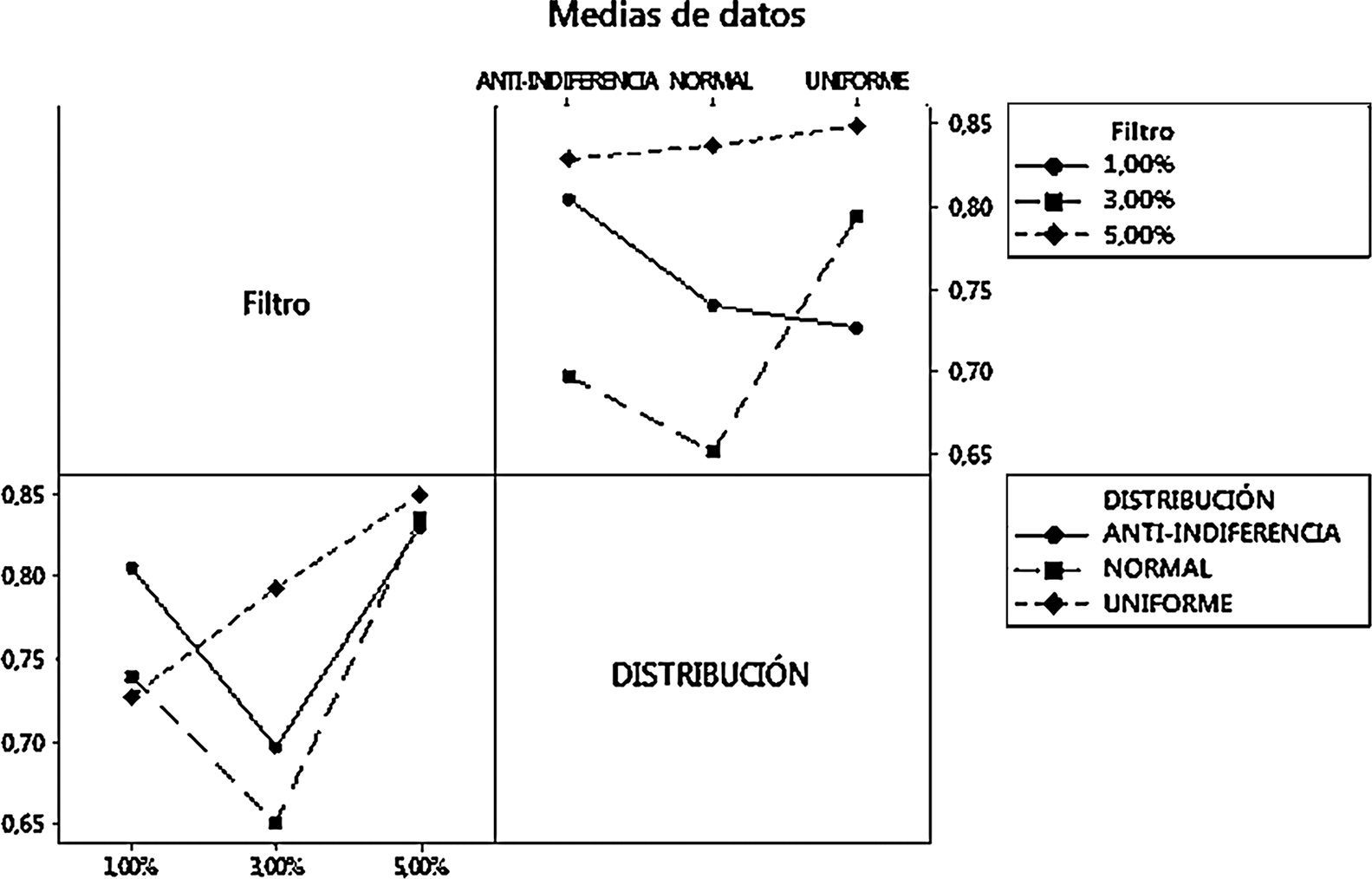
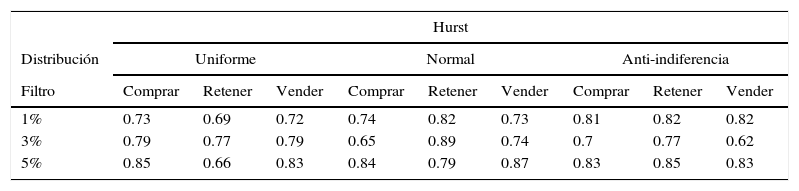
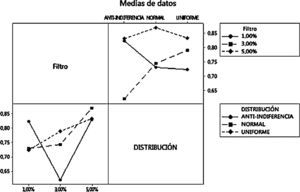
Modelo autómata celular mixtoPara el diseño experimental, como hipótesis inicial H0 se parte de que tenemos que todas las medias de Hurst son iguales y, como H1, que al menos una de estas es diferente; en este caso, existen dos factores y la interacción entre estos. Los coeficientes de Hurst del diseño se encuentran en la tabla 7.
Coeficiente de Hurst promedio del MAC mixto
| Hurst | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Distribución | Uniforme | Normal | Anti-indiferencia | ||||||
| Filtro | Comprar | Retener | Vender | Comprar | Retener | Vender | Comprar | Retener | Vender |
| 1% | 0.73 | 0.69 | 0.72 | 0.74 | 0.82 | 0.73 | 0.81 | 0.82 | 0.82 |
| 3% | 0.79 | 0.77 | 0.79 | 0.65 | 0.89 | 0.74 | 0.7 | 0.77 | 0.62 |
| 5% | 0.85 | 0.66 | 0.83 | 0.84 | 0.79 | 0.87 | 0.83 | 0.85 | 0.83 |
Fuente: elaboración de los autores a partir de MATLAB.
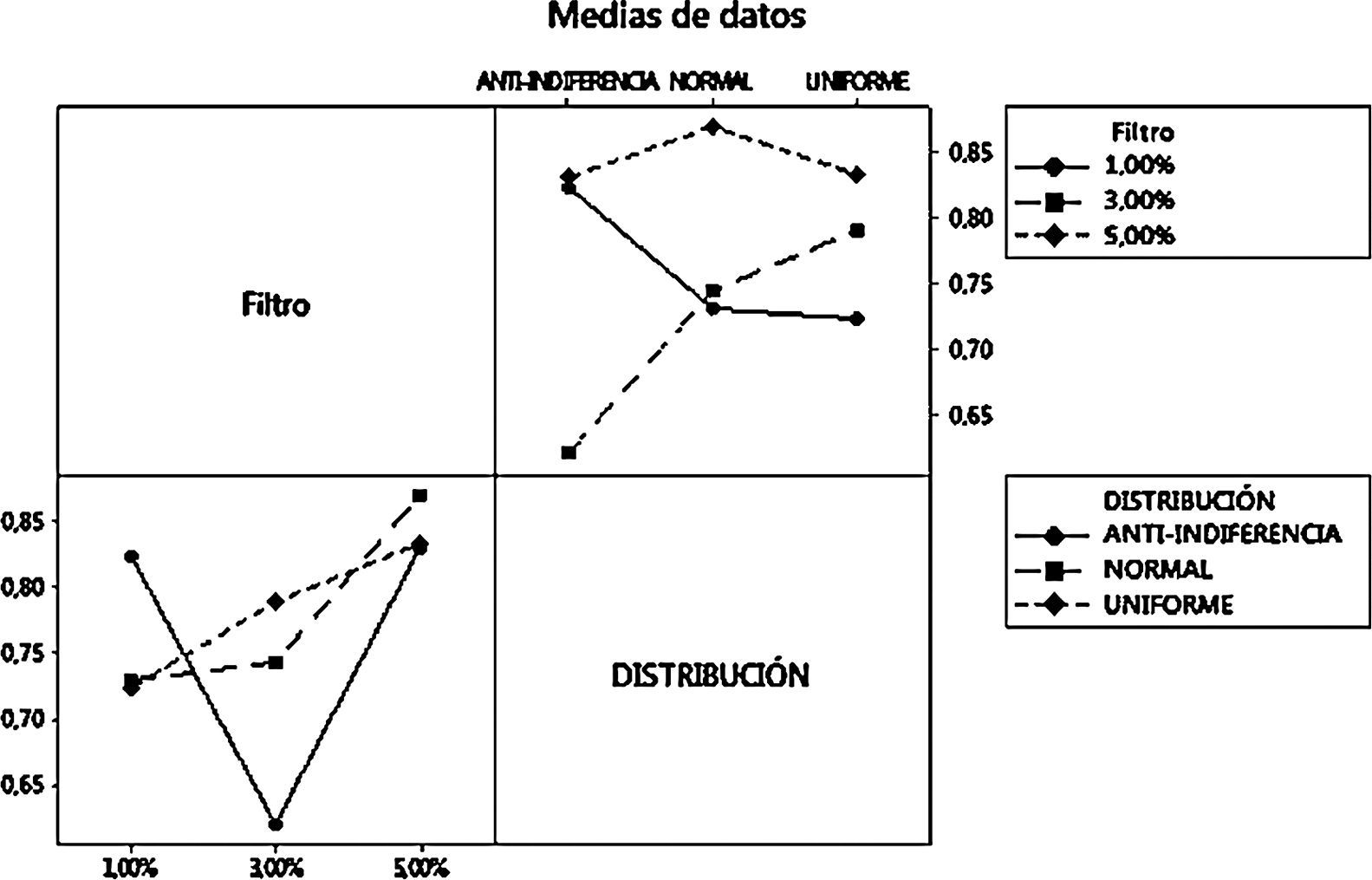
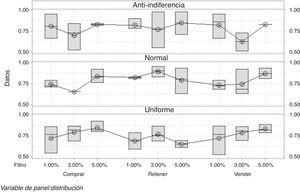
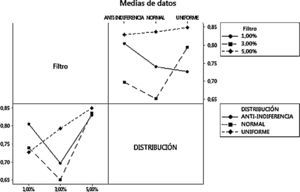
Al tener tres métricas de calidad o variables respuesta, se realiza una MANOVA, encontrando que existe una correlación entre la posición de comprar y la de vender. Por otra parte, el diseño factorial revela que solo para la posición de comprar hay una relación entre el comportamiento del coeficiente de Hurst y el nivel del filtro; la variabilidad del diseño se observa en la figura 5.
En la posición de comprar se aprecia un comportamiento persistente, el cual es menos caótico a medida que aumenta el valor del filtro, comportamiento correlacionado débilmente con la posición de vender. El nivel de eficiencia del mercado en general está directamente relacionado entre las posiciones de comprar y vender (ver Apéndice 1), las cuales en los históricos de datos poseen una correlación negativa, reafirmando el comportamiento de la oferta/demanda en el MAC.
Conclusiones y recomendacionesEste trabajo buscó construir un escenario en el que pueda representarse el comportamiento de un mercado con más de un tipo de agente bursátil bajo la perspectiva de las finanzas conductuales y la incidencia del inversionista en la eficiencia del mismo. Para ello se utilizó el coeficiente de Hurst como indicador del caos y/o memoria mediante la cercanía de la estimación al valor teórico de aleatoriedad H=0.5, el cual representa un mercado eficiente.
En un mercado bursátil virtual netamente conductual como el desarrollado por Fan et al. (2009) la eficiencia es mínima, puesto que las estimaciones del coeficiente de Hurst son cercanas a 0.86, indicando una serie persistente. Gracias a las variantes propuestas en esta investigación se puede determinar que debe existir cierto grado de indiferencia o nivel de racionalidad en los agentes; es decir, en un mercado simulado no debe existir un comportamiento íntegramente conductual: al añadir el componente racional se puede modelar una eficiencia débil.
El modelo autómata celular racional muestra una tendencia al caos o eficiencia en la medida en que el agente modelado es más exigente con la información económica del entorno. Como mejora, la inclusión de un generador de precios y la configuración del macrofactor económico facilitarían su contraste con un mercado real.
Al modelar dos tipos de agentes —racionales y conductuales— se simula el comportamiento hipotético del mercado. Se evidencia una tendencia persistente a la inversión entre más exigente es el filtro, a diferencia del modelo netamente racional. Dicho comportamiento se debe a la disposición de los agentes, puesto que si el valor de decisión z% del mercado va al alza, cada agente conductual adoptaría probablemente la posición de sus vecinos, quienes siempre serían cuatro racionales afectados por z% y, por ende, las capacidades de imitación observadas en las distribuciones normal y anti-indiferencia generarían un efecto manada.
El modelo autómata celular mixto puede ser mejorado al cambiar las disposiciones y la cantidad de cada tipo de agente en el mercado, con el fin disminuir el nivel de persistencia de la serie financiera. También puede adoptar un sistema de castigos e incentivos cuando la posición adoptada por los agentes conductuales responde al comportamiento de la economía en el instante t+1, generando así un modelo autómata celular mixto de aprendizaje.