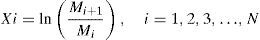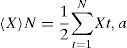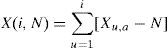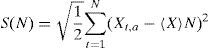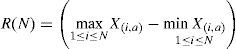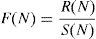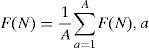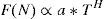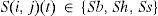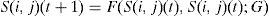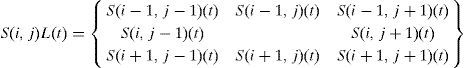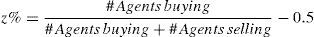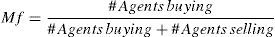The main objective of this article is to develop a Cellular Automaton Model in which more than one type of stockbroker interact, and where the use and exchange of information between investors describe the complexity measured through the estimation of the Hurst exponent. This exponent represents an efficient or random market when it has a value equal to 0.5. Thanks to the various proposals, it can be determined in this investigation that a rational component must exist in the simulator in order to generate an efficient behavior.
El objetivo principal de este artículo es desarrollar un modelo autómata celular en el que interactúen más de un tipo de agentes bursátiles, donde el uso y el intercambio de información entre los inversores describen la complejidad medida a través de la estimación del coeficiente de Hurst, que representa un mercado eficiente o aleatorio al tener un valor igual a 0.5. Gracias a las variantes propuestas en esta investigación se puede determinar que debe existir un componente racional en el simulador con el fin de generar un comportamiento eficiente.
The capacity to find patterns and generate predictions is a natural behavior that has accompanied humanity since its origins, when the first people contemplated the universe in search of guidance and answers. Since ancient times and even up to this day, the increase in the level of certainty has conferred onto mankind a degree of satisfaction and advantage in their surroundings. Similarly, in the field of finances, the ability to decrease uncertainty and to find non-slanted patterns translates into an advantage at the time of investing, increasing the wealth of the investor.
Within the history of the stock market, different studies have been carried out with the purpose of understanding the behavior of the assets, going from deterministic to probabilistic approaches. However, it was not until the Efficient Market Hypothesis (EMH) proposed by Fama (1970)—which has endured for decades as a pillar of classic or rational finances—that a conceptual base was established, which provided evidence on the inability to take advantage in a market that provides the same opportunities to all of its agents. However, there is evidence that indicates that this hypothesis does not manage to explain the real behavior of the stock market.
With the objective of understanding the behavior of the stock market, Mandelbrot (1972) structures the Fractal Market Hypothesis (HMF), which contrasts with the EMH, as it proposes a memory or tendency level to replicate a behavior in the series of prices. This hypothesis was studied by Peter (1994) through a rescaled range analysis to explain the volatility of the real market and the efficiency of the same. On the other hand, a new financial study theory focused on the behavior of the investor and not on the information of the market is proposed by Shiller (2003) in the Theory of Behavioral Finance (TBF), which contrasts with the EMH.
Due to the different hypotheses used to explain the behavior of the series of prices, and in order to analyze the statistical behavior of the same, algorithms emerge in the so-called computational finances (Lebaron, 2006). These programs not only study historical behavior, but also generate new series that emulate a real behavior. Using this methodology, Fan, Ying, Wang, and Wei (2009) propose a Cellular Automaton Model (CAM) to study the flow of information and the manner in which the agents interact from the perspective of a behavioral market with fractal behavior.
The objective of this investigation is to evaluate the influence of investor behavior on an artificial stock market focused on the flow of information and the capability to imitate, anti-imitate or to be indifferent to the environment; said behavior is reflected on the theoretical efficiency of the market. For this, we depart from the CAM and generate scenarios or variables in which behavioral agents interact, changing the dynamic of supply and demand. Subsequently a CAM with rational agents is modeled by adapting Alexander's filters, as well as a mixed CAM in which the agents are affected by the information in the market and the buying, retention or sale position of their neighbors.
This article is structured in the following manner: Second section—general review of the complexity of the market, followed by an analysis of publications related to complex systems and the Cellular Automaton Model. Third section—explanation of the technique applied to measure the memory in the series of data and the general points used to build the variables of the model. Fourth section—description of the considerations for each simulation. Fifth section—discussion of the results obtained. Finally, Conclusions and Appendixes sections.
Review of the literatureReview of the complexity of the marketAt the end of the 1960s, Fama (1965, 1970) structured the efficient market hypothesis, studying the random behavior of the price in different assets through the probabilistic tendency of its profitability, thus defining five characteristics that were jointly present in the markets: magnitude, depth, transparency, freedom, and flexibility. This hypothesis was contrasted by Mandelbrot (1972), who discourses on this, and who discovered that a historic financer retains a short-term memory, which possesses fractal characteristics and, therefore, must be studied through non-linear methodologies. Peter (1994) wrote a book in which he analyzed the behavior of the series of prices, applying a regression method through the estimation of the Hurst exponent, to evidence the fractal characteristics of said series and to find whether these were random, persistent or anti-persistent.
Due to different discrepancies between the theory and reality in the financial series, Bulkley and Harris (1997) study the long-term returns in the market of New York (1982–1990), finding that the volatility in the prices of the Stock Market is related to the over- and under-valuation of the expected gains. Wermers (1999) analyze the behavior of the same market for a different period (1975–1995), finding a tendency to act together, thus evidencing the herd behavior of the investors. On the other hand, Chang, Cheng and Khorana (2000) gathered financial data in the United States (1963–1997), Hong Kong (1981–1995), Japan (1976–1995), South Korea (1978–1995) and Taiwan (1976–1995), and found the same characteristics in the Stock Market, thus concluding that these do not depend on the high or low capitalization of assets.
These anomalies in the expected returns and the behavior of the prices allowed Grinblatt and Keloharju (2000) to carry out a study in Finland to relate the error in valuation to the manner in which the investors make decisions. A category resulting from this investigation are: the ‘momentary agents’, who consider the historical behavior of the prices at the time of selecting; and their counterpart, the domestic investors, who base their decisions on the recent price change. Griffin, Harris, and Topaloglu (2003), based on the work by Wermers and Grinblatt, carry out a study that links the yields of the assets to the assets of the investors, finding that there are significant differences in the way that companies and people commercialize the same assets.
Fromlet (2001) compiles the investigations concerning the behavior of the investors and the classification of the same, presenting the fundaments that go into behavioral finances: heuristics for the processing of information, variable available information, filtering or preference of news, information interpretation, the psychology of transmitted messages, expectations, relevance, overconfidence, illusion of control, the disposition effect, home bias, and the herd effect.
Behavioral finances are consolidated as a variant of classical finances by incorporating the behavior of the agents in the behavior of their investments. Shiller (2003) conducts an investigation based on the volatility of the 1980s using the Standard & Poor's 500 (S&P500) index, and concludes that the changes in the series do not correspond to the behavior of a distinctly rational market. Furthermore, he countered the assumptions of the EMH, suggesting that investigations on finances must take into consideration the weakness of this hypothesis.
For his part, Lo (2005) gathered studies on the behavior of the assets and the way in which agents invest, relating factors such as: the number of competitors in the Stock Market, the size of the opportunities (available benefits) and the adaptive capacity of the participants, finding that said factors relate to the degree of the market efficiency. Thus, he proposed the Adaptive Market Hypothesis (AMH), which Tseng (2006) would later integrate with the EMH, using the concept of limited rationality, behavioral finances and neurofinances to analyze the volatility of the indices: S&P500, Dow Jones Industrial Average (DJIA), and the National Association of Securities Dealers Automated Quotation (NASDAQ) (1971–2005), and concluding that the AMH manages to integrate the psychosocial aspects of the investors along with the concept of perfect competition and market equilibrium.
García (2013) takes up Shiller's work, highlighting the complexity of the market by considering two aspects in particular for the financial decision-making process: overconfidence, and limited cognitive capabilities.
Review of complex systemsGardner (1970) creates the bases for the complex systems and Cellular Automaton Models by disclosing John Conway's Game of Life. However, due to the structure of said model, a bias was generated in the results. Therefore, Ashby (1987) differentiated the modeler of the machine and the environment through stochastic components that act as inputs, allowing the change in status or transformation.
For his part, Peter (1994) studies the stock market based on a complex system, in which information flows in the stock market and the agents receive it by changing position; this, in the context of a chaotic market. For his analysis, he reviews the fractal properties through the scaled range of the data. Complex systems as multiple relations spaces are addressed in a multidisciplinary manner by Tarride (1995), who incorporates fields of knowledge such as information technology, psychology and mathematics, among others, when presenting the trajectory and vision of the modeling of reality through complex systems.
Subsequently, having studied the behavior of the simulated financial series, Lebaron (2006) develops algorithms to represent the stock market through price trackers. Finally, the Cellular Automaton Model is built by Fan et al. (2009), who bring back the bases of Conway's work and apply them to an artificial market in order to study the manner in which the agents (machines) receive the information and how said information causes the change of position (transformed).
MethodologyHurst exponentThe Rescaled Range Analysis focuses on the study of the fractal tendency or memory of a series and its properties across time, thus relating through the value of the Hurst exponent to the complexity or efficiency of a market. This is determined by calculating its variability from the range of the series and its degree of deviation.
Considering that we depart from an {Mt} series with a value between 1≤t≤T (All values in this series are produced by the CAM) to be studied from the perspective of complexity, it is necessary to work with the yields of the same. Subsequently, a new series of X time is generated, which relates to the original data according to its logarithmic smoothing.
This period of X time is divided into A contiguous subperiods with an n longitude, so that A*n=N. Each of the I subperiods or subgroups are named, with a=1,2,3,...,A. Each element in I is labeled Xk,a, so that t=1,2,3,...,n. For each Ia subperiod of an n longitude, the average value is defined by the following expression:
The average Xt is the representative value of the series of data; however, it does not indicate which variable can manage to become said sequence. Therefore, a relation between each value and the difference with its median is calculated.
with the average value and the difference between each X(i,N)yThus, the first element to calculate the Rescaled range is obtained. The second element is the range of the series of time, denominated R(N). This value is given between the maximum and minimum values of the series.
The Rescaled range function F(N) is defined through the relation between the magnitude of values of a series of time and the variability of the same for each subperiod.
In this manner, a unit of measure that scales the range by considering each standard deviation is obtained. This corresponds to a Brownian behavior, where said rescaled function is proportional to n for a series of time in which its values are not correlated with one another. Once all the F(N)a are obtained, they are then averaged in order to obtain an estimation of the scaled variability for the series of time.
The rescaled range function is proportional to the Hurstian T root:
Said ratio can be deduced graphically through the behavior of the series for an Ln T axis compared to the Ln F(T).
When the estimated value of the Hurst exponent approaches 1 in the interval (0.5,1] the series is considered to be persistent; this means that if the values are on the rise, it is most probable that it will continue in this manner. Conversely, in the interval [0,0.5), if it is closer to zero, its behavior will be anti-persistent and if at any moment it goes on the rise, it is likely that it will then begin to decrease; if H=0.5, it is then considered to be a random series.
The development of the code was based on the results of the investigation carried out by Wei, Ying, Fan and Wang in (2009). The basic assumptions are the following:
A CAM represents a stock market. Each location in the grid of the model references a stockbroker in the financial market. The state of the space in the grid is consistent with that of the people. Said state varies and is represented with S(i,j)(t), which prevents the behavioral investment of the people in site (i,j) in time t. Three values can be chosen for this state: Sb represents the state of purchase, Sh represents the state of retention, and Ss represents the state of the sale:
Rules of evolution: generally, the state changes to give way to a new state which shall be determined by its very origin, its neighbors, the previous moment, and the control of variables which can be formulated as follows:
where:Represents the state of the neighbors in their respective locations (only the neighborhood for each agent in the (i,j) position is considered). G is the vector of control variables and F is the rule of evolution of the Cellular Automaton Model. As a common rule, it is assumed that the state in a space of the grid will be affected only by the behavior of its neighbors, which possess their own investment preferences that are represented by R in the model.
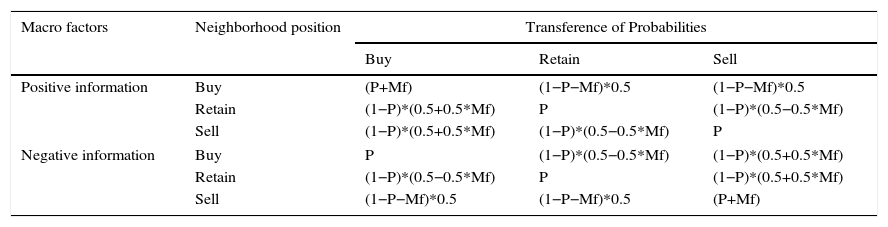
Cellular Automaton Model for behavioral agentsThe artificial stock market focuses on the capability of an agent to imitate, anti-imitate or be indifferent to the position of his neighbors. For the investigation, we worked with an individual transference probability P(i,j) and, according to the original model by Fan et al. (2009), the interaction is studied without considering the market information or Mf. The general matrix of position transference, based on the state of the economy and the individual tendency to replicate or not, is evidenced in Table 1.
Position transference matrix for a behavioral agent.
| Macro factors | Neighborhood position | Transference of Probabilities | ||
|---|---|---|---|---|
| Buy | Retain | Sell | ||
| Positive information | Buy | (P+Mf) | (1−P−Mf)*0.5 | (1−P−Mf)*0.5 |
| Retain | (1−P)*(0.5+0.5*Mf) | P | (1−P)*(0.5−0.5*Mf) | |
| Sell | (1−P)*(0.5+0.5*Mf) | (1−P)*(0.5−0.5*Mf) | P | |
| Negative information | Buy | P | (1−P)*(0.5−0.5*Mf) | (1−P)*(0.5+0.5*Mf) |
| Retain | (1−P)*(0.5−0.5*Mf) | P | (1−P)*(0.5+0.5*Mf) | |
| Sell | (1−P−Mf)*0.5 | (1−P−Mf)*0.5 | (P+Mf) | |
P is the probability of transference in the market, originally defined as a uniform probabilistic variable with a domain between 0 and 1. Mf is the economic Macrofactor or the general state of the economy defined daily. However, for the validation of the model, and for the study of the flow of information, it is ignored, giving it a value equal to zero.
For the construction of a CAM focused on rational agents, a rule of evolution must be defined. In this case, a variant of Alexander's filters was applied, and even though this is a technique that does not apply rigorous statistical inference, it is accepted because it generates a dynamic through the active management of financial series (Duarte & Mascareñas, 2014).
It consists on investing and divesting during a determined period of time based on the rule of purchasing the asset when its price increases x% and selling it when its price falls x%. Nevertheless, since the CAM lacks a price generator, the filter is compared with a z% percentage increase or decrease in the possible purchase.
The change in position of a rational agent relates to the information—free and of quality. The economic Macrofactor or the general state of the economy is then defined as a calculated variable based on the dynamic of the CAM.
This Mf acts as a simile, considering that it does not represent the global economic behavior of a region—as a real macrofactor—it does, however, help analyze the probable tendency of the change. As the Mf is estimated for each iteration, it can be linked to the number of transactions carried out throughout the previous day.1 When Mf≥0.5 the economy is considered to be on the rise.
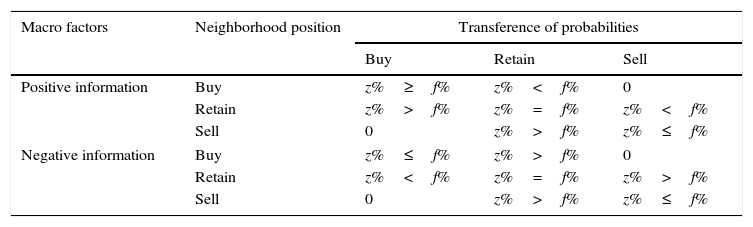
The general position transference matrix, based on the state of the economy and the decision filter, is shown in Table 2.
Position transference matrix for a rational agent.
| Macro factors | Neighborhood position | Transference of probabilities | ||
|---|---|---|---|---|
| Buy | Retain | Sell | ||
| Positive information | Buy | z%≥f% | z%<f% | 0 |
| Retain | z%>f% | z%=f% | z%<f% | |
| Sell | 0 | z%>f% | z%≤f% | |
| Negative information | Buy | z%≤f% | z%>f% | 0 |
| Retain | z%<f% | z%=f% | z%>f% | |
| Sell | 0 | z%>f% | z%≤f% | |
f% represents the value of Alexander's filter. According to the state of the economy, the agent may or may not change position; however, in the case of doing so, said change will always be to the closest position.
In the mixed CAM, the macroeconomic information affects both types of agents, therefore, Eq. (13) is calculated for the two transference matrices (Tables 1 and 2), a disposition is generated by mixing behavioral and rational agents so that each of them has four neighbors of each type. The disposition observed in Figure 1. Spatial distribution of the agents makes it possible for the assets of the behavioral agents to be affected by the nature of the market and the behavior of the rational agents.
Spatial distribution of the agents.
Source: Evaluation of the methodologies for the construction of artificial markets, Talero, Duarte, and Sierra (2015).
According to the CAM designed by Fan et al. (2009), a market of 50*50 cells in which the initial position of the agents is distributed uniformly between Buying, Retaining or Selling an asset is built. The simulation is carried out for 100 iterations to demonstrate the behavior of the final positions of each version of the model. With regard to the analysis of the Hurst exponent and its relation to the complexity or efficiency of the stock market, only the data equivalent to the average longitude of the original cycle described by Fan will be considered. With L=29. Because a higher number of instances generate the loss of original memory (indicating the end of the natural cycle or memory cycle).
Cellular Automaton Model for behavioral agentsThe simulation is done with three types of probabilities to imitate the neighborhood (Table 3). The first is the one proposed in the original model, in which there is no predilection. In the second, the position of the agents tends to avoid being affected by its neighbors and, therefore, the behavioral tendency is to avoid imitating or being contrary, following a Normal distribution. Finally, the third is obliged to go in favor or against the neighborhood, though never to be indifferent, and the probability is symmetric (Fig. 2).
P(i,j) distributions.
| Distribution | Characteristics |
|---|---|
| Uniform | Continues in the [0;1] interval |
| Normal | Median of 0.5 and standard deviation of 0.16, domain [0,1] |
| Anti-Indifference | Probability of indifference (0.5) equal to zero and symmetric, presents the form of Fig. 2 Anti-indifference Distribution domain between [0,1] |
Anti-indifference distribution.
Source: evaluation of the methodologies for the construction of artificial markets, Talero et al. (2015).
The simulation is done with three levels of filters to determine if, in a completely rational market, the agents adopt positions, and if the change in these represents the efficiency of the simulated Stock Market. The first filter is designed with the purpose of emulating a low decision value, which facilitates the dynamic by allowing quick changes between buying, retaining or selling. The second filter is an average point of reference for the filters used. Finally, the third represents a demanding filter, the market will only change when the stock information is reassuring. The three levels of filters f% are described in Table 4.
Mixed Cellular Automaton ModelAn experimental 32 design is developed, with each type of agent being the {Behavioral,Rational} factor, and the variants of the models being the levels to be analyzed. N1={Uniform,Normal,Anti-Indifference}N2={1%,3%,5%} Three experimental replicas were done in order to evidence the variability of the memory or efficiency in the Cellular Automaton Model.
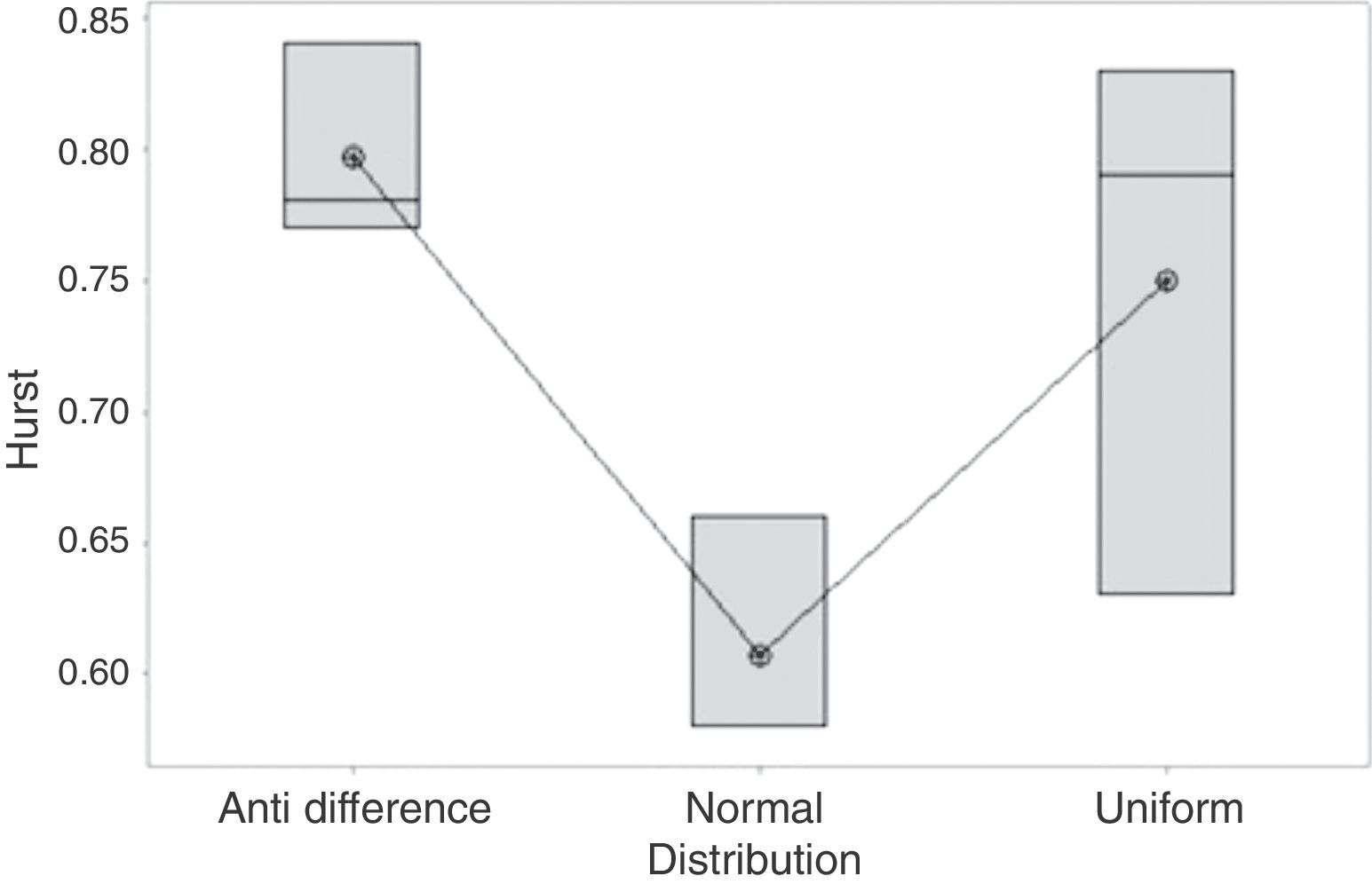
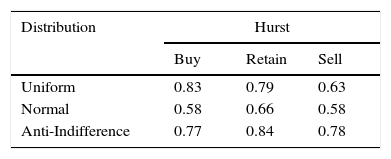
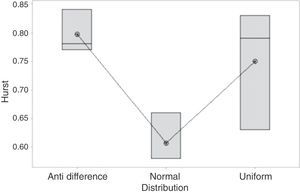
Results analysisCellular Automaton Model for behavioral agentsAs initial hypothesis (H0), we have that all Hurst medians are equal, and as an alternative hypothesis (H1) we have that at least one of these is different. The resulting values from the simulation are shown in Table 5. Hurst exponent for the different P, indicating that there are discrepancies between the original distribution (Uniform) and those that affect the tendency to imitate or not (Fig. 3).
The conceptual difference between the Normal and Anti-Indifference levels is statistically evidenced through ANOVA. However, the uniform distribution can present a similar behavior to both, provided that their probability of changing state is individual.
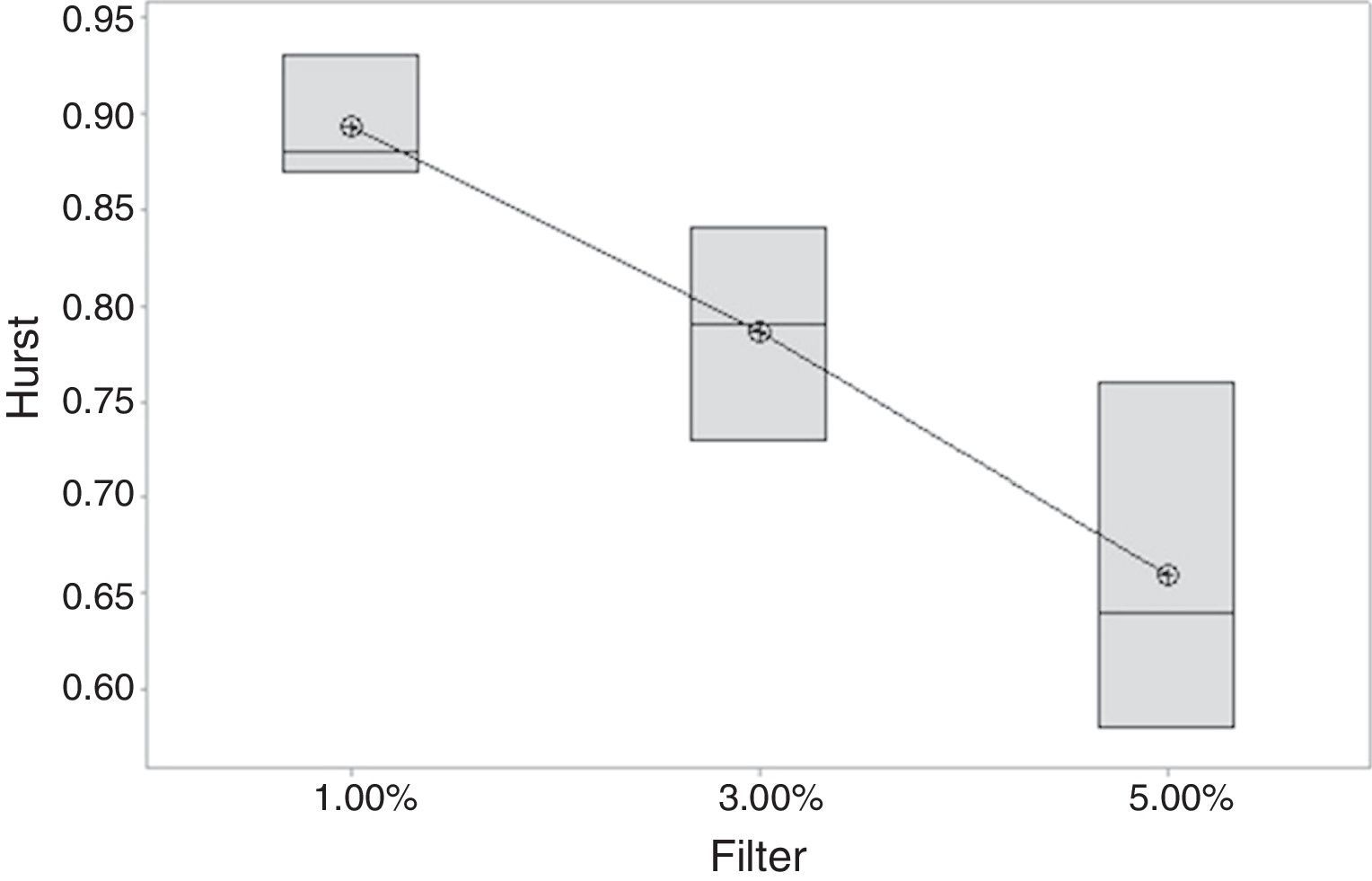
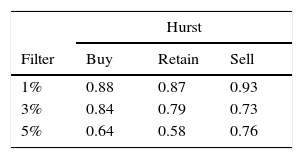
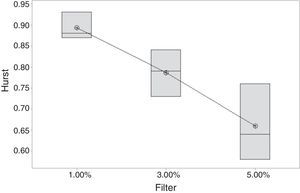
Cellular Automaton Model for rational agentsAs initial hypothesis H0, we have that all Hurst medians are equal, and as H1, we have that at least one of these is different. The estimated coefficients are shown in Table 6. Hurst exponent for different filters indicating that there is a tendency for chaos when the value of the filter is increased (Fig. 4).
A significant difference can be appreciated after the ANOVA between the extreme levels of the filter factor; the value of 3%, due to being an intermediate point between these, could statistically estimate both.
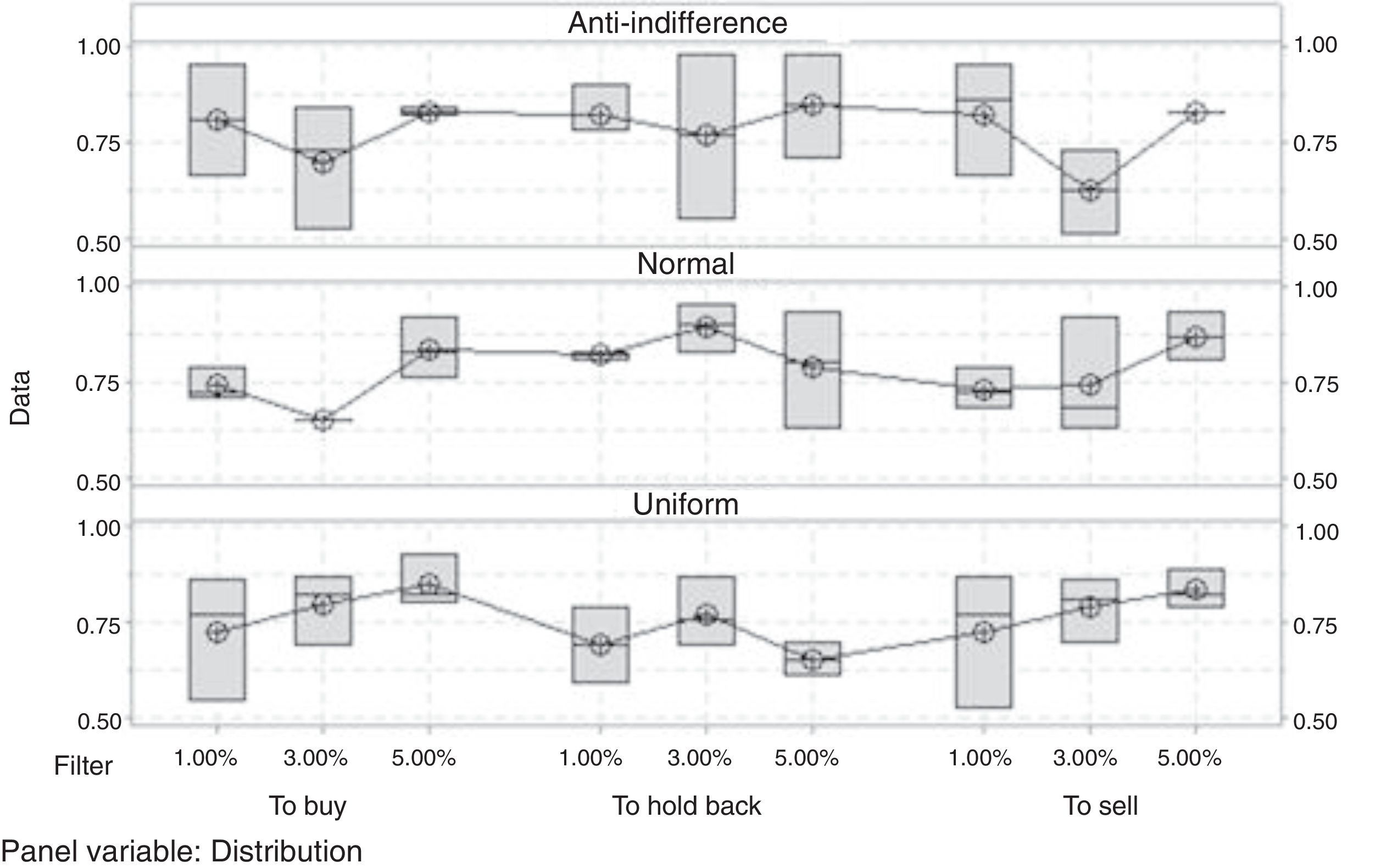
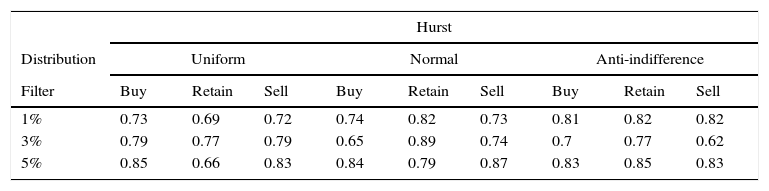
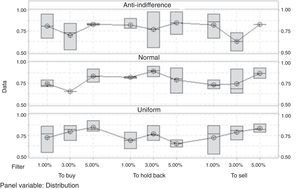
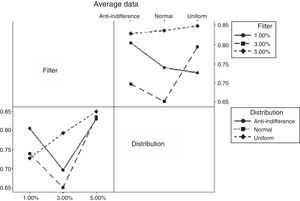
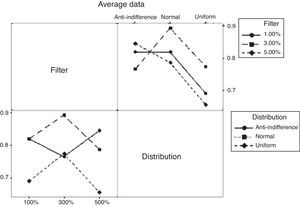
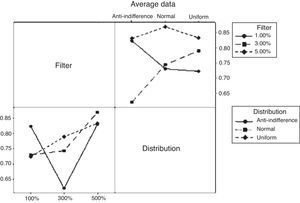
Mixed Cellular Automaton ModelAs initial hypothesis H0 for the experimental design, we have that all Hurst medians are equal; and as H1, we have that at least one of these is different. In this case, there are two factors and the interaction between these. The Hurst exponents of the design are shown in Table 7.
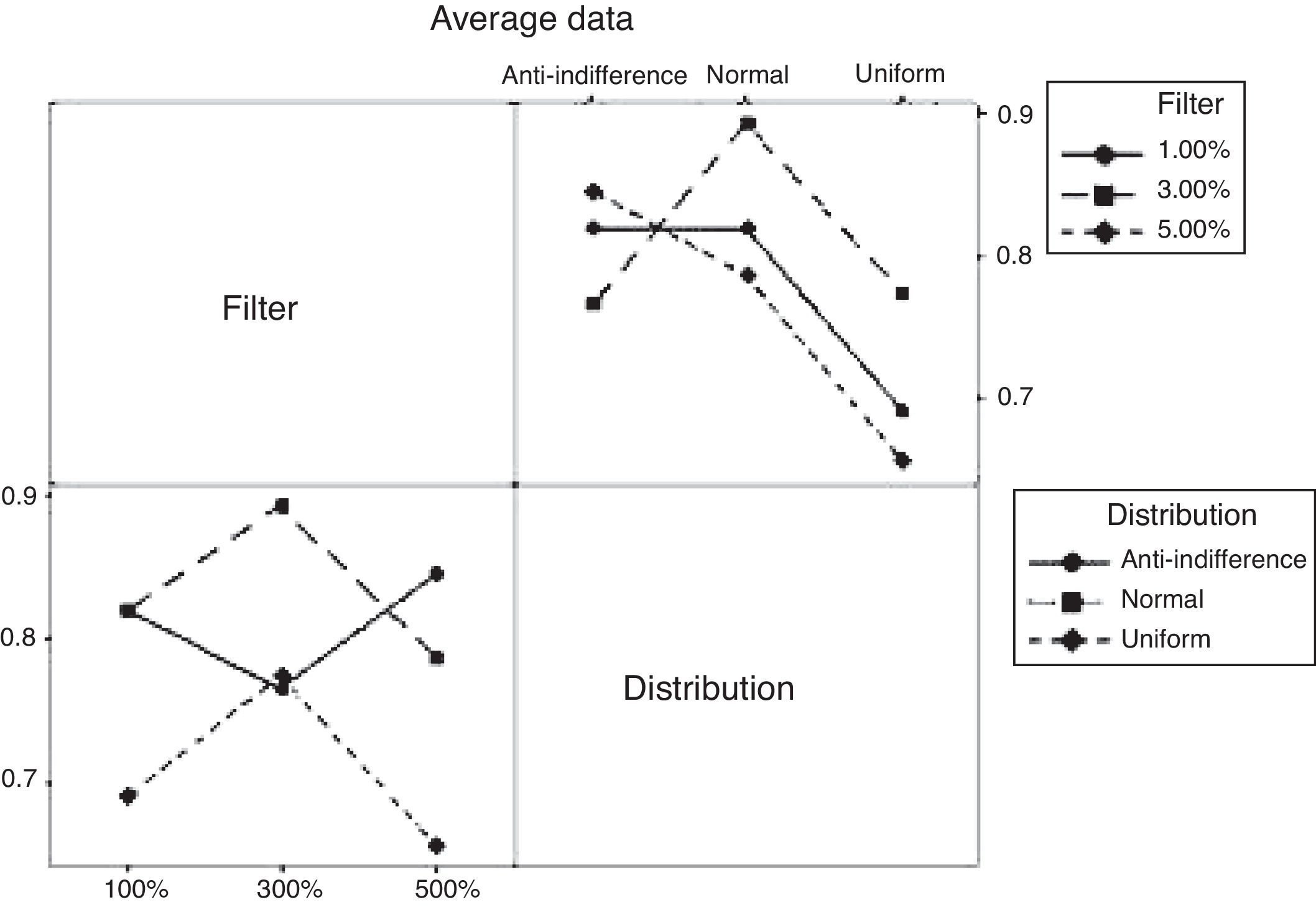
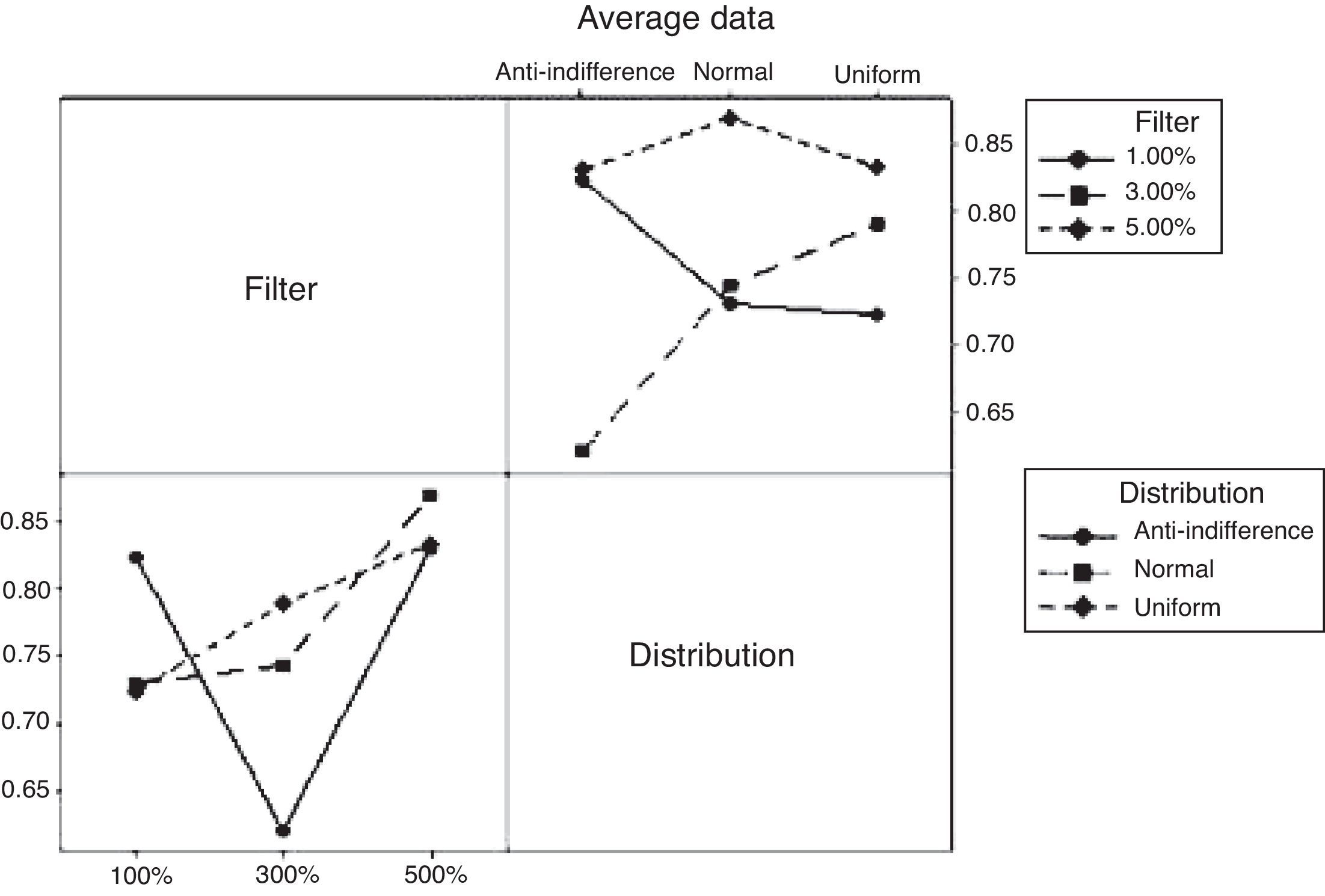
Average Hurst exponent of the mixed CAM.
| Hurst | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Distribution | Uniform | Normal | Anti-indifference | ||||||
| Filter | Buy | Retain | Sell | Buy | Retain | Sell | Buy | Retain | Sell |
| 1% | 0.73 | 0.69 | 0.72 | 0.74 | 0.82 | 0.73 | 0.81 | 0.82 | 0.82 |
| 3% | 0.79 | 0.77 | 0.79 | 0.65 | 0.89 | 0.74 | 0.7 | 0.77 | 0.62 |
| 5% | 0.85 | 0.66 | 0.83 | 0.84 | 0.79 | 0.87 | 0.83 | 0.85 | 0.83 |
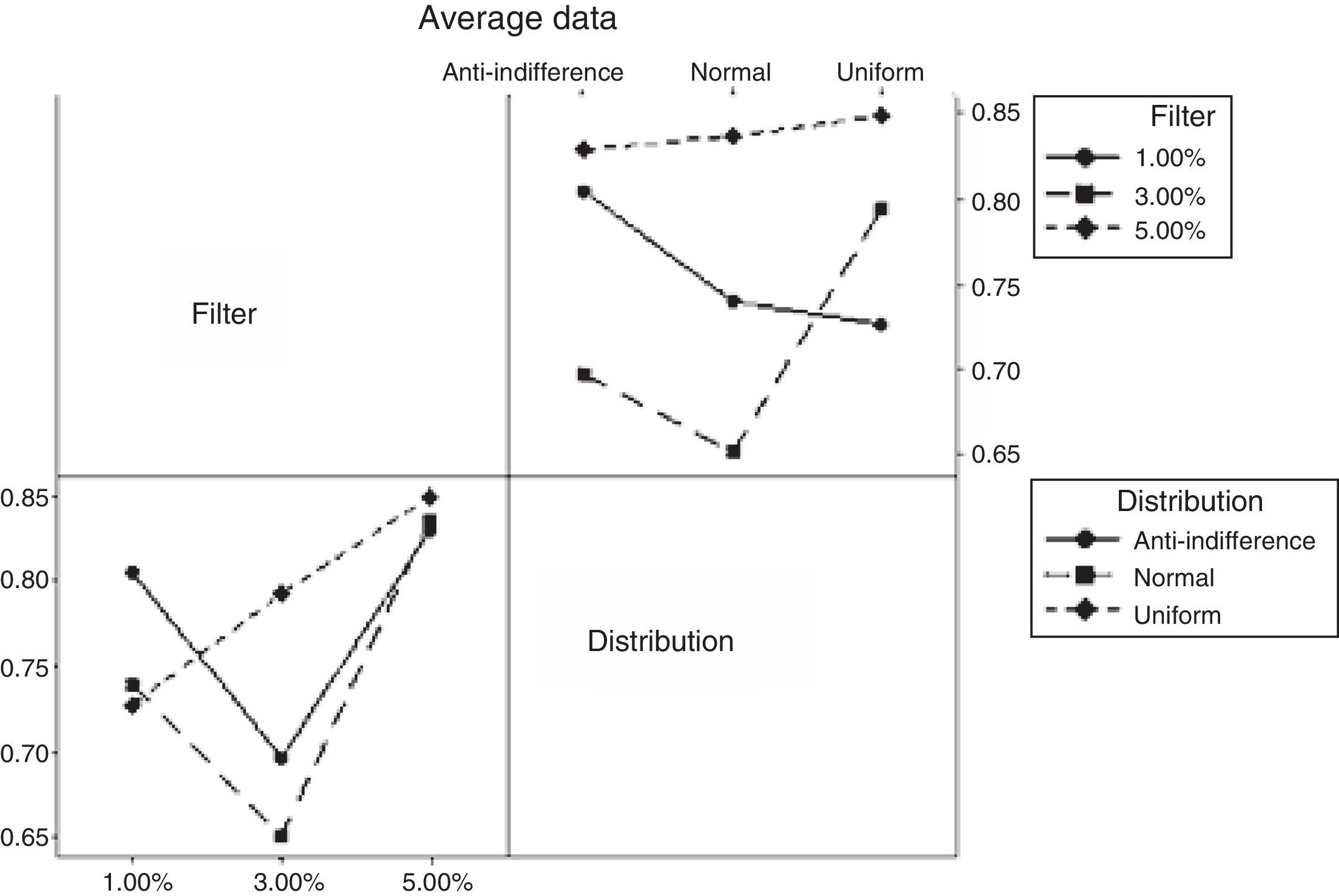
By having three metrics of quality or response variables, a MANOVA is carried out, finding that there is a correlation between the Buy and Sell positions. On the other hand, the factorial design reveals that there is a relation between the behavior of the Hurst exponent and the level of the filter only in the case of the Buy position. The variability of the design is shown in Figure 5.
In the Buy position, a persistent behavior can be observed, which is less chaotic as the value of the filter increases; a behavior that correlates weakly with the Sell position. In general, the level of market efficiency is directly related with the Buy and Sell positions (see Appendix 1), which carry a negative correlation in the historical data confirming the behavior of the supply/demand in the CAM.
Conclusions and recommendationsThis work aimed to build a scenario in which the behavior of a market with more than one type of stock agent could be represented in the context of behavioral finances and the impact of the investor in the efficiency of the same. To this end, the Hurst exponent was used as an indicator of the chaos and/or memory, this through the proximity of the estimation to the theoretical value of randomness H=0.5, which represents an efficient market.
In a distinctly behavioral virtual stock market such as the one developed by Fan, Ying, Wang and Wei (2009), the efficiency is minimal given that the estimations of the Hurst exponent are close to 0.86, indicating a persistent series. Due to the different proposals in this investigation, it can be determined that there should be a degree of indifference or level of rationality in the agents, that is, a simulated market there must not have a fully behavioral behavior. When adding the rational component, a weak efficiency can be modeled.
The rational Cellular Automaton Model will show a tendency for chaos or efficiency depending on whether the modeled agent is more demanding with the contextual economic information. This can be improved with the inclusion of a price generator and the configuration of the economic macrofactor that will facilitate its comparison with a real market.
By modeling two types of agents—rational and behavioral—the hypothetical behavior of the market is simulated. A persistent tendency toward investment can be appreciated when the filter is more demanding, unlike the distinctly rational model. Said behavior is due to the disposition of the agents, given that if the z% decision value of the market is on the rise, each behavioral agent will probably adopt the position of his neighbors, who shall always be four rational affected by z% and, therefore, the capability for imitation observed in the Normal and Anti-Indifference distributions would generate a herd effect.
The mixed Cellular Automaton Model can be improved by changing the dispositions and quantity of each type of agent in the market, in order to decrease the persistence level of the financial series. A system of punishments and incentives could also be adopted when the position adopted by the behavioral agents responds to the behavior of the economy at the t+1 instance, thus generating a Mixed Learning Cellular Automaton Model.
Peer Review under the responsibility of Universidad Nacional Autónoma de México.