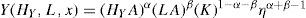El objetivo de este artículo es analizar el papel que juega la innovación tecnológica en la dinámica del crecimiento económico regional en México. Para tal propósito se utiliza un modelo que involucra una función de innovación y una función de producción para establecer el nivel de interacción entre las variables de innovación y de crecimiento económico. Para el análisis econométrico se utiliza información estadística por entidad federativa, correspondiente al periodo de 1994 a 2008. Se estima un modelo con datos de panel, cuyos resultados muestran que existe un efecto positivo y diferenciado entre variables que incorporan en alguna medida la innovación tecnológica, como son las patentes, el gasto en I+D, entre otros, así como el crecimiento del Producto Interno Bruto.
The aim of this paper is to analyze the role of technological innovation in the dynamics of regional economic growth in Mexico. For this purpose, a model which involves a function of innovation and a production function to set the level of interaction between the variables of innovation and economic growth is used. For the econometric analysis statistical information by state is used, for the 1994-2008 period. A model is estimated with panel data, with results that show a positive and differentiated effect between variables that incorporate some degree of technological innovation such as patents, R & D expense, among others, as well as Gross Domestic Product (GDP) growth.
En los últimos años se ha registrado la incorporación masiva de nuevas tecnologías que redefinen completamente no sólo las rutinas innovativas, productivas, comer-ciales, financieras, etc., sino también la propia forma de vida de una parte de los habitantes en todo el mundo. Las llamadas nuevas tecnologías de la comunicación y la información (TCI) son el núcleo de esta transformación, a la cual hay que sumar otras tecnologías todavía menos avanzadas en su desarrollo, pero también de amplios efectos (biotecnología, nuevos materiales, entre otras).1
Al mismo tiempo, la dinámica de la competencia capitalista se ha desplazado visiblemente hacia un peso cada vez mayor de las capacidades tecnológicas como determinantes del desempeño económico y la competitividad de empresas y países. Productos y procesos llegan a la obsolescencia de manera cada vez más rápida, y la capacidad de diferenciación y flexibilidad se han convertido en elementos decisivos para la supervivencia en el mercado. La Organización para la Cooperación y el Desarrollo Económicos (OCDE) confirma en sus últimos reportes que estamos ingresando en la era de las economías basadas en el conocimiento (knowledge-ba- sedeconomies), las cuales —a su vez— se basan directamente en los procesos de innovación tecnológica, uso de conocimiento y de las tecnologías de la información y la comunicación (TIC) (OECD, 1996a).
La relación entre el esfuerzo en I+D, innovación tecnológica y crecimiento económico ha sido estudiada desde dos grandes visiones: en el área de crecimiento económico (macroeconomía) a través de modelos teóricos en los que la innovación tecnológica es un factor endógeno de crecimiento. Se trata de modelos que consideran que la tecnología es un factor de las economías como lo son el capital o el trabajo, y no sólo la forma funcional que establece la relación de estos inputs tradicionales con el producto. La otra visión se enfoca en el área de la organización industrial por medio de modelos que pretenden explicar el comportamiento de las empresas en relación con las actividades relacionadas con la innovación (tanto en su generación como en su adopción) en economía de mercado.
En estos dos tipos de modelos, el grado de innovación tecnológica es resultado de la asignación de recursos a la creación y difusión de conocimientos y, por tanto, de las decisiones de los agentes económicos (Borondo, 2008b). La dinámica consiste en que los agentes económicos establecen su función objetiva y comienzan un proceso de óptima asignación de sus recursos escasos para conseguir la maximización de dicha función objetiva. De este modo, el grado de innovación tecnológica que un agente (una empresa o un país) decide es el nivel óptimo, el cual vendrá determinado tanto por la función objetiva como por las restricciones a las que se enfrente. En este artículo, nos centraremos en la primera aproximación a la Economía de la Innovación Tecnológica.
Los avances tecnológicos son considerados como uno de los principales determinantes del crecimiento económico: Pavitt y Soete (1981), Fagerberg (1988) y Dosi et al. (1988d) muestran de manera empírica que existe una relación muy estrecha entre estas dos variables. La literatura del crecimiento endógeno centra la atención sobre el cambio tecnológico endógeno para explicar los patrones de crecimiento de las economías mundiales. De acuerdo con estos llamados modelos endógenos de crecimiento, iniciados por Romer (1994), la innovación tecnológica se crea en la investigación y desarrollo (I + D) usando capital humano y el stock de conocimientos existentes.
El punto central de estos modelos de crecimiento endógeno plantea que la innovación tecnológica propicia de algún modo el crecimiento económico sostenible, ya que hay rendimientos constantes a la innovación en términos de capital humano empleado en los sectores de investigación y desarrollo. En este trabajo se analiza el papel que juega la innovación tecnológica en el crecimiento económico regional en México. Para el análisis se utiliza una técnica de datos de panel y los datos de diez regiones de México para el periodo 1994-2006; en particular se tiene interés en determinar en qué medida la inversión en I+D propicia la innovación tecnológica y si un aumento en la innovación conduce a un aumento permanente en el producto interno bruto (PIB) per cápita.
Revisión de la literaturaEl propósito de este apartado es proporcionar un ordenamiento de la literatura más significativa que se ha producido recientemente acerca de los determinantes, características y consecuencias de los procesos de innovación y cambio tecnológico. Cabe aclarar que la intención no es presentar una discusión acabada sobre todas las cuestiones vinculadas a dichos temas, sino proponer una guía temática y de lecturas, que ordene los principales campos de debate e indique algunas de las referencias más relevantes actualmente disponibles en cada uno de ellos.2
Si bien no es la intención de este trabajo adentrarse en los debates teóricos internos a nuestra disciplina —la economía— es imposible obviar el hecho de que dentro de ella conviven distintos enfoques conceptuales, cuyas diferencias se extienden, inevitablemente, al área que nos ocupa aquí.
El tratamiento que se hace de la innovación y el cambio tecnológico resulta, a nuestro juicio, menos adecuado y fructífero que los aportes que, desde diferentes perspectivas, han venido realizado desde tiempo atrás varios autores heterodoxos, a los cuales es común ver agrupados —aunque este procedimiento no siempre está justificado— con el nombre de neoschumpeterianos (por referencia a Schumpeter, quien fue uno de los muy pocos economistas de este siglo en hacer de la innovación una preocupación central dentro de su esquema de pensamiento) o evolucionistas.3
Es necesario advertir, en consecuencia, que la mayor parte de la literatura a la que hacemos referencia aquí se ubica dentro, o en las cercanías, de estos enfoques heterodoxos que, de todos modos, parecen comenzar a permear el pensamiento dominante en economía, tal como lo muestran los borradores del próximo informe sobre el desarrollo mundial (World Development Report), muy influyente publicación del Banco Mundial que en su edición del próximo año se dedicará al tema del cambio tecnológico.
La sociedad capitalista ha desarrollado distintos métodos para garantizar la propiedad privada de los beneficios de la innovación. Probablemente el más conocido de ellos es el sistema de patentes que, por otro lado, intenta balancear la apropiabilidad perfecta por tiempo limitado con la apertura (disclosure) pública de su contenido, la cual garantizaría, luego de su expiración, la difusión de sus beneficios. La evidencia muestra, sin embargo, que no siempre son las patentes el medio empleado para proteger las innovaciones.
Levin et al. (1987) presentan los resultados de una amplia encuesta realizada en los EE.UU. sobre los métodos empleados para apropiarse de los resultados de la innovación industrial. Además de las patentes, aparecen el secreto comercial, el tiempo de desarrollo de las nuevas tecnologías (lead time), la rapidez en moverse a lo largo de la curva de aprendizaje y los servicios post venta. La relevancia de los distintos métodos varía según la industria y el tipo de innovación considerada. Al mismo tiempo, en otros trabajos se han señalado otras formas de protección de los retornos de la innovación; por ejemplo, las marcas, el acaparamiento de insumos críticos, el control de canales de distribución, la publicidad y la presencia de economías de escala.
Por otro lado, como señalan David y Foray (1996), desde el punto de vista social importa el poder distributivo (distribution power) de un sistema de innovación, lo cual apunta a facilitar una eficiente distribución y utilización del conocimiento científico y tecnológico disponible en la sociedad. Si por una parte esto implica, por ejemplo, estimular las interacciones entre ciencia y tecnología, también supone que los mismos medios que se usan para asegurar un mayor retorno privado de las actividades innovativas pueden disminuir el poder distributivo del sistema. En consecuencia, puede surgir un trade-off entre apropiabilidad —que favorecería una mayor acumulación de nuevo conocimiento— y poder distributivo —que favorecería que ese conocimiento sea socialmente más útil.
A su vez, Levin et al. (1987) señalan que no siempre un fortalecimiento de la apropiabilidad privada lleva a acelerar el ritmo de surgimiento de las innovaciones y, cuando lo hace, esas innovaciones pueden tener a nivel social un costo excesivo. Otras referencias relevantes: Dasgupta (1988), Foray (1997), Griliches (1990), Primo Braga (1990) y Teece (1987).
La relación positiva entre la innovación y el crecimiento del producto ha sido confirmada por estudios internacionales que utilizan datos de panel tales como Frantzen (2000) y Griffith, Redding y Reenen (2001). También hay fuerte evidencia de que las externalidades de los países industrializados a los países en desarrollo tienen efectos positivos sobre el crecimiento (Coe, Helpman y Hoffmaister, 1995; Griffith, Redding y Reenen, 2001). En un estudio más reciente Zachariadis (2003) compara el efecto de la innovación sobre la producción manufacturera y agregada y encuentra que el efecto de la innovación es mucho mayor para la producción agregada que para el sector manufacturero. Porter y Stern (2000) utilizan datos agregados de patentes para examinar los efectos de la innovación y encuentran que la innovación se relaciona de manera positiva con el capital humano y el stock de conocimientos. También encuentran que existe una relación significativa entre la innovación y el crecimiento del producto.
El eje central de estos modelos reside en que la innovación tecnológica permite un crecimiento económico sostenible debido a que son constantes los retornos a la innovación en términos de capital humano empleado en el sector de I+D. El análisis empírico de esta relación se lleva a cabo habitualmente a partir de la estimación de una función de producción en la que se incluye como variable explicativa el capital tecnológico también llamado stock de conocimientos (Romer, 1990). Este input facilita la generación de nuevas ideas en las empresas, las cuales pueden revertir en un mayor crecimiento de acuerdo con los modelos de crecimiento endógeno.
Por su parte, los modelos basados en I+D, introducido por Romer (1986, 1990) y Grossman y Helpman (1991) dan un paso más al incorporar la competencia imperfecta en los modelos de crecimiento. Estos modelos se basan en tres sectores: el sector de la producción final, el sector de los bienes intermedios y el sector de I+D. El sector de I+D utiliza capital humano para producir nuevas ideas y diseños; después de crear estas ideas las vende al sector de bienes intermedios; éste a su vez patenta estas nuevas ideas y obtiene los derechos de monopolio exclusivo de producir los nuevos productos diseñados por estas ideas; posteriormente, vende estos productos intermedios al sector de la producción final. El sector de I+D es el sector clave en estos modelos para el crecimiento sostenible.
Generalmente, los estudios empíricos de estos modelos implican probar el efecto de las variables de I+D sobre el crecimiento de la productividad. Borondo (2008b) examina los modelos de crecimiento basados en I+D utilizando un modelo de series de tiempo; sin embargo, no encuentra ninguna evidencia de un aumento en el crecimiento de la productividad de los factores a pesar de un continuo aumento de la tasa de crecimiento del número de ingenieros y científicos. Este autor argumenta que dicho resultado es evidencia de los rendimientos decrecientes en la producción de nuevos conocimientos.
Coe, Helpman y Hoffmaister (1995) usan un modelo multipaís para examinar los efectos de derramas de I+D de países industrializados a países en vía de desarrollo sobre el crecimiento de productividad total de los factores. Ellos usan datos para 77 países en vía de desarrollo durante el periodo de 1971-1990 y encuentran que hay derramas sustanciales de I+D de países desarrollados a países en vías de desarrollo. Estas derramas tienen un efecto positivo y significativo sobre la productividad total de factores de países en vías de desarrollo.
Aghion y Howit (1998) proveen razones que justifican por qué un incremento en la tasa de crecimiento del número de ingenieros y científicos no provocó un aumento correspondiente en el crecimiento de la productividad. En primer lugar, la creciente complejidad de la tecnología hace que sea necesario aumentar la I+D con el tiempo justo para mantener el tipo de invención constante para cada producto; en segundo lugar, como el número de productos incrementa, una innovación en un producto afecta directamente una menor proporción de la economía y, por lo tanto, tiene menor efecto indirecto proporcional en las existencias totales de los conocimientos. Estos mismos autores también argumentan que en vez de usar el número de ingenieros y científicos ocupados en los sectores de I+D, la fracción de PIB asignada a I+D debería ser usada probar la implicación de modelos basados en I+D. Ellos prueban la implicación de modelos basados en I+D usando datos sobre gastos de I+D como una fracción del PIB para Estados Unidos y concluyen que en Estados Unidos los modelos de I+D confirman la teoría de crecimiento endógena en lugar de contradecirla.
La relación existente entre I + D y el crecimiento de la productividad en algunos países ha sido también confirmada por los estudios que utilizan datos de panel internacionales, tales como Frantzen (2000) y Griffith, Redding y Reenen (2001). Zachariadis (2003) compara el efecto de la I+D sobre la producción agregada y la producción manufacturera, y él considera que el efecto de la I+D es mucho mayor para la economía global que para el sector manufacturero.
De acuerdo con Aboites y Dutrénit (2003), en México en los últimos años la importancia de la creación de innovaciones tecnológicas ha sido ampliamente reconocida. Este hecho es corroborado por la participación de los gobiernos de subsidiar programas de I+D. Germán-Soto et al. (2009) mencionan que en México se han generado incrementos importantes en la captación de inversiones foráneas con la consiguiente implantación de tecnologías nuevas y sistemas de información. Afirman que la formación de capital humano juega un papel esencial en el desarrollo tecnológico e innovador del país. Por lo tanto, ambos factores (educación e inversiones nuevas) deben constituir elementos explicativos e inseparables del proceso innovador. Con el fin analizar la pertinencia de la intervención pública, en este artículo realizamos estimaciones empíricas del papel que juega la formación de capital humano en el proceso de innovación y de ésta innovación tecnológica en la determinación del crecimiento del PIB per cápita regional utilizando técnica de datos panel para el periodo 1994-2006, debido a la disposición de la información.
Aspectos descriptivosLa formación de recursos humanos, específicamente de investigadores de alto nivel académico, se ha incrementado considerablemente en respuesta a los estímulos gubernamentales y la expansión de las instituciones de educación superior e investigación. Lo anterior se puede observar en la gráfica 1.
En cuanto en el nivel regional, específicamente en cada estado de la República, el número de SNI del Distrito Federal con respecto al resto de los estados es muy evidente, lo cual refleja claramente la concentración de las actividades de investigación y desarrollo.
Las dos graficas anteriores muestran la formación de capital humano de alto nivel, ya que dichos investigadores son la materia prima para realizar proceso de innovación. Michael Porter señala que el nivel de la innovación de una región puede estimarse con la cantidad de patentes generadas. De acuerdo con Porter, en México el nivel de innovación se muestra mediante las patentes concedidas en el periodo 1990-2007, como se muestra en la siguiente gráfica.
Por otra parte, en el nivel estatal la diferencia en patentes solicitadas del Distrito Federal con respecto al resto de los estados es muy grande, tal y como se muestra en el cuadro 1.
Patentes solicitadas por entidad de residencia del inventor (1997-2006)
| Entidad federativa | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|---|---|---|---|---|---|
| Aguascalientes | 8 | 4 | 3 | 3 | 2 | 2 | 6 | 5 | 8 | |
| Baja California | 6 | 9 | 11 | 4 | 4 | 6 | 0 | 0 | 3 | 3 |
| Baja California Sur | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 3 | 1 | 1 |
| Campeche | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 4 | 1 |
| Chiapas | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 6 |
| Chihuahua | 2 | 5 | 9 | 9 | 11 | 17 | 18 | 27 | 15 | 24 |
| Coahuila | 16 | 14 | 13 | 7 | 10 | 11 | 32 | 26 | 18 | 17 |
| Colima | 2 | 4 | 1 | 5 | 8 | 5 | 2 | 4 | 3 | 2 |
| Distrito Federal | 143 | 148 | 181 | 166 | 215 | 206 | 167 | 179 | 212 | 181 |
| Durango | 0 | 0 | 1 | 1 | 3 | 2 | 0 | 1 | 2 | 7 |
| Estado de México | 49 | 70 | 44 | 64 | 55 | 59 | 52 | 58 | 56 | 61 |
| Guanajuato | 9 | 10 | 15 | 12 | 23 | 13 | 26 | 22 | 9 | 14 |
| Guerrero | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 3 |
| Hidalgo | 6 | 12 | 1 | 2 | 2 | 3 | 3 | 1 | 4 | 3 |
| Jalisco | 21 | 25 | 33 | 39 | 41 | 51 | 40 | 59 | 66 | 72 |
| Michoacán | 1 | 5 | 2 | 3 | 4 | 7 | 1 | 10 | 5 | 5 |
| Morelos | 27 | 15 | 14 | 11 | 11 | 10 | 10 | 14 | 10 | 17 |
| Nayarit | 2 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| Nuevo León | 56 | 47 | 38 | 27 | 66 | 44 | 44 | 66 | 75 | 81 |
| Oaxaca | 2 | 3 | 3 | 2 | 5 | 2 | 2 | 4 | 5 | 1 |
| Puebla | 11 | 15 | 16 | 19 | 14 | 15 | 14 | 22 | 15 | 11 |
| Querétaro | 17 | 15 | 24 | 19 | 12 | 17 | 10 | 22 | 21 | 11 |
| Quintana Roo | 0 | 0 | 2 | 1 | 1 | 3 | 2 | 3 | 1 | 5 |
| San Luis Potosí | 3 | 4 | 10 | 8 | 9 | 7 | 3 | 4 | 3 | 9 |
| Sinaloa | 3 | 6 | 3 | 8 | 7 | 8 | 3 | 5 | 7 | 2 |
| Sonora | 3 | 2 | 3 | 4 | 7 | 7 | 1 | 3 | 5 | 10 |
| Tabasco | 3 | 3 | 1 | 5 | 2 | 3 | 3 | 5 | 7 | 1 |
| Tamaulipas | 7 | 6 | 4 | 3 | 8 | 7 | 3 | 7 | 10 | 6 |
| Tlaxcala | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 2 |
| Veracruz | 10 | 9 | 5 | 4 | 8 | 8 | 2 | 5 | 7 | 6 |
| Yucatán | 3 | 3 | 4 | 2 | 1 | 5 | 9 | 8 | 5 | 3 |
| Zacatecas | 0 | 1 | 0 | 0 | 1 | 1 | 4 | 0 | 4 | 0 |
| Sin clasificar* | 8 | 15 | 11 | 0 | 1 | 4 | 2 | 0 | 0 | 4 |
| Total | 420 | 453 | 455 | 431 | 534 | 526 | 468 | 565 | 584 | 574 |
La regionalización debe incluir el conjunto de indicadores cualitativos y cuantitativos que expresen la realidad del territorio. La utilidad máxima de la regionalización es ser la herramienta perfecta para la planificación del territorio —ordenamiento territorial— a partir de la suma de estados y municipios que definan la regionalización socioeconómica funcional del país.
Debido a que no existe uniformidad de criterios con respecto a un esquema exacto de lo que es la región económica y la regionalización, en esta investigación la regionalización propuesta se ha efectuado a partir de criterios de nivel de ingreso y especialización productiva tomadas por Aboites y Dutrénit (2003). De esta forma se obtienen diez regiones para expresar la dinámica territorial del país.
Regiones económicas
| Región | Estados | Región | Estados |
|---|---|---|---|
| Region noroeste | Baja California | Región sur | Chiapas |
| Baja California Sur | Guerrero | ||
| Sonora | Oaxaca | ||
| Sinaloa | |||
| Región norte-central | Chihuahua | Región capital | México |
| Coahuila | Distrito Federal | ||
| Región noreste | Nuevo León | Región este | Veracruz |
| Tamaulipas | Tabasco | ||
| Región centro-norte | Aguascalientes | Región península de Yucatán | Campeche |
| Durango | Quintana Roo | ||
| San Luis Potosí | Yucatán | ||
| Zacatecas | |||
| Región centro-oeste | Colima | Región centro | Hidalgo |
| Guanajuato | Morelos | ||
| Jalisco | Puebla | ||
| Michoacán | Querétaro | ||
| Nayarit | Tlaxcala |
El crecimiento económico regional es producto, por un lado, del distinto peso y dinámica que tienen los sectores productivos en la economía local —componente de estructura sectorial— y, por el otro, de la propia competitividad que registra la actividad en la región de referencia —componente de competitividad—, entre otros factores.
En la siguiente gráfica se puede observar las diferentes tasas de crecimiento del producto interno bruto (PIB) por cada región en el periodo de 1993 a 2006.
En la gráfica anterior se puede observar cómo la región norte central es la que presentó el más alto crecimiento; además, es la región sur la que registra el menor crecimiento. Como se acaba de observar, existen diferentes niveles tasas de crecimiento económico debido a una diversidad en cuanto a la actividad económica desarrollada en cada región. Es importante mencionar que se omiten gráficas de las otras variables y sólo se presentan las anteriores debido a que las otras son las variables complementarias y no quisiéramos ahondar en su análisis.
Los datos relativos a las variables tales como producto interno bruto (Y), la formación bruta de capital fijo (FBKF), salario medidos en unidades monetarias y la inversión en investigación y desarrollo (I+D) se obtuvieron de Inegi, Conacyt y la Secretaría del Trabajo y Previsión Social; mientras que el stock de capital tecnológico se calcula utilizando el método de inventario permanente de la siguiente manera, tomando como referencia a García et al. (1998):
Donde Kit es el capital tecnológico del año anterior, Rit-1 los gastos en I+D en t-1, y δ la tasa de depreciación del capital de conocimiento. Esta expresión supone que el gasto actual en I+D se transforma en conocimiento útil con un rezago de un año.
Entonces para obtener el capital tecnológico recursivamente de la expresión (1) es necesario hacer referencia a la necesidad de calcular el stock de capital tecnológico para el primer año; suponiendo que el año inicial es t, podemos partir de la relación
Donde s es el número de años que el ente económico ha realizado gastos en I+D; así, pues, suponiendo que los gastos en I+D fueron constantes en todos los años anteriores a t, tenemos que
Por lo tanto, el stock de capital tecnológico inicial es
De esta manera, el capital tecnológico inicial se puede calcular con la expresión (4), considerando como el número de años en que se han realizado gastos en I+D y Ri como el gasto promedio en I+D en un determinado periodo de análisis.
Fundamento del análisis empíricoEl modelo empírico construido está basado sobre el modelo de crecimiento de Romer (1990). Este modelo se basa en tres partes: 1) el crecimiento se basa en el cambio tecnológico; 2) el cambio tecnológico surge como resultado de acciones intencionales que toman las personas que responden a los incentivos del mercado; 3) planos (diseños) para la fabricación de nuevos productos no son rivales; es decir, que puede ser replicado sin costo adicional. El modelo tiene tres sectores: el sector de investigación y desarrollo (I+D), el sector de bienes intermedios y el sector de bienes finales. El producto final es producido de acuerdo con una función de producción Cobb-Douglas
Donde H,L,x son el capital humano, el trabajo y bienes durables, respectivamente. Cada bien durable es producido por un monopolio en el sector de bienes intermedios usando η unidades de consumo sacrificado y el diseño de ese bien durable comprado al sector I+D. La creación de nuevos diseños en el sector I+D evoluciona de acuerdo con la siguiente ecuación
Donde HA es el total de capital humano en el sector I+D, A es el stock de conocimientos y A˙ son los nuevos diseños (innovación). El postulado más importante del modelo Romer que conduce a un crecimiento económico sostenible es el hecho de que la producción de nuevos productos es lineal en el capital humano empleado en el sector I+D y stock de conocimientos (i.e, θ = 1). Esto tiene dos implicaciones: dedicar más capital humano para la investigación conduce a una mayor tasa de producción de éstos; cuanto mayor es el stock de diseños y conocimientos, mayor será la productividad de un ingeniero que trabaja en el sector de la investigación.
Después que un nuevo diseño se produce, entra en la economía en dos formas diferentes: un nuevo diseño permite la producción de un nuevo bien intermedio que se puede utilizarse en la producción del producto; también incrementa el stock total de conocimientos y la productividad del capital humano en el sector de investigación. El capital total evoluciona de acuerdo con la siguiente ecuación
Debido a que toma η unidades de consumo sacrificado para crear una unidad de cualquier tipo de bien durable, esta medida de contabilidad de K está relacionado con los bienes duraderos que son realmente utilizados en la producción según la siguiente regla
Además, debido a la simetría en el modelo, todos los bienes durables disponibles son suministrados en el mismo nivel y pueden ser denotados como x. Puesto que A determina el rango de bienes duraderos que se pueden producir, y puesto que η unidades de producto se requieren por unidad de bienes duraderos, es posible despejar x de la ecuación K = ηAx. Posteriormente, sustituyendo x = K / ηA en la función de producción de la ecuación (5) da lugar a la forma final de la función de producción en el modelo de Romer
Los incrementos en los rendimientos a escala se elevan tanto en los sectores de I+D como en el de bienes finales porque ambos sectores usan stock de conocimientos no rival, A, como insumo. A entra en el sector de I+D directamente e indirectamente en el proceso de producción de bienes finales a través de los desbordamientos de los conocimientos. La implicación más importante de este modelo es que los países puedan alcanzar un crecimiento económico perpetuo mediante el fomento del sector I+D y la inversión en capital humano.
De lo dicho anteriormente, es muy importante probar que los avances tecnológicos juegan un papel importante en la explicación, el largo plazo, el crecimiento económico, así como la formación de capital humano juega un papel importante en la generación de innovación. La teoría del crecimiento endógeno visualiza que los esfuerzos orientados a la innovación responden a los incentivos económicos como un importante motor del progreso tecnológico y el crecimiento de la producción.
Este esfuerzo adopta la forma de inversión en capacidad tecnológica, que es la capacidad de hacer un uso eficaz de los conocimientos tecnológicos y generar beneficios indirectos considerables.
Especificación econométricaEn primer lugar, se utiliza un modelo de regresión lineal para estimar la función de innovación porque se pretende explicar el comportamiento de la innovación en función del stock de conocimientos; posteriormente, se utiliza un modelo de datos panel debido a la limitada información existente con respecto a nuestras variables mencionadas anteriormente, razón por la cual también se utiliza una división regional con objeto de tener una mayor cantidad de datos; además de que algunas de las ventajas de usar datos en panel son: a) se toma en cuenta y controla la heterogeneidad individual; b) da más información. Las variaciones de los datos pueden descomponerse en: variaciones entre empresas, estados o individuos (Gujarati, 2004); asimismo, permite analizar los efectos individuales específicos y los efectos temporales.
El análisis empírico, que abarca el periodo 1994-2006, utiliza los datos oficiales publicados; además, cubre diez regiones de México, las cuales a su vez están integradas por diferentes números de estados.
Retomando la ecuación de la creación de nuevos diseños o innovación
Los resultados del flujo de innovación o patentes creadas A˙ dependen de la cantidad de capital humano que se destina a la investigación H, y del stock de conocimientos A. Si aplicamos logaritmos para linealizar la ecuación tenemos
A esta ecuación se le agregan otras variables como el nivel de escolaridad superior y el producto interno bruto, debido a que la sola ecuación posee un alto grado de significatividad. Estas variables ayudan a obtener un modelo más significativo aparte de tener una relación de causalidad de acuerdo con la prueba da causalidad de Granger que se muestra en el cuadro 3, donde la probabilidad menor a 0.05 indica que sí existe causalidad entre las variables.
El modelo por estimar es de la siguiente forma
Donde ln ES y ln PIB representan al nivel educativo superior y al producto inter-no bruto.
Asimismo, el modelo utilizado para probar impacto de la innovación en crecimiento del producto deriva de una manera convencional, pues se da a partir de una función de producción en la que se incluyen la variable patentes del modelo anterior como proxi de innovación para medir el impacto que genera en el crecimiento económico todo el aprendizaje derivado de la acumulación de conocimientos y los efectos asociados a ella, donde se incluye el valor de las externalidades que son los efectos de conocimientos tecnológicos de las regiones más cercanas.
Para estimar esta función, adoptamos una extensión de la función de producción Cobb-Douglas
Luego aplicando logaritmos a la ecuación (13) tenemos la siguiente ecuación de regresión
Donde
yit es el crecimiento del PIB per cápita
lit es salario
kit es el la formación bruta de capital
sit es la innovación
rit es la externalidad
eit es el termino de error
i representa la región 1,2,…,5
t representa el tiempo 1,2,…,13
Análisis de resultados de la estimación econométricaLos resultados de la estimación econométrica del modelo de la ecuación (14) se muestran a continuación.
El cuadro 4 muestra los resultados de la estimación del modelo de innovación. En la primera columna se muestran los parámetros, en la segunda el valor estimado de dichos parámetros y en la tercera columna el valor de la probabilidad al 95% de confianza. El modelo muestra una bondad de ajuste de 0.81. Los resultados de los parámetros β y θ; esto es, del stock de conocimientos y la cantidad de capital humano dedicado a la investigación son los esperados de acuerdo con la teoría del crecimiento endógeno; es decir, son significativos con un efecto positivo en la generación de innovaciones.
El cuadro 5 muestra las estimaciones econométricas de la función de producción mediante datos del panel aplicado para las diez regiones económicas antes mencionadas. La primera columna muestra la estimación en mínimos cuadrados ordinarios; la segunda, la estimación mediante efectos fijos (EF), el cual supone que las diferencias entre regiones no son aleatorias; y en la tercera, la de efectos aleatorios (EA) que supone que las diferencias entre regiones son aleatorias.
Resultados de la estimación del modelo de producción
| Variables | MCO | MEF | MEA |
|---|---|---|---|
| Fbkfp | -0.4159977 | 0.0311349 | 0.029616 |
| (0.0000) | (0.0000) | (0.0000) | |
| Salario | 0.5485608 | 0.1723671 | 0.1829905 |
| (0.0000) | (0.0000) | (0.0010) | |
| Innovación | -0.1614715 | 0.0206109 | 0.0192227 |
| (0.0010) | (0.0000) | (0.0000) | |
| Externalidades | -1.33814 | 0.369835 | 0.3135413 |
| (0.0050) | (0.0000) | (0.0000) | |
| Constante | 21.19938 | 3.5689 | 4.955378 |
| (0.0000) | |||
| (0.0000) | (0.0000) | ||
| F (p-value) | 0.0000 | ||
| LM (p-value) | 0.0000 | ||
| Hausaman (p-value) | 0.8007 | ||
| Observaciones | 480 | 480 | 480 |
| R2+ | 0.21 | 0.30 | 0.30 |
El intervalo superior corresponde al valor del coeficiente y el intervalo inferior en paréntesis corresponde al valor de la probabilidad.
Para determinar cuál de estos tres modelos es mejor, tenemos que compararlos aplicando determinadas pruebas; por ejemplo, para elegir entre el modelo de mínimos cuadrados ordinarios y el modelo de efectos fijos aplica la prueba F, que en este caso tiene un valor de probabilidad menor a 0.05, lo cual indica que el modelo de efectos fijos es preferido. Asimismo, la prueba LM arroja una probabilidad menor a 0.05, lo cual indica que el modelo de efectos aleatorios se prefiere al de mínimos cuadrados y para elegir entre efectos fijos y aleatorios se aplica la prueba Hausman, que en este caso arroja un valor mayor a 0.05, motivo por el cual el modelo el modelo de efectos aleatorios es mejor.
Los resultados en la estimación con efectos fijos y el incremento en el PIB per cápita provocado por la innovación es de 0.02%. En esta regresión, el coeficiente de la externalidad es positivo y significativo; en cuanto a las otras dos, llámese fbkfp y salario, sus coeficientes también son positivos y significativos. Por lo que respecta a la regresión con efectos aleatorios el incremento de 1% en la innovación provoca también un 0.02% de incremento en el PIB per cápita. De igual modo la fbkfp y el salario son positivos y significativos; por su parte, la externalidad también es positivo y significativo.
Como se puede constatar, los resultados arrojados por la estimación econométrica muestran que en las regiones aquí estudiadas los resultados son consistentes con lo mencionado anteriormente de acuerdo con lo predicho por los modelos de crecimiento endógeno, ya que la innovación indica que la mayor dotación de ésta tiene efectos positivos y significativos en el PIB per cápita.
ConclusionesEl objetivo de este trabajo fue analizar el papel que juega la innovación tecnológica en la determinación del crecimiento económico regional. Se utilizó un modelo econométrico de MCO para estimar la función de innovación; asimismo, se utilizan datos panel sobre el PIB per cápita, la fbkfp, el salario, la innovación y las externalidades en el periodo 1993-2008 para estimar la función de producción Cobb-Douglas ampliada.
De los resultados que se obtienen en este trabajo queda claro que los postulados de los modelos de crecimiento endógeno se cumplen significativamente para el caso de México. Los resultados econométricos de la función de innovación proporcionan evidencia empírica suficiente del papel relevante del stock de conocimientos en la generación de innovaciones, situación que es postulada por los modelos de crecimiento endógeno.
Asimismo, el análisis obtenido de las evaluaciones empíricas de la función de producción permite verificar que la incorporación de innovaciones tecnológicas en el proceso productivo impacta de manera positiva en el crecimiento del PIB per cápita en el nivel regional; estos efectos no son los suficientemente significativos para lograr un crecimiento sostenido suficiente debido a los impactos que son muy pequeños, como lo muestran los resultados de la estimación econométrica.
Sin embargo, los resultados reflejan claramente el resultado obtenido por Romer (1990), donde encuentra una relación positiva entre el aumento en el gasto en I+D y el crecimiento económico, deduciendo que la participación de agentes económicos en las actividades de investigación y desarrollo sí está generando condiciones favorables que influyen positivamente en el crecimiento económico. Por lo tanto, se puede concluir que las políticas gubernamentales encaminadas hasta ahora a la generación de nuevas innovaciones tecnológicas no han logrado tener una contribución importante para hacer crecer la economía a un mayor ritmo, lo cual debe llevar a un estudio profundo para verificar las causas de por qué la innovación que se realiza no está contribuyendo de manera significativa al crecimiento económico.
Véase Antonelli, 1992; ATAS, 1995; Borondo, 2008b; Carlsson, 1995; Fransman, 1991; Freeman, 1995; Freeman y Pérez, 1988; Freeman y Soete, 1997; OECD, 1991; Pérez, 1986; Willinger y Zuscovitch, 1988.
Aunque estas referencias se mencionan a lo largo del texto, cabe destacar aquí algunos de los más influyentes artículos, libros y recopilaciones que tratan de presentar —desde diferentes ángulos— una visión global acerca de la economía de la innovación y que son un punto de partida ineludible para aquellos que deseen adentrarse en dicha área (Dosi et al., 1988d; Dosi, 1988a; Edquist, 1997; Freeman, 1975 y 1994; Freeman y Soete, 1997; Heertje, 1984; Landau y Rosenberg, 1986; Lundvall, 1992; Nelson, 2007; OECD, 1992; Rosenberg, 1979a y 1982; y Stoneman, 1995).