Este artículo presenta una metodología para la toma de decisiones en el mercado accionario colombiano utilizando la técnica multicriterio Analytic Hierarchy Process (AHP). La problemática está relacionada con el proceso de inversión en un mercado bursátil considerando criterios de riesgo y rentabilidad. La metodología propuesta incluye la integración de las técnicas tradicionales de decisión de inversión en portafolio de acciones junto con la técnica multicriterio AHP que permite evaluar un número finito de alternativas de manera jerárquica bajo criterios cualitativos y cuantitativos. La metodología ha sido probada en la solución del problema de selección de portafolio de acciones de alta y media bursatilidad que cotizaron en el mercado colombiano durante el periodo de diciembre de 2007 a abril de 2010. Los resultados computacionales muestran la importancia y la eficiencia de la integración exitosa de los criterios tradicionales de inversión en portafolio de acciones junto con la metodología AHP para encontrar un balance apropiado entre rentabilidad y riesgo en el proceso de toma de decisiones de inversión en acciones en el mercado bursátil colombiano.
This paper presents a methodology for decision making in the Colombia stock market by using the Analytic Hierarchy Process (AHP) multicriteria technique. The problem of the research is related to the process for making investment decisions in a stock market by considering risk and profitability criteria. The research methodology includes the integration of traditional techniques for making investment decisions in equity portfolio with the AHP technique. The AHP multicriteria technique allows evaluating a finite number of choices with qualitative and quantitative criteria in a hierarchical way. The methodology has been tested on the solution of the problem of choice an equity portfolio by considering stocks of high and Medium Marketability which quoted in the Colombian stock market from December 2007 to April 2010. The computational results show the importance and efficiency of the successful integration of the traditional criteria of equity portfolio investment with the methodology AHP, for finding an appropriate balance between profitability and risk in the process of stock investment on the Colombian stock market.
El proceso de toma de decisión de inversión en acciones es una de las actividades a la que comúnmente se enfrentan inversionistas que desean incrementar su capital financiero mediante la adquisición o compra de partes del capital social de una empresa constituida como sociedad anónima, las cuales otorgan al titular ciertos beneficios económicos que dependen directamente de la generación de utilidades.
Aun cuando el riesgo es inherente a las actividades de inversión en acciones y la rentabilidad esperada depende del grado de riesgo que se asuma, es importante incluir modelos de decisión más elaborados que abandonen los métodos tradicionales basados en la intuición y la experiencia. En mercados en vías de desarrollo, la aplicación de estos modelos se convierte en un tema vital debido a la inestabilidad de las variables económicas y al temor que genera para los inversionistas el no poder materializar los rendimientos deseados en un lapso determinado.
Este artículo de investigación toma distancia del método imperante y, sin desconocer su existencia, propone un cambio estructural en el proceso de toma de decisiones de inversión en portafolio de acciones al considerar que no es confiable la aplicación de los esquemas tradicionales de decisión. En particular se propone la utilización de metodologías multicriterio racionales que permitan valorar y seleccionar objetivamente portafolios de acciones considerando diversos criterios de rentabilidad y riesgo considerados en Markowitz (1952, emsp 1991), emsp Sharpe (1970), emsp Elton y Gruber (1978), así como Morgan (1996). Algunos de los supuestos y limitaciones de estos métodos se resumen a continuación (tabla 1).
Supuestos principales y limitaciones de los métodos tradicionales para la construcción de portafolios.
| Supuestos | Limitaciones |
|---|---|
| Las rentabilidades se distribuyen normalmente | La serie de tiempo financiera no se puede ajustar a la distribución normal |
| Los análisis se basan en dos parámetros principales: media y desviación estándar | La volatilidad considera las ganancias y las pérdidas de la misma manera |
| El riesgo (volatilidad) es medido por la desviación estándar | La volatilidad por sí sola es una medida del riesgo incompleta |
| Se maximiza la rentabilidad esperada para un nivel de riesgo determinado | Un portafolio de acciones con una baja volatilidad relativa puede presentar una mayor propensión a pérdidas extremas |
| Se asume mercados eficientes e inversionistas racionales | Existe información asimétrica en los mercados |
| El riesgo de un portafolio de acciones con correlación positiva entre títulos es menor que la suma de los riesgos individuales de las acciones que lo conforman | Existen sesgos cognitivos de los inversionistas |
| Las volatilidades y correlaciones están en constante cambio de acuerdo con el dinamismo del mercado | |
| Los valores esperados de las volatilidades pueden variar significativamente de los valores actuales |
Para probar la eficiencia de la metodología propuesta se han seleccionado datos reales e históricos de las cotizaciones de las acciones de media y alta bursatilidad del mercado colombiano con el fin de aplicar distintas teorías y metodologías de selección de acciones y portafolios para encontrar un balance adecuado entre rentabilidad y riesgo. Después de realizar un análisis matemático, se obtendrá como resultado parcial los mejores portafolios de acciones de acuerdo con los principios de cada metodología. A partir de la determinación de las mejores composiciones de inversión en cada portafolio se desglosa un problema de toma de decisiones multicriterio resumido en los siguientes interrogantes: ¿en cuál portafolio de acciones se debe invertir?, ¿qué proporción de capital debo invertir en cada portafolio de acciones?
En este caso en particular, la problemática de decisión se centra en seleccionar el mejor portafolio de acciones entre una serie de opciones determinadas por ciertos criterios financieros de riesgo y rentabilidad. Para hacer frente a dicha problemática, se propone la utilización del esquema de decisión multicriterio Analytic Hierarchy Process (AHP), que permite la comparación de un número finito de alternativas considerando diversos criterios cualitativos y cuantitativos (Saaty, 1990). En particular se desean contrastar las siguientes hipótesis nulas: Hipótesis I: se encuentran soluciones similares (portafolios con los mismos porcentajes de inversión de acciones) al aplicar diversos criterios de riesgo y rentabilidad; Hipótesis II: es imposible integrar dentro de un modelo de decisión multicriterio los resultados obtenidos por diversas metodologías para la selección de portafolio de acciones. La principal contribución del artículo está relacionada con la integración de la metodología de decisión multicriterio AHP con la teoría clásica de inversión de portafolio de acciones para el proceso de toma de decisiones en el mercado bursátil colombiano considerando diversos criterios de rentabilidad y riesgo. De acuerdo con la revisión de la literatura no se han encontrado artículos que combinan efectivamente técnicas multicriterios con criterios de decisión de riesgo y rentabilidad para la conformación de portafolios con aplicabilidad a mercados bursátiles latinoamericanos.
En este trabajo se ha asumido que las rentabilidades diarias de las acciones son normalmente distribuidas. De acuerdo con Li y Li (2012) si el tamaño de muestra es superior a 50, la aproximación de normalidad puede ser usada para la estimación de la rentabilidad esperada y la desviación estándar en un portafolio de acciones. Debido a lo anterior la muestra considerada en esta investigación (precios diarios de cierre para las acciones de alta y media bursatilidad en el mercado colombiano durante el periodo diciembre de 2007-abril de 2010) puede ser considerada como representativa para asumir que las rentabilidades de las acciones se distribuyen normalmente. A pesar de que dicha presunción puede tener limitaciones debido a que la posibilidad de obtener ganancias se considera igualmente probable que el riesgo de encontrar pérdidas en el cálculo de la volatilidad de un portafolio (simetría de la distribución normal), varios trabajos la han asumido como válida, entre ellos Duffie y Pan (1997), emsp Alexander y Baptista (2003), emsp Hyung y De Vries (2005), Bodurtha y Shen (2009), emsp Kumar y Dhankar (2011), emsp Kocak, Calis y Unal (2013), emsp Csakar y Köksalan (2013).
El artículo está organizado de la siguiente manera. A continuación se presenta la revisión de la literatura relacionada con las metodologías de toma decisión de inversión en portafolio de acciones y la metodología multicriterio AHP. Después se presenta la metodología propuesta para el desarrollo de la problemática. Posteriormente se muestran los resultados obtenidos de la aplicación de la metodología propuesta en el mercado bursátil colombiano. Finalmente, se presentan las conclusiones y posibles trabajos futuros derivados de esta línea de investigación.
Revisión de la literaturaPara la selección de acciones individuales es común el uso de indicadores estadísticos y financieros (Escobar y Jaramillo, 2012). En la metodología propuesta se utilizaron los siguientes indicadores relacionados con los rendimientos: valor esperado (1), varianza (2), desviación estándar (3), coeficiente de variación (4) y coeficiente de asimetría (5).
En donde xj es la rentabilidad de la acción x en el periodo j y E(Rj) su probabilidad de ocurrencia. La ecuación (1) mide la rentabilidad esperada de cada título, mientras que las ecuaciones (2) a (5) están relacionadas con la exposición al riesgo, ambos objetivos contradictorios. En particular, un inversionista siempre deseara obtener la máxima rentabilidad al mínimo riesgo.
Para la conformación de portafolios se han considerado los criterios de riesgo y rentabilidad estudiados en Sharpe (1970), emsp Elton y Gruber (1978), emsp Markowitz (1952, emsp 1991), Morgan (1996) y en un esquema de decisión multicriterio jerárquico propuesto por Saaty (1990).
Modelo de valoración de precios de los activos financierosEn Sharpe (1970), se plantea el modelo de valoración de precios de los activos financieros (CAPM); este permite determinar la tasa de retorno de un activo o costo de capital requerido de un activo mediante una función que considera la sensibilidad de la acción a los cambios del mercado, el cual se representa por el símbolo Beta (β). La ecuación (6) representa el costo capital de un activo k3
Donde Rf es la tasa libre de riesgo, βx es el indicador de riesgo sistemático de la acción x y E(Rm) − Rf es la prima de riesgo otorgada al realizar una inversión en la acción x. El coeficiente de riesgo sistemático βx se calcula mediante (7):
Donde CovE(Rx,Rm) es la covarianza entre el rendimiento de la acción x y el rendimiento del mercado y σm2 es la varianza del mercado. De igual forma, en Sharpe (1970) se menciona que el riesgo sistemático o beta del portafolio (βp) y costo capital del portafolio (kp) se puede calcular mediante las ecuaciones (8) y (9):
Donde px es la proporción que se invierte en la acción x yβx es el riesgo sistemático de la acción x.
Teoría de la razón betaEn Elton y Gruber (1978) se plantea una técnica para la selección de acciones, que incluye las siguientes etapas:
1. Calcular el beta (βx) para cada acción x de acuerdo con la metodología propuesta por Sharpe (1970). Luego calcular la razón beta (Rβx) mediante la siguiente ecuación:
2. Calcular el ratio critico C*:
Donde n es el número de acciones consideradas, σm2 es la varianza de la rentabilidad del índice de mercado y Rf es la rentabilidad del título libre de riesgo del país en el cual se está analizando la inversión.
3. Comparar la razón beta Rβx para cada acción x con el valor del ratio crítico C*. Si se cumple la condición de que Rβx > C*, se debería invertir en la acción x.
Teoría clásica de inversión en portafolios de accionesLas nuevas tendencias internacionales enmarcan la necesidad de gestionar y administrar la exposición al riesgo debido a que el mercado de capitales en su proceso de desarrollo ha traído consigo instrumentos más complejos que acrecientan el riesgo para los agentes económicos.
En la actualidad existen variedad de teorías, modelos y técnicas de administración de inversiones, que permiten estructurar los portafolios o carteras de inversión en acciones mediante una valoración rigurosa que disminuye la incertidumbre y, por ende, la vulnerabilidad al riesgo. En este artículo se consideran algunas técnicas para gestionar los riesgos inherentes de la actividad de inversión en acciones. Sin embargo, dada la generalidad y robustez de la metodología propuesta se podrían incluir dentro de ella otras técnicas cualitativas y cuantitativas para la toma de decisiones de inversión en portafolio de acciones.
Ante la aversión al riesgo, los inversionistas desean conformar el mejor portafolio de acciones que genere una alta rentabilidad, pero con un mínimo grado de riesgo. No obstante, la conformación de un portafolio bajo estas condiciones no suele ser tan sencillo, puesto que el mercado generalmente se mueve bajo la premisa que entre mayor es la exposición al riesgo mayor debería ser la rentabilidad esperada.
En Markowitz (1952) se menciona que la conducta racional en la inversión y conformación de portafolios de acciones involucra en esencia la obtención de unos rendimientos financieros. Pero a su vez un inversionista es consciente de que dicha finalidad trae implícito cierta incertidumbre y, por ende, consideración de riesgos, razón por la cual se debe desarrollar una metodología que permita cubrir los eventos inesperados a través de la aplicación de modelos analíticos.
Otro de los criterios considerados en este trabajo es el Value at Risk (VaR), el cual cuantifica la exposición al riesgo dado un nivel de confianza determinado. Se define como la perdida máxima en la que podría incurrir un inversionista al tomar una decisión de inversión en un intervalo de confianza y en un periodo determinado. El origen del concepto VaR fue introducido originalmente por Morgan (1996) como una medida del riesgo de mercado asociado a las posiciones financieras de un banco a través del cálculo de un solo indicador. En la actualidad, el VaR ha sido ampliamente estudiado por la comunidad científica financiera como Alexander y Baptista (2003), emsp Hyung y De Vries (2005), emsp Jorion (2007), entre otros.
Metodología multicriterio Analytic Hierarchy ProcessEn Saaty (1990, 2003), se muestra la metodología multicriterio Analytic Hierarchy Process (AHP); considera la evaluación de una serie finita de alternativas que consecuentemente facilitan el proceso de toma de decisiones. En la actualidad, este método constituye uno de los pilares para la toma de decisiones multicriterio (Saaty, 2008).
La metodología AHP permite evaluar un número finito de alternativas mediante un modelo jerárquico, en el que se desglosa la información de manera escalonada para un problema en particular: el nivel más alto es la meta, los niveles siguientes son los objetivos generales y criterios que afectan al problema, y en el nivel más bajo se sitúan las alternativas por evaluar. Se caracteriza por ajustarse a las necesidades del problema de conformación de portafolio de acciones porque permite comparar tanto aspectos cuantitativos como cualitativos a través de una escala de medida propuesta en Saaty (1990). En dicha escala el decisor puede articular sus preferencias y comentarios respecto a dos elementos de forma verbal y representarlos numéricamente a través de una escala numérica del 1 al 9. La tabla 2 muestra la escala numérica utilizada en la metodología AHP.
Escala numérica AHP.
| Escala numérica | Escala verbal | Explicación |
|---|---|---|
| 1 | Igual importancia | Los dos elementos tienen similar importancia |
| 3 | Moderadamente más importante una alternativa sobre otra | El juicio y la experiencia previa favorecen a un elemento en comparación con el otro |
| 5 | Fuertemente más importante una alternativa sobre otra | El juicio y la experiencia previa favorecen fuertemente a un elemento en comparación con el otro |
| 7 | Mucho más fuerte la importancia de una alternativa sobre otra | Una alternativa domina fuertemente. Su dominación está probada en práctica |
| 9 | Importancia extrema de una alternativa sobre otra | Un alternativamente domina completamente |
En la tabla 2, la primera columna (escala numérica) corresponde al valor numérico que se debe asignar en la comparación de alternativas o criterios, la segunda columna (escala verbal) corresponde a la descripción cualitativa de la comparación y la última columna (explicación) corresponde a la explicación detallada de la escala verbal. Cabe indicar que los valores numéricos pares no son declarados; sin embargo, son permitidos indicando una valoración intermedia dentro de la escala.
El procedimiento AHP involucra la comparación binaria dentro de la escala dando como resultado una matriz de comparaciones pareadas, en donde se enmarca el nivel de preferencia de una alternativa en relación con otra en función de una meta en general. En otras palabras, la escala permite evaluar la proporción que contribuye cada alternativa al nivel inmediatamente superior del cual se desglosa en la jerarquía. Seguidamente se procede al cálculo del vector de prioridad para cada criterio, de manera que se puedan comparar las alternativas entre sí. Finalmente, se obtiene el vector de prioridad de las alternativas, el cual permite establecer la mejor solución al problema de preferencias sobre cada alternativa. Así, se obtiene la mejor alternativa de acuerdos con los criterios considerados. Varias aplicaciones similares pueden ser encontradas en Bahmani, Yamoah, Basseer y Rezvani (1987), emsp Cheng, Chen y Lee (2006), emsp Tiryaki y Ahlatcioglu (2009), emsp Lashgari y Kobra (2012), emsp Charouz y Ramik (2010), emsp Le (2008), emsp Beshkooh y Afshari (2012) y Bahloul y Abid (2013).
En Bahmani et al. (1987) se aplica la metodología AHP para seleccionar una inversión financiera. El modelo de decisión considera factores como las características del inversionista, así como las características y las alternativas de la inversión. En este trabajo se evidencia que la metodología AHP puede adicionar nuevas perspectivas para la selección de portafolio de inversiones proporcionando a los investigadores un mecanismo alternativo para maximizar la utilidad esperada.
En Cheng et al. (2006) se considera una variante de la metodología AHP, denominada Fuzzy Analytic Hierarchy Process (FAHP), para el proceso de selección de inversión en bonos. Otros trabajos en los cuales se considera la metodología FAHP han sido propuestos por Tiryaki y Ahlatcioglu (2009), quienes consideran el problema de selección de un portafolio de acciones considerando qué títulos deben seleccionarse y en qué proporción se debe invertir en cada uno de ellos; por su parte, Lashgari y Kobra (2012) identifican los factores más representativos utilizados en la selección de un portafolio; luego, mediante la metodología Delphi y la técnica FAHP seleccionan la mejor alternativa de inversión de siete posibilidades.
En Charouz y Ramik (2010) se propone una aplicación del AHP para las tareas parciales en la administración de un portafolio. En particular, se estudia la problemática de convertir el portafolio en dinero considerando diversos factores como leyes, contratos, requerimientos internos, entre otros. Le (2008) estudia la problemática de asignación correcta de fondos a diferentes opciones de inversión utilizando la metodología AHP. Beshkooh y Afshari (2012) consideran la combinación de la técnica AHP con la teoría Grey para la selección de cuatro acciones en diferentes industrias. Finalmente, Bahloul y Abid (2013) desarrollan un modelo de decisión integrado combinando la metodología AHP y la programación de metas (GP) para el problema del impacto de mezcla de inversiones en selección de portafolios internacionales.
Metodología propuestaLa metodología propuesta se ha divido en varias etapas, considerando puntos específicos que se deben realizar para el proceso de toma de decisiones de inversión en portafolio de acciones. Las etapas que a continuación se detallan se deben realizar de manera secuencial; sin embargo, dentro de cada una de ellas se pueden realizar actividades específicas de manera paralela. En el detalle de cada etapa se especifica el caso.
Etapa 1. Aplicación de las teorías estadísticas para acciones individualesLa primera etapa de la metodología propuesta está relacionada con los elementos que se deben considerar para seleccionar las acciones individuales. A continuación se detallan:
- 1.
Establecer el periodo de análisis histórico de las cotizaciones de los títulos.
- 2.
Seleccionar las acciones de media y alta bursatilidad para dicho periodo. Se descartan las acciones clasificadas como de baja bursatilidad debido a su poca transabilidad en el mercado financiero.
- 3.
Procesar y organizar la información de las cotizaciones de los títulos.
- 4.
Efectuar el cálculo de los indicadores de rentabilidad, riesgo, coeficiente de variación, coeficiente de asimetría y riesgo diversificable, para cada uno de los títulos utilizando la teoría estadística y financiera descrita en la sección Revisión de la literatura.
- 5.
Determinar el riesgo sistemático y costo de capital de las acciones, como se especifica en el modelo CAPM, descrito anteriormente. Este paso se puede realizar de manera simultánea con el paso 4.
- 6.
Establecer los valores críticos de cada acción, a partir de la implementación de la teoría de la razón beta (Elton y Gruber, 1978). Para realizar este proceso es necesario contar con la información de los betas y los criterios calculados en el paso 4, por lo cual se puede realizar una vez se haya cumplido el paso 4.
A partir de la aplicación de las distintas teorías de análisis de acciones, se procede a evaluar los resultados obtenidos en la etapa 1 para seleccionar los mejores títulos. En particular se proponen seleccionar N acciones. En Vitali y Tapon (2013), se menciona que si N es el total de número de acciones disponibles en el mercado en un determinado tiempo, la n-combinación posible de N acciones es igual a:
El cálculo de todas las posibles combinaciones probablemente incorpora complejidad computacional incluso para el equipo de cómputo más moderno (Vitali y Tapon, 2013). De acuerdo con lo anterior, la metodología propuesta fija un número determinado de acciones N para el análisis de portafolios; sin embargo, el número de títulos no interfiere en el desempeño de la metodología propuesta.
Los pasos para realizar la etapa 2 son los siguientes:
- 1.
Descartar las acciones con rentabilidades negativas. En el caso que se hayan obtenido un total de N acciones o menos se continúa con el paso 6, de lo contrario se ejecuta el paso 2.
- 2.
Seleccionar los títulos que obtuvieron como valor 1, tras la aplicación de la teoría de la razón beta descrita en la sección Teoría de la razón beta. En el caso que se hayan obtenido un total de N acciones o menos se continúa con el paso 6, de lo contrario se ejecuta el paso 3.
- 3.
Elegir los títulos que tienen un riesgo diversificable alto, lo que indica que la proporción de riesgo que se puede administrar es mayor. En el caso que se hayan obtenido un total de N acciones o menos se continúa con el paso 6, de lo contrario se ejecuta el paso 4.
- 4.
Seleccionar los títulos con un riesgo sistemático (βx) menor. En el caso que se hayan obtenido un total de N acciones o menos se continúa con el paso 6, de lo contrario se ejecuta el paso 5.
- 5.
Evaluar la rentabilidad versus el riesgo de los títulos con miras a seleccionar las acciones que se ajusten a las expectativas del inversionista. Si ocurre el caso en que los datos de rentabilidad y riesgo son muy similares, se eligen los títulos con menor coeficiente de variación y menor coeficiente de asimetría.
- 6.
Con los títulos seleccionados a través del análisis de los criterios anteriores, se conforman los portafolios evaluando todas las combinaciones posibles de N acciones o menos.
Fijando las posibles combinaciones de acciones para integrar los portafolios de inversión, se procede a efectuar la aplicación de las teorías de análisis a cada uno de ellos aplicando los siguientes pasos:
1. Determinar los cálculos varianza, desviación estándar, coeficiente de variación, coeficiente de correlación y probabilidad de perdida para cada portafolio utilizando la teoría de portafolio propuesta en Markowitz (1952). A partir de los resultados obtenidos, se establecen los siguientes criterios de selección independientes:
- •
Elegir los portafolios que tengan el mejor balance entre rentabilidad, riesgo y coeficiente de variación. Si dos portafolios tienen la misma rentabilidad se debería seleccionar el que tiene menor riesgo. Si dos portafolios tienen diferente rentabilidad y riesgo se debe seleccionar el que tiene menor coeficiente de variación. En el caso de que ambos tengan igual rentabilidad e igual riesgo se debe seleccionar el que tiene menor coeficiente de asimetría. Este portafolio será catalogado como la primera alternativa para el posterior análisis del AHP.
- •
Elegir los portafolios que tengan menor probabilidad de pérdida. De esta manera, se obtiene otra alternativa para el análisis del AHP.
2. Establecer el riesgo sistemático y costo de capital para cada portafolio tras la implementación del modelo de valoración de precios de los activos financieros (CAPM) descrito anteriormente. Con los resultados derivados de dichos cálculos se fijan los siguientes criterios de selección de manera independiente:
- •
Seleccionar el portafolio con menor costo de capital (kp). De esta manera, se obtiene otra alternativa para el análisis del AHP.
- •
Escoger el portafolio que obtiene el mayor valor de la diferencia de la rentabilidad promedio y el costo de capital (kp). De esta manera, se obtiene otra alternativa para el análisis del AHP.
3. Determinar el valor de riesgo (VaR) y seleccionar los portafolios con menor cuantía o exposición al riesgo, de acuerdo con la teoría descrita en Morgan (1996). El VaR constituye el último indicador de valoración de las opciones de inversión. De esta manera, se obtiene la última alternativa para evaluación mediante la metodología AHP.
En el caso de que todas las alternativas (portafolios) seleccionadas arrojen el mismo resultado en cuanto a títulos de conformación y porcentaje de participación de cada título, se debe seleccionar dicho portafolio como el mejor. En este caso, las metodologías de decisión multicriterio no tendrían peso para el proceso de toma de decisiones en el mercado bursátil. Sin embargo, experimentos computacionales en el caso del mercado bursátil colombiano descritos en la sección Resultados computacionales han demostrado que este caso sería excepcional y con una probabilidad casi nula de ocurrencia. De esta manera, se puede validar la Hipótesis I.
Etapa 4. Aplicación de la metodología Analytic Hierarchy Process para la selección del mejor portafolio considerando las diversas alternativas de decisión- 1.
Construir la estructura jerárquica del proceso de decisión, en la que se vislumbra el problema y se identifican el objetivo, los criterios y las alternativas para llegar al mejor portafolio de acciones para invertir. El problema de decisión se centra específicamente en cuál de las alternativas invertir, cuando todos los criterios de valoración incluyen elementos de análisis totalmente válidos. El objetivo sería seleccionar de entre los diversos portafolios obtenidos en la etapa 3 el mejor para invertir. Las alternativas son los portafolios seleccionados preliminarmente bajo los criterios de análisis y que para efectos de comparación se denotan como P1, P2, P3, P4 y P5.
Los criterios son los indicadores bajo los cuales se seleccionaron las alternativas o portafolios (rentabilidad, riesgo, coeficiente de variación, probabilidad de pérdida, costo de capital, diferencia entre rentabilidad y costo de capital, y valor en riesgo).
- 2.
Elaborar la matriz de comparaciones por parejas para cada criterio de valoración, efectuando evaluaciones binarias entre las alternativas de decisión y la asignación del nivel de preferencia mediante la escala propuesta en Saaty (2003, 2008). En este paso se obtienen los vectores de prioridad de las alternativas para cada criterio.
- 3.
Dado que el vector de prioridad favorece alternativas distintas, se construye la matriz de significancia o de comparaciones binarias, cotejando los criterios de valoración. De esta manera, se aplican los subsiguientes pasos para la matriz de criterios.
- 4.
Calcular un vector resultante de la multiplicación de los vectores de preferencia de cada alternativa con los vectores de preferencia de cada criterio de valoración.
- 5.
A partir de los resultados anteriores, se selecciona la alternativa que obtenga el mayor valor porcentual de preferencia, como mejor opción de inversión. Finalmente, es válida la Hipótesis II.
Para validar la metodología propuesta se han seleccionado los precios diarios de las acciones de ordinarias de media y alta bursatilidad de la Bolsa de Valores de Colombia durante el periodo diciembre de 2007-abril de 2010. En total se han considerado 32 acciones para el análisis (tabla 3), descartando los títulos de Biomax, S.A., Bolsa Nacional Agropecuaria, S.A., Pacific Rubiales Energy y Sociedad de Inversiones de Energía, S.A. A pesar de que dichas acciones fueron catalogadas como de media y alta bursatilidad durante el 2008, su cotización en la bolsa inició en fechas posteriores a diciembre de 2007, lo que afecta la validez y consistencia de los resultados obtenidos en la muestra seleccionada.
Títulos de media y alta bursatilidad que cotizaron en el mercado accionario colombiano durante diciembre, 2007 a abril, 2010.
| NA° | Compañía | Acción |
|---|---|---|
| 1 | Acerías Paz del Rio S.A. | APDR |
| 2 | Admón. de Fondos y Cesantías Protección S.A. | PROT |
| 3 | Almacenes Éxito S.A. | EXIT |
| 4 | Banco Bilbao Vizcaya Colombia S.A. - BBVA | BBVA |
| 5 | Banco Comercial AV Villas S.A. | BAVV |
| 6 | Banco de Bogotá S.A. | BBOG |
| 7 | Banco de Occidente S.A. | BOCC |
| 8 | Banco Santander Colombia S.A. | BSAN |
| 9 | Bancolombia S.A. | BAvCO |
| 10 | Cartón de Colombia S.A. | CARC |
| 11 | Cementos Argos S.A. | CARG |
| 12 | Compañía Colombiana de Inversiones S.A. | COIN |
| 13 | Compañía Colombiana de Tejidos S.A. | COLT |
| 14 | Corporación Financiera Colombiana S.A. | CORF |
| 15 | Ecopetrol S.A. | ECOP |
| 16 | Empresa de Telecomunicaciones de Bogotá S.A. | ETBO |
| 17 | Enka de Colombia S.A. | ENKA |
| 18 | Gas Natural S.A. | GASN |
| 19 | Grupo Aval Acciones y Valores S.A. | AVAL |
| 20 | Grupo de Inversiones Suramericana S.A. | SURA |
| 21 | Grupo Nacional de Chocolates S.A. | CHOC |
| 22 | Interbolsa S.A. | IBOL |
| 23 | Interconexión Eléctrica S.A. | ICEL |
| 24 | Inversiones Argos S.A. | IARG |
| 25 | Isagen S.A. | ISAG |
| 26 | Mineros S.A. | MNOS |
| 27 | Organización de Ingeniería Internacional S.A. | OING |
| 28 | Promigas S.A. | PROM |
| 29 | Tableros y Maderas de Caldas S.A. – Tablemac | TMAC |
| 30 | Textiles Fabricato Tejicondor S.A. | TFAB |
| 31 | Valorem S.A. | VALO |
| 32 | Valores Simesa S.A. | VALS |
Durante el periodo de análisis, el Índice General de la Bolsa de Valores de Colombia (IGBC) tuvo un crecimiento del 17% al pasar de 10 694.18 puntos (diciembre de 2007) a 12 512.61 (abril de 2010). A pesar de lo anterior, el IGBC evidenció una tendencia a la baja desde diciembre de 2007 hasta agosto de 2009, pero el nivel más bajo se registró en octubre de 2008 con un valor de 7 226.03. De acuerdo con el Banco de la República (2010), la Bolsa de Valores de Colombia presentó el mayor dinamismo en Latinoamérica durante el periodo 2007 a 2010 a pesar del limitado número de emisores y su alta concentración en ciertos sectores empresariales. De igual forma, en materia de liquidez –durante el periodo de análisis– el mercado bursátil colombiano obtuvo mayores registros que los obtenidos por mercados financieros como Lima, Buenos Aires y Santiago de Chile (Banco de la República, 2010). Finalmente, la capitalización bursátil del IGBC durante el periodo de análisis muestra un crecimiento gradual y sostenido del mercado de renta variable. Lo anterior si bien no obedece a un aumento en el número de empresas inscritas en bolsa, sí refleja el dinamismo en precios y volumen de las acciones más bursátiles (Ceron, 2012).
Del total de acciones analizadas, el 43.75% presentó valores de rentabilidad promedio inferiores al valor esperado de la rentabilidad del IGBC. Adicionalmente, un 25% del total presentó rentabilidades promedio negativas durante el periodo de análisis. Dado lo anterior, la muestra para el cálculo de los indicadores de riesgo en acciones individuales se redujo a un 56.25% del total de títulos.
Después de aplicar los indicadores de riesgo descritos en la etapa 1 y de realizar el descarte de acciones propuesto en la etapa 2 de la metodología, se llegó a la selección de N = 5 acciones. Dicho número fue determinado con base en la teoría descrita en Beshkooh y Afshari (2012); sin embargo, como se mencionó en la etapa 2, la metodología es lo suficientemente robusta para incluir cualquier número de acciones.
Los resultados obtenidos al final de la aplicación de la etapa 2 se resumen en la tabla 4. Los títulos seleccionados, en general, presentan una rentabilidad promedio superior al IGBC y a su vez no presentan una alta sensibilidad a las variaciones del mercado determinado por bajos factores Beta (βx). El riesgo diversificable es favorable: tienen una baja probabilidad de pérdida y el criterio de la razón beta (Elton y Gruber, 1978) confirma que son títulos apropiados para la conformación de portafolios. De esta forma, se obtienen 26 portafolios que resultan de la combinación de las 5 acciones seleccionadas (tabla 5). Para cada uno de los portafolios se ha calculado el porcentaje de dinero óptimo que se debería invertir en cada título de acuerdo con la metodología descrita en Markowitz (1952).
Conformación de portafolios de 2, 3, 4 y 5 acciones.
| Portafolio | Combinación | Portaf | PROT | BOCC | CORF | ICEL | MNOS |
|---|---|---|---|---|---|---|---|
| 2 Acciones | 1 | E2-1 | X | X | |||
| 2 | E2-2 | X | X | ||||
| 3 | E2-3 | X | X | ||||
| 4 | E2-4 | X | X | ||||
| 5 | E2-5 | X | X | ||||
| 6 | E2-6 | X | X | ||||
| 7 | E2-7 | X | X | ||||
| 8 | E2-8 | X | X | ||||
| 9 | E2-9 | X | X | ||||
| 10 | E2-10 | X | X | ||||
| 3 Acciones | 11 | E3-11 | X | X | X | ||
| 12 | E3-12 | X | X | X | |||
| 13 | E3-13 | X | X | X | |||
| 14 | E3-14 | X | X | X | |||
| 15 | E3-15 | X | X | X | |||
| 16 | E3-16 | X | X | X | |||
| 17 | E3-17 | X | X | X | |||
| 18 | E3-18 | X | X | X | |||
| 19 | E3-19 | X | X | X | |||
| 20 | E3-20 | X | X | X | |||
| 4 Acciones | 21 | E4-21 | X | X | X | X | |
| 22 | E4-22 | X | X | X | X | ||
| 23 | E4-23 | X | X | X | X | ||
| 24 | E4-24 | X | X | X | X | ||
| 25 | E4-25 | X | X | X | X | ||
| 5 Acciones | 26 | E5-26 | X | X | X | X | X |
En el caso de que dos portafolios obtuvieron igual rentabilidad promedio se seleccionó el portafolio con menor riesgo (menor desviación estándar). En el caso de que la rentabilidad promedio y el riesgo (desviación estándar) fueran diferentes, se seleccionaba el portafolio que obtuviera menor coeficiente de variación. Considerando estos criterios, el mejor portafolio es E4-24. Este portafolio fue considerado como la primera alternativa para el análisis multicriterio AHP. De manera similar se realizaron los análisis para los otros criterios descritos en la etapa 3 y se seleccionaron los mejores portafolios para el análisis AHP. La tabla 6 resume los hallazgos del análisis de la etapa 3. Nótese que al aplicar las diversas metodologías que consideran rentabilidad y riesgo para la selección de portafolios se encuentran resultados diversos (diferentes acciones y porcentajes de inversión en cada portafolio). Por lo tanto, se puede rechazar la Hipótesis I.
Portafolios seleccionados de acuerdo con los criterios C1, C2, C3, C4 y C5.
| C1 | C2 | C3 | C4 | C5 | |
|---|---|---|---|---|---|
| 2 Acciones | E2-7 | E2-7 | E2-1 | E2-10 | E2-1 |
| 3 Acciones | E3-16 | E3-19 | E3-11 | E3-15 | E3-12 |
| 4 Acciones | E4-24 | E4-24 | E4-21 | E4-23 | E4-24 |
| 5 Acciones | E5-26 | E5-26 | E5-26 | E5-26 | E5-26 |
| Portaf | E4-24 | E5-26 | E2-1 | E2-10 | E4-24 |
De esta manera, se procede a seleccionar el mejor portafolio de acuerdo con la metodología AHP (etapa 4 de la metodología propuesta). En la figura 1 se puede apreciar el modelo de decisión jerárquico considerado. La metodología AHP permite comparar aspectos de carácter cualitativo y cuantitativo mediante una escala que determina en qué medida contribuye cada alternativa a la escala jerárquica. Esta escala asigna números que van desde el 1 al 9, dependiendo la importancia de un elemento frente a otro. No obstante, la asignación del nivel de preferencia de valoración entre pares de alternativas debe hacerse de manera objetiva para no incluir apreciaciones subjetivas que alteren la eficiencia del modelo de decisión.
La asignación de valores numéricos para cada comparación pareada de alternativas bajo cada criterio se realizó de la siguiente forma:
- 1.
Determinar las alternativas que obtienen el mejor y el peor valor numérico para cada criterio seleccionado. Para los criterios de rentabilidad (Rentab) y diferencia entre rentabilidad y costo de capital (Rentab-kp), la mejor alternativa es la que obtiene el máximo valor; en caso contrario para los demás criterios (riesgo, CV, VaR, kp). Por ejemplo, de acuerdo con la tabla 7, los portafolios que obtienen el mejor y el peor valor para el criterio de rentabilidad son P4 y P3 respectivamente.
Tabla 7.Selección de mejores portafolios de acciones (Percent, Rentab, Riesgo, CV, VaR, kp en %).
N° Portaf Acción Percent Rentab Riesgo CV VaR kp Rentab-kp PROT 37.07 BOCC 32.46 0.086 0.719 839.00 0.049 0.021 0.065 P1 E4-24 ICEL 16.18 MNOS 14.29 PROT 36.37 BOCC 31.78 P2 E5-26 CORF 6.97 0.085 0.714 839.18 0.049 0.021 0.064 ICEL 10.95 MNOS 13.93 PROT 90.00 P3 E2-1 BOCC 10.00 0.056 1.140 2 044.30 0.078 0.020 0.036 P4 E2-10 CORF 13.00 MNOS 87.00 0.161 1.624 1 006.51 0.110 0.021 0.140 PROT 23.15 P5 E4-24 BOCC 25.99 ICEL 19.53 0.104 0.793 759.98 0.054 0.022 0.082 MNOS 31.33 Fuente: elaboración propia. - 2.
Asignar el número máximo de la escala propuesta por Saaty (2008) para la comparación de las alternativas que obtienen el mejor y el peor valor para cada criterio. En este caso, por ejemplo al comparar P4 y P3 bajo el criterio de rentabilidad, se asigna un valor de 9 en la matriz de comparación por parejas.
- 3.
Calcular la diferencia de cada valor obtenido en cada criterio con los valores obtenidos por la mejor y peor alternativa para determinar el nivel de preferencia. Realizar el mismo procedimiento entre las alternativas faltantes hasta completar la matriz de comparación por parejas para cada criterio. Por ejemplo, la tabla 8 muestra la matriz de comparación de parejas obtenida para el criterio de rentabilidad (Rentab).
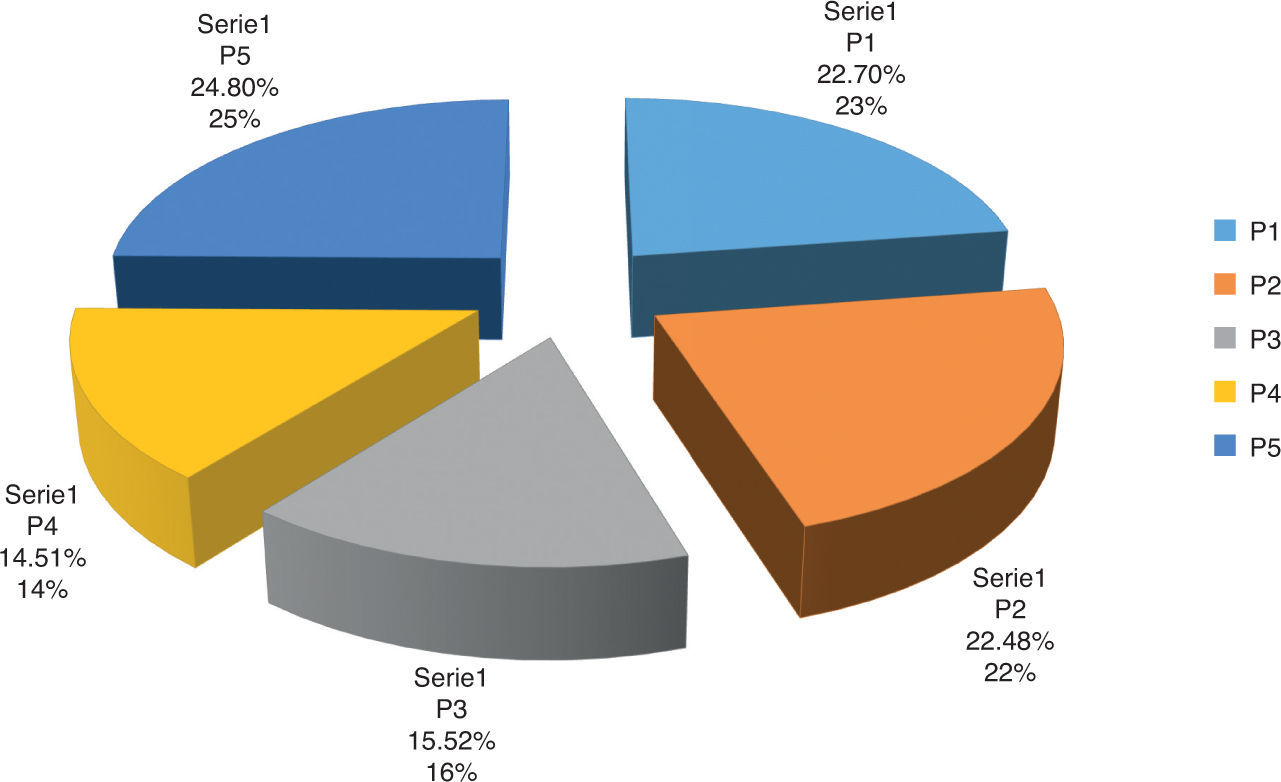
Al aplicar el modelo AHP se obtiene que el mejor portafolio con una preferencia de 25% es P5. La figura 2 muestra los resultados finales obtenidos. De esta manera, se rechaza la Hipótesis Nula II.
Para la validación de resultados del modelo de decisión se realizaron dos tipos de pruebas. En primera instancia se hizo una validación de la estructura de la información, la cual permitió dar el visto bueno a la coherencia en la concatenación de ecuaciones, relaciones de variables y datos de entrada. En segundo lugar, se hizo una verificación de la información de salida u output respecto al comportamiento de los valores ingresados como archivo de datos. El resultado general de todo este proceso fue la completa coherencia entre los resultados obtenidos y la lógica asociada al modelo de decisión.
ConclusionesEn este artículo se propone una metodología efectiva para el problema de selección del mejor portafolio de acciones basado en la combinación de diversos criterios de riesgo y rentabilidad; así como en la metodología multicriterio AHP, que ha sido evaluada con información obtenida del mercado bursátil colombiano. Los experimentos computacionales muestran que la metodología propuesta genera una mayor eficiencia en el proceso de toma de decisiones, en la medida que se eliminan conjeturas y pensamientos intuitivos, tras la implementación de técnicas y herramientas analíticas cuando se cuenta con una serie de alternativas de decisión. La aplicación de la metodología AHP no garantiza la elección de una decisión óptima; sin embargo, ofrece de manera robusta buenas decisiones mediante un proceso heurístico a través de criterios analíticos. Los resultados obtenidos sugieren que la metodología podría ser aplicada a otros mercados bursátiles considerando diferentes criterios de rentabilidad y riesgo.
El perfil del inversionista incide directamente en la metodología de decisión propuesta debido a que la valoración y comparación de las alternativas en cada uno de los criterios puede variar en cada periodo. Para el periodo de análisis considerado, el mejor portafolio es P5 con un 25% promedio de favorabilidad, seguido por el portafolio P1 con un 23% y el portafolio P2 con 22%. Es importante señalar que dichos portafolios siempre consideran las acciones Admón. de Fondos y Cesantías Protección, S.A., Banco de Occidente, S.A., Interconexión Eléctrica, S.A. y Mineros, S.A.
Queda abierto un interesante campo de investigación futuro, en el cual se pueden realizar extensiones a la metodología propuesta: I) considerando la inclusión de otros indicadores cuantitativos y cualitativos para la selección de portafolio de acciones; II) eliminando el supuesto de que las rentabilidades de las acciones en el mercado colombiano siguen una distribución normal; III) analizando el comportamiento de otras metodologías de decisión multicriterio fuzzy; IV) calculando el número de acciones requeridas para conformar portafolios, de manera que se puedan optimizar los beneficios al diversificar; V) analizando portafolios cuyo número de acciones varíe entre subperiodos de acuerdo con la metodología introducida por Vitali y Tapon (2013); y VI) probando la eficiencia de la metodología propuesta en otros mercados bursátiles.
FinanciaciónEste trabajo ha sido parcialmente financiado por el Ministero Istruzione, Università e Ricerca, Italia, la Pontificia Universidad Javeriana Cali, Colombia, y la Universidad del Valle, Cali, Colombia.
AgradecimientosEl autor agradece enormemente a los dos árbitros anónimos por sus valiosos comentarios.
AnexoEn las tablas 3-7, la notación usada es la siguiente:
- •
NAo = Número de la acción.
- •
Compañía = Nombre de la compañía emisora.
- •
Acción = Código de la acción.
- •
Portafolio = Tipos de portafolio de acuerdo con el número de acciones.
- •
- •
Portaf = Código del portafolio.
- •
No = Número del portafolio.
- •
Percent = Porcentajes que se deben invertir en cada acción.
- •
Rentab = Rentabilidad promedio del portafolio.
- •
Riesgo = Riesgo del portafolio (desviación estándar).
- •
CV = Proporción entre riesgo y rentabilidad.
- •
VaR = Valor en riesgo del portafolio.
- •
kp = Costo de capital promedio del portafolio
- •
Rentab – kp = Diferencia entre los resultados Rentab y kp.
- •
C1 = Criterios de máxima rentabilidad (Rentab), mínima desviación estándar (Riesgo) y mínimo coeficiente de variación (CV).
- •
C2 = Criterio de menor probabilidad de perdida.
- •
C3 = Criterio de menor kp.
- •
C4 = Criterio de máxima diferencia entre Rentab – kp.
- •
C5 = Criterio de mínimo VaR.