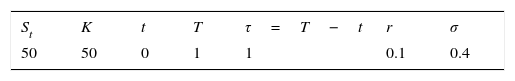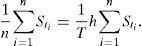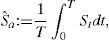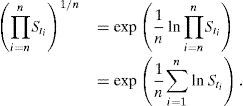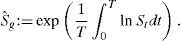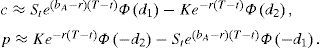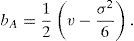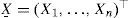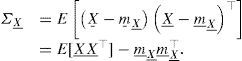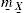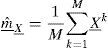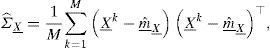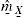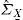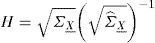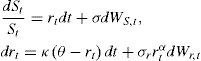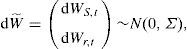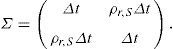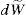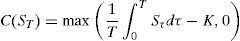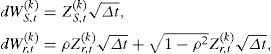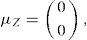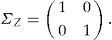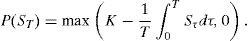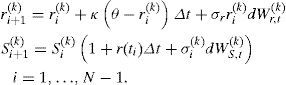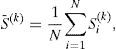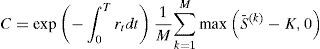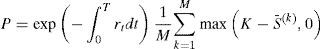Este trabajo propone una metodología para obtener el precio de una opción asiática con subyacente promedio mediante simulación Monte Carlo. Se supone que la tasa de interés es conducida por un proceso de reversión a la media de tipo Vasicek y CIR con parámetros calibrados por máxima verosimilitud. La simulación incluye el remuestreo cuadrático, el cual reduce el uso de recursos computacionales; en particular, el método mejora la generación de la matriz de varianza-covarianza. La metodología propuesta se aplica en la valuación de opciones sobre el precio de AMXL. Los resultados muestran que al comparar los precios de opciones europeas —tanto simulados como con los publicados por MexDer— con sus contrapartes asiáticas, los precios de opciones asiáticas son menores en el caso de opciones de compra y de venta dentro del dinero. Para opciones de venta, los precios simulados fueron menores en todos los casos. Asimismo se encontró que la diferencia se incrementa conforme el plazo al vencimiento de la opción aumenta.
This paper proposes a methodology to obtain the price of an Asian option with underlying average through Monte Carlo simulation. It is assumed that the interest rate is driven by a mean reversion process of Vasicek and CIR type with parameters calibrated by maximum likelihood. The simulation includes the quadratic resampling which reduces the use of computational resources, in particular the method improves the generation of variance covariance matrix. The proposed methodology is applied in the valuation of options on the price of AMXL. The results show that by comparing prices of European options, with both simulated and published by MexDer with their Asian counterparts, Asian options prices are lower in the case of call and put options in the money. For put options simulated prices were lower in all cases. Moreover, it was also found that the difference increases as the time to maturity of the option increases.
Las opciones asiáticas, también conocidas como opciones promedio, están clasificadas dentro de los derivados exóticos; en particular, pertenecen a las opciones dependientes de su trayectoria, es decir, el valor de la opción al vencimiento no solo depende del valor que alcance el activo subyacente al vencimiento, sino también de la evolución que tenga este durante toda la vida del contrato. Se denominan asiáticas puesto que fueron operadas en algunos mercados asiáticos para desmotivar el sobreejercicio al vencimiento1. Asimismo, las opciones asiáticas pueden ser europeas o americanas. Los promedios comúnmente utilizados en los contratos de opción de esta clase son los promedios aritmético o geométrico del subyacente, y la mayoría de estos contratos se negocian con muestreo discreto. Existe una extensa variedad de subyacentes en este tipo de contratos: divisas, acciones, tasa de interés, commodities, seguros y energía (eléctrica). Son diversas las razones por las que son populares, y algunas de ellas se mencionan en el desarrollo de esta investigación.
Las opciones asiáticas son útiles cuando se realizan frecuentes transacciones sobre un mismo activo en un tiempo determinado, es decir, resulta más barato comprar una opción asiática que considere n diferentes precios de un mismo activo (a través de un promedio) al vencimiento, que comprar n opciones del mismo activo a diferentes vencimientos, lo cual considera n diferentes primas, siendo muy costoso, pero en ambas alternativas la cobertura de riesgos es muy similar, por lo cual ofrecen una manera menos costosa de cubrir el riesgo de mercado.
Una manera de clasificar las opciones asiáticas respecto al precio de ejercicio es como sigue: si el precio de ejercicio depende de una cantidad fija, la opción se conoce como una opción asiática con precio de ejercicio fijo u opción con precio promedio. Si el precio de ejercicio es proporcional al precio del activo, entonces es una opción asiática con precio de ejercicio flotante u opción con precio de ejercicio promedio. Otra distinción depende del tipo de promedio utilizado, ya sea aritmético o geométrico, ambos con diferentes pesos en las observaciones previas. El promedio se puede calcular con muestreo discreto, es decir, con un número finito de realizaciones previas, o con muestreo continuo. En la práctica, todos los contratos se suscriben sobre la media aritmética con muestreo discreto, aunque en la literatura la mayoría de los trabajos consideran el caso continuo.
Algunas de las razones que justifican la negociación de opciones asiáticas son las siguientes; debido a que los contratos que solo dependen del precio final del subyacente son más vulnerables a cambios repentinos de gran tamaño o manipulación de precios, las opciones asiáticas son menos sensibles a dichos fenómenos. Algunos agentes prefieren opciones asiáticas como instrumentos de cobertura, ya que pueden estar expuestos a la evolución del subyacente en un intervalo de tiempo. Además, las opciones asiáticas son más baratas que sus contrapartes plain vanilla y son relativamente más fáciles de cubrir. Este último resulta de que si toma en cuenta que la volatilidad del promedio por lo general será menor que la del subyacente; además, conforme más cercana sea la fecha de vencimiento, menor será la variación del promedio. Esto implica una menor sensibilidad de la opción ante cambios en el subyacente que para una opción plain vanilla con el mismo vencimiento.
En lo que concierne a la valuación de opciones con media aritmética, no hay soluciones en forma cerrada mediante el enfoque probabilista. En este enfoque se supone que el subyacente sigue un movimiento geométrico browniano, lo que equivale a suponer que el subyacente sigue una distribución lognormal. A diferencia de que la media geométrica modelada como el producto de variables aleatorias lognormales se distribuye lognormal, la media aritmética es la suma de variables aleatorias lognormales correlacionadas, y es por esto que no existe una expresión en forma cerrada para la función de distribución de dicha suma; véase, por ejemplo, Linetsky (2004). El mismo problema resulta en la valuación de una opción canasta, cuyo precio depende de la media aritmética de varios activos.
El precio de una opción asiática con media aritmética se puede aproximar por su contraparte geométrica de varias maneras. Por ejemplo, Turnbull y Wakeman (1991) aproximan el precio de una opción con media aritmética al coincidir los momentos con sus contrapartes geométricas. Incluso se pueden utilizar métodos de Monte Carlo con reducción de varianza, con el precio de la opción geométrica como la variable de control para calcular el precio de las aritméticas; véase, por ejemplo, Glasserman (2003). Una fórmula de aproximación de opciones asiáticas se muestra en Levy (1992a, b).
Existen en la literatura soluciones en forma cerrada para opciones asiáticas con media geométrica con muestreo continuo; véanse, por ejemplo, Angus (1999), Vorst (1992) y Kwok y Wong (2000). Asimismo, Dai (2003) propone un modelo binomial para valuar opciones de tipo europeo y americano con media geométrica. Estos modelos tienen la ventaja de que la media geométrica de variables aleatorias lognormales resulta tener una distribución lognormal. Una vez que se tiene la función de densidad conjunta del precio del subyacente y la media, el precio de la opción se obtiene mediante la esperanza de la función de pago de la opción bajo una medida neutral al riesgo.
Fouque y Han (2003) combinan los enfoques de Fouque, Papanicolaou y Sircar (2000) y Vecer (2002) para valuar opciones asiáticas bajo la hipótesis de reversión a la volatilidad promedio. Su trabajo propone calibrar los parámetros con precios de mercado de opciones europeas y calcular el precio de la opción con un algoritmo numérico, que consiste en resolver 2 ecuaciones diferenciales parciales con coeficientes dependientes del tiempo. Sin embargo, la precisión de este método no se muestra, pues no proporciona solución analítica para el precio de la opción.
Por otro lado, hay varios artículos que suponen que la tasa de interés para valuar una opción es conducida por un proceso estocástico. El primer trabajo que incorpora tasa de interés estocástica en la valuación de opciones se debe a Merton (1973). En Goldstein y Zapatero (1996) obtienen una fórmula para valuar una opción sobre una acción con el supuesto de que la tasa de interés es conducida por un proceso endógeno de tipo Vasicek en un enfoque de equilibrio de tasas de interés. Kim y Kunitomo (1999) extienden el modelo de Black y Scholes (1973) al modificar la fórmula con tasas de interés determinista y un término de ajuste conducido por la volatilidad de la tasa de interés. Recientemente, Kim, Yoon y Yu (2013) han desarrollado un modelo de valuación de opciones en el que la tasa de interés es conducida por un proceso de tipo Hull y White bajo un enfoque de volatilidad estocástica con el objetivo de evaluar la sensibilidad del precio de la opción ante cambios en la volatilidad de la tasa de interés.
De esta manera en la literatura hay una amplia variedad de métodos para determinar el precio de una opción sobre la media aritmética. En términos generales existen métodos basados en la solución a una ecuación diferencial parcial, aproximaciones analíticas, cotas inferiores y superiores, árboles binomiales, métodos de transformación y métodos de Monte Carlo. Este trabajo no pretende dar una visión completa de los métodos anteriores; en particular se pretende contribuir con una metodología basada en la simulación Monte Carlo.
En la presente investigación se obtiene mediante simulación Monte Carlo el precio de una opción asiática con subyacente promedio con media aritmética. Los supuestos de la metodología propuesta son: la tasa de interés es estocástica y conducida por un proceso de reversión a la media, específicamente, se supone que la dinámica de la tasa de interés es modelada por un proceso de tipo Vasicek y por un proceso de tipo CIR. Para obtener el precio de la opción bajo los supuestos anteriores se hace uso de la simulación de Monte Carlo y la metodología del remuestreo cuadrático de Barraquand (1995), que mejora la precisión de los cálculos y reduce el uso de recursos computacionales.
Este trabajo está organizado como sigue: en la siguiente sección se plantean las funciones de pago de una opción asiática considerando los promedios aritmético y geométrico; asimismo se comparan precios de opciones obtenidos con el modelo de Kemna y Vorst (1990) y Black y Scholes (1973); en el transcurso de la tercera sección se expone el método de remuestreo cuadrático de Barraquand (1995); en la cuarta sección se plantea la metodología para determinar el precio de una opción asiática con subyacente promedio con tasa de interés estocástica conducida por un proceso de reversión a la media; en la quinta sección se realiza un análisis comparativo entre precios de opciones europeas y asiáticas con subyacente promedio obtenidos con la metodología propuesta; por último, se presentan las conclusiones.
Opciones asiáticas con promedio aritmético y geométricoUna opción con precio de ejercicio promedio es una opción asiática en la que su pago depende de un precio de ejercicio igual al promedio aritmético del precio del subyacente durante la vida de la opción. Hay varias maneras de generar valores promedio del precio de un subyacente St. Si se observa el comportamiento de St en intervalos de tiempo discretos ti de manera equidistante durante un intervalo de tiempo h≔T/n, de esta manera se obtiene una serie de precios St1,St2,…,Stn. Por ejemplo, para el promedio aritmético:
Si las observaciones se realizan continuamente durante un intervalo de tiempo 0≤t≤T, la media anterior corresponde a la integral:La mayoría de los contratos de opciones asiáticas son sobre la media aritmética. En otros casos se utiliza la media geométrica, que se puede expresar como:Por lo tanto, la media geométrica con muestreo continuo del precio St es la integral:Si los promedios Sˆa y Sˆg se construyen en el periodo de tiempo 0≤t≤T, entonces corresponde a una opción europea. Si se permite el ejercicio anticipado en t<T, se reescribe a Sˆa y Sˆg, por ejemplo:Con un valor promedio Sˆ dado como la media aritmética en (1) o la media geométrica en (2), las funciones de pago de opciones asiáticas se resumen como se muestra en la tabla 1.Cuadro resumen de funciones de pago de una opción asiática
| Función de pago | Nombre de la opción |
|---|---|
| maxSˆ−K,0 | Opción de compra con subyacente promedio |
| maxK−Sˆ,0 | Opción de venta con subyacente promedio |
| maxST−Sˆ,0 | Opción de compra con precio de ejercicio promedio |
| maxSˆ−ST,0 | Opción de venta con precio de ejercicio promedio |
Fuente: elaboración propia.
Al comparar las funciones de pago anteriores con las de una opción plain vanilla, para una opción asiática con subyacente promedio se tiene que Sˆ sustituye a S, mientras que para una opción asiática con precio de ejercicio promedio Sˆ sustituye a K. Una característica notable de las opciones asiáticas es aprovechar el hecho de que el promedio del subyacente tiene menor volatilidad justo antes de la fecha de vencimiento2.
Fórmula de Kemma y Vorst para aproximar el precio de una opción asiática con media geométrica continuaKemna y Vorst (1990) muestran que las opciones asiáticas con media geométrica continua se pueden valuar con el mismo enfoque de las opciones plain vanilla; solo se deben cambiar los parámetros de volatilidad σ por σa, y el costo de acarreo b por bA.
De acuerdo con Kemna y Vorst, las fórmulas para valuar una opción de compra y una opción de venta son:
con d1 y d2 dados por:La función Φ(d) es la función de distribución acumulada de E∼N(0,1). La volatilidad ajustada es igual a:mientras que el costo de acarreo ajustado es:Como se mencionó en la introducción, el precio de una opción asiática es menor que el de una opción europea con los mismos parámetros, por lo que se procedió a investigar empíricamente tal afirmación. Para lograr tal objetivo, considere los parámetros de la tabla 2.Parámetros empleados para calcular precios de opciones asiáticas de compra y de venta con el modelo de Kemna y Vorst (1990) y el de Black y Scholes (1973)
| St | K | t | T | τ=T−t | r | σ |
|---|---|---|---|---|---|---|
| 50 | 50 | 0 | 1 | 1 | 0.1 | 0.4 |
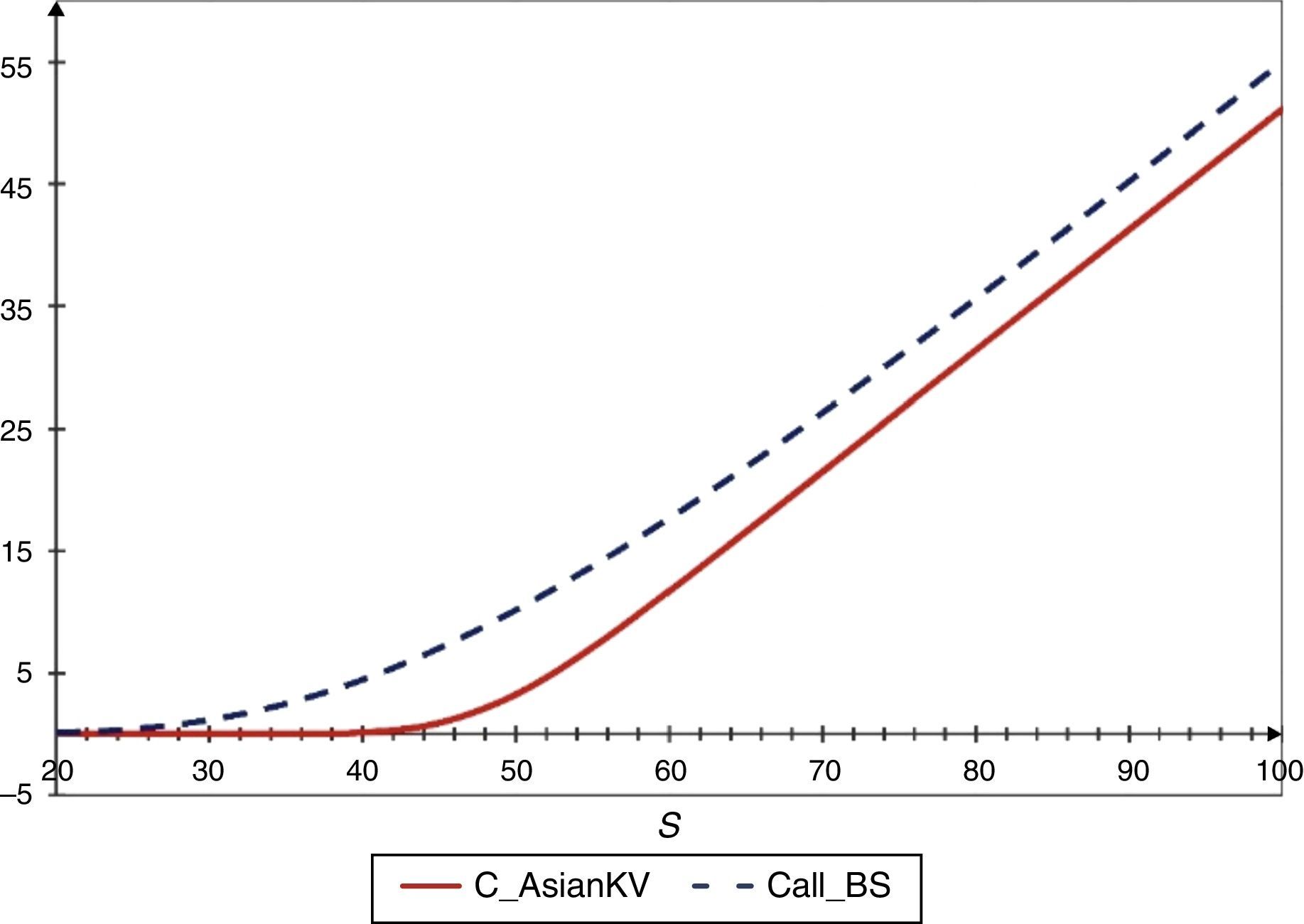
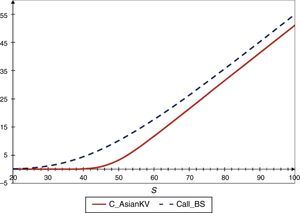
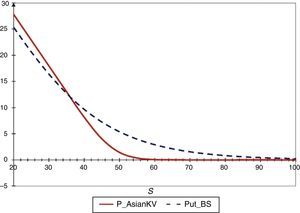
Se calculan los precios de las opciones de compra y de venta de acuerdo con los parámetros de la tabla 2. Los resultados para opciones de compra se muestran en la figura 1, el precio del subyacente se consideró desde St=20 hasta St=100 con incrementos de 5. Se observa que para opciones fuera del dinero el precio de una opción europea de compra es mayor que el de una opción de asiática, y para opciones dentro del dinero el precio de una opción europea de compra es mayor que el de una asiática con los mismos parámetros, y lo mismo se observa para opciones en el dinero. Análogamente con las opciones de venta se calculan los precios. Los resultados se muestran en la figura 2.
Comparación entre precios de opciones asiáticas de compra obtenidos con el modelo de Kemna y Vorst (1990) y con el modelo de Black y Scholes (1973).
Fuente: elaboración propia.
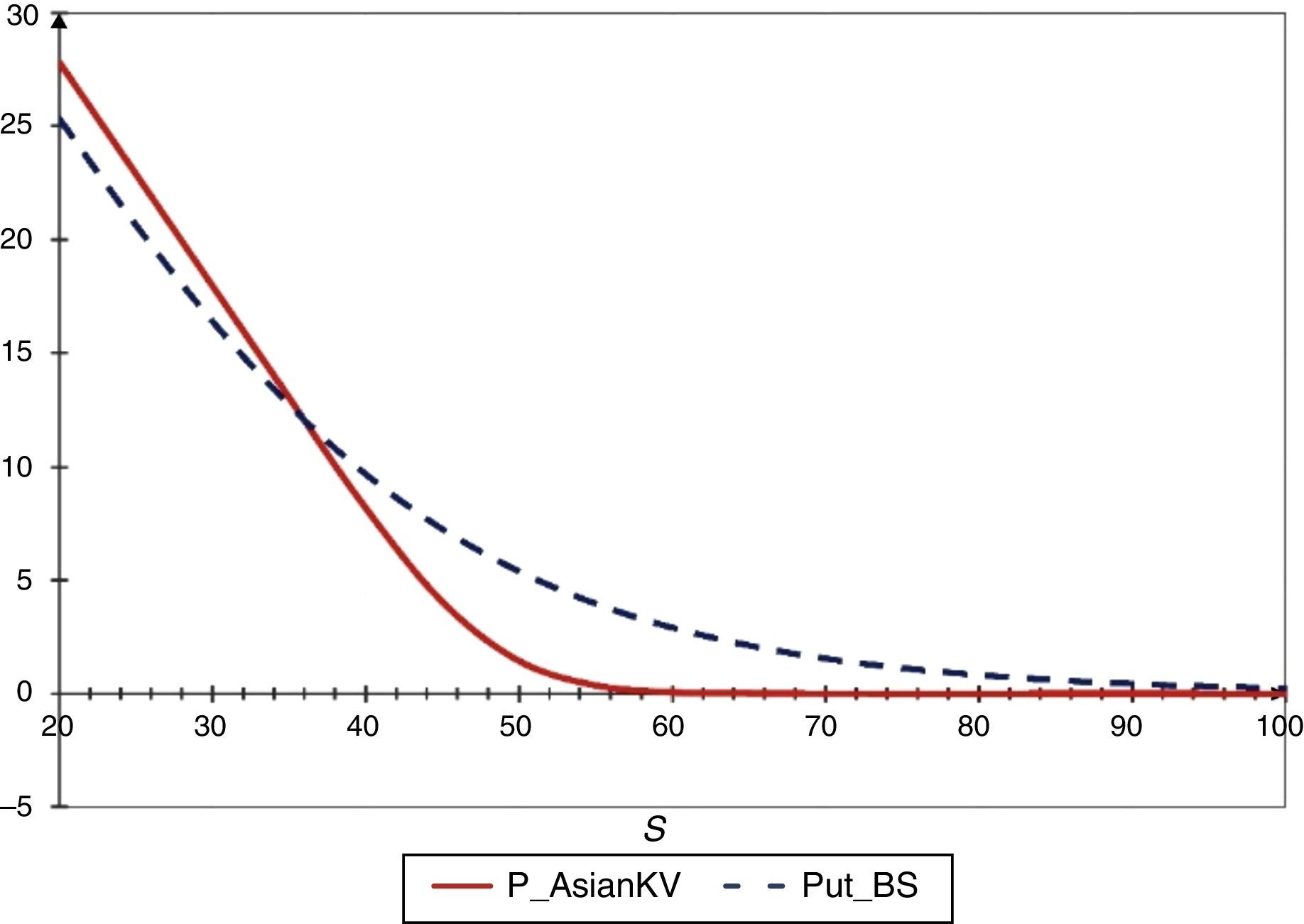
Comparación entre precios de opciones asiáticas de venta con el modelo de Kemna y Vorst (1990) y con el modelo de Black y Scholes (1973).
Fuente: elaboración propia.
Según los resultados obtenidos para opciones de venta en la figura 2, se observa que para opciones fuera del dinero, en el dinero y dentro del dinero el precio de una opción asiática de venta es menor que el de una opción de venta europea en todos los casos. Sin embargo, para opciones muy dentro del dinero el precio de la asiática es mayor que el de la europea.
Remuestreo cuadráticoUno de los temas más representativos de las finanzas computacionales es la determinación del precio de un activo que no tiene una fórmula cerrada. Esta metodología generalmente consiste en calcular la esperanza matemática de una función de pago; por ejemplo, la función de pago de una opción. La simulación Monte Carlo3 es una herramienta ampliamente utilizada en la práctica: la idea básica consiste en estimar la esperanza de funciones de variables aleatorias por medio del promedio de un número considerable de muestras obtenidas de dichas simulaciones, aunque para obtener una precisión adecuada se requiere incrementar el número de simulaciones, y con los recursos de cómputo actuales ese punto no es problema. Sin embargo, en situaciones complejas en las que se requiere simular un proceso con varias variables, los cálculos computacionales se convierten en un tema que merecen especial atención.En este contexto, Barraquand (1995) señala que cuando se generan variables aleatorias, se obtienen estadísticas de la muestra que en general no coinciden con las estadísticas teóricas. Para aprovechar las propiedades de las fórmulas teóricas que contienen tales estadísticas es necesario transformar los datos con el propósito de establecer una igualdad entre los parámetros de la muestra y los parámetros teóricos. Sin duda el parámetro clave es la matriz de varianza-covarianza de un vector aleatorio. A continuación se muestra dicha técnica. Sea X_=X1,…,Xn⊤ un vector aleatorio de dimensión n con media:
y matriz de varianza-covarianza:Para estimar m_X_ y ΣX_, se ejecutan M simulaciones y luego calcular las estadísticas de la muestra como son:ydonde X_k es el vector de la k-ésima simulación. Al desarrollar la expresión de la varianza muestral resulta:De acuerdo con la ley de los grandes números, cuando M es muy grande, mˆ_X_ y ΣˆX_ están muy cercanas a m_X_ y ΣX_ con buena precisión.Si M es pequeña, la precisión no es significativa. Sin embargo, es posible modificar los datos en X_ de tal manera que la media muestral y la matriz de varianza-covarianza coincidan con la media y la matriz de varianza-covarianza teóricas. Al hacer las estimaciones con datos ΣˆX_ es una matriz cuadrada definida positiva y simétrica, por lo cual la raíz cuadrada de la matriz ΣˆX_ existe y es regular.
Considere la matriz:
y el vector:Si se ejecutan M simulaciones el nuevo vector es:y la media muestral de Y_k se convierte en:Al desarrollar la suma obtenemos una igualdad entre la media muestral de Y_ y la media teórica de X_:Análogamente, la matriz de varianza-covarianza de Y_ es:Esta transformación implica que la media de la muestra Y_k es idéntica a la media teórica de X_ y la matriz de varianza-covarianza de Y_k es idéntica a la matriz de varianza-covarianza teórica de X_. Para ejecutar esta transformación es necesario conocer la matriz de varianza-covarianza teórica de X_. En estas condiciones esta transformación mejora la precisión de los cálculos obtenidos de la simulación Monte Carlo.Opción asiática con subyacente promedio y tasa de interés estocásticaUna manera de considerar la naturaleza estocástica de la tasa de interés es modelarla por medio de procesos de reversión a la media, como por ejemplo con modelos de tasa corta ampliamente citados en la literatura como son el modelo de Vasicek (1977) y Cox, Ingersoll y Ross (1985), entre otros. En lo que respecta a la calibración de estos modelos se encuentran el método generalizado de momentos y series de tiempo. Un método alternativo para calibrar los parámetros de los modelos de tasa de interés es el propuesto por Overbeck y Rydn (1997). En términos prácticos este método consiste en la estimación de un conjunto de parámetros dentro de la esperanza condicional de un proceso estocástico: E[Xt|Xt−1]. Posteriormente los valores estimados se usan como valores iniciales en un enfoque de máxima verosimilitud que acelera la convergencia a un óptimo global.
Por otra parte, una de las metodologías para determinar el precio de una opción es por medio de simulación Monte Carlo. La flexibilidad de la metodología aquí propuesta radica en que, con el supuesto de que el precio del subyacente es conducido por un movimiento geométrico browniano, se plantea la función de pago de la opción, se genera un número particular de trayectorias del subyacente y se trae a valor presente con la tasa libre de riesgo el promedio de las trayectorias; es así como se puede determinar el precio de una opción europea, de opciones exóticas, entre otras, y además es muy útil cuando no se tiene una fórmula cerrada. Para fines de este trabajo, se supone que la tasa de interés con la cual se calcula la esperanza de la función de pago para una opción europea de compra y venta, y de una opción asiática con subyacente promedio, es estocástica y se modela con un proceso de reversión a la media. A continuación se desarrolla la metodología para determinar el precio de una opción asiática con subyacente promedio sin pago de dividendos mediante simulación Monte Carlo.
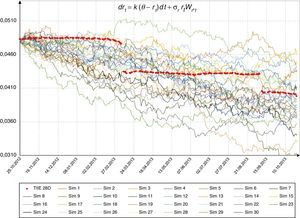
Suponga que el precio del subyacente St es conducido por un movimiento geométrico browniano con tasa de interés estocástica rt conducida por proceso de reversión a la media, y que ambos procesos están correlacionados como sigue:
donde Wr,t es un proceso de Wiener correlacionado con WS,t, i.e., Cov(dWr,t, dWS,t)=ρdt. Si α=0, entonces la dinámica de la tasa corta de interés es conducida por un modelo Vasicek y se considera α=0.5 para un proceso de tipo CIR.Al hacer la analogía con los modelos de volatilidad estocástica, los parámetros θ, κ y σr se interpretan como la tasa de largo plazo, la velocidad de reversión a la tasa de largo plazo y la volatilidad de la varianza de la tasa de interés (a menudo denominada como la volatilidad de la volatilidad), respectivamente.
Para ejecutar la simulación de ambos procesos es necesario generar trayectorias con una estructura dada por:
con:Para hacer lo anterior, se calcula L, dado que Σ=LL⊤, y simular dZ∼N(0, I2) para obtener dW˜=LdZ, se elige un número para la partición del plazo al vencimiento de la opción, por ejemplo N=100 y mediante el método de remuestreo cuadrático generar dZ, que involucra a dW˜ por construcción. Sean μZ y ΣZ la media teórica y la matriz de covarianza de dZ, respectivamente:yCon las ecuaciones anteriores se generan las trayectorias del sistema de ecuaciones diferencial estocásticas planteado en (16).El precio de una opción de compra con subyacente promedio está dado por la función de pago:
y el precio de una opción de venta con subyacente promedio está dado por:Si el subyacente es conducido por el sistema dado en (16), entonces el algoritmo para determinar los precios de las opciones de compra y de venta es:- 1)
Generar dWS,t y dWr,t como:
- 2)
Discretizar el sistema de ecuaciones diferenciales estocásticas como:
- 3)
Definir la media aritmética de las trayectorias generadas:
- 4)
Calcular el precio de la opción como:
ydonde M denota el número de trayectorias simuladas y N el número de precios generados.
En esta sección se calculan por medio de simulación Monte Carlo precios de opciones asiáticas con subyacente promedio. El subyacente es el precio de la acción de AMX-L, y se compara con los precios de opciones que se publicaron en el boletín de MexDer del día 25 de octubre de 2013. Se supone que la tasa de interés es conducida por procesos de reversión a la media de tipo Vasicek y de tipo CIR, y para la estimación de los parámetros iniciales se considera el método de máxima verosimilitud propuesto por Overbeck y Rydn (1997).
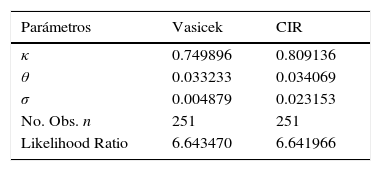
La muestra de la tasa de interés TIIE28 para calibrar los modelos comprende del 25 de octubre de 2012 al 25 de octubre de 2013. Con datos obtenidos de la página web de Banxico, los parámetros estimados con el modelo de Vasicek y CIR son los que figuran en la tabla 3.
De los resultados del cuadro anterior se puede verificar que se cumple la condición de Feller, es decir: 2κθ>σ2 en los 2 casos, lo cual es importante, ya que implica que las trayectorias del proceso que conduce la tasa de interés son siempre positivas.
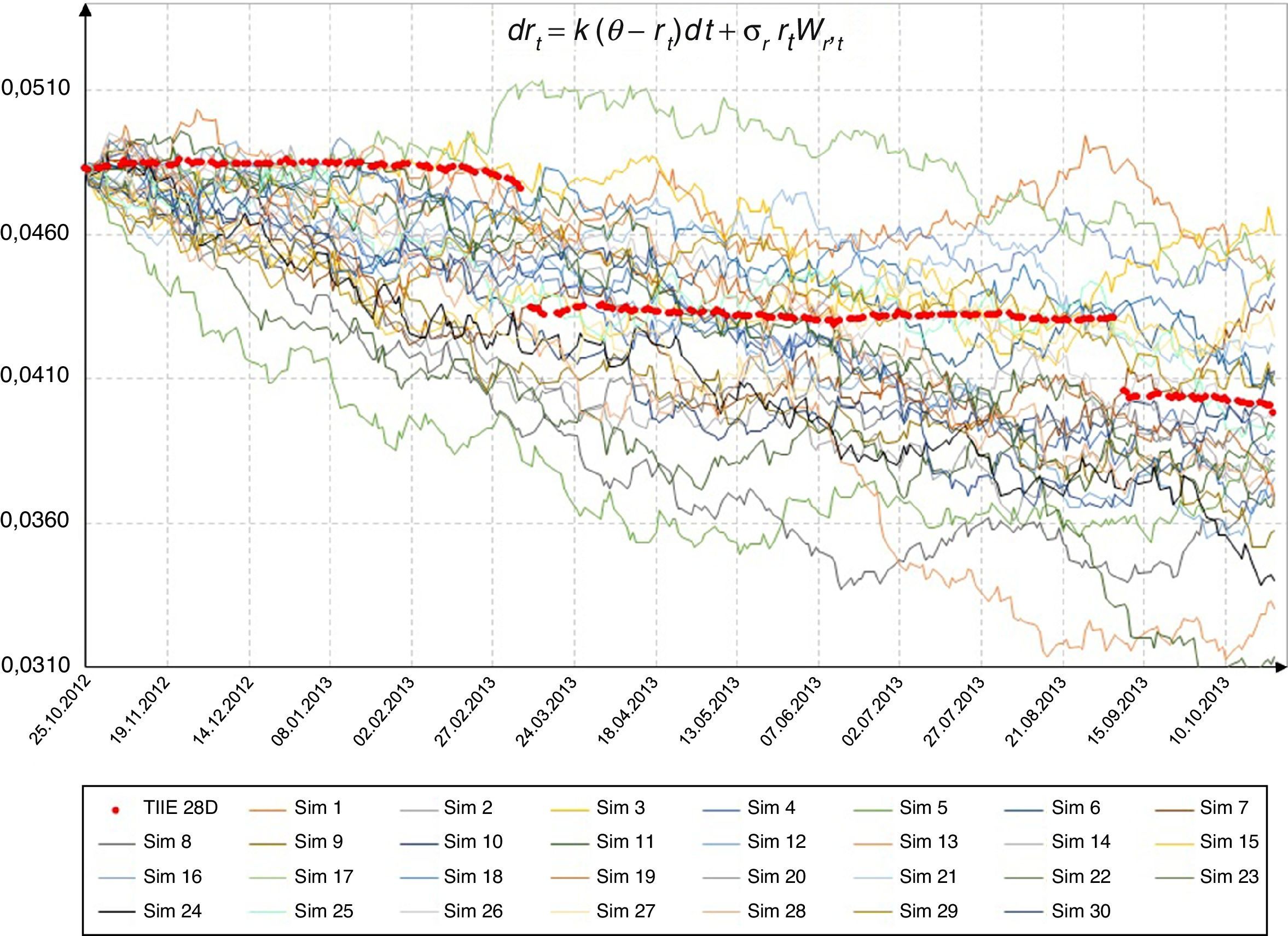
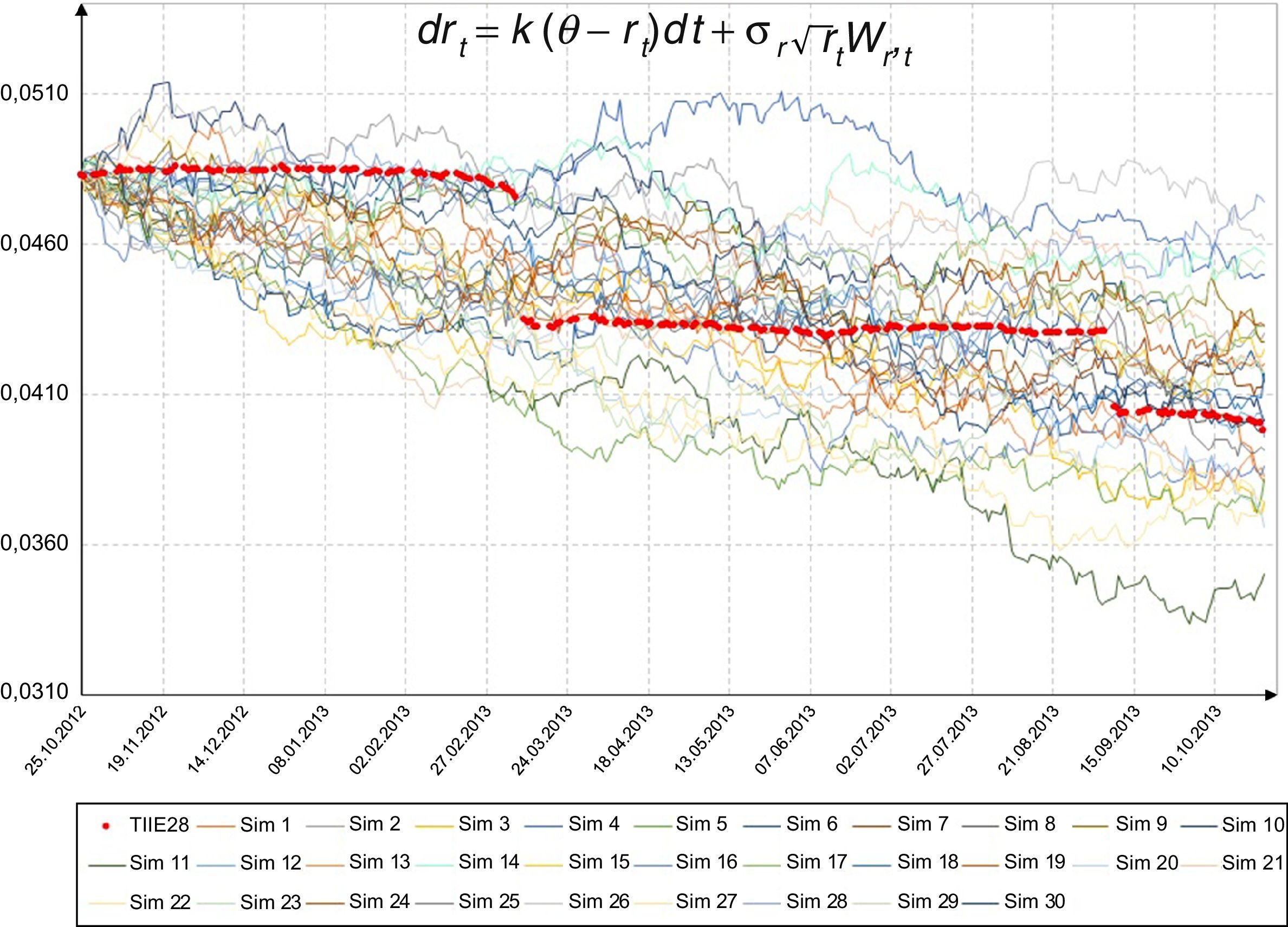
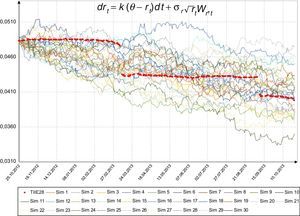
La figura 3 muestra la serie original de la tasa libre de riesgo y 30 trayectorias simuladas con los parámetros dados por el modelo de Vasicek, y la figura 4 con parámetros dados por el modelo CIR. En ambos casos se observa la tendencia de la tasa hacia la baja; además, la serie original muestra 2 cambios significativos: el primero de 4.7550 a 4.3450% el día 11 de marzo de 2013 y el segundo de 4.3075 a 4.0570% el 9 de septiembre de 2013.
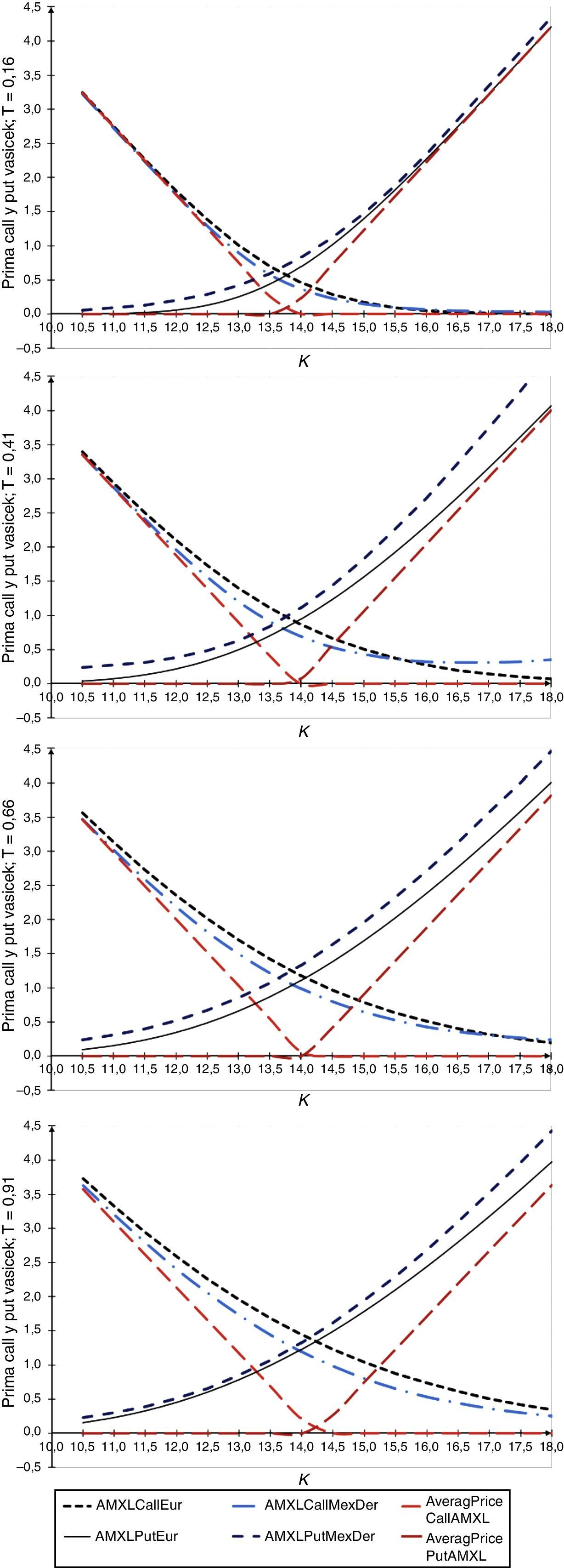
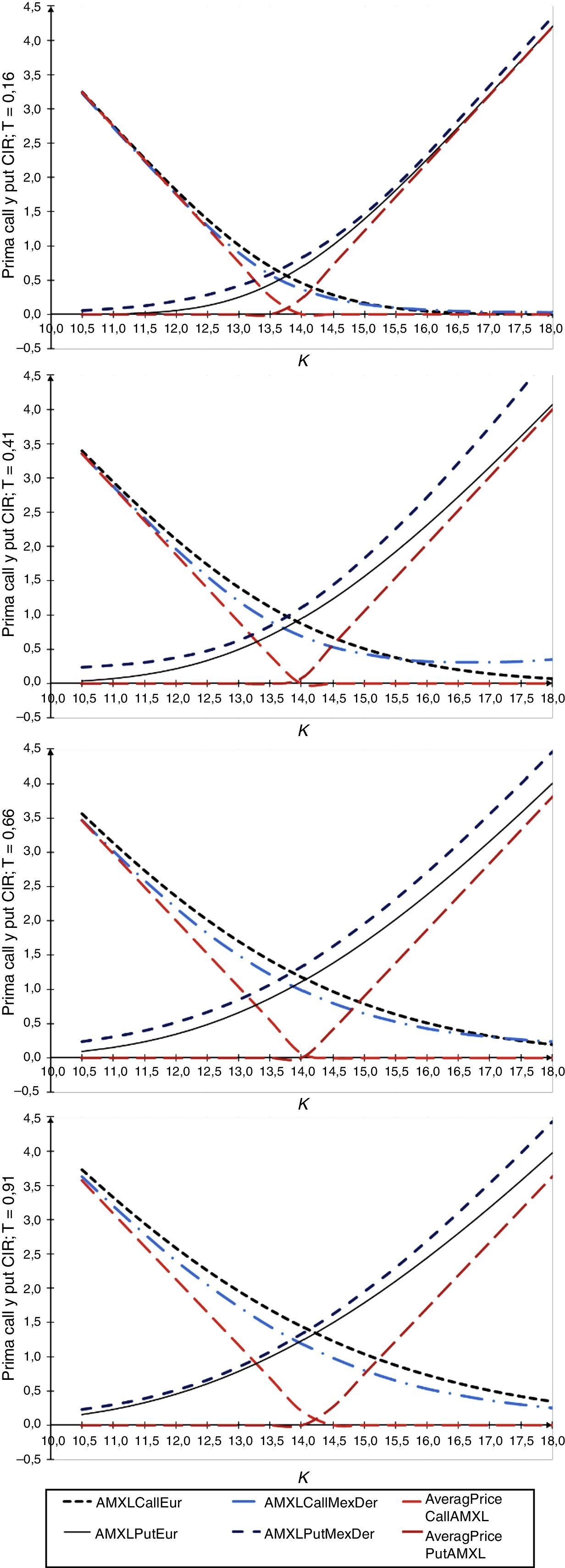
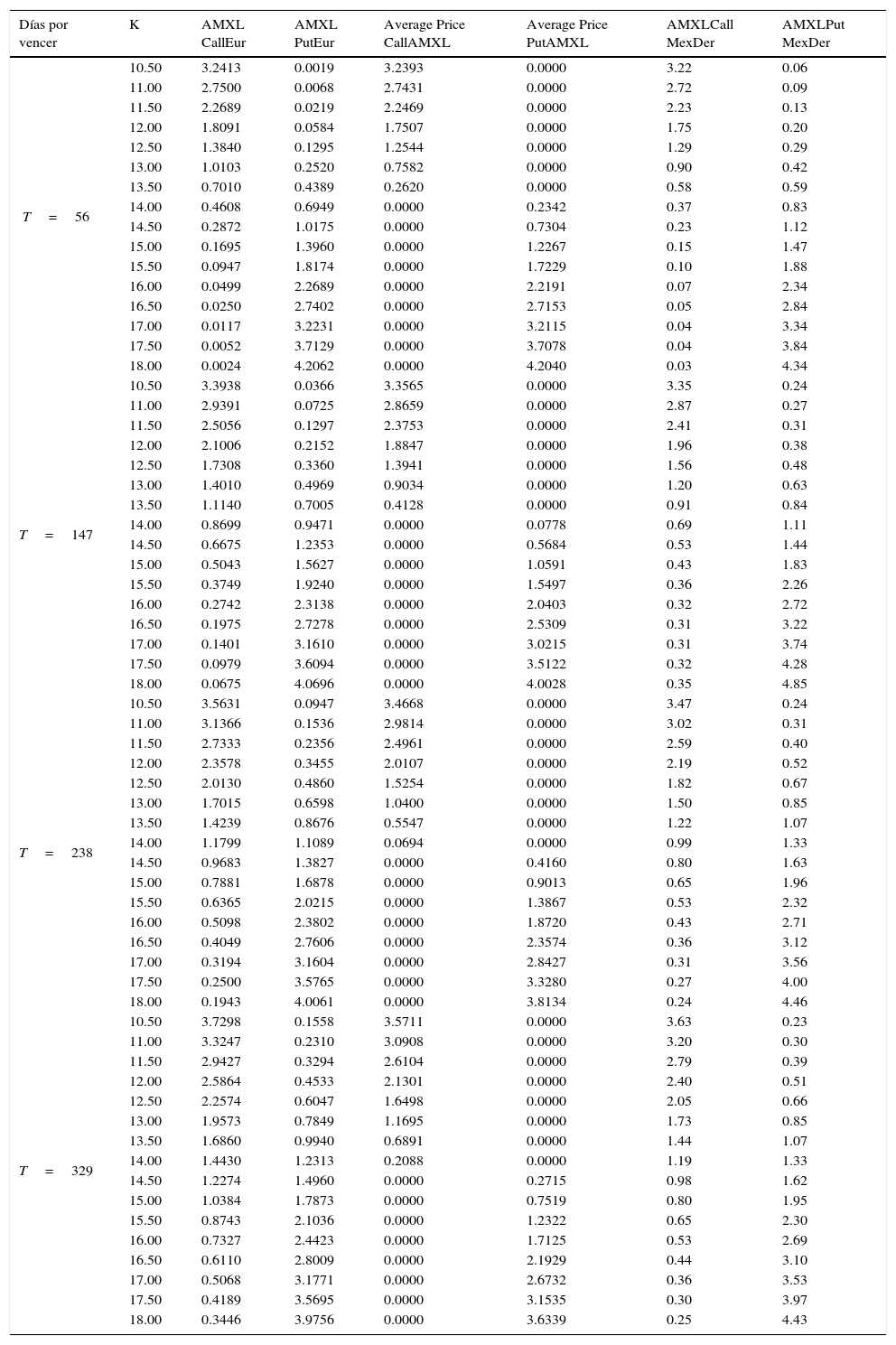
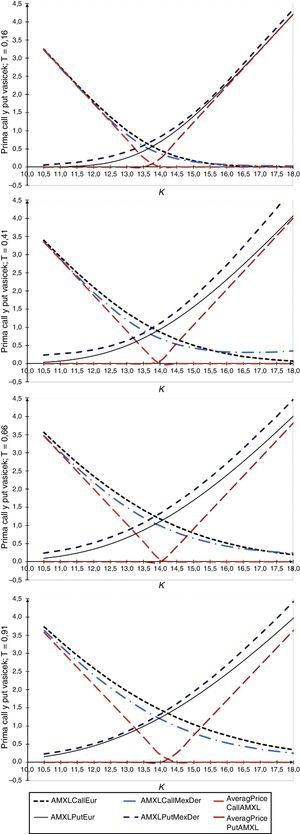
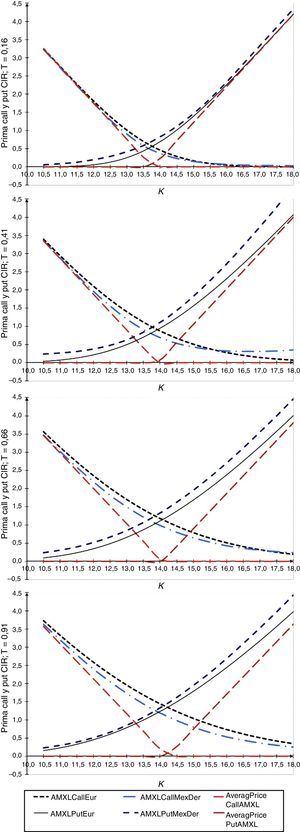
Los resultados de la aplicación se muestran en el Anexo. La figura 5 muestra precios de opciones obtenidos con el modelo de Vasicek y la figura 6 precios de opciones obtenidos con el modelo CIR; en ambos casos los plazos son desde T=56, 147, 238 y 329 días, y los precios de ejercicio varían desde $10.50 hasta $18.00, con incrementos de $0.50, asimismo el precio de AMX-L=$13.66 para el día 25 de octubre de 2013. El número de trayectorias que se simularon para determinar los precios de las opciones fue de 100,000. Un resultado relevante es que, al comparar los precios de opciones europeas —tanto simulados como con los publicados por MexDer— con sus contrapartes asiáticas, los precios de opciones asiáticas son menores en el caso de opciones de compra y de venta dentro del dinero, en el dinero y fuera del dinero.
En la figura 5 se muestran los precios de opciones de compra y de venta europeas, y precios de opciones con subyacente promedio, ambas con tasa de interés estocástica con parámetros calibrados con el modelo de Vasicek. Tales precios se comparan con precios de opciones de compra y de venta sobre AMXL publicados por MexDer. Se tienen 16 precios de ejercicio, de los cuales 7 están dentro del dinero para opciones de compra y 9 están dentro del dinero para opciones de venta. Se observa que para opciones al plazo de T=56 días en los primeros 4 precios de ejercicio, los precios de opciones de compra con subyacente promedio resultaron mayores que los precios publicados por MexDer. Para los demás plazos, los precios de opciones de compra y de venta simulados son menores en comparación con los precios de las publicadas por MexDer.
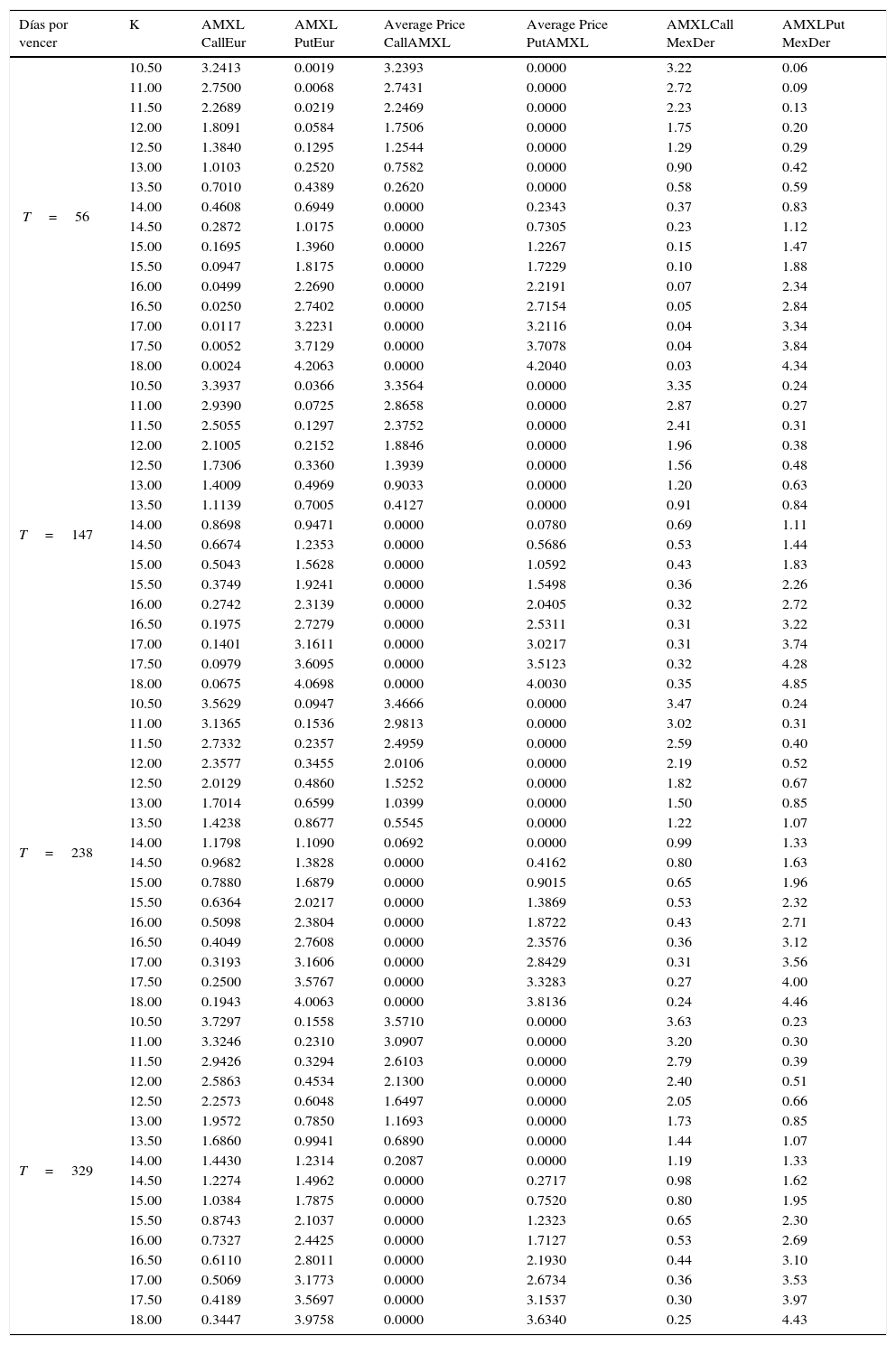
En la figura 6 se muestran los resultados con parámetros calibrados con el modelo de CIR, y los resultados son similares a los obtenidos con el modelo de Vasicek. Un análisis de las tablas A.1 y A.2 (Anexo) y las figuras anteriores revela que no se observan diferencias significativas en precios para ambos modelos. Además, se observa que los precios de opciones de venta y de compra con subyacente promedio son menores conforme el plazo al vencimiento de la opción se incrementa en ambos casos.
ConclusionesUna clase particular de las opciones asiáticas son aquellas en las que el subyacente es el precio promedio durante un período de tiempo. Con esta característica, las opciones asiáticas tienen una menor volatilidad y, por lo tanto, son más baratas en comparación con las opciones europeas. Se negocian principalmente sobre divisas y commodities que tengan bajos volúmenes de negociación. Fueron utilizados originalmente en 1987, cuando la oficina del Banco Trust en Tokio las utilizó para determinar el precio de opciones sobre el precio promedio del barril de petróleo, y por ello la opción se conoce como «asiática».
Las opciones asiáticas se pueden clasificar en 3 categorías, según sea el promedio que se tome: promedio aritmético, promedio geométrico y ambos se pueden ponderar de varias formas, en el que un peso determinado se aplica a cada subyacente del cual se calcule el promedio. Esto puede ser útil para determinar el promedio de una muestra con una distribución muy sesgada. Una característica adicional de las opciones asiáticas es que el subyacente puede ser el precio promedio, o bien el precio de ejercicio sea el promedio del subyacente que tome durante la vigencia del contrato.
En esta investigación por medio de simulación Monte Carlo y con el método de remuestreo cuadrático de Barraquand (1995) se determinaron precios de opciones europeas de compra y de venta, y precios de opciones de compra y de venta con subyacente promedio, también conocidas como average price (call and put); además, se supone que la tasa de interés es estocástica y conducida por un proceso de reversión a la media de tipo Vasicek y CIR. En la estimación de los parámetros iniciales se consideró el método de máxima verosimilitud propuesto por Overbeck y Rydn (1997), y en ambos casos resultó que se cumple la condición de Feller, es decir, las trayectorias del proceso que conduce la tasa de interés son positivas.
Al analizar los resultados obtenidos se encontró que al comparar los precios de opciones europeas con diferentes precios de ejercicio, tanto simulados como con los de publicados por MexDer, con sus contrapartes asiáticas, los precios de las asiáticas son menores en el caso de opciones de compra y de venta tanto para tasa de interés estocástica de tipo Vasicek y CIR. Sin embargo, al plazo de T=56 días en los primeros 4 precios de ejercicio los precios de opciones de compra con subyacente promedio resultaron mayores que los precios publicados por MexDer. Para los demás plazos, los precios de opciones de compra y de venta con subyacente promedio simulados son menores en comparación con los precios de las publicadas por MexDer. Asimismo, para opciones con tasa de interés estocástica de tipo Vasicek y CIR se encontró que los precios de opciones de compra y de venta con subyacente promedio son menores conforme el plazo al vencimiento de la opción se incrementa.
Por último, de la aplicación de la metodología propuesta resultó que todas las primas calculadas por simulación son menores que las publicadas por MexDer, lo cual implica que es deseable que se listaran instrumentos de esta clase como alternativa de cobertura, como en otros mercados de derivados.
Precios de opciones europeas de compra y de venta sobre AMXL, obtenidos con parámetros calibrados para la tasa de interés con el modelo de Vasicek
| Días por vencer | K | AMXL CallEur | AMXL PutEur | Average Price CallAMXL | Average Price PutAMXL | AMXLCall MexDer | AMXLPut MexDer |
|---|---|---|---|---|---|---|---|
| T=56 | 10.50 | 3.2413 | 0.0019 | 3.2393 | 0.0000 | 3.22 | 0.06 |
| 11.00 | 2.7500 | 0.0068 | 2.7431 | 0.0000 | 2.72 | 0.09 | |
| 11.50 | 2.2689 | 0.0219 | 2.2469 | 0.0000 | 2.23 | 0.13 | |
| 12.00 | 1.8091 | 0.0584 | 1.7507 | 0.0000 | 1.75 | 0.20 | |
| 12.50 | 1.3840 | 0.1295 | 1.2544 | 0.0000 | 1.29 | 0.29 | |
| 13.00 | 1.0103 | 0.2520 | 0.7582 | 0.0000 | 0.90 | 0.42 | |
| 13.50 | 0.7010 | 0.4389 | 0.2620 | 0.0000 | 0.58 | 0.59 | |
| 14.00 | 0.4608 | 0.6949 | 0.0000 | 0.2342 | 0.37 | 0.83 | |
| 14.50 | 0.2872 | 1.0175 | 0.0000 | 0.7304 | 0.23 | 1.12 | |
| 15.00 | 0.1695 | 1.3960 | 0.0000 | 1.2267 | 0.15 | 1.47 | |
| 15.50 | 0.0947 | 1.8174 | 0.0000 | 1.7229 | 0.10 | 1.88 | |
| 16.00 | 0.0499 | 2.2689 | 0.0000 | 2.2191 | 0.07 | 2.34 | |
| 16.50 | 0.0250 | 2.7402 | 0.0000 | 2.7153 | 0.05 | 2.84 | |
| 17.00 | 0.0117 | 3.2231 | 0.0000 | 3.2115 | 0.04 | 3.34 | |
| 17.50 | 0.0052 | 3.7129 | 0.0000 | 3.7078 | 0.04 | 3.84 | |
| 18.00 | 0.0024 | 4.2062 | 0.0000 | 4.2040 | 0.03 | 4.34 | |
| T=147 | 10.50 | 3.3938 | 0.0366 | 3.3565 | 0.0000 | 3.35 | 0.24 |
| 11.00 | 2.9391 | 0.0725 | 2.8659 | 0.0000 | 2.87 | 0.27 | |
| 11.50 | 2.5056 | 0.1297 | 2.3753 | 0.0000 | 2.41 | 0.31 | |
| 12.00 | 2.1006 | 0.2152 | 1.8847 | 0.0000 | 1.96 | 0.38 | |
| 12.50 | 1.7308 | 0.3360 | 1.3941 | 0.0000 | 1.56 | 0.48 | |
| 13.00 | 1.4010 | 0.4969 | 0.9034 | 0.0000 | 1.20 | 0.63 | |
| 13.50 | 1.1140 | 0.7005 | 0.4128 | 0.0000 | 0.91 | 0.84 | |
| 14.00 | 0.8699 | 0.9471 | 0.0000 | 0.0778 | 0.69 | 1.11 | |
| 14.50 | 0.6675 | 1.2353 | 0.0000 | 0.5684 | 0.53 | 1.44 | |
| 15.00 | 0.5043 | 1.5627 | 0.0000 | 1.0591 | 0.43 | 1.83 | |
| 15.50 | 0.3749 | 1.9240 | 0.0000 | 1.5497 | 0.36 | 2.26 | |
| 16.00 | 0.2742 | 2.3138 | 0.0000 | 2.0403 | 0.32 | 2.72 | |
| 16.50 | 0.1975 | 2.7278 | 0.0000 | 2.5309 | 0.31 | 3.22 | |
| 17.00 | 0.1401 | 3.1610 | 0.0000 | 3.0215 | 0.31 | 3.74 | |
| 17.50 | 0.0979 | 3.6094 | 0.0000 | 3.5122 | 0.32 | 4.28 | |
| 18.00 | 0.0675 | 4.0696 | 0.0000 | 4.0028 | 0.35 | 4.85 | |
| T=238 | 10.50 | 3.5631 | 0.0947 | 3.4668 | 0.0000 | 3.47 | 0.24 |
| 11.00 | 3.1366 | 0.1536 | 2.9814 | 0.0000 | 3.02 | 0.31 | |
| 11.50 | 2.7333 | 0.2356 | 2.4961 | 0.0000 | 2.59 | 0.40 | |
| 12.00 | 2.3578 | 0.3455 | 2.0107 | 0.0000 | 2.19 | 0.52 | |
| 12.50 | 2.0130 | 0.4860 | 1.5254 | 0.0000 | 1.82 | 0.67 | |
| 13.00 | 1.7015 | 0.6598 | 1.0400 | 0.0000 | 1.50 | 0.85 | |
| 13.50 | 1.4239 | 0.8676 | 0.5547 | 0.0000 | 1.22 | 1.07 | |
| 14.00 | 1.1799 | 1.1089 | 0.0694 | 0.0000 | 0.99 | 1.33 | |
| 14.50 | 0.9683 | 1.3827 | 0.0000 | 0.4160 | 0.80 | 1.63 | |
| 15.00 | 0.7881 | 1.6878 | 0.0000 | 0.9013 | 0.65 | 1.96 | |
| 15.50 | 0.6365 | 2.0215 | 0.0000 | 1.3867 | 0.53 | 2.32 | |
| 16.00 | 0.5098 | 2.3802 | 0.0000 | 1.8720 | 0.43 | 2.71 | |
| 16.50 | 0.4049 | 2.7606 | 0.0000 | 2.3574 | 0.36 | 3.12 | |
| 17.00 | 0.3194 | 3.1604 | 0.0000 | 2.8427 | 0.31 | 3.56 | |
| 17.50 | 0.2500 | 3.5765 | 0.0000 | 3.3280 | 0.27 | 4.00 | |
| 18.00 | 0.1943 | 4.0061 | 0.0000 | 3.8134 | 0.24 | 4.46 | |
| T=329 | 10.50 | 3.7298 | 0.1558 | 3.5711 | 0.0000 | 3.63 | 0.23 |
| 11.00 | 3.3247 | 0.2310 | 3.0908 | 0.0000 | 3.20 | 0.30 | |
| 11.50 | 2.9427 | 0.3294 | 2.6104 | 0.0000 | 2.79 | 0.39 | |
| 12.00 | 2.5864 | 0.4533 | 2.1301 | 0.0000 | 2.40 | 0.51 | |
| 12.50 | 2.2574 | 0.6047 | 1.6498 | 0.0000 | 2.05 | 0.66 | |
| 13.00 | 1.9573 | 0.7849 | 1.1695 | 0.0000 | 1.73 | 0.85 | |
| 13.50 | 1.6860 | 0.9940 | 0.6891 | 0.0000 | 1.44 | 1.07 | |
| 14.00 | 1.4430 | 1.2313 | 0.2088 | 0.0000 | 1.19 | 1.33 | |
| 14.50 | 1.2274 | 1.4960 | 0.0000 | 0.2715 | 0.98 | 1.62 | |
| 15.00 | 1.0384 | 1.7873 | 0.0000 | 0.7519 | 0.80 | 1.95 | |
| 15.50 | 0.8743 | 2.1036 | 0.0000 | 1.2322 | 0.65 | 2.30 | |
| 16.00 | 0.7327 | 2.4423 | 0.0000 | 1.7125 | 0.53 | 2.69 | |
| 16.50 | 0.6110 | 2.8009 | 0.0000 | 2.1929 | 0.44 | 3.10 | |
| 17.00 | 0.5068 | 3.1771 | 0.0000 | 2.6732 | 0.36 | 3.53 | |
| 17.50 | 0.4189 | 3.5695 | 0.0000 | 3.1535 | 0.30 | 3.97 | |
| 18.00 | 0.3446 | 3.9756 | 0.0000 | 3.6339 | 0.25 | 4.43 |
Precios de opciones europeas de compra y de venta sobre AMXL, obtenidos con parámetros calibrados para la tasa de interés con el modelo de CIR
| Días por vencer | K | AMXL CallEur | AMXL PutEur | Average Price CallAMXL | Average Price PutAMXL | AMXLCall MexDer | AMXLPut MexDer |
|---|---|---|---|---|---|---|---|
| T=56 | 10.50 | 3.2413 | 0.0019 | 3.2393 | 0.0000 | 3.22 | 0.06 |
| 11.00 | 2.7500 | 0.0068 | 2.7431 | 0.0000 | 2.72 | 0.09 | |
| 11.50 | 2.2689 | 0.0219 | 2.2469 | 0.0000 | 2.23 | 0.13 | |
| 12.00 | 1.8091 | 0.0584 | 1.7506 | 0.0000 | 1.75 | 0.20 | |
| 12.50 | 1.3840 | 0.1295 | 1.2544 | 0.0000 | 1.29 | 0.29 | |
| 13.00 | 1.0103 | 0.2520 | 0.7582 | 0.0000 | 0.90 | 0.42 | |
| 13.50 | 0.7010 | 0.4389 | 0.2620 | 0.0000 | 0.58 | 0.59 | |
| 14.00 | 0.4608 | 0.6949 | 0.0000 | 0.2343 | 0.37 | 0.83 | |
| 14.50 | 0.2872 | 1.0175 | 0.0000 | 0.7305 | 0.23 | 1.12 | |
| 15.00 | 0.1695 | 1.3960 | 0.0000 | 1.2267 | 0.15 | 1.47 | |
| 15.50 | 0.0947 | 1.8175 | 0.0000 | 1.7229 | 0.10 | 1.88 | |
| 16.00 | 0.0499 | 2.2690 | 0.0000 | 2.2191 | 0.07 | 2.34 | |
| 16.50 | 0.0250 | 2.7402 | 0.0000 | 2.7154 | 0.05 | 2.84 | |
| 17.00 | 0.0117 | 3.2231 | 0.0000 | 3.2116 | 0.04 | 3.34 | |
| 17.50 | 0.0052 | 3.7129 | 0.0000 | 3.7078 | 0.04 | 3.84 | |
| 18.00 | 0.0024 | 4.2063 | 0.0000 | 4.2040 | 0.03 | 4.34 | |
| T=147 | 10.50 | 3.3937 | 0.0366 | 3.3564 | 0.0000 | 3.35 | 0.24 |
| 11.00 | 2.9390 | 0.0725 | 2.8658 | 0.0000 | 2.87 | 0.27 | |
| 11.50 | 2.5055 | 0.1297 | 2.3752 | 0.0000 | 2.41 | 0.31 | |
| 12.00 | 2.1005 | 0.2152 | 1.8846 | 0.0000 | 1.96 | 0.38 | |
| 12.50 | 1.7306 | 0.3360 | 1.3939 | 0.0000 | 1.56 | 0.48 | |
| 13.00 | 1.4009 | 0.4969 | 0.9033 | 0.0000 | 1.20 | 0.63 | |
| 13.50 | 1.1139 | 0.7005 | 0.4127 | 0.0000 | 0.91 | 0.84 | |
| 14.00 | 0.8698 | 0.9471 | 0.0000 | 0.0780 | 0.69 | 1.11 | |
| 14.50 | 0.6674 | 1.2353 | 0.0000 | 0.5686 | 0.53 | 1.44 | |
| 15.00 | 0.5043 | 1.5628 | 0.0000 | 1.0592 | 0.43 | 1.83 | |
| 15.50 | 0.3749 | 1.9241 | 0.0000 | 1.5498 | 0.36 | 2.26 | |
| 16.00 | 0.2742 | 2.3139 | 0.0000 | 2.0405 | 0.32 | 2.72 | |
| 16.50 | 0.1975 | 2.7279 | 0.0000 | 2.5311 | 0.31 | 3.22 | |
| 17.00 | 0.1401 | 3.1611 | 0.0000 | 3.0217 | 0.31 | 3.74 | |
| 17.50 | 0.0979 | 3.6095 | 0.0000 | 3.5123 | 0.32 | 4.28 | |
| 18.00 | 0.0675 | 4.0698 | 0.0000 | 4.0030 | 0.35 | 4.85 | |
| T=238 | 10.50 | 3.5629 | 0.0947 | 3.4666 | 0.0000 | 3.47 | 0.24 |
| 11.00 | 3.1365 | 0.1536 | 2.9813 | 0.0000 | 3.02 | 0.31 | |
| 11.50 | 2.7332 | 0.2357 | 2.4959 | 0.0000 | 2.59 | 0.40 | |
| 12.00 | 2.3577 | 0.3455 | 2.0106 | 0.0000 | 2.19 | 0.52 | |
| 12.50 | 2.0129 | 0.4860 | 1.5252 | 0.0000 | 1.82 | 0.67 | |
| 13.00 | 1.7014 | 0.6599 | 1.0399 | 0.0000 | 1.50 | 0.85 | |
| 13.50 | 1.4238 | 0.8677 | 0.5545 | 0.0000 | 1.22 | 1.07 | |
| 14.00 | 1.1798 | 1.1090 | 0.0692 | 0.0000 | 0.99 | 1.33 | |
| 14.50 | 0.9682 | 1.3828 | 0.0000 | 0.4162 | 0.80 | 1.63 | |
| 15.00 | 0.7880 | 1.6879 | 0.0000 | 0.9015 | 0.65 | 1.96 | |
| 15.50 | 0.6364 | 2.0217 | 0.0000 | 1.3869 | 0.53 | 2.32 | |
| 16.00 | 0.5098 | 2.3804 | 0.0000 | 1.8722 | 0.43 | 2.71 | |
| 16.50 | 0.4049 | 2.7608 | 0.0000 | 2.3576 | 0.36 | 3.12 | |
| 17.00 | 0.3193 | 3.1606 | 0.0000 | 2.8429 | 0.31 | 3.56 | |
| 17.50 | 0.2500 | 3.5767 | 0.0000 | 3.3283 | 0.27 | 4.00 | |
| 18.00 | 0.1943 | 4.0063 | 0.0000 | 3.8136 | 0.24 | 4.46 | |
| T=329 | 10.50 | 3.7297 | 0.1558 | 3.5710 | 0.0000 | 3.63 | 0.23 |
| 11.00 | 3.3246 | 0.2310 | 3.0907 | 0.0000 | 3.20 | 0.30 | |
| 11.50 | 2.9426 | 0.3294 | 2.6103 | 0.0000 | 2.79 | 0.39 | |
| 12.00 | 2.5863 | 0.4534 | 2.1300 | 0.0000 | 2.40 | 0.51 | |
| 12.50 | 2.2573 | 0.6048 | 1.6497 | 0.0000 | 2.05 | 0.66 | |
| 13.00 | 1.9572 | 0.7850 | 1.1693 | 0.0000 | 1.73 | 0.85 | |
| 13.50 | 1.6860 | 0.9941 | 0.6890 | 0.0000 | 1.44 | 1.07 | |
| 14.00 | 1.4430 | 1.2314 | 0.2087 | 0.0000 | 1.19 | 1.33 | |
| 14.50 | 1.2274 | 1.4962 | 0.0000 | 0.2717 | 0.98 | 1.62 | |
| 15.00 | 1.0384 | 1.7875 | 0.0000 | 0.7520 | 0.80 | 1.95 | |
| 15.50 | 0.8743 | 2.1037 | 0.0000 | 1.2323 | 0.65 | 2.30 | |
| 16.00 | 0.7327 | 2.4425 | 0.0000 | 1.7127 | 0.53 | 2.69 | |
| 16.50 | 0.6110 | 2.8011 | 0.0000 | 2.1930 | 0.44 | 3.10 | |
| 17.00 | 0.5069 | 3.1773 | 0.0000 | 2.6734 | 0.36 | 3.53 | |
| 17.50 | 0.4189 | 3.5697 | 0.0000 | 3.1537 | 0.30 | 3.97 | |
| 18.00 | 0.3447 | 3.9758 | 0.0000 | 3.6340 | 0.25 | 4.43 |
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.
Se comercializaron por primera vez en 1987, cuando la oficina de Bankers Trust en Tokio las utilizó para valuar opciones con precio promedio sobre contratos del barril de petróleo (Venezia, 2010).
Una descripción más detallada de las ventajas del uso de promedios está en Wilmott (2006).
Véase Boyle, Broadie y Glasserman (1997) respecto al uso de la simulación Monte Carlo en finanzas computacionales.