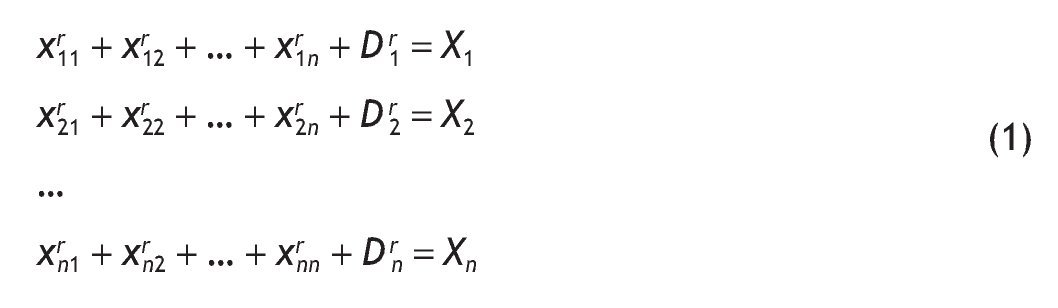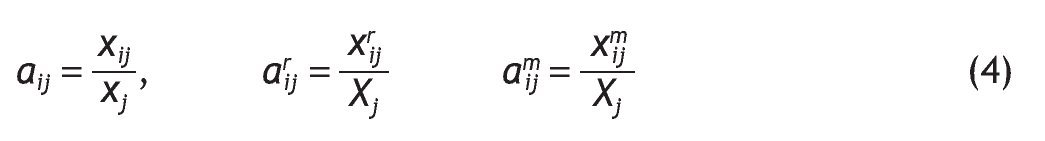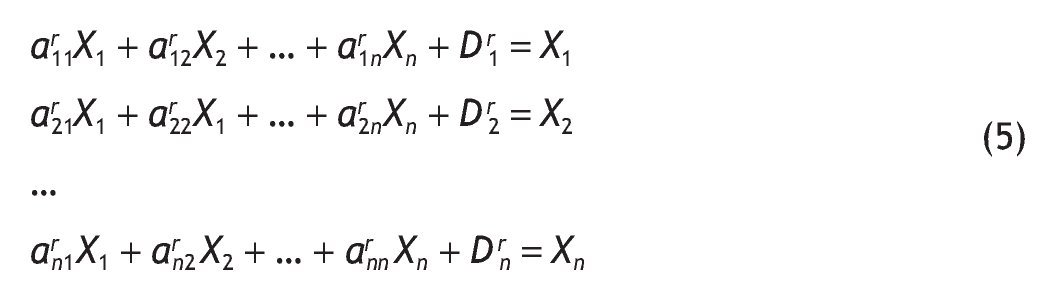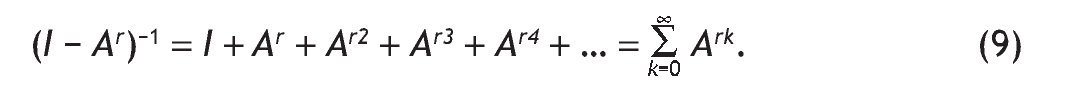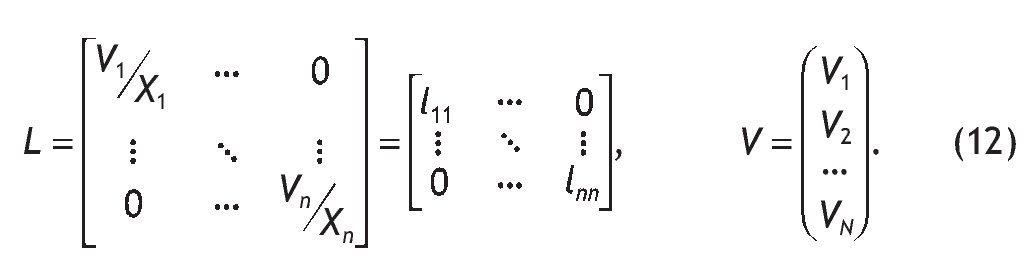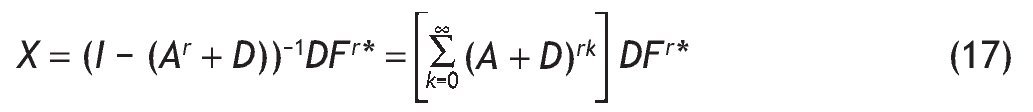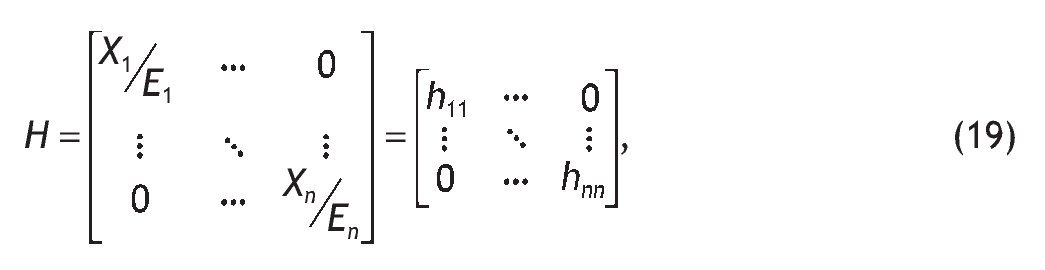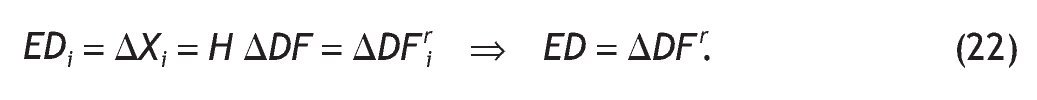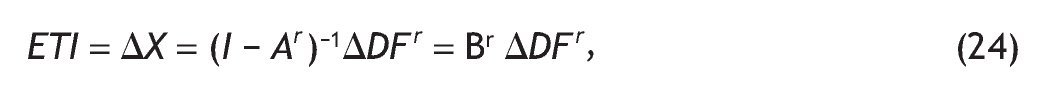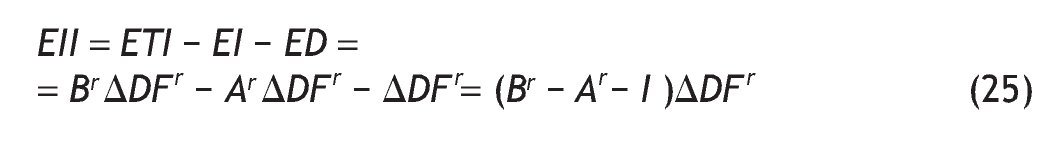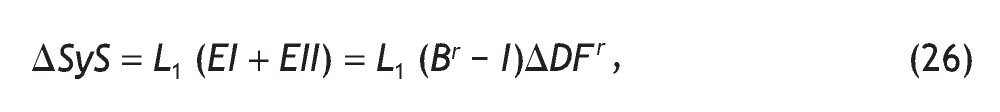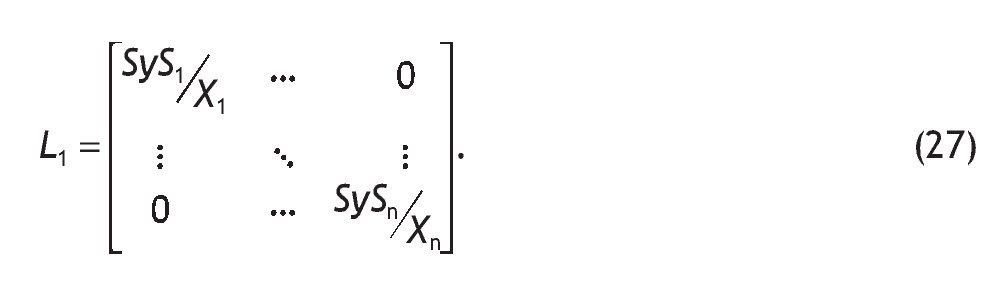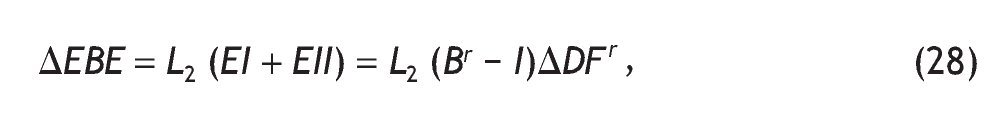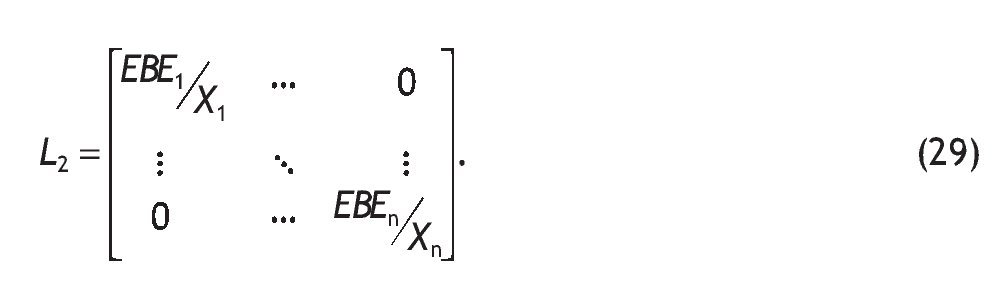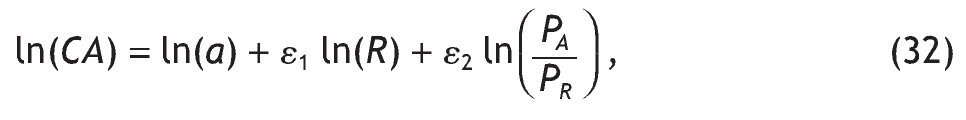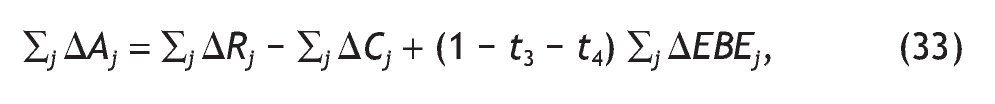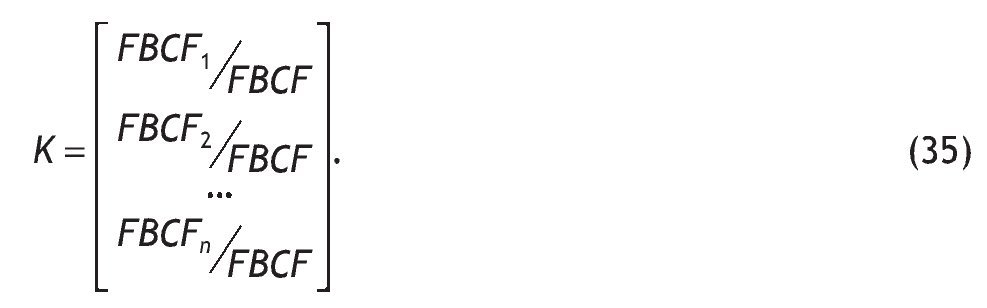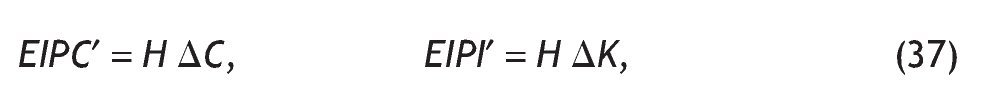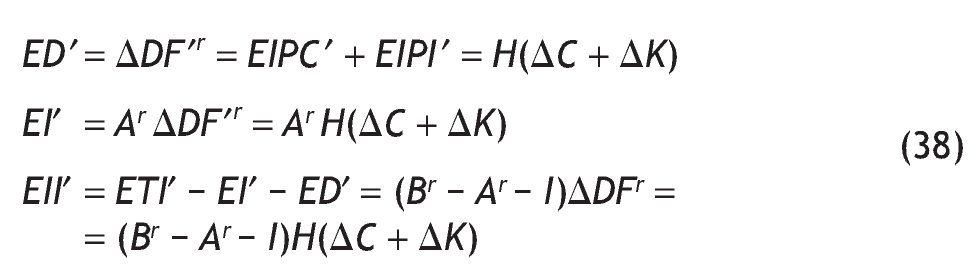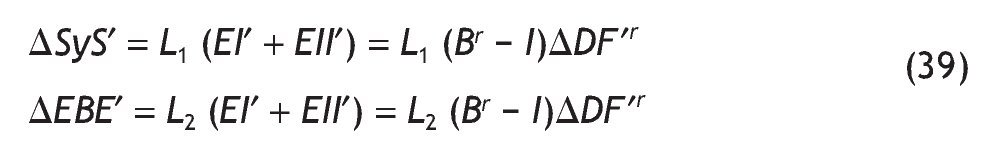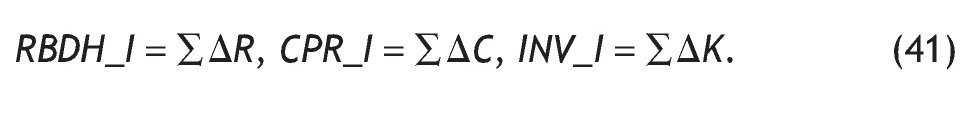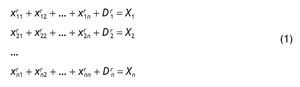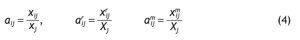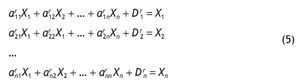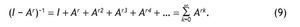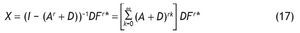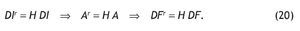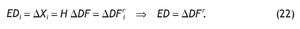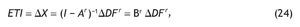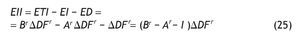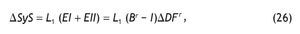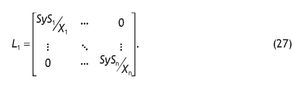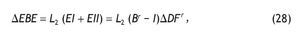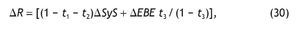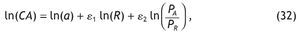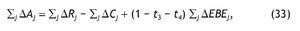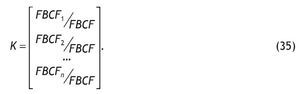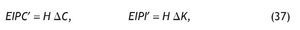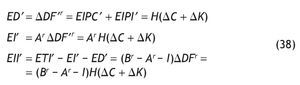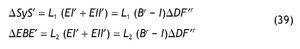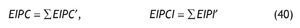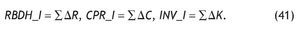Partiendo de la cuenta satélite de las tecnologías de la información y la comunicación: CS-TIC 2005-2009, se presenta en este artículo un modelo de simulación basado en técnicas input-output, que permite calcular los efectos directos, indirectos e inducidos ligados al aumento de demanda final en bienes y servicios TIC, establecer los efectos macroeconómicos de la implantación de nuevas industrias TIC o de una sustitución de importaciones por producción interna de bienes TIC. Como novedad del modelo, además de incorporar el consumo de los hogares de forma endógena, se introduce también el ahorro y su distribución en el flujo circular, derivando funciones de impacto inducido asociadas a la producción de bienes de capital mediante un proceso iterativo. Bajo este esquema, los impactos o efectos macroeconómicos asociados a los efectos inducidos se subdividen a su vez en tres magnitudes: iniciales, producción-consumo y producción-inversión.
This study presents a simulation model, based on input-output techniques, using the Spanish satellite account on Information and Communications Technologies (ICT): CS-TIC 2005¿2009, for calculating the direct, indirect and induced effects related to an increase in final demand in ICT goods and services. The macroeconomic effects of the implementation of new ICT industries are determined, as well as to analyze import substitution for domestic production of ICT goods. The main novelty of the model, besides including endogenous household consumption, is the introduction of savings and their distribution in the circular flow, and the derivation of functions, through an iterative process, for the induced impact associated to the production of capital goods. Under this scheme, the macroeconomic impacts associated with the induced effects can be further divided into three separate magnitudes: initial, production-consumption, and production-investment.
1. Introducción
En el esquema conceptual del análisis input-output se asume que una alteración de la demanda de un grupo de población provoca múltiples efectos en cascada en el conjunto de la economía (en la inversión, el empleo, los beneficios empresariales, etc.). El modelo de simulación que va a desarrollarse está basado en las tablas de origen, destino y simétrica elaboradas en la CS-TIC para 2007 por Vicente y Zofío (2012), con las que se realiza una simulación a fin de predecir el posible comportamiento de los sectores económicos ante un aumento de la demanda final de hogares en bienes y servicios TIC de un 10%.
Como en cualquier simulación del modelo de demanda, este nuevo consumo de los hogares en bienes y servicios TIC provocará un aumento de los ingresos, de los beneficios y del empleo en el sector, derivado de la nueva producción. Como consecuencia, las empresas TIC incrementarán las compras a sus empresas suministradoras, en sectores que, al ver aumentada su demanda, verán a su vez incrementar también su actividad, lo que generará, en un efecto multiplicador, un nuevo incremento del empleo y de la demanda en los sectores que les suministran materias primas, etc., es decir, se producirá un crecimiento general y en cascada de la renta y del empleo, que se traducirá nuevamente en aumentos de la demanda, tanto de las empresas como de los particulares.
Las variaciones en las demandas finales, establecidas en las Tablas Input-Output a través de los multiplicadores que se derivan de la matriz de coeficientes técnicos, determinan los niveles de oferta y de rentas generadas en el marco de una economía, Miller y Blair (1985). Por tanto, en las simulaciones que se proponen en este estudio se actuará tanto sobre las demandas finales, como variables exógenas, como sobre los parámetros del modelo.
El objetivo del artículo es, pues, estudiar los efectos directos, indirectos e inducidos de un hipotético shock de demanda final en bienes y servicios TIC en el conjunto de la economía, tanto en términos de empleo, de renta y de un conjunto de variables macroeconómicas de especial interés: impuestos, cotizaciones, valor añadido, etc.
En artículo se estructura de la siguiente forma: en la próxima sección metodológica se formula matricialmente el modelo de Leontief (1936, 1966, 1986), que constituye la base del proceso del modelo de simulación utilizado, y que tiene como antecedentes la propuestas de Miyazawa (1976), y el modelo MICAL (MInería del CArbón en León), de extracción hipotética, desarrollado al objeto de analizar el impacto que provocaría en la economía de la provincia de León, la desaparición o reducción del sector minero, Muñoz (1997).
En la tercera sección se presenta el análisis asociado a los nuevos efectos inducidos que se proponen: producción-consumo y producción-inversión, ampliando el modelo al objeto de incluir los impactos derivados del ahorro en el flujo circular; impactos que se traducen en un aumento de la demanda de inversión y, por tanto, de la producción de nuevos bienes de capital. En el cuarto apartado se exponen y comentan los resultados de la simulación realizada poniendo de manifiesto la importancia del sector de las TIC en el conjunto de la economía nacional mediante la cuantificación de los efectos propuestos. El quinto y último cierra con las conclusiones más relevantes.
2. Metodología
2.1. Estructura de la Tabla Input¿Output
En el SEC¿95, el Marco Input¿Output queda definido por las Tablas de Origen y Destino por ramas de actividad, las Tablas que relacionan las Tablas de Origen y Destino y las Cuentas de los sectores, y las Tablas Input-Output simétricas por ramas homogéneas (por productos).
Las Tablas de Origen y Destino son matrices (donde las filas corresponden a productos y las columnas a ramas de actividad) que reflejan la desagregación de la producción de las ramas de actividad por tipos de productos, y la distribución de la oferta de bienes y servicios interiores e importados entre los diferentes empleos intermedios o finales, incluidas las exportaciones. Asimismo, la Tabla de Destino muestra por ramas de actividad la estructura de los costes de producción y la renta generada.
En la Tabla de Origen se muestra la oferta de bienes y servicios por producto y tipo de proveedor, distinguiendo la producción de las ramas de actividad interiores y las importaciones. En la Tabla de Destino se muestran los empleos de bienes y servicios por producto y tipo de empleo, es decir, como consumos intermedios (por rama de actividad), Consumo Final, formación bruta de capital, o exportaciones. Además, en la Tabla se muestran los componentes del Valor Añadido Bruto, es decir, la remuneración de los asalariados, los otros impuestos menos las subvenciones sobre la producción, la renta mixta neta, el Excedente de Explotación neto y el Consumo de Capital Fijo.
La Tabla Input-Output (TIO) producto por producto (o Tabla simétrica) es la Tabla más importante del marco Input-Output definido en el SEC¿95, fundamentalmente por constituir la herramienta básica para la elaboración de modelos de simulación. Esta Tabla puede elaborarse mediante una conversión de las Tablas de Origen y Destino, ambas a precios básicos. La conversión consta de tres fases:
1) La asignación de los productos secundarios de la Tabla de Origen a las ramas de actividad en las que son productos principales.
2) La reordenación de las columnas de la Tabla de Destino, para pasar de los insumos de las ramas de actividad a los insumos de las ramas homogéneas1 (sin agregación de las filas).
3) La agregación, en su caso, de los productos detallados (filas) de la nueva Tabla de Destino a las ramas homogéneas que figuran en las columnas.
La Tabla Input-Output (TIO) simétrica de la CS-TIC elaborada por Vicente y Zofío (2012), se estructura, al igual que la Tabla de Destino, en tres matrices independientes: la matriz de consumos intermedios o de demanda intermedia (DI), la matriz de demanda final (DF) y la matriz de inputs primarios (IP).
La matriz DI contabiliza las relaciones de intercambio entre las distintas ramas productivas, donde bajo el esquema de tabla simétrica, es una matriz cuadrada, con el mismo número de filas que de columnas. La matriz DF recoge la parte de la producción de bienes y servicios que se destina a los usuarios finales (demanda de consumo, demanda de inversión y demanda exterior de bienes producidos en la economía nacional). Finalmente, en la matriz IP se registran los pagos que realizan las empresas y las administraciones por utilizar los factores originarios de la producción: rentas del trabajo (RAj), excedentes empresariales (EBEj) y los otros impuestos netos sobre la producción (OIj). La matriz IP proporciona el valor añadido de cada rama que se obtiene deduciendo del valor de la producción el total de consumos intermedios.
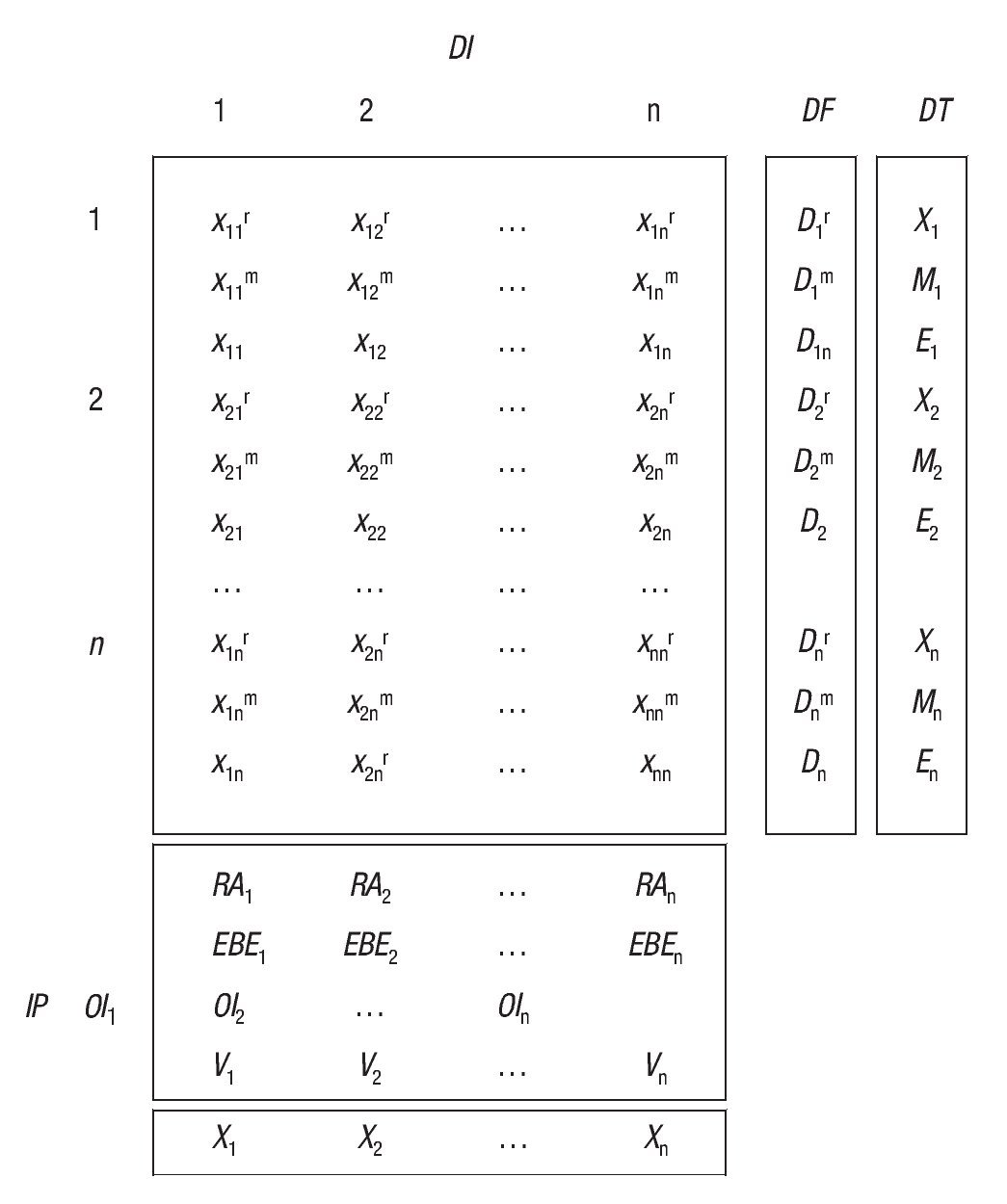
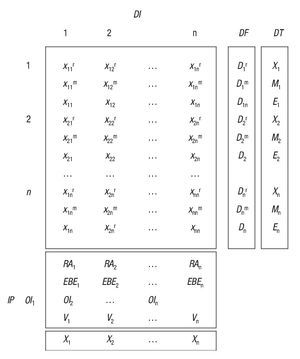
En la figura 1 se representa matemáticamente la estructura de una TIO, apareciendo diferenciadas las tres matrices anteriores.
Figura 1 Esquema matricial de una tabla input-outp. Fuente: Muñoz et al. (2001) y elaboración propia.
Cada elemento xij de la matriz DI recoge los consumos de productos de la rama i que hace la rama j. Si estos consumos son originarios de empresas residentes en el área territorial de referencia de la TIO, es decir, tienen el carácter de interior, se referencian con el superíndice r, los importados desde unidades no residentes se referencian con el superíndice m. La producción que realiza una rama (Xj) se obtiene como suma de los elementos que figuran en cada columna: consumos intermedios de unidades residentes, importaciones y valor añadido (Vj).
Por filas, en el vector DT, aparecen los destinos de la producción interior (Xi) y de las importaciones (Mi), siendo Ei el total de empleos o demanda total del producto i2. Estos destinos son la demanda intermedia (las compras que realizan otros sectores, Sjxij) y la demanda final (Di); es decir, DT = DI + DF.
Simplificando, sí se lee la tabla por filas, se obtienen las salidas o ventas del sector de la fila a los sectores de las columnas (los llamados outputs), y si se lee por columnas, se obtienen las entradaVVs o compras del sector columna a los sectores de las filas (los denominados inputs). Así pues, en el cuadro de n sectores se tendrán todas las relaciones interindustriales y la cifra de cada casilla del cuadro (xij), refleja las ventas del sector i al sector j o a las compras del sector j al sector i, que lógicamente, darán la misma cifra.
Dado el equilibrio contable establecido en la TIO simétrica en donde el valor de producción por columnas ha de igualarse con la producción distribuida o empleada en cada fila, se puede también representar la estructura formal de la TIO a través del siguiente sistema de ecuaciones lineales:
Este sistema de ecuaciones en notación matricial, queda expresado por:
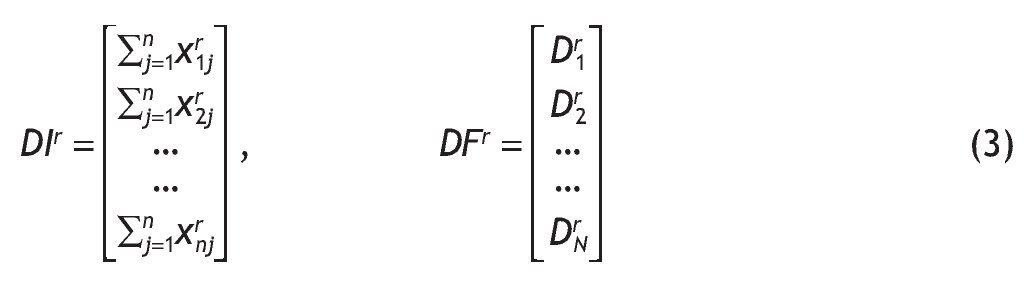
siendo DIr y DF r los siguientes vectores:
Definimos el coeficiente técnico aij como la relación entre la cantidad consumida de un input y el valor de producción de una rama:
obteniendo un nuevo sistema de ecuaciones:
Este nuevo sistema, en notación matricial, permite expresar la ecuación (2) de la siguiente forma:
Operando convenientemente se transforma en:
en donde I es la matriz identidad; y de forma que
La matriz Br = (I - Ar)-1 se corresponde con la matriz inversa de Leontief, cuyos elementos brij constituyen una medida del esfuerzo de producción requerido a la rama i por parte de la rama j para abastecer una unidad de demanda final de esta última. Cada elemento de la matriz inversa de Leontief representa pues los efectos acumulativos (directos e indirectos) que subyacen en la estructura productiva que la TIO representa. Téngase en cuenta que:
De igual modo, si consideramos las filas correspondientes al total del consumo, interior e importado, obtenemos:
2.2. Modelo de demanda y sus formas
Las ecuaciones (8) y (10) caracterizan el modelo abierto de Leontief o modelo de Tipo I. En este modelo, podemos definir los efectos directos e indirectos en la distribución de la renta como:
siendo
En la década de los setenta, diversos autores formularon modelos input-output ampliados de distribución de renta, véase Golladay y Haveman (1976), Paukert et al. (1976) y Rose (1977). En Miyazawa (1976) los efectos de la distribución de la renta sobre los multiplicadores input-output pueden ser incorporados partiendo del modelo abierto de Leontief, lo que da lugar a la denominada matriz de Leontief Tipo II3. Además de la hipótesis de que los coeficientes técnicos son constantes, en el modelo derivado de la matriz de Leontief Tipo II (modelo cerrado Tipo II), es necesario también suponer que lo es la conducta de los consumidores, tanto en lo relativo al consumo como al ahorro. Esto implica una función de consumo lineal y homogénea, donde todos los hogares tienen las mismas propensiones al consumo y, por ende, los mismos ingresos salariales.
Para salvar estas limitaciones, Miyazawa propuso una desagregación del sector hogares en k clases de niveles de renta, expresando el consumo de los hogares, CPr, como:
siendo C(n·k) la matriz de coeficientes de consumo y VA(k·n) la matriz de ratios de valor añadido, dando lugar a los modelos cerrados de Tipo III, donde la matriz de Leontief toma ahora el valor:
Bajo este esquema, puede asimismo derivarse una matriz que relaciona la renta con la demanda final exógena, que Miyazawa denominó matriz de multiplicadores de formación de renta. Ejemplos de utilización de esta matriz pueden consultarse en Henry y Martin (1984), Rose y Beaumont (1988) y Fuentes (2009).
Una formulación alternativa simplificada, si no se dispone de la información relativa al nivel de consumo, renta y valor añadido según tramos de niveles de renta de los hogares, sería suponer que el consumo realizado de los bienes y servicios producidos por un sector es una proporción constante del VAB total (Ricardo, 2005), obteniendo:
donde ki es una constante que indica la proporción del VAB que se dedica al consumo de bienes y servicios producidos por el sector i-ésimo y l´ es un vector cuyo elemento i-ésimo indica para cada sector la proporción que representa el VAB sobre la producción total Xi, de manera que el producto l´X es el VAB agregado.
Por tanto, en notación matricial, sería:
donde la matriz de Leontief de Tipo III se calcula ahora como (I - Ar- K)-1.
Así, endogeneizar el consumo bajo el esquema de este tipo de modelos implica derivar los nuevos niveles de producción:
siendo D = C V A o D = K, respectivamente.
En Muñoz (1997), con el objetivo de analizar el impacto que provocaría en la economía de la provincia de León la desaparición o reducción del sector minero (Modelo MICAL [MInería del CArbón en León]), se propone un modelo en donde el consumo de los hogares se endogeiniza a partir de la elasticidad renta-consumo. Este modelo inicial, ha sido posteriormente adaptado a la evaluación del gasto sanitario en España (Santos et al., 1999), al estudio del efecto de la liberalización de la telefonía en España (Muñoz et al., 2000), a la simulación del impacto del gasto turístico en diversas comunidades autónomas (Canarias, Baleares, Murcia, Andalucía, Cataluña, Valencia y Madrid), a la simulación de los efectos macroeconómicos de los presupuestos del Gobierno de Baleares, a valorar el impacto de la inmigración en diferentes comunidades autónomas (Cortiñas et al., 2007; Vicente, 2010), y a evaluar los efectos directos, indirectos e inducidos del paro juvenil sobre la economía española (Vicente y Muñoz, 2012). La polivalencia demostrada por este modelo y la validez de los resultados obtenidos, hacen de él una herramienta que se adapta a los objetivos que se persiguen en este trabajo.
Estos modelos presuponen que el consumo es exclusivamente realizado por los hogares a través de las rentas del trabajo que obtienen, sin considerar las remuneraciones ajenas al trabajo (pensiones y prestaciones), que también obtienen los hogares. De cara a superar este inconveniente, se han desarrollado otros trabajos, donde cabe citar a Batey (1985), y Batey y Rose (1990), los cuales desagregan al sector de los hogares en: empleados, subempleados y desempleados e inactivos, considerando modelos de Tipo III.
A pesar de esta limitación, hay que tener presente que el objeto del análisis es ver la contribución del sector TIC a la generación de empleo y PIB, por lo que los efectos de la producción de bienes y servicios TIC entendemos deben de contemplarse a través de las rentas asociadas a la producción y no a la distribución de rentas, como es el caso del sistema de pensiones y prestaciones. No obstante al igual que se endogeiniza el consumo asociado a los trabajadores que directa o indirectamente contribuyen a la producción de bienes y servicios TIC (en este caso teniendo en cuenta estimaciones de elasticidades consumo-renta), cabe introducir también el ahorro y su distribución en el flujo circular, derivando funciones de impacto inducido asociadas a la producción de bienes de capital mediante un proceso iterativo.
3. Efecto inducido producción¿consumo y efecto inducido producción¿inversión
Dado que la CS-TIC elaborada por Vicente y Zofío (2012) solo permite la obtención de la tabla simétrica total, se parte de la siguiente hipótesis de trabajo para realizar la simulación:
Es decir, se supone un comportamiento similar en el consumo intermedio y final en las preferencias sobre productos interiores e importados. Esta hipótesis, como es lógico, no invalida el desarrollo teórico que exponemos a continuación y, cabe esperar que no afecte en gran medida a los resultados obtenidos en la simulación. Bajo esta hipótesis, vamos a considerar la matriz diagonal formada por los siguientes elementos:
estimando DIr, DFr y Ar del siguiente modo:
Los impactos o efectos macroeconómicos totales (ET) a que da lugar un aumento de la demanda final de un sector (ya sea motivado por un shock de consumo de los hogares, la instalación de un nuevo complejo industrial o el aumento de la demanda externa) en el conjunto de la economía, se pueden dividir en tres tipos:
— Un efecto directo (ED) provocado por el aumento de la demanda final del sector, el cual provoca un aumento de la producción de las ramas de actividad que lo componen con objeto de satisfacer la nueva demanda.
— Unos efectos indirectos (EI) en el resto de ramas de actividad que suministran inputs a las ramas que forman el sector, las cuales, ante el aumento de demanda, realizarán mayores pedidos a sus proveedores para poder aumentar su producción.
— Unos efectos inducidos producidos a causa del aumento de demanda de inputs que realizan las ramas afectadas por los efectos indirectos, que se transmiten al conjunto de sectores de la economía, y del correspondiente consumo e inversión generada.
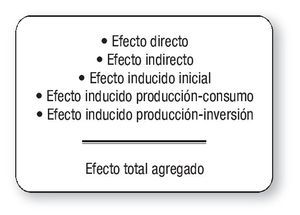
Finalmente, los efectos inducidos pueden a su vez dividirse en tres tipos:
— Efecto inducido inicial (EII).
— Efecto inducido producción-consumo (EIPC).
— Efecto inducido producción-inversión (EIPI).
Por lo tanto, el impacto macroeconómico final será igual a:
El efecto inducido inicial se deriva directamente de la aplicación de la inversa de Leontief, recogiendo la producción inducida en el conjunto de la economía necesaria para abastecer a las ramas que a su vez proveen a aquellas que producen los nuevos productos demandados.
Derivado de esta nueva producción (indirecta e inducida), se generará a su vez un incremento de las rentas salariales y de los excedentes empresariales. En función de los supuestos de consumo, como variable dependiente de la renta, y de inversión, como variable dependiente del ahorro y los excedentes empresariales, se producirán aumentos del consumo y de la inversión, lo que da como resultado nuevos aumentos de demanda final. Estos efectos son los que hemos denominado efecto inducido producción-consumo y efecto inducido producción-inversión.
Matemáticamente, estos efectos se obtienen de la siguiente manera.
El aumento de la demanda final del sector i tiene como efecto directo inmediato el aumento de la producción sectorial para satisfacerla. Es decir:
Dichos efectos se reparten proporcionalmente a cada rama del sector en función de los consumos intermedios del mismo.
El segundo de los efectos (efecto indirecto) se deduce de los coeficientes técnicos de producción, los cuales nos miden el consumo de mercancía necesaria del sector i para obtener una unidad del sector j. En notación matricial:
Dado que el efecto total inicial (ETI) viene determinado por la resolución del siguiente modelo matricial (modelo de Leontief):
podemos obtener el efecto inducido inicial (EII) como la diferencia entre el efecto total inicial y los efectos directo e indirecto:
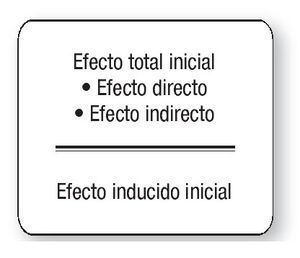
según lo ilustrado en la figura 2.
Figura 2 Cálculo del Efecto Inducido Inicial.
Por último, los efectos inducidos producción-consumo y producción-inversión se obtienen a partir del siguiente proceso iterativo:
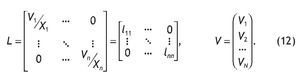
• El efecto indirecto e inducido inicial producirán un aumento de renta salarial (ΔSyS), que se calcula de la siguiente manera:
siendo L1 la matriz diagonal formada por los ratios de salarios sobre producción en cada rama.
• Análogamente, se producirá un aumento de los excedentes empresariales (ΔEBE):
donde L2 denota en este caso a la matriz diagonal con los ratios de excedente bruto de explotación sobre producción.
• La renta disponible para el consumo de los hogares (ΔR), derivada de los efectos directo e inducido, se calcula ahora como:
donde t1 representa el tipo impositivo aplicado en el IRPF, t2 la tasa de cotizaciones sociales a la Seguridad Social y, por último, t3 el porcentaje de rentas distribuidas de las sociedades, en forma de dividendos, a los hogares. Los valores considerados para t1 y t2 son de 18% y 6,35% respectivamente, mientras que t3 se ha obtenido a partir de la tasa registrada en las Cuentas del total de la economía y de los sectores institucionales de la Contabilidad Nacional de España, que para 2007 toma un valor de 11,1%.
• Dicho aumento de las rentas disponibles se traduce en un aumento del consumo final de los hogares (ΔCP) igual a:
siendo th el vector que representa para cada producto el porcentaje del precio básico sobre el precio de adquisición4 y kh las elasticidades consumo-renta5. En este caso, las elasticidades de consumo-renta se han ajustado a las generalmente aceptadas de acuerdo con las estimaciones de otros autores, realizadas con series temporales. En el caso de España, las estimaciones dan una propensión marginal al consumo de 0,8.
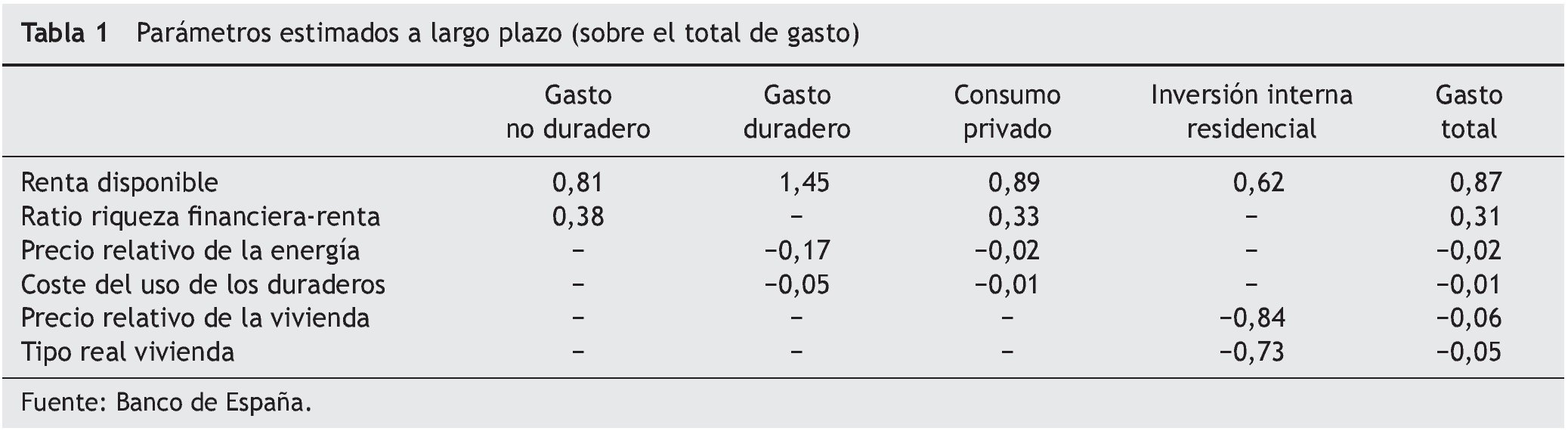
Como una primera referencia se dispone de las estimadas para la economía nacional en los modelos MOISEES (Andrés et al., 1990, 1991) y HERMIN (Herce y Sosvilla-Rivero, 1994, 1995). También referido al caso español el trabajo de Raymond y Uriel (1987) discute ampliamente diversas estimaciones de funciones de consumo. Estrada y Buisán (1999) realizaron uno de los estudios más detallados de las decisiones de gasto de las familias españolas a nivel agregado. Según estos autores, el consumo privado se ve afectado positivamente en el largo plazo por la renta disponible y por la ratio riqueza financiera¿renta; en cambio, el coste de uso de los bienes duraderos (es decir, el tipo de interés real) y el precio relativo de la energía influyen negativamente.
La elasticidad estimada respecto a la renta disponible es, aproximadamente, 0,89, ligeramente inferior a la obtenida por Andrés et al. (1991); la semielasticidad respecto a la ratio riqueza financiera¿renta (0,33) es también comparable con la obtenida en dicho trabajo y aparecen dos factores adicionales: el coste de uso de los bienes duraderos, con una elasticidad de -0,01, y el precio relativo de la energía, cuya elasticidad se evalúa en torno a -0,02 (tabla 1).
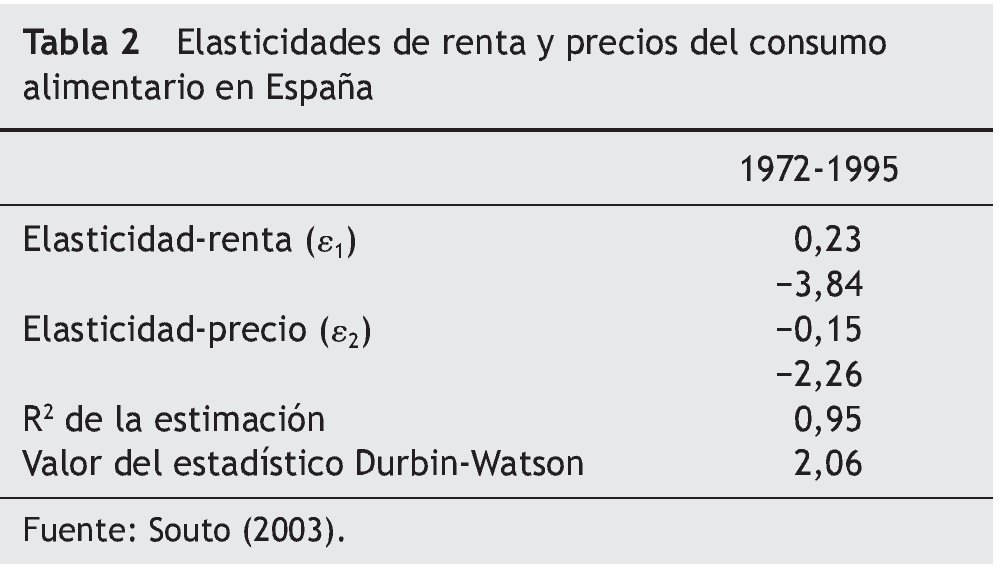
En relación con el consumo alimentario no son muchas las referencias bibliográficas que incluyan cálculos econométricos de dicha elasticidad, destacar si cabe la estimación de la función de demanda de los alimentos que realizó Souto (2003),
donde el gasto en alimentación depende de una constante (a), de la renta disponible (R) y de los precios relativos de los alimentos con respecto al resto de bienes (PA/PR).
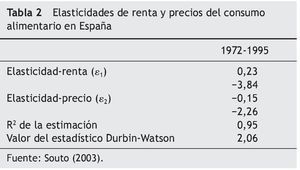
Los resultados obtenidos se muestran en la tabla 2, donde se establecen las elasticidades renta y precios del consumo alimentario en España que se muestra a continuación.
Por otro lado, se han incluido las estimaciones de las elasticidades de demanda precio y de demanda renta de los servicios de comunicación utilizados en Alvarez et al. (2000); dicho calculo era de 1,32 para incrementos unitarios de la renta disponible.
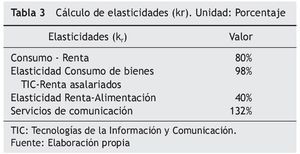
Finalmente, las elasticidades (kr) consideradas son las que se muestran en la tabla 3:
• El ahorro total generado (Sj ΔAj), atendiendo a los cálculos efectuados, se estima del siguiente modo:
siendo ahora t4 el tipo impositivo medio en el impuesto sobre sociedades, considerando para la simulación un valor del 20%. Suponiendo que este ahorro se invierte íntegramente, la nueva inversión generada (ΔK) por los efectos EI y EII es igual a:
donde K es un vector de reparto, cuyo elemento i-ésimo indica la proporción de la formación bruta de capital fijo para cada producto registrado en la tabla.
• En consecuencia, los efectos EI y EII generan un aumento en la demanda final (ΔDF´) equivalente a:
Los efectos inducidos producción-consumo (EIPC´) y producción-inversión (EIPI´) serán, por tanto:
generándose unos nuevos efectos directos, indirectos e inducidos, lo cual nos llevará a un nuevo cálculo de ΔSyS y ΔEBE:
y, por tanto:
• Iterando el proceso hasta un punto en el cual los aumentos de demanda final dejan de ser significativos, es decir,ΔDF ´r @ 0, o equivalentemente EIPC´ @ 0 y EIPI´ @ 0, obtenemos los efectos EIPC y EIPI como la suma de los sucesivos aumentos de demanda final interior provocados por el aumento del consumo y la inversión.
siendo los efectos inducidos sobre la renta disponible de los hogares (RBDH_I), el consumo (CPR_I), y la inversión INV_I:
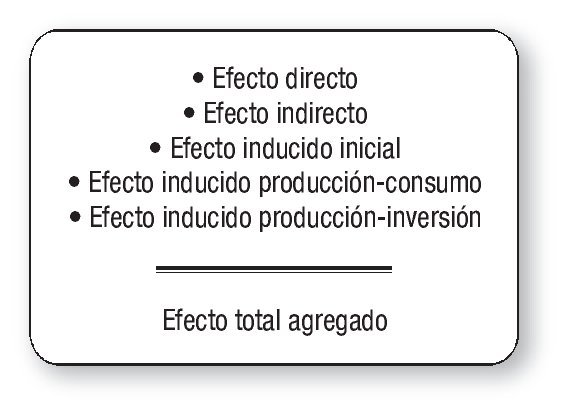
Finalmente, el efecto total agregado del aumento de demanda final inicial se obtiene a partir de la expresión que se muestra en la figura 3.
Figura 3 Cálculo del Efecto Total Agregado.
Bajo este esquema, determinados los niveles de las producciones y de los valores añadidos, se deducen los nuevos niveles de la renta disponible de los hogares, compatibles con el nuevo volumen de sueldos y salarios, y de excedentes empresariales. Estas son las variables que van a integrar el nivel de demanda final, puesto que de ellas dependen el nivel del consumo e inversión.
Tanto el bloque de producción, como el de renta de los hogares e inversión, se resuelven simultáneamente hasta encontrar una solución estable. En este proceso se requiere repartir el total del consumo y la inversión estimada entre los diversos productos procedentes de las ramas de la TIO.
Así, por ejemplo, una hipotética variación, al alza o a la baja, de las rentas de los trabajadores se transmitirá inmediatamente (en función de las propensiones consideradas) al consumo. De acuerdo con la teoría permanente del consumo, ante un cambio en el nivel de las rentas familiares los consumidores tratarán de mantener el nivel de ahorro, siendo el consumo la variable de ajuste. El modelo asume que el resto de las variables que determinan rentas y consumo permanecen inalteradas, por lo que ni el efecto riqueza, ni los tipos de interés, ni los precios relativos juegan papel alguno en la simulación.
Como es sabido, las relaciones entre consumo y renta disponible se establecen en términos reales. Sin embargo, ante la desaparición de las referencias temporales, se asume que el año de las simulaciones (2007) es la fecha base de referencia en precios y cantidades, con lo que los primeros son iguales a la unidad. Mientras en la simulación no intervengan variables nominales, en tanto que las alteraciones de los valores añadidos y de la remuneración de asalariados se deban a efectos reales de la demanda, no hay modificaciones en los índices de precios. Por todo ello, se considera que las variaciones en todas las variables se producen en términos reales, incluso en el caso de la renta disponible de los hogares.
4. Simulación de los efectos de un incremento de la demanda de los bienes y servicios de Tecnologías de la Información y Comunicación
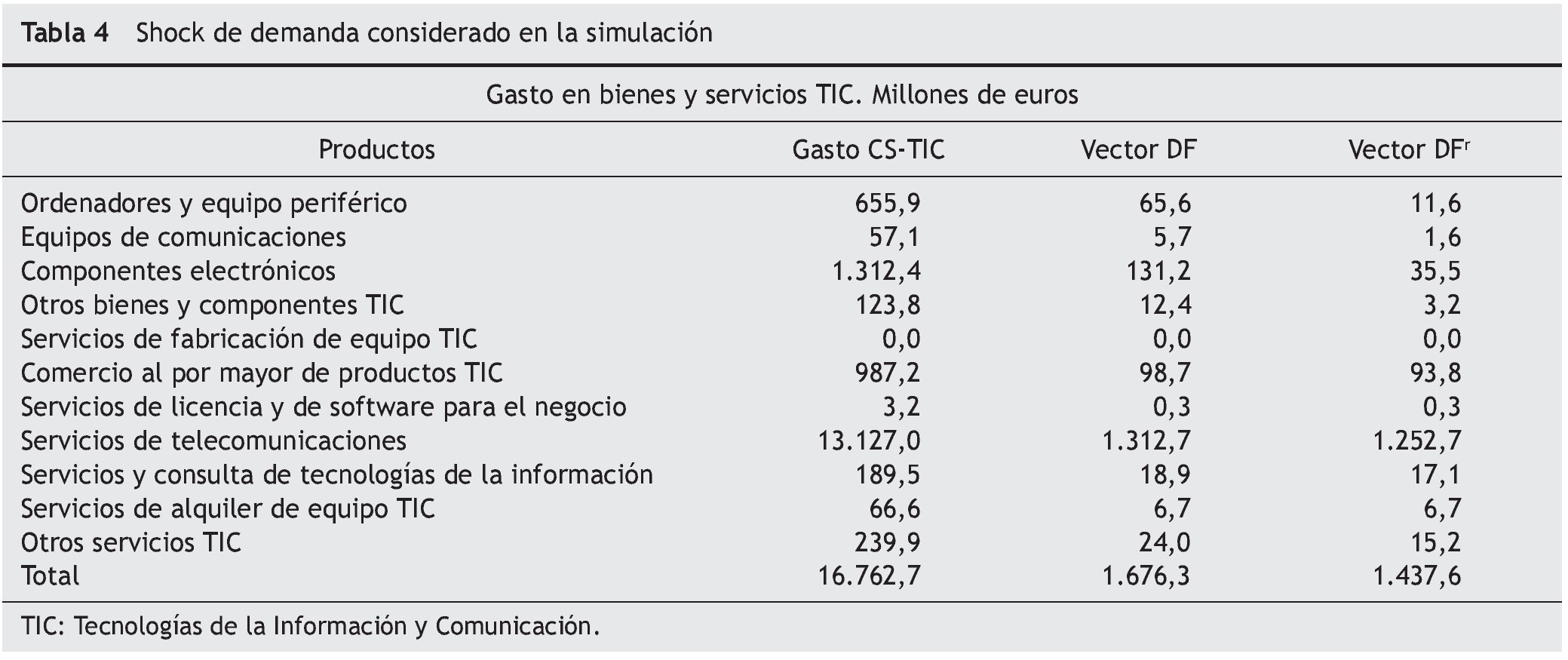
Según la CS-TIC, el consumo privado en bienes y servicios TIC en 2007 asciende a 16.763 millones de euros. Considerando un shock equivalente al 10% y la misma distribución por productos, la variable exógena DFr sería entonces la mostrada en la tabla 4.
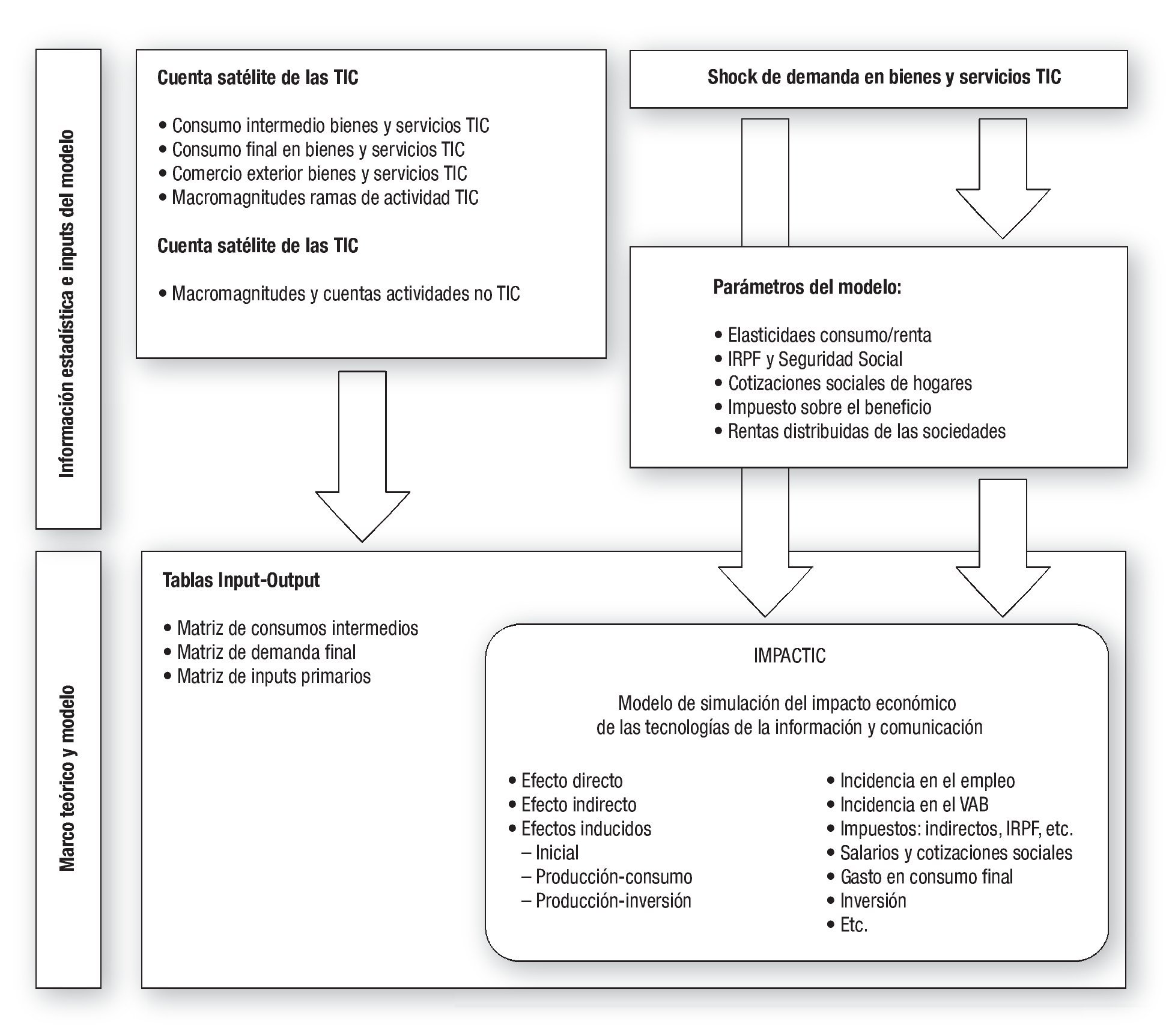
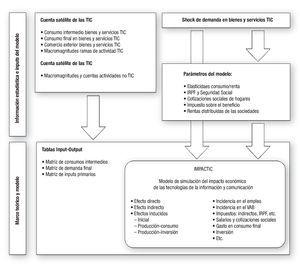
La simulación proporciona las estimaciones de los efectos derivados del nuevo volumen de producción sobre las macromagnitudes de la Contabilidad Nacional (consumos intermedios, valor añadido a precios básicos, otros impuestos netos sobre la producción, excedente bruto de explotación, empleo, consumo de hogares, inversión y renta) y las variaciones en los niveles de cotizaciones sociales e impuestos, que se deducen de sus tipos efectivos medios y de las alteraciones de sus bases imponibles estimadas con el modelo (fig. 4).
Figura 4 Síntesis del modelo.
Los resultados relativos a la demanda final se ofrecen según productos de la tabla, mientras que los que hacen referencia a macromagnitudes por el lado de la oferta (producción, consumos intermedios, valor añadido, salarios, excedente bruto de explotación, otros impuestos netos sobre la producción y empleo) según las ramas de actividad definidas en la CS¿TIC (11 ramas de actividad y 14 agrupaciones de productos).
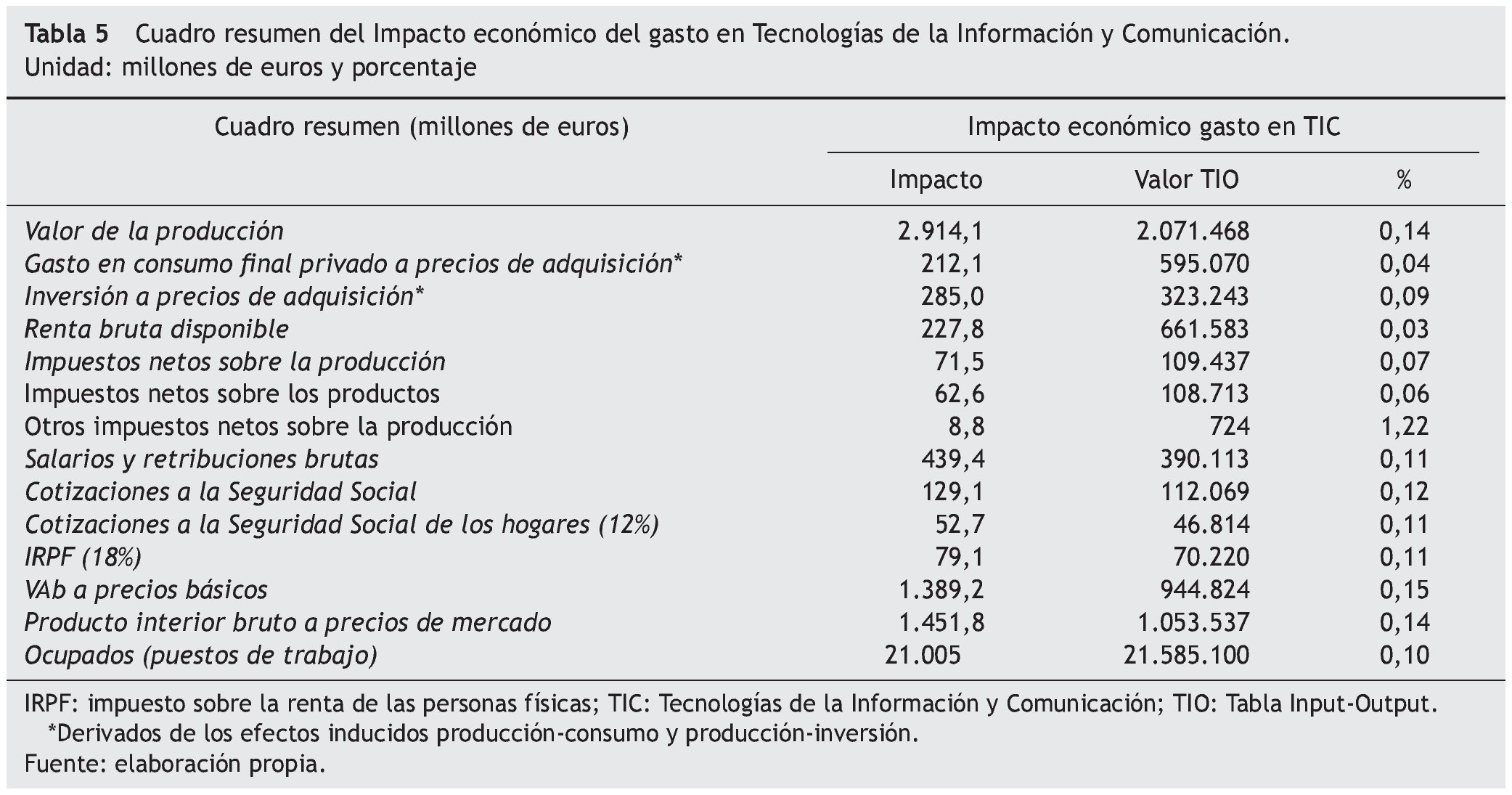
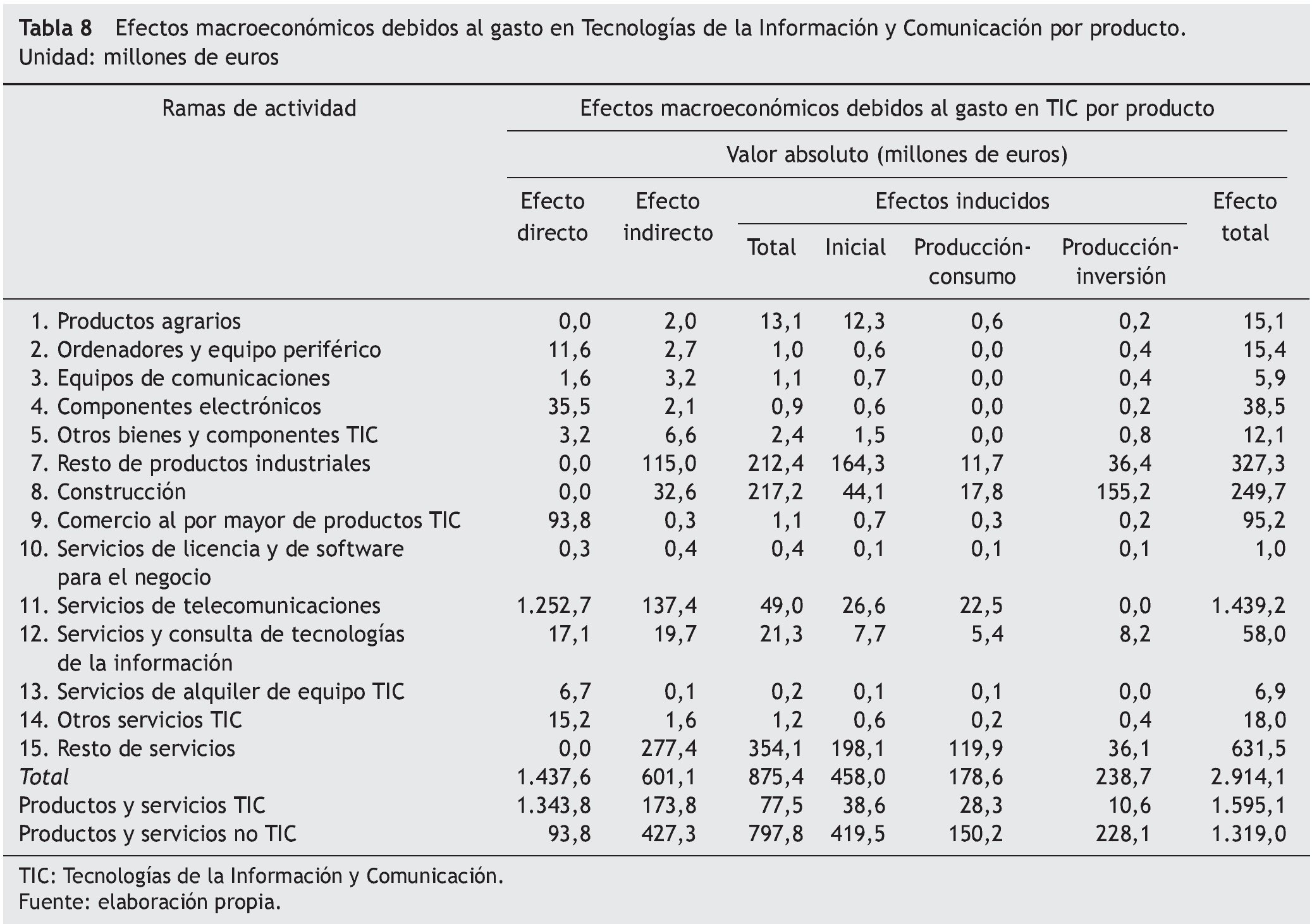
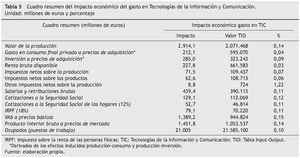
Los resultados recogidos en la tabla 5, muestran que partiendo de un aumento del gasto privado de 1.676,3 millones de euros, al ser en parte satisfecho a través de productos y/o servicios importados, 238,7 millones de euros, se le supone un aumento de la demanda interior de 1.437,6 millones de €; el modelo asocia un aumento del valor de producción a precios básicos de 2.914,1 millones de euros, es decir, un 73,8% superior. El P.I.B. vinculado a esta producción final asciende a 1.451,8 millones de euros y el empleo a 21.005 ocupados.
El gasto en consumo final de los hogares y la inversión inducida por los sucesivos aumentos de demanda final se estiman en 212,1 y 285,0 millones de euros respectivamente. El impacto sobre los impuestos netos sobre la producción es de 71,5 millones de euros, y sobre las cotizaciones sociales de 181,9.
El volumen de los nuevos puestos de trabajo directos, indirectos e inducidos, generan un valor añadido bruto a precios básicos de 1.389,2 millones de euros, percibiendo salarios por valor de 439,4.
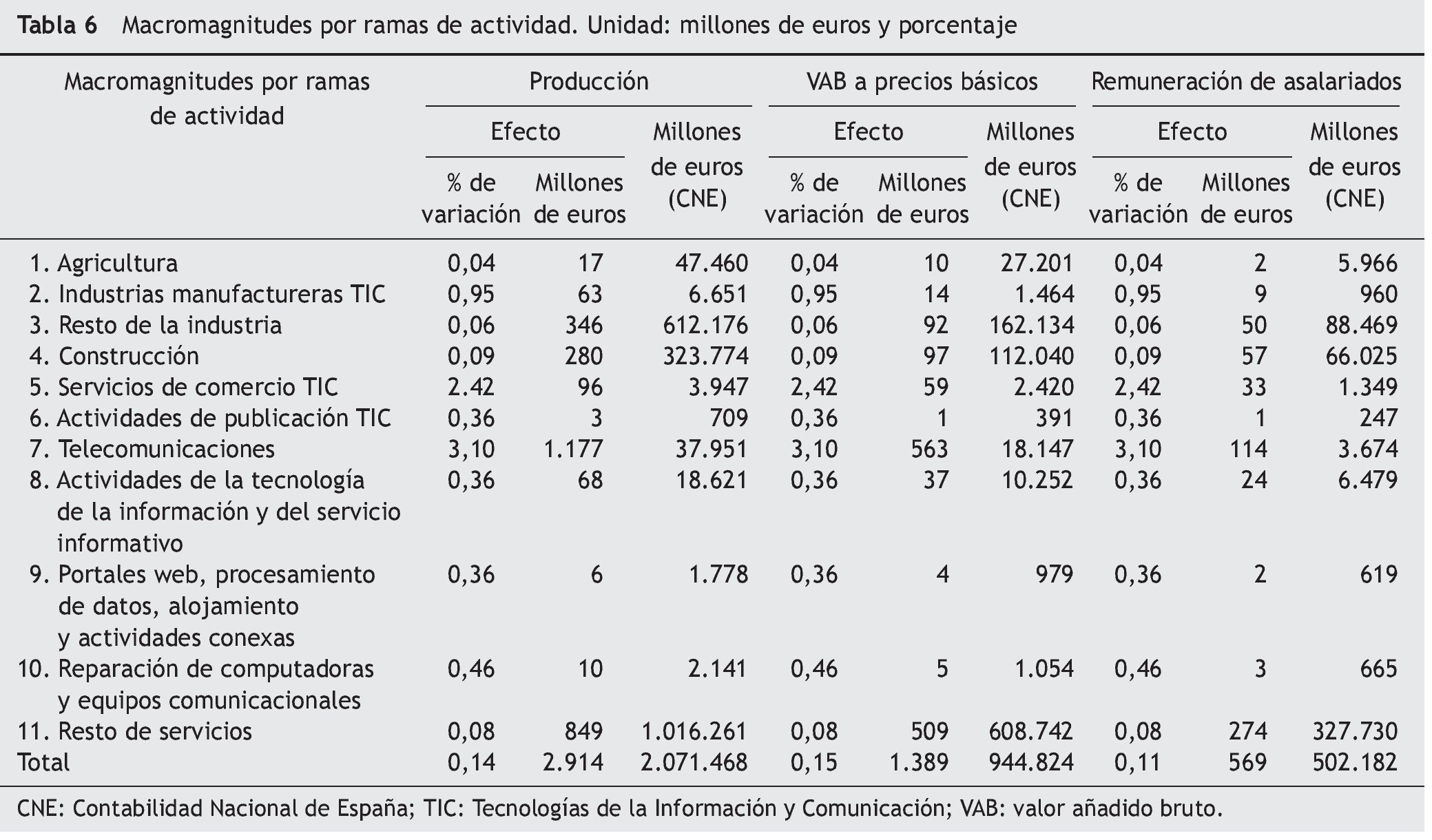
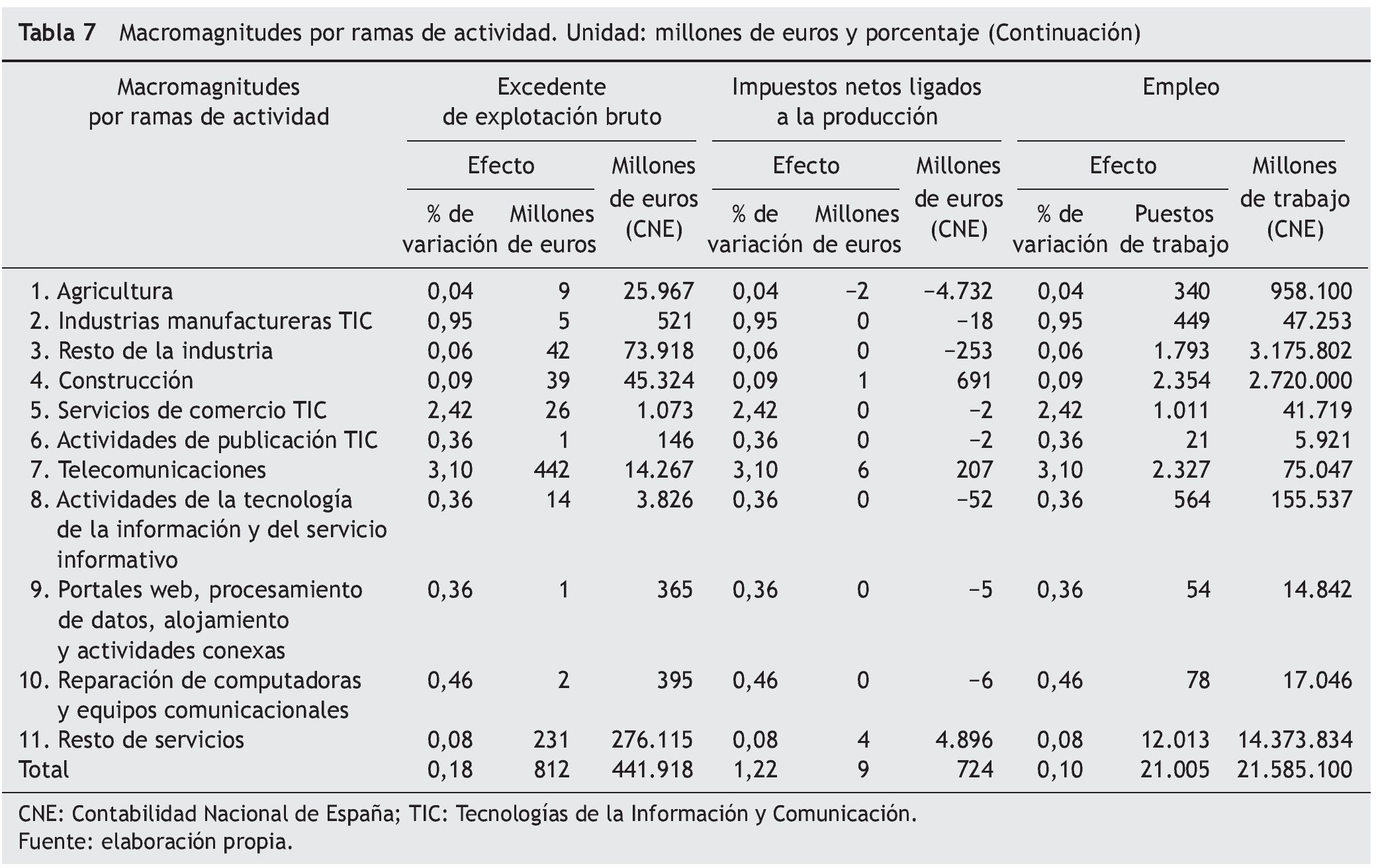
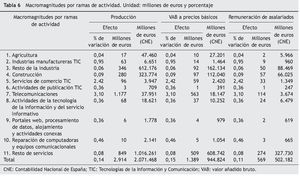
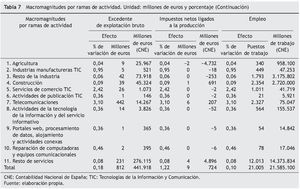
Por ramas de actividad, las tablas 6 y 7 muestran que la que recibe el mayor impacto es la de los servicios de telecomunicaciones, que con 562,7 millones de euros aporta un 40,5% al nuevo valor añadido bruto. Este resultado se deriva del hecho de que esta rama de actividad es la que genera la mayor parte del consumo privado en bienes y servicios TIC, el 78,3% del total de gasto según la CS-TIC.
Destaca también la rama correspondiente al resto de los servicios, que recibe un 36,6% del impacto, con 508,8 millones de euros, debido a las fuertes interrelaciones existentes entre las ramas de actividad TIC con las correspondientes al resto del sector servicios.
En general, las actividades donde se observa el mayor impacto son las telecomunicaciones, el resto de los servicios, el resto de la industria, los servicios de comercio de productos TIC y la construcción, esta última por el impacto recibido a partir del efecto producción-inversión.
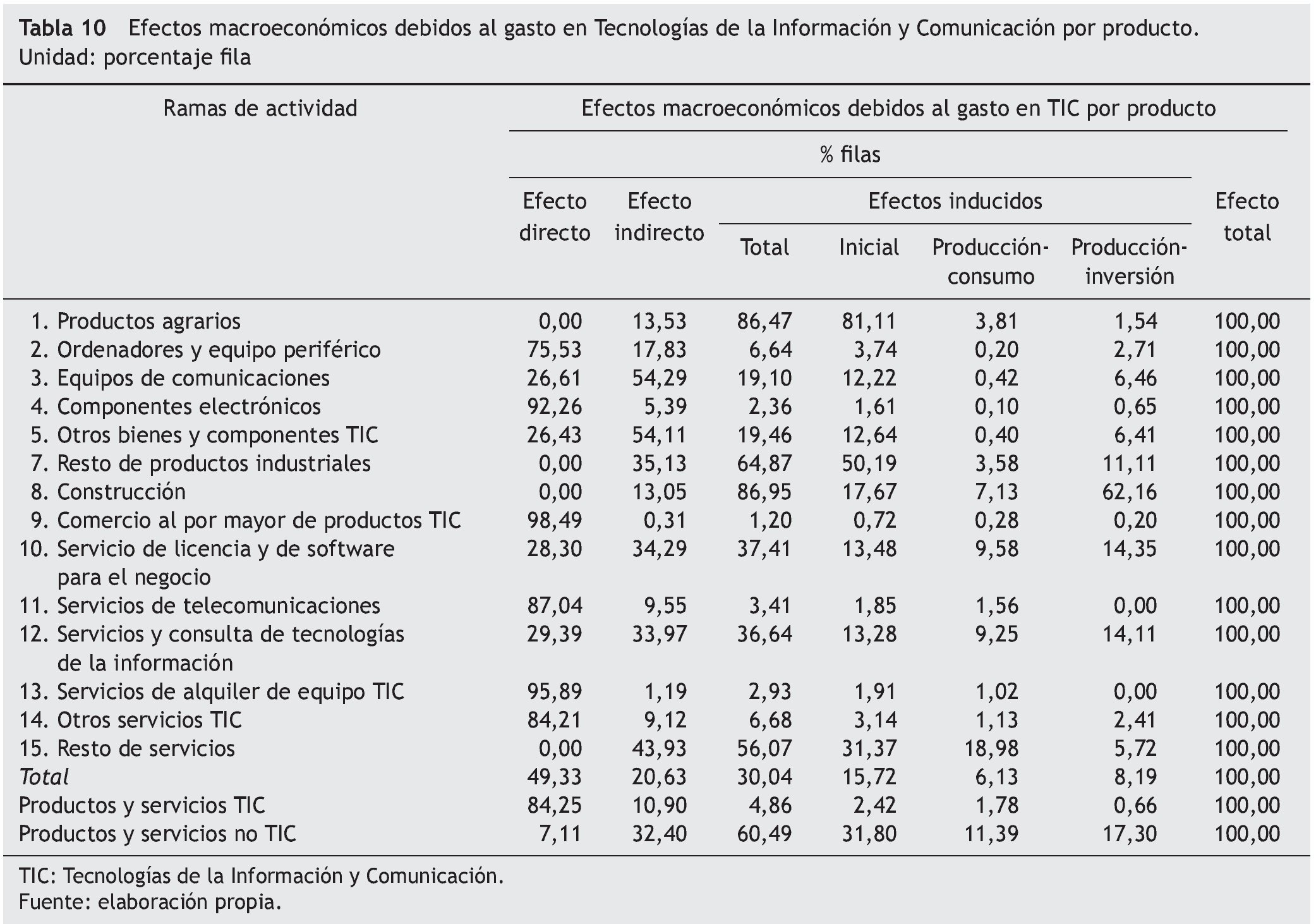
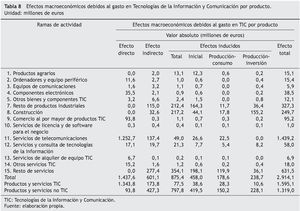
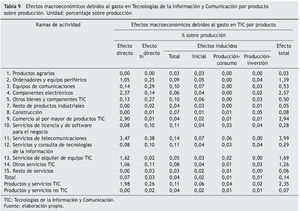
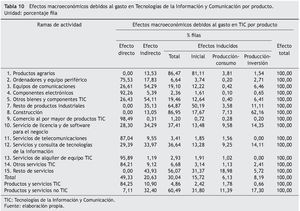
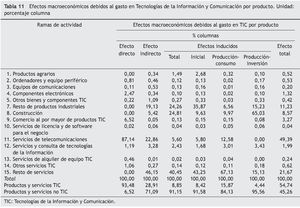
Las tablas 8 a 11 muestran los efectos directos, directos e inducidos, tanto en valor, como en porcentaje de la producción y su distribución porcentual por filas y columnas. Como ya se ha señalado, el efecto directo, o producción a generar por la economía debido al aumento de la demanda final interior, genera en primera instancia un efecto indirecto que se evalúa como el volumen de consumo intermedio doméstico que las ramas de actividad que producen los productos demandados (ramas de actividad TIC en nuestro caso) necesitan para producir. El volumen de producción indirecta se estima en 601,1 millones de euros, lo que supone el 20,6% del total del impacto generado (véanse las tablas 8 y 10, respectivamente).
La demanda de la producción necesaria para satisfacer los consumos intermedios de las empresas que a su vez suministran los productos intermedios a las ramas de actividad TIC, es la que origina los denominados efectos inducidos iniciales. El volumen de nueva producción debida e este tipo de efectos supone, con 458,0 millones de euros, el 15,7% del efecto total (véanse, de nuevo, las tablas 8 y 10, respectivamente).
Por ultimo, la generación de la nueva producción indirecta e inducida lleva consigo un incremento de las rentas salariales y no salariales que, de acuerdo a los supuestos considerados en nuestro modelo, generarán nuevos efectos debido al incremento esperado de los bienes y servicios de consumo e inversión. El incremento de la producción generada debido al aumento del consumo de los hogares, o efecto producción-consumo, se cifra en 178,6 millones de euros, lo que supone el 6,1%, mientras que el efecto de la producción-inversión representa el 8,2%, con 238,7 millones (véanse, una vez más, las tablas 8 y 10, respectivamente).
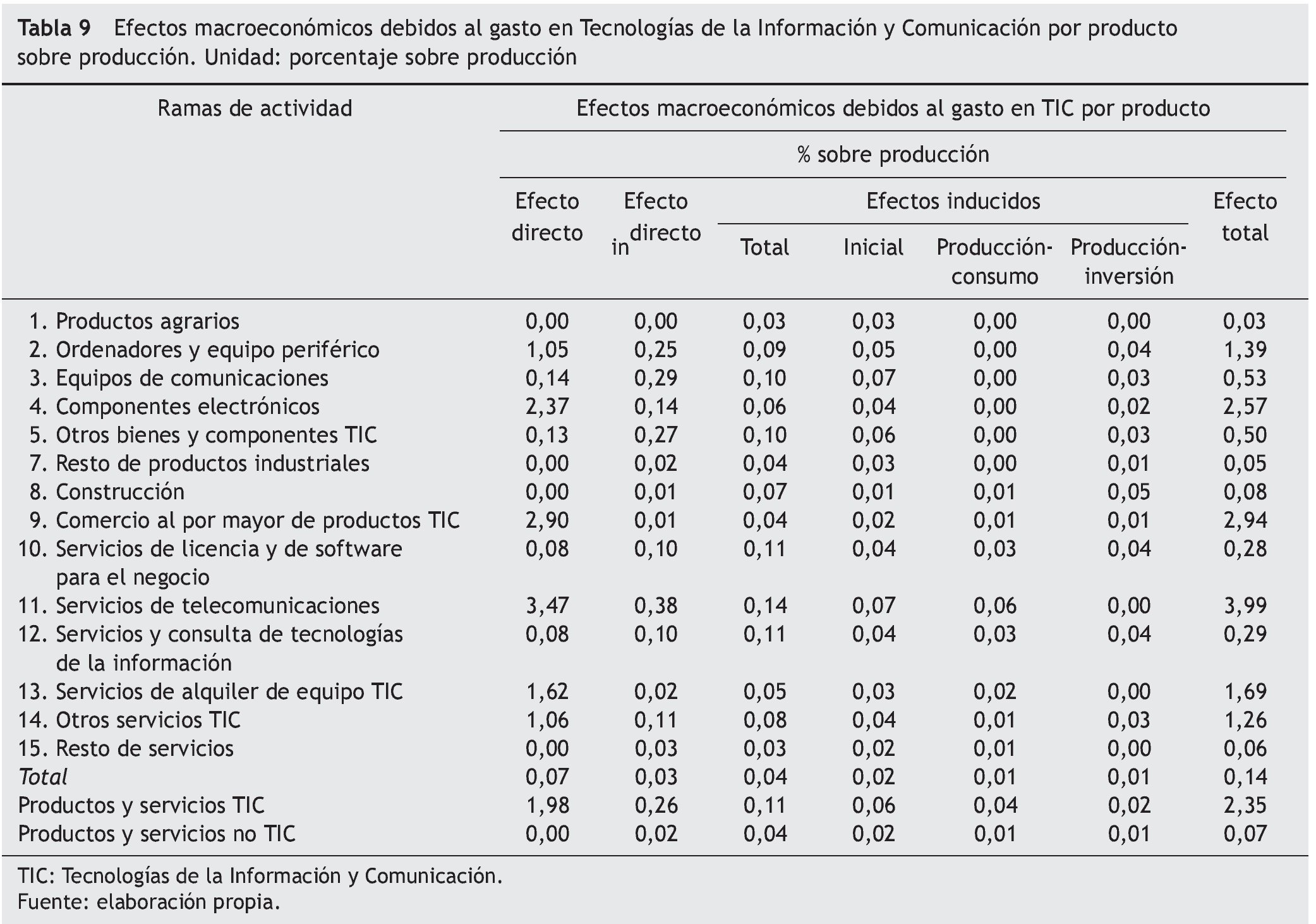
Las actividades donde se producen los mayores impactos relativos son las telecomunicaciones, con un incremento de su producción del 3,99%, el comercio al por mayor de productos TIC, con un 2,94%, y las actividades de fabricación de componentes electrónicos, con un 2,57%, donde la media global es del 0,14% (tabla 9).
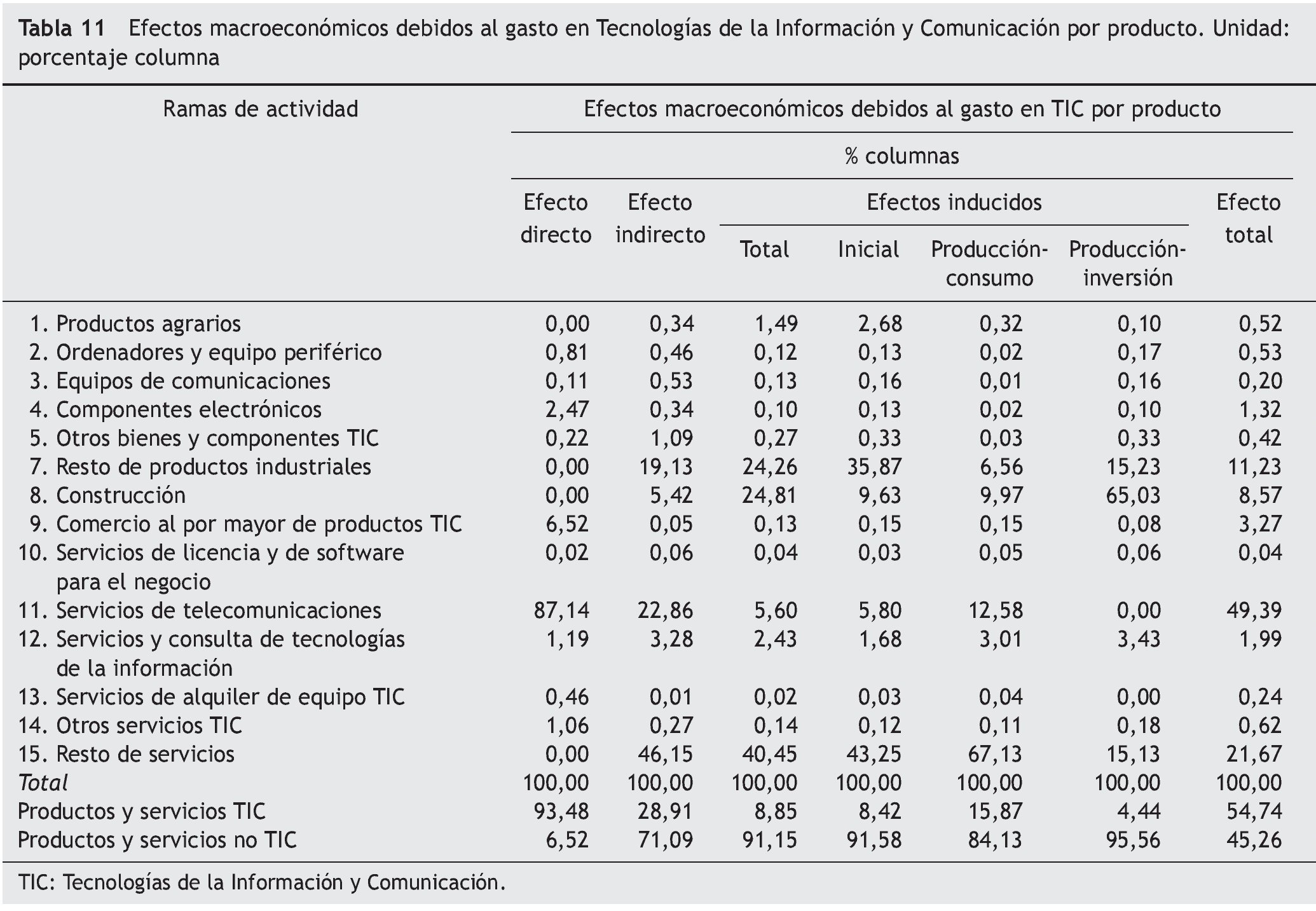
La rama de actividad que recibe la mayor parte de los efectos indirectos es la del resto de servicios, con un 46,2% del total de producción indirecta. También destacan las actividades de telecomunicaciones, el resto de la industria y la construcción, con participaciones del 22,9%, 19,1% y 5,4% respectivamente (tabla 11).
Como es lógico, el efecto inducido se concentra en las actividades no TIC, que absorben el 91,1% del total. Señalar que la construcción acumula el 65,0% del efecto producción-inversión, mientras que el impacto generado por el efecto-producción-consumo está más repartido entre todas las actividades (de nuevo mostrados en la tabla 11).
Respecto al impacto total, las principales actividades, que concentran el 90,9%, son las telecomunicaciones, 49,4%, el resto de los servicios, 21,7%, el resto del sector industrial, 11,2%, y la construcción, con un 8,6% (una vez más en la tabla 11).
Como complemento al análisis realizado, se presupone ahora que todo el shock de demanda va a ser satisfecho por nueva producción nacional, es decir:
Adicionalmente, también puede suponerse que la demanda inducida de bienes y servicios TIC también será satisfecha por producción interior:
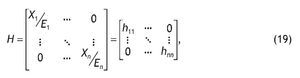
Estas suposiciones equivalen simplemente a modificar la matriz H introducida previamente en (19), de la siguiente manera:
siendo
Recuérdese que al no disponer la CS-TIC de Ar, se ha procedido en nuestro modelo a estimarla a partir de la expresión (20); es decir, Ar = H A. Podemos suponer, asimismo, que los consumos intermedios inducidos de actividades TIC son satisfechos por producción nacional, estimando una nueva matriz Ar:
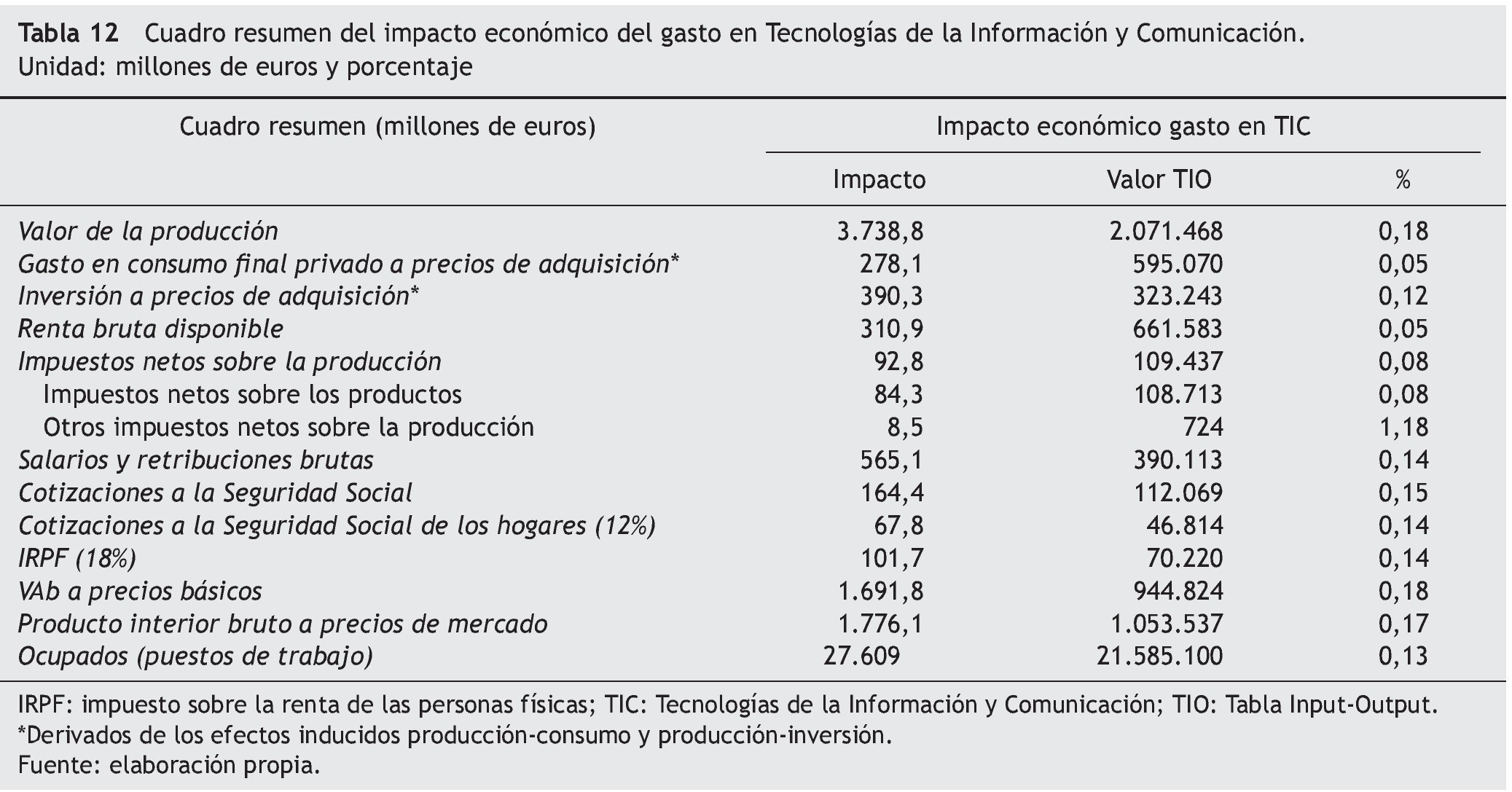
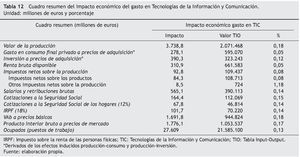
Bajos estos supuestos, los resultados quedan reflejados en la tabla 12, donde, como es posible observar, el PIB generado asciende ahora a 1.776,1 millones de euros. El incremento de producción, respecto al supuesto anterior sería del 28,3%, que sería el efecto cifrado de la sustitución de producción importada por nacional.
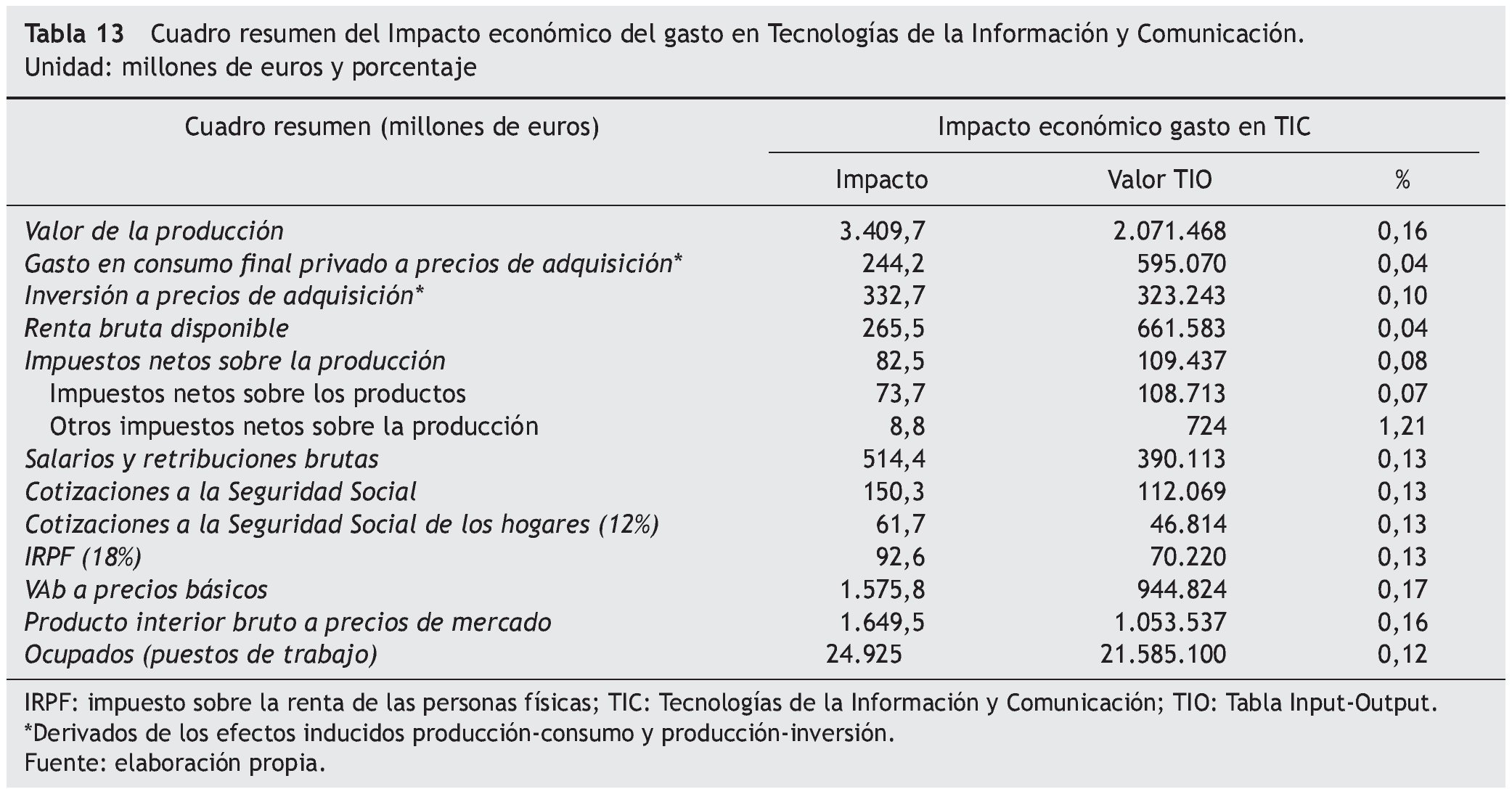
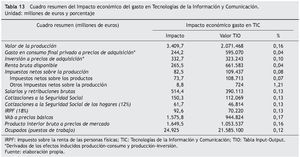
Por último, si solo suponemos que el shock de demanda es satisfecho por producción nacional, manteniendo la propensión a importar en los productos intermedios y la demanda final inducida, los resultados serían los reflejados en la tabla 13.
5. Conclusiones y futuras líneas de investigación
El modelo de simulación planteado estima los efectos macroeconómicos inducidos por un shock de demanda de consumo de hogares de un 10% sobre el total de consumo en bienes y servicios TIC, según la nueva CS-TIC de 2007, equivalente a 1.676,3 millones de euros.
Bajo el aumento de esta demanda, el P.I.B. generado se cifra en 1.451,8 millones de euros adicionales (un 0,14% sobre el total del P.I.B. de la economía), con 21.005 nuevos puestos de trabajos directos, indirectos e inducidos, percibiendo salarios por valor de 439,4 millones de euros. Asimismo, este aumento de demanda inducirá sucesivos incrementos en la demanda de bienes de consumo e inversión, estimados en 212,1 y 285,0 millones de euros respectivamente.
Las nuevas rentas inducidas, disponibles para el consumo y ahorro de los hogares, se estiman en 227,8 millones de euros, que generarían un incremento impositivo de 79,1 millones en IRPF, 71,5 millones en impuestos netos sobre la producción y 181,9 millones de euros en cotizaciones sociales.
Asumiendo que la nueva demanda sea satisfecha íntegramente por producción nacional, el PIB generado ascendería entonces a 1.776,1 millones de euros, es decir, las nuevas rentas generadas en el circuito económico serían un 6% superiores al propio shock de demanda, lo cual sitúa al sector de las TIC como un sector clave de cara al impulso de la actividad económica.
En lo que se refiere a la modelización planteada, esta puede considerarse como punto de partida para futuras líneas de investigación en esta materia. En este sentido, al considerar constantes los coeficientes técnicos, no se contempla la posibilidad de una mayor capitalización de las empresas que les permita generar más producción con el mismo nivel de empleo, es decir, no se evalúan los posibles incrementos de la capacidad productiva, así como tampoco se plantea el cambio en los niveles de precios ante alteraciones de la demanda, tanto intermedia como final.
1. Los valores de las operaciones correspondientes a las ramas homogéneas (formadas por unidades teóricas que solo producen un determinado tipo de producto) son diferentes de los que aparecen en la tabla de destino, aunque si coinciden los totales para todas las operaciones contables (producción, valor añadido, componentes de la demanda final, etc.).
2. Como puede deducirse de la notación utilizada, en una tabla simétrica el total del empleo interior coincide con la producción de las ramas de actividad.
3. La matriz (I-A′r)-1 se denomina matriz de Leontief Tipo II, siendo la matriz A′r una matriz de dimensión (n+1) · (n+1), donde la columna n+1 y la fila n+1 representan el consumo final interior y los salarios y compensaciones del sector hogares por unidad de producto, y el elemento (n+1, n+1), correspondiente a los reempleos, puede ser igualado a 0 dada su escasa magnitud. Entonces: X = = (I-A′r)-1DFr*, siendo DFr* la suma del consumo público interior, la formación bruta de capital interior y las exportaciones.
4. Los servicios de comercio de productos TIC se calculan aplicando los márgenes comerciales medios derivados en la CS-TIC.
5. No se excluye en este caso la posible utilización del procedimiento de Miyazawa (1976) o de Batey y Rose (1990) si se dispusiera de la información desagregada por productos y sectores asociada al nivel de consumo, renta y VAB para los grupos de hogares que definen.
6. En el caso de disponer de Ar, la operativa sería sustituir en las filas correspondientes a las actividades TIC el valor arij por el correspondiente a aij.
Recibido el 29 de mayo de 2012; aceptado el 14 de noviembre de 2012
* Autor para correspondencia.
Correo electrónico: javicente@cee.uned.es (J.A. Vicente Vírseda).
Bibliografía
Alvarez, N., Muñoz, A., Parra, F., 2000. A measurement of effects of telecommunications on income and employment by the input-output models applied to Spain. ITS Conference, July 2000, Buenos Aires.
Andrés, J., Molinas, C., Taguas, D., 1990. Una función de consumo privado para la economía española. Aplicación del análisis de cointegración. Cuadernos Económicos del ICE 44, 173-212.
Andrés, J., Molinas, C., Taguas, D., 1991. Una función de consumo privado para la economía española. En: Molinas, C., Zabalza, A. (Eds.), La economía española. Una perspectiva macroeconó-mica. Antoni Bosch, Barcelona.
Batey, P.W.J., 1985. Input-output models for regional demographic-economic analysis: Some structural comparisons. Environment and Planning A 17, 73-99.
Batey, P.W.J., Rose, A.Z., 1990. Extended input¿output models: Progress and potential. International Regional Science Review 13, 27-49.
Cortiñas, P., Parra, F., Vicente, J.A., Valdivia, A., 2007. Impact of migration on a regional economy. The case of the Balearic Islands, Spain. 16th International Input-Output Conference. Istambul.
Estrada, A., Buisán, A., 1999. El gasto de las familias en España. Estudios Económicos 65. Servicio de Estudios. Banco de España, Madrid.
Golladay, F., Haveman, R., 1976. Regional and distributional effects of a negative income tax. The American Economic Review 66, 629-641.
Fuentes, N.A., 2009. Encadenamientos intersectoriales de la industria maquiladora de exportación en California. Región y Sociedad XXI, 171-194.
Henry, M.S., Martin, T.L., 1984. Estimating income distribution effects on regional input-output multipliers. Journal of Regional Analysis and Policy 14, 33-45. Regional Science Perspectives 12.
Herce, J.A., Sosvilla-Rivero, S., 1994. The effects of the community support framework 1994-99 on the Spanish economy: An analysis based on the HERMIN model. Documento de Trabajo 94-10R, FEDEA.
Herce, J.A., Sosvilla-Rivero, S., 1995. HERMIN Spain. Economic Modeling 12, 295-311.
Leontief, W., 1936. Quantitative Input and output relations in the economic system of the United States. The Review of Economic Statistics 18, 105-125.
Leontief, W., 1966. Input¿output economics. Oxford University Press, New York.
Leontief, W. 1986. Input¿output economics. 2nd ed. Oxford University Press, New York.
Miller, R.E., Blair, P., 1985. Input-output analysis. Foundations and extensions. Prentice¿Hall, New Jersey.
Miyazawa, K., 1971. An analysis of the interdependence between service and goods-producing sectors. Hitotsubashi Journal of Economics 12, 10-21.
Miyazawa, K., 1976. Input-output analysis and the structure of income distribution. Springer Verlag, Berlin.
Muñoz, A. 1997. Estimación del impacto económico de la minería del carbón en la provincia de León. Acto de clausura del curso académico 1996-97. Facultad de Ciencias Económicas y Empresariales. Universidad de León, León.
Muñoz, A., Parra, F., Santos, J., 2001. Métodos de construcción de contabilidades nacionales y tablas input-output en España. Técnicas de análisis input-output. Cuadernos de la UNED, Universidad Nacional de Educación a Distancia, Madrid.
Paukert, F., Skolka, J., Malton, J., 1976. Redistribution of income patterns, consumption, and employment. En: Polenske, K., Skolka, J., (Eds.), Advances in input output analysis. Balinger, Cambridge.
Raymond, J.L., Uriel, E., 1987. Investigación econométrica aplicada: un caso de estudio. Editorial AC, Madrid.
Ricardo, A. 2005. Tópicos sobre el modelo de insumo-producto: teoría y aplicaciones. Serie: Estudios estadísticos y prospectivos. Naciones Unidas-CEPAL, Santiago de Chile.
Rose, A. 1977. Economic impact of geothermal energy development. Dry Lands Research Institute. University of California, Riverside, CA.
Rose, A., Beaumont, P., 1988. Interrelational income-distribution multipliers for the West Virginia economy. Journal of Regional Science 28, 461-476.
Santos, J., Cortiñas, P., Muñoz, A., 1999. La medición de la incidencia de la sanidad pública en la economía mediante el análisis input-output en efectos económicos del gasto público en sanidad. PriceWaterhouse, Madrid.
Souto, G. 2003. Tasas de descuento para la evaluación de inversiones públicas: estimaciones para España. P. T. N.º 8/03. Instituto de Estudios Fiscales, Madrid.
Vicente, J.A., 2010. Inmigrantes y Extranjeros en La Rioja. Año 2009 — Part 3: Estimación del impacto económico de la inmigración en La Rioja. Gobierno de La Rioja, Logroño.
Vicente, J.A., Muñoz, A., 2012. Estimación de los efectos directos, indirectos e inducidos del paro juvenil sobre la economía española mediante el empleo de la Contabilidad Nacional y de las tablas input-output. Revista Estudios de Juventud 94, 13-36 (monográfico: jóvenes y trabajo social).
Vicente, J.A., Zofío, J.L., 2012. Elaboración de una cuenta satélite de las TIC en España. Años 2005-2009. XXXIII Congreso Nacional de Estadística e Investigación Operativa, VII Jornadas de Estadística Pública, Madrid.