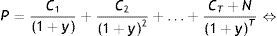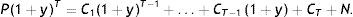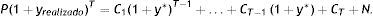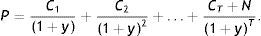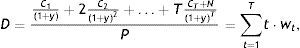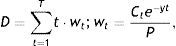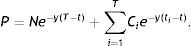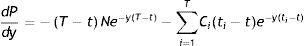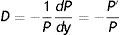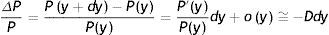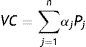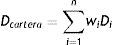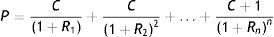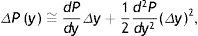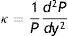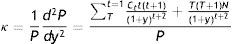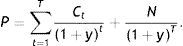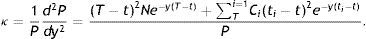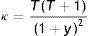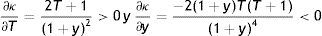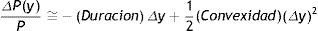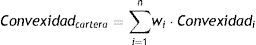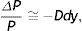La estructura temporal de los tipos de interés: estrategias de negociación en renta fija

Resumen

En este trabajo ofrecemos una visión general y actualizada sobre diferentes estrategias de negociación en activos de renta fija que hacen uso de la estructura temporal de tipos de interés (ETTI) en su implementación. Con dicho propósito, hemos comenzado analizando el riesgo de tipos de interés, para posteriormente resumir un conjunto de estrategias de gestión pasiva y activa sobre carteras de renta fija.

Abstract

The paper reviews the literature on how the term structure of interest rates (TSIR) can be used to implement passive and active fixed income portfolio strategies. This is done by defining the concept, explaining the risk of interest rates, and detailing several fixed income portfolio strategies.

1

Estructura temporal de los tipos de interés

La estructura temporal de tipos de interés (ETTI) o curva de tipos al contado (spot) se define como la relación funcional entre el tipo de interés nominal en los préstamos sin riesgo de la economía y el tiempo hasta su vencimiento (Pérez-Rodríguez et al., 2002). Los bonos cupón cero, emitidos al descuento, son los títulos de renta fija que mejor reflejan esta relación funcional, ya que garantizan un único pago, denominado valor facial o nominal, al vencimiento establecido en una fecha futura conocida. La forma funcional de la ETTI debería poseer, por sus importantes implicaciones para la teoría financiera, 2 características básicas: continuidad y suavidad. La suavidad garantiza la continuidad de la ETTI a plazo (forward implícito), lo cual es un requerimiento para la hipótesis de no arbitraje en el contexto financiero.

Los profesionales del mercado, los inversores, los bancos centrales y las autoridades monetarias están interesados en conocer la ETTI, ya que esta estructura muestra la información del consenso del mercado sobre la futura evolución de los tipos de interés, es decir, permite cuantificar lo que piensa el mercado sobre lo que sucederá en el futuro con los tipos de interés.

De forma sintética cabría señalar que los principales usos de la ETTI son los siguientes:

• •

  Establecer los rendimientos de todos los instrumentos del mercado de deuda.

• •

  Actuar como indicador de futuros niveles de tipos de interés e instrumento esencial de la política monetaria.

• •

  Valoración y comparación de rendimientos a lo largo del espectro de vencimientos.

• •

  Indicar el valor relativo de diferentes bonos de similar vencimiento.

• •

  Cobertura de riesgos y valoración de derivados sobre tipos de interés.

• •

  Estrategias de negociación para la gestión de carteras de renta fija.

La amplia aplicabilidad que presenta la ETTI conduce a que los diversos aspectos de su estimación pueden estar sujetos al uso que pretenda hacerse de ella. En este sentido, cabría señalar que cuando el uso fundamental de la ETTI sea la política gubernamental más que la valoración de instrumentos financieros, su estimación debería basarse en los siguientes criterios: el método de estimación debería tener como objetivo primordial ajustar los tipos forward implícitos y no los tipos spot, y la curva de tipos forward resultante debería ser tan suave como fuera posible porque el objetivo es proporcionar información sobre futuros niveles de los tipos de interés y las expectativas en la política monetaria del banco central.

El presente trabajo tiene como objetivo los inversores y gestores de carteras de renta fija, centrándose en las posibilidades que proporciona un conocimiento preciso de la ETTI de cara al desarrollo de estrategias de negociación empleadas en la gestión de carteras de renta fija. En este sentido, hemos realizado un análisis actualizado de diferentes estrategias de negociación de carteras de renta fija, donde la ETTI será un instrumento esencial para la implementación de dichas estrategias. Para entender las formas de estimación de la ETTI, recomendamos la lectura de Fabozzi (1993, 1997), Martellini et al. (2003), Yallup (2012) y Andrada-Félix et al. (2013a), entre otros.

Los profesionales del mercado utilizan desde hace mucho tiempo numerosas estrategias de renta fija, y de forma paralela se ha ido desarrollando una prolija literatura académica con el fin de buscar evidencia empírica a dichas estrategias de inversión. El trabajo seminal de donde arranca la posibilidad de construir estrategias de renta fija inmunizadas frente a los cambios en los tipos de interés hay que buscarlo en Macaulay (1938), quien introduce el concepto de duración, aunque asociado a la gestión de fondos de pensiones. En general, un fondo de pensiones se encuentra inmunizado con respecto a sus responsabilidades de pago si tiene suficiente liquidez para atender sus compromisos a pesar de los movimientos que se produzcan en los tipos de interés, y la forma de conseguir tal inmunización no era otra que conseguir que la duración de los pasivos del fondo igualase a la duración de sus activos.

En los años setenta Fisher y Weil (1971) criticaron la duración propuesta por Macaulay proponiendo un nuevo concepto de duración que tendría amplias repercusiones en el diseño de una cartera de renta fija inmune a los movimientos paralelos de la ETTI.

No obstante, la inmunización propuesta por Fisher y Weil solo protege una inversión de los posibles desplazamientos paralelos de la ETTI, por eso el diseño de estrategias de cobertura ante movimientos más complejos de la curva de tipos se puso muy pronto en el ojo de la literatura; en este sentido es digno de mención un remarcable estudio empírico sobre los tipos de desplazamiento que se producen en la ETTI realizado por Jones (1991), quien encuentra que los desplazamientos paralelos y los torcimientos de la ETTI son responsables del 91,6% de los rendimientos del Tesoro, el 3,4% de los rendimientos es atribuible a desplazamientos en mariposa y el resto a factores desconocidos. Tales resultados son consistentes con los ofrecidos por Litterman y Scheinkman (1991); por su parte, Mann y Ramanlal (1997) también encuentra evidencia relativa del buen comportamiento de diversas estrategias de renta fija. Una visión crítica acerca de la evidencia empírica del análisis de duración como forma de garantizar la inmunización de las carteras también se encuentra en Ilmanen (1996c).

Cuando se usa la duración de una cartera y su convexidad como medidas de su exposición al tipo de interés, se suponen desplazamientos paralelos de la curva de tipos de interés. Para caracterizar el riesgo de tipos de interés en caso de movimientos no paralelos se han diseñado medidas capaces de considerar la sensibilidad de la cartera ante los cambios producidos en el tipo spot para cada vencimiento de la curva de tipos de interés. Aparece así la idea de considerar una aproximación generalizada a la duración por medio de un vector de duraciones; en esta rama de la literatura destacan, entre otros, los trabajos de Chambers y Carleton (1988), Reitano (1990) y Ho (1992).

El éxito del uso de estrategias de renta fija más complejas que el simple análisis de duración se ha visto incrementado en la medida que se ha producido una mejora en el ajuste de la curva de tipos de interés. La modelización de la función de descuento a partir de los precios de los bonos y no de sus rentabilidades internas es una línea metodológica de calidad superior iniciada por McCulloch (1971,1975) empleando los splines cuadráticos y cúbicos. Con posterioridad se han desarrollado otros procedimientos de suavizado entre los que destaca el modelo de Nelson y Siegel (1987), extendido posteriormente por Svensson (1994, 1995); estos modelos proporcionan una parametrización concisa de la curva cupón cero y abren la puerta a formalizar estrategias de cobertura contra los riesgos de movimiento del nivel, la pendiente y la curvatura de la ETTI. En este sentido, Willner (1996) presenta nuevas herramientas de gestión de renta fija basadas en el uso del nivel, la pendiente y la curvatura. Poco después Grieves (1999) realizó un análisis profundo de las estrategias «butterfly» o mariposas, destinadas a aprovechar variaciones en la curvatura de la curva de tipos de interés; en este punto también cabría citar a Devers (1999) como referencia práctica y menos académica.

Muchos otros procedimientos de ajuste de la ETTI han sido implementados en las 2 últimas décadas. Una perspectiva sobre las distintas técnicas de suavizado puede encontrarse en Adams y van Deventer (1994) y Frishling y Yamamura (1996). Finalmente, también han sido desarrollados complejos algoritmos de aprendizaje estadístico que ayudan al suavizado de la ETTI, como el proporcionado por Fernández-Rodríguez (2006).

El entendimiento de la información contenida dentro de la curva de tipos de interés, así como el papel de los tipos forward como predictores de los tipos al contado en el futuro, han sido objeto de una larga investigación académica con amplia influencia en las estrategias de inversión de renta fija. En este terreno destacan, entre otros, los trabajos de Fama (1984), Ilmanen (1995,1996b), Buser et al. (1996), Ilmanen e Iwanowski (1997) y Dolan (1999). Desde el punto de vista práctico puede verse también Ilmanen (1995, 1996a, 1997) y González et al. (2013).

No obstante, de cara a estudiar las bases que sustentan la rentabilidad en la toma de posiciones en estrategias de renta fija, la literatura académica ha profundizado en la investigación de los fundamentos económicos del mercado de bonos, la forma de predecir sus movimientos y las posibles formas que puede presentar la ETTI en el tiempo y que están relacionadas con el estado del ciclo económico. Aquí habría que citar, entre otros, a Cox et al. (1985), a Renshaw (1995, 1996), a Fleming y Remolona (1999), a Litterman y Scheinkman (1991), a Litterman et al. (1988) y a Boyd y Mercer (2010). Más recientemente, Diebold et al. (2006) realizan un profundo estudio sobre la influencia de la ETTI en la macroeconomía, empleando una novedosa aproximación metodológica de factores latentes dinámicos.

En épocas recientes también se han desarrollado estrategias de negociación basadas en la predicción de la ETTI mediante modelos econométricos. Un trabajo seminal en este sentido ha sido el de Diebold y Li (2006), quienes mostraron que el modelo de 3 factores de Nelson y Siegel (1987) puede usarse para predecir la ETTI, estudiando la dinámica de dichos factores, periodo a periodo, siendo estos capaces de capturar la evolución en la forma de la ETTI. Usando una metodología similar a la de Diebold y Li (2006), Fabozzi et al. (2005) analizan si resulta beneficiosa la predicción dinámica de la ETTI, evaluando diferentes estrategias mariposas capaces de capturar dichos movimientos. Otros autores también analizan estrategias de negociación basadas en la predicción de la evolución dinámica de la ETTI; entre ellos podemos destacar a Ferstl y Weissensteiner (2011), a Hays et al. (2012) y a Andrada-Félix et al. (2013b).

La literatura al respecto para el mercado de deuda pública española no es tan extensa, destacando los trabajos de Soto (2001), Balbás et al. (2002), Díaz et al. (2008) y Díaz et al. (2009), entre otros, quienes analizan diferentes tipos de estrategias de inmunización sobre la curva de tipos de interés española. Todos ellos encuentran que las estrategias inmunizadoras aplicadas sobre el mercado de deuda pública española proporcionan un buen desempeño.

Además de los estudios académicos sobre estrategias de inversión mediante la ETTI mencionados hasta ahora, hay que destacar el desarrollo entre los operadores del mercado de un amplio conjunto de técnicas y estilos de inversión. Como manuales sobresalientes que recogen una amplia panorámica, tanto teórica como práctica, de la inversión en renta fija habría que citar, entre otros, a Tuckman (1992), Fabozzi (1993, 1997), Choudhry (2001) y Martellini et al. (2003). Como técnicas y estilos de inversión véase también Lowenstein (2000), Ilmanen et al. (1996) y Perold (1999). Como forma de usar los indicadores económicos para mejorar el análisis de las inversiones, véase Tainer (1998). Para entender los diferentes procedimientos de estimación de la ETTI se recomienda Martellini et al. (2003), BIS (2005) y Yallup (2012).

Por último, habría que citar que la información contenida dentro de la ETTI también es susceptible de ser empleada en la toma de posiciones en los mercados bursátiles, pues la información contenida en los componentes de la curva de tipos de interés (resumida en el nivel, la pendiente y la curvatura de la ETTI) tiene importante poder predictivo sobre la situación económica, y por tanto sobre el mercado de acciones (ver Resnick y Shoesmith, 2002, y Chen, 2009). En este sentido, existe una amplia evidencia empírica que documenta la relación existente entre la pendiente de la ETTI y los mercados bursátiles, usándose ambos como indicadores adelantados de los ciclos económicos. Fama y French (1989), por ejemplo, encuentran una relación positiva entre la pendiente de la ETTI de Estados Unidos y las acciones bursátiles estadounidenses, siendo aquella una variable representativa (proxy) de las sorpresas o shocks en los tipos de descuento, implícitos en la valoración de las acciones. De forma similar, Boudoukh et al. (1993) y Ostdiek (1998) detectan que las primas de riesgo de las acciones de Estados Unidos y una cartera global de acciones suelen ser negativas en periodos precedidos por una ETTI con pendiente negativa. Por su parte, Resnick y Shoesmith (2002), estudiando la probabilidad de las tendencias bajistas (bear market) a través de un modelo Probit, en lugar de predecir los futuros rendimientos bursátiles encuentran que la pendiente de la ETTI tiene una gran habilidad predictiva sobre las tendencias bajistas en el índice Standard & Poors 500 de la Bolsa de Nueva York dentro de varios periodos. Aunque la literatura al respecto para otros países es escasa, esta revela una relación similar entre la pendiente de la ETTI y los mercados bursátiles (Asprem, 1989; McCrown, 2001).

Demostrada la habilidad predictiva de la pendiente de la ETTI, la literatura reciente va más allá, encontrando que no solo la pendiente de la ETTI, sino los diferentes componentes de la misma (reflejando el nivel, la pendiente y la curvatura de la ETTI) incorporan una información relevante sobre los movimientos futuros de los principales agregados macroeconómicos (véanse Ang et al., 2006; Diebold et al., 2006; Ferreira et al., 2008, y Moench, 2012, entre otros).

Para el caso español, Fernández-Pérez et al. (2013) extienden el análisis de Resnick y Shoesmith (2002) sobre el índice IBEX 35.

2

Riesgo de tipos de interés

A continuación comenzaremos explicando el riesgo de tipos de interés, con el consecuente análisis de los conceptos de la duración y la convexidad.

El riesgo de tipos de interés, conocido también como riesgo de mercado de un activo de renta fija, es un concepto que intenta valorar la posible variación del precio del activo como consecuencia de variaciones en los tipos de interés. Por ejemplo, las inversiones que ofrecen un rendimiento constante son sensibles a las fluctuaciones de los tipos de interés, ya que el precio teórico de un activo de renta fija varía inversamente con aquellas. Por consiguiente, la mayor o menor sensibilidad del precio ante las variaciones que se puedan producir en los tipos de interés de mercado dependerán de las características propias del activo, que en el caso de un bono con cupón serían el plazo de amortización, los flujos de caja y su periodicidad, entre otras. Así, si los tipos de interés descienden, el precio teórico de un bono con cupones sube incrementado la ganancia de capital para el inversor, mientras que el incremento de los tipos provoca una caída en su precio teórico y las consecuentes pérdidas de capital.

Supongamos un inversor que desea invertir hoy sus recursos con el fin de tener disponible una determinada cantidad de dinero unos años más adelante. Si realiza su inversión en una cartera de bonos, el problema no queda plenamente resuelto debido a los cambios que se pueden producir en los tipos de interés después de que los bonos hayan sido adquiridos. En el caso de que un inversor compre un bono con un vencimiento diferente a su horizonte de inversión³, este estará expuesto a un riesgo de reinversión o a un riesgo de capital. Supongamos entonces que su horizonte de inversión fuese de 9 meses. Si, por ejemplo, comprase un bono cupón cero a 6 meses incurrirá en un riesgo de reinversión porque, a partir del sexto mes, tendrá que reinvertir el capital resultante durante los 3 meses restantes a un tipo que hoy desconoce. De igual forma, si compra un bono de idénticas características a un año incurrirá en un riesgo de pérdida de capital, porque el precio al que podrá vender el bono dentro de 9 meses también es hoy desconocido. Por tanto, la única forma de que el riesgo de reinversión y el riesgo de capital se cancelen mutuamente sería comprando un bono cupón cero con vencimiento igual al horizonte de inversión, que en este ejemplo sería un bono cupón cero de 9 meses.

A continuación van a considerarse por separado la existencia de estos 2 tipos de riesgo de mercado: el riesgo de reinversión de flujos intermedios y el riesgo de precio o de capital.

2.1.1

Riego de reinversión de flujos intermedios

Sea un bono de precio P y una tasa interna de rendimiento (TIR) igual a y:

La anterior expresión indica que para generar la TIR prometida por un bono es necesario mantener el bono hasta su vencimiento y reinvertir los cupones al tipo y. Si una vez comprado el bono se produce un inmediato descenso en el tipo de interés hasta y* < y, la TIR calculada inicialmente ya no se realizará, y el rendimiento compuesto realizado (y_realizado) que se obtiene será:

El riesgo de reinversión de flujos intermedios surge porque en la mayoría de los casos los cupones han de ser reinvertidos a unas tasas diferentes a la TIR, lo que altera el rendimiento del bono. En concreto, el impacto exacto en el rendimiento del bono producido por un cambio en la TIR es una función de los cupones y del tiempo de vencimiento que tiene 2 características esenciales: cuanto mayor es el vencimiento del bono, mayor es este tipo de riesgo; y cuanto mayor es el tipo de cupón, mayor es la dependencia del rendimiento del bono de la reinversión de los pagos de cupón.

2.1.2

Riesgo de precio o riesgo de pérdida de capital

Este riesgo se resume de modo que cuando los tipos de interés suben, el precio del bono baja y se produce una pérdida inmediata de capital, y viceversa.

Hay una interacción entre el riesgo de pérdida de capital y el riesgo de reinversión de flujos intermedios, por lo que un cambio en los tipos tiene efectos contrapuestos.

Por un lado, si los tipos caen y se mantienen, hay ganancias de capital con una inmediata apreciación en el valor de la cartera, pero las ganancias por reinversión de los cupones que produce la cartera caen, pues estos crecen entonces a una tasa más lenta hasta el vencimiento.

Llamando H al horizonte temporal del inversor (tiempo que desea mantener la inversión) e y a la TIR del bono, se tendrá lo siguiente:

• •

  Si y baja y H es pequeño: las ganancias de capital son mayores que las pérdidas por reinversión.

• •

  Si y baja y H es grande: las ganancias de capital son menores que las pérdidas por reinversión.

Por otro lado, si los tipos suben y se mantienen, hay una pérdida de capital inmediata, pero las ganancias por reinversión que proporciona la cartera crecen más rápidamente durante el tiempo que quede hasta el vencimiento. De forma que:

• •

  Si y sube y H es pequeño: las pérdidas de capital son mayores que las ganancias por reinversión.

• •

  Si y sube y H es grande: las pérdidas de capital son menores que las ganancias por reinversión.

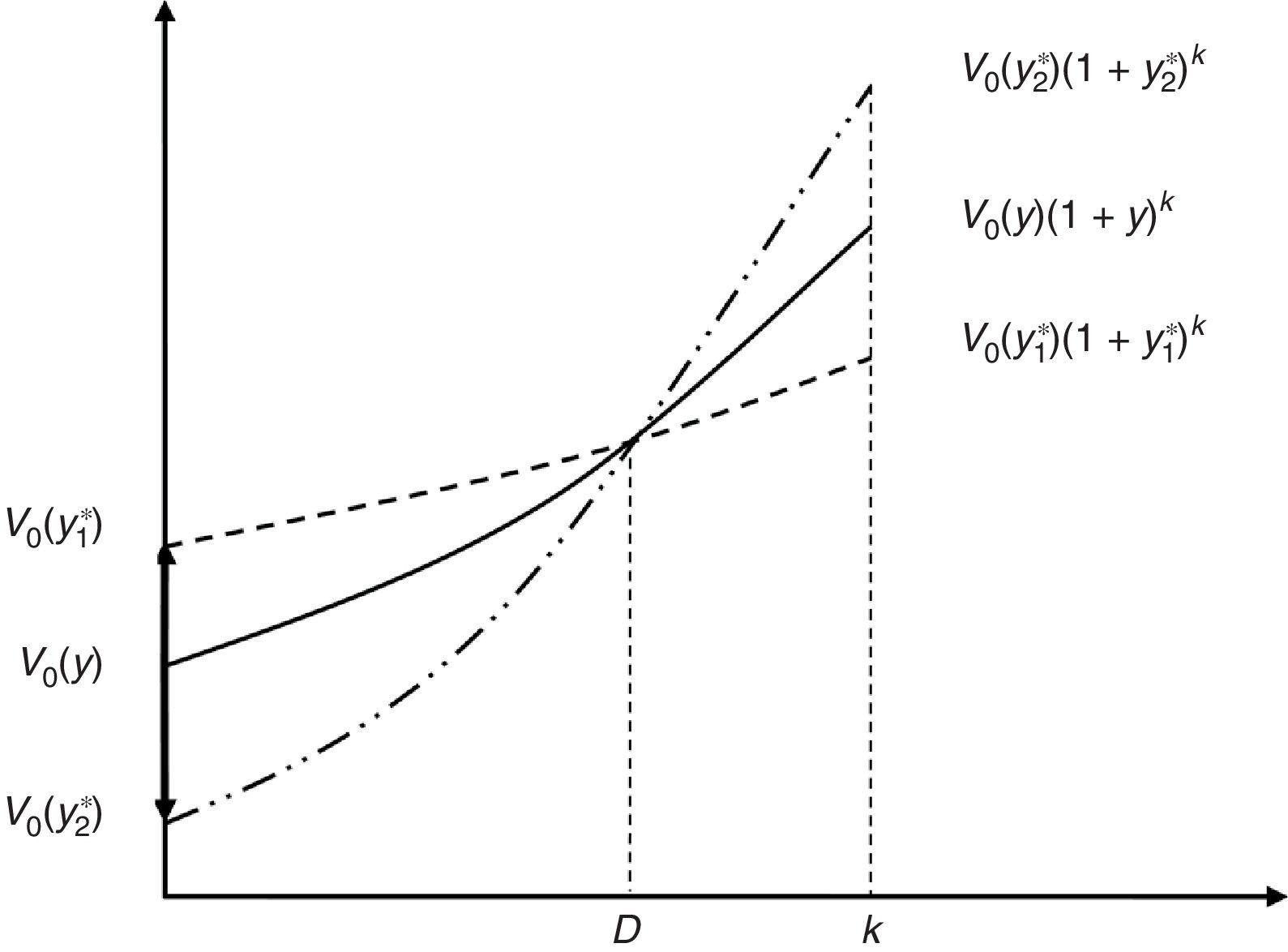
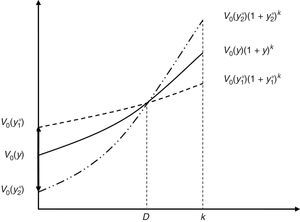
Existe, por tanto, un horizonte D tal que estos 2 riesgos se cancelan mutuamente. En dicho horizonte temporal de inversión, a los inversores no les importará que los tipos suban o bajen (para pequeños cambios paralelos de la curva de tipos). Es decir, para ese horizonte D las pérdidas de capital son iguales a las ganancias por reinversión.

Suponiendo que la TIR del bono baja desde y hasta un valor y1* y sube hasta y2*, donde y1*V₀ al valor inicial del bono, todos estos efectos se pueden reflejar en la figura 1.

Figura 1.

Horizonte temporal del inversor y evolución del capital.

A continuación vamos a analizar con más detalle dicho horizonte temporal de inversión D, el cual se conoce como «duración».

2.2

Duración

Inicialmente se utilizaba la vida pendiente del título hasta su amortización (tiempo hasta el vencimiento, T – t) como la variable indicadora de la sensibilidad del precio del activo respecto a las variaciones de los tipos de interés. Dicha variable refleja fielmente en los bonos cupón cero el tiempo que el poseedor del bono ha invertido su dinero. Sin embargo, para bonos con cupón, el vencimiento es una medida incorrecta del tiempo en que se inmoviliza la inversión debido a los pagos de cupón. Por ello, posteriormente se introdujo un concepto más elaborado que el tiempo de vencimiento para describir dicha sensibilidad. Este concepto se conoce como «duración». Según la idea original que desarrolló Macaulay (1938), la duración de un bono es una medida del tiempo medio de espera del poseedor de un bono antes de recibir el flujo de pagos. Esta variable es clave para explicar la sensibilidad de los precios de los bonos a las fluctuaciones de los tipos de interés.

Si se considera un bono con cupón como un paquete de bonos cupón cero, la duración de Macaulay (1938) se define como un promedio ponderado de los vencimientos de los bonos cupón cero que subyacen en un bono con cupón, donde los pesos que se aplican a cada vencimiento son el valor presente de los correspondientes bonos cupón cero, usando la TIR para calcular la tasa de descuento. De manera más formal, consideremos la expresión de la TIR de un bono con cupones:

Teniendo en cuenta la expresión anterior, la duración se define dividiendo el promedio ponderado de los vencimientos entre P de forma que la combinación lineal sea convexa:

donde el factor que se aplica a cada vencimiento wt=Ct(1+y)−tP es el valor presente del correspondiente bono cupón cero entre P. De la expresión (1) se deriva que la duración es un valor intrínsecamente positivo, ya que todos sus elementos así lo son.

En el caso de capitalización continua, la duración de Macaulay (1938) se define como:

e igualmente consiste en una combinación lineal convexa del tiempo hasta los pagos de cupón ponderada por unos factores w_t proporcionales al valor presente de cada cupón.

Como los pesos son proporcionales a los cupones, un bono que paga inicialmente cupones bajos y cupones altos al final tendrá una duración más alta que otro bono que paga cupones altos al principio y bajos al final. Un caso especial es el de un bono cupón cero, cuya duración es igual a su vencimiento.

Si un inversor compra un bono cupón cero con un vencimiento igual a su horizonte de inversión no se verá afectado por los movimientos de los tipos de interés; entonces se dice que está inmunizado ante variaciones de los tipos de interés. Por este motivo, también se puede considerar la duración de un bono como aquel horizonte de inversión (tiempo que se desea mantener la inversión) tal que los inversores con dicho horizonte son indiferentes a que los tipos de interés suban o bajen, siempre que se produzcan pequeños cambios paralelos en la curva de tipos. En otras palabras, el riesgo de pérdida de capital es compensado por el riesgo de reinversión de flujos intermedios.

Retomando la ecuación (2), y considerando el precio de un bono en el instante t que paga cupones en t₁, t₂, …, t_n = T, el cual viene dado en función de la TIR por la expresión:

Si se deriva respecto a la TIR, y, se obtiene:

Dividiendo a continuación entre P, y teniendo en cuenta la expresión (2), se obtiene otra importante expresión para la duración⁴ conocida como duración modificada o duración relativa, o sencillamente duración:

La expresión (4) de la duración permite obtener una aproximación del cambio porcentual en el valor del bono para pequeños movimientos en la TIR (en general, de los tipos de interés), pues:

La relación (5) indica que cuanto mayor sea la duración de un bono, mayor será su sensibilidad para un cambio dado de la TIR.

En esa misma línea se observa que en un bono cupón cero el efecto negativo que tiene sobre él una subida de tipos de interés prevalecerá durante toda la vida del bono. En cambio, en un bono con poca duración (que tenga mucho tiempo hasta el vencimiento y page altos cupones al principio) el efecto de la subida de tipos es menor que en un bono cupón cero (con el mismo tiempo hasta el vencimiento), pues en el primero podemos reinvertir los intereses de los cupones a un tipo más elevado.

El significado de la expresión (5) puede resumirse señalando que si se espera un incremento en los tipos de interés, los inversores deberán recortar la duración de su cartera. Sin embargo, si se espera una bajada de tipos de interés, los inversores deberán aumentar la duración de su cartera. Ambas operaciones se pueden realizar modificando los constituyentes de la cartera de bonos, es decir, cambiándolos o variando los pesos de estos en la cartera, o a través del mercado de derivados de renta fija.

Finalmente debe observarse que la bondad de la duración como medida de sensibilidad depende de 2 factores: primero, si la ETTI es completamente plana, en este caso la TIR sería una representación exacta de la estructura temporal; y segundo, si la ETTI solo experimenta pequeños desplazamientos paralelos.

2.2.1

Duración de una cartera de bonos e inmunización

Sea una cartera formada por n bonos cuyo valor es proporcional a los precios de los bonos que la conforman:

donde α_j es el número de participaciones del bono j de precio P_j y VC es el valor de la cartera. En tal caso el porcentaje de participación, o peso, de cada bono en la cartera es:

wi=αjPjVC, con i = 1, 2, …, n,

y donde ∑i=1nwi=1.

Su duración es un operador lineal, y no es más que el promedio ponderado de las duraciones de cada uno de los bonos:

Aunque la duración de un bono es una cantidad intrínsecamente positiva, en el caso de una cartera de bonos donde es posible la existencia de posiciones largas (compras) y cortas (ventas) la duración podría ser negativa o nula, como ocurre con un banco que presta y pide prestado, y donde los flujos pueden ser positivos o negativos. En tal caso, la cartera será insensible a los movimientos de los tipos de interés, en el instante presente, cuando su duración sea cero. Debido a la linealidad que tiene la duración, este hecho es equivalente a que la duración de los activos de la cartera sea igual a la duración que tengan sus pasivos, por lo que se dice que la cartera está inmunizada.

Muchas estrategias de renta fija persiguen el objetivo de duración cero, por ejemplo en la estrategia butterfly o mariposa, donde se toma una posición vendedora en un bono de vencimiento medio y una posición compradora en 2 bonos, uno de vencimiento corto y otro de largo. Por otro lado, si la cartera solo contuviese posiciones largas, esta se puede inmunizar haciendo que su duración iguale al horizonte de planificación de la inversión (HPI). En ese caso, y si la ETTI solo sufre pequeños movimientos paralelos, el inversor asegurará desde el instante inicial el montante final de su inversión, siendo este el resultante de capitalizar la inversión inicial a los tipos de la fecha inicial, es decir, haciendo que se cumplan los tipos de hoy al finalizar el HPI. Otra forma de decirlo sería que al inmunizar su cartera al HPI, el inversor estará cubierto, para pequeños cambios paralelos en la ETTI, frente al riesgo de capital y al riesgo de reinversión de flujos intermedios.

3

Estrategias de inversión y gestión de carteras de renta fija

El proceso de gestión de una inversión para cualquier tipo de institución financiera lleva consigo 5 pasos (Fabozzi, 1993):1. Establecer los objetivos de la inversión. Los objetivos de una inversión varían con el tipo de institución financiera. Por ejemplo, para el caso de un fondo de pensiones, el objetivo de inversión es generar suficiente flujo de caja con las inversiones de modo que se satisfagan las obligaciones de las pensiones. En cambio, para una compañía de seguros de vida, el objetivo es satisfacer las obligaciones estipuladas en las pólizas. Por su parte, en el caso de las instituciones bancarias, estas obtienen sus fondos gracias a depósitos ordinarios, certificados de depósitos, instrumentos del mercado de dinero o préstamos a tipo variable, siendo su objetivo el de ganar un rendimiento en los fondos invertidos que sea mayor que el coste de adquisición de dichos fondos. En todos estos casos, los objetivos están determinados fundamentalmente por la naturaleza de sus obligaciones con los perceptores de pensiones, los asegurados y los depositantes. En cambio, para las sociedades de inversión (fondos de inversión) pueden no existir tales obligaciones específicas.2. Establecer la política de inversión. Se trata de establecer las líneas maestras de los objetivos de inversión. En este sentido, las decisiones comienzan en cómo deben ser asignados y distribuidos los fondos de la institución entre las diferentes clases de inversión: efectivo, acciones, renta fija y títulos extranjeros.3. Seleccionar la estrategia de inversión. Las estrategias de inversión pueden clasificarse entre estrategias activas y pasivas. En las estrategias activas es esencial la especificación de las expectativas sobre los factores que influyen en el comportamiento de cada clase de activos. En cambio, las estrategias pasivas involucran unas expectativas mínimas.4. Seleccionar los activos. La selección de unos activos específicos de renta fija requiere una cuidadosa e individualizada evaluación de cada uno de ellos, examinando sus características tales como cupones, vencimiento, duración, convexidad, calidad crediticia u opciones inmersas. Recopilar esta información puede ayudar a encontrar activos mal valorados.5. Evaluar el desempeño o performance de la inversión. Una inversión precisa comparar sus rendimientos obtenidos con alguna otra cartera de referencia, la cual se denomina benchmark.

3.1

Fuentes de rendimiento en activos de renta fija

En este apartado se analizan las fuentes de rendimiento de los activos de renta fija y su relación con la ETTI (ver Navarro y Nave, 2001). La fórmula de valoración de un bono que paga n cupones, y cuyo valor facial es la unidad, responde a la expresión:

A partir de esta, se puede considerar que un activo de renta fija tiene 3 fuentes de rentabilidad: a) la renta procedente de los pagos de cupones; b) la renta procedente de la reinversión de los cupones, y c) las ganancias o pérdidas de capital debidas al cambio de precio en el bono. Si no se produce la quiebra del emisor del bono, la primera de las fuentes de rentabilidad se conoce con certeza, mientras que las otras 2 fuentes son inciertas y dependen de cambios en los tipos de interés. Por un lado, las ganancias o pérdidas de capital dependerán de la evolución de los tipos de interés, a menos que el inversor desee mantener el bono hasta su vencimiento. Por otro lado, la renta procedente de la reinversión de los cupones será siempre incierta, y nadie garantiza al inversor poder obtener la TIR inicial del bono. Aunque el nivel de tipos permanezca inalterado sobre el HPI, el precio de un bono puede subir o bajar debido a la convexidad y a la estrategia de cabalgamiento (roll down return), que son sensibles a cambios en la forma de la ETTI. Esta estrategia de cabalgamiento basa sus ganancias en la caída de los rendimientos, típica de un bono que se acerca a su vencimiento. Dado que bajo circunstancias normales la ETTI tiene una estructura creciente, si esta forma creciente no cambia con el paso del tiempo, cuando el bono se acerca a su vencimiento, el precio del mismo aumentará por efecto de la caída de su rendimiento. Así, la compra de bonos de largo vencimiento puede producir ganancias de capital con el paso del tiempo si la ETTI mantiene su inclinación, siendo este efecto más acusado a medida que la ETTI sea más empinada.

Otra posible fuente de beneficios es el coste neto de financiación (carry) de la operación, que es la diferencia entre el cupón pagado por el bono y el interés pagado para financiar la posición. Así pues, un coste neto de financiación positivo es un colchón frente a las pérdidas derivadas de las caídas del precio de los bonos (subidas de tipos). Por el contrario, un coste neto de financiación negativo significa que la posición puede perder dinero incluso si aumenta el precio del bono.

4

Gestión de inversión en carteras de renta fija

Para construir una cartera, un gestor de renta fija puede elegir, a la hora de seleccionar su estrategia de inversión, entre estrategias activas o pasivas. En una estrategia activa los gestores pueden sacar ventaja en la gestión de carteras de su información, de la técnica empleada o de su habilidad para predecir los tipos de interés o detectar ineficiencias del mercado. En cambio, en una estrategia de inversión pasiva los gestores aceptan los precios del mercado de los títulos como adecuados, y suponen plena eficiencia⁵ en el mercado. En este tipo de estrategias los gestores no intentan batir al mercado explotando su habilidad o mejor información; simplemente intentan mantener un equilibrio apropiado riesgo-rentabilidad según las circunstancias del mercado, controlando al mismo tiempo el riesgo de tipo de interés en sus carteras de renta fija.

4.1

Estrategias pasivas de inversión

Existen 2 procedimientos clásicos de gestión pasiva de una cartera de renta fija con el fin de cubrir el riesgo de interés (ver Fabozzi, 1993; Navarro y Nave, 2001; Martellini et al., 2003, entre otros): el emparejamiento de activos y pasivos (cash-flow matching) y la estrategia inmunizadora, cuyo objetivo es aislar la cartera del riesgo de tipo de interés.

4.1.1

Correspondencia entre flujos de tesorería: cash-flow matching

La estrategia de correspondencia entre los flujos de tesorería o emparejamiento de activos y pasivos es una estrategia de inversión pasiva que persigue la construcción y el mantenimiento de una cartera de bonos, también conocida como dedicated portfolio, que tenga una estructura de flujos de tesorería que se corresponda con la estructura de la corriente futura de pagos. Dicho de otra forma, se trata de intentar emparejar las deudas con las inversiones, igualando las posiciones cortas en bonos con las posiciones largas en bonos, de modo que los cupones en las posiciones largas sean idénticos en tamaño y ritmo a los pagos requeridos por sus responsabilidades. Por ello, en esta estrategia los bonos cupón cero juegan un papel muy importante.

4.1.2

Inmunización

Una estrategia alternativa de inversión pasiva consiste en construir una cartera de posiciones largas en bonos cuya duración iguale a la duración de la cartera de responsabilidades de pago. Este sería el problema de la inmunización simple de Fisher y Weil (1971), el cual consiste en la formación de una cartera de renta fija que asegure una rentabilidad al menos tan grande como la que se habría obtenido si durante el horizonte temporal de la inversión se verificase la curva de tipos de interés implícitos observada al construir la cartera, con independencia de las fluctuaciones de los tipos de interés. Dicho de forma más simplificada, debe asegurarse una rentabilidad al menos tan grande como la que se habría obtenido si la curva de tipos se mantuviese inalterada durante el horizonte temporal de la inversión.

El teorema de Fisher y Weil (1971) afirma que si para un instante t entre los instantes iniciales y finales de la inversión, t₀ < t < T, la ETTI solo sufre desplazamientos paralelos⁶, una cartera de flujos no negativos está inmunizada en el instante t₀ si su duración Dt0 es igual al horizonte temporal de la inversión T – t₀.

Dado que para proceder a la inmunización instantánea de una cartera de bonos es preciso recurrir a posiciones cortas en bonos, considérese una cartera de bonos donde existen posiciones largas y cortas, tal como ocurre con un banco donde tienen una cartera de pasivos con vencimientos a la vista (depósitos) y una cartera de activos con vencimientos a 30 o 30 años (préstamos hipotecarios). En tal caso, tiene sentido buscar una composición adecuada de la cartera de bonos de modo que quede inmunizada en el instante presente contra las variaciones de los tipos de interés, de modo que su valor sea insensible a los desplazamientos paralelos de la curva de tipos de interés en ese instante.

4.1.2.1

Limitaciones de la inmunización mediante la duración

La inmunización basada en la duración debe ser empleada con cautela por 2 razones: la primera es que se suponen desplazamientos paralelos en la curva de tipos de interés, no obstante, históricamente los movimientos en los intereses a corto plazo tienden a ser mayores que los movimientos a plazos más largos; y segunda, mediante el uso de la derivada primera del desarrollo de Taylor, tal como hace la duración, solo se puede dar cuenta del efecto sobre los precios de pequeños cambios en la TIR del bono, por lo que, para considerar el efecto de movimientos mayores, se debe tener en cuenta la derivada segunda (convexidad).

Entre las diversas formas clásicas de corregir las limitaciones que tiene la estrategia pasiva de la inmunización de una inversión, cabe citar:1. Estrategias de inmunización dinámica. Con el transcurso del tiempo y el pago de los cupones, o el vencimiento de algún activo, la duración de una cartera se verá afectada sin remedio. Por ello, las estrategias de inmunización dinámica persiguen que la duración de la cartera al comienzo de cada periodo planificador sea igual al tiempo restante del periodo al que se planifica la inversión. Por ejemplo, si el periodo planificador es inicialmente T, el inversor coloca hoy, t = 0, sus fondos en una cartera de duración igual a T, D = T. En el periodo siguiente (t = 1), la duración de la cartera habrá de ajustarse de modo que el periodo planificador sea igual a T – 1. En general, transcurridos t periodos habrá de ajustarse de modo que aquel sea igual a T – t. En la práctica, se reajusta la duración de la cartera cada vez que cualquier activo de la misma genere algún flujo, como por ejemplo en cada pago de cupón o cuando algún activo de la cartera llegue al vencimiento.2. Convexidad. A la hora de afrontar las limitaciones de la inmunización mediante la duración, el procedimiento más efectivo, por su simplicidad, consiste en considerar el término de segundo orden en el desarrollo de Taylor de la función que relaciona el incremento del precio de un bono frente al incremento de la TIR. Con ello se obtiene una medida del error de cobertura del proceso de inmunización, mediante la duración, que se llama convexidad.

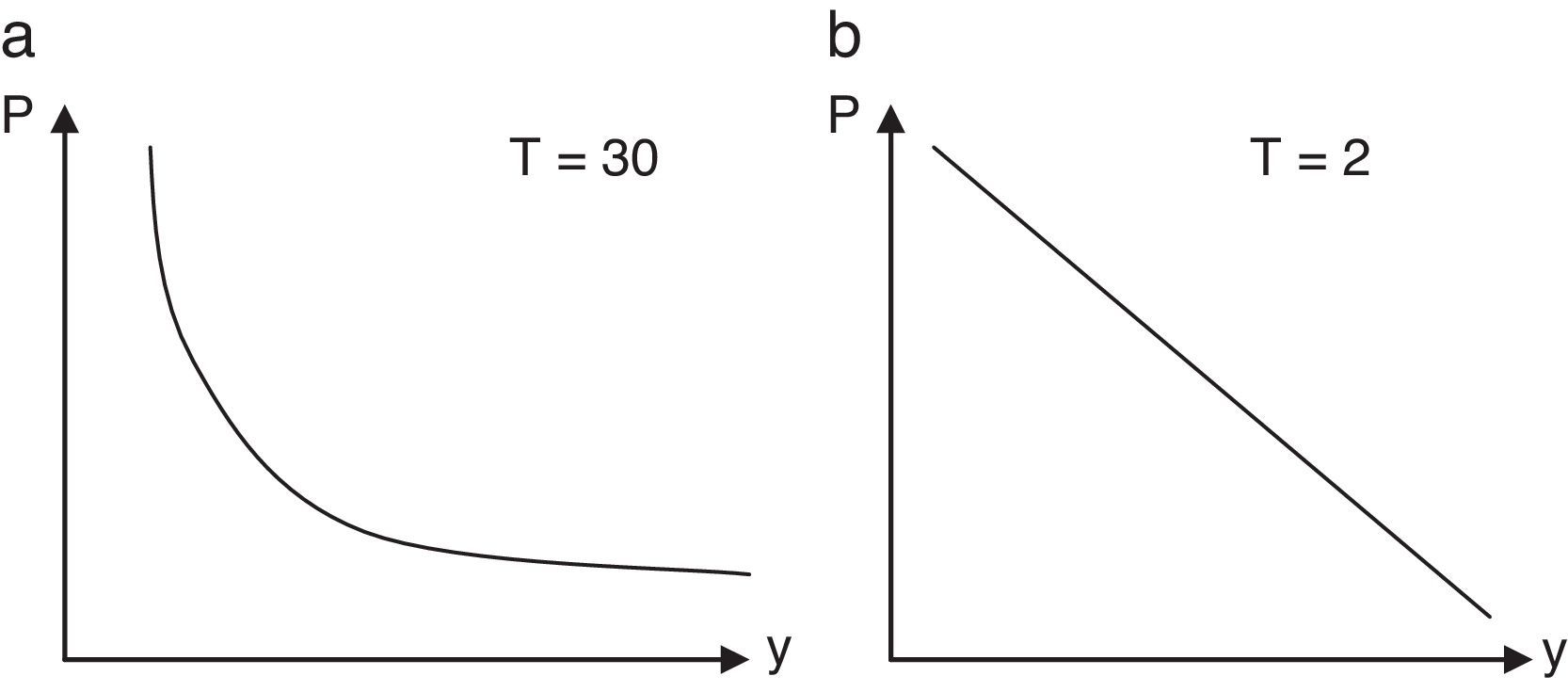
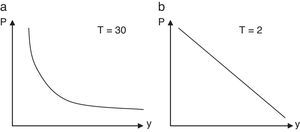
Si se representa el precio de un bono cupón cero hasta su vencimiento frente a su TIR, tanto en el supuesto de capitalización discreta, donde P=11+yT, como en el de capitalización continua, donde P = e^−yT, es fácil observar cómo varía dicha relación con el tiempo de vencimiento. Por ejemplo, en las gráficas de la figura 2 se observa que el precio de los bonos al descuento (cupón cero) a 30 años tiene una pronunciada curvatura (a). Ello implica que la sensibilidad del precio del bono a los cambios en la TIR no es constante. En cambio, para los bonos a 2 años, su precio es una función casi lineal de la TIR (b).

Figura 2.

Sensibilidad del precio de un bono frente a su TIR.

Estas gráficas señalan una serie de importantes propiedades de la relación del precio de un bono con respecto a su TIR, y, y cómo puede cambiar la volatilidad del precio de los bonos que no tienen opciones inmersas en función de su vencimiento. Así, a través de estas gráficas puede observarse que:

1. Aunque el precio de los bonos se mueve en dirección opuesta a los cambios en el tipo de interés, el porcentaje de cambios no es el mismo para todos los bonos.

2. Para pequeños cambios en los tipos de interés, el cambio en el precio de un determinado bono es el mismo, con independencia de que los tipos asciendan o desciendan.

3. Para grandes cambios en los tipos, el cambio en el precio no es el mismo para un incremento en los tipos que para un descenso. Concretamente, el incremento de los precios de los bonos con una bajada de los tipos es superior al descenso de los precios de los bonos con una subida de tipos, es decir, para un cambio grande en los tipos de interés, la apreciación del precio de los bonos será mayor que la depreciación.

La explicación del comportamiento asimétrico de los bonos que se describe en esta última propiedad aludida se debe a la forma convexa de la relación precio/tipo de interés que presentan los bonos sin opciones inmersas. Dicha convexidad aumenta con el tiempo hasta el vencimiento, y vendrá recogida en la derivada segunda del precio respecto al tipo de interés.

Tal como se advertía, la inmunización basada en la duración debe ser empleada con cautela porque supone pequeños desplazamientos paralelos en los tipos de interés. Por el contrario, la convexidad ayuda a ampliar la perspectiva de la inmunización, pues constituye una medida del error de cobertura en un proceso de inmunización. Es decir, si se produce un cambio instantáneo en los tipos de interés, un bono con convexidad cero se comportará en línea con su duración. Por el contrario, en un bono con convexidad positiva se espera que su comportamiento mejore el cambio que pronostica su duración.

De modo más formal, considérese el desarrollo de Taylor del precio de un bono en relación a su TIR:

Si se dividen ambos miembros entre P, se obtiene el cambio relativo en el valor del precio del bono:

A partir de esta expresión se define la convexidad relativa, o más sencillamente la convexidad de un bono como:

donde, para el caso de capitalización discreta, esta expresión adopta la forma de:

con:

Asimismo, para el caso de capitalización continua la expresión de la convexidad adopta la forma:

Como caso particular, la convexidad de un bono cupón cero, en el supuesto de capitalización discreta, es:

donde dicha convexidad es creciente con el tiempo hasta el vencimiento, T, y decreciente con el tipo de interés, y, tal como puede comprobarse fácilmente estudiando el signo de sus derivadas parciales:

En resumen, la convexidad permite añadir una aproximación de segundo orden que considere el impacto relativo en el precio del cambio en la TIR, siendo entonces la expresión que recoge el valor relativo de dicho impacto la siguiente:

Convexidad de una cartera de bonos. Al igual que con la duración, la convexidad relativa es un operador lineal; por tanto, la convexidad de una cartera formada por n bonos en la misma moneda con pesos w_i es la suma ponderada de las convexidades relativas de cada bono, es decir:

con ∑i=1nwi=1.

Críticas a la convexidad. La convexidad juega también un papel importante en la inmunización de una cartera. Igual que la gamma es una medida de la estabilidad de la delta de una opción, la convexidad es una medida de la estabilidad de la duración, de forma que una convexidad alta significa que un desplazamiento en la ETTI tendrá un efecto relativamente grande en la duración de un bono. Así, un gestor de inversiones que tuviese inmunizada su cartera, pero tal que la convexidad de las posiciones cortas y largas de los bonos no se igualase, debería esperar que tras un gran desplazamiento en los tipos de interés la cartera dejara de estar inmunizada.

Igualmente, la convexidad puede resultar perjudicial si existe incertidumbre sobre cómo evolucionará la curva de tipos de interés. Este hecho es debido a que el efecto de los cambios de la pendiente de la ETTI en la duración de un bono será mayor cuanto mayor sea la convexidad. Esto se produce porque una mayor convexidad implica una dispersión mayor de los flujos de caja. Por ello, esa mayor convexidad implicaría que existe una mayor incertidumbre sobre cómo la duración del bono se comporta cuando se produzcan cambios no paralelos en la curva de tipos de interés. En definitiva, el éxito de las estrategias de cobertura basadas en la duración y la convexidad depende de 2 factores cruciales: primero, que la ETTI pueda considerarse plana, y segundo, que sus desplazamientos sean paralelos.

4.2

Estrategias activas de inversión

En una estrategia de inversión pasiva los gestores aceptan los precios del mercado de los títulos como adecuados y suponen plena eficiencia en el mercado. Dicho de otra forma, los gestores no intentan batir al mercado explotando su habilidad o su mejor información; simplemente buscan mantener un equilibrio apropiado entre el riesgo y la rentabilidad, según las circunstancias del mercado. En este sentido, el procedimiento clásico de gestión pasiva es una estrategia inmunizadora, ya explicada anteriormente, que tiene como objetivo aislar la cartera del riesgo de tipo de interés. En cambio, en las estrategias activas los gestores pueden sacar ventaja en la gestión de carteras de su información, de la técnica empleada, de su habilidad para predecir los tipos de interés o detectar ineficiencias del mercado.

Un gestor de carteras que persiga una estrategia de inversión activa tomará posiciones en su cartera con el fin de capitalizar sus expectativas sobre la futura evolución de los tipos de interés. Asimismo, el mercado en su conjunto también tiene unas expectativas sobre los futuros tipos de interés que se manifiestan en el precio de mercado de los bonos. Por tanto, el resultado de una estrategia activa no solo dependerá de que sea capaz de anticiparse al mercado sino también de la medida en que sus expectativas difieran de las del resto de agentes que constituyen el mercado. Siguiendo a Martellini et al. (2003), hay 2 tipos de estrategias activas:

• •

  Tomar posiciones derivadas de las predicciones sobre los tipos de interés (market timing). Estas estrategias utilizan las previsiones de los tipos de interés con el fin de predecir los movimientos del mercado de bonos.

• •

  Tomar posiciones sobre las ineficiencias observadas en el mercado (bond picking). Estas estrategias buscan identificar los sectores particulares del mercado que tienen un precio relativamente bajo y/o alto.

A continuación se examinarán con más detenimiento los diferentes tipos de estrategias activas.

4.2.1

Tomar posiciones derivadas de las predicciones sobre los tipos de interés

En una cartera de renta fija existen 3 fuentes para la obtención de rendimientos: la renta procedente de los pagos de cupones, la renta procedente de la reinversión de los cupones y las ganancias o pérdidas de capital debidas al cambio de precio en el bono.

A su vez, los diversos cambios que pueden afectar a estas fuentes de rendimiento son los cambios en el nivel de los tipos de interés, en la forma de la curva de rentabilidades, en el spread de rentabilidades entre los diferentes sectores de bonos, en el spread de rentabilidades para un bono en particular y en la asignación de activos dentro de un sector de bonos.

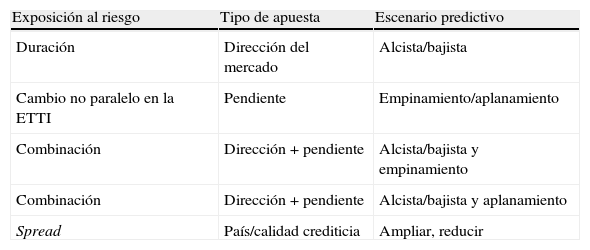
La tabla 1 muestra diversos factores de riesgo y tipos de apuestas predictivas que se pueden realizar frente al cambio de dichos factores. Asimismo, muestra los posibles escenarios predictivos en estrategias activas de renta fija basadas en las predicciones sobre los futuros movimientos de los tipos de interés.

Tabla 1.

Fuentes de exposición, tipo de apuesta y escenario

Exposición al riesgo	Tipo de apuesta	Escenario predictivo
Duración	Dirección del mercado	Alcista/bajista
Cambio no paralelo en la ETTI	Pendiente	Empinamiento/aplanamiento
Combinación	Dirección + pendiente	Alcista/bajista y empinamiento
Combinación	Dirección + pendiente	Alcista/bajista y aplanamiento
Spread	País/calidad crediticia	Ampliar, reducir

Fuente: Martellini et al. (2003).

Igualmente, en la selección de una estrategia los inversores pueden tener diferente actitud frente al riesgo. Este hecho lleva a considerar diferentes formas de negociación:

• •

  Negociación básica, representando inversores de riesgo neutro con objetivos centrados en el rendimiento total como ocurre con los fondos de pensiones, compañías de seguros y bancos comerciales.

• •

  Negociación conservadora, realizada por inversores más aversos al riesgo con objetivos de acumulación de renta.

• •

  Negociación arriesgada, realizada por inversores con un perfil de riesgo elevado y con objetivos de ganancias de capital como los hedge funds.

4.2.2

Tomar posiciones sobre las ineficiencias observadas en el mercado

Los gestores pueden hacer algunas apuestas sobre los cambios en la curva de tipos de interés o sobre un segmento particular de aquella. En este sentido, podemos definir 4 principales tipos de apuestas:

• a)

  Sobre la ausencia de cambios en la curva de tipos de interés.

• b)

  Sobre el nivel de los tipos de interés.

• c)

  Basadas en la pendiente de los tipos de interés.

• d)

  Basadas en movimientos de la curvatura de los tipos de interés.

Estas apuestas se materializan en alterar la composición de la cartera en relación con un índice amplio del mercado de bonos que se utiliza como benchmark⁷. En consecuencia, al suponer que el índice representa al mercado, estas apuestas intentan aprovechar diversas ineficiencias de aquel. En definitiva, son apuestas sobre errores que puede estar cometiendo el mercado en su valoración.

A continuación se examinan cada una de ellas con más detenimiento.

4.2.2.1

Estrategias sobre la ausencia de cambios en la curva de tipos de interés

La estrategia de comprar un activo de renta fija de tiempo hasta el vencimiento muy largo y venderlo antes de su vencimiento suele denominarse estrategia de cabalgar sobre la curva de tipos (riding the yield curve). Así, si la curva de tipos es relativamente creciente y los tipos de interés se mantienen estables en el futuro, un gestor de inversión puede beneficiarse de cabalgar la curva de tipos de interés respecto a la estrategia de comprar y mantener instrumentos a corto plazo hasta el vencimiento. La razón para que se prefiera esta estrategia es la siguiente:

Si la curva de tipos de interés tiene una pendiente positiva y se supone que dicha pendiente se mantendrá en el futuro, un inversor puede ganar dinero comprando activos de renta fija con vencimientos superiores al horizonte temporal de inversión y venderlos para beneficiarse de los rendimientos descendentes de los bonos (y consiguiente aumento de su precio) que se producirá con el paso del tiempo cuando decrezcan los vencimientos de los bonos. Por ejemplo, si el inversor compra hoy bonos a 2 años con precio P₂, y suponiendo que la actual curva de tipos de interés se mantenga dentro de un año, estos bonos tendrán un vencimiento de un año y un precio P₁ > P₂ porque y₁ < y₂.

El éxito de este tipo de estrategias contradice la teoría de las expectativas, ya que si la teoría de las expectativas es cierta, una curva de tipos de interés con pendiente creciente indica que los futuros tipos de interés a corto plazo subirán. Por tanto, un inversor no obtendrá rendimientos superiores comprando bonos de alto vencimiento en lugar de bonos de corto vencimiento. Sin embargo, la teoría de las expectativas puede no funcionar perfectamente en la práctica. Con respecto a ello, existe una amplia discusión académica sobre si la estrategia de cabalgar sobre la curva de tipos de interés es rentable o no (ver Martellini et al., 2003:235, y Galvani y Landon, 2013).

4.2.2.2

Estrategias sobre el nivel de los tipos de interés

Las estrategias basadas en los cambios en el nivel de los tipos de interés suponen que existe un solo factor que origina todos los movimientos de la curva de tipos de interés, por lo que la ETTI solo se verá afectada por 2 posibles desplazamientos paralelos, uno creciente y otro decreciente.

Un gestor convencido de que puede predecir con precisión el nivel futuro de los tipos de interés alterará la sensibilidad de su cartera ante los cambios en los tipos de interés. Así, incrementará (reducirá) la duración de la cartera ante expectativas de caídas (subidas) de los tipos, en relación a su benchmark:1. Expectativas de caída de tipos de interés. Si el inversor tiene expectativas de que caerá el nivel de los tipos, teniendo en cuenta que:

podría apostar por un aumento de las ganancias de capital alargando la duración de la cartera. Este cambio de la duración de una cartera puede realizarse cambiando sus bonos por otros de modo que se alcance el nuevo objetivo de duración para la cartera.2. Expectativas de subida de tipos de interés. Si el inversor tiene expectativas de que el nivel de los tipos subirá, puede apostar por aumentar las ganancias de capital acortando la duración de la cartera. En este aspecto, existen diversas formas de alterar la duración de una cartera; entre ellas, las formas más típicas son la compra o venta de bonos, el uso de swaps sobre tipos de interés, y comprar o vender futuros sobre tipos de interés.

Hay que observar que la literatura académica no sostiene la visión de que los tipos de interés puedan ser predichos de manera que pueda obtenerse, de forma consistente, un exceso de rendimiento sin incrementar el riesgo. Además, existe una tendencia por parte de ciertos gestores a realizar apuestas sobre la evolución de los tipos de interés para ocultar, en los periodos finales del horizonte de inversión, las performances de la inversión inferiores al benchmark. Una forma de evitar este tipo de juegos por parte de los clientes es imponer restricciones sobre la cuantía en que la duración de la cartera puede variar en relación al benchmark.

4.2.2.3

Estrategias basadas en cambios específicos de la curva de tipos de interés

Históricamente se han observado 3 tipos de desplazamientos en la ETTI: paralelos, cambios en la pendiente y cambios en la curvatura. Los desplazamientos paralelos son aquellos donde el cambio en la rentabilidad para todos los vencimientos es el mismo. No obstante, la curva de tipos puede estar potencialmente afectada por otros 2 desplazamientos no paralelos, universalmente reconocidos en la literatura, como son los desplazamientos en la pendiente y en la curvatura de la ETTI.

Los cambios en la pendiente se refieren al aplanamiento o escarpamiento de la curva de tipos de interés. En la práctica, existen varias formas de obtener la pendiente de la curva de tipos. Por un lado, se mide como el spread existente entre algún rendimiento de largo vencimiento, como el tipo de interés a 10 o 30 años, y un rendimiento de corto vencimiento, como el tipo de interés a 3 meses o a un año, donde el aplanamiento indica que el spread disminuye y el escarpamiento aumenta. Por otro lado, se puede extraer la pendiente de la ETTI a través de algún modelo de estimación de la ETTI, como por ejemplo el modelo de Nelson y Siegel (1987), el cual dispone de un parámetro específico que representa a la pendiente de la ETTI.

El otro tipo de desplazamiento no paralelo se refiere a cambios en la curvatura, también denominado desplazamiento en mariposa (butterfly). Esta se puede obtener como la diferencia entre 2 veces el tipo a medio plazo, como puede ser el rendimiento a 2 años, menos un rendimiento de corto vencimiento y menos un rendimiento de largo vencimiento (ver Diebold et al., 2006). Asimismo, se puede hacer uso del parámetro del modelo de Nelson y Siegel (1987) que representa la curvatura.

En este sentido, cabría destacar el trabajo de Jones (1991), quien analiza los tipos de desplazamiento en la ETTI entre 1979 y 1990. Jones observa que los 3 tipos de desplazamientos no son independientes, siendo los 2 tipos más comunes de desplazamiento de la ETTI⁸:

• •

  Un desplazamiento hacia arriba combinado con un aplanamiento (presentan una correlación de 0,41).

• •

  Un desplazamiento hacia abajo combinado con un escarpamiento.

Además, Jones (1991) encuentra que el desplazamiento hacia arriba combinado con un aplanamiento está correlacionado con una mariposa positiva (menor curvatura). Por otra parte, un desplazamiento hacia abajo combinado con un escarpamiento está correlacionado con una mariposa negativa (mayor curvatura). Este autor también ofrece evidencia empírica de la importancia de los cambios en la ETTI para la determinación de los bonos en varios sectores de vencimiento, haciendo uso del Merrill Lynch Treasury Bond Index. Así, encuentra que los desplazamientos paralelos y los torcimientos de la ETTI son responsables del 91,6% de los rendimientos del Tesoro, el 3,4% de los rendimientos es atribuible a desplazamientos en mariposa y el resto a factores desconocidos. Tales resultados son consistentes con los ofrecidos por Litterman y Scheinkman (1991).

Por tanto, las estrategias basadas en el comportamiento de la ETTI requieren una predicción de la dirección del desplazamiento y una predicción sobre el tipo de torsión. En este respecto, se podría observar que 2 carteras con la misma duración pueden comportarse de forma muy diferente ante el mismo desplazamiento en la ETTI, por lo que el factor clave es el espaciamiento del vencimiento de los bonos dentro de la cartera que puede emplearse para controlar el riesgo ante desplazamientos de la ETTI. El otro factor clave que afecta el comportamiento de la cartera es la magnitud del desplazamiento de la curva de tipos.

Las diferentes estructuras de vencimiento empleadas en la construcción de una cartera se corresponderán con diferentes estrategias de posicionamiento, según las expectativas de los inversores, ante posibles desplazamientos de la curva de tipos de interés, tomando posiciones respecto a ciertos vencimientos a lo largo de todo el espectro. En este sentido, existen 4 estrategias clásicas denominadas bullet, barbell, ladder y butterfly. Cada una de ellas tendrá diferente comportamiento en función del tipo y de la magnitud del desplazamiento que sufra la ETTI, por lo que no se puede decir de antemano cuál es la estrategia óptima. También hay que observar que 2 estrategias que tienen la misma duración pueden dar lugar a diferente desempeño o performance si no tienen la misma convexidad, dependiendo también de la magnitud de los cambios que se produzcan en la ETTI.

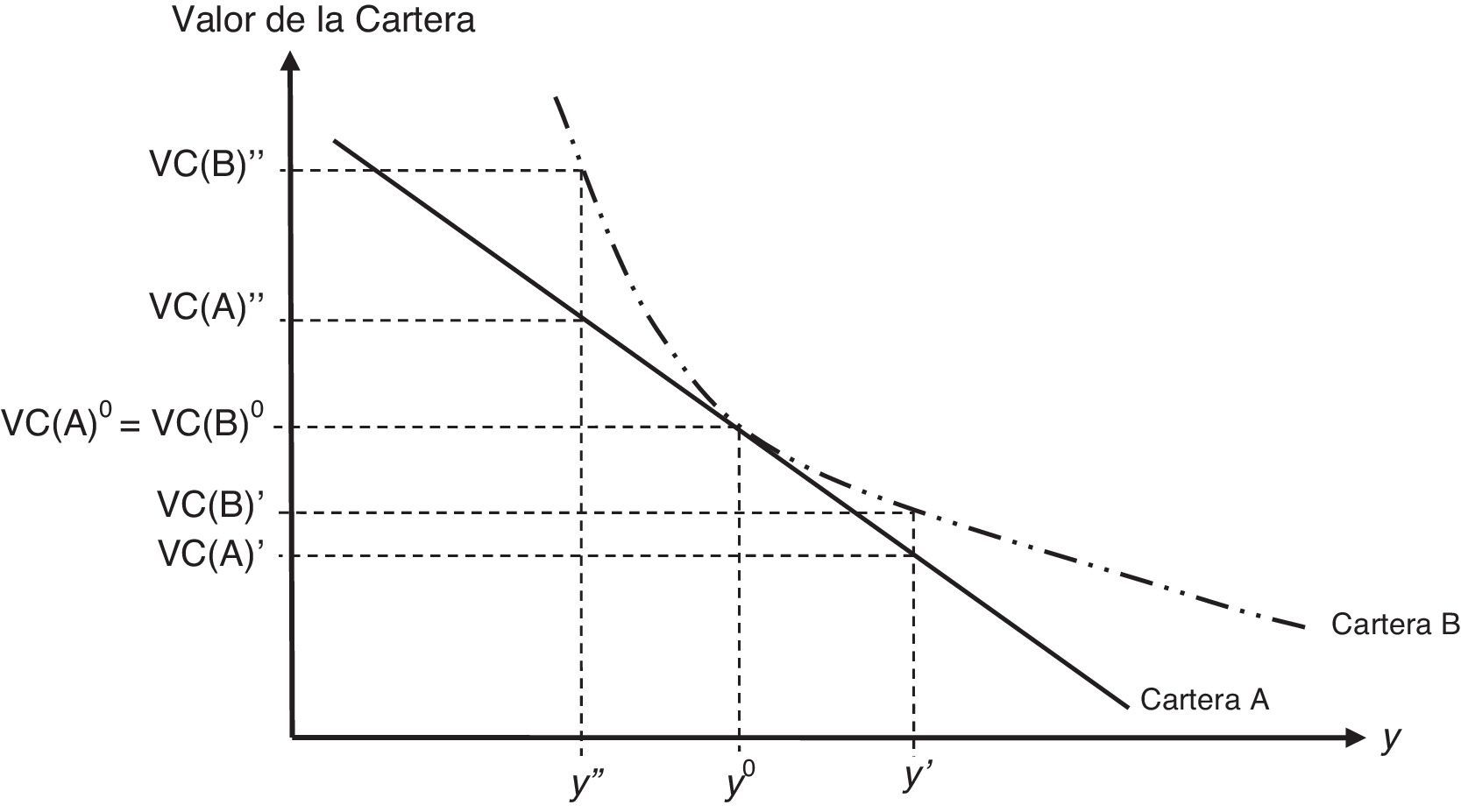
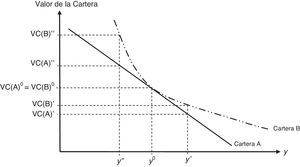
Para reflejar lo anterior, supongamos 2 carteras, que llamaremos cartera A y cartera B, iguales en todos los aspectos excepto en la convexidad, es decir, ambas carteras tienen igual duración y valor en el instante inicial, t = 0, pero la cartera B tiene mayor convexidad que la cartera A. En la figura 3 se muestra la variación en el valor de ambas carteras ante grandes desplazamientos en los tipos de interés, específicamente ante un aumento en los tipos desde y⁰ a y’, y ante un descenso en los tipos desde y⁰ a y”, es decir, y” < y⁰ < y’, siendo y⁰ el tipo de interés en el instante inicial.

Figura 3.

Evolución en el valor de las carteras ante cambios en los tipos de interés.

Como se puede observar en la figura 3, la cartera B siempre estará mejor que la cartera A ante cualquier movimiento de los tipos de interés. Por tanto, 2 carteras con igual duración y valor, pero con diferentes convexidades, obtendrán diferente performance ante grandes cambios en los tipos de interés. Concretamente, la cartera con mayor convexidad siempre superará a la de menor convexidad.

• Estrategia bullet. La estrategia bullet (cuerpo de la mariposa) consiste en concentrar la inversión en un vencimiento particular, usualmente vencimiento medio, de la curva de tipos de interés. Si dicha bullet es neutral a la duración, tendrá la misma exposición al riesgo del mercado que el benchmark. En cambio, si su duración difiere de la del benchmark, el bullet sería una apuesta sobre la dirección del mercado. Por tanto, el punto de vencimiento seleccionado del bullet afectará a la performance de la cartera dependiendo del tipo de desplazamiento en la ETTI (Martellini et al., 2003).

• Estrategia barbell. La estrategia barbell (alas de la mariposa) consiste en concentrar la inversión en los vencimientos a corto plazo y a largo plazo de la curva de tipos de interés (Martellini et al., 2003). Esta estrategia puede construirse de modo que sea neutral a la duración en relación al benchmark objetivo.

Los bonos a largo plazo de la barbell tienen un alto interés, mientras que los bonos a corto plazo aseguran que se tendrá la oportunidad de reinvertir en cualquier otro producto si hay una bajada de tipos de interés. De forma que si se produce un desplazamiento en la ETTI, una barbell tendrá un rendimiento total en un horizonte dado bastante diferente de las respectivas carteras de vencimiento a corto y a largo plazo por separado. Así, si se compara la barbell con la bullet, se suele observar que una cartera bullet tiene un mejor comportamiento que una barbell de la misma duración en un entorno de apuntamiento de la ETTI debido a la convexidad, aunque en realidad su comportamiento relativo depende de cómo es el desplazamiento de la ETTI y de su magnitud. De modo intuitivo, es mejor tener más convexidad que menos, como se ha reflejado en la figura 3. Sin embargo, el mercado encarece los bonos de mayor convexidad haciendo que disminuya su rendimiento. En la práctica, el beneficio de la convexidad depende de la magnitud del cambio en los rendimientos. Tanto es así que para pequeños desplazamientos paralelos un bullet de pequeña convexidad puede mejorar a una cartera barbell. No obstante, para hacer un análisis preciso del comportamiento relativo de ambas estrategias es necesario evaluar diferentes escenarios de desplazamiento de la ETTI, con el fin de analizar de forma precisa la exposición al riesgo y la performance de ambas estrategias.

• Estrategia ladder. La estrategia ladder (escalera) consiste en repartir la inversión en proporciones iguales sobre bonos con diferentes vencimientos, por ejemplo entre uno y 15 años (Martellini et al., 2003), de forma que si se produce el vencimiento de los bonos a un año, la escalera se mantendrá comprando bonos de vencimiento a 15 años. Dependiendo del vencimiento de los bonos en que se invierte, se pueden construir diferentes tipos de ladder. Por ejemplo, se puede construir el ladder concentrándose en vencimientos entre un mes y un año o, alternativamente, distribuyendo la inversión entre vencimientos de corto, medio y largo plazo. Otra característica de ladder es que se puede emplear con fines especulativos si se anticipa la caída en paralelo de la ETTI. No obstante, el propósito final del ladder es obtener una cartera con rendimientos cercanos a los bonos a largo plazo y con riesgo sustancialmente inferior.

Un ladder es una sencilla forma de diversificar una inversión en bonos. Por un lado, la corriente de rentas que proporciona un ladder permanecerá relativamente constante en el tiempo porque solo una pequeña proporción de la cartera vencerá y será reemplazada cada año. Por otro, la cartera incluirá bonos comprados en periodos de tipos de interés altos y bajos, y así se reducirá el riesgo de reinversión, ya que el dinero está siendo reinvertido a través de un ciclo completo de tipos de interés. Desde esta perspectiva, cualquier momento es bueno para aplicar una estrategia ladder.

4.3

Arbitraje de renta fija

El arbitraje de renta fija busca identificar inconsistencias entre los precios de los diferentes activos. Esta aproximación difiere de la negociación direccional que intenta anticipar los cambios en los tipos de interés.

El arbitraje de renta fija toma posiciones cortas y largas con el fin de aprovechar los desajustes temporales entre activos relacionados. Debido a que dichos desajustes son muy pequeños, es frecuente el uso del apalancamiento⁹. Además, las carteras se construyen de modo que estén cubiertas frente a movimientos paralelos de los tipos de interés tratando de conseguir que su duración sea la menor posible (cero si fuese posible), o alternativamente, igual al horizonte de planificación del inversor. Normalmente, las posiciones de arbitraje suelen abrirse sobre activos cuyos precios estén correlacionados y que resulten mal valorados como consecuencia de eventos externos. Dichos activos son de una amplia gama, como por ejemplo los bonos del Tesoro, corporativos, hipotecarios, de países emergentes, etc. Por otro lado, el mercado de renta fija está segmentado debido a que los grandes inversores institucionales —como los fondos de pensiones, las compañías de seguros y los bancos centrales— tienen diferentes restricciones y objetivos de inversión. Estas anomalías estructurales y efectos de segmentación pueden ser aprovechados mediante el uso de modelos analíticos, más o menos sofisticados, con el fin de detectar las malas valoraciones.

Las principales formas de arbitraje de renta fija son las siguientes (Fabozzi, 1993):

• •

  Arbitraje de emisión. Se anticipa que el precio de los bonos de la última emisión y los precios de la siguiente emisión convergerán por tener una duración muy similar. Sin embargo, existe un pequeño diferencial entre los precios de ambos tipos de bonos, ya que los emitidos hace pocos meses son menos líquidos y se negocian con un ligero descuento sobre los bonos que van a emitirse.

• •

  Arbitraje sobre el diferencial entre 2 mercados de deuda pública. Se negocia sobre el diferencial existente entre 2 curvas de tipos de interés que pueden estar denominadas en distinta moneda. Tal es el caso de realizar arbitraje entre la deuda pública de diferentes países, como por ejemplo tomar una posición larga en bonos del Tesoro a 10 años alemanes (Bund) y una posición corta en bonos a 10 años de Estados Unidos (T-Bond). En tal caso, se apuesta por un aumento del diferencial de las rentabilidades de la deuda pública en Alemania y en Estados Unidos.

• •

  Arbitraje basado en futuros. Se busca sacar ventaja de las incongruencias entre el precio de un contrato de futuros y el instrumento subyacente que debe ser entregado al vencimiento. Dado que la parte vendedora de un contrato de futuros (venta de un callable o compra de un puttable bond) puede elegir para su entrega al vencimiento del bono del Tesoro más barato (Cheapest to Delivery, CTD), existirá un margen para el arbitraje.

• •

  Arbitraje basado en opciones. Los spreads entre bonos con opciones inmersas y bonos sin opciones inmersas (bonos callables y no callables), así como sus cupones, cambian como resultado de cambios esperados en la dirección de los tipos de interés y en la volatilidad de los tipos de interés. Por tanto, una caída esperada en el nivel de los tipos de interés ampliará dicho spread por las expectativas de que el emisor ejercite la opción de compra. En cambio, una subida esperada de los tipos de interés reduce el spread. De la misma manera, un incremento en la volatilidad de los tipos de interés aumenta el valor de las opciones inmersas, y por tanto el spread entre los bonos que tienen opciones inmersas y los que no las tienen.

• •

  Arbitraje sobre el diferencial de swaps. Se aprovecha el diferencial entre el tipo swap y el de la deuda del Estado de similar duración con el fin de obtener oportunidades de arbitraje.

• •

  Arbitraje sobre la estructura de capital. Las obligaciones de pago de una empresa con los diferentes acreedores están subordinadas en función del grado relativo de obligatoriedad en dicho pago. Tanto es así que a la hora de cobrar en una situación de quiebra, tendrían preferencia en el cobro las deudas bancarias, seguidas de los distintos tipos de poseedores de bonos, según su preferencialidad, y los accionistas serían los últimos en cobrar. Por tanto, es posible sacar ventaja entre las disparidades de precios de 2 instrumentos de deuda emitidos por una misma empresa tomando posiciones compradoras en unos y vendedoras en otros.

• •

  Arbitraje sobre diferenciales de crédito. Los diferenciales de crédito entre bonos de empresas con diferente calidad crediticia pueden resultar beneficiosos. Así, es posible implementar estrategias cortas y largas por medio de los swaps de morosidad de crédito (Credit Default Swap, CDS) que permiten ir corto o largo sobre una determinada compañía sin negociar con sus bonos. En este caso, el comprador de un swap de morosidad sobre una empresa toma una posición corta sobre el crédito de dicha empresa, ganando dinero si la calidad crediticia de la empresa se deteriora, denominándose como evento de crédito. En cambio, el vendedor toma una posición larga sobre el crédito de la empresa, y gana dinero si no empeora su calidad crediticia. En este sentido, existen fondos de inversión libre (Hedge Funds) especializados en analizar la calidad crediticia de las empresas y a anticiparse a las agencias de calificación, donde la predicción de cambios en la calificación da lugar a oportunidades de inversión del tipo pair trading¹⁰. Para ello se consideran 2 empresas de un mismo sector y se toman posiciones largas en la deuda de las empresas cuya calidad crediticia (o rating) puede aumentar y posiciones cortas en la deuda de la empresa cuya calidad crediticia puede descender.

• •

  Carry trades. Consiste en la compra de bonos con rendimientos mayores que el coste del dinero que se pide prestado para comprarlos, aunque, como es natural, esta estrategia entraña riesgos. La estrategia adopta 2 formas: la intra-curva y la inter-curva. La intra-curva consiste, por ejemplo, en pedir prestado al tipo a 3 meses para comprar bonos a 20 años. La inter-curva consiste, por ejemplo, en pedir prestado en dólares en Estados Unidos y comprar deuda del Estado español. En el último caso, resulta crítico valorar también el riesgo de tipo de cambio.

• •

  Arbitraje con equilibrio de inflación. Hoy día existen algunos tipos de deuda del Tesoro cuyos rendimientos están protegidos contra la inflación, como los TIPS (Treasury Inflation Protection Securities). Donde sí se considera que la inflación va a subir, se irá largo en TIPS y corto en deuda tradicional, y viceversa. De esta forma se consigue una estrategia asociada a la capacidad de predecir la inflación y cuyos rendimientos no están correlacionados con los tipos de interés.

• •

  Arbitraje de diferente valor en 2 divisas. Una misma empresa puede emitir bonos con rentabilidades distintas según la moneda de su denominación. Sin embargo, los diferenciales de rentabilidad respecto a sus respectivos activos libres de riesgo deben ser únicos porque ambos bonos tienen la misma probabilidad de impago y la prima de riesgo debería ser la misma. Si estas divergencias entre los diferenciales de rentabilidad persisten en el tiempo proporcionan oportunidades de arbitraje. Por ejemplo, si el diferencial de crédito es superior en Estados Unidos, se puede ir largo en los bonos denominados en dólares (cubriéndose ante la exposición a los tipos con una posición corta en bonos del Tesoro de Estados Unidos) e ir corto en los bonos denominados en euros (cubriéndose ante la exposición a los tipos con una posición larga en bonos europeos). Nótese que esta estrategia no tiene exposición al riesgo de interés ni de impago, y si se cumple el efecto Fisher internacional¹¹, tampoco tendrá exposición al tipo de cambio.

• •

  Treasure over Eurodollars spread (TED). Consiste en tomar una posición larga en bonos del Tesoro de Estados Unidos y una posición corta en contratos de eurodólares con el mismo vencimiento. Igualmente puede concebirse como una inversión en bonos gubernamentales cubierta con swaps denominados en la misma divisa. En general, puede buscarse el diferencial entre los bonos gubernamentales y algún tipo de interés interbancario. como el LIBOR, con el mismo vencimiento.

4.4

Estrategias de negociación sobre la curva de tipos de interés

Se trata de una de las estrategias de negociación de renta fija más universalmente empleadas. En ella se toman posiciones cortas y largas sobre los diferentes vencimientos de la ETTI para beneficiarse de malas valoraciones de los bonos en dichos tramos. Dichas valoraciones erróneas conducen a distorsiones en la curva de tipos de interés que representan oportunidades de inversión. En estas estrategias pueden negociarse activos de renta fija sobre la ETTI en un solo país (intra-curva) o en varios países, realizando arbitraje entre la curva de tipos de dichos países (inter-curva).

En la práctica suelen distinguirse 2 subtipos de estrategias intra-curva: apuestas sobre la pendiente de la ETTI y apuestas sobre la curvatura de la ETTI (o butterfly).

4.4.1

Apuestas sobre la pendiente de la estructura temporal de los tipos de interés

Las estrategias que se refieren a apuestas sobre el cambio en la pendiente de la ETTI implican la asignación de activos en el espectro de vencimientos de forma diferente a como lo hace el benchmark, replicando al mismo tiempo la duración del mismo. Una forma de alterar la asignación de vencimientos de una cartera sería a través de diferentes combinaciones de bullets y barbells.

A continuación se describen las apuestas por el aplanamiento y el empinamiento en la pendiente de la ETTI.

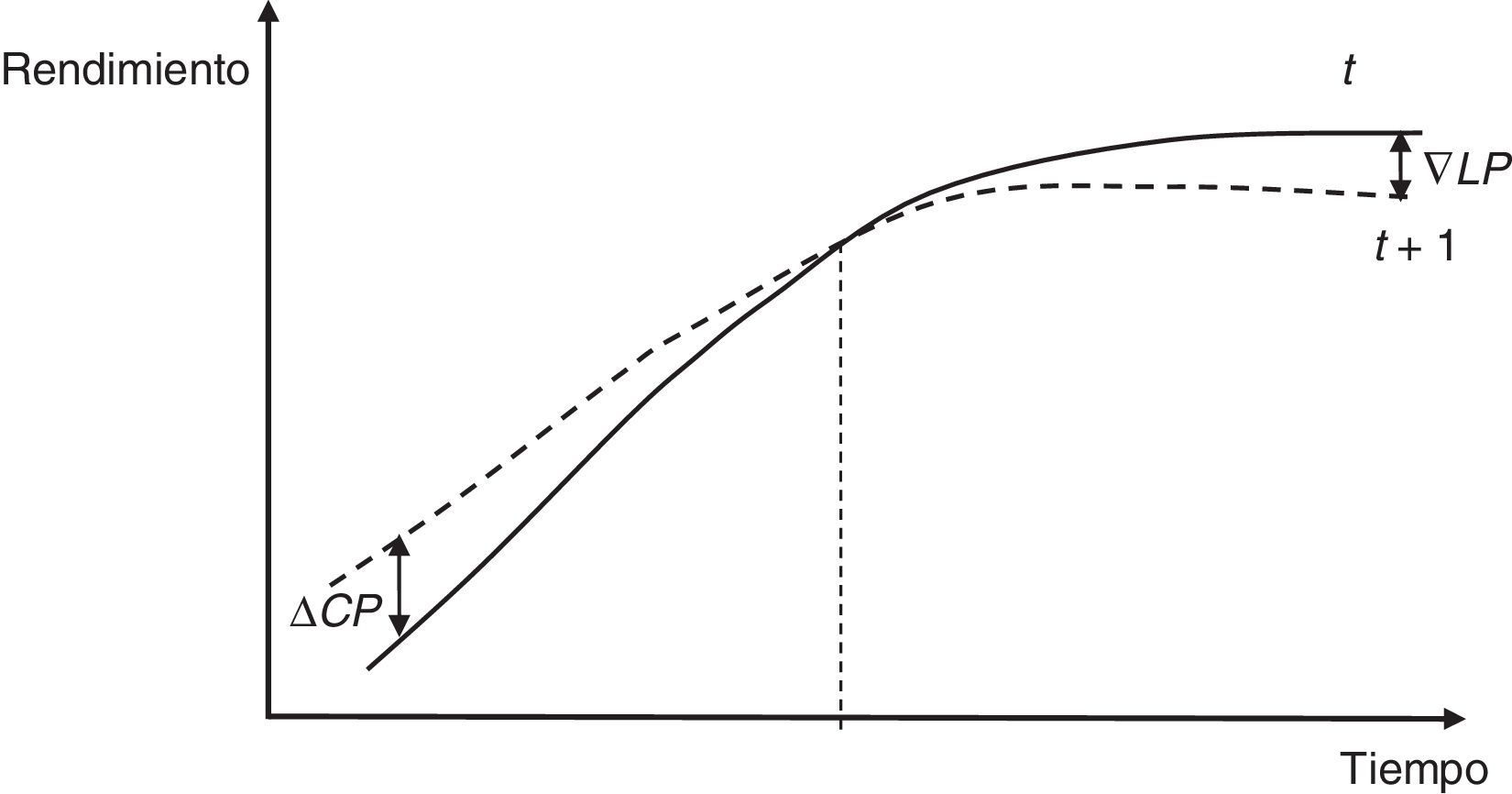
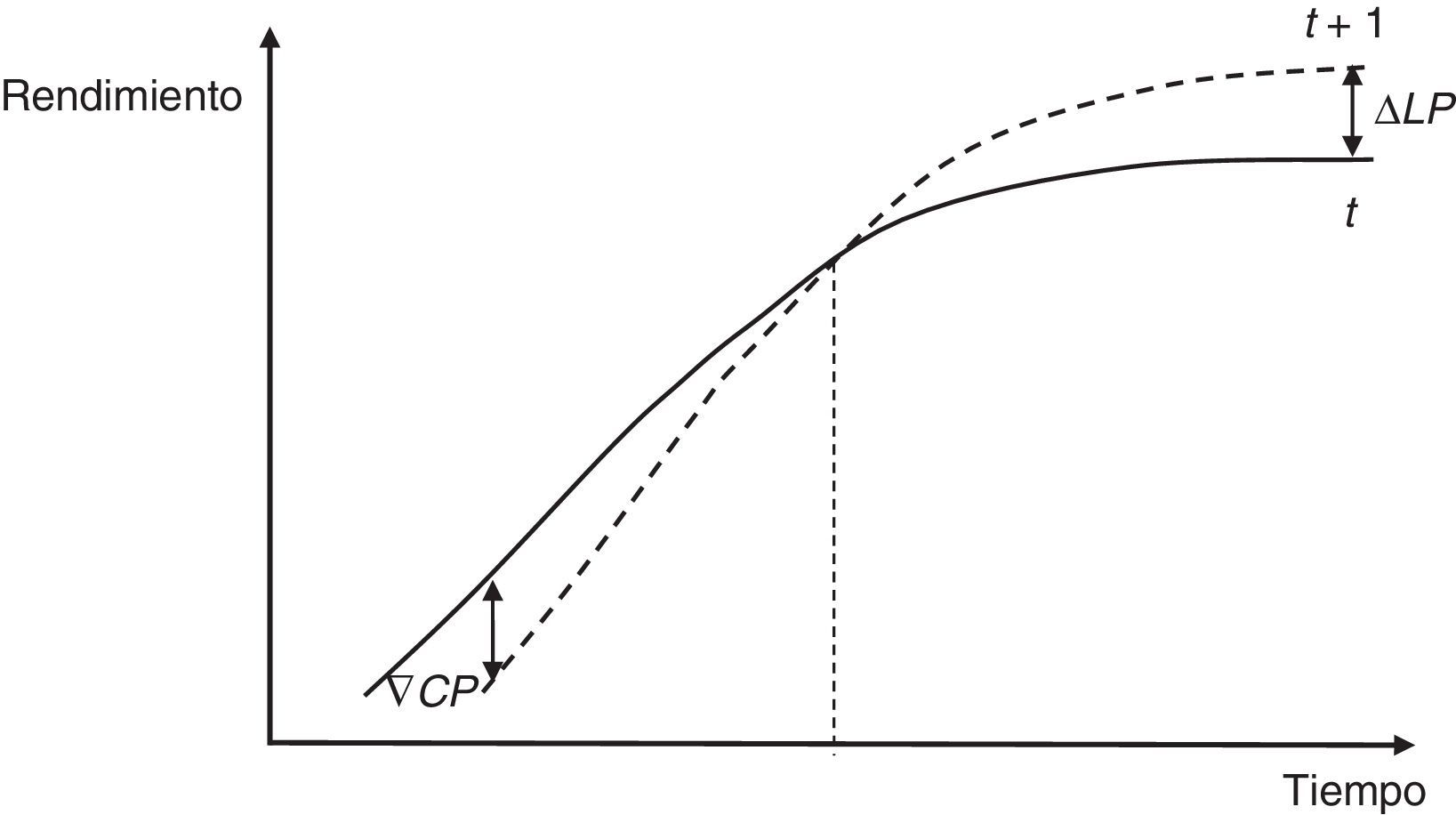
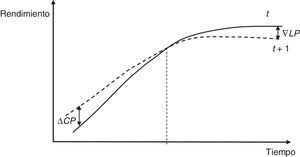
4.4.1.1

Apuestas sobre el aplanamiento de la estructura temporal de los tipos de interés

En este caso se toman posiciones cortas, o vendedoras, sobre bonos próximos a la expiración (se piensa que subirán los tipos de interés a corto plazo) y posiciones largas, o compradoras, sobre bonos con expiración a largo plazo (se piensa que bajarán los tipos de interés a largo plazo). Asumiendo que no se producen movimientos paralelos en el nivel, en la figura 4 se puede observar el movimiento en aplanamiento de la ETTI.

Figura 4.

Movimiento en aplanamiento de la ETTI.

Hay que observar que si se consigue que la duración de la cartera en la apuesta por el aplanamiento de la ETTI sea igual al horizonte de planificación del inversor, entonces la estrategia estará inmunizada frente a desplazamientos paralelos en el nivel de los tipos.

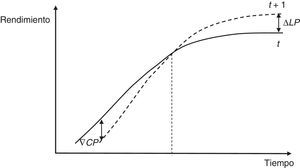
4.4.1.2

Apuesta por empinamiento de la estructura temporal de los tipos de interés

En este caso se toman posiciones largas en bonos próximos al vencimiento y cortas en bonos de largo vencimiento. De nuevo, la estrategia estará inmunizada frente a desplazamientos paralelos de la ETTI si su duración es cero o igual al horizonte de planificación del inversor. Igual que en la figura 4, no asumimos desplazamientos paralelos en el nivel de la ETTI (fig. 5).

Figura 5.

Movimiento en empinamiento de la ETTI.

El aplanamiento o empinamiento de la ETTI depende de factores macroeconómicos como la inflación, el producto interior bruto y la política monetaria perseguida por el banco central. Así, las posiciones direccionales tomadas sobre la ETTI expresan el punto de vista macroeconómico del gestor, quien realiza predicciones sobre la forma de la ETTI, y no sobre el nivel de la curva de tipos de interés (Fabozzi, 1993; Martellini et al., 2003, entre otros).

4.4.2

Apuestas sobre la curvatura de la estructura temporal de los tipos de interés

Este tipo de estrategia, denominada mariposa o butterfly, consiste en combinar una barbell (alas de la mariposa) y un bullet (cuerpo de la mariposa) donde se supone que se vende el cuerpo (bono de vencimiento intermedio) y se compran las alas¹² (bonos de vencimientos cortos y largos). Así, el propósito es ajustar el peso de estos componentes de manera que la estrategia sea autofinanciada y tenga una duración igual a cero, lo que garantiza la inmunización ante pequeños desplazamientos paralelos de la curva de tipos. Asimismo, si la butterfly se estructura de forma que tenga una convexidad positiva, generará ganancias positivas si se producen largos desplazamientos paralelos de la ETTI.

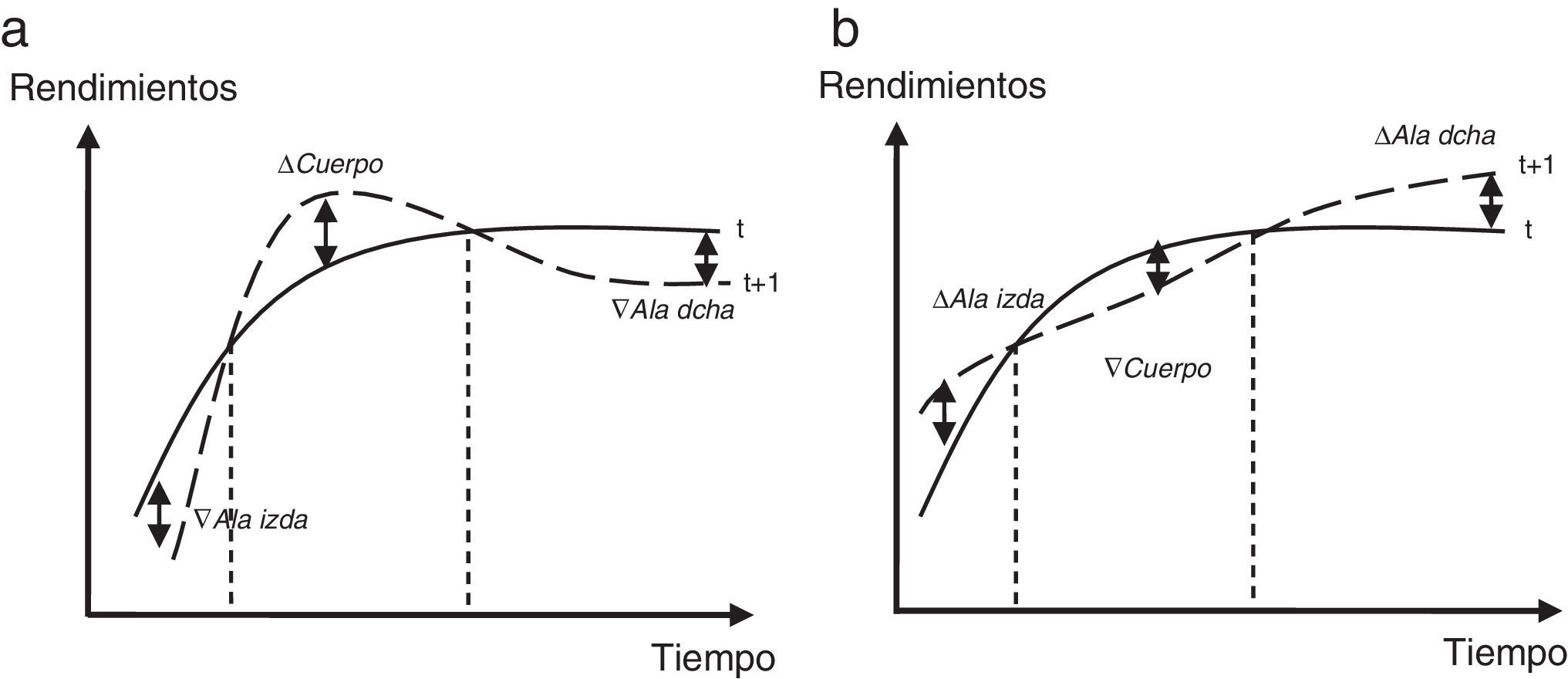
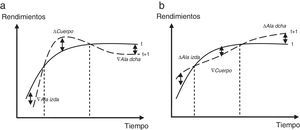
En resumen, las butterflies tienen como objetivo la cobertura frente a cambios en la pendiente o convexidad de la ETTI, es decir, la estrategia está diseñada para explotar malas valoraciones de bonos, mientras que se controla el riesgo de tipos de interés. En la figura 6 se puede observar un aumento de la curvatura de la ETTI (a) y una disminución de la misma (b).

Figura 6.

Movimientos de la curvatura de la ETTI.

En todos los casos, tanto si aumenta la curvatura (a) como si disminuye (b), se obtienen beneficios si la ETTI en el futuro toma una forma más suave con independencia de sus desplazamientos paralelos, pues las butterflies pueden elegirse con duración cero o igual al HPI, dependiendo de si se quiere inmunizar instantáneamente la cartera o inmunizarla al HPI. Pese a todo, una butterfly no es una máquina de hacer dinero sin riesgo, y puede producir rendimientos negativos si se producen movimientos complejos en la curva de tipos de interés tales como desplazamientos no paralelos o cambios en su convexidad.

Las butterflies tienen numerosos usos, incluyendo la implementación de estrategias de negociación, la creación de opciones sintéticas y la realización de apuestas sobre la volatilidad y la forma de la ETTI.

En Martellini et al. (2002) se muestran las formas de inmunizar los diferentes tipos de butterflies contra diferentes movimientos específicos de la ETTI que pueden afectar a su pendiente y a su curvatura.

4.5

Análisis del valor relativo de los bonos

El análisis del valor relativo de los bonos consiste en detectar bonos que están infravalorados (sobrevalorados) por el mercado con el fin de comprarlos (venderlos). Para detectar la mala valoración suelen emplearse 2 métodos: la comparación de bonos con una cartera de bonos segregables (strips), y la detección de bonos caros y baratos.

4.5.1

Comparación de bonos con una cartera de bonos segregables o strips

En diversos países, los cupones individuales de los bonos del Tesoro pueden ser negociados de forma separada del principal. A estos se los conocen como strips (separate trading of register interest and principal), los cuales son instrumentos financieros con rendimiento implícito creados a partir de la segregación de los flujos que originan los bonos. Por ejemplo, un bono que paga m cupones más el nominal al vencimiento, puede convertirse en m + 1 bonos cupón cero a través de los strips, donde el único flujo de caja distribuido por cada uno de los m + 1 bonos cupón cero que componen el strip es el principal en su fecha de vencimiento. Estos bonos cupón cero son atractivos para inversores a largo plazo, como los fondos de pensiones y compañías de seguros, y su propósito fundamental es asegurar un rendimiento en un horizonte de inversión a largo plazo. Tanto es así que los strips a largo plazo son interesantes en la medida en que es difícil encontrar bonos cupón cero de tan largo vencimiento, y en contraste con los bonos con cupón, aquellos no tienen riesgo de reinversión de flujos intermedios.

En este análisis del valor relativo de los bonos se trata de detectar oportunidades de arbitraje comparando los precios de un bono con cupón y la suma de los strips que reconstruyen exactamente el bono, es decir, 2 instrumentos que son equivalentes en términos de futuros flujos de caja. Por tanto, si el mercado es eficiente y no hay oportunidades de arbitraje, tal bono puede descomponerse en una suma de bonos cupón cero o strips. Así, el precio del bono debe ser igual a la suma de strips descontados.

Este arbitraje no es fácil de detectar, porque el arbitrajista ha de tener en cuenta la horquilla de precios bid-ask y el tipo repo en su cálculo. En este sentido, Jordan et al. (2000) han encontrado diversas oportunidades de arbitraje en el mercado de strips del Tesoro en Estados Unidos.

4.5.2

Detección de bonos caros y baratos: bond picking

En este análisis del valor relativo de los bonos se trata de buscar bonos que históricamente presenten rendimientos anormales en su vencimiento, tomando como referencia de buen comportamiento una curva teórica de tipos cupón cero ajustada con los precios de los bonos. Siguiendo a Martellini et al. (2003), el primer paso de esta metodología es, entonces, estimar una curva de tipos cupón cero usando datos de activos con las mismas características en términos de liquidez y riesgo; por ejemplo:

• •

  Bonos de un país específico usando la curva de tipos cupón cero del tesoro de dicho país como referencia; por ejemplo, bonos del Tesoro de Estados Unidos usando T-bills y T-bonds para construir la curva de tipos de interés del Tesoro estadounidense.

• •

  Bonos de una zona financiera unificada (con una única divisa) usando los bonos emitidos en esta zona para obtener una curva de tipos cupón cero adecuada; por ejemplo, eurobonos del Tesoro usando bonos franceses, alemanes y holandeses para construir la curva de tipos del Tesoro europeo.

• •

  Bonos corporativos de un país específico o zona financiera unificada con la misma clasificación crediticia (rating) y sector económico; por ejemplo, bonos de Telecom BBB de la zona euro usando el mismo tipo de bonos para construir la curva de tipos de interés euro Telecom BBB.

• •

  Bonos corporativos de una sola firma; por ejemplo, usar solo bonos de France Telecom para construir la curva de tipos de France Telecom.

Una vez estimada la curva de rendimientos cupón cero que servirá de referencia, se calcula el precio teórico de cada activo como suma de sus flujos de caja descontados usando los tipos cupón cero de los correspondientes vencimientos. Entonces se calcula la TIR que proporciona el mercado y se compara con la TIR obtenida teóricamente.

Finalmente, la dispersión (spread) entre la TIR del mercado y la TIR teórica permitirá la identificación de activos caros (dispersión negativa) o activos baratos (dispersión positiva), todo ello cuando las posiciones cortas sean viables. Nótese que resulta indiferente usar la TIR o el precio de los activos. Sin embargo, al usar el precio de los activos debemos tener en cuenta que un activo caro se correspondería con una dispersión positiva (el precio de mercado es superior al precio teórico), mientras que un activo barato se correspondería con una dispersión negativa (el precio de mercado es inferior al precio teórico).

En resumen, estos métodos pretenden obtener beneficios a partir de ineficiencias o malas valoraciones detectadas en el mercado considerando que la curva de tipos de interés teórica es la correcta.

Finalmente, hay que señalar que los problemas que puede presentar esta estrategia derivan de la dificultad de modelizar correctamente las curvas de tipos de interés, ya que dependiendo del modelo de estimación de la ETTI empleado, los activos caros y/o baratos pueden variar (ver cómo varían las curvas de tipos de interés dependiendo del modelo de estimación en Yallup, 2012).

5

Apalancamiento y elección de un benchmark

El apalancamiento consiste en el incremento de la posición en el mercado por encima de la cantidad del dinero que realmente se invierte. Una forma de aumentar los rendimientos de una cartera es mediante la petición de dinero prestado con el fin de tomar una posición en el mercado que es mayor que si solo se invierte dinero en efectivo. Por tanto, una cartera en la que se ha tomado dinero prestado para su formación se dice que está apalancada.

El principio básico para usar apalancamiento es que se espera ganar un rendimiento en los fondos prestados que es superior al coste que habrá que pagar por pedirlos prestados. En consecuencia, el riesgo del apalancamiento es que el rendimiento generado por los fondos prestados sea menor que su coste. Algunos gestores de inversión usan el apalancamiento para beneficiarse de los cambios de precios, magnificando los beneficios obtenidos de pequeños cambios de precio por medio del apalancamiento. Así, ante expectativas de bajadas de tipos de interés es posible pedir fondos prestados para incrementar la posición en bonos.

Nótese, en este sentido, que la petición de fondos prestados incrementa la duración de la cartera. Si se considera, por ejemplo, una cartera de 100 € invertidos en bonos de duración 2 años, un cambio de 100 puntos básicos en los tipos producirá un cambio en la cartera de 2 €. Si se piden prestados otros 100 €, el fondo apalancado tendrá una inversión total de 200 €. Por tanto, si se invierte en un bono de duración 2 años, un cambio de 100 puntos básicos en los tipos producirá, ahora, un cambio de 4 € en la cartera, es decir, la nueva duración de la cartera será ahora igual a 4 años.

Existen 2 formas de crear apalancamiento. La primera forma es por medio del uso de instrumentos derivados, y la segunda es crear el apalancamiento por medio del mercado de repos, o en el caso específico del mercado español, por medio de las operaciones simultáneas, lo que confiere una mayor libertad para negociar con los activos que lo que permite el mercado de repos.

Una operación repo (en inglés, repurchase agreement, pacto de recompra) es un acuerdo, que se negocia en un mercado OTC (over the counter) para vender algún activo (normalmente letras, bonos y obligaciones del Estado) a otra parte y recomprarlo a un precio especificado en una determinada fecha futura. La diferencia entre el precio de compra y de venta da lugar a un tipo de interés llamado tipo repo. Por su parte, una operación simultánea es la operación constituida por 2 compraventas vinculadas de sentido contrario, contratadas al mismo tiempo pero con momentos de liquidación distintos. En ambos casos, para el participante que compra los valores en la primera transacción de la operación doble se trata de una adquisición temporal, mientras que para su contrapartida se trata de una cesión temporal, sobre el mismo tipo de activo y por el mismo importe nominal. La característica principal de las operaciones simultáneas es que el comprador tiene plena disponibilidad de los valores adquiridos, con independencia de la fecha en que se ha contratado la operación de retorno. Esta característica hace que esta sea el activo ideal para la toma de posiciones cortas en renta fija.

La principal diferencia entre la operación simultánea y la repo está en que, a efectos legales, en el caso de la operación repo el comprador no ostenta la propiedad del mismo ante la ley, mientras que en el caso de la operación simultánea sí es propietario del bono, pudiendo disponer de él en la forma que desee hasta la fecha de vencimiento. Es decir, en el caso de la operación simultánea el comprador del bono puede revenderlo, siempre que lo recompre para devolverlo en la fecha de vencimiento, mientras que en el caso de la operación repo esto no es posible, teniendo solo derecho a disfrutar de los cupones que pagase el bono. En resumen, tanto el mercado de repos como el de operaciones simultáneas son mercados que permiten que se pidan fondos prestados mediante un acuerdo donde se ofrece otro activo como colateral del préstamo. Así, un acuerdo de recompra es un préstamo colateralizado donde el colateral es el activo vendido y posteriormente comprado (suelen ser títulos del Tesoro) y donde la diferencia entre el precio de recompra y el precio de venta es el coste del préstamo que genera el llamado tipo repo, o tipo de la operación simultánea.

Gracias a la existencia de un colateral, el tipo repo y simultáneo será, generalmente, inferior al tipo interbancario o el tipo de los Bancos Centrales, debido a que estas últimas transacciones carecen de colateral y no están aseguradas. Por tanto, esto representa una ventaja para un dealer, ya que el tipo del mercado de repos o el simultáneo, usado para pedir prestado a corto plazo, será inferior que el coste, y por consiguiente menor que la financiación bancaria.

Existen 2 posiciones en una operación simultánea: una posición larga, donde se piden fondos prestados entregando un activo que se devolverá en el futuro, y una posición corta, también conocida como repo inverso. En el repo inverso se entregan los fondos a cambio de los activos mediante los cuales se pueden tomar posiciones cortas, siempre y cuando se recompren y se entreguen en la fecha de finalización de la operación simultánea. Nótese que ambos acuerdos son transacciones que permiten financiar las posiciones cortas y largas, normalmente en deuda pública.

No existe un único tipo repo o simultáneo, pues puede variar en cada transacción dependiendo de diversos factores, como son la calidad del colateral, el plazo, la curva de tipos de interés, los requerimientos de entrega, la disponibilidad del colateral y los tipos de interés interbancarios predominantes.

Finalmente es necesario hacer alguna consideración sobre cómo evaluar los rendimientos de una inversión. La forma más sencilla de hacerlo es compararlos con los de otra cartera denominada benchmark; se trata de una cartera, real o conceptual, que se emplea para comparar los rendimientos de una inversión. El benchmark desempeña el papel de dirigir el riesgo de los activos. Fundamentalmente existen 4 tipos de benchmarks:

• •

  Un índice de mercado o cartera de mercado, tal como el de Barclays Capital Aggregate Bond Index. Estas son carteras simuladas, y no reales, que no tienen gastos ni costes de transacción asociados. Hay un amplio menú de elecciones de índices de referencia en el mercado de bonos, y cada uno representa características de riesgo ligeramente diferentes. Normalmente, se pueden tomar posiciones sobre aquellos a través de ETF (exchange-traded fund).

• •

  Las carteras reales gestionadas cuyos rendimientos son promediados según el tipo de cartera —por ejemplo, Morningstar and Lipper— crean categorías de fondos mutuos de renta fija tales como corto plazo, índice de bonos de alta calidad, índice de bonos de baja calificación de vencimiento intermedio, etc.

• •

  Los pasivos de una institución pueden usarse como benchmark.

• •

  La cartera resultante de aplicar una estrategia pasiva, como puede ser la estrategia de la inmunización.

La elección de un benchmark es el factor más importante en la determinación del perfil de riesgo y del nivel de rendimiento de una cartera de renta fija. En este sentido, los 4 factores de riesgo que definen a la mayoría de los benchmarks son la duración, el sector, el crédito y las divisas. En cuanto a la duración, esta debe ser similar a la de la estrategia que se quiera evaluar; así, el benchmark y dicha estrategia serán equivalentes en términos de riesgo. Por su parte, el benchmark y la estrategia a comparar deben pertenecer al mismo sector, tener igual riesgo de crédito y estar evaluadas en la misma divisa; por ejemplo, una estrategia activa y un benchmark sobre activos de la deuda pública de España. En este ejemplo, ambas carteras pertenecen al mismo sector (deuda pública española), de igual crédito (el que tenga en ese momento el Tesoro español) e igual divisa (euros).

6

Consideraciones finales

La estructura temporal de los tipos de interés (ETTI) se define como la relación funcional entre el tipo de interés nominal en los préstamos sin riesgo de la economía y el tiempo hasta su vencimiento, manifestando así la dependencia entre los tipos de interés y su plazo de amortización. La ETTI es una herramienta esencial tanto en la política monetaria, debido a la información implícita que recoge sobre las expectativas de los agentes en la futura evolución de los tipos de interés, como en su implementación en estrategias de negociación sobre carteras de renta fija.

Con este trabajo hemos pretendido contribuir a la literatura existente ofreciendo un resumen actualizado de diferentes estrategias de negociación sobre carteras de renta fija, implementadas con el uso de la ETTI.

7

Financiación

Esta investigación ha recibido ayuda financiera del Ministerio de Ciencia y Educación de España a través del proyecto de investigación ECO2010-21318.

Agradecimientos

Los autores agradecen la ayuda financiera del Ministerio de Ciencia y Educación de España.