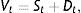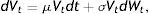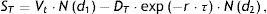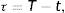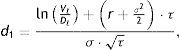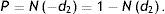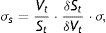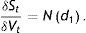Se utiliza la metodología de Merton (1974) para obtener la probabilidad de incumplimiento de las obligaciones de pago de un conjunto de empresas españolas no financieras que cotizan en bolsa, desde enero de 2002 hasta diciembre de 2011, con el objetivo de analizar si la actual crisis económica ha tenido repercusión en el valor de las probabilidades de default. A partir del número, del precio y de la volatilidad de las acciones y del valor facial de la deuda a corto y largo plazo de cada empresa se obtienen, mediante métodos de resolución numéricos, los valores y las volatilidades para el conjunto de empresas de la muestra, que permiten cuantificar las probabilidades de default con frecuencia mensual y para todo el plazo analizado. Las probabilidades obtenidas han permitido constatar, empíricamente, la influencia negativa del actual contexto económico sobre el riesgo de crédito de las empresas, especialmente en las del sector de Servicios Financieros e Inmobiliarios.
This work focuses on obtaining default probabilities for the Spanish case, in order to study the impact of the current economic situation on company credit risk. Using Merton's model (1974) we estimate the likelihood that outstanding non-financial companies listed on the Spanish stock exchange market would have to default on its debt obligations over the period from January 2002 to December 2011. Based upon the number of shares of each company, the observable price of a share and its volatility, and the short and long term debt face value, we computed company values and volatility. These data are used to determine the monthly time series of default probabilities for selected companies over the period analyzed. The analysis carried out reveals a negative impact of the economic crisis over these probabilities, especially in the sector of Financial Services and Real Estate.
El riesgo es un concepto que depende del contexto y de la disciplina científica en que es utilizado. Por ello, existen diferentes medidas del riesgo. Es habitual describir el riesgo como la desviación típica del rendimiento esperado o como el valor esperado de la pérdida. Sin embargo, la acepción más habitual es la desviación negativa del resultado esperado. Si se considera el riesgo en el ámbito financiero, siguiendo a Duffie y Singleton (2003) se establece la siguiente tipología de riesgos financieros: riesgo de mercado, riesgo de liquidez, riesgo operacional, riesgo sistémico y riesgo de crédito. Algunos autores (Ruiz et al., 2000) también consideran el riesgo legal como un riesgo financiero.
La influencia negativa de factores externos e internos en los mercados implica variaciones desfavorables en los precios. Estas variaciones negativas son las que generan un riesgo de variación de precios o riesgo de mercado, que puede ser de tipo de cambio, de cotización bursátil, de tipo de interés o de mercaderías, entre otros. El riesgo de liquidez es el asociado a la ocasional falta de capacidad del mercado de transformar un activo en efectivo; errores provocados por la operativa de los sujetos que llevan a cabo las operaciones o errores debidos a la tecnología conllevan un riesgo operacional. El riesgo sistémico hace referencia a una caída general en la liquidez del mercado financiero o a una reacción en cadena de sucesos de incumplimiento; faltas en la formalización o legalidad contractual de las operaciones pueden ocasionar un riesgo legal en las mismas. Y finalmente, el riesgo de crédito es el riesgo de pérdida que se puede producir por el incumplimiento de las obligaciones de pago del sujeto obligado a ello en la operación financiera o por la disminución de la calidad crediticia de la contraparte. Según Duffie y Singleton (2003), el riesgo de crédito es el riesgo de quiebra o de reducciones en el valor de mercado causadas por cambios en la calidad crediticia de los emisores y contrapartes.
Este trabajo se centra en el riesgo de crédito, ya que en los últimos años ha adquirido una especial importancia, como pone de manifiesto la abundante literatura existente sobre este tema y que queda reflejada también en los acuerdos de Basilea, uno de cuyos principales objetivos es mitigar este riesgo, adecuando las exigencias de recursos propios al capital en riesgo real de las empresas. De hecho, desde sus inicios, los acuerdos de Basilea han intentado cubrir posibles pérdidas inesperadas debidas al riesgo de crédito y han asentado la premisa de que debe disponerse de un sistema que lo mida correctamente. El principal objetivo de los diferentes acuerdos de Basilea es que los requerimientos de capital sean más sensibles al riesgo de crédito. En el primer acuerdo (Basilea, 1988) se fijaba un coeficiente de solvencia fijo del 8% de los activos, ponderados por un factor de riesgo, determinado de una forma simple y poco realista. En el segundo y tercero (Basilea, 2004; Basilea, 2011) se permite medir el riesgo de crédito a partir de métodos más rigurosos, como el método de calificaciones internas o internal rating based approach (IRB). Para este último método un input principal son las probabilidades de incumplimiento o probabilidades de default.
Obviamente, esta importancia es aún mayor en un contexto de crisis económica, donde los derivados de riesgo de crédito tienen un papel relevante. En la valoración de estos activos derivados, las probabilidades de default son una pieza fundamental (Bermúdez et al., 2009).
El objetivo de este estudio es obtener las probabilidades de default de Merton (1974) para el mercado español y para los años 2002-2011 y poder observar, así, si la cuantificación de estas probabilidades ha reflejado los años de crisis económica. Aunque se han publicado trabajos que obtienen probabilidades de default para el mercado español (Martín y Trujillo, 2005; Badía et al., 2007; Samaniego et al., 2007; Caicedo et al., 2012) y para otros mercados internacionales (Caicedo et al., 2011; Dietsch y Petey, 2004), no existe ningún estudio publicado que efectúe este análisis para el caso español y para un amplio horizonte temporal, que incluya los años anteriores, de inicio y de consolidación de la crisis.
Este trabajo se estructura de la siguiente forma: primero se revisan los principales modelos de riesgo de crédito. A continuación se describe el modelo de Merton (1974). En el cuarto apartado se describe la muestra utilizada para la aplicación empírica del modelo, que se lleva a cabo en el siguiente apartado, donde también se analizan los resultados obtenidos. Finalmente se extraen las conclusiones más relevantes.
2Modelos de riesgo de créditoEl riesgo de crédito de una entidad se puede valorar a partir de características cualitativas, es decir, analizando ciertas cualidades inherentes a la capacidad de cumplimiento de pago de las entidades. Algunas de estas cualidades son el conocimiento del sujeto de crédito, la capacidad de pago derivada de un análisis financiero del mismo, el capital de la entidad, el conocimiento de las garantías de crédito de la firma y las condiciones cíclicas que pueden determinar la exposición al riesgo de crédito de las empresas. Ahora bien, de forma paralela, un posible análisis cuantitativo del riesgo de crédito consiste en el cálculo de las probabilidades de default o de incumplimiento. Estas, aparte de proporcionar información sobre la capacidad de cumplimiento de pago de las empresas, posibilitan estrategias de cobertura y sirven, evidentemente, para la cuantificación y la valoración de derivados de crédito. Es por ello que los modelos que calculan estas probabilidades han adquirido más importancia en los últimos años.
Existen, básicamente, 2 metodologías que determinan probabilidades de default: la de los modelos estructurales y la de los modelos reducidos. Los modelos estructurales se basan en el valor de la empresa para determinar el suceso de crédito y utilizan información relativa a la cotización de las acciones y a su volatilidad. El modelo de Merton (1974) es el primero en desarrollar esta metodología. Posteriormente, tomando como base y referencia este modelo se desarrollan otros modelos estructurales, entre los que destacan Geske (1977), CreditMetrics de JP Morgan (1977), Longstaff y Schwartz (1995) y el modelo Vasicek-Kealhofer (Vasicek, 1984; Kealholfer, 2003a; Kealholfer, 2003b) implementado por Moody's KMV (2003), entre otros. En los modelos reducidos, el suceso de crédito está supeditado a información exógena de la empresa, como es la información de mercado relacionada con los títulos de la entidad de referencia. Destacan, entre otros, los trabajos de Jarrow y Turnbull (1995); Duffie y Singleton (1999); Kijima y Muromachi (2000); Hughston y Jarrow (2001) y Zhu y Chiu (2007).
Existen trabajos que revisan y comparan los distintos modelos de riesgo de crédito, estructurales y reducidos: Crouhy et al. (2000); Giesecke (2004); Elizalde (2005); Hao et al. (2010).
Una ventaja de los modelos estructurales es la utilización de una metodología ampliamente desarrollada en los últimos años como es la teoría de valoración de opciones financieras. A partir de datos del balance de la empresa y de información del mercado de renta variable, estos modelos obtienen el valor de la empresa y su volatilidad, y para cuantificar la probabilidad de incumplimiento comparan el valor de la empresa deducido con un determinado umbral de su deuda. Además, tanto los inputs como los outputs obtenidos son variables económicas reales.
Este trabajo obtiene las probabilidades de default asociadas al modelo estructural de Merton (1974), que es uno de los más utilizados en la práctica de mercado. Así, por ejemplo, tanto los acuerdos de Basilea II y III como el modelo desarrollado por Moody's analizan el riesgo de crédito a partir de este modelo. Por otra parte, para cuantificar las probabilidades de default de Merton se precisa de información contable y bursátil de fácil acceso. Además, la bolsa es un mercado más activo que el mercado de renta fija, base de los modelos reducidos. Respecto a otros modelos estructurales, una ventaja del modelo de Merton (1974) es que no presenta una alta complejidad analítica derivada de la aplicación del modelo de valoración de opciones de Black y Scholes (1973).
3Modelo de MertonMerton (1974) considera una empresa financiada mediante recursos propios, representados por una acción, y recursos ajenos o deuda formalizada por una obligación cupón cero. Tanto la acción como la obligación se negocian en un mercado financiero en el que no hay posibilidades de arbitraje, ni costes de transacción, ni impuestos, ni restricciones a la venta al descubierto, y los activos son infinitamente divisibles. Se supone una economía en tiempo continuo y que el tipo de interés libre de riesgo r es constante y cierto. Existe además la posibilidad de prestar y endeudarse al mismo tipo de interés.
En un momento t∈0,T se cumple, según Modigliani y Miller (1958), que el valor de los activos de la empresa, Vt, es la suma del valor de la acción St y el valor de la deuda Dt con vencimiento en T:
de manera que Vt también puede considerarse un activo negociable en el mercado.La economía está representada por el espacio de probabilidad Ω,ℱt,P, donde Ω es el conjunto de sucesos posibles ωi, ℱt es una filtración en t que genera un proceso browniano y P es la medida de probabilidad objetiva asociada.
Bajo estas hipótesis, la dinámica del valor de la empresa queda descrita mediante la siguiente ecuación diferencial estocástica:
que define un proceso browniano geométrico donde μ es la tendencia instantánea de los cambios en la variable Vt, σ es la volatilidad instantánea o coeficiente de difusión del proceso y dWt es el proceso de Wiener estandarizado, definido en el espacio de probabilidad.Bajo estas hipótesis la acción representa una opción call sobre el activo de la empresa con vencimiento T y precio de ejercicio DT. Así, el valor de la acción en un instante t es, bajo la hipótesis de no arbitraje, la solución de Black-Scholes:
donde:La probabilidad neutra al riesgo de que la entidad sufra un suceso de crédito en T es la probabilidad de que los accionistas no puedan ejercer su opción. Esta probabilidad viene dada por:
Para obtener estas probabilidades de default es preciso calcular previamente el valor y la volatilidad de la empresa. Dichas variables se determinan a partir del valor y la volatilidad de la acción. Así pues, a efectos de cálculo, se trata de considerar en primer lugar la expresión de la volatilidad de la acción:
relación que se obtiene al aplicar el lema de Itô sobre el valor de la acción.Por otra parte, la expresión de la variación del valor de la acción respecto del valor de la empresa viene dada por:
4DatosEl objetivo de este trabajo es obtener, para el plazo 2002-2011 y para cada mes, las probabilidades de default o incumplimiento a un año1 de las empresas españolas no financieras que cotizan en el Sistema de Interconexión Bursátil Español (SIBE), para constatar si estas probabilidades han sabido capturar el contexto de crisis económica actual. Una vez obtenidas estas probabilidades se efectúa un análisis sectorial de las mismas para comprobar si los efectos de la crisis han sido los mismos en todos los sectores. En 2002, el número de empresas no financieras incluidas en el SIBE era de 154. De estas, se ha podido obtener la información necesaria para todo el plazo considerado para 75 empresas, ya que el resto o bien han desaparecido, o se han fusionado, o simplemente se han dado de baja del SIBE. Tampoco se han considerado las empresas que se han incorporado al SIBE con posterioridad al 2002.
La obtención de las probabilidades de default a partir de la expresión (7), detallada en el apartado anterior, ha implicado la recopilación para cada una de las 75 empresas y para todo el plazo de estudio y con frecuencia mensual, de los siguientes datos: número, precio y volatilidad en base 250 de las acciones, valor facial de la deuda a corto y a largo plazo, y tipo de interés libre de riesgo a un año.
Los datos relativos a las acciones se han obtenido a partir del informe mensual que proporciona la Sociedad de Bolsas2. A partir del número y del precio de las acciones se ha podido calcular el valor de capitalización para cada mes del plazo 2002-2011 y para cada empresa.
El valor de la deuda a corto y a largo plazo, hasta el año 2004 incluido, se ha obtenido a partir de los balances consolidados anuales de la base de datos AMADEUS. Como hipótesis de trabajo, estos importes se han considerado como los correspondientes valores mensuales de cada año. A partir de 2005 esta información se obtiene de los balances consolidados semestrales publicados por la Comisión Nacional del Mercado de Valores3 o por la Bolsa de Barcelona4. En este caso, al ser esta información semestral, se ha efectuado la hipótesis de que el valor de la deuda del primer semestre es válido para los 6 primeros meses del año y el valor del segundo semestre lo es para los 6 últimos meses del año. A partir de la deuda a corto y a largo plazo se ha determinado la deuda total suponiendo que su vencimiento es a un año. En este estudio, tal como se ha comentado anteriormente, la totalidad de las empresas de la muestra son no financieras para disponer de información homogénea del pasivo de las mismas.
El tipo de interés libre de riesgo se ha tomado del mercado interbancario. En concreto, se ha considerado cada mes el Euribor a un año publicado por el Instituto Nacional de Estadística5. Como este tipo de interés es nominal para un plazo anual, se ha calculado su equivalente instantáneo.
El número de observaciones de cada variable y para una empresa es 120. Como para cada empresa se ha recogido información de 5 variables, el número total de observaciones por empresa ha ascendido a 600. Al considerar 75 empresas, la base de datos con la que se ha trabajado ha sido de 45.000 inputs. A este número debería sumarse la serie temporal del tipo de interés, que también es de 120 observaciones.
En el anexo 1 se presentan las empresas de la muestra organizadas por sectores, los mismos que los del mercado de renta variable español. Estos sectores son los siguientes:
- •
Sector 1. Petróleo y Energía.
- •
Sector 2. Materiales Básicos, Industria y Construcción.
- •
Sector 3. Bienes de Consumo.
- •
Sector 4. Servicios de Consumo.
- •
Sector 5. Servicios Financieros e Inmobiliarios.
- •
Sector 6. Tecnología y Telecomunicaciones.
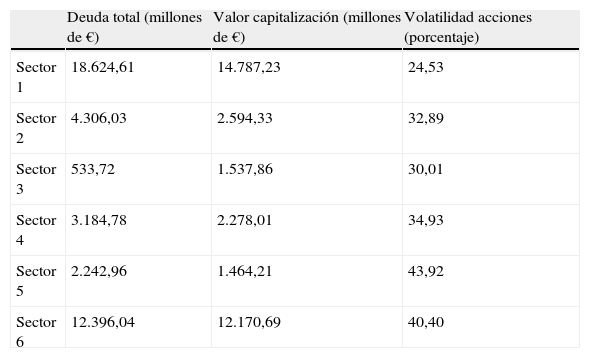
El valor medio anual, para cada sector y para el total del plazo considerado, de la deuda total, del valor de capitalización y de la volatilidad de la acción se muestra en la tabla 1.
Valores medios sectoriales
| Deuda total (millones de €) | Valor capitalización (millones de €) | Volatilidad acciones (porcentaje) | |
| Sector 1 | 18.624,61 | 14.787,23 | 24,53 |
| Sector 2 | 4.306,03 | 2.594,33 | 32,89 |
| Sector 3 | 533,72 | 1.537,86 | 30,01 |
| Sector 4 | 3.184,78 | 2.278,01 | 34,93 |
| Sector 5 | 2.242,96 | 1.464,21 | 43,92 |
| Sector 6 | 12.396,04 | 12.170,69 | 40,40 |
Fuente: elaboración propia.
Una vez recopilados todos estos datos se ha procedido a calcular, en primer lugar y para cada mes, la volatilidad y el valor de cada una de las 75 empresas. Estos valores se han calculado resolviendo simultáneamente las ecuaciones (8) y (9). Como el anterior sistema de ecuaciones no tiene solución analítica ha sido necesario, para cada mes y para cada empresa, utilizar un método numérico para su resolución (Löffler y Posch, 2007).
Así, a partir de los valores observados en t del valor y la volatilidad de la acción, St y σS, y del valor facial de la deuda, DT, se obtiene un valor de empresa Vt* calculado como Vt*=St+DT y una volatilidad de empresa calculada como σ*=σS⋅StVt*. Los valores calculados de Vt* y σ* sirven únicamente para iniciar el proceso de iteración del método numérico aplicado para la obtención de Vt y σ. Es decir, con estos valores calculados y aplicando Black-Scholes se obtienen d1, d2, St y σS a partir de las expresiones (5), (6), (3) y (8), respectivamente. Estos valores de la acción y su volatilidad, resultado de la aplicación del modelo, difieren, obviamente, de los valores observados en el mercado. El método de resolución numérico aplicado llega a la solución del sistema cuando la diferencia entre los valores obtenidos por Black-Scholes y los valores observados para St y σS es 0. El criterio aplicado es el de mínimos cuadrados, que consiste en minimizar la suma de las diferencias relativas al cuadrado, entre los valores que proporciona el modelo y los valores observados, del valor y la volatilidad de la acción. Para conseguir este objetivo se ha utilizado la función solver de Microsoft Excel. Con estos valores para estas variables se han obtenido los valores definitivos de d1 y d2, que son los que en última instancia permiten calcular las probabilidades de default.
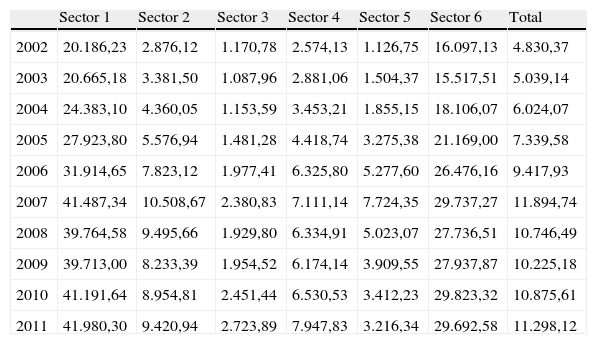
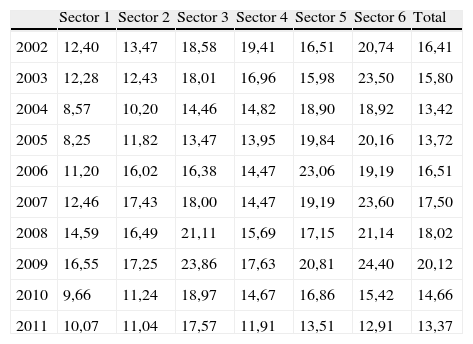
En las tablas 2 y 3 se presentan los valores medios del valor y la volatilidad de la empresa obtenidos a través de la aplicación del modelo. Son datos anuales para la totalidad de la muestra y se presentan por sectores.
Valor de empresa medio por sector (millones de €)
| Sector 1 | Sector 2 | Sector 3 | Sector 4 | Sector 5 | Sector 6 | Total | |
| 2002 | 20.186,23 | 2.876,12 | 1.170,78 | 2.574,13 | 1.126,75 | 16.097,13 | 4.830,37 |
| 2003 | 20.665,18 | 3.381,50 | 1.087,96 | 2.881,06 | 1.504,37 | 15.517,51 | 5.039,14 |
| 2004 | 24.383,10 | 4.360,05 | 1.153,59 | 3.453,21 | 1.855,15 | 18.106,07 | 6.024,07 |
| 2005 | 27.923,80 | 5.576,94 | 1.481,28 | 4.418,74 | 3.275,38 | 21.169,00 | 7.339,58 |
| 2006 | 31.914,65 | 7.823,12 | 1.977,41 | 6.325,80 | 5.277,60 | 26.476,16 | 9.417,93 |
| 2007 | 41.487,34 | 10.508,67 | 2.380,83 | 7.111,14 | 7.724,35 | 29.737,27 | 11.894,74 |
| 2008 | 39.764,58 | 9.495,66 | 1.929,80 | 6.334,91 | 5.023,07 | 27.736,51 | 10.746,49 |
| 2009 | 39.713,00 | 8.233,39 | 1.954,52 | 6.174,14 | 3.909,55 | 27.937,87 | 10.225,18 |
| 2010 | 41.191,64 | 8.954,81 | 2.451,44 | 6.530,53 | 3.412,23 | 29.823,32 | 10.875,61 |
| 2011 | 41.980,30 | 9.420,94 | 2.723,89 | 7.947,83 | 3.216,34 | 29.692,58 | 11.298,12 |
Fuente: elaboración propia.
Volatilidad de empresa media por sector (porcentaje)
| Sector 1 | Sector 2 | Sector 3 | Sector 4 | Sector 5 | Sector 6 | Total | |
| 2002 | 12,40 | 13,47 | 18,58 | 19,41 | 16,51 | 20,74 | 16,41 |
| 2003 | 12,28 | 12,43 | 18,01 | 16,96 | 15,98 | 23,50 | 15,80 |
| 2004 | 8,57 | 10,20 | 14,46 | 14,82 | 18,90 | 18,92 | 13,42 |
| 2005 | 8,25 | 11,82 | 13,47 | 13,95 | 19,84 | 20,16 | 13,72 |
| 2006 | 11,20 | 16,02 | 16,38 | 14,47 | 23,06 | 19,19 | 16,51 |
| 2007 | 12,46 | 17,43 | 18,00 | 14,47 | 19,19 | 23,60 | 17,50 |
| 2008 | 14,59 | 16,49 | 21,11 | 15,69 | 17,15 | 21,14 | 18,02 |
| 2009 | 16,55 | 17,25 | 23,86 | 17,63 | 20,81 | 24,40 | 20,12 |
| 2010 | 9,66 | 11,24 | 18,97 | 14,67 | 16,86 | 15,42 | 14,66 |
| 2011 | 10,07 | 11,04 | 17,57 | 11,91 | 13,51 | 12,91 | 13,37 |
Fuente: elaboración propia.
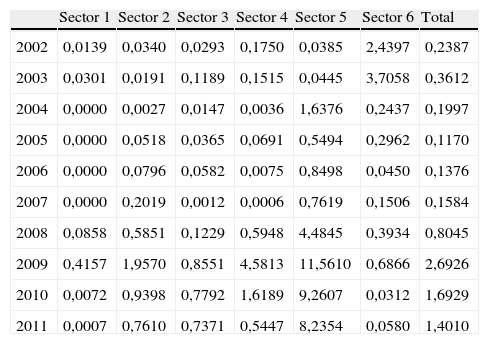
Se han obtenido las probabilidades de incumplimiento para cada empresa desde enero de 2002 hasta diciembre de 2011: en total 120 probabilidades por empresa. A partir de dichas probabilidades mensuales se han calculado las probabilidades medias de cada sector y para cada año del plazo analizado. También se ha calculado la probabilidad anual para el conjunto de las 75 empresas. Estas probabilidades se presentan, en porcentaje y aproximadas con 4 decimales, en la tabla 4.
Probabilidades de incumplimiento por sector (porcentaje)
| Sector 1 | Sector 2 | Sector 3 | Sector 4 | Sector 5 | Sector 6 | Total | |
| 2002 | 0,0139 | 0,0340 | 0,0293 | 0,1750 | 0,0385 | 2,4397 | 0,2387 |
| 2003 | 0,0301 | 0,0191 | 0,1189 | 0,1515 | 0,0445 | 3,7058 | 0,3612 |
| 2004 | 0,0000 | 0,0027 | 0,0147 | 0,0036 | 1,6376 | 0,2437 | 0,1997 |
| 2005 | 0,0000 | 0,0518 | 0,0365 | 0,0691 | 0,5494 | 0,2962 | 0,1170 |
| 2006 | 0,0000 | 0,0796 | 0,0582 | 0,0075 | 0,8498 | 0,0450 | 0,1376 |
| 2007 | 0,0000 | 0,2019 | 0,0012 | 0,0006 | 0,7619 | 0,1506 | 0,1584 |
| 2008 | 0,0858 | 0,5851 | 0,1229 | 0,5948 | 4,4845 | 0,3934 | 0,8045 |
| 2009 | 0,4157 | 1,9570 | 0,8551 | 4,5813 | 11,5610 | 0,6866 | 2,6926 |
| 2010 | 0,0072 | 0,9398 | 0,7792 | 1,6189 | 9,2607 | 0,0312 | 1,6929 |
| 2011 | 0,0007 | 0,7610 | 0,7371 | 0,5447 | 8,2354 | 0,0580 | 1,4010 |
Fuente: elaboración propia.
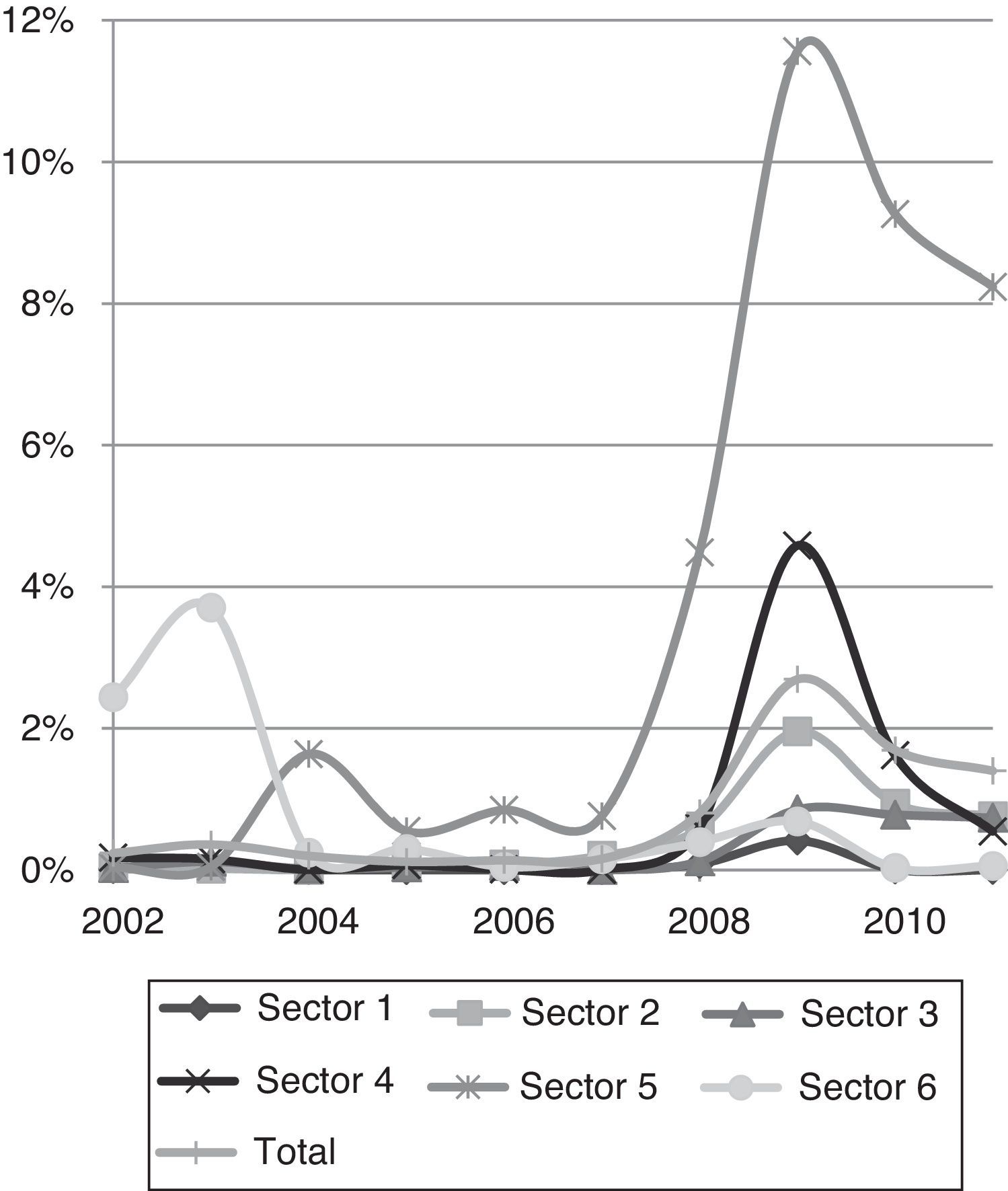
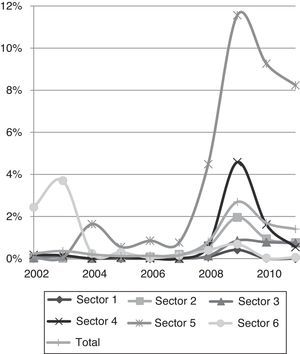
La evolución de las probabilidades de default a lo largo de los años analizados se muestra en la figura 1.
Aunque muchos analistas consideran que la actual crisis económica se inició en el año 2008, es a partir del año 2007 que todos los sectores presentan una tendencia alcista en sus probabilidades de incumplimiento. El año 2009 es el que recoge las probabilidades de default más elevadas para todos los sectores y para todo el plazo analizado, excepto el sector 6 de Tecnología y Comunicaciones, que entre los años 2002 y 2004 había presentado valores superiores. De los datos obtenidos se constata, como era de esperar, que el sector donde las probabilidades de default son considerablemente más elevadas es el de Servicios Financieros e Inmobiliarios, sector 5, cuya probabilidad media anual alcanza el 11,5610% en el año 2009. Es importante tener en cuenta que en la muestra no se han incluido las entidades bancarias y que, por tanto, la actividad predominante en este sector es la inmobiliaria. Por el contrario, el sector donde menos repercusión ha tenido la crisis sobre la probabilidad de incumplimiento es el sector 1, de Petróleo y Energía. En este sector, la probabilidad media anual de default es del 0,0000% desde 2004 a 2007 inclusive, y el valor máximo lo alcanza en 2009, con una probabilidad de 0,4157%.
En los años 2010 y 2011 se aprecia una disminución de las probabilidades de incumplimiento, pero estas continúan siendo superiores a las de los años previos al inicio de la crisis en los sectores 2, 4 y 5: sectores de Materiales Básicos, Industria y Construcción, Servicios de Consumo, y Servicios Financieros e Inmobiliarios, respectivamente. En cambio, este descenso no se observa en el sector 3, de Bienes de Consumo, que a partir del año 2009 ha mantenido la probabilidad de incumplimiento media estable. En los sectores 1 (Petróleo y Energía) y 6 (Tecnología y Telecomunicaciones) se han recuperado los valores previos a la crisis, y en este último sector incluso los valores son inferiores.
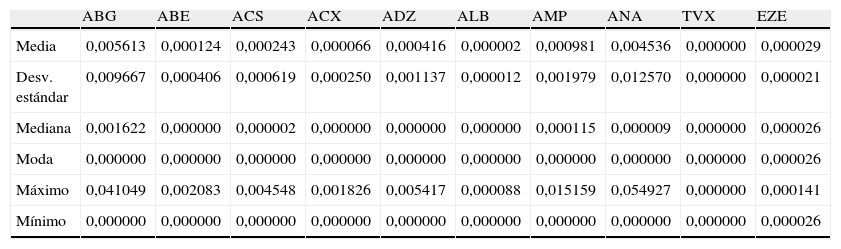
Para analizar de una forma más precisa el comportamiento de las probabilidades de incumplimiento se han calculado los principales estadísticos descriptivos, a partir de las 120 probabilidades a un año obtenidas para cada mes del plazo estudiado y para cada una de las 75 empresas de la muestra. Estos estadísticos se presentan en el anexo 2.
La moda para el conjunto de la muestra es el valor nulo. Dado que el periodo de estudio empieza en el año 2002, para la mayoría de las empresas y para un amplio recorrido, estas probabilidades son cero. Los valores diferentes a 0 se concentran a partir del año 2007, 2008 o 2009, según la empresa.
La probabilidad de incumplimiento media del conjunto de la muestra es 0,7849%. La probabilidad media más alta es de 6,9186% que corresponde a la empresa Urbas (UBS), perteneciente al sector inmobiliario.
El valor máximo que ha alcanzado la probabilidad de incumplimiento a lo largo del plazo estudiado ha sido del 55,3870%, que se corresponde con la observación, en abril de 2010, de la empresa Nyesa (NYE), perteneciente al sector de Servicios Financieros e Inmobiliarios. Esta empresa, dedicada a la promoción inmobiliaria residencial, entró en pre-concurso de acreedores en septiembre de 2011, confirmando el concurso en marzo de 2012. Cabe mencionar que es precisamente esta empresa la que presenta una mayor desviación estándar. El segundo valor más elevado lo alcanza Reyal Urbis (REY) en enero de 2010, y es del 43,1748%. Esta empresa, perteneciente también al sector inmobiliario, presentó pre-concurso de acreedores en octubre de 2012 y el concurso definitivo en febrero de 2013. Estos 2 valores son un buen ejemplo de la bondad de estimación de estas probabilidades.
En líneas generales, y avanzando ya la conclusión de este trabajo, se constata, como ya se ha comentado anteriormente en el análisis sectorial, que la mayoría de las empresas concentran los valores más altos de estas probabilidades alrededor del año 2009. El comportamiento de la probabilidad de incumplimiento, salvando la particularidad de algunas empresas, es parecido para todas ellas, de manera que se aprecia que a partir de 2007 dichas probabilidades empiezan a tomar valores sensiblemente superiores a los registrados hasta entonces.
6ConclusionesEl objetivo principal de este trabajo ha sido el cálculo de las probabilidades de incumplimiento o de default para las empresas españolas no financieras que cotizan en bolsa y así poder analizar el impacto de la crisis económica en la cuantificación de las mismas.
Para la consecución de dicho objetivo se ha escogido un horizonte temporal comprendido entre el año 2002 y 2011. Ello ha permitido comparar los niveles de probabilidad de los años previos a la crisis con los alcanzados a partir del inicio de la misma. El modelo elegido para tal fin es el modelo de Merton (1974), ya que es uno de los más utilizados en la investigación financiera actual y es también el que tiene una repercusión de mercado más importante.
A partir de los datos recogidos para el conjunto de las 75 empresas que han formado parte de la muestra se han aplicado métodos numéricos que han permitido obtener la volatilidad y el valor de estas empresas. Estas variables se han utilizado para calcular, para cada mes desde de enero de 2002 y hasta diciembre de 2011, las probabilidades de default a un año para cada una de las empresas.
Una primera conclusión que se extrae de este trabajo es que las probabilidades de incumplimiento empiezan a mostrar una tendencia alcista a partir del año 2007 y que los valores más altos se concentran, para la práctica totalidad de las empresas, en el año 2009. A partir de entonces se observa que las probabilidades disminuyen pero sin llegar a alcanzar los niveles previos a la crisis, donde estas probabilidades eran prácticamente nulas para la inmensa mayoría de las empresas consideradas.
Del análisis sectorial realizado se observa que el subsector de las empresas inmobiliarias y de cartera incluidos en el sector de Servicios Financieros e Inmobiliarios es el que presenta las probabilidades de default más elevadas a partir del año 2004.
Por otra parte, del análisis de los datos obtenidos se muestra, empíricamente, la bondad del modelo de Merton para la cuantificación de las probabilidades de default, puesto que estas han capturado la repercusión negativa de la actual crisis sobre los estados financieros de las empresas.
Para finalizar, se ha obtenido una base de 9.000 probabilidades de default de empresas españolas, base que en este trabajo se ha utilizado para analizar si la crisis económica ha tenido repercusión sobre dichas probabilidades. Ahora bien, obviamente, estas probabilidades pueden utilizarse en otras áreas como la valoración de activos derivados de crédito o el diseño de estrategias de cobertura de riesgo de crédito, aplicaciones propias de las probabilidades de default.
- •
Sector 1. Petróleo y Energía: Compañía Española de Petróleos (CEP), Endesa (ELE), Enagas (ENG), Gas Natural (GAS), Iberdrola (IBE), Red Eléctrica de España (REE) y Repsol (REP).
- •
Sector 2. Materiales Básicos, Industria y Construcción: Abengoa (ABG), Actividades de Construcción y Servicios ACS (ACS), Acerinox (ACX), Acciona (ANA), Azkoyen (AZK), Befesa Medio Ambiente (BMA), Construcciones y Auxiliar de Ferrocarriles (CAF), CIE Automotive (CIE), Cementos Portland Valderrivas (CPL), European Aeronautic Defence (EAD), Ercros (ECR), Elecnor (ENO), Fomento de Construcciones y Contratas (FCC), Ferrovial (FER), Gamesa Corporación Tecnológica (GAM), Lingotes Especiales (LGT), Duro Felguera (MDF), Nicolás Correa (NEA), Obrascon Huarte Lain (OHL), La Seda de Barcelona (SED), Tubacex (TUB), Uralita (URA), Sacyr (SCYR) y Zardoya Otis (ZOT).
- •
Sector 3. Bienes de Consumo: Adolfo Domínguez (ADZ), Grupo Tavex (TVX), Baron de Ley (BDL), Campofrío Food Group (CFG), ENCE Energía y Celulosa (ENC), Faes Farma (FAE), Ebro Foods (EBRO), Iberpapel Gestión (IBG), Indo Internacional (IDO), Industria de Diseño Textil INDITEX (ITX), Miquel & Costas & Miquel (MCM), Natra (NAT), Natraceutical (NTC), Papeles y Cartones de Europa EUROPAC (PAC), Pescanova (PVA), Bodegas Riojanas (RIO), Sniace (SNC), Deoleo (OLE), Adveo Group International (ADV), Vidrala (VID), Viscofan (VIS) y Zeltia (ZEL).
- •
Sector 4. Servicios de Consumo: Abertis (ABE), Funespaña (FUN), International Consolidated Airlines Group (IAG), Prosegur Compañía de Seguridad (PSG), NH Hoteles (NHH), Meliá Hotels International (MEL), Service Point Solutions (SPS) y Promotora de Informaciones (PRISA) (PRS).
- •
Sector 5. Servicios Financieros e Inmobiliarios: Corporación Financiera Alba (ALB), Nyesa Valores Corporación (NYE), Inmobiliaria Colonial (COL), Metrovacesa (MVC), Sotogrande (STG), Testa Inmuebles en Renta (TST), Urbas Grupo Financiero (UBS) y Reyal Urbis (REY).
- •
Sector 6. Tecnología y Telecomunicaciones: Amper (AMP), Grupo Ezentis (EZE), Tecnomcom, Telecomunicaciones y Energía (TEC), Indra Sistemas (IDR), Jazztel (JAZ) y Telefónica (TEF).
| ABG | ABE | ACS | ACX | ADZ | ALB | AMP | ANA | TVX | EZE | |
| Media | 0,005613 | 0,000124 | 0,000243 | 0,000066 | 0,000416 | 0,000002 | 0,000981 | 0,004536 | 0,000000 | 0,000029 |
| Desv. estándar | 0,009667 | 0,000406 | 0,000619 | 0,000250 | 0,001137 | 0,000012 | 0,001979 | 0,012570 | 0,000000 | 0,000021 |
| Mediana | 0,001622 | 0,000000 | 0,000002 | 0,000000 | 0,000000 | 0,000000 | 0,000115 | 0,000009 | 0,000000 | 0,000026 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000026 |
| Máximo | 0,041049 | 0,002083 | 0,004548 | 0,001826 | 0,005417 | 0,000088 | 0,015159 | 0,054927 | 0,000000 | 0,000141 |
| Mínimo | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000026 |
| AZK | BDL | NYE | BMA | CAF | CEP | TEC | CIE | COL | CFG | |
| Media | 0,000354 | 0,000000 | 0,065770 | 0,011880 | 0,000006 | 0,000183 | 0,000216 | 0,002417 | 0,044332 | 0,000102 |
| Desv. estándar | 0,000926 | 0,000001 | 0,126080 | 0,022166 | 0,000018 | 0,000736 | 0,000393 | 0,006167 | 0,077076 | 0,000382 |
| Mediana | 0,000000 | 0,000000 | 0,012387 | 0,000770 | 0,000001 | 0,000000 | 0,000023 | 0,000061 | 0,000019 | 0,000000 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| Máximo | 0,006121 | 0,000006 | 0,553870 | 0,092196 | 0,000092 | 0,005418 | 0,002021 | 0,027010 | 0,288604 | 0,002630 |
| Mínimo | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| CPL | EAD | ECR | ELE | ENC | ENG | ENO | FAE | FCC | FER | |
| Media | 0,001524 | 0,000262 | 0,011438 | 0,000468 | 0,002305 | 0,000018 | 0,000429 | 0,000006 | 0,000791 | 0,006587 |
| Desv. estándar | 0,002804 | 0,000877 | 0,019419 | 0,001100 | 0,006585 | 0,000060 | 0,001148 | 0,000018 | 0,001865 | 0,015272 |
| Mediana | 0,000000 | 0,000000 | 0,003988 | 0,000000 | 0,000000 | 0,000000 | 0,000007 | 0,000000 | 0,000015 | 0,000028 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| Máximo | 0,013271 | 0,005064 | 0,085205 | 0,004534 | 0,031373 | 0,000278 | 0,005293 | 0,000133 | 0,007583 | 0,063591 |
| Mínimo | 0,000000 | 0,000000 | 0,000177 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| FUN | GAM | GAS | EBRO | IBE | IBG | IAG | IDO | IDR | ITX | |
| Media | 0,000016 | 0,006152 | 0,000866 | 0,000002 | 0,001592 | 0,000004 | 0,005512 | 0,014486 | 0,000006 | 0,000000 |
| Desv. estándar | 0,000041 | 0,014927 | 0,002953 | 0,000007 | 0,004907 | 0,000016 | 0,011417 | 0,021273 | 0,000017 | 0,000000 |
| Mediana | 0,000000 | 0,000078 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000570 | 0,000337 | 0,000000 | 0,000000 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| Máximo | 0,000283 | 0,064108 | 0,015610 | 0,000047 | 0,021301 | 0,000136 | 0,049930 | 0,072770 | 0,000090 | 0,000002 |
| Mínimo | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000003 | 0,000000 | 0,000000 |
| LGT | MCM | JAZ | MDF | MVC | NAT | NEA | NHH | NTC | OHL | |
| Media | 0,000356 | 0,000026 | 0,046903 | 0,000312 | 0,036448 | 0,002255 | 0,002314 | 0,008604 | 0,000781 | 0,004448 |
| Desv. estándar | 0,000657 | 0,000079 | 0,073032 | 0,000635 | 0,077986 | 0,004726 | 0,004518 | 0,017434 | 0,002287 | 0,010224 |
| Mediana | 0,000019 | 0,000000 | 0,010541 | 0,000008 | 0,000233 | 0,000221 | 0,000093 | 0,000017 | 0,000001 | 0,000098 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| Máximo | 0,003724 | 0,000384 | 0,269446 | 0,002872 | 0,337866 | 0,022060 | 0,021859 | 0,075556 | 0,017089 | 0,040887 |
| Mínimo | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| PAC | PRS | PSG | PVA | REE | REP | RIO | SED | SNC | MEL | |
| Media | 0,000472 | 0,033209 | 0,000047 | 0,000683 | 0,000009 | 0,000738 | 0,000001 | 0,039798 | 0,007785 | 0,010356 |
| Desv. estándar | 0,001053 | 0,066301 | 0,000147 | 0,002067 | 0,000031 | 0,001988 | 0,000006 | 0,074428 | 0,008092 | 0,023602 |
| Mediana | 0,000008 | 0,000161 | 0,000000 | 0,000006 | 0,000000 | 0,000001 | 0,000000 | 0,000192 | 0,003941 | 0,000146 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,100481 | 0,000000 | 0,000000 |
| Máximo | 0,005104 | 0,250193 | 0,000746 | 0,008759 | 0,000179 | 0,008415 | 0,000056 | 0,277683 | 0,031242 | 0,094512 |
| Mínimo | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000001 | 0,000000 |
| OLE | SPS | STG | TEF | TST | TUB | ADV | URA | UBS | REY | |
| Media | 0,030544 | 0,004106 | 0,003348 | 0,000165 | 0,015958 | 0,001230 | 0,000000 | 0,000001 | 0,069186 | 0,064340 |
| Desv. estándar | 0,054467 | 0,004664 | 0,007529 | 0,000465 | 0,039916 | 0,003107 | 0,000001 | 0,000010 | 0,086870 | 0,116806 |
| Mediana | 0,000000 | 0,002906 | 0,000000 | 0,000000 | 0,000002 | 0,000002 | 0,000000 | 0,000000 | 0,034565 | 0,000000 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| Máximo | 0,197565 | 0,019661 | 0,038924 | 0,002436 | 0,201600 | 0,016261 | 0,000010 | 0,000108 | 0,327030 | 0,431748 |
| Mínimo | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000001 | 0,000000 |
| SCYR | VID | VIS | ZEL | ZOT | |
| Media | 0,013852 | 0,000171 | 0,000001 | 0,000465 | 0,000000 |
| Desv. estándar | 0,024161 | 0,000537 | 0,000002 | 0,001363 | 0,000000 |
| Mediana | 0,000445 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| Moda | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
| Máximo | 0,089217 | 0,002818 | 0,000016 | 0,006876 | 0,000000 |
| Mínimo | 0,000000 | 0,000000 | 0,000000 | 0,000000 | 0,000000 |
Fuente: elaboración propia.
En los acuerdos de Basilea también se calculan probabilidades a un año.