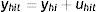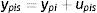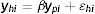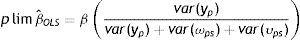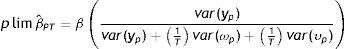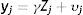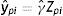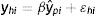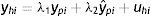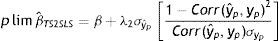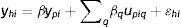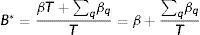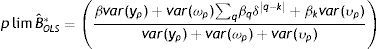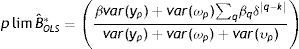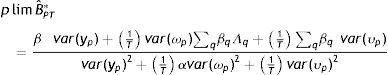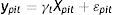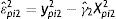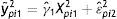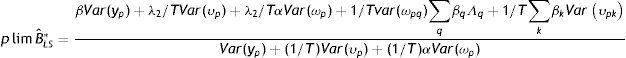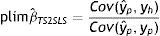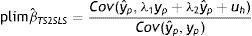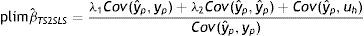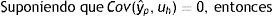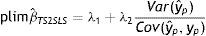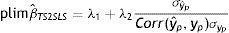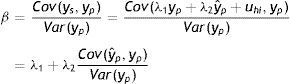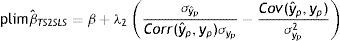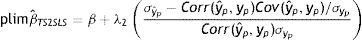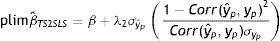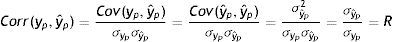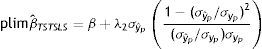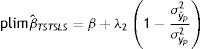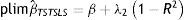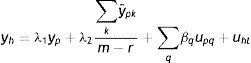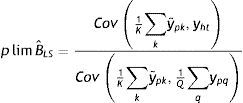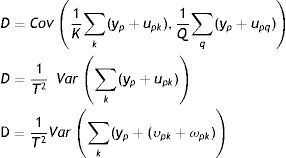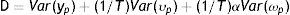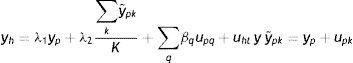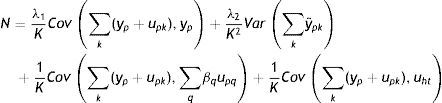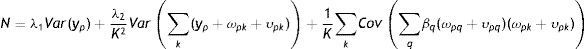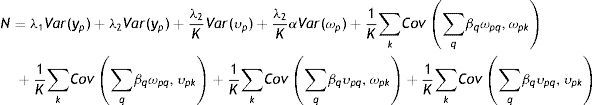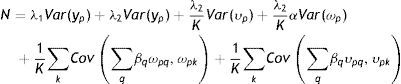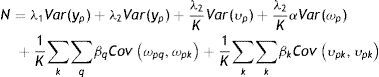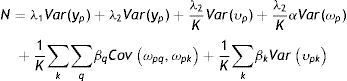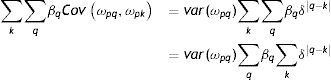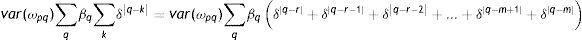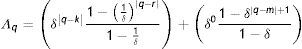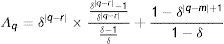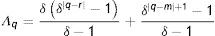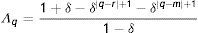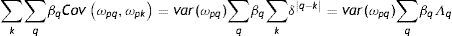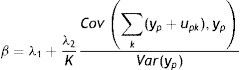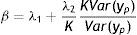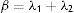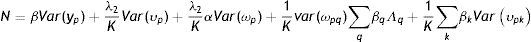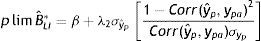El principal objetivo de este artículo es evaluar la performance, a partir de datos para Chile y Argentina, de distintos estimadores de la elasticidad intergeneracional del ingreso (EII) que constituye la medida de inmovilidad de ingresos entre padres e hijos más utilizada en la literatura empírica. A fin de computar la EII se considera no solo el modelo intergeneracional tradicional sino también un modelo alternativo, y se propone una nueva estrategia de estimación para datos cross-section. Asimismo se realiza un análisis comparativo de la movilidad del ingreso entre generaciones para Chile y Argentina a partir de estimaciones metodológicamente comparables. Para ello se utilizan los datos de la Encuesta Panel CASEN 1996-2001-2006 de Chile, que constituye uno de los paneles de datos más largo disponible para un país Latinoamericano. También se emplean los datos de diversas encuestas disponibles para Argentina. Los resultados obtenidos de la estimación del modelo tradicional de ingreso permanente sugieren que los niveles de movilidad intergeneracional del ingreso (MII) tienden a ser menores en Chile que en Argentina. Sin embargo, cuando se considera el modelo intergeneracional alternativo, las estimaciones obtenidas con el nuevo método sugieren que los niveles de MII son similares en ambos países y relativamente bajos.
The main objective of this article is to evaluate the performance, based on data for Chile and Argentina, of different estimators of the intergenerational elasticity of income (IGE), which is the measurement of immobility of incomes between parents and children most commonly used in the empirical literature. In order to compute the IGE, not only the traditional intergenerational model is considered, but also an alternative model and a new estimation strategy is proposed for cross-sectional data. A comparative analysis of income mobility between generations for Chile and Argentina is also made from methodologically comparable estimates. For this, the data are taken from the CASEN Panel Survey 1996-2001-2006 of Chile that constitutes one of the longest data panels available for a Latin American country, as well as data from various surveys available for Argentina. The estimation results of the traditional model of permanent income suggest that intergenerational income mobility (IIM) tends to be lower in Chile than in Argentina. However, when considering the alternative intergenerational model, the estimates obtained with the new method suggest that IIM levels are similar in both countries, and are relatively low.
La movilidad intergeneracional se refiere a la relación que existe entre el nivel socioeconómico de padres e hijos, medido generalmente a través de su educación o de sus ingresos (Conconi et al., 2008). En este artículo, la medida del status socioeconómico de padres e hijos se determina por sus ingresos. Los motivos para examinar la transmisión del ingreso entre generaciones son varios. El análisis de la movilidad intergeneracional del ingreso (MII) complementa las investigaciones sobre la desigualdad del ingreso que estudian la distribución desde un punto de vista estático. Por otra parte, comprender el grado de movilidad generacional es un primer paso para entender las consecuencias de la desigualdad de ingresos. Rosen (1985) va más allá al afirmar que si existe suficiente movilidad del ingreso no es necesario preocuparse de cuán desigualmente están distribuidos los ingresos.
El principal objetivo de este artículo es evaluar la performance, a partir de datos para Chile y Argentina, de distintos estimadores de la elasticidad intergeneracional del ingreso (EII) que constituye la medida de inmovilidad de ingresos entre padres e hijos más utilizada en la literatura empírica. A fin de computar la EII se considera no solo el modelo intergeneracional tradicional sino también un modelo alternativo. A diferencia de lo sostenido por el primer modelo, la idea central del nuevo enfoque propuesto por Muller (2010) es que la transmisión relevante entre generaciones no solo tiene lugar en relación al componente permanente del ingreso, sino también a través de los ingresos transitorios1. Esto, a su vez, tiene varias implicancias relevantes. Por un lado, sugiere que las comparaciones realizadas entre países, en base al modelo estándar de transmisión intergeneracional del ingreso permanente, ignoran una fuente potencial de heterogeneidad inobservada que podría afectar las estimaciones de la MII: la edad de los hijos en la que se mide el ingreso de sus padres. Por otra parte, si es posible identificar que los componentes transitorios del ingreso de los padres tienen un efecto significativo en las oportunidades económicas futuras de los niños, las implicancias de política serían más inmediatas. Si el ingreso transitorio afecta el ingreso futuro de los niños, esto indicaría que el ingreso de los padres per se tiene un efecto en sus oportunidades, lo que generalmente es incompatible con las formulaciones incluso más débiles del enfoque de igualdad de oportunidades. Entonces, cuanto mayor sea la importancia del ingreso transitorio con relación al permanente en el proceso de transmisión intergeneracional, mayor será el campo para la intervención pública (Muller, 2008).
La estimación de este modelo alternativo, al igual que el tradicional, es particularmente problemática en países en los que las bases de datos disponibles no incluyen información sobre el ingreso de los padres para los individuos encuestados, en edades centrales del ciclo vital de ambos. Aunque contienen datos sobre otras características de los padres, como su educación. Si bien, una solución ampliamente utilizada para estimar la EII en este caso es implementar el método Two-Sample Intrumental Variable (TSIV), esta técnica no sería adecuada para el modelo alternativo porque instrumenta el ingreso permanente pero no resuelve el problema de la exclusión del ingreso transitorio del modelo estimado. Por eso, en esta investigación se propone una nuevo enfoque metodológico que combina algunas características del método TSIV para estimar el componente permanente del ingreso parental y del enfoque propuesto por Dang et al. (2014)2 que permite considerar también su componente transitorio, particularmente durante la niñez y la adolescencia de los hijos. Bajo determinados supuestos, con esta técnica podría obtenerse un límite inferior y superior de la EII en el contexto del modelo alternativo.
Asimismo, a fin de valorar la magnitud del grado promedio de persistencia de ingresos entre generaciones observado en Argentina, se realiza también un análisis comparativo con Chile. Además de los motivos metodológicos, esta comparación es, en sí misma, un ejercicio interesante por diversas razones. En primer lugar, la obtención de estimaciones metodológicamente comparables permite evaluar si los niveles de MII en Argentina pueden considerarse relativamente altos o bajos en relación con los computados para Chile, evaluando así el desempeño relativo del país en esta dimensión dinámica del bienestar. Esto, a su vez, permite eliminar el efecto de distintas muestras de padres e hijos y métodos en las diferencias que pueden observarse. Por otra parte, las características comunes y disímiles que presentan estos dos países limítrofes y que, según los modelos teóricos, son susceptibles de tener un efecto importante sobre el proceso de transmisión intergeneracional, podrían permitir elaborar futuras hipótesis susceptibles de explicar las potenciales diferencias o similitudes observadas en los niveles de MII entre ambos países. Así, por ejemplo, aunque ambos países comparten políticas sociales universalistas, los patrones de crecimiento económico que experimentaron no han sido convergentes. Además, conforme con la evidencia reportada por Gasparini et al. (2007), para la década de los noventa y principios de los 2000, mientras en Argentina los cambios en el ingreso han sido negativos y claramente desigualadores, Chile ha experimentado un crecimiento sostenido a lo largo de toda la distribución de ingresos. La evolución de la incidencia de la pobreza también muestra marcadas heterogeneidades entre Chile y Argentina, durante los noventa y principios de los 2000. Así, mientras en Chile se observan reducciones significativas (al igual que en Brasil, El Salvador, Jamaica y Nicaragua), Argentina muestra un gran incremento de la tasa de pobreza en ese período. Por otra parte, ambos países han experimentado significativos cambios políticos y económicos en las últimas décadas. Después de una profunda recesión a principios de los ochenta, durante los noventa la economía chilena exhibió un sustancial y sostenido crecimiento económico que llevó a una mejora significativa de las condiciones de vida en el país. El lado oscuro de esta exitosa historia es la persistente desigualdad económica, que ha sido históricamente elevada; otra característica que comparte con la economía argentina, en la que, en cambio, el crecimiento económico no fue tan elevado ni sostenido como el chileno3. El patrón de desigualdad chileno está caracterizado por una alta concentración de los ingresos entre los estratos más ricos de la población, mientras que las diferencias entre los sectores pobres y los de ingresos medios son mucho menos pronunciadas que las observadas en naciones industrializadas (Torche, 2005).
A partir del 2000, concretamente entre 2002 y 2008, la desigualdad comenzó a disminuir en casi todas las economías de América Latina, incluyendo Chile y Argentina, después de la tendencia creciente observada durante la denominada «década perdida» de los ochenta, las reformas estructurales de los noventa y las crisis ocurridas al cambiar el siglo (Gasparini y Lustig, 2014). No obstante, tanto en los noventa como en los 2000 los niveles de desigualdad del ingreso en Chile fueron mayores que los observados en Argentina4. Si la desigualdad y la movilidad están relacionadas, siendo la primera un factor muy importante para la configuración de la segunda, más que, por ejemplo, los niveles de crecimiento económico, se espera que Chile muestre niveles de persistencia intergeneracional mayores o relativamente similares a Argentina.
Los resultados obtenidos de la estimación del modelo tradicional de ingreso permanente sugieren que los niveles de MII tienden a ser menores en Chile que en Argentina. Sin embargo, cuando se considera el modelo intergeneracional alternativo, las estimaciones obtenidas con el nuevo método sugieren que los niveles de MII son similares en ambos países y relativamente bajos.
Por lo tanto, se considera que este artículo hace tres contribuciones interesantes. La primera consiste en evaluar la performance de estimadores de dos modelos intergeneracionales diferentes. La segunda contribución es metodológica y se relaciona con la extrapolación del método propuesto por Dang et al. (2014) para estimar el modelo alternativo ya mencionado a partir de datos cross-section. Por último, la tercera es una contribución al estudio de la movilidad entre generaciones en países en desarrollo a partir del análisis comparativo de los niveles de MII en Argentina y en Chile.
2La movilidad intergeneracional del ingreso: una breve revisión de los antecedentes para Chile y ArgentinaLa mayoría de los estudios empíricos que cuantifican y analizan la transmisión intergeneracional del ingreso en un cierto país o región están referidos a países desarrollados, principalmente por la mayor disponibilidad de datos para esos países. Entre estos, se destacan como antecedentes el artículo de Atkinson et al. (1983) para Inglaterra, así como los trabajos de Solon (1992) y Zimmerman (1992) para Estados Unidos. Sin embargo, en los últimos años esta literatura ha crecido y se ha extendido en diferentes lugares5.
A partir de la revisión de la literatura se advierte una desproporcionada cantidad de estudios realizados para países desarrollados en comparación con los existentes para países en desarrollo. En particular, los estudios sobre MII en Argentina son muy escasos. Si bien existen estudios de movilidad intergeneracional específicos para el país, la mayoría no examina la movilidad del ingreso sino la movilidad ocupacional o educativa entre generaciones6. El antecedente más directo de la investigación desarrollada en este artículo para Argentina es el estudio de FIEL (2008), que examina los efectos de un indicador del nivel socioeconómico de los padres en el ingreso de los hijos pero a partir de una encuesta específica del 2007 para el Gran Buenos Aires. Según los resultados obtenidos por los autores, la movilidad intergeneracional de la condición socioeconómica7 puede considerarse moderada con respecto a los países más avanzados pero mayor que la observada en Brasil y Colombia, aunque con un desempeño similar al de México y Brasil, en la región latinoamericana.
En el caso de Chile, en cambio, existen algunos estudios que examinaron la MII8, como los de Núñez y Risco (2004) y Núñez y Miranda (2011) y el más reciente de Celhay et al. (2010). Con excepción de este último, los anteriores utilizaron datos cross-section, implementando la estrategia de estimación con dos muestras en dos etapas (TSIV) a partir de los microdatos provenientes de Encuesta de Empleo y Desempleo. En cambio, en esta investigación se explotará el panel más largo disponible para Chile: la Encuesta Panel Casen 1996-2001-2006. Además, a diferencia del estudio de Celhay et al. (2010), que también utiliza esta base de datos, los objetivos de esta investigación son distintos. En primer lugar, se pretende obtener estimaciones de los niveles de MII comparables en Chile y Argentina y, en segundo lugar, evaluar la performance de los métodos de estimación basados en datos cross-section como la técnica TSIV, así como un nuevo método aquí propuesto para examinar un modelo intergeneracional alternativo.
Por otra parte, las investigaciones que, como esta, obtuvieron estimaciones comparables de los niveles de MII entre países de América Latina son casi inexistentes. Una excepción es el estudio desarrollado por Grawe (2004), que incluye dos países de la región —Ecuador y Perú— además de Nepal, Pakistán, Malasia, Estados Unidos, Canadá, Alemania y Reino Unido. Como el autor implementa el método TSIV en el caso de los cinco países en desarrollo que considera, estas estimaciones, aunque comparables entre sí, no lo son con las realizadas para los otros cuatros países desarrollados incluidos. Los resultados obtenidos por Grawe (2004) sugieren que la persistencia intergeneracional de ingresos es mayor en Ecuador y en Perú que en Nepal y en Pakistán. Además, mientras en estos dos últimos países los niveles de MII son mayores en los cuantiles más altos de la distribución, lo contrario se observa en Ecuador y en Perú.
Al igual que las investigaciones sobre movilidad social intergeneracional en un país en desarrollo, las que realizan comparaciones entre países latinoamericanos consideraron en su mayoría como variable de resultado la educación (Dahan y Gaviria, 2001; Andersen, 2001; Conconi et al., 2008; Ferreira et al., 2013).
Un problema que ninguno de los estudios revisados advirtió al realizar las comparaciones es la posibilidad de la existencia de una heterogeneidad inobservada producto del momento en el ciclo de vida de los hijos en que se observa el ingreso parental. Esta observación realizada recientemente por Muller (2010)9 lleva a cuestionar el modelo intergeneracional tradicional de ingreso permanente, dando lugar a un modelo alternativo que será examinado en Chile y en Argentina, a partir de un nuevo método de estimación aquí propuesto.
3Análisis de los modelos empíricos intergeneracionales del ingreso y sus métodos de estimaciónEn esta sección se describen, en primer lugar, los modelos y métodos de estimación propuestos en la literatura para obtener uno de los indicadores de inmovilidad o persistencia intergeneracional más utilizados en la literatura: la elasticidad intergeneracional del ingreso (EII), prestando especial atención a los potenciales sesgos que puede presentar. Para esto se derivan los límites en probabilidad de distintos estimadores utilizados. Luego se presenta un modelo alternativo recientemente formulado por Muller (2010) que aún no ha sido evaluado empíricamente para otro país. Con este fin, se propone una nueva técnica de estimación de la EII, en el contexto de este modelo, utilizando datos de corte transversal que, en muchos países, como Argentina, son la única fuente de información disponible.
Al comparar los niveles de MII entre países deben tenerse en cuenta varias cuestiones. En la descripción de cada una de ellas que se realiza a continuación se resaltan además algunos puntos ignorados o que se considera tuvieron un tratamiento erróneo en la mayoría de los estudios aplicados.
3.1Modelo intergeneracional clásico de ingreso permanenteEl modelo estadístico tradicional considerado en la literatura que estima la EII es el siguiente:
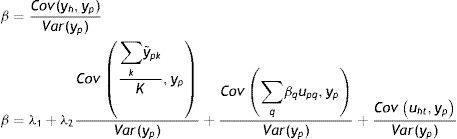
donde yhit es el ingreso corriente del hijo en el año t y ypis es el ingreso corriente del padre en el año s expresados como una función del ingreso permanente (yhiyypi) que refleja la verdadera capacidad de ingresos a largo plazo y un término de error (uhit=ωhit+υpisyupis=ωpis+υpis) con componentes que capturan shocks transitorios en los ingresos (ωhtyωps) y componentes de ruido blanco (υhityυpis)10. La ecuación (3) es el modelo intergeneracional de interés que relaciona el ingreso permanente de hijos y padres y β es la EII, esto es, una medida del grado de persistencia del ingreso permanente de padres e hijos. La EII también puede interpretarse como la fracción de la brecha de ingresos entre padres con distintos niveles de ingresos que, en promedio, persiste a través de las generaciones. En otras palabras, β resume en un solo número el grado de inmovilidad generacional del ingreso en una sociedad. De esta forma, el nivel de MII o el grado con el cual los ingresos no están asociados entre generaciones es medido a partir de (1−β).
Este modelo, definido por las ecuaciones (1), (2) y (3), asume implícitamente que no hay correlación entre los componentes permanentes y transitorios del ingreso de padres e hijos11. De manera que los componentes permanentes capturarán el impacto de factores constantes como la educación, características y atributos genéticos de los padres y cualquier efecto causal del componente permanente del ingreso en sí mismo. Por tanto, es importante aclarar, antes de analizar los distintos estimadores propuestos para la EII, que esta no constituye (ni se espera que sea) una medida del efecto causal del ingreso de los padres en el resultado económico de los hijos. En general, es inevitable que la EII sobrestime cualquier relación causal que exista como resultado de la correlación entre el ingreso de los padres y otras variables explicativas en la ecuación estructural del ingreso (o, en general, del resultado económico) de los hijos. No obstante, aun así, la EII es una medida relevante de inmovilidad intergeneracional. Pero debe recordarse que este tipo de modelos deja pendiente la exploración de los determinantes de esa inmovilidad.
La estimación por Ordinary Least Squares (OLS) de (3) usando los ingresos corrientes en lugar de los permanentes (yhiyypi) produce estimaciones sesgadas de la EII. Formalmente, el límite en probabilidad de la EII estimada por OLS12 es:
En este caso, la estimación por OLS estará sujeta al tradicional sesgo de atenuación por error de medición en las variables13. Las dos soluciones propuestas y más utilizadas en la literatura para este problema clásico de error14 en las variables fueron la técnica de promediar los ingresos del padre a lo largo de un período T determinado (PT) y el método Instrumental Variable (IV).
Usando un promedio a lo largo de T años del ingreso del padre como variable independiente en (3), el límite en probabilidad de la EII así estimada es15:
Es decir, este procedimiento reduce el sesgo en la estimación de β, pues el promedio elimina el componente transitorio de los ingresos del padre. Cuanto mayor sea el número de períodos, T, a lo largo de los cuales se tome el promedio, mayor es la reducción en el sesgo (Zimmerman, 1992). Pero, como advierten Solon (1992) y Zimmerman (1992), el efecto de reducción del sesgo de atenuación como resultado de promediar el ingreso a lo largo de un período T es mitigado si existe una correlación entre los componentes transitorios.
En cambio, conforme con los supuestos asumidos por Solon (1992), el método IV produciría un estimador inconsistente que sobrestima β. De manera que los estimadores OLS y IV de la EII en (3) ofrecerían un límite inferior y superior, respectivamente, para β. Sin embargo, el estimador IV de β sobrestimará la verdadera EII, como afirman Solon (1992) y Zimmerman (1992)16, siempre que se cumplan ciertas condiciones. Para ver esto, supongamos que el ingreso permanente de los padres es una función de un vector de características o variables explicativas que incluye variables, como la educación de los padres, que pueden esperarse que tengan un efecto directo sobre el ingreso de los hijos, además del efecto indirecto que puedan tener a través de su correlación con el ingreso del padre. Entonces, si se estima la ecuación (3) usando la predicción del ingreso permanente de los padres a partir del método IV con la educación como instrumento, el estimador IV de β sobrestimará la verdadera EII si la educación del padre tiene un efecto no-negativo en el ingreso de los hijos y si la correlación entre el ingreso y la educación de los padres esté acotada entre cero y uno17.
Un problema adicional que se presenta para estimar (3) en el caso de varios países, como es el caso de Argentina, es la falta de información sobre el ingreso de los padres para todos los individuos incluidos en la base de datos disponible. Una solución para esto consiste en implementar una estrategia de estimación alternativa que constituye una extensión del método IV tradicional en la que los momentos muestrales necesarios para estimar el coeficiente de interés (β) son tomados de dos muestras diferentes. Se utiliza, entonces, una muestra principal en la que se observa el ingreso de los hijos y ciertas características de los padres (generalmente, su educación u ocupación) y una muestra secundaria o auxiliar con información del ingreso y las mismas características para un conjunto de individuos18. Así, es posible predecir el ingreso de los padres a partir de los parámetros estimados con la muestra secundaria y de las características de los padres observadas o reportadas por los hijos en la muestra principal. Esos ingresos predichos son usados en la segunda etapa del procedimiento como regresores del modelo del ingreso de los hijos que se estima con la muestra principal.
Este método denominado Two Sample Instrumental Variable (TSIV) o Two-Sample Two-Stage Least Squares (TS2SLS)19 fue propuesto por primera vez por Klevmarken (1982)20. Siguiendo a Jerrim et al. (2014), supongamos que se dispone de una muestra auxiliar secundaria J que cumple las siguientes condiciones: a)contiene una medida del ingreso permanente de los entrevistados21; b)es obtenida de la misma población que la muestra principal, y c)contiene las mismas variables instrumentales Z que la muestra principal. Entonces, usando esta muestra secundaria J es posible estimar el siguiente modelo de regresión por OLS:
Usando los coeficientes estimados es posible predecir el ingreso permanente del padre en la muestra principal I:
De esta forma, la ecuación (3) ahora puede ser estimada a partir de:
Las dos variables instrumentales más comúnmente utilizadas son la educación y la ocupación. Sin embargo, ambas variables probablemente sean endógenas, es decir, influyan en el ingreso de los hijos. En este caso, el ingreso de los hijos estará dado por:
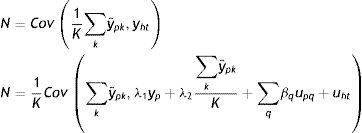
donde λ1 es el impacto directo del ingreso permanente del padre sobre el ingreso del hijo y λ2 es el efecto del ingreso predicho del padre sobre el ingreso de los hijos. Entonces, realizando una derivación similar a la que se utiliza para el estimador IV y suponiendo que Cov(yˆp,uh)=0, el límite en probabilidad del estimador TS2SLS de la EII22 es:
A partir de esta ecuación se aprecia la similitud entre el límite en probabilidad de los estimadores IV y TSIV (o 2SLS y TS2SLS), en particular cuando el instrumento utilizado para predecir el ingreso paterno es su educación. Asimismo, se deduce que βˆTSTSLS sobrestimará β siempre que el efecto directo de las características paternas utilizadas como instrumento para predecir su ingreso, generalmente su educación, sobre el ingreso del hijo sea positivo (λ2>0) y que la correlación entre la educación del padre (ponderada por su retorno) y el ingreso paterno sea positiva pero no igual a 1. Sin embargo, si en línea con los hallazgos de Sewell y Hauser (1975), Corcoran et al. (1992) y Mazumder (2005), el efecto directo de la educación del padre sobre el ingreso del hijo no es estadísticamente distinto de cero, una vez que se controla por el ingreso del padre promediado durante varios años, la estimación TSIV o TS2SLS de la EII sería consistente.
Otro punto a tener en cuenta cuando se comparan las EII es que los datos en diferentes países incluyen muestras de padres e hijos de distintas edades. Varios estudios (Mazumder, 2005; Haider y Solon, 2006; Núñez y Miranda, 2011, entre otros) han investigado los efectos de cambiar las edades en las cuales los ingresos de los hijos y/o de los padres son observados. Los resultados obtenidos en estas investigaciones indican que las estimaciones de la persistencia intergeneracional medida con la EII varían con la edad en la cual el ingreso de los padres e hijos son medidos. Este problema es denominado en la literatura como life-cycle bias. Las estimaciones de Haider y Solon (2006), así como de Böhlmark y Lindquist (2006), sugieren que tanto el ingreso de padres como el de hijos deberían medirse óptimamente en las edades centrales de su ciclo de vida. Sin embargo, incluso así podría existir un sesgo de atenuación en el estimador OLS de la EII. Por otra parte, tanto el estimador IV como el estimador TS2SLS, en este caso, pueden sobrestimar como subestimar la verdadera EII23. Sin embargo, si el ingreso corriente de hijos y padres es observado en sus edades centrales, entonces el life-cylcle bias desaparece o disminuye y el estimador IV, así como el TS2SLS, sobrestimarían la EII bajo los supuestos previamente mencionados.
3.2Un modelo intergeneracional alternativo y un nuevo método de estimaciónEl modelo intergeneracional tradicionalmente considerado en la literatura sobre MII, así como sus generalizaciones antes descriptas, está basado en el concepto de ingreso permanente y en el supuesto de que esta es la única variable relevante cuando se evalúa la persistencia de ingresos entre generaciones. Esto excluye implícitamente otra clase de modelos estructurales, como aquellos que incorporen la posibilidad de que el ingreso de los padres en los primeros años de la niñez tenga una contribución diferencial a la EII o que el efecto de las restricciones crediticias de los padres sobre los ingresos posteriores de los hijos sea diferente en determinadas edades de los hijos. Si estos supuestos son correctos, las estimaciones de la EII podrían variar debido a la heterogeneidad inobservada previamente no tomada en consideración. Para contemplar esta posibilidad, Muller (2010) propuso la siguiente modificación de la regresión intergeneracional estándar (3) que permite que el ingreso permanente de los hijos sea una función de las desviaciones del ingreso permanente de los padres (upiq):
donde upiq=ypiq−βypi=ωpia+υpiayq∈Q, s∈S, Q⊂S.
Los años que conforman la niñez y en los que es medido el ingreso de los padres son indexados por q y s, respectivamente. El coeficiente β puede variar de forma tal que el ingreso transitorio puede tener diferentes impactos dependiendo de la etapa de la niñez en que ocurra.
Como el ingreso permanente es el mismo en cada año, la EII en este modelo está ahora definida como la suma del efecto del ingreso permanente (β) y un promedio de los βq:
Cuando βq=0, ∀q, el modelo se reduce al modelo tradicional definido en (1), (2) y (3). Si el modelo alternativo es el correcto, un punto importante en su estimación es considerar explícitamente si el ingreso de los padres es observado durante la niñez (y adolescencia)24 o fuera de ella. Si el ingreso de los padres es observado en un único año y dentro del período de la niñez (y adolescencia) del hijo, el límite en probabilidad del estimador OLS está dado por25:
En cambio, si el ingreso de los padres es observado en un único año (k) pero fuera de la niñez (y adolescencia) del hijo, se tiene:
El segundo término en el numerador de (13) y (14) representa la suma de los coeficientes sobre el ingreso transitorio para cada año de la niñez, ponderados por δq−k, que es una función de la correlación (δ) en el componente transitorio del ingreso del padre (ωp) y de la proximidad entre ese año y el año en el que se observa el ingreso paterno q−k. Si no existiera correlación serial en el ingreso transitorio, δ=0 y el ingreso es observado en un año fuera de la niñez y adolescencia del hijo, el plim en (14) sería igual al definido en (4), de manera que no se capturaría nada del impacto del ingreso transitorio. En cambio, si el ingreso es observado en un año perteneciente a la niñez y adolescencia, el impacto del componente de ruido blanco del ingreso paterno (υp) para el año particular usado es parte del coeficiente calculado. Además, en (13), como k está más cercano a q, el segundo término será mayor que el término equivalente en (14). Por lo tanto, las estimaciones de la EII basadas en ingresos observados dentro de la niñez y adolescencia de los hijos deberían ser mayores que las que usan ingresos fuera de ese período. Entonces, la recomendación para el análisis empírico en el que se usa procedimientos de estimación basados en el ingresos de los padres observados en un único año es usar los ingresos percibidos durante la niñez y adolescencia de los hijos y, si esto no es factible, al menos tratar de medir los ingresos en un año que sea lo más cercano posible a ese período. Además, como el objetivo es también comparar las estimaciones entre países, Chile y Argentina, en este caso, el ingreso del padre en ambos países debería ser medido en el mismo período de la niñez o adolescencia del hijo.
Según Muller (2008, 2010), los métodos de estimación disponibles en la literatura no permiten estimar correctamente (12). Sin embargo, bajo determinados supuestos, es posible derivar un límite inferior y superior que contenga la verdadera EII (B*). En este caso, las derivaciones ofrecidas por Muller (2008) sugieren que la utilización de un promedio del ingreso corriente de los padres en múltiples años de la niñez o adolescencia de los hijos podría sobrestimar el verdadero coeficiente, ofreciendo un límite superior para la EII verdadera. Formalmente, el límite en probabilidad de la EII estimada considerando como variable explicativa el promedio del ingreso de los padres durante todos los años relevantes de la niñez o adolescencia de los hijos (T), denotada por BˆPT*, es:
donde Λq=1+δ−δq−r+1−δq−m+11−δ y α=1+2δT−δT−1+δTT(1−δ)2
Siendo r y m el primer y último año usado en el promedio, que se supone coinciden con el primer y último año de la niñez y adolescencia de los hijos.
Conforme se mencionó al comenzar el artículo, las implicancias de este modelo alternativo son relevantes tanto para el diseño de políticas públicas como para las comparaciones entre países, pues pone de relieve una fuente potencial de heterogeneidad inobservada previamente ignorada: la edad de los hijos en la que se mide el ingreso de los padres. Además, la importancia de considerar que el ingreso transitorio de los padres puede tener un efecto en las oportunidades futuras de los hijos, particularmente si ocurren durante su niñez y adolescencia, es mayor en países en desarrollo como Argentina y Chile que en los más desarrollados. En estos últimos países la mayor y más adecuada provisión pública de salud, educación y otros servicios sociales, así como el acceso al mercado de créditos y a oportunidades de empleo menos volátiles, disminuyen la importancia de los componentes transitorios como permanentes del ingreso. En consecuencia, se espera que el sesgo que surge de excluir los ingresos transitorios del modelo intergeneracional estándar en las estimaciones de los niveles de persistencia del ingreso entre generaciones sea mayor en las sociedades menos desarrolladas.
3.2.1Método de estimación propuestoLa estimación del modelo (11) plantea problemas en países en los que las bases de datos disponibles no incluyen información sobre el ingreso de los padres durante varios años de la niñez y adolescencia de los individuos encuestados, aunque contienen datos sobre otras características de los padres, como su educación. Si bien previamente se mencionó que una solución para estimar la EII en este caso es implementar el método TSIV26, esta técnica, por sí sola, no sería adecuada para el modelo alternativo porque instrumenta el ingreso permanente pero no resuelve el problema de la exclusión del ingreso transitorio del modelo estimado. No obstante, bajo determinados supuestos el método TSIV ofrece una estimación apropiada de la EII permanente. Por tanto, teniendo en cuenta que la EII propuesta por este nuevo modelo está dada por (12) como la suma entre β y las elasticidades correspondientes al componente transitorio del ingreso paterno, el estimador TSIV ofrece un límite inferior de B*. Para esto, conforme con el plim de este estimador dado en (10) es necesario que se cumpla que λ2=0, teniendo en cuenta la ecuación (9), y si la educación se utiliza como variable instrumental, esto implica asumir que el efecto directo de la educación del padre sobre el ingreso del hijo es nulo, una vez que se controla por una medida de su ingreso a largo plazo. Como ya se mencionó, los hallazgos de Sewell y Hauser (1975), Corcoran et al. (1992) y Mazumder (2005) respaldan el cumplimiento de este supuesto.
Para derivar el límite superior de B*, en cambio, se propone una nueva técnica de estimación que combina algunas características del método TSIV y de un enfoque recientemente propuesto por Dang et al. (2014) para el análisis de la movilidad intrageneracional, concretamente de los movimientos dentro y fuera de la pobreza27. Bajo determinados supuestos, este método permitiría derivar un límite superior de la verdadera EII en el contexto del modelo alternativo antes descripto.
Supongamos que disponemos de dos ondas de una encuesta cross-section que son muestras aleatorias de la población subyacente de interés. Sea Xpit un vector de características determinísticas o invariantes en el tiempo del i-ésimo padre observadas en la onda t=1, 2 como edad, sexo, educación, lugar de nacimiento, entonces la proyección lineal del ingreso observado del padre, en la onda t, ypit en Xpit está dada por:
Para los hijos de la muestra principal de la onda 2 solo se dispone de información de características determinísticas o invariantes en el tiempo del i-ésimo padre pero no de su ingreso permanente ni transitorio cuando eran niños o adolescentes. Una forma de solucionar este problema es estimando este ingreso inobservado utilizando una muestra alternativa de un momento en el pasado en que los hijos de la muestra principal eran niños o adolescentes. En base a esta muestra secundaria (de la onda 1) es posible predecir el ingreso permanente de los padres en el pasado a partir de los parámetros estimados en esa muestra auxiliar y de las características observadas de los padres en la muestra principal (de la onda 2). La diferencia con el método TSIV antes mencionado es que también se utiliza la información de dos muestras para estimar el componente transitorio del ingreso (εpit) en la niñez o adolescencia de los hijos de la muestra principal. Para esto, se deben realizar dos supuestos. El primero requiere que la muestra de la onda 1 y de la onda 2 sea de la misma población subyacente28. El segundo supuesto se refiere al comportamiento del término de error en (16), específicamente del componente que captura los shocks transitorios. Conforme con los supuestos realizados es posible derivar un límite superior de la EII definida en (12). Según postula el modelo alternativo, es razonable asumir que εpi1 está correlacionado con εpi2. Existen dos razones por las que esto podría suceder. La primera, previamente analizada, es que los shocks en el ingreso pueden ser persistentes y estar positivamente correlacionados, siguiendo, por ejemplo, un proceso AR(1), esto es, εpis=δεpis−1+ξpis. La segunda razón es que el término de error contenga un efecto fijo individual (Dang et al., 2014). Con el objetivo de ofrecer un límite superior para la EII (y por lo tanto inferior para la MII) se asume que los términos de error presentan una autocorrelación positiva perfecta29. Es decir, δ=1yεpi2=εpi1. Los pasos para estimar la EII en este caso son:
1.°. Usando la muestra auxiliar de padres «representativos» de la onda 1, estimar por OLS una regresión de ypi11 en Xpi11, donde el superíndice denota que estas son observaciones para los individuos observados en la onda 1 solamente. A partir de esta estimación obtener el estimador γˆ1 del vector de coeficientes γ1. Luego, usando la muestra principal de padres de la onda 2, estimar una regresión de ypi22 y Xpi22 y obtener los residuos OLS:
2.°. Usar el estimador OLS γˆ1 de la onda 1 junto con los valores conocidos de Xpi22 para estimar el ingreso de los padres en la onda 1, esto es, en algún año de la niñez o adolescencia de los hijos como sigue:
3.°. Estimar la ecuación (18) para la mayor cantidad de años en la niñez o adolescencia de los hijos que sea posible, utilizando como ingreso de los padres en la niñez o adolescencia de sus hijos y˜pi12 en lugar del inobservado ypi12 y obtener un promedio de los ingresos estimados de los padres en distintos años de la niñez y adolescencia de sus hijos. Con este ingreso promedio como variable independiente, obtener la EII estimada denotada por BˆLs* que constituye el límite superior de la verdadera B*. Bajo determinados supuestos (especificados en el anexo B.2), el límite en probabilidad de este estimador30 está dado por:
donde Λq=1+δ−δq−r+1−δq−m+11−δ y α=1+2δT−δT−1+δTT(1−δ)2
De esta forma, dados los estimadores propuestos para el límite inferior y el límite superior y bajo los supuestos examinados, el método aquí presentado podría aportar una técnica para obtener un intervalo cerrado de la EII bajo el modelo alternativo (B*).
4DatosLa datos utilizados para examinar la MII en Chile provienen de la Encuesta Panel CASEN (EPCASEN) que nació en 2001 con el seguimiento31 de una muestra representativa de los hogares de las regiones III, VII, VIII y Metropolitana, a partir de la Encuesta de Caracterización Socioeconómica Nacional (CASEN) 1996. El aporte que supone la onda 2006 de la encuesta es importante, en el contexto de Chile y de los países menos desarrollados, por el tamaño de su muestra y por el período de tiempo que abarca: 10 años32. La población objetivo de la EPCASEN son todas las personas residentes en hogares privados de las de las regiones III, VII, VIII y Metropolitana, en múltiples momentos del tiempo, correspondiendo estos a las ondas de recolección de los datos: 1996, 2001 y 2006. Un total de 20.942, 18.857 y 14.568 personas fueron encuestadas en 1996, 2001 y 2006, respectivamente. La muestra de 1996 representa aproximadamente al 60% de la población total. El total de individuos seguidos entre 1996 y 2001 es de 15.038 y 10.287 personas en las 3 ondas (1996-2001-2006). Esta disminución en el tamaño de la muestra inicial se traduce en una tasa de atrición de 28,2% entre 1996 y 2001, y de un 50,9% entre 1996 y 200633. La primera onda de la EPCASEN fue realizada entre noviembre y diciembre de 1996, la segunda, entre noviembre y diciembre de 2001, en tanto que la última onda se realizó entre noviembre y diciembre de 2006 y enero y febrero de 2007. La encuesta contiene información sobre educación, ingresos, salud, participación en el mercado laboral, empleo, historia laboral y características de la vivienda (Bendezú et al., 2007).
Con el objetivo de implementar la técnica TSIV así como el método propuesto en esta investigación, para evaluar su performance y realizar comparaciones con Argentina, se dividió el panel en dos submuestras, una correspondiente a la onda 1996 y otra, a la onda 2006, usando cada submuestra como dos encuestas cross-section repetidas. La encuesta de la onda 2006 del EPCASEN contiene información retrospectiva, para todos los jefes y cónyuges de hogar, sobre educación y ocupación de los padres. Esta muestra constituye, entonces, la denominada muestra principal de hijos del método TSIV. Por tanto, la muestra secundaria de padres «representativos» de los hijos de la muestra primaria se obtuvo de la onda 1996.
Otros datos empleados para Chile, a fin de realizar un análisis de robustez de las estimaciones obtenidas con el nuevo método aquí propuesto, se obtuvieron de las Encuestas CASEN para los años 1987, 1990, 1992, 1994, 1996, 1998, 2000 y 2006. Esta encuesta de hogares, con cobertura nacional (urbano-rural), cuya onda de 1996 sirvió de base para la EPCASEN 1996-2001-2006, contiene una gran variedad de información sobre características demográficas, laborales y socioeconómicas de la población. Las encuestas CASEN se realizan en noviembre y diciembre desde 1987, con periodicidad bianual o trianual, utilizando un muestreo estratificado, por conglomerados compacto (manzana de viviendas) y polietápico.
Los microdatos utilizados para Argentina provienen de distintas fuentes de información. Por una parte, la Encuesta Permanente de Hogares (EPH) de los mismos años que los cubiertos por la EPCASEN. A diferencia de esta última, la EPH es una encuesta repetida de sección cruzada de los principales aglomerados urbanos del país que incluye información sobre ingresos y otras características sociodemográficas para padres e hijos corresidentes. Esto permite la implementación de la técnica TSIV, de forma similar que la muestra seleccionada, con fines comparativos, de hijos y padres corresidentes del 2006 en la EPCASEN. A partir de la EPH del 2006 se obtiene la denominada «muestra principal de hijos y padres» y de la EPH de 1996 se deriva la «muestra secundaria o representativa».
Otra fuente de datos utilizada para Argentina es la Encuesta de Percepción de Planes Sociales (EPPS), que contiene información retrospectiva sobre los padres para todos los individuos encuestados, independientemente de que estos residan o no, al momento de la encuesta, en la misma vivienda que sus padres34. Este encuesta fue realizada entre mediados de junio y mediados de agosto de 2007 por Equipos MORI Argentina y el Centro de Estudios Distributivos, Laborales y Sociales de la Universidad Nacional de La Plata (CEDLAS). La muestra de la EPPS consiste de 2.500 jefes de hogar y cónyuges residentes en hogares particulares de todo el país. Por lo tanto, la muestra es representativa de hogares a nivel nacional (urbano-rural)35. Por esto, en el ejercicio de comparación con Chile, la muestra secundaria necesaria para implementar el método TSIV con los datos de la EPPS es obtenida de la Encuesta de Desarrollo Social (EDS) realizada en octubre de 1997 que es aproximadamente representativa de la población nacional. Asimismo, en el contexto del presente estudio, la principal ventaja de la EPPS es la información que provee sobre la edad y educación de los padres para todos los encuestados. De forma similar, la EPCASEN, además de los datos sobre los padres que se derivan de la estructura longitudinal, incluye información retrospectiva sobre la educación y la ocupación de los padres para los jefes y cónyuges de hogar encuestados. Además, los años de realización de ambas encuestas están separados por un intervalo de 10años, similar al período de tiempo cubierto por la EPCASEN. La EPPS permite también analizar la robustez de los resultados derivados con la EPH.
Como la EPH recolecta información solo de los centros urbanos más importantes del país en términos de tamaño de población, las muestras son representativas de las ciudades pero no de toda la población nacional. Esto podría llevar a una sobrestimación de la movilidad generacional en el país, porque esta encuesta no representa grupos de la población para quienes se espera que la persistencia generacional de ingresos sea mayor, tales como los que viven en áreas rurales o pequeñas ciudades. No obstante, en Argentina un elevado porcentaje de la población total habita en centros urbanos y la muestra de la EPH actualmente representa aproximadamente al 70% de la población urbana y al 60% de la población total del país. Además, como análisis de robustez de los resultados obtenidos se realizaron estimaciones utilizando una muestra secundaria obtenida a partir de la EDS de 1997 que tiene mayor cobertura geográfica.
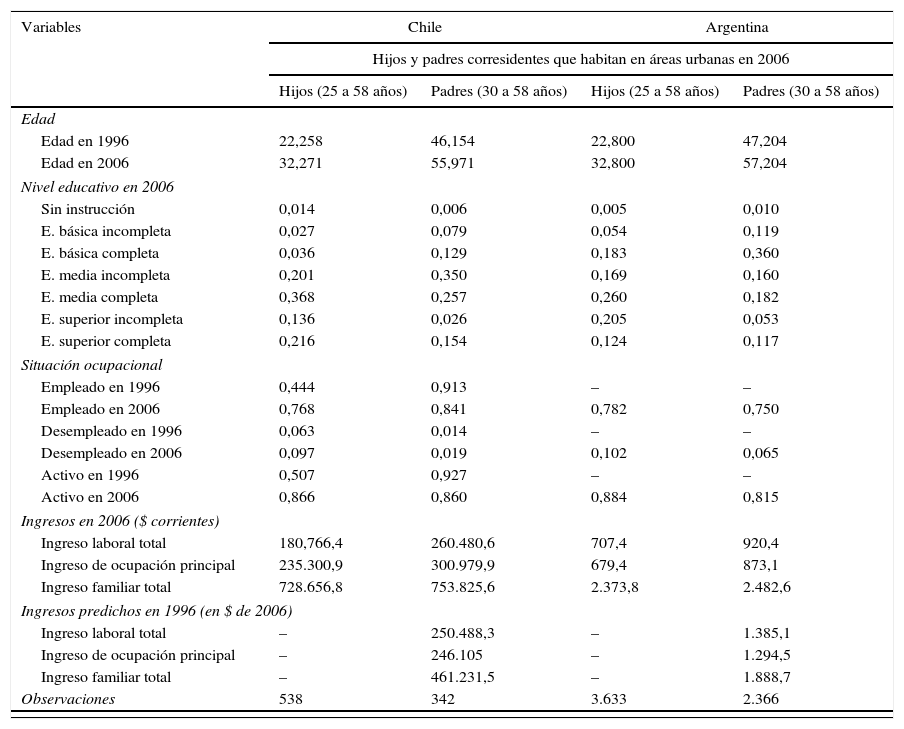
En la tabla 1 y la tabla A.1 del anexo A se observan las principales características de las muestras de padres e hijos con las que se desarrolla el análisis comparativo de los niveles de persistencia intergeneracional de ingresos entre Chile y Argentina. Como se observa en la tabla 1, solo se consideraron hijos varones, dados los problemas de sesgo de selección muestral normalmente asociados con la participación femenina en el mercado laboral36.
Características de las muestras de hijos varones y padres. Chile y Argentina
| Variables | Chile | Argentina | ||
|---|---|---|---|---|
| Hijos y padres corresidentes que habitan en áreas urbanas en 2006 | ||||
| Hijos (25 a 58 años) | Padres (30 a 58 años) | Hijos (25 a 58 años) | Padres (30 a 58 años) | |
| Edad | ||||
| Edad en 1996 | 22,258 | 46,154 | 22,800 | 47,204 |
| Edad en 2006 | 32,271 | 55,971 | 32,800 | 57,204 |
| Nivel educativo en 2006 | ||||
| Sin instrucción | 0,014 | 0,006 | 0,005 | 0,010 |
| E. básica incompleta | 0,027 | 0,079 | 0,054 | 0,119 |
| E. básica completa | 0,036 | 0,129 | 0,183 | 0,360 |
| E. media incompleta | 0,201 | 0,350 | 0,169 | 0,160 |
| E. media completa | 0,368 | 0,257 | 0,260 | 0,182 |
| E. superior incompleta | 0,136 | 0,026 | 0,205 | 0,053 |
| E. superior completa | 0,216 | 0,154 | 0,124 | 0,117 |
| Situación ocupacional | ||||
| Empleado en 1996 | 0,444 | 0,913 | – | – |
| Empleado en 2006 | 0,768 | 0,841 | 0,782 | 0,750 |
| Desempleado en 1996 | 0,063 | 0,014 | – | – |
| Desempleado en 2006 | 0,097 | 0,019 | 0,102 | 0,065 |
| Activo en 1996 | 0,507 | 0,927 | – | – |
| Activo en 2006 | 0,866 | 0,860 | 0,884 | 0,815 |
| Ingresos en 2006 ($ corrientes) | ||||
| Ingreso laboral total | 180,766,4 | 260.480,6 | 707,4 | 920,4 |
| Ingreso de ocupación principal | 235.300,9 | 300.979,9 | 679,4 | 873,1 |
| Ingreso familiar total | 728.656,8 | 753.825,6 | 2.373,8 | 2.482,6 |
| Ingresos predichos en 1996 (en $ de 2006) | ||||
| Ingreso laboral total | – | 250.488,3 | – | 1.385,1 |
| Ingreso de ocupación principal | – | 246.105 | – | 1.294,5 |
| Ingreso familiar total | – | 461.231,5 | – | 1.888,7 |
| Observaciones | 538 | 342 | 3.633 | 2.366 |
| Variables | Hijos jefes y cónyuges de hogar con información sobre sus padres | |||
|---|---|---|---|---|
| Hijos (25 a 58 años) | Hijos (30 a 45 años) | Hijos (25 a 58 años) | Hijos (30 a 45 años) | |
| Edad | 43,151 | 38,089 | 42,288 | 37,537 |
| Nivel educativo | ||||
| Sin instrucción | 0,003 | 0,002 | 0,004 | 0,005 |
| E. básica incompleta | 0,069 | 0,056 | 0,065 | 0,033 |
| E. básica completa | 0,033 | 0,020 | 0,248 | 0,236 |
| E. media incompleta | 0,317 | 0,358 | 0,207 | 0,214 |
| E. media completa | 0,280 | 0,332 | 0,261 | 0,253 |
| E. superior incompleta | 0,084 | 0,046 | 0,084 | 0,114 |
| E. superior completa | 0,214 | 0,186 | 0,130 | 0,146 |
| Nivel educativo del padre | ||||
| Sin instrucción | 0,142 | 0,176 | 0,081 | 0,098 |
| Primaria incompleta | 0,277 | 0,281 | 0,240 | 0,195 |
| Primaria completa | 0,200 | 0,201 | 0,399 | 0,442 |
| Secundaria incompleta | 0,133 | 0,139 | 0,077 | 0,074 |
| Secundaria completa | 0,188 | 0,153 | 0,154 | 0,147 |
| Universitaria incompleta | 0,016 | 0,021 | 0,014 | 0,018 |
| Universitaria completa | 0,044 | 0,029 | 0,036 | 0,026 |
| Ingresos familiares totales ($ corrientes) | 630,794,6 | 579.348,6 | 1.930,76 | 1.946,46 |
| Ingresos familiares totales predichos de su padre 10 años antes (en $ año muestra ppal.) | 350.555,7 | 449.544,8 | 1.937,92 | 2.039,44 |
| Observaciones | 1.089 | 551 | 666 | 317 |
Los ingresos predichos de los padres se obtuvieron empleando como instrumento su nivel educativo. El promedio de los ingresos predichos laborales y de la ocupación principal de ambos padres es la media de la suma del ingreso laboral del padre y de la madre. El ingreso laboral total incluye los ingresos mensuales de la ocupación principal y los ingresos mensuales de las ocupaciones secundarias (sueldos o salarios, bonificaciones, gratificaciones y remuneraciones en especie).
Fuente: elaboración propia sobre la base de EPCASEN, EPH, EPPS y EDS.
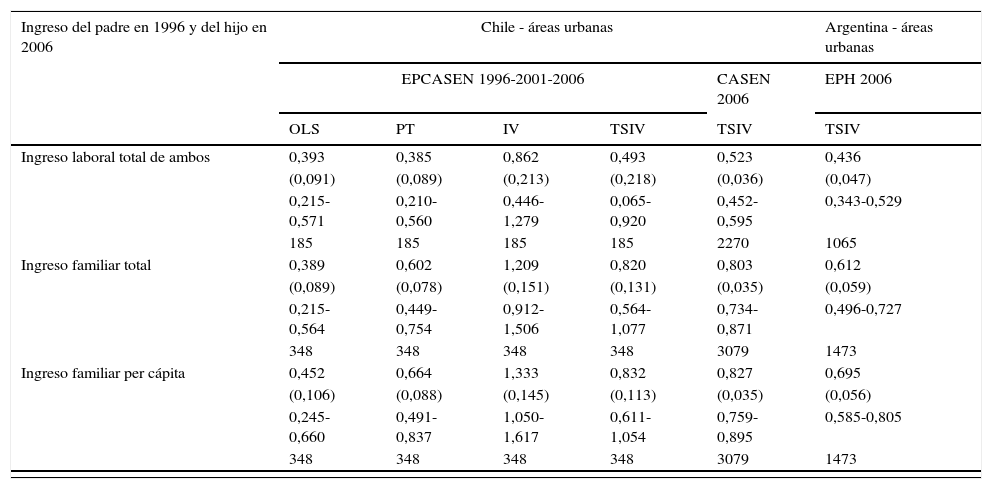
Las EII que se reportan en la tabla 2 y se analizan en este apartado fueron estimadas en base al modelo intergeneracional del ingreso permanente, siguiendo a la gran mayoría de la literatura teórica y empírica37.
Elasticidades intergeneracionales del ingreso (EII) estimadas entre hijos varones de 25 a 58 años y padres corresidentes en 2006. Chile y Argentina
| Ingreso del padre en 1996 y del hijo en 2006 | Chile - áreas urbanas | Argentina - áreas urbanas | ||||
|---|---|---|---|---|---|---|
| EPCASEN 1996-2001-2006 | CASEN 2006 | EPH 2006 | ||||
| OLS | PT | IV | TSIV | TSIV | TSIV | |
| Ingreso laboral total de ambos | 0,393 | 0,385 | 0,862 | 0,493 | 0,523 | 0,436 |
| (0,091) | (0,089) | (0,213) | (0,218) | (0,036) | (0,047) | |
| 0,215-0,571 | 0,210-0,560 | 0,446-1,279 | 0,065-0,920 | 0,452-0,595 | 0,343-0,529 | |
| 185 | 185 | 185 | 185 | 2270 | 1065 | |
| Ingreso familiar total | 0,389 | 0,602 | 1,209 | 0,820 | 0,803 | 0,612 |
| (0,089) | (0,078) | (0,151) | (0,131) | (0,035) | (0,059) | |
| 0,215-0,564 | 0,449-0,754 | 0,912-1,506 | 0,564-1,077 | 0,734-0,871 | 0,496-0,727 | |
| 348 | 348 | 348 | 348 | 3079 | 1473 | |
| Ingreso familiar per cápita | 0,452 | 0,664 | 1,333 | 0,832 | 0,827 | 0,695 |
| (0,106) | (0,088) | (0,145) | (0,113) | (0,035) | (0,056) | |
| 0,245-0,660 | 0,491-0,837 | 1,050-1,617 | 0,611-1,054 | 0,759-0,895 | 0,585-0,805 | |
| 348 | 348 | 348 | 348 | 3079 | 1473 | |
| Ingreso del padre en 1996 y del hijo en 2006 | Chile - áreas urbanas y rurales | ||||
|---|---|---|---|---|---|
| EPCASEN 1996-2001-2006 | CASEN 2006 | ||||
| OLS | PT | IV | TSIV | TSIV | |
| Ingreso laboral total | 0,469 | 0,478 | 0,724 | 0,506 | 0,522 |
| (0,084) | (0,083) | (0,189) | (0,168) | (0,031) | |
| 0,304-0,633 | 0,315-0,641 | 0,353-1,095 | 0,176-0,836 | 0,461-0,583 | |
| 247 | 247 | 247 | 247 | 3.606 | |
| Ingreso familiar total | 0,415 | 0,601 | 0,989 | 0,748 | 0,793 |
| (0,072) | (0,060) | (0,115) | (0,100) | (0,029) | |
| 0,273-0,556 | 0,483-0,719 | 0,764-1,214 | 0,552-0,945 | 0,736-0,851 | |
| 436 | 436 | 436 | 292 | 4.837 | |
| Ingreso familiar per cápita | 0,461 | 0,653 | 1,098 | 0,729 | 0,810 |
| (0,084) | (0,066) | (0,115) | (0,083) | (0,027) | |
| 0,297-0,626 | 0,524-0,783 | 0,872-1,324 | 0,567-0,892 | 0,757-0,862 | |
| 436 | 436 | 436 | 436 | 4.837 | |
Se reportan entre paréntesis los errores estándar computados con la técnica de bootstrap, debajo, el intervalo de confianza al 95% y en la última fila de cada panel, el número de observaciones con el que se realizó cada estimación. Las EII fueron estimadas a partir de un modelo intergeneracional que incluye además del ingreso de hijos y padres (observado o predicho en base a su nivel educativo, según el método de estimación), controles cuadráticos para la edad de padres e hijos.
Fuente: elaboración propia sobre la base de EPCASEN, Encuesta CASEN 2006 y EPH.
En el caso de Chile además de la técnica TSIV pueden implementarse los métodos OLS e IV, utilizando la información longitudinal de la EPCASEN. En cambio, en Argentina, si el ingreso de los padres intenta medirse en un momento de su ciclo vital lo más similar a aquel en el que se observa el ingreso de sus hijos, disminuyendo así el denominado life-cycle bias, ante la falta de datos de panel de largo alcance debe recurrirse a una muestra auxiliar en el pasado, cuando los padres de la muestra principal eran más jóvenes. Es decir, debe implementarse el método TSIV. Para esto se utilizan los microdatos provenientes de la EPH de 2006 y de 199638. Con fines comparativos, la muestra utilizada para ambos países está conformada por padres e hijos corresidentes en 2006.
En base a las distintas estimaciones realizadas, se decidió que el rango etario en el que se mide el ingreso de los hijos sea de 25 a 58años, y el de los padres, de 30 a 55años. Se espera que esta selección permita minimizar el life-cycle bias sin reducir demasiado el número de observaciones, en particular las incluidas en la muestra de hijos de la EPCASEN.
Las EII estimadas por IV y por TSIV se realizaron utilizando como instrumento la educación del padre, concretamente su nivel educativo39. Para la implementación del método TSIV, en ambos países, se utilizó como muestra principal la de hijos y padres corresidentes en 2006 y como muestra secundaria la conformada por hijos y padres «representativos» entrevistados en 1996 y de la misma cohorte de nacimiento que los incluidos en la muestra principal. La razón de la elección de este último año es que se corresponde al primer año de la EPCASEN. En otras palabras, la cobertura temporal del panel chileno impide medir el ingreso de los padres en años previos a 1996. Sin embargo, esto sería recomendable dado que, conforme surge de las características de la muestra de hijos y padres corresidentes, reportadas en la tabla 1, los padres, en 1996, año en que se mide su ingreso (o la correlación entre este y su nivel educativo, en el caso del método IV o TSIV) tienen, en promedio, 10años más que sus hijos en 2006. Esto impide que el life-cycle bias pueda ser completamente eliminado. En efecto, una forma de eliminarlo es midiendo el ingreso de padres e hijos en la misma edad. Esto implica, en términos empíricos, que el ingreso de los padres debería ser medido 20años antes, en promedio, al momento en que se observa el ingreso de sus hijos. No obstante, la edad promedio de los hijos (32años en la muestra chilena y 34años en Argentina) y la de los padres (45años en Chile y 46años en Argentina) pertenece al intervalo en que, según las estimaciones de Haider y Solon (2006) y Böhlmark y Lindquist (2006), el life-cycle bias disminuye o desaparece.
Conforme con los límites en probabilidad presentados en la sección 3, y en línea con los hallazgos encontrados por otros estudios (Solon, 1992; Zimmerman, 1992, entre otros), cuando se consideran las EII estimadas para la muestra chilena de hijos y padres varones, que habitan tanto en áreas urbanas como rurales, el estimador OLS parece subestimar la verdadera EII, en tanto que, el estimador IV tiende a sobrestimarla. En cambio, la EII obtenida con la técnica de TSIV toma en muchos casos valores intermedios al intervalo configurado por los estimadores anteriores. Por tanto, bajo determinados supuestos, podría estar más cerca de la verdadera EII que la computada con ellos.
Dados los problemas de sesgo de selección muestral normalmente asociados con la participación femenina en el mercado laboral, y como este problema es menor entre los varones, por sus mayores tasas de participación en el mercado laboral (87% en Chile y 88% en Argentina), se considera que las comparaciones de las EII estimadas con el método TSIV para la muestra de padres e hijos varones, que habitan en zonas urbanas, son más apropiadas. En general, las EII estimadas con el mismo método (TSIV) para Chile superan las obtenidas para Argentina, pero las diferencias no resultan, en su mayoría, estadísticamente significativas40. Cuando la variable utilizada es el ingreso laboral total41, las EII son de 0,49 en Chile y de 0,44 en Argentina. Esta última, aunque menor en 0,05, no es estadísticamente diferente de la primera.
Las estimaciones de la EII para el ingreso laboral obtenidas para Chile, con la EPCASEN y la CASEN 2006, son similares a las reportadas por otros estudios empíricos que implementaron el método TSIV, utilizando la educación y la experiencia como instrumentos. Así, Núñez y Risco (2004) estiman, a partir de la Encuesta de Empleo y Desempleo del 2004, para el área de Gran Santiago, una elasticidad de 0,55 para una muestra de hijos de 23 a 35años y de 0,58 para hijos de 23 a 55años. En tanto que Núñez y Miranda (2011) obtienen una EII de 0,54, para hijos de 23 a 65años, en base a la Encuesta de Empleo y Desempleo de 2004, y de 0,71 para hijos de 23 a 40años, utilizando la Encuesta CASEN de 2006.
Cuando la persistencia intergeneracional de ingresos se evalúa considerando el ingreso familiar total42, nuevamente, la EII en Chile (0,8) resulta mayor, en 0,2 aproximadamente, a la estimada en Argentina (0,6), siendo esta diferencia significativa43. Este hallazgo podría ser particularmente relevante teniendo en cuenta que el ingreso familiar ofrece una medida más amplia de los recursos del hogar que el ingreso laboral44 y está menos sujeto a los problemas de medición asociados con las fluctuaciones transitorias en los ingresos45. De allí que, en línea con los resultados obtenidos por varios estudios empíricos46, se observa que tanto en Chile como en Argentina el ingreso familiar está más altamente asociado entre generaciones que el ingreso laboral. Esto podría ser el resultado de varios factores como el efecto sobre el ingreso familiar de los ingresos de capital o de fuentes de ingresos no laborales, las variaciones en la oferta de trabajo de la madre que afecta la distribución de ingresos familiares y el emparejamiento selectivo (o assortative mating) que es especialmente pronunciado entre las parejas con altos niveles educativos y puede incrementar las desigualdades entre las familias.
Sin embargo, las limitaciones de las muestras con las que se obtuvieron estas EII para ambos países, concretamente el potencial sesgo de selección por corresidencia presente en las estimaciones, impiden llegar a una conclusión definitiva porque no es posible determinar si el método implementado para corregir por este problema es efectivo.
Una forma de evaluar la robustez de ese resultado es utilizar una muestra alternativa que no presente este problema de selección. Una muestra de hijos que cumple con esta característica es la conformada por todos los jefes de hogar y cónyuges entrevistados en la EPCASEN de Chile, así como en la EPPS relevada en Argentina, a quienes se consultó por algunas características de sus padres. Concretamente, en ambas encuestas, se preguntó por el nivel educativo del padre47. Como la información sobre el ingreso de los padres solo está disponible, en la EPCASEN, para los hijos corresidentes y no lo está en el caso de la EPPS48, se implementó el método TSIV, utilizando como instrumento la educación del padre, reportada por todos los jefes de hogar y cónyuges encuestados. Asimismo, dado que la única variable de ingreso disponible en la EPPS es el ingreso familiar, las estimaciones se realizaron, para la muestra argentina, considerando esta variable que, además, es de particular interés en este caso.
Las EII se estimaron para todos los jefes y cónyuges de hogar de dos grupos de edad, 25 a 58años y 30 a 45años, considerando rangos etarios similares para los padres «representativos» de la muestra auxiliar o secundaria. Esta última muestra fue obtenida de la onda de 1996 de la EPCASEN, en el caso de Chile, y de la EDS49 de 1997, en el caso de Argentina.
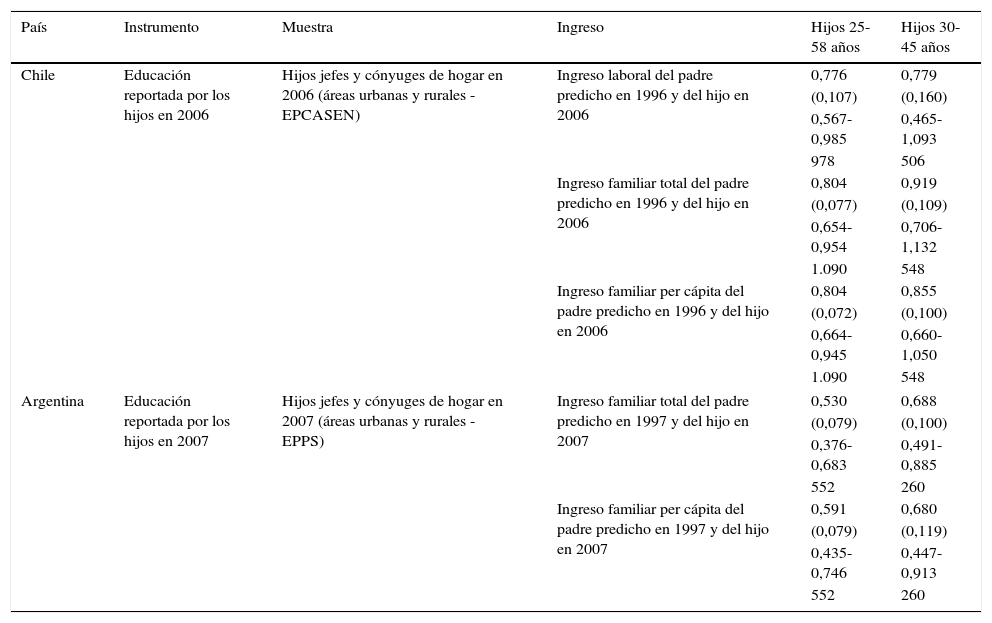
Las EII reportadas en la tabla 3 confirman el resultado anterior derivado a partir de las elasticidades computadas con la muestra de hijos y padres corresidentes (tabla 2). Esto es, la persistencia intergeneracional del ingreso familiar parece ser mayor en Chile que en Argentina. Así, las elasticidades intergeneracionales del ingreso familiar total estimadas para hijos chilenos de 25 a 58años, así como para aquellos de 30 a 45años (0,78), superan en 0,3 y 0,2 las computadas entre hijos argentinos del mismo rango etario (0,53 y 0,69). Estas pronunciadas diferencias resultan significativas desde un punto de vista tanto económico como estadístico. Un resultado similar se obtiene al considerar como variable de resultado el ingreso familiar per cápita.
Elasticidades intergeneracionales del ingreso (EII) estimadas para hijos varones jefes y cónyuges de hogar. Chile y Argentina
| País | Instrumento | Muestra | Ingreso | Hijos 25-58 años | Hijos 30-45 años |
|---|---|---|---|---|---|
| Chile | Educación reportada por los hijos en 2006 | Hijos jefes y cónyuges de hogar en 2006 (áreas urbanas y rurales - EPCASEN) | Ingreso laboral del padre predicho en 1996 y del hijo en 2006 | 0,776 | 0,779 |
| (0,107) | (0,160) | ||||
| 0,567-0,985 | 0,465-1,093 | ||||
| 978 | 506 | ||||
| Ingreso familiar total del padre predicho en 1996 y del hijo en 2006 | 0,804 | 0,919 | |||
| (0,077) | (0,109) | ||||
| 0,654-0,954 | 0,706-1,132 | ||||
| 1.090 | 548 | ||||
| Ingreso familiar per cápita del padre predicho en 1996 y del hijo en 2006 | 0,804 | 0,855 | |||
| (0,072) | (0,100) | ||||
| 0,664-0,945 | 0,660-1,050 | ||||
| 1.090 | 548 | ||||
| Argentina | Educación reportada por los hijos en 2007 | Hijos jefes y cónyuges de hogar en 2007 (áreas urbanas y rurales - EPPS) | Ingreso familiar total del padre predicho en 1997 y del hijo en 2007 | 0,530 | 0,688 |
| (0,079) | (0,100) | ||||
| 0,376-0,683 | 0,491-0,885 | ||||
| 552 | 260 | ||||
| Ingreso familiar per cápita del padre predicho en 1997 y del hijo en 2007 | 0,591 | 0,680 | |||
| (0,079) | (0,119) | ||||
| 0,435-0,746 | 0,447-0,913 | ||||
| 552 | 260 | ||||
Se reportan entre paréntesis los errores estándar computados con la técnica de bootstrap, debajo, el intervalo de confianza al 95% y en la última fila de cada panel, el número de observaciones con el que se realizó cada estimación.
Fuente: elaboración propia sobre la base de EPCASEN, EPPS y EDS.
Por otra parte, cabe destacar algunos resultados metodológicamente relevantes. En primer lugar, dada la mayor cobertura geográfica de la EPPS, con relación a la EPH, que incluye, a diferencia de esta última, zonas rurales, podría esperarse que los niveles de persistencia intergeneracional del ingreso y, por tanto, las EII sean mayores que las reportadas en la tabla 2. En principio, se espera que los procesos de transmisión intergeneracional sean más fuertes en las poblaciones rurales donde las oportunidades de inversión en capital humano de los hijos, así como sus posibilidades de acceder a mejores puestos laborales que los poseídos por sus padres son, en general, más limitadas. Sin embargo, cuando se comparan estas estimaciones para hijos y padres varones de 25 a 58años, los resultados no muestran diferencias significativas entre ellas. Así, mientras las EII computadas con los datos de la EPPS son 0,5 para el ingreso familiar total y 0,6 para el familiar per cápita, las obtenidas a partir de la EPH son 0,6 y 0,69, respectivamente. Este resultado podría estar relacionada con el bajo porcentaje de población total que habita en zonas rurales en Argentina (menos del 40% según las estimaciones del último censo nacional de población del 2010). Este hallazgo sugiere, entonces, que los indicadores de movilidad intergeneracional obtenidos para Argentina, como la EII, utilizando la EPH son aproximadamente similares a lo que podrían derivarse a partir de una encuesta con cobertura geográfica urbana y rural.
Asimismo, el resultado anterior también sugeriría que las estimaciones realizadas con una muestra de padres e hijos que residen juntos (como la obtenida de la EPH) no son estadísticamente diferentes a las estimadas a partir de una muestra de hijos con información retrospectiva de sus padres y sin sesgo de selección por corresidencia (como la derivada de la EPPS 2007). Una forma de apreciar el efecto aislado de este sesgo en las estimaciones es comparando las EII de la tabla 2 y la tabla 3 estimadas a partir de las muestras disponibles para Chile que presentan la misma cobertura geográfica e incluyen hijos del mismo grupo etario. Así, las EII obtenidas de la EPCASEN, para el ingreso familiar, a partir de una muestra de hijos y padres corresidentes son aproximadamente similares a las computadas con la muestra de hijos jefes y cónyuges de hogar, no sujetas a ese problema de sesgo de selección50. Así, las elasticidades intergeneracionales del ingreso familiar total y per cápita estimadas por TSIV para Chile, utilizando la muestra de hijos corresidentes con sus padres, son iguales a 0,79 y 0,81, en tanto que las obtenidas con la muestra de jefes y cónyuges de hogar (habiten o no con sus padres), del mismo rango etario y con el mismo método de estimación, son iguales a 0,8. Por tanto, estas EII no presentan diferencias estadísticamente significativas.
Además, las EII computadas para hijos varones de 30 a 45años resultan, en general, mayores que las obtenidas con la muestra de 25 a 58años. Aunque este resultado es esperable, dado que los hijos del primer grupo etario están, en promedio, en las edades en que, en teoría, el life cycle bias desaparece o es menor, las diferencias no son estadísticamente significativas. Este hallazgo confirma, entonces, que los resultados obtenidos con la muestra de hijos de 25 a 58años no llevan a conclusiones diferentes que las que podrían derivarse considerando la muestra de hijos en el primer rango etario.
5.2Evaluación del nuevo modelo intergeneracional y su método de estimaciónEn esta sección se evalúa el nuevo modelo intergeneracional formulado por Muller (2008). Conforme con este, no solo el ingreso permanente de los padres sino también sus ingresos transitorios pueden ser relevantes en la determinación del conjunto de oportunidades futuras de los hijos. A fin de obtener una estimación de la EII correspondiente a este modelo alternativo se estiman, a partir del nuevo método de estimación propuesto, los límites inferiores y superiores de esta EII. La principal ventaja de este nuevo método es la posibilidad de estimar, utilizando encuestas cross-section repetidas, un intervalo de confianza de la movilidad o persistencia intergeneracional de ingresos que se derivaría en caso de disponer de datos de panel de largo alcance. En el caso de Chile, la EII que surge del modelo alternativo, a diferencia de las derivadas a partir del modelo tradicional, no puede obtenerse con los datos longitudinales de la EPCASEN 1996-2001-2006 de Chile porque no se dispone de información sobre el ingreso del padre durante un número suficiente de años durante la niñez o adolescencia de los hijos adultos entrevistados en 2006, sino solo para dos años previos: 1996 y 2001.
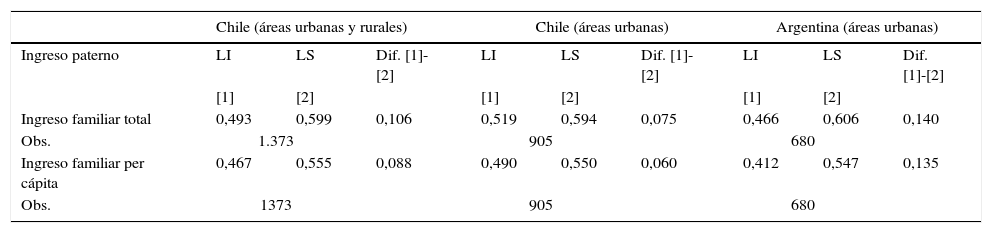
Las estimaciones reportadas en la tabla 4 se obtuvieron a partir de una muestra de hijos adultos que tenían entre 25 y 35 años en 2006, de forma tal que eran niños y jóvenes antes de 1996. Este rango etario elegido para los hijos responde a los argumentos de Muller (2008) relacionados con la relevancia de estimar la EII en la niñez o adolescencia de los hijos. La ampliación del rango etario de los hijos implica medir el ingreso de los padres fuera de la etapa vital considerada a priori relevante que es la de su niñez y adolescencia. En este punto resulta importante recordar que la hipótesis subyacente del modelo intergeneracional alternativo para considerar los shocks en el ingreso o los ingresos transitorios de los padres (además del ingreso permanente) es que se espera tengan un efecto en las oportunidades futuras de los hijos, particularmente si ocurren durante su niñez y adolescencia, posibilidad que es mayor en países en desarrollo como Argentina y Chile. Este supuesto está fundamentando por una variedad de evidencia empírica y el fuerte consenso que existe en la literatura acerca de que las experiencias de los primeros años de vida son fundamentales para determinar las oportunidades posteriores. Estos estudios analizan cómo el desarrollo en los primeros años y la adolescencia genera un proceso acumulativo de experiencias y factores que afecta los resultados futuros obtenidos por los hijos. Entre estos antecedentes se encuentra el estudio de Cameron y Heckman (2001) que analizan el efecto del ingreso familiar sobre la educación de los hijos, encontrando resultados que sugieren que el ingreso familiar en las primeras etapas de la niñez, y no luego, es el que afecta las probabilidades de asistencia a la universidad de los hijos51. Según Raczinsky (2006) la niñez temprana es una ventana de oportunidad para la adquisición de capacidad y aprendizaje que pueden lograrse a edades más avanzadas pero a un mayor costo. Sin embargo, algunos, como Heckman y Masterov (2007), entienden que hay habilidades cognitivas que solo pueden alcanzarse al inicio de la vida y, por tanto, no hay modo de remediar las fallas en esa etapa. Esto tiene implicancias directas de políticas pues sugiere mover su foco hacia la familia y la primera infancia. Además, según Cunha et al. (2006), las intervenciones a edad temprana promueven mejoras acumulativas —así como la falta de intervenciones producen desventajas que se acumulan—, aumentando la productividad de la educación secundaria para los hijos de familias pobres que, en ausencia de restricciones crediticias, decidirían continuar sus estudios (FIEL, 2008).
Límites de la elasticidad intergeneracional del ingreso (EII) del modelo alternativo. Hijos varones de 25 a 35 años en 2006
| Chile (áreas urbanas y rurales) | Chile (áreas urbanas) | Argentina (áreas urbanas) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ingreso paterno | LI | LS | Dif. [1]-[2] | LI | LS | Dif. [1]-[2] | LI | LS | Dif. [1]-[2] |
| [1] | [2] | [1] | [2] | [1] | [2] | ||||
| Ingreso familiar total | 0,493 | 0,599 | 0,106 | 0,519 | 0,594 | 0,075 | 0,466 | 0,606 | 0,140 |
| Obs. | 1.373 | 905 | 680 | ||||||
| Ingreso familiar per cápita | 0,467 | 0,555 | 0,088 | 0,490 | 0,550 | 0,060 | 0,412 | 0,547 | 0,135 |
| Obs. | 1373 | 905 | 680 | ||||||
Los modelos intergeneracionales estimados tienen como variable dependiente el ingreso laboral de los hijos e incluyen como controles un polinomio cuadrático en la edad de los hijos.
Fuente: elaboración propia sobre la base de EPCASEN 1996-2001-2006, CASEN 1987, 1992, 1994, 1996, 2006 y EPH 1987, 1992, 1994, 1996, 2006.
Como se mencionó en la sección 3, el método TSIV permite, bajo determinados supuestos, estimar consistentemente la EII permanente. A partir de la ecuación (10) se observa que el estimador TSIV de la EII (β) es consistente si la educación del padre no tiene un efecto directo sobre el ingreso del hijo, después de controlar por el ingreso permanente del padre. Los estudios de Sewell y Hauser (1975), Corcoran et al. (1992) y Mazumder (2005) muestran que el efecto directo de la educación del padre sobre el ingreso del hijo no es estadísticamente distinto de cero, una vez que se controla por el ingreso del padre promediado durante varios años52. Si esto es así, el método TSIV permitiría obtener el límite inferior (LI) de la EII correspondiente al nuevo modelo intergeneracional puesto que solo capturar el impacto del componente permanente del ingreso paterno.
Por otra parte, el límite superior (LS) de la EII se obtuvo implementando el nuevo método de estimación propuesto en esta investigación. Con este objetivo, se utilizaron cinco muestras secundarias distintas a partir de los datos de la encuesta CASEN de Chile y de la EPH de Argentina de los años 198753, 1990, 1992, 1994 y 1996. Como los hijos adultos de la muestra principal de 2006 tienen entre 25 y 35años, el ingreso predicho de los padres a partir de su nivel educativo54 se computó en distintas etapas de su niñez y juventud. Así, por ejemplo, si la muestra secundaria es obtenida de la encuesta de 1987, el ingreso de los padres es estimado cuando los hijos tenían de 6 a 16años, mientras que si se obtiene de la encuesta del año 1996, la estimación del ingreso paterno se realiza cuando los hijos tenían entre 15 y 25años. Los ingresos paternos en cada uno de los cinco años mencionados se estimaron implementando los diferentes pasos del método aquí propuesto para derivar el LS bajo el supuesto de que los términos de error están perfecta y positivamente correlacionados en el tiempo. Luego, los ingresos así estimados se promediaron para obtener la EII correspondiente al LS.
Por otra parte, debe señalarse que las estimaciones se realizaron a partir una muestra de hijos que residen con su padre55. Si bien esto puede generar un sesgo en las estimaciones, de acuerdo con los resultados de la sección 5.1, este parece no tener un efecto significativo sobre las EII. Además no hay razones para suponer que la magnitud de este potencial sesgo sea distinta en las estimaciones obtenidas para Argentina en comparación con las derivadas para Chile utilizando el mismo método. Entonces, si el sesgo afecta las estimaciones de la misma forma, la diferencia entre ellas no lo incluiría. De esta forma, las comparaciones de las EII serían válidas.
En la tabla 4 se reportan los límites inferiores y superiores de la EII correspondientes al modelo alternativo aquí evaluado para Chile y Argentina, considerando como medida de ingreso de los hijos su ingreso laboral56 y como medida de ingreso de los padres su ingreso familiar total y per cápita57. Debe mencionarse también que para reducir el denominado life-cycle bias en las estimaciones se incluyó a padres en edades centrales de 30 a 45años.
En todos los casos, el LS de la EII del nuevo modelo supera el LI, es decir, la estimación de la EII correspondiente al modelo tradicional de ingreso permanente tanto para el ingreso familiar total como para el ingreso familiar per cápita. Esto es consistente con la hipótesis de Muller (2008) sobre la importancia de considerar el ingreso transitorio de los padres, particularmente durante la niñez y adolescencia de los hijos. Además, las diferencias entre el LS y LI no son superiores a 0,11 en el caso de Chile y a 0,14 en el caso de Argentina. Teniendo en cuenta que LI no captura ningún efecto de los ingresos transitorios en tanto que el LS podría sobreestimar su efecto, este resultado sugiere que los ingresos transitorios de los padres explicarían como máximo el 18% y el 25% de la correlación del ingreso entre padres e hijos en Chile y Argentina, respectivamente. Según las estimaciones de Muller (2010), la contribución de los βq de la ecuación (11) a la EII total es del 0,11, de manera que el 20% o más de la elasticidad intergeneracional en Estados Unidos puede responder al denominado ingreso transitorio de los padres.
Por otra parte, a partir de los límites estimados para la EII del modelo alternativo no se observan diferencias significativas en los niveles de persistencia intergeneracional del ingreso entre Chile y Argentina cuando se considera la correlación entre el ingreso laboral de los hijos varones y el ingreso familiar en su niñez y juventud.
6ConclusionesUna forma de evaluar la magnitud del grado de persistencia intergeneracional del ingreso observado en Argentina es contrastándolo con el existente en otro país. Con este fin se realizó un ejercicio de comparación con Chile a partir de estimaciones metodológicamente confrontables. Las características comunes y diferentes que presentan Argentina y Chile, susceptibles de tener un efecto importante en el proceso de transmisión intergeneracional, como sus niveles de crecimiento y desigualdad económica, hacen que este ejercicio empírico sea particularmente interesante. Así, una de las hipótesis que podrían evaluarse es si, dados los comparativamente mayores niveles de desigualdad históricamente observados en Chile, y si la desigualdad y la movilidad están estrechamente relacionadas, siendo la primera un factor muy importante para la configuración de la segunda, más que, por ejemplo, los niveles de crecimiento económico, los niveles de persistencia intergeneracional son mayores en Chile o relativamente similares a los observados en Argentina. Los resultados obtenidos, a partir de las distintas técnicas de estimación de la EII, sugieren que los niveles de movilidad intergeneracional son mayores en Chile que en Argentina cuando se considera como medida de ingreso el ingreso familiar total o per cápita. Así, las EII estimadas para hijos chilenos de 25 a 58años (0,8), así como para los de 30 a 45años (0,9), superan en aproximadamente 0,2-0,3 las computadas entre hijos argentinos del mismo rango etario (0,5-0,6 y 0,7). Sin embargo, cuando se utiliza como medida de resultado económico para los hijos su ingreso laboral no se observan diferencias significativas en los niveles promedio de inmovilidad intergeneracional de ingresos de Chile y Argentina. Conforme a estimaciones comparables, la EII laboral asciende a 0,5 en Chile y a 0,44 en Argentina.
En el artículo también se analizaron formalmente las propiedades de los distintos métodos disponibles para estimar la EII que, como ya fue señalado, constituye uno de los indicadores de persistencia o inmovilidad de ingreso entre generaciones más utilizado en la literatura empírica. En este análisis se destacaron las ventajas y se derivaron los sesgos potencialmente presentes en los distintos estimadores. Algunos de estos fueron ignorados por la mayoría de los estudios disponibles. Asimismo, se evaluó empíricamente la performance de distintos estimadores de la EII, tanto los más utilizados en la literatura empírica como los obtenidos con un nuevo método aquí propuesto, utilizando uno de los paneles de datos más largo disponibles para un país de América Latina, como la Encuesta Panel CASEN 1996-2001-2006 (EPCASEN) de Chile. Los resultados obtenidos sugieren, en línea con los hallazgos de otros estudios empíricos (Solon, 1992, Zimmerman, 1992, entre otros), que las EII estimadas por OLS, utilizando un solo período para medir el ingreso paterno, tienden a subestimar la verdadera, ocurriendo lo contrario con las estimaciones IV. Si esto es así, entonces el método TSIV presentaría una buena performance, puesto que en la mayoría de los casos muestra valores intermedios, superiores a los computados con el método OLS pero inferiores a los obtenidos con la técnica IV. Esto es particularmente relevante, puesto que el método TSIV permite computar y analizar los niveles de MII en países que, como Argentina, no disponen de datos longitudinales de largo alcance.
El principal objetivo del artículo fue evaluar empíricamente un modelo intergeneracional alternativo, recientemente propuesto por Muller (2010) y poco explorado en la literatura, y contrastar estos resultados con los derivados del modelo tradicional. La idea central de este nuevo enfoque es que, a diferencia de lo sostenido por el modelo intergeneracional tradicional, la transmisión relevante entre generaciones no solo tiene lugar en relación al componente permanente del ingreso, sino también a través de los ingresos transitorios. Este modelo tiene varias implicancias relevantes, como se mencionó previamente. Por un lado, sugiere que las comparaciones realizadas entre países en base al modelo estándar de transmisión intergeneracional del ingreso permanente ignoran una fuente potencial de heterogeneidad inobservada que podría afectar las estimaciones de la EII: la edad de los hijos en la que se mide el ingreso de sus padres. Por otra parte, las implicancias de política de este modelo alternativo son más inmediatas. Si el ingreso transitorio afecta el ingreso futuro de los niños, esto indicaría que el ingreso de los padres per se tiene un efecto en sus oportunidades, lo que generalmente es incompatible con las formulaciones incluso más débiles del enfoque de igualdad de oportunidades. Entonces, cuanto mayor sea la importancia del ingreso transitorio con relación al permanente en el proceso de transmisión intergeneracional, mayor será el campo para la intervención pública (Muller, 2008).
Como la estimación de este modelo alternativo, al igual que el tradicional, es particularmente problemática en países en los que las bases de datos disponibles no incluyen información sobre el ingreso de los padres para los individuos encuestados, en edades centrales del ciclo vital de ambos, se propuso en esta investigación un método novedoso de estimación. Este nuevo enfoque metodológico combina algunas características del método TSIV para estimar el componente permanente del ingreso parental y del enfoque propuesto por Dang et al. (2014) que permite estimar su componente transitorio, particularmente durante la niñez y la adolescencia de los hijos. Bajo determinados supuestos, con este método puede obtenerse un límite inferior y uno superior de la verdadera EII en el contexto del modelo alternativo. Las estimaciones obtenidas con la implementación de la nueva técnica indican que los ingresos transitorios de los padres explicarían como máximo el 18% y el 25% de la correlación del ingreso observada entre padres e hijos en Chile y Argentina, respectivamente. En definitiva, considerando que las principales inversiones en el capital humano de los hijos tienen lugar en su niñez y adolescencia, y que tanto los componentes permanentes como transitorios del ingreso son relevantes para determinar las oportunidades futuras de los hijos, esos resultados sugieren que los niveles reales de MII en ambos países son similares y relativamente bajos. No obstante, estos resultados deben ser interpretados con precaución, dados los supuestos bajo los cuales fueron derivados. Sin embargo, más allá de las limitaciones del método propuesto se considera que este puede constituir un primer aporte para una línea de investigación sobre formas alternativas de analizar la MII en países con fuentes de información limitada. En particular, se trata de una propuesta metodológica inicial para examinar un aspecto relevante pero poco explorado en la literatura empírica como el impacto de los componentes transitorios del ingreso paterno sobre los resultados económicos obtenidos por sus hijos. Por lo tanto queda relegado para una investigación futura el estudio de otras técnicas de estimación que permitan relajar los supuestos del enfoque aquí propuesto.
AgradecimientosAgradezco las observaciones de Leonardo Gasparini, así como los comentarios realizados por el Comité de Doctorado de la Universidad Nacional de La Plata (UNLP), por los asistentes al Seminario de Doctorado de la UNLP y los recibidos durante la XLVII Reunión Anual de la Asociación Argentina de Economía Política (AAEP).
.
Característica de la muestra de hijos y padres corresidentes en áreas urbanas y rurales. Chile, 2006
| Variables | Hijos (25 a 58 años) | Padres (30 a 58 años) |
|---|---|---|
| Edad | ||
| Edad en 1996 | 22,413 | 46,242 |
| Edad en 2006 | 32,419 | 56,040 |
| Nivel educativo en 2006 | ||
| Sin instrucción | 0,017 | 0,011 |
| E. básica incompleta | 0,036 | 0,112 |
| E. básica completa | 0,041 | 0,132 |
| E. media incompleta | 0,226 | 0,342 |
| E. media completa | 0,360 | 0,233 |
| E. superior incompleta | 0,124 | 0,023 |
| E. superior completa | 0,196 | 0,147 |
| Situación ocupacional | ||
| Empleado en 1996 | 0,467 | 0,920 |
| Empleado en 2006 | 0,787 | 0,843 |
| Desempleado en 1996 | 0,065 | 0,013 |
| Desempleado en 2006 | 0,090 | 0,017 |
| Activo en 1996 | 0,532 | 0,933 |
| Activo en 2006 | 0,876 | 0,860 |
| Ingresos en 2006 ($ corrientes) | ||
| Ingreso laboral total | 174.037,1 | 252.044,8 |
| Ingreso de ocupación principal | 218.591,3 | 284.807,7 |
| Ingreso familiar total | 696.647,6 | 726.620,3 |
| Ingresos predichos en 1996 (en $ de 2006) | ||
| Ingreso laboral total | – | 229.116,6 |
| Ingreso de la ocupación principal | – | 226.071,6 |
| Ingreso familiar total | – | 434.418,4 |
| Observaciones | 668 | 411 |
Fuente: elaboración propia sobre la base de EPCASEN.
Dado el modelo definido en las ecuaciones (1), (2), (3), (6) y (9), el límite en probabilidad del estimador TSIV, utilizando la educación de los padres como instrumento de su ingreso permanente, es:
Multiplicando y dividiendo el denominador por σyˆpσyp=Var(yˆp)Var(yp) se tiene:
Dada la relación entre β y los parámetros λ1 y λ2 de la ecuación (6):
Y reemplazando λ1 según (B.2) en (B.1), se obtiene:
Esta es la ecuación (6) de la sección 3.1.
Siguiendo a Jerrim et al. (2014), es posible obtener una expresión más simple para el límite en probabilidad de βˆTSTSLS, bajo el supuesto de que la covarianza entre el ingreso predicho del padre y el real es igual a la covarianza entre el ingreso predicho del padre y este mismo. En este caso, se tiene:
donde R es la raíz cuadrada de la varianza explicada (R2) en el modelo de la primera etapa (11). Entonces, el límite en probabilidad del estimador sería:
El modelo a estimar está definido por las ecuaciones (1), (2), (6) y (11). El parámetro de interés es la EII definida en la ecuación (12) (B*). Según Muller (2010), una forma de obtener un límite superior de esta EII que surge del modelo intergeneracional alternativo es utilizando un promedio del ingreso del padre durante varios años de la niñez o adolescencia de los hijos. Sin embargo, debe recordarse que, dada las limitaciones de información existentes para Argentina, es necesario obtener primero una estimación de ese promedio. La estrategia propuesta en esta investigación consiste en estimar (11) utilizando yˆp=γˆ Zp y εˆp en lugar del ingreso permanente (yp) y del ingreso transitorio (up) inobservados del padre. Específicamente, a partir de los pasos descriptos en la sección 3.2 y bajo el supuesto de perfecta correlación entre los componentes transitorios del término de error, es posible obtener BˆLS utilizando una estimación del ingreso paterno en diferentes años k de la niñez y adolescencia de los hijos, definido por y˜pk=γˆpkXpk+εˆpk.
Asimismo, si se utilizan la educación o la ocupación del padre como variable instrumental (Zp), dado que probablemente estas variables sean endógenas entonces el ingreso de los hijos estará dado por:
A continuación se deriva el plim del estimador propuesto para el límite superior de la EII que surge del modelo alternativo (B*)5858 Para no complejizar las ecuaciones se deja de lado en la derivación la consideración del potencial lyfe-cycle bias. No obstante, es posible mostrar que su efecto en el plim del estimador es similar al analizado previamente bajo el modelo tradicional.
Se analiza en primer lugar el denominador de (B.5), siguiendo las derivaciones de Muller (2008) para el estimador PT del modelo (1), (2), (6) y (11). Teniendo en cuenta que y˜pk=γˆpkXpk+εˆpk=ypk=yp+upk y que ypq=yp+upq, suponiendo que K=Q=T, el denominador es igual a:
donde α=1+2δT−δT−1+δTT(1−δ)2
No obstante, con relación al supuesto K=Q debe aclararse que existen varios escenarios posibles en términos de los solapamientos que pueden presentarse entre el conjunto de los ingresos medidos en la niñez de los hijos (Q) y el conjunto de los ingresos usados en la regresión (K). En el caso en que se utilicen en la regresión una medida del ingreso de los padres para todos los años de la niñez de los hijos, se cumplirá que K=Q.
Queda por determinar ahora el plim del numerador. Reemplazando:
se tiene:Dado que Cov(upk,yp)=0 ∀k, suponiendo que Cov(yp,uht)=0 ∀t y Cov(upk,uht)=0 ∀k,t y entonces:
Teniendo en cuenta que υpq, υpk y υpk son componentes de ruido blanco, entonces υpq
Dado que ωpq sigue un proceso AR(1), de acuerdo con las derivaciones de Muller (2008) se tiene:
Por tanto,
Supongamos que K=m – r, donde m es el último año y r es el primer año de la niñez de los hijos, entonces:
En el caso en que K=Q, la serie entre paréntesis es primero creciente y luego decreciente en δq−k.
Para un año q dado dividimos la suma entre paréntesis en dos series geométricas finitas como seguidos.
Por otra parte, la relación entre los parámetros β y λ1 y λ2 es la siguiente:
Teniendo en cuenta los siguientes supuestos: Cov(upq,yp)=0 ∀q y Cov(upt,yp)=0 ∀t, se tiene
Reemplazando (B.9) y (B.8) en (B.7), se tiene:
Por lo tanto, de (B.6) y (B.10) se obtiene finalmente:
donde Λq=1+δ−δq−r+1−δq−m+11−δ y α=1+2δT−δT−1+δTT(1−δ)2Por otra parte, como se mencionó previamente en el texto, teniendo en cuenta que la EII propuesta por este nuevo modelo es la suma entre β y las elasticidades correspondientes al componente transitorio del ingreso paterno, el estimador TSIV ofrece un límite inferior de B*, pues solo captura la elasticidad referida al componente permanente. Dado el modelo definido en (1), (2), (6) y (11) y el límite en probabilidad del estimador TS2SLS dado en (B.11) se tiene que:
Bajo el supuesto de que λ2=0, se observa a partir de (B.12) que este estimador ofrece una medida de la EII permanente y, entonces, constituye un límite inferior del parámetro de interés, B*, dado por (11). En tanto que, según (B.11)BˆLS constituye un límite superior de B*. Asimismo, debe observarse que esto también ocurre cuando λ2>0. Ahora bien, como ya se mencionó, cuando se utiliza como instrumento para predecir el ingreso del padre su educación, es razonable suponer que su efecto sobre el ingreso del hijo capturado por λ2 es positivo. Además, teniendo en cuenta que según los resultados obtenidos por Sewell y Hauser (1975), Corcoran et al. (1992) y Mazumder (2005), el efecto directo de la educación del padre en el ingreso del hijo no es estadísticamente distinto de cero, una vez que se controla por el ingreso del padre promediado durante varios años, el supuesto de que λ2=0 también resulta razonable.
Como señala Muller (2010), a quienes no están demasiado familiarizados con la literatura específica de MII les podría resultar sorprendente descubrir que la posibilidad de que el ingreso parental de cualquier tipo (permanente o transitorio) tenga un efecto causal en las oportunidades futuras de los hijos no sea ampliamente aceptada.
Los autores proponen este enfoque para analizar los movimientos intrageneracionales dentro y fuera de la pobreza.
En Argentina, la desigualdad aumentó significativamente desde mediados de la década de los setenta hasta mediados de los años 2000. En el estudio de Gasparini y Lustig (2014) puede encontrarse un examen detenido de la evolución temporal de la desigualdad de ingresos en América Latina.
Así, por ejemplo, en 1996 y 2006, dos años particularmente relevantes en esta investigación, el coeficiente de Gini del ingreso familiar per cápita fue de 0,486 y 0,475 en Argentina, mientras que en Chile ascendió a 0,548 y 0,518, respectivamente, siendo las diferencias entre los coeficientes de ambos países, para los mismos años, estadísticamente significativas.
Para una revisión exhaustiva de los estudios existentes sobre MII a nivel internacional, ver Jiménez (2011a).
En Jiménez (2011b) puede consultarse una revisión detallada de los estudios sobre movilidad ocupacional y movilidad educativa intergeneracional disponibles para Argentina.
La movilidad intergeneracional socioeconómica es medida a través de la elasticidad intergeneracional y del coeficiente de correlación intergeneracional de ingresos. Sin embargo, para aproximar la medida del ingreso permanente se construyó un índice de nivel socioeconómico que sintetiza la situación patrimonial, educativa y de empleo para cada uno de los encuestados.
Al igual que para Argentina, en Chile son más numerosas las investigaciones que examinan la movilidad educativa u ocupacional intergeneracional (Torche, 2005).
Si bien Muller (2008) reconoce que hay varios estudios previos que consideran la relevancia de medir el ingreso paterno durante la niñez antes que en cualquier otro período, su discusión está estrictamente desvinculada de la estructura implícita del modelo intergeneracional asumido que sólo permite una relación entre el ingreso permanente de padres e hijos.
Se asume para simplificar la notación y sin pérdida de generalidad que los ingresos están escritos como desvíos de las medias (por esto no se incluyen constantes en los modelos).
En el siguiente apartado se cuestiona este supuesto, considerando un modelo alternativo propuesto por Muller (2010).
Los detalles de la derivación de la ecuación (4) están a disposición del lector que los requiera.
No obstante, como advierten Nybom y Sthuler (2016), el estimador OLS estrictamente podría subestimar como sobrestimar la verdadera EII si el término de error incluye un shock transitorio correlacionado con el ingreso permanente.
Algunos estudios, reconociendo el problema de error de medición, propusieron como forma de solucionarlo introducir controles por la edad de padres e hijos en la ecuación (3), cuando se utilizaran los ingresos corrientes en lugar de los permanentes. Sin embargo, Haider y Solon (2006) mostraron que la inclusión de controles por edad y experiencia en una regresión media como (3) controlará solamente por los efectos promedios de la edad o la experiencia y no capturará la variación heterogénea del crecimiento en los ingresos alrededor de la tasa de crecimiento promedio (Nybom y Sthuler, 2016).
Los detalles de la derivación de la ecuación (5) están a disposición del lector que los requiera.
Estos son los dos estudios seminales de una segunda generación de estudios empíricos que implementaron las estrategias de estimación allí propuestas (los métodos PT y IV) para corregir el problema de error de medición del ingreso permanente del padre.
La derivación formal de este argumento y del límite en probabilidad del estimador IV de la EII está a disposición del lector que la requiera. Debe señalarse también que, según las observaciones de Nybom y Sthuler (2016), para que el estimador IV de la EII constituya un límite superior debe cumplirse también que la educación de los padres no esté correlacionada (o tenga una correlación positiva) con el error de medición del ingreso permanente conformado por un componente que captura los shocks transitorios y un ruido blanco conforme con (1) y (2).
En general, esta segunda muestra corresponde a un momento en el pasado en el que los padres eran más jóvenes. Esto permite obtener una predicción del ingreso de los padres en edades centrales y reducir, así, el denominado lyfe-cycle bias que se describe en la próxima sección.
Este estimador puede ser considerado como una clase especial dentro de los estimadores IV. También puede pensarse en esta técnica como un procedimiento de imputación cold-deck o como parte de un enfoque para generar regresores inobservado (Jerrim et al., 2014).
El método TS2SLS es similar al 2SLS excepto porque las estimaciones de la primera etapa son tomadas de una muestra diferente que las de la segunda etapa.
En la práctica suele utilizarse como medida del ingreso permanente el ingreso promedio a lo largo de varios años. La derivación y el análisis formal del límite en probabilidad del estimador TS2SLS para el caso en que no se cumple esta condición, es decir, cuando no se observa el ingreso permanente sino el ingreso corriente de padres e hijos, están a disposición del lector que lo requiera.
En efecto, como advierte Stuhler (2010), el hecho que los individuos altamente educados tiendan a tener un mayor crecimiento en los ingresos a lo largo del ciclo de vida complica la interpretación del estimador IV. La derivación formal de los límites en probabilidad de los estimadores OLS, IV y TSIV o TS2SLS de la EII bajo el supuesto de existencia del life-cycle bias está a disposición del lector que la requiera.
Muller (2010) supone que la niñez (y adolescencia) se extiende desde que el niño está en el seno materno hasta que alcanza 20años de edad. En realidad, esta es una cuestión que, en este contexto, debe resolverse empíricamente.
Los detalles de la derivación de los plim del estimador OLS de la EII bajo este modelo alternativo pueden consultarse en Muller (2008).
El método de IV tampoco sería adecuado por la misma razón.
Cruces et al. (2015) realizaron un ejercicio de validación de este método para tres países de América Latina (Chile, Nicaragua y Perú), confirmando que los límites inferiores y superiores derivados con esta técnica funcionan como un intervalo de las verdaderas estimaciones de movilidad intrageneracional que podrían obtenerse con un conjunto de datos de panel. De igual forma, Martinez et al. (2013) implementaron, entre otros, el método de Dang et al. (2014) para evaluar distintos índices de movilidad intrageneracional.
Según Dang et al. (2014), una forma de comprobar el cumplimiento de este supuesto en la práctica es examinando si las características invariantes en el tiempo de una cohorte cambian significativamente de una onda a otra de la encuesta utilizada para obtener la muestra auxiliar. El supuesto parece cumplirse para los datos de las encuestas de sección cruzada utilizadas en el ejercicio empírico de la sección 5.2.
En realidad, Solon (1992) y Muller (2008, 2010), entre otros, asumen que δ=0,5 en base a estimaciones previas. Por lo tanto, el supuesto de δ=1 nos asegura la obtención de un límite superior para la EII, al menos en este aspecto.
En el anexo B.2 pueden consultarse los detalles de la derivación del plimBˆLs*.
La encuesta busca seguir a los hogares iniciales de la encuesta. Sin embargo, hay incorporación de individuos que no fueron encuestados en la primera onda. Esto se debe a nacimientos y a personas que no participaron en la nueva encuesta pero que se fueron a vivir con un hogar que sí fue entrevistado. La encuesta solo sigue a los miembros originales de la muestra, siempre y cuando sigan viviendo en las regiones especificadas, sin importar si pasaron a vivir en un hogar distinto (Bendezú et al., 2007).
Solo 5 de 44 países de bajo desarrollo humano y 7 de los 66 países de desarrollo humano intermedio cuentan con datos de este tipo de encuestas, y ninguna de estas cubre un período tan largo (Bendezú et al., 2007).
Como estas tasas de atrición pueden considerarse elevadas y, principalmente, dado que la atrición afecta variables que resultan relevantes en esta investigación (como el ingreso), en las estimaciones se utilizaron las ponderaciones longitudinales corregidas por la probabilidad de volver a responder en la siguiente encuesta. Para detalles del método utilizado para corregir los factores de expansión por el problema de atrición, ver Bendezú et al. (2007).
Esto elimina el problema de sesgo de selección por corresidencia potencialmente existente en las estimaciones de movilidad intergeneracional obtenidas a partir de muestras de padres e hijos que cohabitan en una misma vivienda, como, por ejemplo, las provenientes de la EPH.
Esta es una gran ventaja respecto de la EPH, que solo es representativa de los centros urbanos más poblados del país.
Como la participación laboral femenina en Chile es inusualmente baja, al menos en el contexto latinoamericano, sería riesgoso asignar una interpretación económica a las diferencias observadas entre las EII para las mujeres de Argentina y Chile. Conforme con las estadísticas obtenidas, la tasa de actividad femenina (en zonas urbanas) es del 72% en Chile y del 77% en Argentina. Entre los varones, en cambio, las tasas de participación en el mercado laboral son mayores: 87% en Chile y 88% en Argentina.
En la siguiente sección se examinarán las tasas de persistencia del ingreso entre generaciones a la luz del modelo alternativo sugerido por Muller (2010) que, además del efecto del componente permanente del ingreso, incorpora el impacto potencial de los shocks transitorios.
Estrictamente, la información disponible en la EPH permitiría estimar la EII por OLS e IV también para Argentina, pero la muestra de hijos utilizada resultaría demasiado joven, incrementando considerable el denominado life-cycle bias. Para más detalles, ver sección 3.1.
Se decidió instrumentar el ingreso de los padres utilizando dummies por nivel educativo porque si bien la EPCASEN incluye suficiente información sobre los años de educación formal, en el caso de la EPH la variable está truncada en la cola superior, dado que no se consulta al encuestado por los años aprobados en el caso de la educación superior de grado (terciaria o universitaria) ni de posgrado finalizadas.
Debe señalarse, no obstante, que en algunos casos la magnitud de las diferencias puede considerarse significativa desde el punto de vista económico pero, como consecuencia de los elevados errores estándares asociados con las estimaciones obtenidas, en particular los computados con las muestras obtenidas de la EPCASEN de menor tamaño, no resultan estadísticamente significativas.
El ingreso laboral total incluye los ingresos mensuales de la ocupación principal y los ingresos mensuales de las ocupaciones secundarias (sueldos o salarios, bonificaciones, gratificaciones y remuneraciones en especie). La principal razón para utilizar el ingreso laboral es que, conceptualmente, la capacidad de generar este tipo de ingresos (habilidades, esfuerzos, gustos o preferencias) no puede ser transferida de padres a hijos de la misma forma que una casa o un activo financiero. En este sentido, la movilidad con respecto a los ingresos laborales ofrece una mejor medida de las oportunidades sociales con relación al mérito individual. Además, desde una perspectiva teórica, los economistas no han analizado los efectos intergeneracionales del ingreso no laboral (Mazumder, 2005).
Se ha controlado que los ingresos laborales o familiares incluyan los mismos conceptos y hayan sido medidos de forma relativamente similar en las bases de datos de ambos países, en este caso Chile y Argentina.
Un resultado similar se obtiene al considerar el ingreso familiar per cápita, puesto que las EII estimadas para Chile utilizando esta medida de ingreso (0,872 y 0,760) también superan las obtenidas para Argentina (0,714 y 0,679), aunque en este caso las diferencias no son significativas, al menos al 5%.
Si la movilidad depende de cuánto pueden invertir los padres en el capital humano de sus hijos, es más adecuado y relevante concentrarse en el ingreso familiar total. Además, en el modelo tradicional de ingreso permanente el deseo de suavizar el consumo a lo largo del tiempo sugiere que las familias usarían fuentes de ingresos no laborales para compensar shocks transitorios en los ingresos laborales. Por lo tanto, usar los ingresos familiares para estimar la EII constituye un enfoque alternativo para solucionar los problemas de medición asociados con las fluctuaciones transitorias en los ingresos laborales. Esto podría ser particularmente cierto en la parte inferior de la distribución del ingreso laboral de los padres, donde los individuos pueden percibir ingresos no laborales (como subsidios provenientes de planes sociales) en períodos en los que no perciben ingresos laborales (Mazumder, 2005).
La utilización del ingreso familiar también reduce el problema de sesgo de selección dentro del empleo que podrían presentar las estimaciones derivadas a partir del ingreso laboral, particularmente en el caso de las mujeres.
Por ejemplo, Solon (1992) y Mazumder (2005), entre otros.
Además, a diferencia de la EPPS, en la EPCASEN también se consulta por la educación de la madre.
Las diferencias en el año en el que se obtuvo la muestra principal de hijos: 2006, EPCASEN y 2007; EPPS no se espera que afecte la comparabilidad de los resultados, entre otras razones porque la información de la onda 2006 de la EPCASEN se relevó entre noviembre y diciembre de 2006 y febrero y marzo de 2007.
Ver sección 4 para más detalles sobre esta encuesta y las razones de su elección.
En cambio, la EII estimada con el ingreso laboral de los hijos es marcadamente menor cuando se utiliza la muestra con el potencial sesgo por corresidencia en comparación con la computada sin este sesgo y reportada en la tabla 4. Sin embargo, debe tenerse en cuenta que esta última, a diferencia de la anterior, fue obtenida de una muestra conformada por jefes y cónyuges de hogar que tienen una edad promedio mayor (tabla 1). Este hecho, por tanto, podría también explicar, en parte, la diferencia observada entre las elasticidad intergeneracionales del ingreso laboral que se están comparando.
La explicación de este resultado está relacionada principalmente con el impacto acumulado del ingreso familiar desde el nacimiento hasta la adolescencia durante muchos años sobre la habilidad y el capital humano general adquirido por el hijo antes de asistir a la universidad. Esto, a su vez, sugiere que el alcance de políticas educativas que promocionan la asistencia universitaria estará limitado por los efectos de largo plazo del ingreso familiar disponible durante la primera infancia, niñez y adolescencia.
Con los datos de la EPCASEN también se obtuvo evidencia empírica a favor de este supuesto a partir de una regresión para el ingreso de los hijos que incluye entre las variables explicativas además de la educación del padre, un promedio del ingreso observado del padre durante los dos primeros años del panel. El coeficiente estimado de la educación del padre no resultó estadísticamente diferente de cero.
Aunque sería recomendable obtener la muestra de encuestas previas al año 1987, a fin de estimar el ingreso paterno durante la primera infancia de los hijos adultos de la muestra principal del 2006, no se dispone de una encuesta CASEN más antigua para Chile.
Si bien, de acuerdo con lo señalado por Dang et al. (2014), podría ser conveniente utilizar otras características paternas invariantes en el tiempo para predecir su ingreso como su lugar de residencia o sector de ocupación en años previos, no se dispone de esta información retrospectiva en las bases de datos utilizadas para Argentina. Además, se desconoce la posible dirección del sesgo presente en los estimadores de la EII (B*) cuando se utilizan otras variables instrumentales diferentes al nivel educativo.
La posible dirección de este sesgo no es clara a priori. En Jiménez (2011a) se examinaron los métodos disponibles en la literatura para su corrección y se utilizó la técnica de dos etapas de Heckman. No obstante, no se consideró conveniente implementarlo aquí dados los supuestos restrictivos bajo los cuales este método solucionaría el problema y las limitaciones informativas de las bases de datos disponibles.
No se consideró como medida de resultado para los hijos su ingreso familiar porque, al tratarse de muestras de padres e hijos corresidentes, la muestra de padres utilizada para estimar su ingreso transitorio incluiría en ese caso también a los hijos, sesgando las estimaciones.
No se utiliza el ingreso laboral del padre para evitar los problemas de sesgo de selección asociados con la participación laboral. Además, el ingreso familiar es una medida más adecuada de los recursos del hogar (Mazumder, 2005).
Para no complejizar las ecuaciones se deja de lado en la derivación la consideración del potencial lyfe-cycle bias. No obstante, es posible mostrar que su efecto en el plim del estimador es similar al analizado previamente bajo el modelo tradicional.