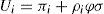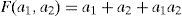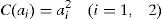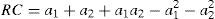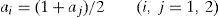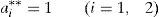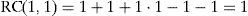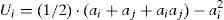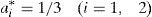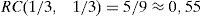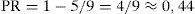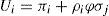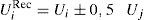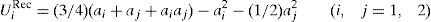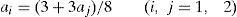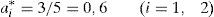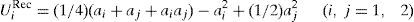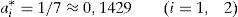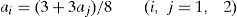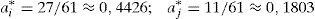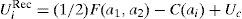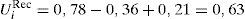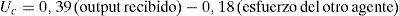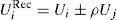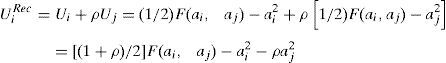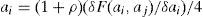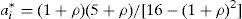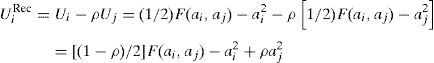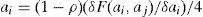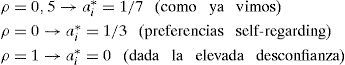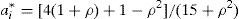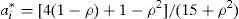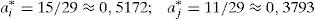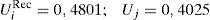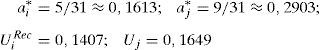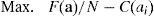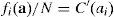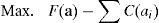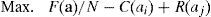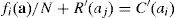Las preferencias y la conducta del cooperante recíproco en un contexto empresarial

Resumen

El propósito de este trabajo es analizar el dilema entre cooperación y conflicto que aparece en las acciones colectivas, a partir de un modelo de preferencias para los agentes económicos implicados, alternativo al de la persona egoísta (self-regarding) que habitualmente usa la literatura. El aspecto esencial que abordamos es el comportamiento cooperativo en el seno de una organización empresarial. En concreto proponemos una función de utilidad para un cooperante recíproco en un contexto empresarial y aplicamos esta función a un modelo de coalición formado por dos agentes.

Abstract

This paper aims to analyse the tension between cooperation and conflict in collective actions, based on a model of the preferences of economically involved agents versus the self-regarding person, who usually uses the literature. The key topic discussed is cooperative behaviour within managerial organisations. We propose a utility function for a reciprocal cooperative agent in a managerial context and apply this function to a coalition model composed of two agents.

1

Introducción

El propósito de este trabajo es analizar el dilema entre cooperación y conflicto que aparece en las acciones colectivas, a partir de un modelo de preferencias para los agentes económicos implicados, alternativo al de la persona egoísta (self-regarding) que habitualmente usa la literatura. Alchian y Demsetz (1972) plantean las ventajas ex ante de la colaboración entre múltiples propietarios de recursos en presencia de complementariedades entre las aportaciones de cada uno (tecnología de equipo). En el mismo trabajo los autores demuestran los problemas de motivación que surgen entre los agentes que colaboran cuando la retribución de cada uno se determina en función de la producción del grupo (la tecnología de equipo impide saber cuál es la producción final que le corresponde a cada uno). Para Alchian y Demsetz, la empresa capitalista, donde el empresario asume la capacidad de supervisión y retribuye a cada participante en función de lo que aporta a la acción colectiva, surge precisamente como respuesta a los problemas de motivación que tienen su origen en la empresa colectivista o autogestionada. Una hipótesis central en los resultados de Alchian y Demsetz es que las personas que colaboran bajo la tecnología de equipo son personas egoístas para las que el bienestar de cada una depende únicamente de la riqueza neta que recibe a cambio de la colaboración. En este trabajo se analizan las consecuencias de los modelos autogestionados de empresa bajo otros supuestos sobre las preferencias de los agentes que colaboran a través de ella.

El supuesto de que una persona, en el momento de decidir sus aportaciones a la acción colectiva de la empresa, solo tiene en cuenta las consecuencias que tendrán para sí mismo las diferentes alternativas que dispone parece poco realista, si tenemos en cuenta que la reiteración en las relaciones humanas deriva en sentimientos de amistad o de solidaridad ampliamente reconocidos por la psicología del comportamiento. Por otra parte, hay que reconocer que el tipo self-regarding existe en el mundo real, pero no creemos que sea predominante. Pensamos que una gran mayoría de personas se sitúan en el medio, entre el egoísta puro (que solo piensa en sí mismo) y el altruista puro (que le da tanta importancia al bienestar de los demás como al suyo propio). Por otro lado, y en relación con lo anterior, está el nivel de confianza que se tenga en el resto de los componentes del grupo.

Debemos caminar, y esa es nuestra intención, hacia un modelo más general, que permita la inclusión de todo grado de egoísmo. Para ello seguiremos la propuesta de Gintis et al. (2005), que se basa en un agente de comportamiento recíproco, lo que significa que tiende a adoptar un comportamiento de cooperación, es decir, acorde con los intereses colectivos del grupo de que forma parte, siempre que los demás también lo hagan.

Por tanto, el aspecto esencial que abordamos en este trabajo es el comportamiento cooperativo en el seno de una organización empresarial. En este punto existe en la teoría una especie de disociación que se ha convertido en un importante obstáculo para el desarrollo teórico. Por un lado está la visión mayoritaria de una empresa formada por individuos que solo tratan de obtener el mayor bienestar individual posible de su participación en la organización, sin tener en cuenta en ningún grado el comportamiento de los otros participantes. Este punto de vista casi conduce a un callejón sin salida a las empresas cooperativas que renuncian a estructuras jerárquicas, condenándolas a su desaparición, cosa que no ha ocurrido hasta el momento.

Por otro lado está la perspectiva de los que tratan de justificar la existencia de dichas empresas en la presencia de unos valores cooperativos que no son fáciles de descubrir en el mundo real. Por ejemplo, Aranzadi (2003) defiende que una de las razones del éxito de la Cooperativa de Mondragón reside en los valores cooperativos que siempre ha llevado consigo. Entre ellos destaca la democracia cooperativa (los socios, y no el capital, son los que dirigen la empresa) y la solidaridad, lo que implica mutua ayuda para los socios, coincidencia con los intereses generales de la comunidad, principio de «puerta abierta» (aumento del empleo) y la defensa de los débiles.

Nuestro tratamiento del problema será algo más neutral. Consideraremos que las personas que forman una empresa buscan su propio bienestar, pero que ello no les impide tener en cuenta el bienestar del resto de participantes y, lo que es más importante, su comportamiento. Entendemos que la conducta cooperativa es consustancial al ser humano y, sin embargo, la teoría económica más ortodoxa no le ha prestado la debida atención.

Después de esta breve introducción, el trabajo tiene los siguientes epígrafes. En el siguiente proponemos una función de utilidad para un cooperante recíproco en un contexto empresarial; posteriormente aplicamos esta función a un modelo de coalición formado por dos agentes, y por último terminamos con el habitual apartado de conclusiones.

2

Las preferencias de un cooperante recíproco

Siguiendo el trabajo original de Alchian y Demsetz, una buena parte de las investigaciones llevadas a cabo han estado encaminadas a demostrar la presencia del escaqueo (free-rider), lo que hace que los miembros de la organización aporten un nivel de esfuerzo por debajo del correspondiente a la eficiencia colectiva. Veremos un ejemplo numérico de esto en el siguiente apartado. La ya comentada solución aportada por estos autores (la introducción de un supervisor que controla el esfuerzo aportado por el resto de los agentes) no siempre se da en la realidad, lo que parece indicar que el modelo no es del todo válido.

Holmstrom (1982) abordó el problema desde una óptica de agencia, llegando prácticamente a la misma conclusión: el escaqueo puede ser ampliamente resuelto mediante la separación entre propiedad y trabajo en la empresa. Esto coloca en situación de ventaja a la empresa capitalista frente a las cooperativas. En concreto, en su modelo demuestra que no hay reparto posible que satisfaga las condiciones de esfuerzo eficiente por parte de los agentes.

En estos dos textos existe poco espacio para considerar en las preferencias individuales argumentos que tengan que ver con el bienestar de los demás individuos que participan en la organización, a pesar de que la vida real está llena de ejemplos en los que las personas deciden no solo en función de las consecuencias que tengan sus decisiones para sí mismas. En este sentido, algunos autores distinguen entre motivaciones intrínsecas y extrínsecas (Pelligra, 2004).

Para solventar este problema consideraremos el concepto de reciprocidad. Esta característica define a personas que tienen predisposición a cooperar con los otros, y a castigar (con coste personal, si es necesario) a aquellos que violan las normas de cooperación, incluso cuando aquellos costes son irrecuperables. Por tanto, la reciprocidad se diferencia de otros tipos de comportamientos —como la cooperación o la represalia— en que en estos casos los actores persiguen beneficios materiales, y en el caso de la reciprocidad los actores responden a acciones amigables u hostiles, incluso cuando no existen esperanzas para obtener ganancias materiales por ello. Por otra parte, se diferencia del altruismo en que este se trata de una actitud bondadosa incondicional que no responde a acciones beneficiosas o perjudiciales (Fehr y Gächter, 2000).

El desarrollo de estas ideas se basa fundamentalmente en el libro Moral Sentiments and Material Interests: The foundations of cooperation in economic life (Gintis et al., 2005). La metodología de estos autores se basa en experimentos de laboratorios sobre el comportamiento humano. Uno de ellos, quizás el más explícito, es el juego del ultimátum, en el que dos jugadores se reparten una determinada suma de dinero. Uno de ellos (el proponente) lanza una oferta de reparto al otro (el responder). El primero solo puede hacer una oferta y el segundo solo puede aceptarla o rechazarla, pero en este caso los dos se quedarían sin nada. Los resultados demuestran que el comportamiento egoísta (ofrecer una pequeña cantidad) es minoritario. La oferta modal es el 50%, y los responders frecuentemente rechazaban ofertas inferiores al 30%. Los proponentes ofrecen el 50% porque son altruistas o el 40% porque temen el comportamiento castigador por parte del responder. Para apoyar esto último se repetía el experimento haciendo de proponente un ordenador (y esto lo sabía el responder): las ofertas bajas eran muy raramente rechazadas (también se varió el juego: el proponente podía quedarse con la parte que había propuesto para sí y los responders nunca rechazaban la oferta, por muy baja que fuera). No obstante, hay que advertir que algunos estudios han encontrado un porcentaje significativo (entre el 20 y el 30%) de sujetos que demuestran un comportamiento completamente egoísta (Fehr y Gächter, 2000).

Otro juego interesante es el de bienes públicos. En él los jugadores comenzaban aportando la mitad de sus dotaciones al bien público, pero esas contribuciones iban decayendo a medida que se acercaba el final del juego. Este comportamiento se aleja del supuesto jugador egoísta (que no contribuiría con nada desde el principio), generalmente defendido en la teoría económica más ortodoxa.

Después de finalizado el juego, se preguntaba a los jugadores por qué iban reduciendo su cooperación, y contestaban que lo hacían como castigo a los que estaban contribuyendo menos que ellos, lo que confirma el carácter recíproco del comportamiento cooperativo. Para apoyar esta interpretación se varió el juego, permitiendo el castigo (sin reducir la cooperación) a los free riders, y efectivamente, la cooperación no se reducía.

Por otra parte, la mayoría de los agentes que mostraban este comportamiento cooperativo lo hacían motivados por las intenciones de su compañeros, más que por los resultados de sus acciones, aunque una fracción significativa sí se preocupa del resultado (exclusivamente o además de la intención del compañero). En este sentido, algunos autores han diseñado juegos psicológicos que permiten analizar escenarios estratégicos en los que las expectativas y las emociones de los jugadores tienen un papel crucial (Geanakoplos et al., 1989). Para estos autores la utilidad de los jugadores depende de los resultados obtenidos (como en la literatura estándar), así como de sus creencias sobre las intenciones del resto de los jugadores. Por ejemplo, el jugador i no valora igual dos acciones del jugador j que tienen idéntico perjuicio para él, cuando las opciones de las que dispone el jugador j son diferentes, por lo que las creencias sobre las intenciones del jugador j también lo son.

En Geanakoplos et al. (1989) las únicas creencias que influyen en la utilidad de los jugadores y, por tanto, en la evolución del juego son las iniciales. Sin embargo, Dufwenberg y Kirchsteiger (2004) diseñaron un juego en el que las creencias de los jugadores cambian a medida que el juego avanza. Es decir, el carácter dinámico de su modelo permite a los jugadores aprender observando el comportamiento de los demás, por lo que sus creencias se van modificando a medida que el juego transcurre. Cada jugador decide su próxima acción a partir de las acciones anteriores de los otros jugadores, de las que deduce sus intenciones, lo que puede dar lugar a modificaciones en las creencias iniciales del primero. Estos autores demuestran la existencia de un sequential reciprocity equilibrium (SRE) en todo juego psicológico con reciprocidad, que es la estrategia que garantiza la maximización de la utilidad por parte de todos los jugadores, dadas sus creencias iniciales y el aprendizaje posterior.

Por otro lado, la principal diferencia entre Geanakoplos et al. (1989) y Rabin (1993) está en que los primeros incorporan las emociones a las funciones de utilidad de los agentes, mientras que el segundo las deriva de los pagos materiales recibidos. Esto hace que su análisis tenga una aplicación más general y, por tanto, que sea más fácil su comparación con el análisis más convencional. Las dos hipótesis de partida del trabajo de Rabin, que casi podemos generalizar al conjunto de los estudios sobre reciprocidad, son los siguientes: por un lado, que la mayoría de la gente está dispuesta a sacrificar parte de su bienestar material para ayudar (castigar) a aquellos que tienen un buen (mal) comportamiento; por otro lado, que las motivaciones anteriores tendrán un mayor efecto sobre el comportamiento cuanto menor sea el coste material en el que se ha de incurrir.

La importancia del comportamiento recíproco para las ciencias sociales no depende de si es interpretado como una desviación del comportamiento egoísta o como una forma de racionalidad limitada; es importante porque afecta fundamentalmente al funcionamiento de los mercados, las organizaciones, los incentivos y las acciones colectivas (Fehr y Fischbacher, 2005).

Dicha importancia puede verse, por ejemplo, si se aumenta el número de responders en el juego del ultimátum ya comentado. En principio, si todas las partes fueran egoístas, la introducción de la competencia entre responders no afectaría a la parte del excedente que estos obtendrían (una conclusión, por otra parte, muy poco intuitiva). Los experimentos realizados demuestran, sin embargo, que añadir más responders tiene como consecuencia que la proporción obtenida por estos es más pequeña a medida que el número de responders aumenta.

En cualquier caso, la cuestión clave para conocer los problemas relativos a la cooperación está en la interacción entre los diferentes tipos de preferencias presentes en la vida económica, particularmente entre los tipos egoísta (o self-regarding) y recíproco fuerte, y en cómo dicha interacción está seriamente influida por el entorno institucional. Entendemos por reciprocidad fuerte la predisposición a cooperar con el resto de los agentes, pero también a castigarlos (con coste personal, si es necesario) cuando se percibe su violación de las normas de cooperación, incluso cuando se tiene la certeza de que dichos costes son irrecuperables.

Por otra parte, Rotemberg (2006) propone una función de utilidad que permite resolver, entre otros, el ya comentado juego del ultimátum sin necesidad de recurrir a valores extremos. Para él, la utilidad obtenida depende de los pagos materiales logrados, así como de la diferencia entre el nivel de altruismo esperado por el resto de los individuos con los que se interactúa y el nivel de altruismo realmente manifestado por ellos.

Nosotros, sin embargo, seguiremos la propuesta de Falk y Fischbacher (2005), titulada Modeling Strong Reciprocity, incluido en el texto ya comentado, que propone la siguiente modelización del comportamiento cooperativo recíproco. Según estos autores, la estructura básica del comportamiento recíproco consiste en la recompensa de los comportamientos cooperativos y el castigo de los no cooperativos. Por tanto, dicha estructura puede expresarse en la siguiente fórmula:

Donde π_i son los pagos materiales del jugador i; ρ_i es el parámetro de reciprocidad, que captura la fortaleza de las preferencias recíprocas del jugador i (si ρ_i = 0, el jugador tiene las preferencias del homo economicus, como las supuestas por la teoría estándar); φ es el término de bondad, que mide la bondad que el jugador i experimenta de las acciones de los otros jugadores (si φ > 0, la acción del jugador j es considerada como cooperativa, y si φ < 0, la acción del jugador j es considerada como no cooperativa); σ es el término de reciprocidad, que mide la respuesta recíproca del jugador i (como una primera aproximación, σ es simplemente el pago recibido por el jugador j).

Los dos últimos términos, es decir φ y σ, miden la utilidad recíproca. Si φ > 0 el jugador i puede, ceteris paribus, incrementar su utilidad si elige una acción que incremente el pago del jugador j. Lo contrario ocurrirá si φ < 0. En este segundo escenario, el jugador i tiene un incentivo para reducir el pago del jugador j (p. ej., rechazo del jugador recíproco i de una oferta muy baja en el juego del ultimátum).

En el artículo de Falk y Fischbacher (2005) se afirma que toda teoría de la reciprocidad debería incorporar las siguientes cuestiones:

• •

  Las distribuciones equitativas constituyen una referencia estándar, es decir, son la clave para considerar si una oferta es justa o injusta.

• •

  La evaluación de la bondad de una acción depende de las intenciones de la misma, aunque también de sus consecuencias.

• •

  El deseo de venganza (por no cooperar) es mucho más importante que el deseo de reducir la desigualdad para justificar el castigo.

• •

  La gente evalúa la bondad no respecto a la media del grupo, sino con respecto a los individuos que lo componen, con quienes ellos interactúan.

En el siguiente epígrafe aplicaremos esta modelización del comportamiento recíproco en el contexto de un modelo de coalición. Consideraremos varias hipótesis con respecto a las preferencias de los dos agentes que componen la organización.

3

Una aplicación: el cooperante recíproco en un modelo de producción en equipo

Supongamos una empresa formada por dos agentes, a los que denominaremos por los subíndices 1 y 2, con la siguiente función de producción que cumple con la condición de tecnología de equipo:

donde las a_i (i = 1, 2) representan las cantidades de esfuerzo aportadas por los agentes. El coste de dicho esfuerzo viene dado por:

donde C′ > 0 (el coste es creciente con el esfuerzo) y C″ > 0 (el coste de la última unidad de esfuerzo aportada siempre es superior a la anterior). Por tanto la riqueza creada por dicha empresa se puede expresar de la siguiente manera:

Para obtener la riqueza potencial, máximo nivel de riqueza que se podría crear con esta organización, maximizamos [4] y deducimos las funciones de reacción de los agentes:

por lo que el esfuerzo de los agentes que maximiza la riqueza será:

Sustituyendo estas cantidades de esfuerzo en [4] tenemos la máxima riqueza buscada:

El problema está en que estos agentes no tienen por qué asumir la maximización de dicha riqueza como objetivo individual. Desde esta perspectiva, cada uno de ellos tratará de maximizar su función de utilidad. Si suponemos que el output final se reparte equitativamente (es decir, r_i(a₁,a₂) = F(a₁, a₂)/2, para i = 1,2), dicha función tendrá la siguiente expresión, suponiendo individuos egoístas:

cuya maximización nos permite obtener las funciones de reacción:

lo que, a su vez, nos permite calcular los esfuerzos aportados por los agentes en este caso:

y sustituyendo de nuevo en [4] veremos que ahora la riqueza creada por esta empresa es menor:

Es decir, la atención exclusiva en los intereses individuales lleva a los agentes a aportar una cantidad de esfuerzo inferior a la eficiente, lo que impide alcanzar la riqueza potencial. Dicho de otra manera, su comportamiento egoísta genera una pérdida residual, que en nuestro caso es igual a:

Es decir, es el problema ya comentado, conocido en la literatura como de incentivos (o de escaqueo, remoloneo o de free-rider). Tiene su origen en las interdependencias existentes en la producción en equipo (reflejadas en nuestro ejemplo por el término a₁a₂ de la ecuación [2]), que tienen una doble consecuencia: por un lado, la producción conjunta es superior a la suma de las producciones individuales de los agentes (Alchian y Demsetz, 1972) y, por otro lado, la producción de cada agente no solo depende de su propio esfuerzo, sino también del esfuerzo del otro (Petersen, 1992). La producción en equipo (solución de empresa) será preferible a múltiples intercambios bilaterales (solución de mercado), solo si existe un incremento neto de productividad resultante del trabajo en equipo, una vez descontado el coste de disciplinar a sus miembros (Alchian y Demsetz, 1972).

Esta situación nos parece real, aunque insuficiente, ya que estamos suponiendo que ambos agentes se comportan en forma self-regarding. Esto implica que en sus preferencias no se incluyen argumentos referentes al comportamiento del otro agente. Parece que cada uno de ellos actuará sin importarle lo más mínimo cómo lo hará el otro. Como si se tratara de un juego de una sola tirada y no hubiera posibilidad de saber lo que hará el otro agente hasta que obtengamos la producción final.

3.1

Las preferencias de un agente recíproco

Veamos a continuación qué ocurriría si introducimos en nuestro análisis las preferencias de tipo recíproco, vistas en el apartado anterior. Repetimos la expresión [1]:

en donde π_i es ahora la utilidad del agente que estemos considerando en caso de comportamiento self-regarding; ρ_i = 0,5, que es un valor concreto que consideramos plausible, que implica que cada agente pondera en un 50% la utilidad del otro (supondremos otros valores de ρ posteriormente); φ es igual a 1 o –1, en función de que se piense que el otro agente coopera o no coopera, respectivamente; σ_j es la utilidad del otro agente. Esta función nos permite recoger el impacto del comportamiento del agente j sobre el comportamiento del agente i en dos aspectos conceptualmente diferentes: la confianza o desconfianza que exista entre ellos y el grado de egoísmo o generosidad que cada uno de ellos tenga. Nuestro análisis se va a centrar en el primero de estos aspectos.

Por tanto, las funciones de utilidad, en el caso de cooperantes recíprocos (con ρ_i = 0,5), tendrán la siguiente expresión:

Se pueden dar tres tipos de situaciones: 1) ambos agentes piensan que el otro también coopera; 2) ambos agentes piensan que el otro no coopera, y 3) un agente piensa que el otro coopera pero este piensa que aquel no coopera. Veamos cada una de ellas por separado.

• 1)

  Aplicando [8] con signo positivo en el lado derecho de la ecuación, vemos que la función de utilidad de los agentes tiene la siguiente expresión:

  
  es decir, que el output que le corresponde (recordemos que es la mitad) le proporciona una utilidad superior a su valor y, por otro lado, el esfuerzo del otro agente le resta utilidad, aunque en menor medida que el suyo propio. Maximizando [9] obtenemos las funciones de reacción de los agentes:
  
  y resolviendo logramos las aportaciones de esfuerzo de los agentes que hacen máxima su utilidad individual:
  

• 2)

  Procediendo de igual forma que en el caso anterior, pero ahora con signo negativo en el lado derecho de la ecuación [8]:

  
  que es la nueva fórmula de la función de utilidad. Ahora el output recibido aporta una utilidad inferior a su valor y el esfuerzo del otro agente aumenta la utilidad del agente que estemos considerando. Maximizando [11], tenemos:
  
  y resolviendo deducimos las aportaciones de los agentes en este caso:
  

• 3)

  En este último caso suponemos que el agente i piensa que j coopera, pero este cree que i no coopera. Por tanto, las dos funciones de reacción ya no son simétricas:

  
  

  Resolviendo:

  
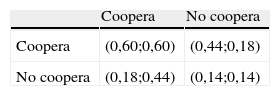
  es decir, que el agente que piensa que el otro coopera aporta más esfuerzo que aquel que cree que el otro no coopera. Un resumen de los resultados obtenidos en estos tres casos lo tenemos en las siguientes tablas.

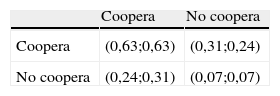
En las filas de la tabla 1 tenemos lo que piensa el agente i sobre el proceder del agente j, y en las columnas, las creencias del agente j sobre la predisposición, o no, a cooperar por parte del agente i. Sustituyendo estos valores en las correspondientes funciones de utilidad obtenemos los niveles de utilidad alcanzados, con los que construimos la tabla 2. En este se puede apreciar que el tradicional dilema del prisionero, que se produce cuando cada agente maximiza su función de utilidad individual (con agentes self-regarding), desaparece.

Tabla 1.

Esfuerzo aportado por los agentes

	Coopera	No coopera
Coopera	(0,60;0,60)	(0,44;0,18)
No coopera	(0,18;0,44)	(0,14;0,14)

Tabla 2.

Nivel de utilidad de los agentes

	Coopera	No coopera
Coopera	(0,63;0,63)	(0,31;0,24)
No coopera	(0,24;0,31)	(0,07;0,07)

En un contexto institucional más jerárquico, la cuestión de la cantidad de esfuerzo aportada a la organización se resuelve en la interacción supervisor (empresario) - trabajador. En este caso la reciprocidad se manifiesta en la posibilidad de castigar al otro, con salario (por parte del empresario) o esfuerzo (por parte del trabajador) bajo, cuando se considera que no tiene un comportamiento «adecuado», o de premiarlo en caso contrario. En principio, los trabajadores podrían aprovecharse del carácter incompleto de los contratos, exigiendo salarios altos, pero la existencia de una proporción no despreciable de trabajadores self-regarding les obliga a aceptar salarios por debajo del nivel deseado (Fehr y Gächter, 2000).

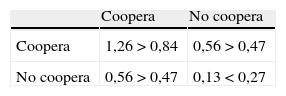
3.2

La confianza como generador de bienestar

Con agentes recíprocos la confianza en el compañero, y por tanto la seguridad de que va a tener un comportamiento cooperativo, es fuente de bienestar. Podemos decir lo contrario de la desconfianza. Para ver esto con mayor nitidez hemos construido la tabla 3, donde tenemos la utilidad total (en primer término) y la riqueza creada (en segundo) para cada una de las cuatro situaciones posibles. Podemos apreciar que en caso de que los dos agentes consideren que el otro también coopera, la utilidad total está significativamente por encima de la riqueza creada (considerada esta como la diferencia entre el output recibido y el coste del esfuerzo). Este incremento de bienestar (1,26 – 0,84 = 0,42) procede de la confianza que cada agente pone en el otro. Por lo que podemos considerar 1,26 como la máxima utilidad posible, o utilidad potencial. Por el contrario, como vemos en la misma tabla, si los dos agentes opinan que el otro no coopera, se produce una disminución de la utilidad total originada en la desconfianza mutua.

Tabla 3.

Utilidad total y riqueza creada

	Coopera	No coopera
Coopera	1,26 > 0,84	0,56 > 0,47
No coopera	0,56 > 0,47	0,13 < 0,27

Por tanto, en el modelo de coalición con agentes recíprocos y reparto igualitario del output final, la utilidad del agente i-ésimo tiene la siguiente expresión:

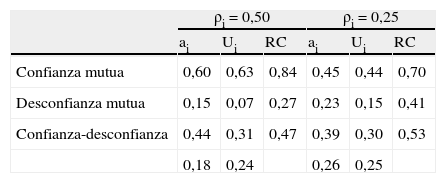
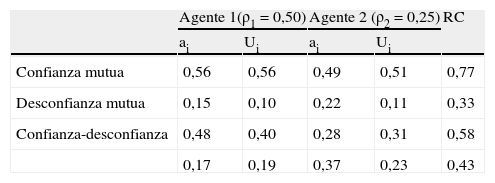
donde Uc representa la utilidad procedente de la confianza (o desconfianza) en el otro agente. Este término, que puede tener signo positivo o negativo en función de las creencias del agente sobre el comportamiento del otro, tiene a su vez dos partes: la utilidad proveniente de la parte de la producción recibida, por un lado, y la provocada por el esfuerzo del otro agente. En caso de confianza, la primera parte será positiva y superior a la segunda (con signo negativo), pero en caso de desconfianza ocurrirá todo lo contrario. Por ejemplo, en el caso de confianza mutua la expresión [15] tendrá el siguiente valor:

donde las 21 centésimas de U_c tienen el siguiente desglose:

Los resultados obtenidos hasta aquí son para un ρ_i = 0,5. Lo que significa que cada agente tiene un 50% de reciprocidad o, lo que es lo mismo, solo tiene en cuenta la mitad del bienestar del otro agente en sus propias preferencias. Obviamente, no todos los individuos tendrán el mismo nivel de reciprocidad, por lo que sería conveniente aplicar el modelo para valores diferentes de ρ_i. Hemos repetidos los cálculos anteriores para ρ_i = 0,25 y presentamos sus resultados en la tabla 4, en la que repetimos los anteriores para facilitar su comparación.

Tabla 4.

Resultados para dos valores distintos de ρ_i

	ρi = 0,50			ρi = 0,25
	ai	Ui	RC	ai	Ui	RC
Confianza mutua	0,60	0,63	0,84	0,45	0,44	0,70
Desconfianza mutua	0,15	0,07	0,27	0,23	0,15	0,41
Confianza-desconfianza	0,44	0,31	0,47	0,39	0,30	0,53
	0,18	0,24		0,26	0,25

De nuevo vemos que los niveles de esfuerzo, utilidad y riqueza creada son superiores en la situación de confianza mutua, comparadas con la situación de desconfianza mutua. Sin embargo, los primeros son inferiores y los segundos superiores con respecto a los obtenidos con ρ_i = 0,5. Es decir, la menor reciprocidad implica que la confianza o desconfianza que se tenga en el otro tiene un menor efecto sobre dichos niveles. En lo que respecta al escenario de confianza-desconfianza podemos decir prácticamente lo mismo, aunque la riqueza creada aumenta, indicando que el efecto positivo sobre ella de una menor desconfianza es superior al efecto negativo de una menor confianza.

Por otra parte, también podemos considerar con este modelo agentes con ρ_i diferentes. Supongamos, por ejemplo, que ρ₁ = 0,5 y ρ₂ = 0,25. Esto significa que el agente 1 es más sensible respecto al comportamiento del otro.

Los resultados aparecen en la tabla 5. De nuevo la riqueza creada es muy superior en la situación de confianza mutua con respecto a la de desconfianza mutua, quedando en el medio los dos posibles escenarios de confianza-desconfianza. En el primero de ellos (cuarta fila) el que confía es el agente con mayor reciprocidad (el agente 1), lo que justifica la superior creación de riqueza con respecto al segundo (quinta fila). Por otra parte, queremos también resaltar que esta mayor sensibilidad respecto al otro agente genera niveles de esfuerzo y utilidad superiores en la situación de confianza mutua, e inferiores en la de desconfianza mutua.

Tabla 5.

Resultados del modelo con agentes que tienen diferentes ρ_i

	Agente 1(ρ1 = 0,50)		Agente 2 (ρ2 = 0,25)		RC
	ai	Ui	ai	Ui
Confianza mutua	0,56	0,56	0,49	0,51	0,77
Desconfianza mutua	0,15	0,10	0,22	0,11	0,33
Confianza-desconfianza	0,48	0,40	0,28	0,31	0,58
	0,17	0,19	0,37	0,23	0,43

3.3

Expresión general de las preferencias de un agente recíproco

Una expresión general de la función de utilidad del agente recíproco es la siguiente:

Nuestro objetivo en este subapartado es obtener las expresiones de los esfuerzos aportados por los agentes, en cada uno de los casos posibles, en función del parámetro ρ y comprobar cómo evolucionan aquellos ante movimientos en este.

• 1)

  Confianza mutua.

  En este caso la función de utilidad es:

  
  de las que se obtienen las condiciones de primer orden:
  

  Resolviendo en [18] tenemos el esfuerzo aportado por el agente i-ésimo en función del parámetro ρ:

  
  expresión en la que si sustituimos 0,5 como valor de ρ obtenemos 0,6 como cantidad de esfuerzo proporcionada (calculada anteriormente; véase la tabla 4). Si en lugar de ello hacemos ρ = 0 (no hay lugar en la función de utilidad propia para el comportamiento del otro), tenemos que ai=1/3, que es la solución del modelo con preferencias self-regarding. Y si ρ = 1 (las preferencias del otro tienen tanto peso como las del otro), entonces ai=1, las aportaciones de la solución de eficiencia.

• 2)

  Desconfianza mutua.

  
  cuya maximización nos da:
  
  y resolviendo:
  
  donde, si sustituimos los tres mismos valores anteriores, tenemos:
  

• 3)

  Para un contexto de confianza-desconfianza utilizamos las fórmulas [18] y [21] para obtener, por un lado:

  
  que es la aportación de esfuerzo del agente que confía, y, por otro lado:
  
  que es la aportación de esfuerzo del agente que no confía.

  Derivando en [19], [22], [23] y [24], podemos observar cómo se modifican los ai ante variaciones en el parámetro de reciprocidad ρ.

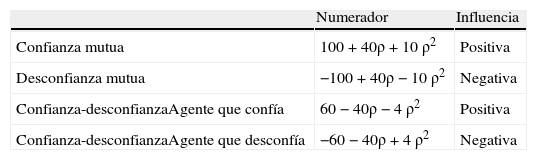
  En la tabla 6 tenemos los numeradores de las cuatro derivadas, y dado que los numeradores son todos positivos, las influencias del parámetro ρ sobre los ai. Vemos que en caso de confianza, aunque el otro agente desconfíe, cuanto mayor sea la misma (es decir, cuanto mayor sea ρ) mayor será el esfuerzo aportado (ai), aunque este será mayor en caso de confianza mutua. Podemos decir el mismo comentario, pero en sentido inverso, para la situación de desconfianza.

  Tabla 6.

  Relación ai−ρ

  	Numerador	Influencia
  Confianza mutua	100 + 40ρ + 10 ρ^2	Positiva
  Desconfianza mutua	−100 + 40ρ − 10 ρ^2	Negativa
  Confianza-desconfianzaAgente que confía	60 − 40ρ − 4 ρ^2	Positiva
  Confianza-desconfianzaAgente que desconfía	−60 − 40ρ + 4 ρ^2	Negativa

3.4

La convivencia entre diferentes tipos de agentes

Por último consideremos brevemente la convivencia entre un agente recíproco y otro self-regarding. Si el agente recíproco confía y ρ = 0,5, utilizamos las expresiones [7] y [10] para obtener las cantidades de esfuerzo aportadas:

de los agentes recíproco y self-regarding, respectivamente. De nuevo, la persona que más confía en la otra es la que más esfuerzo aporta. Si sustituimos estos valores en [6] y [9] observamos que también el que se esfuerza más es el que mayor nivel de utilidad alcanza:

Por otra parte, si mantenemos el mismo grado de reciprocidad pero con un agente desconfiado, y procediendo de igual forma, obtenemos:

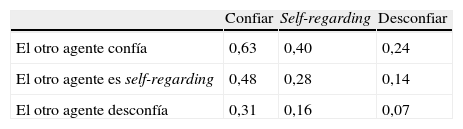
siendo ahora superiores el esfuerzo y la utilidad del agente self-regarding. Asimismo queremos resaltar que de nuevo la suma de las utilidades de ambos agentes supera el nivel de riqueza creada en el primer caso (cuando el agente recíproco confía) y es inferior en el segundo caso (cuando dicho agente desconfía).

Los últimos resultados nos permiten construir la tabla 7, donde tenemos los niveles de utilidad alcanzados en el caso de la convivencia de ambos tipos de agentes. ¿Cuál es la conducta preferida? Vemos que en los tres casos posibles (filas) el mayor valor corresponde a la primera columna (confiar), por lo que parece que la cooperación es la mejor opción. Además, vemos que tanto las columnas como las filas son decrecientes, lo que pone de manifiesto una vez más que la mejor situación que puede darse es la de que ambos agentes confíen, mientras que la peor es la de que ambos desconfíen.

Tabla 7.

Utilidades obtenidas en la convivencia de ambos tipos de agentes (ρ = 0,5)

	Confiar	Self-regarding	Desconfiar
El otro agente confía	0,63	0,40	0,24
El otro agente es self-regarding	0,48	0,28	0,14
El otro agente desconfía	0,31	0,16	0,07

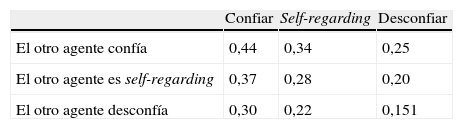
Por otra parte, si bajamos el nivel de reciprocidad (ρ = 0,25) la coherencia de los resultados se mantiene (tabla 8), aunque ahora el rango de variación se reduce, lo que también parece bastante realista.

Tabla 8.

Utilidades obtenidas en la convivencia de ambos tipos de agentes (ρ = 0,25)

	Confiar	Self-regarding	Desconfiar
El otro agente confía	0,44	0,34	0,25
El otro agente es self-regarding	0,37	0,28	0,20
El otro agente desconfía	0,30	0,22	0,151

3.5

Generalización

Nuestro modelo se puede generalizar a N trabajadores y a cualquier función de producción. El problema a resolver por parte de un agente egoísta es el siguiente (Kandel y Lazear, 1992):

que tiene las siguientes condiciones de primer orden:

Sin embargo, desde el punto de vista de la eficiencia colectiva, el problema consiste en:

cuyas condiciones de primer orden son:

Dado que C″ > 0, las a_i que resuelven [26] (1/3 en nuestro ejemplo) son inferiores a las a_i que resuelven [28] (1 en nuestro ejemplo). Este es el planteamiento clásico del problema de free-rider. Sin embargo, en el modelo que hemos desarrollado, cada agente se enfrenta al siguiente problema:

donde R(a_j) representa la reciprocidad del agente i-ésimo con respecto al resto de sus compañeros. La condición de primer orden de [29] es:

que implica un esfuerzo inferior al óptimo pero superior al que aportaría un individuo self-regarding (es decir, entre 1/3 y 1, en nuestro ejemplo) si R’(a_j) es positivo, es decir, si hay confianza en el resto de los agentes.

4

Conclusiones

En esencia, lo que hemos llevado a cabo en este trabajo es la aplicación de la reciprocidad a un modelo de coalición, caracterizado por una organización empresarial, formada por dos agentes maximizadores de sus respectivas utilidades individuales. Dicha aplicación ha dotado al modelo de un mayor grado de realismo. De hecho, la modelización con agentes self-regarding no deja de ser un caso particular de nuestro modelo, donde ρ = 0.

Por otra parte, nuestra propuesta permite superar el escenario de dilema del prisionero, habitual en la literatura, y además implica que el mejor comportamiento individual es la cooperación. Estos dos resultados se derivan de la generación de bienestar por parte de la confianza puesta en el otro agente (y viceversa), lo que conlleva una utilidad total superior a la riqueza creada (confianza mutua) o inferior a la misma (desconfianza mutua) en todos los casos considerados.

El papel de la confianza (desconfianza) como fuente de bienestar (malestar) se debe al protagonismo que tiene en nuestro modelo el comportamiento cooperativo. En el modelo con agentes self-regarding no hay lugar para este comportamiento, que es un aspecto innato a la naturaleza humana. Véase, por ejemplo, la aportación voluntaria (en tiempo y dinero) por parte de los socios de las ONG, o la actitud solidaria durante los desastres naturales (terremotos, incendios, etc.).

No obstante, esta conducta cooperativa no es un cheque en blanco a favor del otro agente. Depende fundamentalmente de lo que piensa cada agente sobre la actitud del otro. Un supuesto bastante realista: colaboramos siempre y cuando los otros también lo hagan. Desde el momento en que detectamos que el otro se escaquea, nosotros lo «castigamos» haciendo lo mismo. Pensamos que este comportamiento es muy generalizado. En cualquier caso, lo que demuestran nuestros resultados es que una actitud de confianza de partida es lo más conveniente para todos.

En nuestro modelo juega un papel importante la interacción entre ambos agentes. Presuponiendo diferentes actitudes de partida (confianza, desconfianza), combinado con los diferentes grados de reciprocidad que puedan darse, pensamos que gana realismo, si lo comparamos con el modelo utilizado en la literatura más convencional, que aborda el tema desde la óptica de la ausencia de reciprocidad, algo que parece escasamente plausible en la vida cotidiana.

Por otra parte, nuestro modelo podría ganar más generalidad si permitiéramos a los agentes repetir «jugada», es decir, si lo hiciéramos dinámico. Esto nos conduciría al estudio del surgimiento y la evolución de la confianza (o desconfianza) entre los agentes. La intuición nos dice que en dicho surgimiento y evolución resulta fundamental la interacción recurrente entre ambos. Debido a esta interacción, las soluciones que pueden esperarse ante las oportunidades de colaboración de los agentes son mucho más diversas que la solución de empresa capitalista y jerarquizada. La diversidad de formas de empresa es una realidad empírica irrefutable, y basándose en ella el realismo del supuesto sobre preferencias recíprocas, realizado en este trabajo, gana fuerza como factor relevante a tener en cuenta para el estudio de las relaciones productivas.

Agradecimientos

Quisiera agradecer las aportaciones y sugerencias de los profesores de mi Departamento Vicente Salas y Marisa Ramírez.