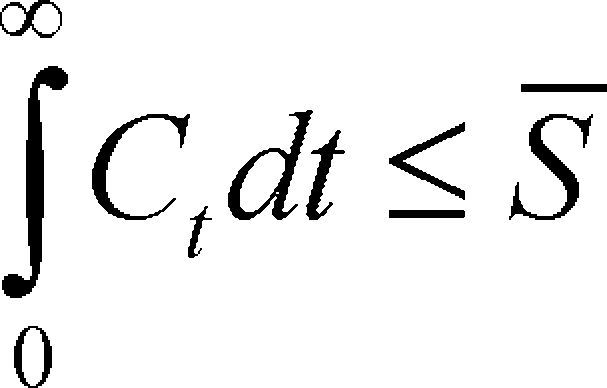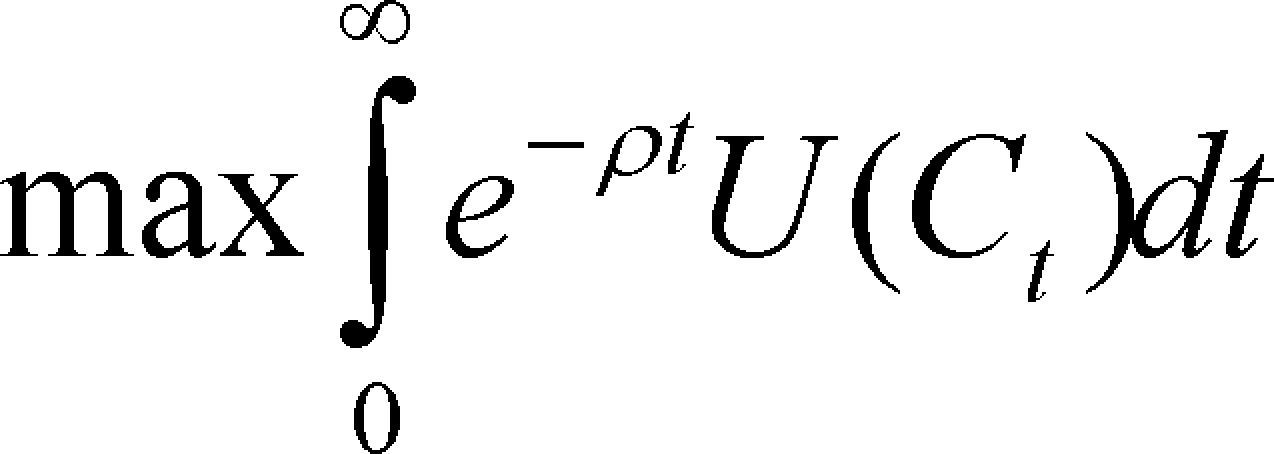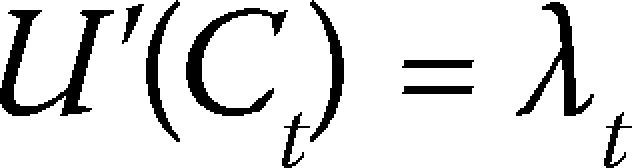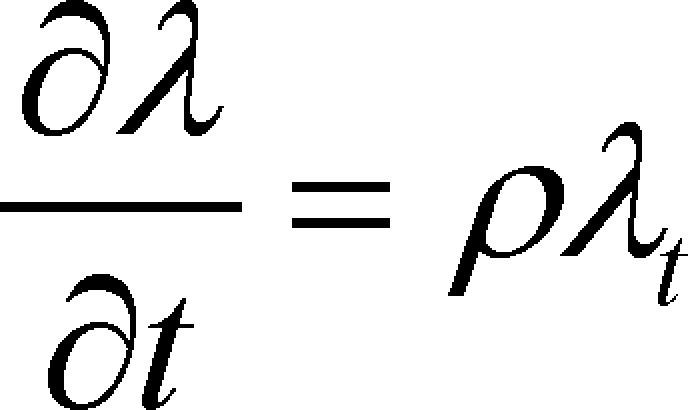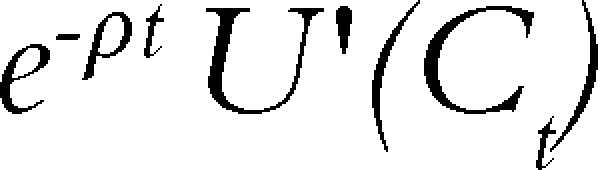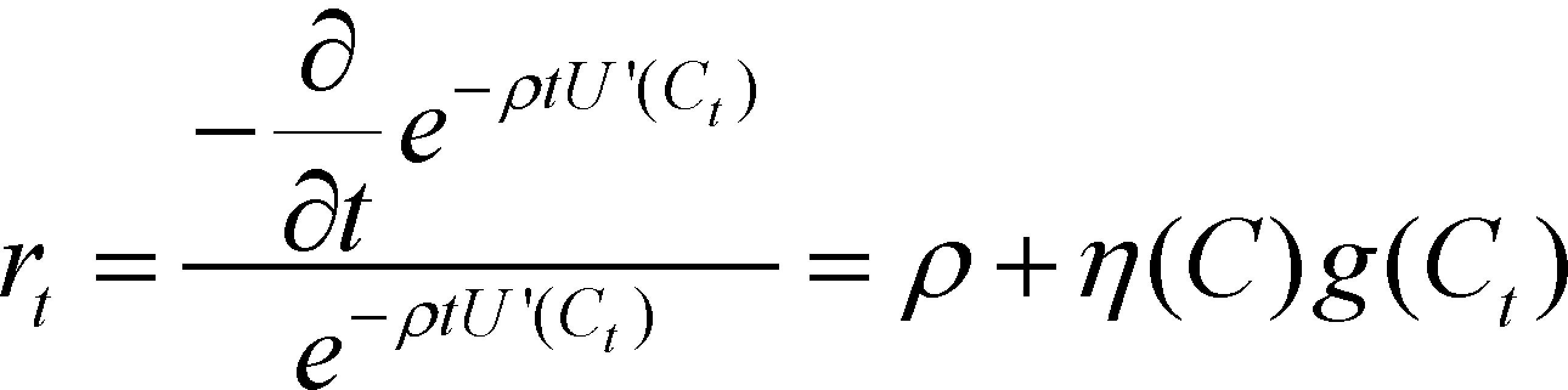Este documento explora con motivación didáctica un modelo simple que expone algunos elementos básicos de la economía del cambio climático que han suscitado debate académico en la última década. A raíz de la publicación en 2006 del llamado Reporte Stern, la literatura académica ha centrado el debate en dos aspectos fundamentales de la modelación de ese problema global: la elección particular de algunos parámetros como microfundamentos que reflejan comportamientos más bien éticos sobre el tratamiento del futuro y la desigualdad, y la modelación de los aspectos estocásticos asociados a fenómenos que ocurren en el futuro relativamente distante. Este documento expone con un modelo sencillo los elementos asociados al primer aspecto. La pretensión es la de acercar a los estudiantes de economía algunas de las consecuencias éticas y analíticas del proceder convencional en la teoría económica dedicada al estudio del problema climático global. A esta breve introducción siguen tres secciones: la primera expone el modelo de referencia con una implementación numérica ilustrativa, la segunda discute asuntos asociados al descuento del futuro y las nociones de equilibrio utilizadas en la modelación estándar, y la tercera presenta brevemente una discusión sobre la consistencia del proceder paramétrico convencional. Una última sección incluye breves reflexiones a modo de cierre.
This paper explores a simple model that highlights for a wider audience some of the main elements of the economics of climate change that have motivated academic debate over the last decade. After the release in 2006 of the Stern Report, academic economists have argued over two crucial aspects involved in economic modeling of this global problem: the particular choice as microfoundations of certain parameters describing ethical behaviors regarding both the future and inequality, and the particular strategies for modeling variables that exhibit stochastic nature in the distant future. The simple model herein exposed is able to deal with many of the issued of the first aspect. The motivation is to make available to students of economics some of the ethical and analytical consequences of economic theory's conventional strategy utilized in models to analyze the economics of global climate change. The first section of the paper presents an exhibit of the model that includes a numerical representation for illustration purposes. Section two links the choice over the discount rate to two notions of economic equilibrium. Section three presents a brief discussion on the consistency of the parametrical choices conventionally made in the economic literature on climate change. Finally, some words are included for concluding purposes.
El problema económico esencial asociado al cambio climático se puede representar por medio del modelo canónico de la economía de los recursos naturales no renovables.1 En dicho modelo, la utilización de los recursos es esencial desde el punto de vista de la producción económica y las características físicas de los recursos implican que los acervos existentes son finitos para las escalas relevantes de su utilización económica. La representación del problema climático con esa modelación pasa por considerar, primero, que la capacidad de almacenamiento atmosférico de gases de efecto invernadero (geis) es un recurso finito y no renovable y, segundo, que dicho recurso es esencial para el sistema económico: el bienestar humano requiere utilizar en todo momento dicha capacidad.
El modelo climático, entonces, incluye los siguientes tres elementos. Primero, la sociedad necesita consumir en todo momento algún monto positivo de la capacidad atmosférica de almacenamiento de geis. Dicha necesidad se puede representar por medio de una función de bienestar que dependa de dicho consumo con los supuestos tradicionales: incrementos en el consumo llevan a incrementos en el bienestar sujetos a rendimientos decrecientes. Formalmente, U(Ct) exhibe U’(Ct)>0 y U”(Ct)<0 para todo momento t, donde U representa el bienestar en t asociado al nivel de consumo Ct. Además, la esencialidad del consumo del recurso implica que limC→0U′(Ct)=∞. Segundo, la capacidad atmosférica de almacenamiento de geis se comporta como un recurso no renovable de acervo finito. Entonces, si el horizonte de planeación es infinito, la finitud del recurso implica que el monto consumido en la totalidad de dicho horizonte no pueda superar el monto total del acervo disponible. Formalmente,
Esta formulación permite incorporar el hecho de que existen magnitudes para la concentración atmosférica de geis que los climatólogos han definido como relativamente seguras para evitar las consecuencias indeseables del cambio climático.2 En el modelo, la variable S¯ puede entonces definirse para representar la acumulación atmosférica de emisiones consistente con esa capacidad. Tercero, el problema dinámico se resuelve tomando en cuenta el bienestar de las generaciones presentes y de las generaciones futuras, pero se asume impaciencia temporal de la sociedad actual, que es la que resuelve el problema, lo que implica que el bienestar futuro recibe una ponderación menor que el bienestar presente. Dicho de otro modo, la sociedad descuenta el futuro a tasas positivas, y la función de bienestar total calcula el valor presente del flujo de bienestar en cada t en todo el horizonte de planeación. Formalmente,
donde ρ representa la tasa de preferencia temporal de la sociedad. El problema económico consiste entonces en alcanzar el valor máximo posible de B sujeto a la restricción 1. Esta formulación hace dos supuestos implícitos que no alteran los objetivos de la modelación. Primero, se asume que las emisiones de geis, que se representan por Ct, se acumulan linealmente en la atmósfera. Es decir, si se emiten 10 unidades de geis, se utilizan las mismas 10 unidades de la capacidad de almacenamiento S¯. Segundo, se hace caso omiso a las tasas de decaimiento que puedan corresponder a los diferentes geis acumulados en la atmósfera. Es decir, se asume que una vez que una unidad de Ct se encuentra en la atmósfera se queda allí para siempre.3
Antes de mirar la estrategia de solución del problema descrito, conviene realizar una conversión de variables para facilitar su tratamiento analítico. Sea que la variable Rt mide el monto de capacidad atmosférica remanente y disponible a partir del tiempo t. Rt es la diferencia entre el total del acervo disponible S¯ y la acumulación de gases hasta el tiempo t. Formalmente,
Diferenciamos con respecto a t para ver la dinámica de Rt:
La expresión (3’) indica de modo simple que la capacidad disponible de almacenamiento atmosférico de geis disminuye en cada t en el mismo monto en el que de hecho se emiten geis a la atmósfera en t. Esta modificación permite escribir el problema del siguiente modo, que resulta un tanto más simple:
sujeto a
El algoritmo de solución requiere formular la siguiente función Hamiltoniana:
con λt representando la variable de co-estado. Dicha variable mide también el precio sombra de la capacidad atmosférica en términos de la función de bienestar B. De la condición de primer orden para maximizar (4) se obtiene
y del principio del máximo se sigue que
que es una ecuación diferencial con solución en
La función (7) implica que el precio sombra de la capacidad atmosférica de acumulación de geis crece a una tasa constante equivalente a la tasa de preferencia temporal a la que la sociedad descuenta el futuro.4 El algoritmo de solución prosigue con la diferenciación de (5) con respecto a t y su combinación con (6), de lo que se obtiene la siguiente expresión que describe la dinámica de la política óptima de consumo
Donde η(C)=−U″(C)U′(C)C mide la elasticidad-consumo de la utilidad marginal.5 La expresión (8) mide la tasa de cambio temporal del consumo y caracteriza la política óptima: dado que ρ y η(C) son parámetros no negativos, las emisiones óptimas de geis son decrecientes en el tiempo. Por este motivo, las generaciones presentes disfrutan de un bienestar más alto derivado de emisiones más altas con respecto a las generaciones futuras, que deberán reducir las emisiones y, por tanto, su bienestar. El resultado obtenido en (8), y sus implicaciones para la dinámica de (4), han llevado a la literatura (por ejemplo, Farzin 2002) a concluir que una economía que depende últimamente de un recurso no-renovable (llamada también “cake-eating economy”) simplemente no puede ser sustentable, ya sea que para ello requiera acceso igualitario al acervo del recurso (siguiendo a Brundtland), ya sea requiriendo constancia en el producto neto que, siguiendo a Weitzman (1976), estaría aquí representado por la función Hamiltoniana (4), a la sazón claramente decreciente en el óptimo.
La inclusión de supuestos adicionales permite obtener mayor información respecto la política óptima de emisiones y su dependencia a diferentes valores de los parámetros ρ y η(C). Si U(Ct) pertenece a la familia de funciones de utilidad isoelásticas, entonces η(C) es constante. Podemos analizar el caso en el que U(Ct)=ln(Ct), lo que implica que η(C)=1.6 En este caso, operaciones de rutina permiten ver que la política óptima {Ct}∞t=0 queda explícita en la siguiente expresión:
A pesar de su sencillez, la expresión (9) permite representar numéricamente algunos de los aspectos más importantes del debate académico-político alrededor de la economía del cambio climático, señaladamente aquél que sigue a la publicación del Reporte Stern en 2006. La Figura 1 y 2 muestran la sensibilidad de la política óptima de emisiones, expresión (9), y de su acumulación atmosférica, expresión (1), a diferentes valores del parámetro ρ que reflejan diferentes actitudes respecto del futuro.7 La Figura 1 muestra claramente cómo la tasa de preferencia temporal afecta no sólo la tasa a la que declina el consumo óptimo periodo a periodo, sino el monto inicial al inicio del periodo de planeación: entre más elevada la tasa de descuento (lo que refleja mayor ponderación al presente que al futuro en (2)), mayores las emisiones de geis en el presente y mayor la tasa a la que decaen en el futuro.
La Figura 2 muestra la acumulación óptima de emisiones en la atmósfera asociada a cada una de las políticas óptimas de la Figura 1, y muestra claramente los efectos de la tasa de preferencia temporal. Al 3%, casi el total de S¯ se agota en alrededor de 150 años; al 1% se requieren 4 siglos para casi agotar el total de S¯; al 0.1% se requieren algunos miles de años para agotar el acervo. Es de notar que la forma de las políticas óptimas de emisiones desplegadas en las figuras 1 y 2 reproduce las características de la política óptima de los modelos integrales de cambio climático (como el famoso modelo DICE de Nordhaus): estas políticas implican iniciar desde el presente con la reducción de emisiones, pero dejar la mayor parte de la mitigación para el futuro. Este hecho ha llevado a Weitzman a notar que la forma de rampa de la política óptima (ver Figura 2) es consecuencia de la estrategia de modelación (suavizamiento del consumo sobre el horizonte de planeación), y no consecuencia de conocimiento crucial sobre las interacciones de los sistemas climático y económico (Weitzman, 2007).
La dependencia de la política de emisiones y de su acumulación atmosférica sobre el parámetro de aversión a la desigualdad η(C) se muestra en las figuras 3 y 4. Se asumen tres valores arbitrarios: η=0.5, η=1 y η=2. La Figura 3 muestra la política óptima de (8) para cada uno de estos valores. Como se ve, entre menor sea la elasticidad-consumo de la utilidad marginal mayor es el consumo presente respecto al futuro y, por tanto, menor la aversión a la desigualdad intergeneracional. La política que suaviza temporalmente el consumo en mayor grado es cuando se asume η=2, lo que implica una aversión a la desigualdad intergeneracional alta.
Los comportamientos de la Figura 3 implican las concentraciones atmosféricas desplegadas en la Figura 4. Como se ve, los efectos sobre la acumulación de emisiones son significativos pero mucho menores a aquellos que puedan asociarse a la tasa de preferencia temporal (Figura 2). Aún así, el suavizamiento del consumo provocado por mayor aversión a la desigualdad puede retrasar por unos tres siglos el agotamiento de la capacidad atmosférica de almacenamiento de geis: cuando η=0.5, y dicha aversión es débil, el acervo prácticamente se agota en menos de 100 años; cuando η=2, y dicha aversión es más fuerte, se requieren casi 4 siglos para agotar el acervo. Es de notar que el efecto del parámetro η mitiga o amplifica los efectos de la tasa de preferencia temporal: un valor η=0.5 equivale a duplicar el valor de ρ, mientras que un valor η=2 equivale a reducir a la mitad el valor de ρ (ver ecuación 8).
Con todo, este breve modelo recoge algunos de los puntos importantes del debate académico de la economía del cambio climático: la dependencia de la política óptima al espacio paramétrico. Dado que prácticamente no existen calibraciones a escala de economía mundial para estimar el valor de los parámetros ρ y η que puedan aplicarse a modelos definidos para esa misma escala, sus valores prácticamente están al arbitrio del investigador en turno. La Figura 5 muestra esto gráficamente para la concentración atmosférica con los valores de los parámetros aquí asumidos con un par de combinaciones extremas: ρ=3% y η=0.5 para describir una sociedad temporalmente impaciente (ponderando más al presente que al futuro) y no-aversa a la desigualdad en el consumo (le va perfectamente bien con patrones de consumo temporalmente no suavizados); y ρ=0.1% y η=2 para describir a una sociedad con paciencia temporal (que pondera más equitativamente presente y futuro) y aversa a la desigualdad (prefiere patrones de consumo suavizados en el tiempo).
En la primer combinación de parámetros (ρ=3% y η=0.5, representando a una sociedad temporalmente impaciente y no aversa a la desigualdad), casi el total de la capacidad atmosférica de almacenamiento se agota en unos 75 años: las generaciones presentes de esta sociedad se agotan el recurso y dejan a las generaciones futuras casi sin consumo posible.8 En la segunda combinación de parámetros (ρ=0.1% y η=2, representando a una sociedad temporalmente paciente y aversa a la desigualdad), el 50% de la capacidad atmosférica está disponible para uso incluso 15 siglos en el futuro: las generaciones presentes son prudentes y consumen de a muy poco, posibilitando el consumo futuro incluso varios siglos hacia adelante.9 De hecho, la Figura 5 despliega un espacio paramétrico muy amplio en el que prácticamente cualquier política de reducción de emisiones puede definirse como óptima para la combinación de parámetros adecuada.
IIDescuento social del futuro, nociones de equilibrio, y cambio climáticoEl descuento del futuro en el contexto del cambio climático ha recibido mucha de la atención en las últimas décadas, pero el estudio de su analítica y sobre sus implicaciones para economías que optimizan dinámicamente es mucho más antiguo. Ramsey (1928), por ejemplo, realiza una famosa crítica a la práctica de utilizar tasas de descuento positivas,10Koopmans (1974) explica un caso en el que la práctica del descuento es desastrosa en el sentido de adelantar el final del horizonte de planeación, cuando éste se asume finito. Más aún, Gale (1967) nota que, a pesar de la crítica de argumento ético que ya se encontraba disponible cuando él escribía, un modelo de economía “cake-eating” con horizonte infinito, como el descrito en la sección previa, requiere de tasas de preferencia temporal positivas para tener sentido analítico (de otro modo, no existe política óptima posible).11
Pero existe un concepto adicional para la tasa de descuento que ha atraído la atención en estos asuntos: la tasa de descuento social, que es diferente a la tasa privada de descuento, ρ. De acuerdo con Perman et al., (2003), o con Heal (1998 y 2008), dicha tasa se puede definir como el negativo de la tasa a la que cambia el valor de un incremento marginal en el consumo conforme su temporalidad se atrasa marginalmente. Dicho de otro modo, la tasa social es una medida de la diferencia entre la utilidad marginal en algún tiempo t y otro tiempo t+¿, para un ¿ arbitrariamente pequeño. Si B, en la expresión (2), es la tasa de utilidad social, el valor presente de la utilidad marginal es, simplemente,
Entonces, el negativo de la tasa de cambio de (10) es:
El parámetro η(Ct) es la elasticidad-consumo de la utilidad marginal, definida igual que antes, y el parámetro g(Ct) es la tasa de crecimiento del consumo. Si ambos parámetros son positivos, entonces la tasa social rt será mayor que la tasa privada ρ, y tendrá sentido ético que la sociedad descuente el futuro a una tasa mayor que la utilizada por los individuos.12 La razón es sencilla, si el consumo futuro será mayor que el consumo presente, si las generaciones venideras serán más ricas que las del presente, entonces tiene sentido tratar el incremento en su bienestar con una ponderación menor que el incremento en el bienestar presente. En este caso, como se ve en (11), tiene sentido siempre utilizar una tasa positiva para descontar el futuro incluso si los individuos tratan de forma equitativa presente y futuro (es decir, incluso si ρ=0).
Este aparente embrollo conceptual y ético se resuelve aclarando cuáles variables se asumen exógenas y cuáles endógenas en (11). Dicho de otro modo, se requiere aclarar si el análisis es de equilibrio parcial o si lo es general. En un modelo de equilibrio parcial, en el que se estudian comportamientos sin implicaciones sistémicas, la tasa g(Ct) puede asumirse exógena, y los parámetros de (11) pueden calibrarse a partir de otros estudios empíricos existentes, incluso si atienden motivaciones analíticas diferentes. Adicionalmente, si se asume que rt debe aproximar a la tasa de interés observada en el mercado, entonces se pueden elegir ρ y η(Ct) tal que la ecuación (11) se mantenga. Las preferencias a favor de tasas sociales de descuento positivas y mayores a las privadas (como las de Schelling o Baumol) pueden estar fundamentadas en nociones de equilibrio parcial, pero dicha noción de equilibrio no resulta robusta para analizar acciones que tienen motivación de cambio sistémico, como la mitigación de gases de efecto invernadero.
En contraste, si se asume una modelación de equilibrio general, como la mostrada muy simplificadamente en el apartado previo, entonces rt y es g(Ct) son endógenas y determinadas por los valores de ρ y η(Ct) que se hayan fijado. En el caso particular del modelo presentado, es fácil ver que la tasa social de descuento rt es cero en todo el horizonte de planeación independientemente de la elección de valores para dichos parámetros: éstos siempre se cancelan al sustituir la expresión (8) en la (11). Este resultado se explica en que en el modelo de la sección previa no existen usos alternativos del consumo (es decir, no existe inversión ni capital). Si se incluyera el capital, es rutinario verificar que los flujos óptimos de consumo e inversión se eligen tal que la productividad marginal del capital sea equivalente a rt tal y como está definida en la expresión (11),13 lo que implica un equilibrio dinámico en el que el costo en bienestar de retrasar cierto monto de consumo de un t hacia un t+¿ es exactamente igual a la ganancia derivada de invertir ese monto en aumentar el acervo de capital entre t y t+¿.
En el contexto del cambio climático, dicho equilibrio dinámico en un modelo de equilibrio general con acervos de capital implicaría que las reducciones en bienestar asociadas a caídas en la producción de geis se asocian con aumentos equivalentes en el bienestar derivados de incrementos adecuados en el acervo de capital. En otras palabras, se asume cierta sustituibilidad entre la capacidad atmosférica de almacenar geis con algunos acervos de capital manufacturado, supuesto que, en términos de su factibilidad técnica, puede resultar heroico. Esta discusión genera dos lecciones generales. Primero, se aclara cómo tratar la expresión (11). En equilibrio parcial, como ecuación: conocidos rt y g(Ct), se eligen ρ y η(Ct) tal que (11) se mantenga. En equilibrio general, como definición, elegir ρ y η(Ct) arbitrariamente y dejar que g(Ct) se defina por (8) y que rt se determine endógenamente.
Segundo, en el contexto del cambio climático no lleva mucho sentido asumir tasas de crecimiento económico exógenas en modelos de equilibrio parcial. Al contrario, como Heal (2008) expone, precisamente porque la economía del cambio climático analiza acciones que deben tener repercusiones sistémicas, la tasa de crecimiento g(Ct) debe ser endógena y el modelo debe ser de equilibrio general. Estas dos lecciones, sin embargo, no aclaran cómo han de elegirse los valores para los parámetros ρ y η(Ct) para incorporarse en un modelo de equilibrio general, por lo que la discusión de la tasa social de descuento no resuelve el problema de la dependencia de la política óptima al espacio paramétrico mostrado en la Figura 5.
IIIElecciones paramétricas y modelación consistenteLa modelación de los apartados previos, si bien contiene los resultados generales que han resultado más polémicos en la discusión académica reciente, es un tanto simplificada respecto la utilizada en los estudios de la literatura relevante. En general, los modelos económico-climáticos son una variación de la estrategia Ramsey-Koopmans-Cass para modelar crecimiento económico en economías que optimizan dinámicamente basadas en comportamientos de suavizamiento temporal en el consumo (ver, por ejemplo, Nordhaus, 2007a y 2007b). En particular, esta estrategia involucra un problema de optimización dinámica que maximiza una función de bienestar social con restricciones dinámicas que están sujetas a la externalidad climática asociada a la emisión de geis que, a su vez, es tratada endógenamente con los llamados “modulos” climáticos que vinculan analíticamente modelos de circulación global con la producción económica. No obstante la mayor complejidad de estos modelos, la estrategia pronto tiene que lidiar con la llamada ecuación de Ramsey, que deviene de vincular las expresiones (8) y (11) del modelo de las secciones previas.
Como allí se ve, la ecuación de Ramsey vincula cuatro elementos: la tasa social de descuento, los parámetros de comportamiento ético (ρ y η(Ct)), y un “dato” económico (la tasa g(Ct)). En la sección previa se aclara el tratamiento (exógeno o endógeno) de dichas variables y parámetros dependiendo de la noción de equilibrio utilizada (parcial o general, respectivamente). Esta sección trata de dos elementos adicionales a dicha discusión. El primero tiene que ver con la consistencia paramétrica respecto a algún modelo de equilibrio general determinístico, el segundo tiene que ver con el tratamiento estocástico de las variables climáticas futuras. Estos dos aspectos han llevado a los economistas a pensar que la modelación basada en políticas óptimas que suavizan el consumo, muy comunes en otros campos de la economía, no son la mejor estrategia para estudiar el problema dinámico supuesto por el cambio climático. Veámos cada uno por separado.
La Tabla 1 muestra las elecciones comunes hechas en algunos estudios relevantes para los parámetros involucrados en la ecuación de Ramsey descrita arriba, y sus consecuencias cuando se combinan con una tasa de crecimiento económico constante de 1.3% anual (tal y como en Dasgupta, 2007). La quinta columna muestra la tasa de descuento social resultante de los supuestos hechos en las otras columnas, y dichos valores concentran la mayor parte de las críticas realizadas a los modelos asociados. Para ilustrar, dichas tasas implican que $1 de costos climáticos 150 años en el futuro equivalen a $0.05 en Cline (1992), a $0.002 en Nordhaus (1994), y a $0.12 en Stern (2006). Esta diferencia es lo que origina la política activista pro mitigación en el presente sugerida en Stern, y la que ha sido el centro de la crítica académica hacia él dirigida.
Elecciones paramétricas en la ecuación de Ramsey en diversos estudios climáticos
| Estudio | ρ | η(Ct) | g(Ct) | rt | Razones |
|---|---|---|---|---|---|
| Cline (1992) | 0 | 1.5 | 1.3% | 1.95% | Éticas |
| Nordhaus (1994) | 3% | 1 | 1.3% | 4.3% | Calibración con economías de mercado |
| Stern (2006) | 0.1% | 1 | 1.3% | 1.4% | Éticas |
Fuente: elaboración propia con base en Dasgupta (2007).
Para evaluar la consistencia de las elecciones paramétricas de la Tabla 1, Dasgupta (2007) las inserta en un modelo determinístico de consumo-ahorro para concluir que todas ellas son “mala economía”, “mala filosofía”, y “mala ética”. En dicho modelo, la relación de la inversión al producto depende de dichos parámetros (también Weitzman 2007 alerta sobre este resultado): bajo la elección de Stern (2006) la relación inversión-producto es de 0.97, implicando que el 97% del producto debe ahorrarse e invertirse en la trayectoria óptima, lo que resulta un absurdo, según Dasgupta (2007). Y mientras la elección de Nordhaus pueda resultar en una relación inversión-producto con más sentido económico, Dasgupta la descalifica por basarse en calibraciones con datos observados de economías de mercado, lo que es un proceder conceptualmente inadecuado en el contexto del masivo problema de los comunes del cambio climático: los precios de mercado, como se sabe, no son buenos indicadores de escasez o de preferencias en presencia de externalidades.
A modo de cierreEste artículo interpreta el modelo canónico de dependencia a recursos naturales no renovables en el contexto del cambio climático para exponer algunos elementos clave del debate académico de la última década. En particular, el modelo presentado muestra la dependencia de la política óptima de emisiones de geis a la elección de valores para dos parámetros de comportamiento particulares: la tasa de descuento subjetiva, que describe la impaciencia temporal de la sociedad, y la elasticidad-consumo de la utilidad marginal, que describe la aversión de la sociedad a la desigualdad. La política óptima de emisiones asociada a la combinación paramétrica que describe a una sociedad impaciente y no aversa a la desigualdad consume en el presente la totalidad de la capacidad atmosférica de almacenamiento de geis, y deja para las generaciones futuras la tarea de lograr una drástica mitigación de emisiones. En contraste, la política óptima asociada a una sociedad paciente y aversa a la desigualdad, emite menos geis a la atmósfera en el presente y asegura un trato más igualitario a las generaciones futuras. Como queda claro en las figuras de las secciones previas, cualquier política de emisiones de geis que ponga más o menos énfasis en el presente o en el futuro puede defenderse como óptima: solo basta elegir aquellos valores paramétricos para los que dicha política resuelva el problema de una economía que optimice dinámicamente.
La simulación numérica aquí presentada, además, muestra que la política óptima de emisiones es mucho más sensible a la tasa de descuento que a la aversión de desigualdad intergeneracional. Por lo que se tomó en cuenta la discusión sobre la elección de la tasa de descuento, introduciendo el concepto de tasa social de descuento. La utilización de este último tiene más sentido analítico cuando la estrategia de modelación se apega a la noción de equilibrio parcial, que asume como exógenas algunas variables cruciales, como la tasa de crecimiento de la economía. El artículo sugiere que la preferencia sobre la utilización de tasas sociales positivas para el descuento del futuro, preferencia mostrada por algunos economistas notables, pasa por la asunción, más o menos tácita, de un modelo de equilibrio parcial que asume con certeza tasas positivas de crecimiento económico futuro. No obstante, dado que la modelación económico-climática estudia el impacto de cambios sistémicos significativos, es preferible apegarse a la noción de equilibrio general, de modo que dichas variables cruciales (como la tasa de crecimiento de la economía) sean más bien endógenas.
Este proceder implica que la elección de los parámetros que describen comportamientos éticos queda a final de cuentas al arbitrio del investigador en turno. El artículo muestra algunas de las elecciones paramétricas existentes en la literatura y expone los argumentos de crítica más importantes. En general, dichas elecciones resultan ser inconsistentes con criterios económicos básicos (como que la inversión debe ser una fracción del producto), o metodológicamente inadecuados (al basarse en calibraciones de mercado con precios que no recogen toda la información que es relevante). Con todo, estos problemas han llevado a algunos economistas a sugerir que la estrategia de modelación económica seguida hasta ahora en la economía del cambio climático ha topado con pared, por así decir: la optimización dinámica y el suavizamiento temporal del consumo no permiten resolver de modo convincente el problema intertemporal del cambio climático. Y estas críticas aún no incluyen los asuntos asociados al tratamiento de la incertidumbre, que este artículo dejó de lado.
Profesor de teoría económica en la División de Estudios Profesionales de la Facultad de Economía de la unam.
Debido al contexto al que pudiera aplicarse, este modelo suele denominarse en la literatura como describiendo una “cake eating economy”. La lectora o el lector interesados pueden encontrar en Dasgupta y Heal (1974) una exposición seminal, y en López-Morales (2003) una aplicación en el contexto del desarrollo sustentable.
Por ejemplo, el reconocido climatólogo James Hansen, quien obtuvo en décadas recientes relevancia internacional por su militancia académica y política desde el Instituto Goddard para Estudios Espaciales de la nasa a favor del combate al cambio climático, ha establecido el famoso umbral de las 350 partes por millón (ppm) de CO2 como aquel que asegura las condiciones climáticas planetarias de la era pre-industrial. En contraste, las observaciones recientes ubican dicha concentración en alrededor de 400 ppm.
Si bien pudieran incorporarse tasas positivas de decaimiento atmosférico, éstas resultan ser muy bajas: algunas estimaciones encuentran que incluso el 15% de las emisiones actuales se encontrarán acumuladas atmosféricamente 500 años en el futuro. Los lectores interesados pueden encontrar en Maier-Reimer y Hasselman (1987) y en Azar y Sterner (1996) algunos modelos climáticos que explicitan estos asuntos. En López-Morales (2008) se puede observar una implementación de estos modelos en el contexto de la discusión sobre el costo social marginal del carbono.
Los lectores azuzados notarán que esta condición no es otra distinta a la famosa regla de Hotelling (1931) para la explotación de los recursos no renovables. En Perman et al. (2002) se puede encontrar una exposición de libro de texto de dicho modelo.
En otras palabras, η(C) mide la respuesta porcentual de la utilidad marginal ante el cambio de un punto porcentual en el consumo. En términos matemáticos η(C) es una medida de la curvatura de la función de utilidad marginal. Usualmente se le interpreta como el grado de aversión ante la desigualdad en el consumo: entre mayor sea dicha respuesta mayor será el incentivo a suavizar temporalmente consumo, lo que se asocia a aversión a la desigualdad alta. Los lectores interesados pueden encontrar en Bekerman (2011) ésta y otras interpretaciones éticas de la economía en el contexto del cambio climático y de otros problemas no menos polémicos.
Es claro que, además, U(Ct) = ln(Ct) cumple con los requisitos para U(Ct): la utilidad marginal es positiva pero decreciente, y es infinita para el caso límite en el que Ct=0.
La simulación que se reporta ahora asume tres valores para ρ: 3%, 1% y 0.1%. Además, se ha fijado arbitrariamente la capacidad de almacenamiento atmosférico en 10 000 unidades.
En términos éticos, para decirlo con el filósofo español Manuel Sacristán, esta primer combinación paramétrica puede representar el comportamiento de una sociedad que en su expansión establece la semilla de su autodestrucción. Sacristán la llamó “la especie exagerada, la especie de la hybris” (Sacristan, 1979).
Para seguir con las imágenes sacristanianas, esta combinación paramétrica puede representar el comportamiento de una sociedad que se autocontrola y que se establece límites, no sin renunciar al disfrute mesurado de los recursos escasos. Esta sociedad puede definirse bien como si fuera parte del rebaño de Epicuro (ver Riechmann, 2006).
“Uno debe enfatizar un asunto de modo más particular: se asume que no debemos descontar el disfrute futuro en comparación con el disfrute presente, que es una práctica éticamente indefendible y que deriva únicamente de la debilidad de la imaginación…” (Ramsey, 1928).
Lo que resulta, además, fácil de ver: si ρ=0, la expresión (8) informa de una tasa constante de consumo de un acervo finito en horizonte temporal infinito, lo que claramente es no factible al violar la condición (1).
Entre otros, este proceder es defendido por Thomas Schelling (1995), premio Nobel de Economía, y expuesto desde William Baumol (1968), quien ha dicho que poner una tasa social con valor menor que la tasa privada para descontar el futuro es de hecho una redistribución del presente hacia el futuro y, en suma, una actividad tipo Robin Hood pero puesta de cabeza: quitarle a los pobres (las generaciones presentes) para darle a los ricos (las generaciones futuras).